A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ethics Statement
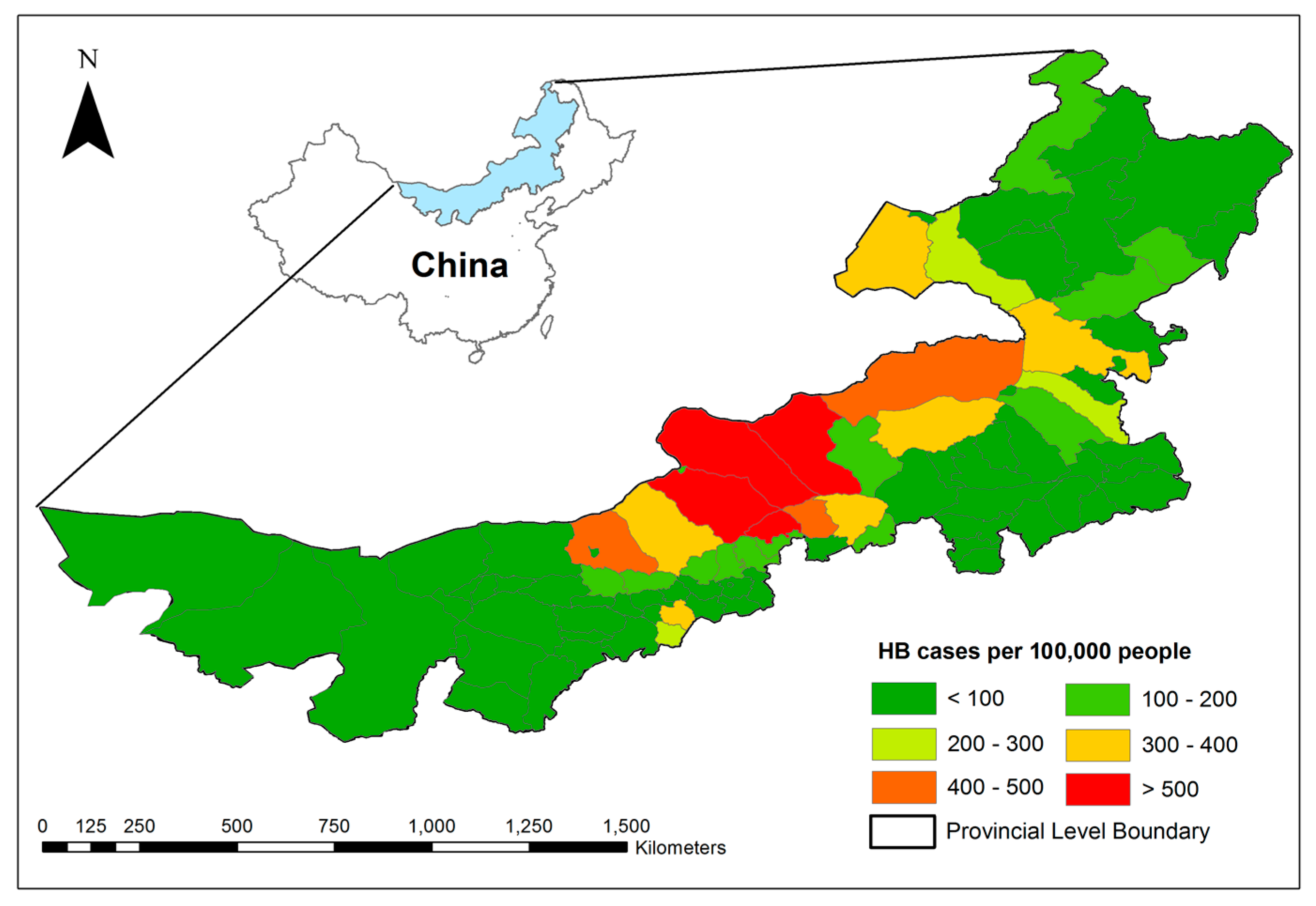
2.2. Study Area
2.3. Data Sources
2.3.1. Epidemiological Data
2.3.2. Human and Animal Population Data
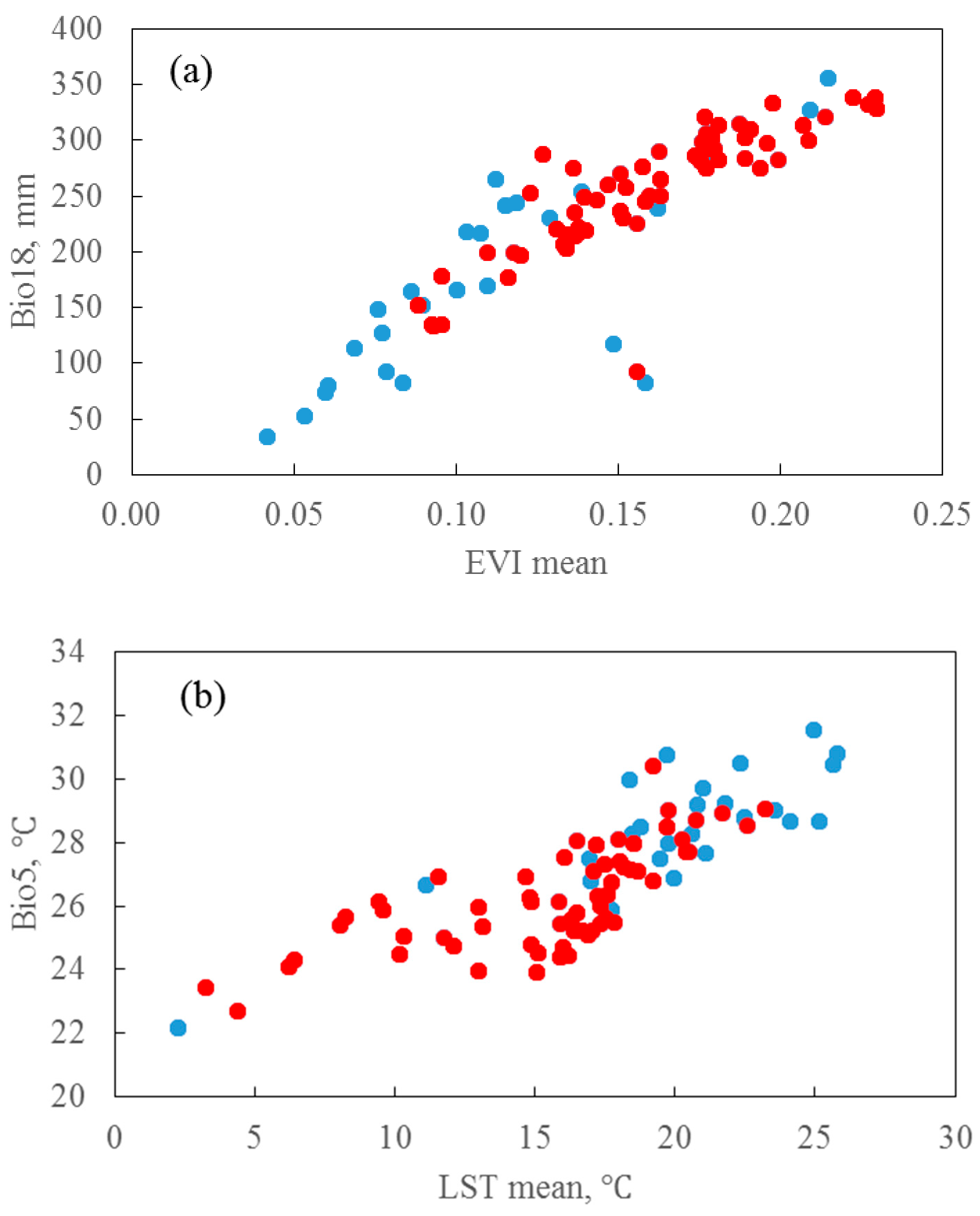
2.3.3. Environmental Variables
2.4. Statistical Analysis
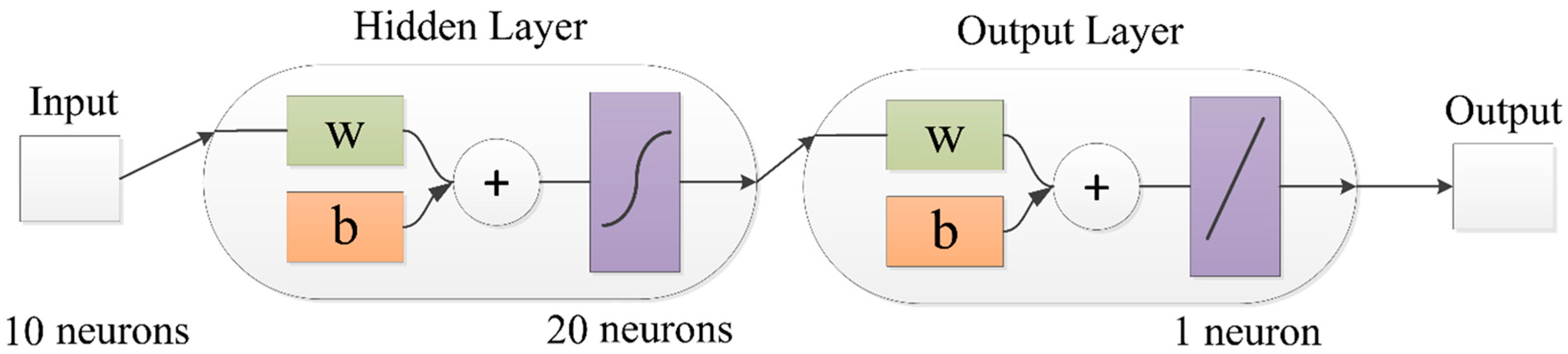
2.5. ANN Model
2.5.1. Model Development
2.5.2. Model Assessment
2.6. Sensitivity Analysis
3. Results
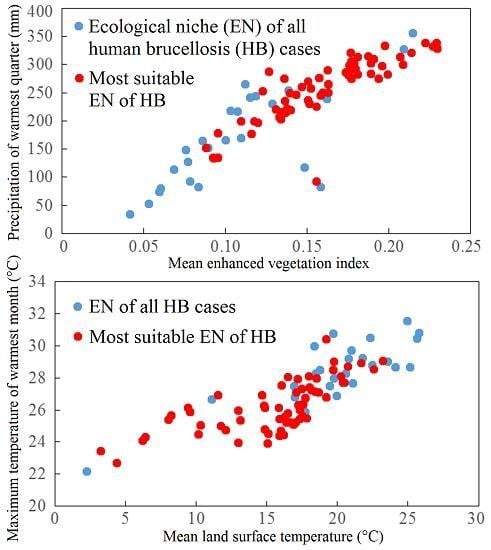
3.1. Predictors of HB
3.2. Model Development
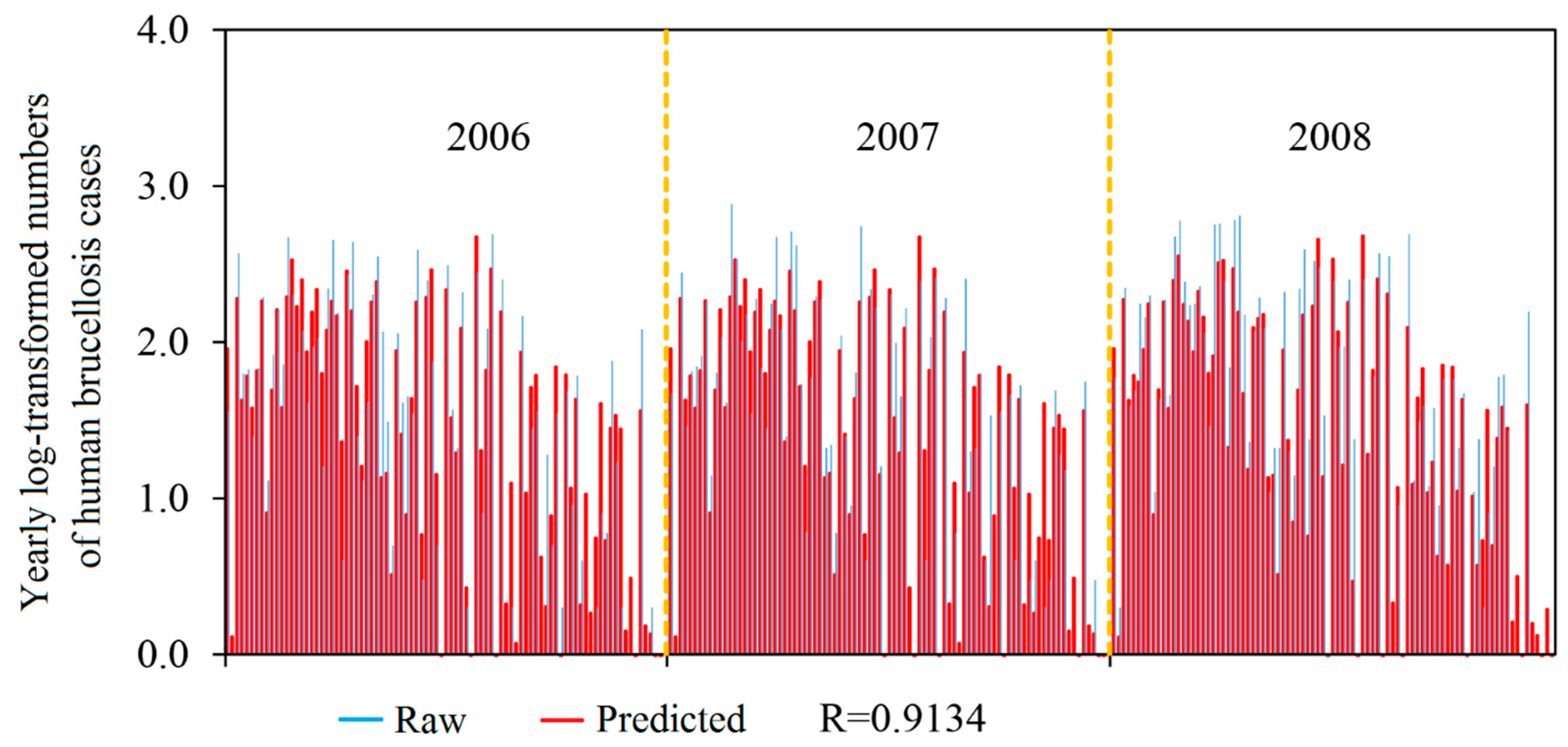
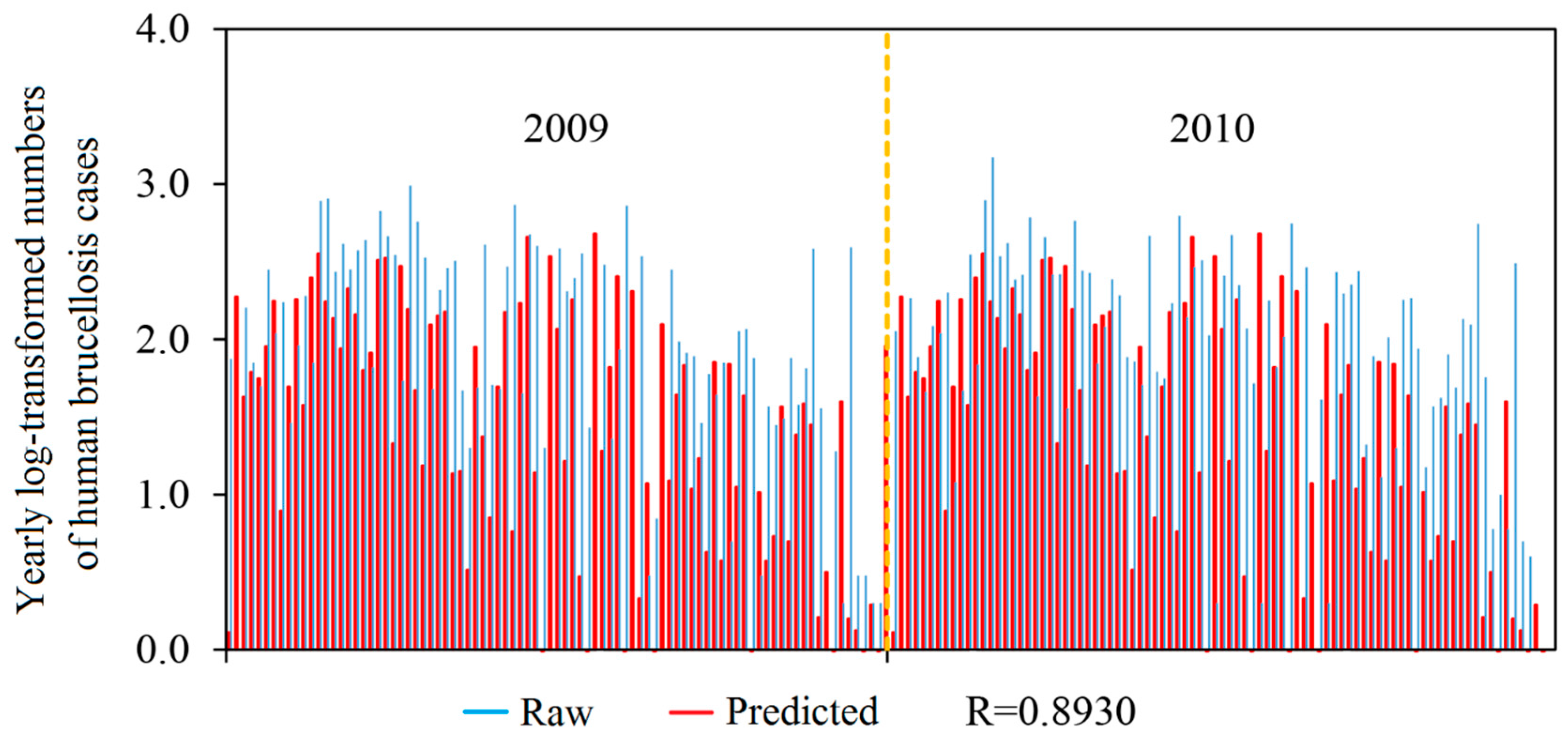
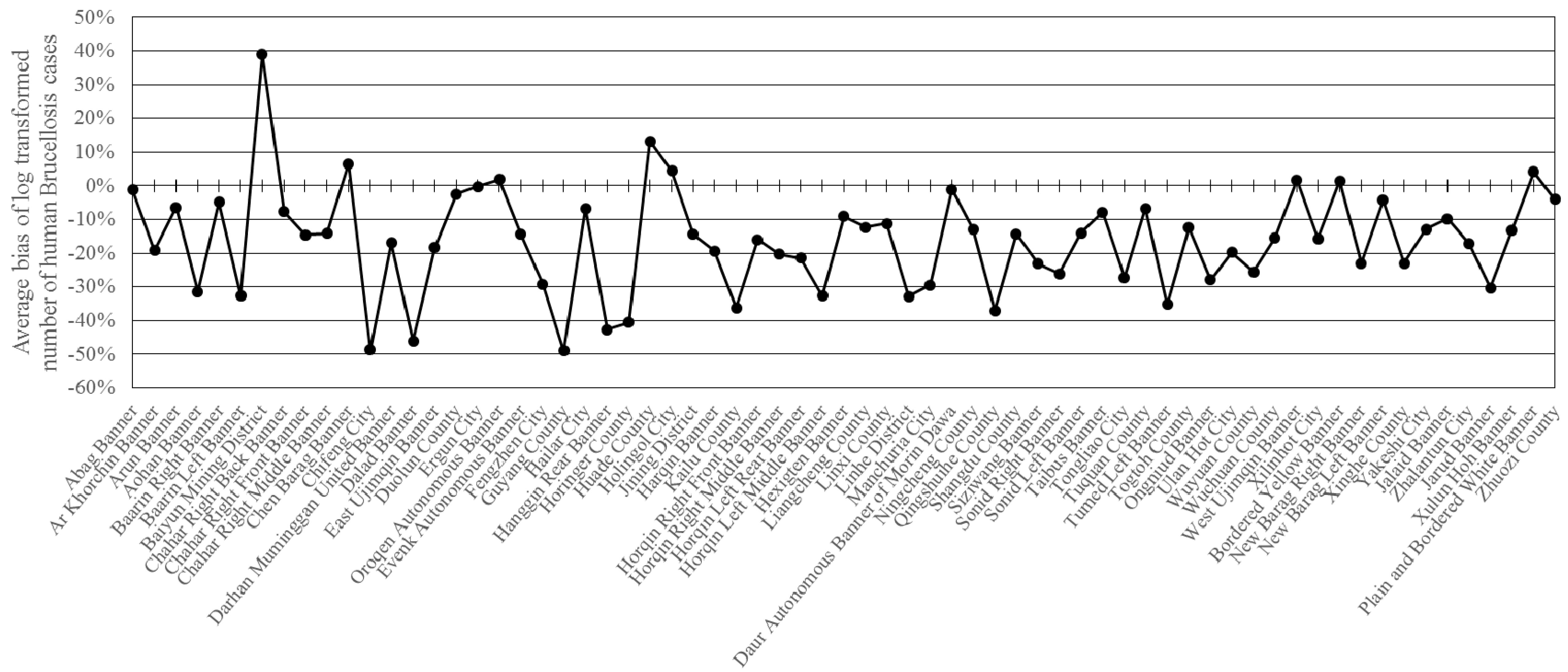
3.3. Model Assessment
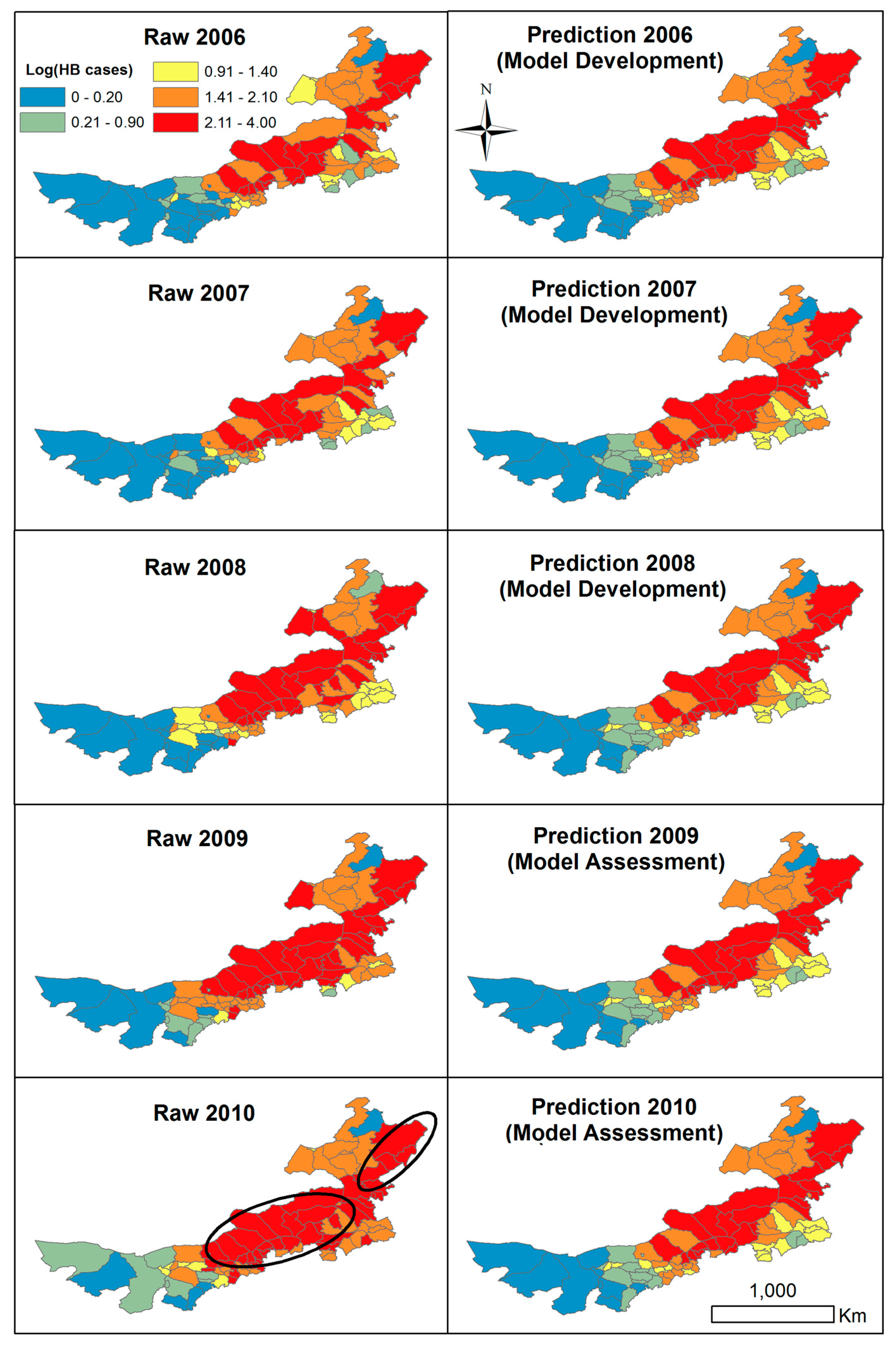
3.4. Model Estimation
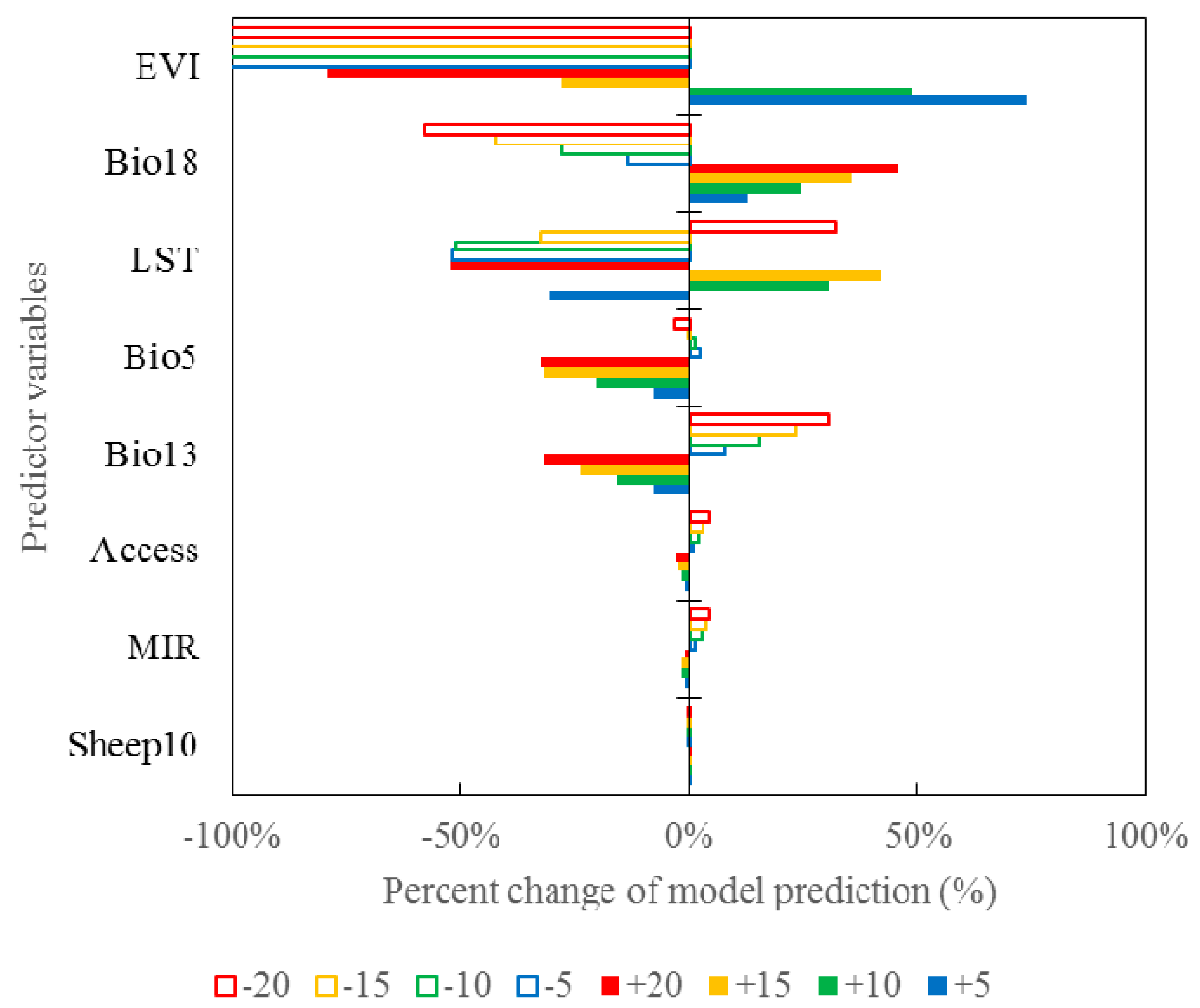
3.5. Sensitivity Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jia, P.; Joyner, A. Human brucellosis occurrences in Inner Mongolia, China: A spatio-temporal distribution and ecological niche modeling approach. BMC Infect. Dis. 2015, 15, 36. [Google Scholar] [CrossRef] [PubMed]
- Pappas, G.; Papadimitriou, P.; Akritidis, N.; Christou, L.; Tsianos, E.V. The new global map of human brucellosis. Lancet Infect. Dis. 2006, 6, 91–99. [Google Scholar] [CrossRef]
- Mufinda, F.C.; Boinas, F.; Nunes, C. Prevalence and factors associated with human brucellosis in livestock professionals. Rev. Saude Publica 2017, 51, 57. [Google Scholar] [CrossRef] [PubMed]
- Sanjuan-Jimenez, R.; Colmenero, J.D.; Morata, P. Lessons learned with molecular methods targeting the bcsp-31 membrane protein for diagnosis of human brucellosis. Clin. Chim. Acta 2017, 469, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Franco, M.P.; Mulder, M.; Gilman, R.H.; Smits, H.L. Human brucellosis. Lancet Infect. Dis. 2007, 7, 775–786. [Google Scholar] [CrossRef]
- Abdullayev, R.; Kracalik, I.; Ismayilova, R.; Ustun, N.; Talibzade, A.; Blackburn, J.K. Analyzing the spatial and temporal distribution of human brucellosis in Azerbaijan (1995–2009) using spatial and spatio-temporal statistics. BMC Infect. Dis. 2012, 12, 185. [Google Scholar] [CrossRef] [PubMed]
- Cascio, A.; Iaria, C. Brucellar aortitis and brucellar spondylitis. Lancet Infect. Dis. 2015, 15, 145. [Google Scholar] [CrossRef]
- Riethmuller, P.C.; Chalermpao, N. Some Issues Associated with the Livestock Industries of the Asia-Pacific Region; Food and Agriculture Organization of the United Nations, Regional Office for Asia and the Pacific Animal Production and Health Commissionfor Asia and the Pacific (APHCA): Bangkok, Thailand, 2002. [Google Scholar]
- Shang, D.; Xiao, D.; Yin, J. Epidemiology and control of brucellosis in China. Vet. Microbiol. 2002, 90, 165–182. [Google Scholar]
- Zhong, Z.; Yu, S.; Wang, X.; Dong, S.; Xu, J.; Wang, Y.; Chen, Z.; Ren, Z.; Peng, G. Human brucellosis in the people’s Republic of China during 2005–2010. Int. J. Infect. Dis. 2013, 17, E289–E292. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.G.; Di, D.D.; Wang, M.; Liu, R.H.; Zhao, H.Y.; Piao, D.R.; Tian, G.Z.; Fan, W.X.; Jiang, H.; Cui, B.Y.; et al. MLVA genotyping characteristics of Human Brucella melitensis isolated from Ulanqab of Inner Mongolia, China. Front. Microbiol. 2017, 8, 6. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yin, F.; Zhang, T.; Yang, C.; Zhang, X.; Feng, Z.; Li, X. Spatial analysis on human brucellosis incidence in mainland China: 2004–2010. BMJ Open 2014, 4, e004470. [Google Scholar] [CrossRef] [PubMed]
- Merow, C.; Smith, M.J.; Silander, J.A. A practical guide to maxent for modeling species’ distributions: What it does, and why inputs and settings matter. Ecography 2013, 36. [Google Scholar] [CrossRef]
- Royle, J.A.; Chandler, R.B.; Yackulic, C.; Nichols, J.D. Likelihood analysis of species occurrence probability from presence-only data for modelling species distributions. Methods Ecol. Evol. 2012, 3, 545–554. [Google Scholar] [CrossRef]
- Warren, D.; Seifert, S. Ecological niche modelling in maxent: The importance of model complexity and the performance of model selection criteria. Ecol. Appl. 2011, 21, 235–342. [Google Scholar] [CrossRef]
- Merow, C.; Silander, J.A. A comparison of maxlike and maxent for modelling species distributions. Methods Ecol. Evol. 2014, 5, 215–225. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophy. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Theory of Statistical Separability in Cognitive Systems; Cornell Aeronautical Laboratory, Inc.: Buffalo, NY, USA, 1958. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 93–202. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Werbos, P.J. Beyond regression: New tools for prediction and analysis in the behavioral sciences. J. Shandong Inst. Commer. Technol. 1975, 29, 65–78. [Google Scholar]
- Zhang, Z.; Deng, Z.; Rusch, K.A. Modeling fecal coliform bacteria levels at gulf coast beaches. Water Qual. Expo. Health 2015, 7, 255–263. [Google Scholar] [CrossRef]
- Baronchelli, A.; Ferrericancho, R.; Pastorsatorras, R.; Chater, N.; Christiansen, M.H. Networks in cognitive science. Trends Cogn. Sci. 2013, 17, 348–360. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Deng, Z. Modeling and prediction of oyster norovirus outbreaks along gulf of Mexico coast. Environ. Health Perspect. 2015, 124, 627–633. [Google Scholar] [CrossRef] [PubMed]
- Bastiaanssen, W.G.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: examples from research and possible applications. Agric. Water Manag. 2010, 46, 137–155. [Google Scholar] [CrossRef]
- Jia, P.; Nie, Y.; Song, G. Detection of underground remains by remote sensing and geophysics. In Proceedings of the IEEE 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Jia, P.; Nie, Y.; Yang, L. Recognition and extraction of the ancient sites covered by thick vegetation in Hainan Province of China. IEEE Geosci. Remote Sens. Symp. 2010. [Google Scholar] [CrossRef]
- Zhu, J.; Jia, P.; Nie, Y. Analysis of the ancient river system in Loulan period in Lop Nur region. Proc. SPIE 2010, 8203, 820313. [Google Scholar]
- Xu, M.; Cao, C.; Li, Q.; Jia, P.; Zhao, J. Ecological niche modeling of risk factors for H7N9 human infection in China. Int. J. Environ. Res. Public Health 2016, 13, 600. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Anderson, J.D.; Leitner, M.; Rheingans, R. High-resolution spatial distribution and estimation of access to improved sanitation in Kenya. PLoS ONE 2016, 11, e0158490. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Stein, A. Using remote sensing technology to measure environmental determinants of non-communicable diseases. Int. J. Epidemiol. 2017, 46, 1343–1344. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Joyner, T.A.; Sun, Y. Short-term associations between accumulated rainfall and atmospheric moisture during landfall of three Atlantic hurricanes. Geogr. Bull. 2014, 55, 49–62. [Google Scholar]
- Xue, Y. The impact of desertification in the Mongolian and the Inner Mongolian grassland on the regional climate. J. Clim. 1996, 9, 2173–2189. [Google Scholar] [CrossRef]
- Li, Y.J.; Li, X.L.; Liang, S.; Fang, L.Q.; Cao, W.C. Epidemiological features and risk factors associated with the spatial and temporal distribution of human brucellosis in China. BMC Infect. Dis. 2013, 13, 547. [Google Scholar] [CrossRef] [PubMed]
- Center for International Earth Science Information Network (CIESIN), Columbia University; International Food Policy Research Institute (IFPRI); The World Bank; Centro Internacional de Agricultura Tropical (CIAT). Global Rural-Urban Mapping Project, Version 1 (GRUMPV1): Population Density Grid; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2011. [Google Scholar]
- Jia, P.; Sankoh, O.; Tatem, A.J. Mapping the environmental and socioeconomic coverage of the indepth international health and demographic surveillance system network. Health Place 2015, 36, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Nelson, A. Estimated Travel Time to the Nearest City of 50,000 or More People in Year 2000. Available online: http://bioval.jrc.ec.europa.eu/products/gam/ (accessed on 10 January 2012).
- Scharlemann, J.P.; Benz, D.; Hay, S.I.; Purse, B.V.; Tatem, A.J.; Wint, G.W.; Rogers, D.J. Global data for ecology and epidemiology: A novel algorithm for temporal Fourier processing MODIS data. PLoS ONE 2008, 3, e1408. [Google Scholar] [CrossRef] [PubMed]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Baptista-Rosas, R.C.; Hinojosa, A.; Riquelme, M. Ecological niche modeling of Coccidioides spp. In western North American deserts. Ann. N. Y. Acad. Sci. 2007, 1111, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, C.; Wang, O.; Strutz, S.E.; Gonzalez-Salazar, C.; Sanchez-Cordero, V.; Sarkar, S. Climate change and risk of leishmaniasis in North America: Predictions from ecological niche models of vector and reservoir species. PLoS Negl. Trop. Dis. 2010, 4, e585. [Google Scholar] [CrossRef] [PubMed]
- IBM Corp. IBM SPSS Statistics for Windows, Version 22.0; IBM Corp: Armonk, NY, USA, 2013. [Google Scholar]
- MathWorks. Global Optimization Toolbox: User’s Guide (2013a); MathWorks: Natick, MA, USA, 2013. [Google Scholar]
- Grandin, T.; Deesing, M.J. Chapter 4—Genetics and behavior during handling, restraint, and herding. In Genetics and the Behavior of Domestic, 2nd ed.; Academic Press: San Diego, CA, USA, 2014; pp. 115–158. [Google Scholar]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soriaauza, R.W.; Zimmermann, N.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Gaughan, A.E. Dasymetric modeling: A hybrid approach using land cover and tax parcel data for mapping population in alachua county, florida. Appl. Geogr. 2016, 66, 100–108. [Google Scholar] [CrossRef]
- Jia, P.; Qiu, Y.; Gaughan, A.E. A fine-scale spatial population distribution on the high-resolution gridded population surface and application in Alachua County, Florida. Appl. Geogr. 2014, 50, 99–107. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Linard, C.; Jia, P.; Tatem, A.J. High resolution population distribution maps for southeast Asia in 2010 and 2015. PLoS ONE 2013, 8, e55882. [Google Scholar] [CrossRef] [PubMed]
- Tatem, A.J.; Gaughan, A.E.; Stevens, F.R.; Patel, N.N.; Jia, P.; Pandey, A.; Linard, C. Quantifying the effects of using detailed spatial demographic data on health metrics: A systematic analysis for the AfriPop, AsiaPop, and AmeriPop projects. Lancet 2013, 381, S142. [Google Scholar] [CrossRef]

| Model | Variables Entered | Variables Removed | R Square | Significance of F Value Change |
|---|---|---|---|---|
| 1 | Sheep10 | 0.129 | 0.000 | |
| 2 | Bio5 | 0.237 | 0.000 | |
| 3 | Bio8 | 0.283 | 0.000 | |
| 4 | EVImin | 0.296 | 0.004 | |
| 5 | LSTmin | 0.333 | 0.000 | |
| 6 | Bio13 | 0.386 | 0.000 | |
| 7 | LSTmean | 0.419 | 0.000 | |
| 8 | Access | 0.435 | 0.000 | |
| 9 | EVImean | 0.445 | 0.006 | |
| 10 | Bio8 | 0.443 | 0.313 | |
| 11 | MIRmin | 0.455 | 0.002 | |
| 12 | Bio18 | 0.460 | 0.044 |
| Statistical Measure | Raw | Predicted |
|---|---|---|
| Linear correlation coefficient (LCC) | NA | 0.9134 |
| Root mean square error (RMSE) | NA | 0.3664 |
| Standard deviation of bias (SDB) | NA | 0.3656 |
| Arithmetic mean (AM) | 1.3998 | 1.3745 |
| Median | 1.5682 | 1.5826 |
| Statistical Measure | Raw | Predicted |
|---|---|---|
| Linear correlation coefficient (LCC) | NA | 0.8930 |
| Root mean square error (RMSE) | NA | 0.5603 |
| Standard deviation of bias (SDB) | NA | 0.3793 |
| Arithmetic mean (AM) | 1.8190 | 1.4067 |
| Median | 1.9370 | 1.5993 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Jia, P.; Cuadros, D.F.; Xu, M.; Wang, X.; Guo, W.; Portnov, B.A.; Bao, Y.; Chang, Y.; Song, G.; et al. A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis. Remote Sens. 2017, 9, 1018. https://doi.org/10.3390/rs9101018
Wang J, Jia P, Cuadros DF, Xu M, Wang X, Guo W, Portnov BA, Bao Y, Chang Y, Song G, et al. A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis. Remote Sensing. 2017; 9(10):1018. https://doi.org/10.3390/rs9101018
Chicago/Turabian StyleWang, Jiao, Peng Jia, Diego F. Cuadros, Min Xu, Xianliang Wang, Weidong Guo, Boris A. Portnov, Yuhai Bao, Yushan Chang, Genxin Song, and et al. 2017. "A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis" Remote Sensing 9, no. 10: 1018. https://doi.org/10.3390/rs9101018
APA StyleWang, J., Jia, P., Cuadros, D. F., Xu, M., Wang, X., Guo, W., Portnov, B. A., Bao, Y., Chang, Y., Song, G., Chen, N., & Stein, A. (2017). A Remote Sensing Data Based Artificial Neural Network Approach for Predicting Climate-Sensitive Infectious Disease Outbreaks: A Case Study of Human Brucellosis. Remote Sensing, 9(10), 1018. https://doi.org/10.3390/rs9101018