Modeling the Effects of the Urban Built-Up Environment on Plant Phenology Using Fused Satellite Data
Abstract
:1. Introduction
- (1)
- In our study area, is there an observable difference in key phenological parameters (Start of Season (SOS), End of Season (EOS), and Length of Season (LOS)) between the urban and exurban areas when using fused imagery over several years and how sensitive those differences to base pair selection?
- (2)
- If there is an observable difference in SOS, EOS, or LOS between the urban and exurban areas when using fused imagery, how often do these differences appear?
- (3)
- Does the amount of impervious area at a location affect any observable differences in SOS, EOS, or LOS between the urban and exurban areas when using fused imagery?
2. Materials and Methods
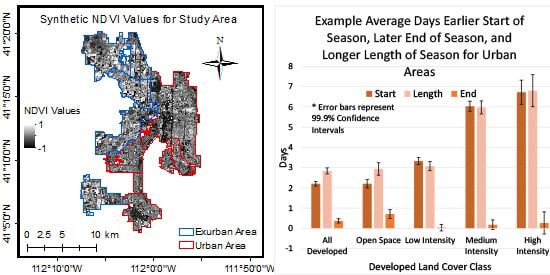
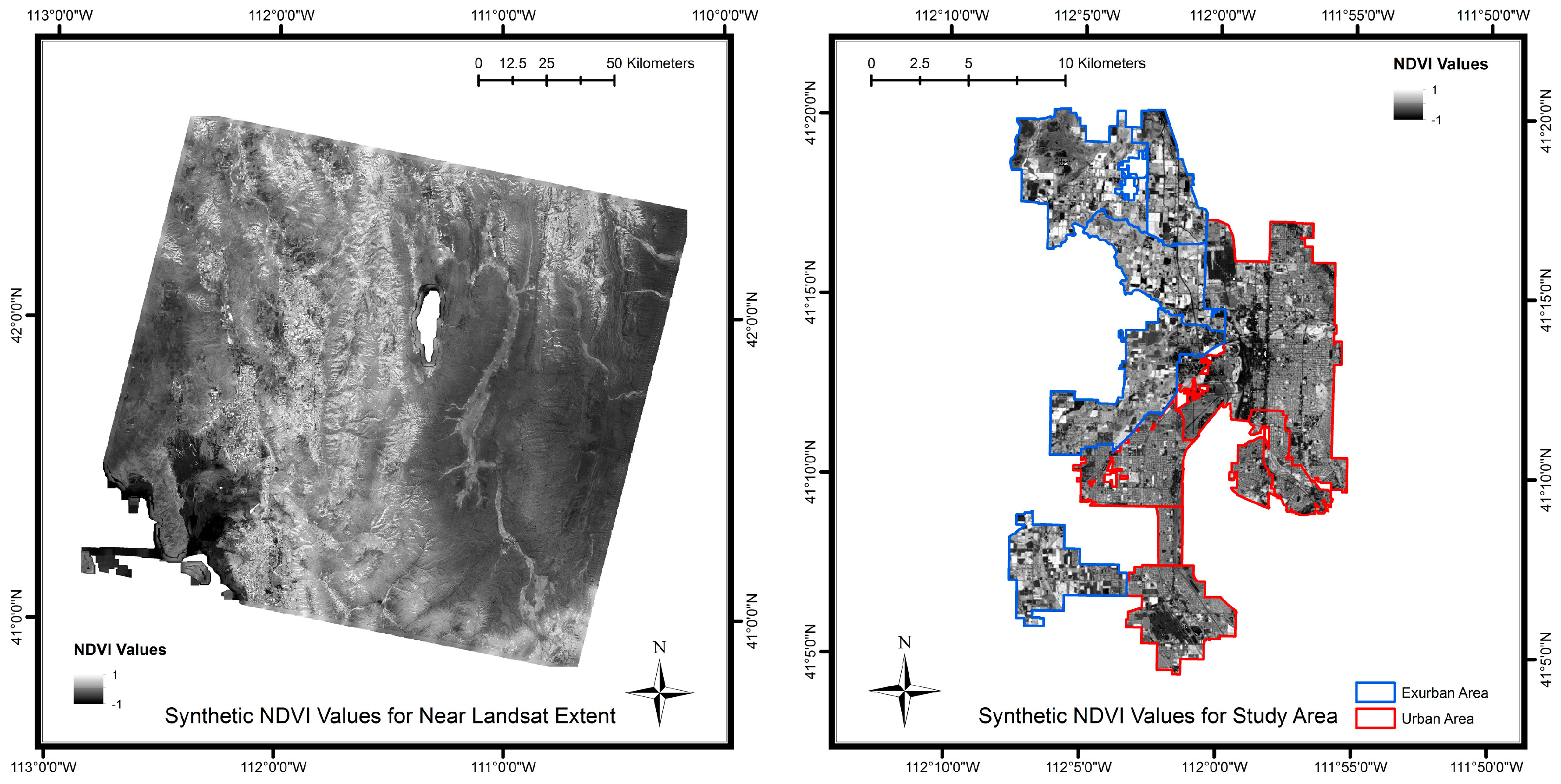
2.1. Study Area
2.2. STARFM Model Description
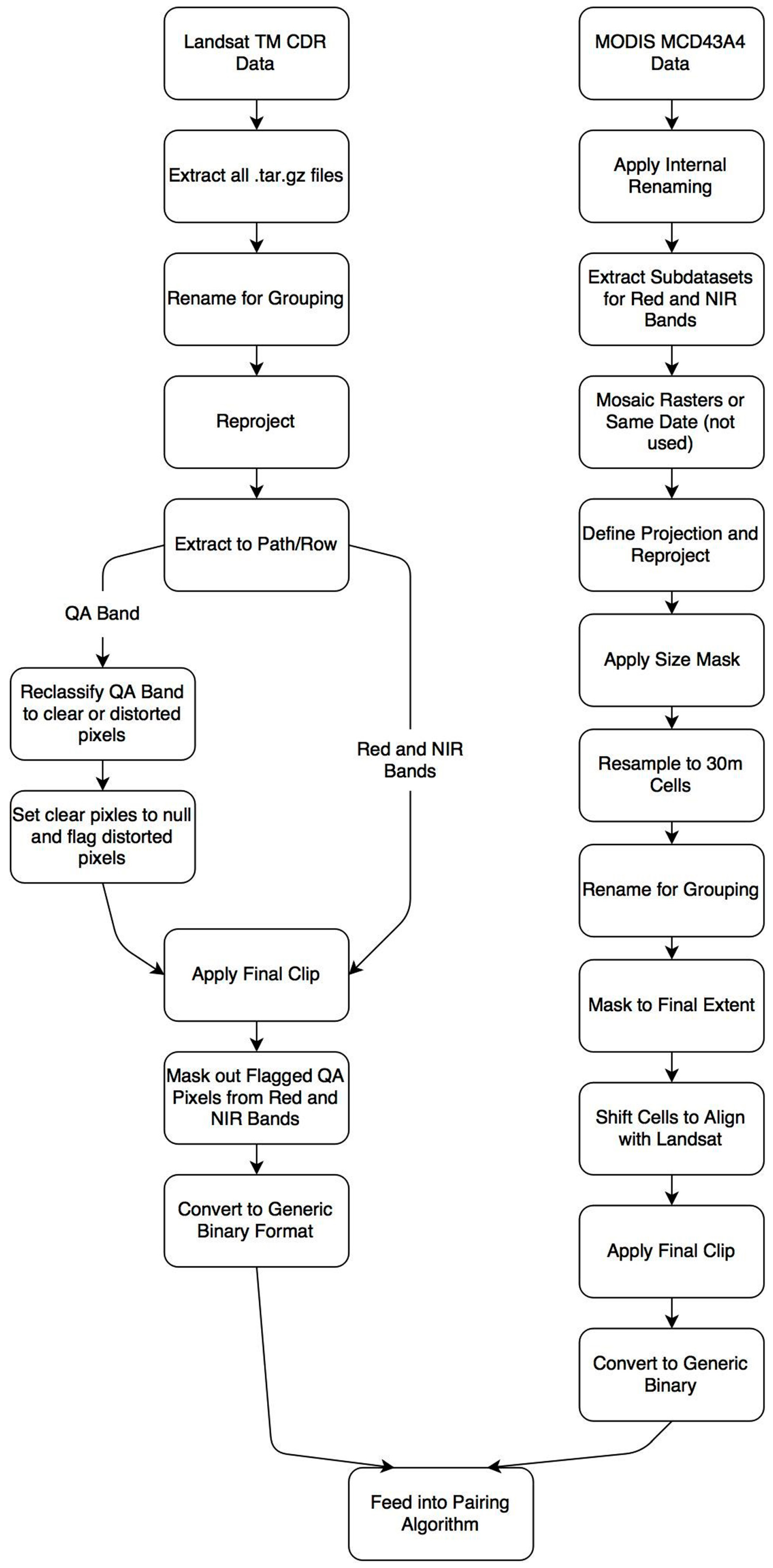
2.3. Satellite Data Processing
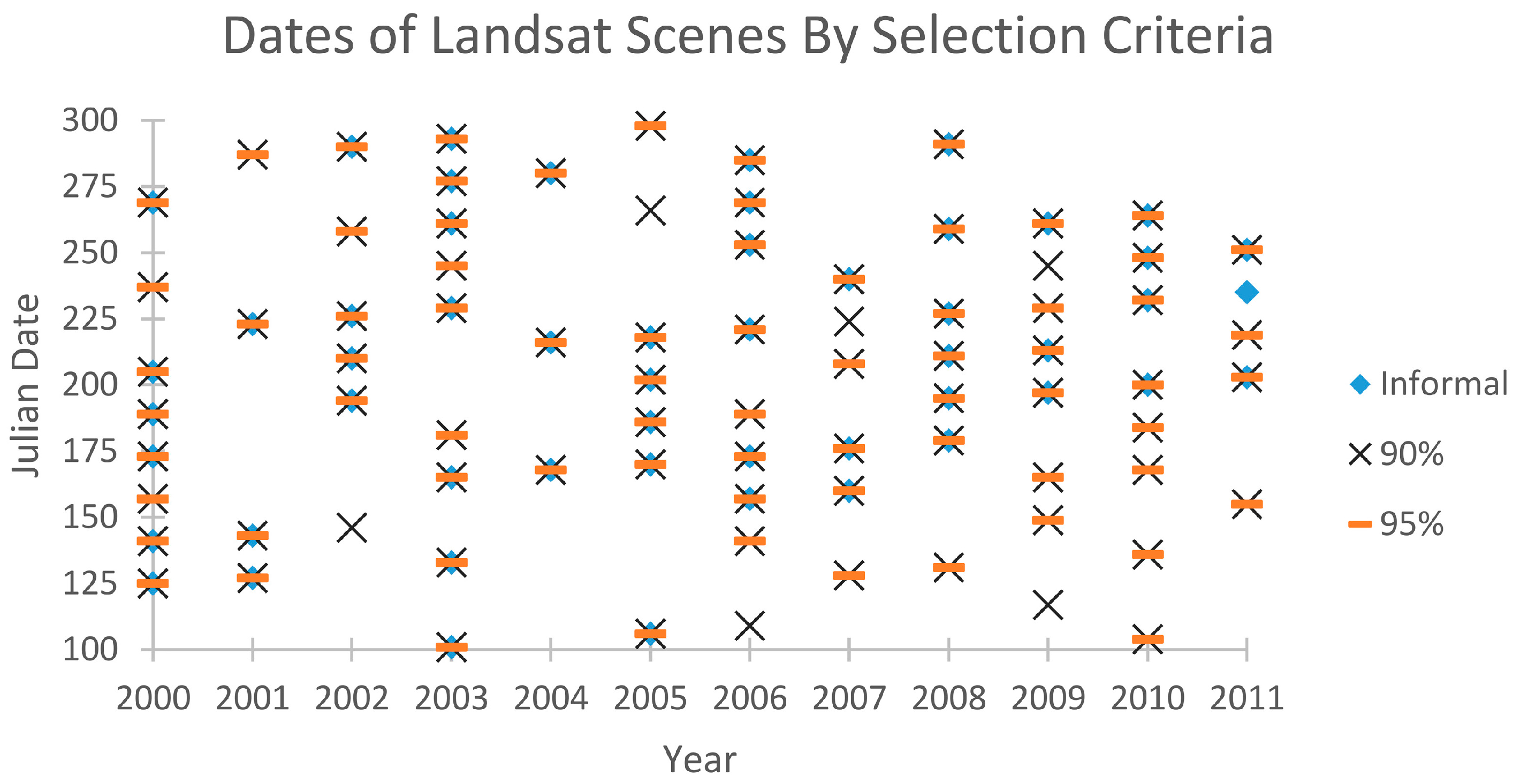
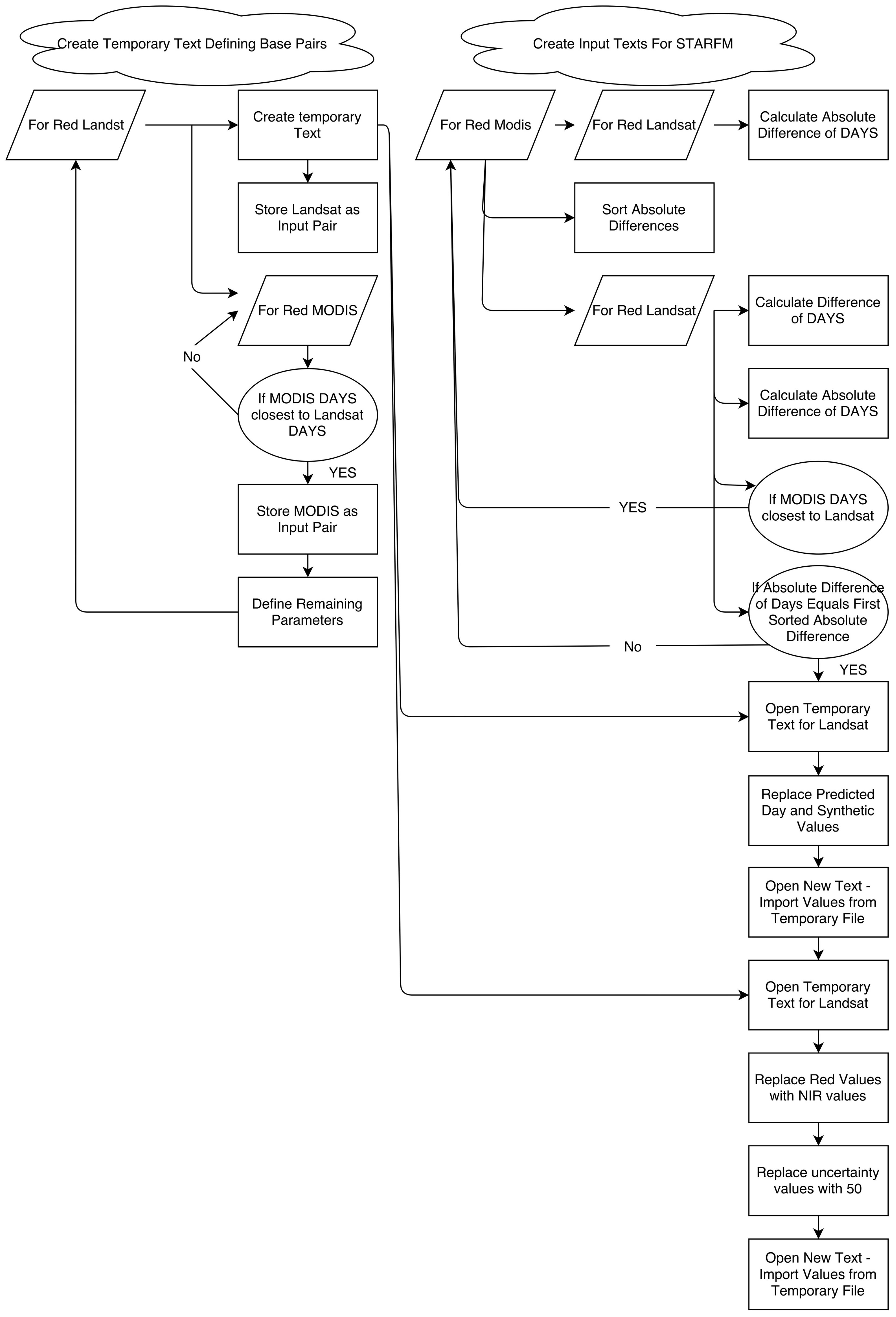
2.4. STARFM Parameters and Input Text Creation
2.5. NDVI Time Series Preparation and Seasonality Extraction
2.6. Dates of Phenological Events for Developed Areas
2.7. Statistical Analyses
3. Results
3.1. Accuracy Assessment of STARFM
3.2. Descriptive Statistics
3.3. Tests for Variance Equality and Normality
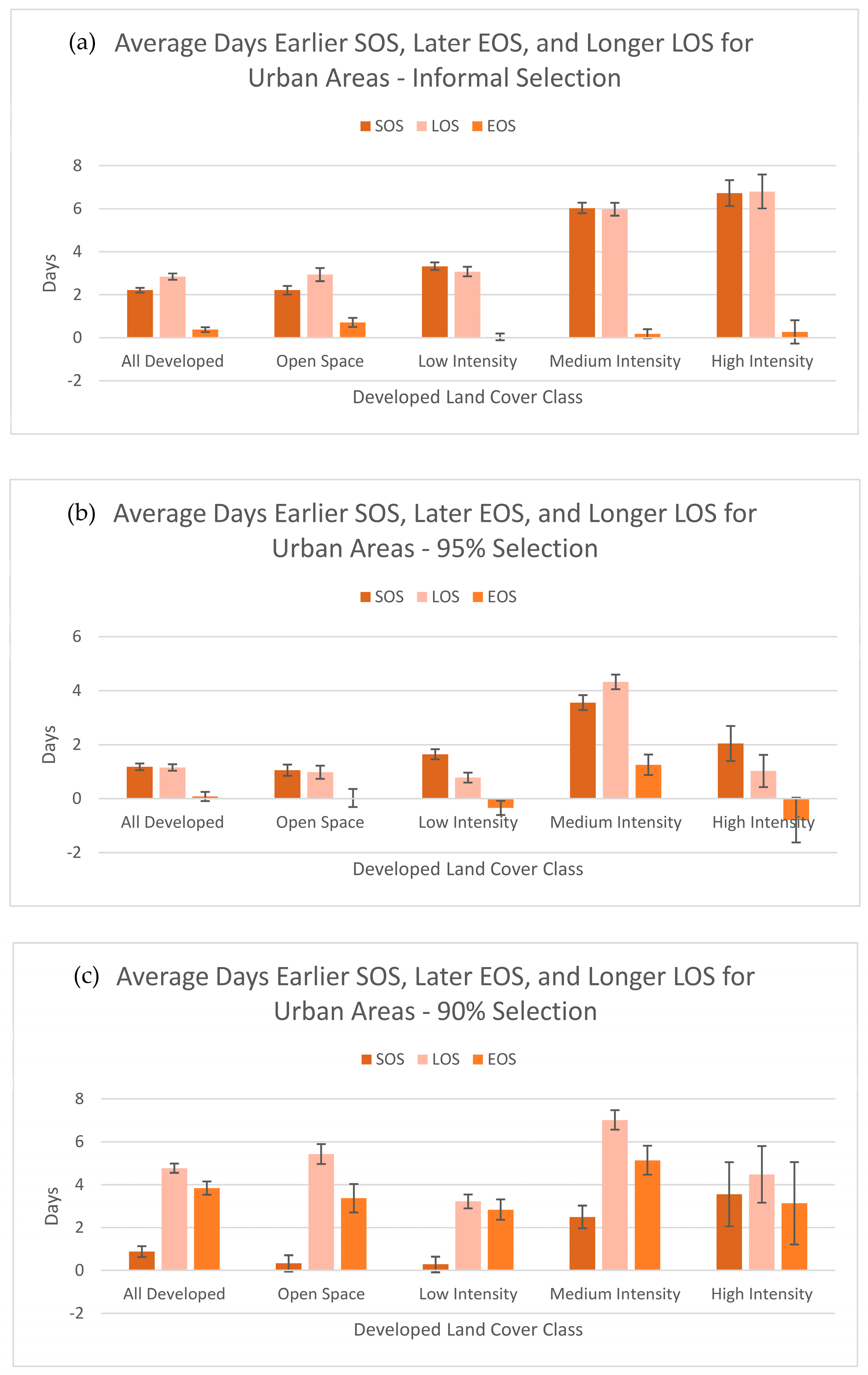
3.4. Tests for Inequality of Phenological Parameters
4. Discussion
4.1. Start of Season
4.2. End of Season
4.3. Length of Season
4.4. Study Assumptions and Potential Limitations
4.5. Future Work
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United Nations. United Nations World Urbanization Prospects; the 2014 Revision; United Nations: New York, NY, USA, 2014. [Google Scholar]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Luo, Z.; Asproudi, C. Subsurface urban heat island and its effects on horizontal ground-source heat pump potential under climate change. Appl. Therm. Eng. 2015, 90, 530–537. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 159–254. [Google Scholar]
- Tan, M.; Li, X. Quantifying the effects of settlement size on urban heat islands in fairly uniform geographic areas. Habitat Int. 2015, 49, 100–106. [Google Scholar] [CrossRef]
- Jochner, S.; Menzel, A. Urban phenological studies—Past, present, future. Environ. Pollut. 2015, 203, 250–261. [Google Scholar] [CrossRef] [PubMed]
- Ziska, L.H.; Gebhard, D.E.; Frenz, D.A.; Faulkner, S.; Singer, B.D.; Straka, J.G. Cities as harbingers of climate change: Common ragweed, urbanization, and public health. J. Allergy Clin. Immunol. 2003, 111, 290–295. [Google Scholar] [CrossRef] [PubMed]
- Walker, J.J.; de Beurs, K.M.; Henebry, G.M. Land surface phenology along urban to rural gradients in the U.S. Great Plains. Remote Sens. Environ. 2015, 165, 42–52. [Google Scholar] [CrossRef]
- Badeck, F.-W.; Bondeau, A.; Böttcher, K.; Doktor, D.; Lucht, W.; Schaber, J.; Sitch, S. Responses of spring phenology to climate change. New Phytol. 2004, 162, 295–309. [Google Scholar] [CrossRef]
- Häkkinen, R.; Linkosalo, T.; Hari, P. Effects of dormancy and environmental factors on timing of bud burst in Betula pendula. Tree Physiol. 1998, 18, 707–712. [Google Scholar] [CrossRef] [PubMed]
- Wesołowski, T.; Rowiński, P. Timing of bud burst and tree-leaf development in a multispecies temperate forest. For. Ecol. Manag. 2006, 237, 387–393. [Google Scholar] [CrossRef]
- Perry, T.O. Dormancy of trees in winter. Science 1971, 171, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Heide, O.M. Growth and dormancy in Norway Spruce Ecotypes (Picea abies) I. Interaction of photoperiod and temperature. Physiol. Plant. 1974, 30, 1–12. [Google Scholar] [CrossRef]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology feedbacks on climate change. Science 2009, 324, 887–888. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Schwartz, M.D.; Karl, T.R. Spring phenology: Nature’s experiment to detect the effect of “green-up” on surface maximum temperatures. Mon. Weather Rev. 1990, 118, 883–890. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I. Responses to a warming world. Science 2001, 294, 793–795. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Hollinger, D.Y.; Dail, D.B.; Lee, J.T.; Munger, J.W.; O’keefe, J. Influence of spring phenology on seasonal and annual carbon balance in two contrasting New England forests. Tree Physiol. 2009, 29, 321–331. [Google Scholar] [CrossRef] [PubMed]
- Primack, R.B.; Ibáñez, I.; Higuchi, H.; Lee, S.D.; Miller-Rushing, A.J.; Wilson, A.M.; Silander, J.A., Jr. Spatial and interspecific variability in phenological responses to warming temperatures. Biol. Conserv. 2009, 142, 2569–2577. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M. Land surface phenology, climatic variation, and institutional change: Analyzing agricultural land cover change in Kazakhstan. Remote Sens. Environ. 2004, 89, 497–509. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Schneider, A. The footprint of urban climates on vegetation phenology. Geophys. Res. Lett. 2004, 31, L12209. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M. Atmospheric correction of Landsat ETM+ land surface imagery—Part I: Methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2490–2498. [Google Scholar] [CrossRef]
- Van de Voorde, T.; Jacquet, W.; Canters, F. Mapping form and function in urban areas: An approach based on urban metrics and continuous impervious surface data. Landsc. Urban Plan. 2011, 102, 143–155. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Sensitivity of vegetation phenology detection to the temporal resolution of satellite data. Int. J. Remote Sens. 2009, 30, 2061–2074. [Google Scholar] [CrossRef]
- Pohl, C.; Van Genderen, J.L. Multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat-MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Liang, L.; Schwartz, M.D.; Wang, Z.; Gao, F.; Schaaf, C.B.; Tan, B.; Morisette, J.T.; Zhang, X. A Cross Comparison of spatiotemporally enhanced springtime phenological measurements from satellites and ground in a Northern U.S. mixed forest. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7513–7526. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef]
- Shen, H.; Huang, L.; Zhang, L.; Wu, P.; Zeng, C. Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data: A 26-year case study of the city of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Olexa, E.M.; Lawrence, R.L. Performance and effects of land cover type on synthetic surface reflectance data and NDVI estimates for assessment and monitoring of semi-arid rangeland. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 30–41. [Google Scholar] [CrossRef]
- National Land Cover Database 2011 (NLCD2011). Available online: https://www.mrlc.gov/nlcd11_data.php (accessed on 19 January 2017).
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- USGS. Query Form for the United States and Its Territories. Available online: http://geonames.usgs.gov/apex/f?p=gnispq (accessed on 29 August 2016).
- NOAA. Salt Lake City Climate Book. Available online: http://www.wrh.noaa.gov/slc/climate/slcclimate/SLC/index.php (accessed on 29 August 2016).
- Walker, J.J.; de Beurs, K.M.; Wynne, R.H.; Gao, F. Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sens. Environ. 2012, 117, 381–393. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). USGS Product Guide: Landsat 4-7 Climate Data record (CDR) Surface Reflectance; version 6.0; United States Geological Survey: Sioux Falls, SD, USA, 2015.
- ArcGIS Desktop, Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2010.
- Martonchik, J.V.; Bruegge, C.J.; Strahler, A.H. A review of reflectance nomenclature used in remote sensing. Remote Sens. Rev. 2000, 19, 9–20. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- NASA. MODIS/Terra Data Outages. Available online: http://modaps.nascom.nasa.gov/services/production/outages_terra.html (accessed on 29 August 2016).
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Marchetti, Z.Y.; Minotti, P.G.; Ramonell, C.G.; Schivo, F.; Kandus, P. NDVI patterns as indicator of morphodynamic activity in the middle Paraná River floodplain. Geomorphology 2016, 253, 146–158. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT 3.2 with Parallel Processing Software Manual; Lund University: Lund, Sweden, 2015. [Google Scholar]
- Zipper, S.C.; Schatz, J.; Singh, A.; Kucharik, C.J.; Townsend, P.A.; Loheide II, S.P. Urban heat island impacts on plant phenology: Intra-urban variability and response to land cover. Environ. Res. Lett. 2016, 11, 054023. [Google Scholar] [CrossRef]
- RStudio Team. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2015. [Google Scholar]
- Öztuna, D.; Elhan, A.H.; Tüccar, E. Investigation of Four different normality tests in terms of type 1 error rate and power under different distributions. Turk. J. Med. Sci. 2006, 36, 171–176. [Google Scholar]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at Landsat resolution: Scaling from the field to the satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
- Melaas, E.K.; Wang, J.A.; Miller, D.L.; Friedl, M.A. Interactions between urban vegetation and surface urban heat islands: A case study in the Boston metropolitan region. Environ. Res. Lett. 2016, 11, 054020. [Google Scholar] [CrossRef]
- White, M.A.; Nemani, R.R.; Thornton, P.E.; Running, S.W. Satellite evidence of phenological differences between urbanized and rural areas of the Eastern United States deciduous broadleaf forest. Ecosystems 2002, 5, 260–273. [Google Scholar] [CrossRef]
- Wickham, J.D.; Stehman, S.V.; Gass, L.; Dewitz, J.; Fry, J.A.; Wade, T.G. Accuracy assessment of NLCD 2006 land cover and impervious surface. Remote Sens. Environ. 2013, 130, 294–304. [Google Scholar] [CrossRef]
- Fu, D.; Zhang, L.; Chen, H.; Wang, J.; Sun, X.; Wu, T. Assessing the effect of temporal interval length on the blending of Landsat-MODIS surface reflectance for different land cover types in Southwestern Continental United States. ISPRS Int. J. GeoInf. 2015, 4, 2542–2560. [Google Scholar] [CrossRef]
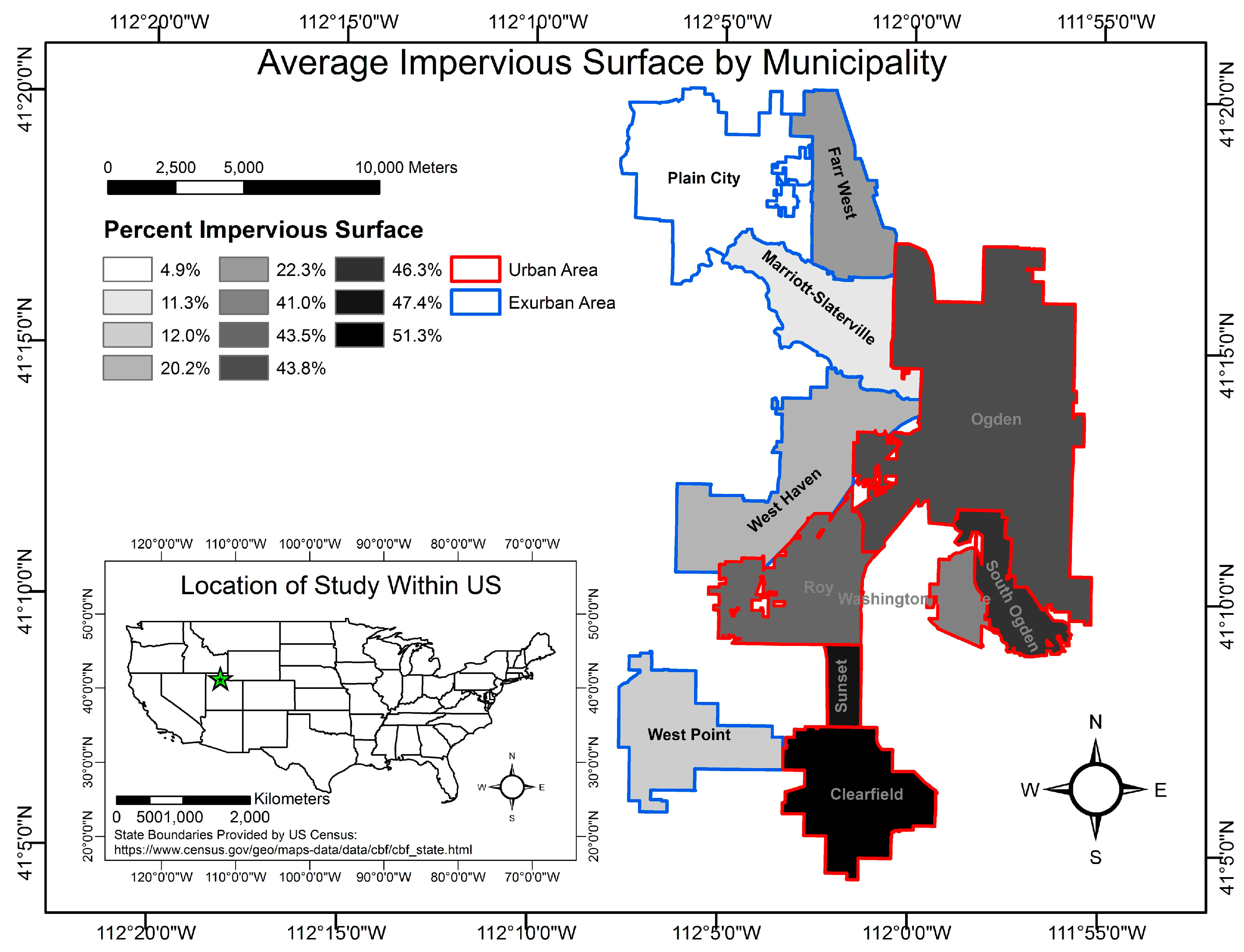
| Urban Municipal Name | Area (km2) | Exurban Municipal Name | Area (km2) |
|---|---|---|---|
| Sunset | 3.8 | West Point | 18.5 |
| Clearfield | 20.0 | West Haven | 26.8 |
| Roy | 20.3 | Marriott-Slaterville | 19.1 |
| Ogden | 70.4 | Plain City | 31.2 |
| Washington Terrace | 5.2 | Farr West | 15.3 |
| South Ogden | 9.6 | ||
| Total | 129.3 | 110.9 |
| Day 21, Year 2003 | Day 181, Year 2003 | Day 245, Year 2003 | Day 58, Year 2005 | Day 298, Year 2005 | Day 48, Year 2007 | Day 128, Year 2007 | Day 208, Year 2007 | |
| Mean Exurban Temp. (°C) | 5.5 | 36.8 | 28.9 | 11.0 | 22.2 | 8.4 | 28.1 | 30.2 |
| Mean Urban Temp. (°C) | 5.5 | 39.3 | 30.3 | 12.5 | 22.2 | 9.9 | 29.9 | 33.2 |
| Degrees Celsius Warmer Urban | −0.01 | 2.47 | 1.38 | 1.54 | 0.06 | 1.53 | 1.77 | 2.93 |
| Informal Selection | Day 21, Year 2003 | Day 181, Year 2003 | Day 245, Year 2003 | Day 58, Year 2005 | Day 298, Year 2005 | Day 48, Year 2007 | Day 128, Year 2007 | Day 208, Year 2007 | |||||
| Mean Abs. Diff. All Areas | 0.07 | 0.04 | 0.05 | 0.07 | 0.07 | 0.12 | 0.06 | 0.04 | |||||
| Mean Abs. Diff. Urban Locations | 0.07 | 0.04 | 0.04 | 0.06 | 0.06 | 0.11 | 0.05 | 0.04 | |||||
| Mean Abs. Diff. Exurban Locations | 0.09 | 0.06 | 0.07 | 0.08 | 0.08 | 0.14 | 0.07 | 0.04 | |||||
| R2 All areas | 0.59 | 0.85 | 0.87 | 0.72 | 0.72 | 0.36 | 0.81 | 0.89 | |||||
| R2 Urban Locations | 0.66 | 0.91 | 0.92 | 0.77 | 0.8 | 0.41 | 0.84 | 0.91 | |||||
| R2 Exurban Locations | 0.45 | 0.69 | 0.8 | 0.63 | 0.54 | 0.28 | 0.71 | 0.85 | |||||
| Statistical Selection Method | Day 21, 2003: 95% Selection | Day 250, 2005: 95% Selection | Day 250, 2005: 90% Selection | Day 43, 2011: 95% Selection | Day 43, 2011: 90% Selection | ||||||||
| Mean Abs. Diff All Areas | 0.05 | 0.04 | 0.04 | 0.11 | 0.17 | ||||||||
| Mean Abs. Diff Urban Locations | 0.05 | 0.04 | 0.04 | 0.11 | 0.22 | ||||||||
| Mean Abs. Diff Exurban Locations | 0.05 | 0.05 | 0.06 | 0.11 | 0.15 | ||||||||
| R2 All areas | 0.68 | 0.88 | 0.87 | 0.46 | 0.16 | ||||||||
| R2 Urban Locations | 0.72 | 0.9 | 0.92 | 0.54 | 0.19 | ||||||||
| R2 Exurban Locations | 0.57 | 0.82 | 0.76 | 0.35 | 0.13 | ||||||||
| All Developed | Open Space | Low Intensity | Medium Intensity | High Intensity | ||
| Informal Base Pair Selection | SOS Urban | 18.4 | 16.6 | 16.3 | 17.7 | 21.7 |
| SOS Exurban | 17.7 | 16.0 | 16.4 | 17.6 | 22.9 | |
| EOS Urban | 17.6 | 17.9 | 16.1 | 16.5 | 22.0 | |
| EOS Exurban | 19.7 | 19.3 | 18.6 | 20.2 | 25.3 | |
| LOS Urban | 24.5 | 24.9 | 22.3 | 23.3 | 29.9 | |
| LOS Exurban | 26.2 | 25.8 | 24.5 | 25.9 | 35.1 | |
| 95% Clear Base Pair Selection | SOS Urban | 19.0 | 16.4 | 16.8 | 18.6 | 26.0 |
| SOS Exurban | 19.2 | 17.5 | 18.4 | 19.8 | 22.3 | |
| EOS Urban | 19.1 | 20.1 | 17.6 | 17.9 | 23.7 | |
| EOS Exurban | 21.7 | 21.7 | 20.8 | 22.4 | 24.1 | |
| LOS Urban | 26.1 | 25.7 | 23.7 | 25.2 | 34.0 | |
| LOS Exurban | 29.4 | 29.5 | 28.5 | 29.9 | 31.9 | |
| 90% Clear Base Pair Selection | SOS Urban | 28.3 | 22.7 | 27.3 | 28.8 | 35.5 |
| SOS Exurban | 24.6 | 22.0 | 24.3 | 26.1 | 29.4 | |
| EOS Urban | 24.4 | 26.3 | 23.8 | 22.9 | 30.4 | |
| EOS Exurban | 27.3 | 27.3 | 26.3 | 28.4 | 31.9 | |
| LOS Urban | 36.8 | 36.6 | 35.9 | 36.5 | 47.3 | |
| LOS Exurban | 36.9 | 36.5 | 35.8 | 38.6 | 42.8 |
| Years with Earlier Urban SOS | Informal Selection | 95% Selection | 90% Selection |
|---|---|---|---|
| All Developed Areas | 9 | 8 | 7 |
| Developed Open Space | 9 | 8 | 8 |
| Developed Low Intensity | 8 | 8 | 6 |
| Developed Medium Intensity | 10 | 7 | 7 |
| Developed High Intensity | 11 | 8 | 8 |
| Years with Later Urban EOS | |||
| All Developed Areas | 7 | 6 | 8 |
| Developed Open Space | 9 | 7 | 8 |
| Developed Low Intensity | 6 | 7 | 8 |
| Developed Medium Intensity | 7 | 8 | 9 |
| Developed High Intensity | 3 | 3 | 6 |
| Years with longer Urban LOS | |||
| All Developed Areas | 7 | 7 | 6 |
| Developed Open Space | 10 | 6 | 8 |
| Developed Low Intensity | 9 | 6 | 6 |
| Developed Medium Intensity | 8 | 7 | 7 |
| Developed High Intensity | 8 | 6 | 6 |
| Parameter | Total Sample Size | Percent Remaining at 500 m Inward | Percent Remaining at 1500 m Inward | |
|---|---|---|---|---|
| Informal Selection | SOS | 1,241,726 | 56 | 12 |
| EOS | 1,681,156 | 56 | 13 | |
| >95% Selection | SOS | 1,263,499 | 56 | 13 |
| EOS | 1,632,057 | 57 | 13 | |
| >90% Selection | SOS | 511,615 | 45 | 5 |
| EOS | 634,573 | 44 | 5 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gervais, N.; Buyantuev, A.; Gao, F. Modeling the Effects of the Urban Built-Up Environment on Plant Phenology Using Fused Satellite Data. Remote Sens. 2017, 9, 99. https://doi.org/10.3390/rs9010099
Gervais N, Buyantuev A, Gao F. Modeling the Effects of the Urban Built-Up Environment on Plant Phenology Using Fused Satellite Data. Remote Sensing. 2017; 9(1):99. https://doi.org/10.3390/rs9010099
Chicago/Turabian StyleGervais, Norman, Alexander Buyantuev, and Feng Gao. 2017. "Modeling the Effects of the Urban Built-Up Environment on Plant Phenology Using Fused Satellite Data" Remote Sensing 9, no. 1: 99. https://doi.org/10.3390/rs9010099
APA StyleGervais, N., Buyantuev, A., & Gao, F. (2017). Modeling the Effects of the Urban Built-Up Environment on Plant Phenology Using Fused Satellite Data. Remote Sensing, 9(1), 99. https://doi.org/10.3390/rs9010099