Gross Primary Production of a Wheat Canopy Relates Stronger to Far Red Than to Red Solar-Induced Chlorophyll Fluorescence
Abstract
:1. Introduction
- -
- to investigate both diurnal and seasonal dynamics of RSIF and FRSIF during a complete vegetative cycle of a crop,
- -
- to analyze the relationship between SIF and GPP according to emission wavelength, time scale, and phenological stage,
- -
- to investigate the factors that potentially control the relationship between SIF and GPP using independent measurements of APAR on one hand, and of fluorescence and photochemical yield by active methods on the other hand.
2. Materials and Methods
2.1. Experimental Site
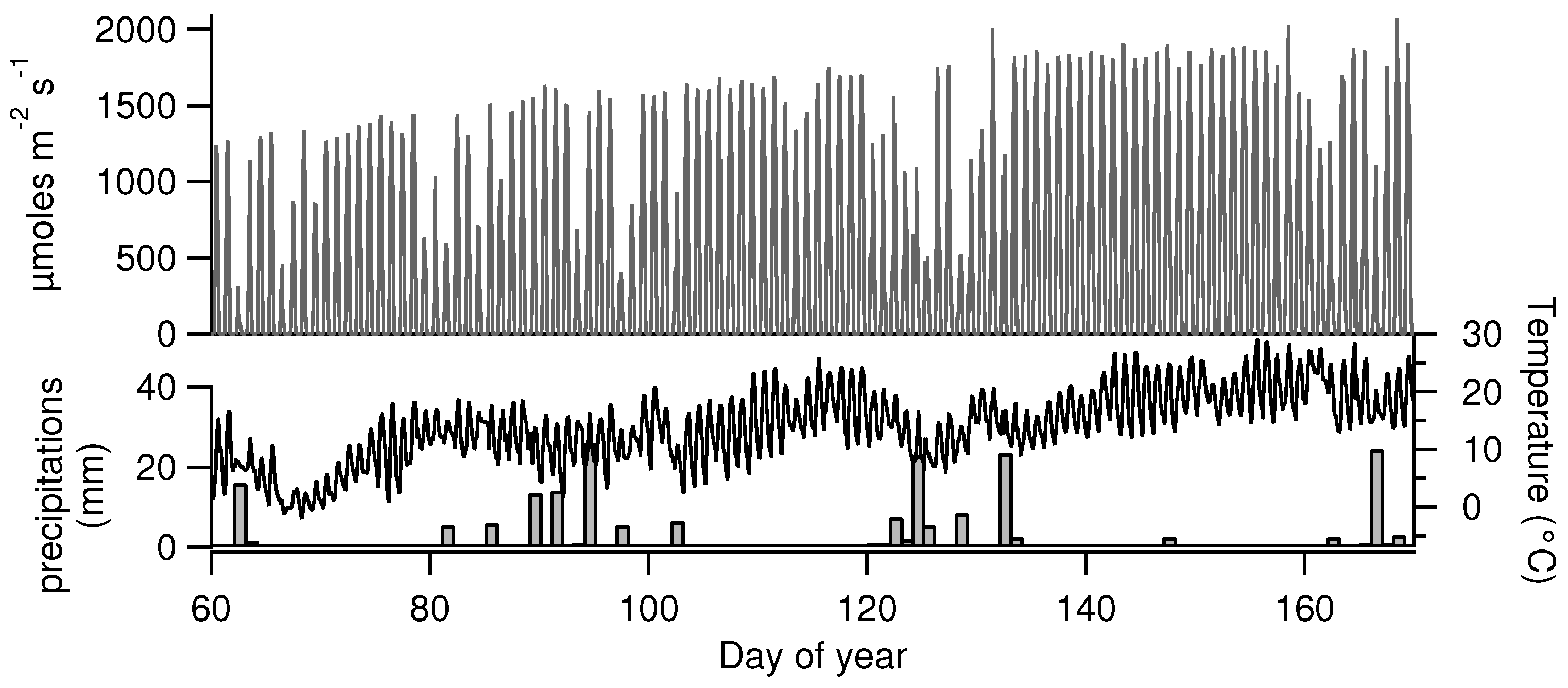
2.2. Canopy Characterization and Environmental Data
2.3. Passive Remote Sensing of SIF and Reflectance
2.3.1. Instrumental Setup and Retrieval of Fluorescence
2.3.2. Derivation of Other Remote Sensing Parameters
2.4. Measurements of Canopy Transmittance and Absorbed PAR
2.5. Measurements of CO2 Fluxes
2.6. Active Fluorometry in the Field
2.7. SIF and GPP Models
2.8. Statistical Analysis
3. Results
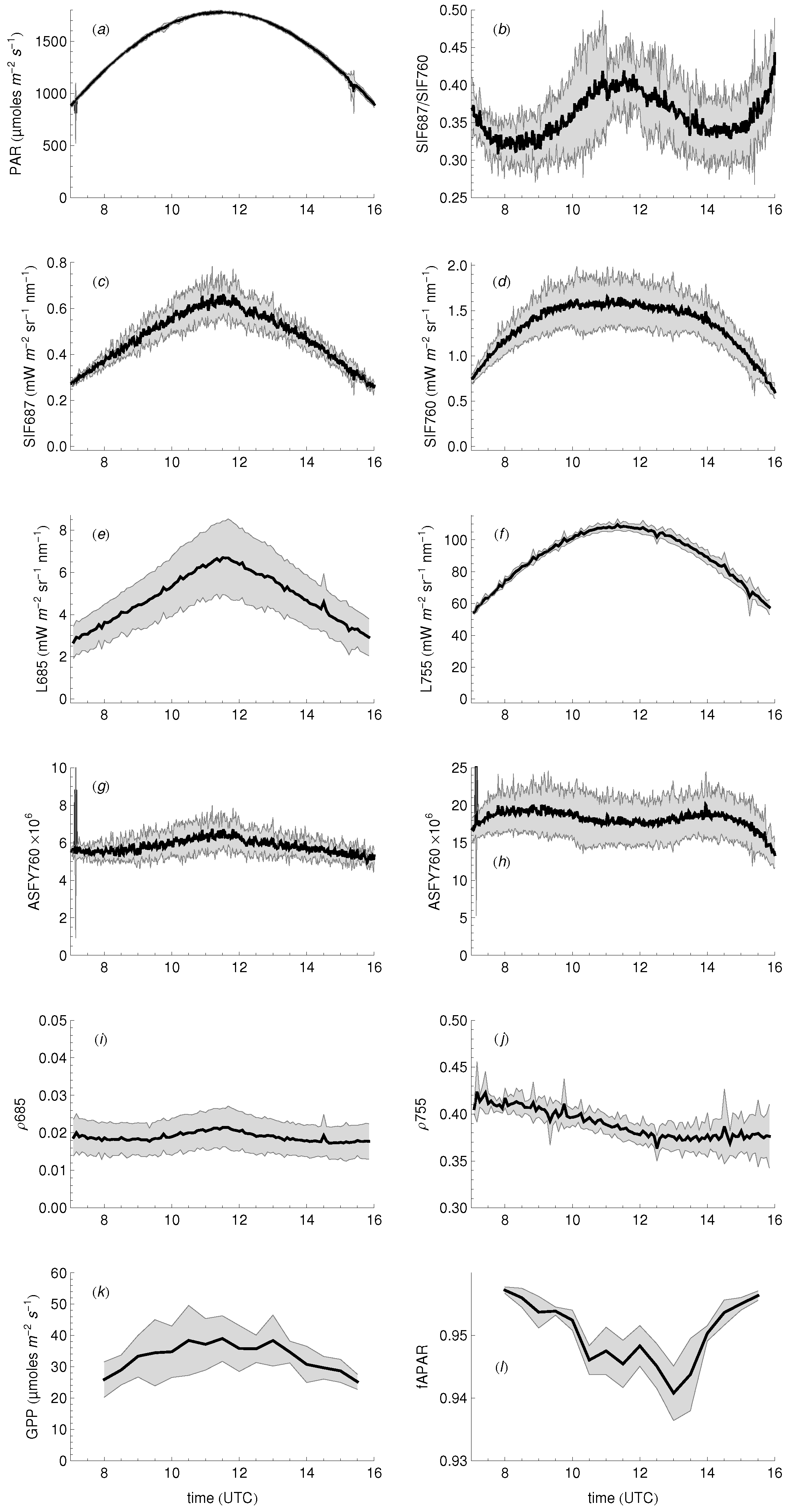
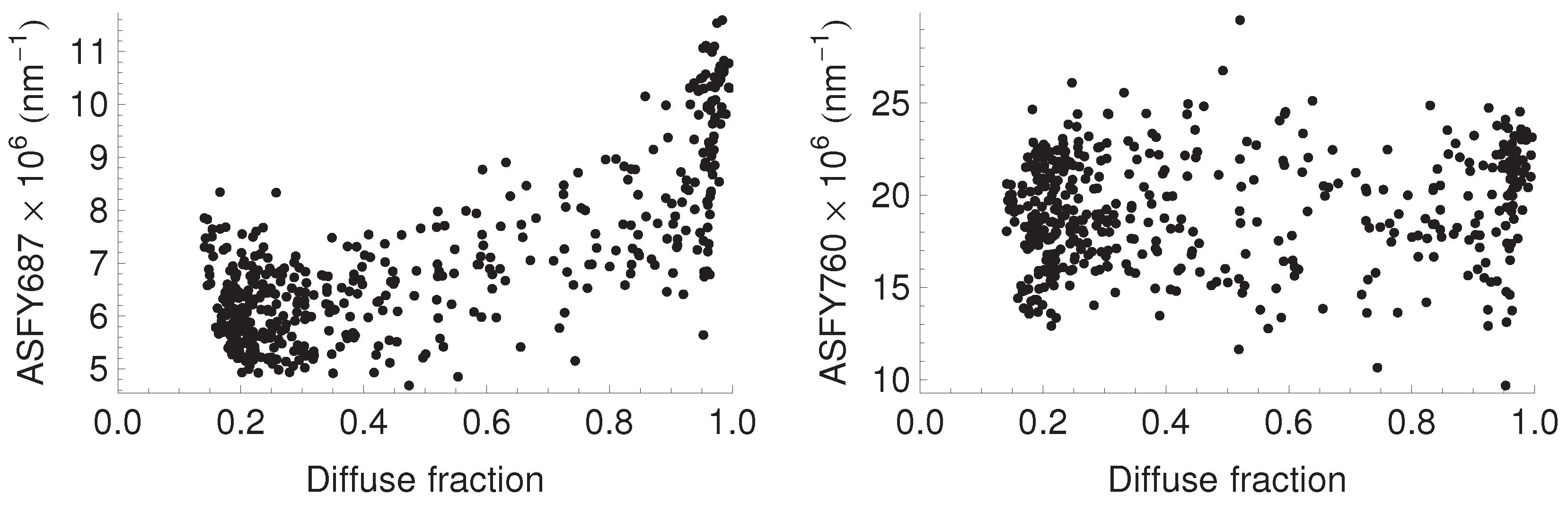
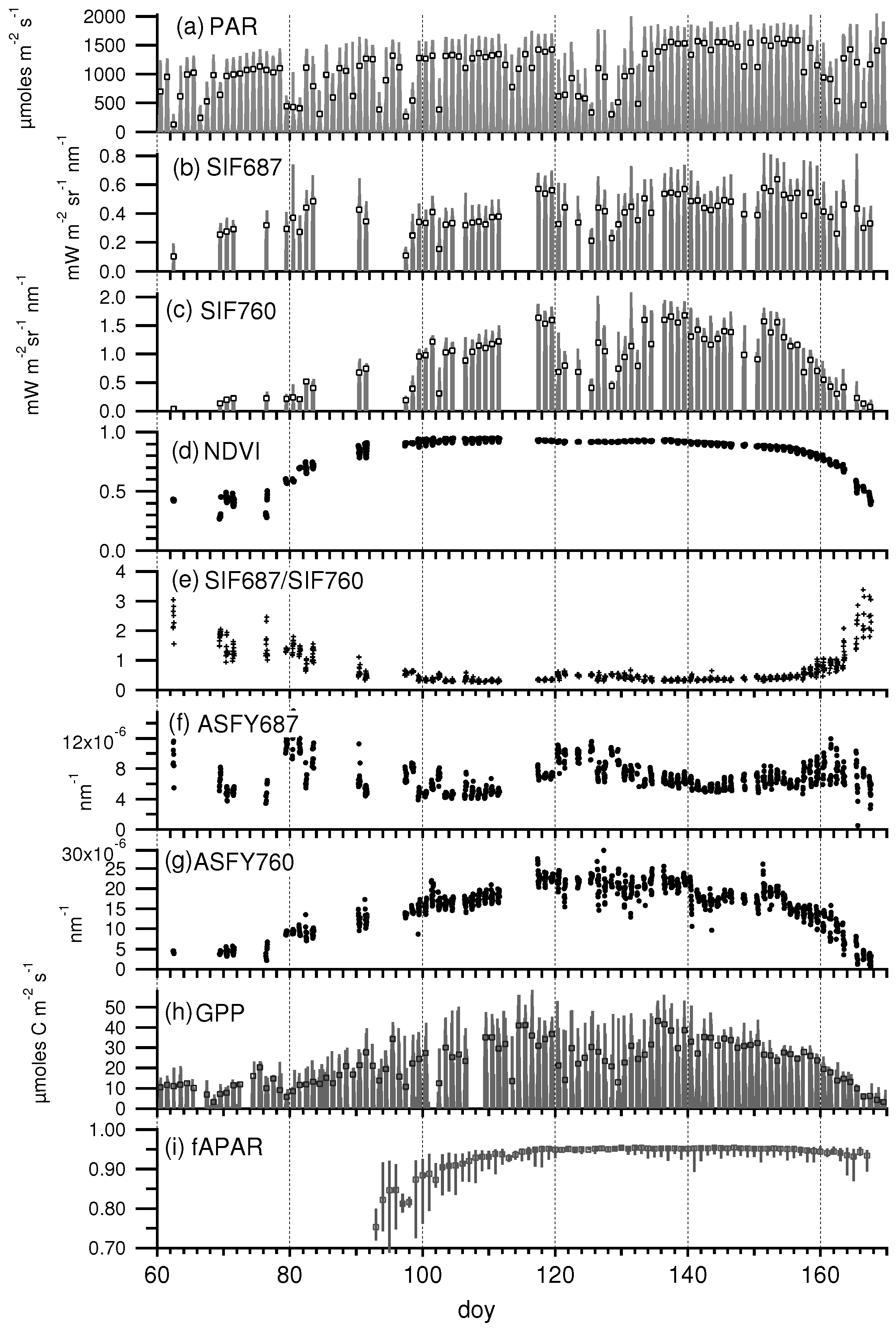
3.1. Daily Cycles of Fluorescence
3.2. Seasonal Patterns of Fluorescence
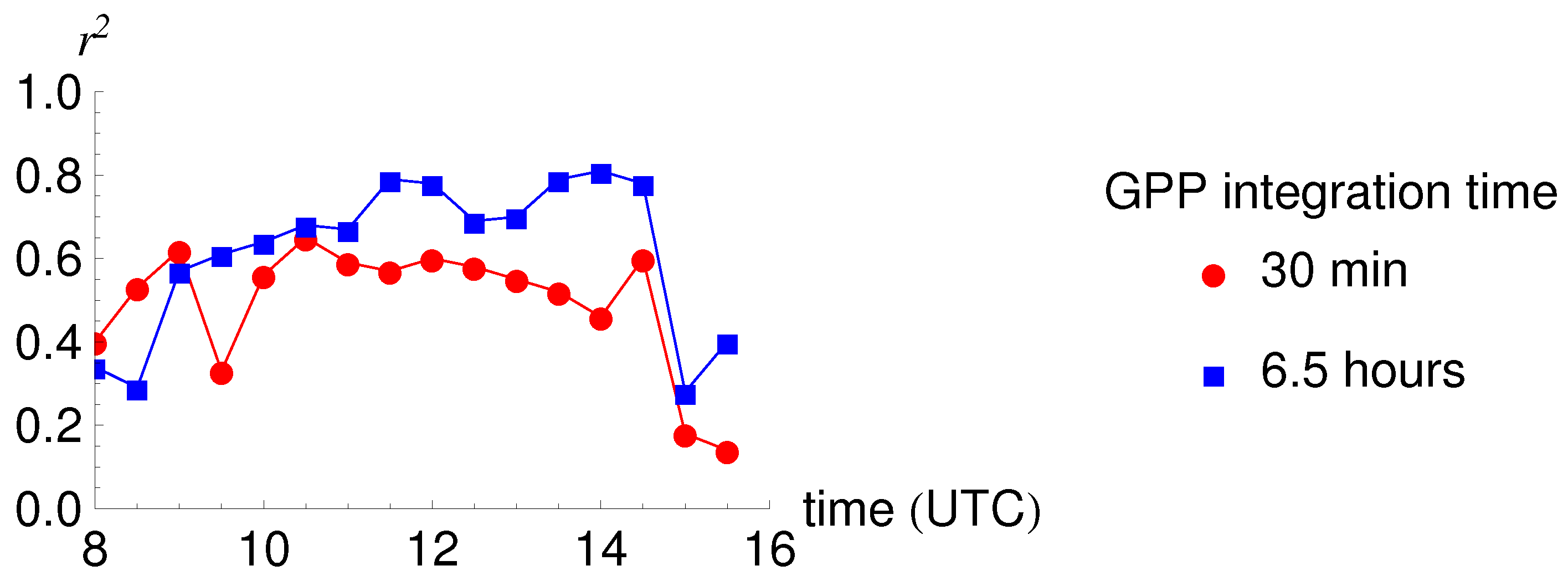
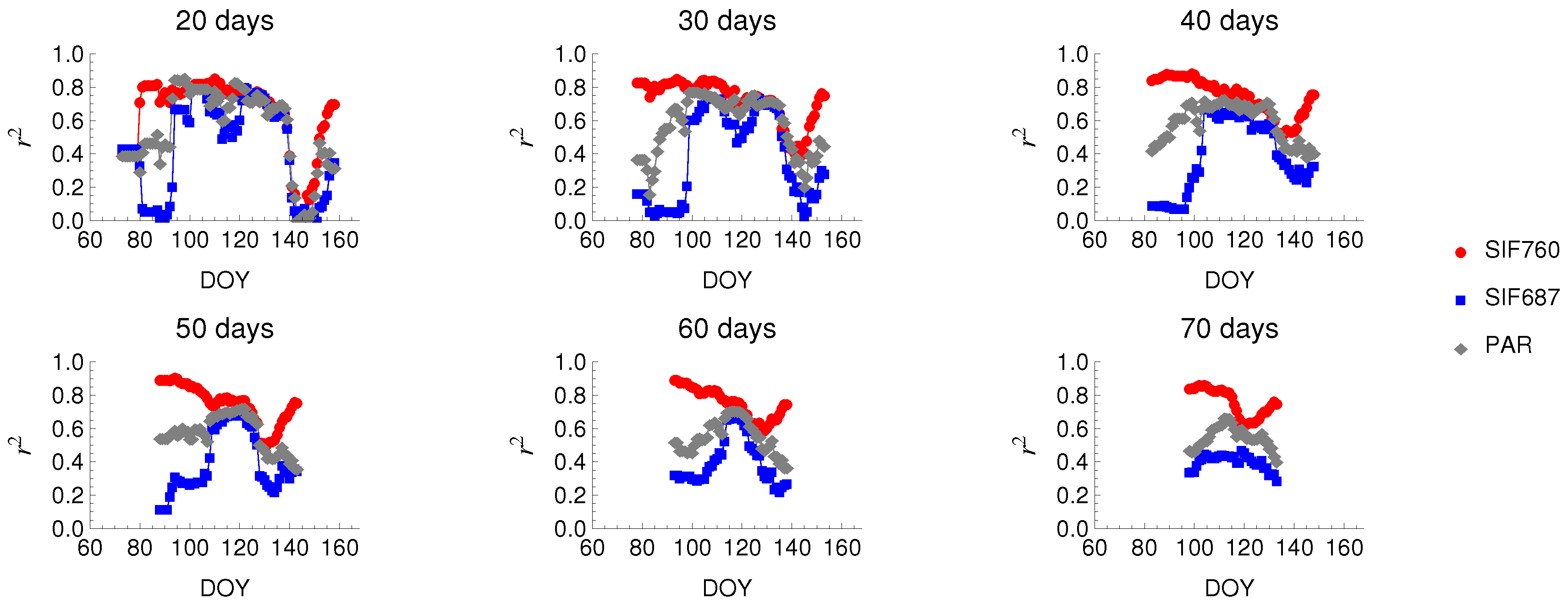
3.3. Relationship between SIF and GPP
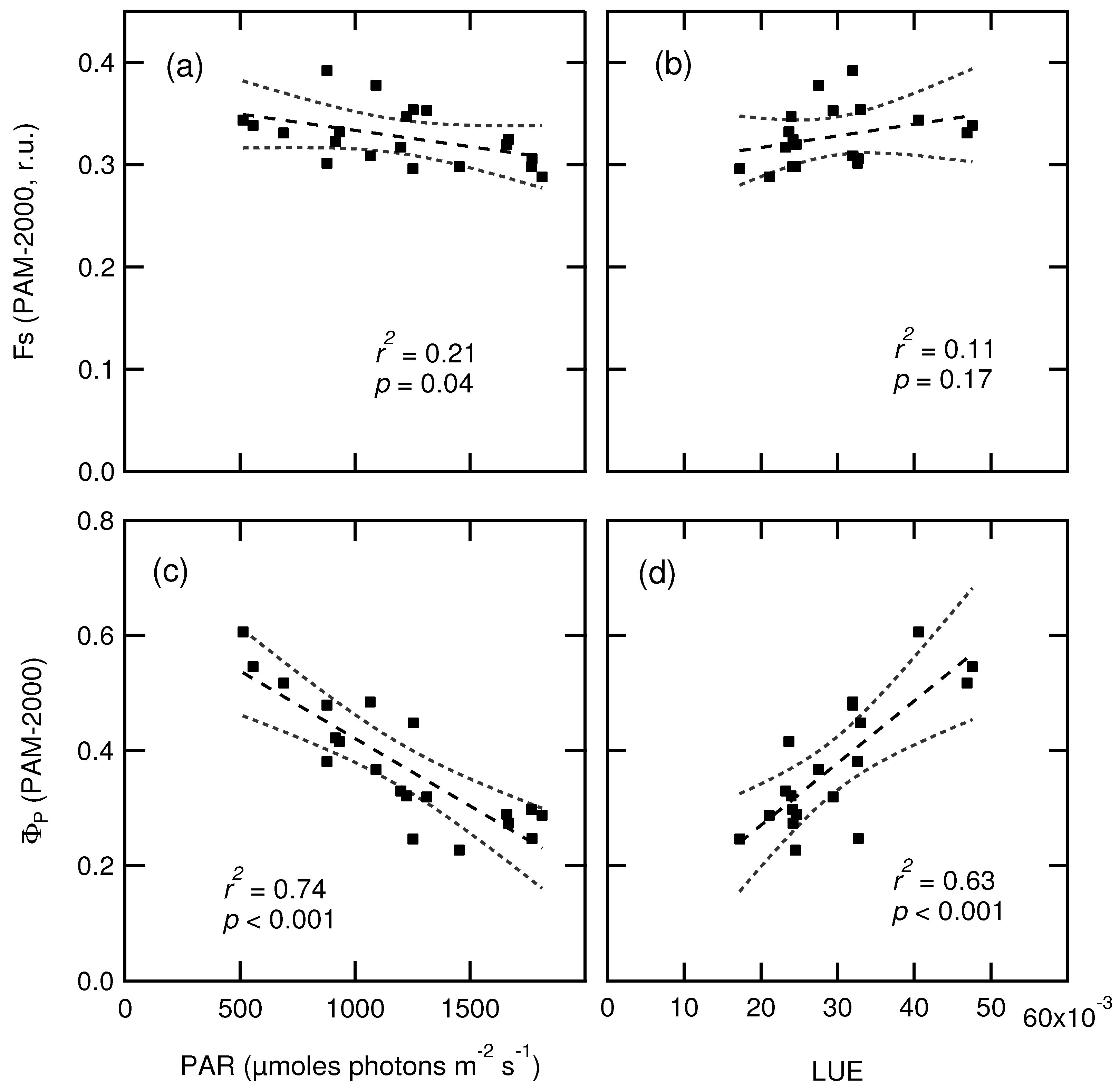
3.4. Relationship between Fluorescence Yield, Photochemistry, and Light Use Efficiency
4. Discussion
4.1. Fluorescence Retrieval in the O2-A and O2-B Bands
4.2. Diurnal Cycles and Short Term Changes in Fluorescence
4.3. Seasonal Changes in Fluorescence
4.4. The SIF–GPP Relationship
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANOVA | ANalysis Of VAriance |
| APAR | Absorbed PAR |
| ASFY | Apparent Spectral Fluorescence Yield |
| Chl | Chlorophyll |
| ChlF | Chlorophyll Fluorescence |
| DOY | day of the year |
| EC | Eddy Covariance |
| ESA | European Space Agency |
| fAPAR | fraction of APAR |
| FLD | Fraunhofer Line Discrimination |
| FRF | Far Red Fluorescence |
| FRSIF | Far Red SIF |
| FWHM | Full Width at Half-Maximum |
| GPP | Gross Primary Production |
| LAI | Leaf Area Index |
| LUE | Light Use Efficiency |
| NDVI | Normalized Difference Vegetation Index |
| NEE | Net Ecosystem Exchange |
| PAR | Photosynthetically Active Radiation |
| PRI | Photochemical Reflectance Index |
| PSI, PSII | Photosystem I, Photosystem II |
| RF | Red Fluorescence |
| RSIF | Red SIF |
| SFM | Spectral Fitting Method |
| SFY | Spectral fluorescence yield |
| SIF | Sun-Induced Fluorescence |
| TOC | Top Of Canopy |
| UTC | Coordinated Universal Time |
Appendix A. Fluorescence Retrieval
Appendix A.1. Description of the Fluorescence Retrieval Method
Appendix A.2. Performance of the Retrieval Algorithm

| SCOPE Variable | Values | Unit | Description |
|---|---|---|---|
| PROSPECT | |||
| Cab | g · | Chlorophyll ab content | |
| Cca | g · | Carotenoid content. Usually 25% of Cab | |
| Cdm | g · | Dry matter content | |
| Cw | Leaf water equivalent layer | ||
| Cs | fraction | Senescent material fraction | |
| N | Leaf thickness parameters | ||
| Leaf_Biochemical | |||
| Vcmo | mol | Maximum carboxylation capacity (at optimum temperature) | |
| m | Ball–Berry stomatal conductance parameter | ||
| Type | Photochemical pathway: 0 = C3, 1 = C4 | ||
| kV | Vertical extinction coefficient of Vcmax | ||
| Rdparam | Respiration = Rdparam × Vcmcax | ||
| Tparam | Five parameters specifying the temperature response. | ||
| Tyear | °C | Mean annual temperature | |
| beta | Fraction of photons partitioned to PSII | ||
| kNPQs | Rate constant of sustained thermal dissipation | ||
| qLs | Fraction of functional reaction centers | ||
| stressfactor | Stress factor to reduce Vcmax (1 = no reduction) | ||
| Fluorescence | |||
| fqe | Fluorescence quantum yield efficiency at photosystem level | ||
| Soil | |||
| spectrum | Spectrum number (column in the database soil_file) | ||
| Canopy | |||
| LAI | Leaf area index | ||
| hc | Vegetation height | ||
| LIDFa | Leaf inclination | ||
| LIDFb | Variation in leaf inclination | ||
| leafwidth | Leaf width | ||
| Meteorological | |||
| z | Measurement height of meteorological data | ||
| Rin | Broadband incoming shortwave radiation (0.4–2.5 m) | ||
| Ta | °C | Air temperature | |
| p | Air pressure | ||
| ea | Atmospheric vapor pressure | ||
| u | Wind speed at height z | ||
| Ca | Atmospheric CO2 concentration | ||
| Angles | |||
| tts | ° | Solar zenith angle | |
| tto | ° | Observation zenith angle |
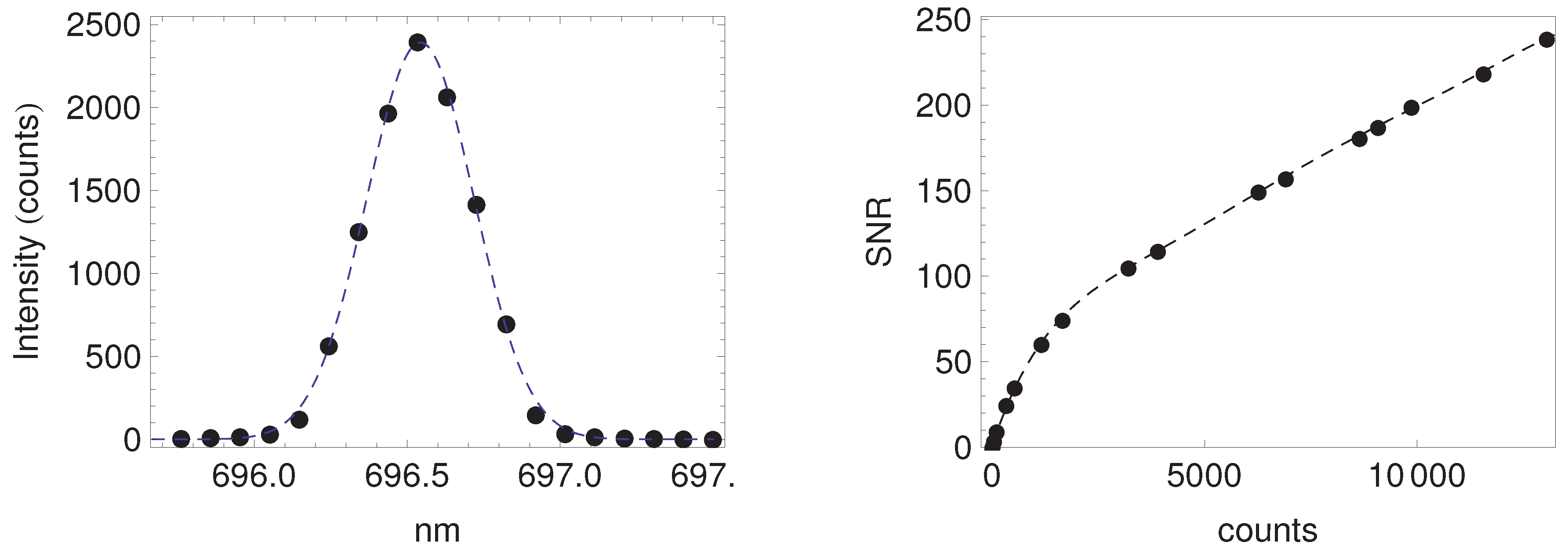
| O2-A | O2-B | |||||||
|---|---|---|---|---|---|---|---|---|
| Central wavelength () | 757.86 | 760.51 | 770.46 | 683.14 | 685.00 | 686.97 | 697.06 | |
| Channel width () | 0.5 | 0.8 | 0.9 | 0.5 | 0.7 | 0.1 | 0.9 | |
| Number of spectral samples | 5 | 8 | 9 | 5 | 7 | 1 | 9 |
| Band | -B | -B | -A |
|---|---|---|---|
| Number of channels | 3 | 4 | 3 |
| Mean bias () | 0.13 | −0.038 | 0.015 |
| Median bias () | 0.12 | −0.057 | 0.013 |
| 0.15 | 0.061 | 0.022 |
References
- Lichtenthaler, H.K.; Rinderle, U. The role of chlorophyll fluorescence in the detection of stress conditions in plants. CRC Crit. Rev. Anal. Chem. 1988, 19, 29–85. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll fluorescence—A practical guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, G.; Govindjee. Chlorophyll a Fluorescence. A Signature of Photosynthesis; Advances in Photosynthesis and Respiration; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Moya, I.; Guyot, G.; Goulas, Y. Remotely sensed blue and red fluorescence emission for monitoring vegetation. ISPRS J. Photogram. Remote Sens. 1992, 47, 205–231. [Google Scholar] [CrossRef]
- Moya, I.; Camenen, L.; Evain, S.; Goulas, Y.; Cerovic, Z.G.; Latouche, G.; Flexas, J.; Ounis, A. A new instrument for passive remote sensing: 1. Measurements of sunlight-induced chlorophyll fluorescence. Remote Sens. Environ. 2004, 91, 186–197. [Google Scholar] [CrossRef]
- Plascyk, J. The MK II Fraunhofer line discriminator (FLD-II) for airborne and orbital remote sensing of solar-stimulated luminescence. Opt. Eng. 1975, 14, 339–346. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Daumard, F.; Goulas, Y.; Champagne, S.; Fournier, A.; Ounis, A.; Olioso, A.; Moya, I. Continuous monitoring of canopy level sun-induced chlorophyll fluorescence during the growth of a sorghum field. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4292–4300. [Google Scholar] [CrossRef]
- Louis, J.; Ounis, A.; Ducruet, J.M.; Evain, S.; Laurila, T.; Thum, T.; Aurela, M.; Wingsle, G.; Alonso, L.; Pedros, R.; et al. Remote sensing of sunlight-induced chlorophyll fluorescence and reflectance of Scots pine in the boreal forest during spring recovery. Remote Sens. Environ. 2005, 96, 37–48. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R. Leaf level detection of solar induced chlorophyll fluorescence by means of a subnanometer resolution spectroradiometer. Remote Sens. Environ. 2006, 103, 438–448. [Google Scholar] [CrossRef]
- Moya, I.; Camenen, L.; Latouche, G.; Mauxion, C.; Evain, S.; Cerovic, Z. An instrument for the measurement of sunlight excited plant fluorescence. In XIth International Congress Photosynthesis; Garab, G., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; Volume V, pp. 4265–4370. [Google Scholar]
- Moya, I.; Daumard, F.; Moise, N.; Ounis, A.; Goulas, Y. First airborne multiwavelength passive chlorophyll fluorescence measurements over La Mancha (Spain) fields. In Proceedings of the 2nd International Symposium on Recent Advances in Quantitative Remote Sensing: RAQRS’II, Torrent, Spain, 25–29 September 2006.
- Rascher, U.; Agati, G.; Alonso, L.; Cecchi, G.; Champagne, S.; Colombo, R.; Damm, A.; Daumard, F.; de Miguel, E.; Fernandez, G.; et al. CEFLES2: The remote sensing component to quantify photosynthetic efficiency from the leaf to the region by measuring sun-induced fluorescence in the oxygen absorption bands. Biogeosciences 2009, 6, 1181–1198. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Corp, L.A.; Middleton, E.M. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Report for Mission Selection: FLEX; Technical Report ESA SP-1330/2; European Space Agency: Paris, France, 2015; p. 197. [Google Scholar]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gómez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
- Cheng, Y.B.; Middleton, E.; Zhang, Q.; Huemmrich, K.F.; Campbell, P.K.E.; Corp, L.; Cook, B.D.; Kustas, W.P.; Daughtry, C.S.T. Integrating solar induced fluorescence and the photochemical reflectance index for estimating gross primary production in a cornfield. Remote Sens. 2013, 5, 6857–6879. [Google Scholar] [CrossRef]
- Damm, A.; Elbers, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A.; et al. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Wagle, P.; Zhang, Y.G.; Jin, C.; Xiao, X.M. Comparison of solar-induced chlorophyll fluorescence, light-use efficiency, and process-based GPP models in maize. Ecol. Appl. 2016, 26, 1211–1222. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.G.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kohler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Tang, J.W.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Genty, B.; Wonders, J.; Baker, N.R. Nonphotochemical quenching of F0 in leaves is emission wavelength dependent—Consequences for quenching analysis and its interpretation. Photosynth. Res. 1990, 26, 133–139. [Google Scholar] [CrossRef] [PubMed]
- Palombi, L.; Cecchi, G.; Lognoli, D.; Raimondi, V.; Toci, G.; Agati, G. A retrieval algorithm to evaluate the Photosystem I and Photosystem II spectral contributions to leaf chlorophyll fluorescence at physiological temperatures. Photosynth. Res. 2011, 108, 225–239. [Google Scholar] [CrossRef] [PubMed]
- Daumard, F.; Champagne, S.; Fournier, A.; Goulas, Y.; Ounis, A.; Hanocq, J.F.; Moya, I. A field platform for continuous measurement of canopy fluorescence. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3358–3368. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Cerovic, Z.G.; Masdoumier, G.; Ben Ghozlen, N.; Latouche, G. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Fournier, A.; Daumard, F.; Champagne, S.; Ounis, A.; Goulas, Y.; Moya, I. Effect of canopy structure on sun-induced chlorophyll fluorescence. ISPRS J. Photogramm. Remote Sens. 2012, 68, 112–120. [Google Scholar] [CrossRef]
- Anderson, G.P.; Berk, A.; Acharya, P.K.; Matthew, M.W.; Bernstein, L.S.; Chetwynd, J.H.; Dothe, H.; Adler-Golden, S.M.; Ratkowski, A.J.; Felde, G.W.; et al. MODTRAN4: Radiative transfer modeling for remote sensing. In Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; Shen, S.S., Descour, M.R., Eds.; Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE); SPIE: Bellingham, WA, USA, 2000; Volume 4049, pp. 176–183. [Google Scholar]
- Daumard, F.; Goulas, Y.; Ounis, A.; Pedros, R.; Moya, I. Measurement and correction of atmospheric effects at different altitudes for remote sensing of sun-induced fluorescence in oxygen absorption bands. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5180–5196. [Google Scholar] [CrossRef]
- Huang, W.; Niu, Z.; Wang, J.; Liu, L.; Zhao, C.; Liu, Q. Identifying crop leaf angle distribution based on two-temporal and bidirectional canopy reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3601–3609. [Google Scholar] [CrossRef]
- Yanli, L.; Shaokun, L.; Jihua, W.; Carol, J.; Ruizhi, X.; Zhijie, W. Differentiating wheat varieties with different leaf angle distributions using NDVI and canopy cover. N. Z. J. Agric. Res. 2007, 50, 1149–1156. [Google Scholar] [CrossRef]
- Louis, J.; Cerovic, Z.; Moya, I. Quantitative study of fluorescence excitation and emission spectra of bean leaves. J. Photochem. Photobiol. B Biol. 2006, 85, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Baret, F.; Vanderbilt, V.C.; Rondeaux, G.; Pettigrew, R.E.; Hanocq, J.F.; Biehl, L.L.; Sarrouy, C.; Daughtry, C.S.T.; Steven, M.D.; Sarto, A.W.; et al. Directional and Temporal Variability of the Apar/vi Relationships. The case of a sunflower canopy. In Proceedings of the 1992 International Geoscience and Remote Sensing Symposium, IGARSS ’92, Houston, TX, USA, 26–29 May 1992; Volume 2, pp. 1468–1470.
- Dolman, A.J.; Tolk, L.; Ronda, R.; Noilhan, J.; Sarrat, C.; Brut, A.; Piguet, B.; Durand, P.; Butet, A.; Jarosz, N.; et al. The CarboEurope regional experimentstrategy. Bull. Am. Meteorol. Soc. 2006, 87, 1367–1379. [Google Scholar] [CrossRef]
- Kowalski, S.; Sartore, M.; Burlett, R.; Berbigier, P.; Loustau, D. The annual carbon budget of a French pine forest (Pinus pinaster) following harvest. Glob. Chang. Biol. 2003, 9, 1051–1065. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.; Baker, N. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Alonso, L.; Gomez-Chova, L.; Vila-Frances, J.; Amoros-Lopez, J.; Guanter, L.; Calpe, J.; Moreno, J. Improved fraunhofer line discrimination method for vegetation fluorescence quantification. IEEE Geosci. Remote Sens. Lett. 2008, 5, 620–624. [Google Scholar] [CrossRef]
- Meroni, M.; Busetto, L.; Colombo, R.; Guanter, L.; Moreno, J.; Verhoef, W. Performance of spectral fitting methods for vegetation fluorescence quantification. Remote Sens. Environ. 2010, 114, 363–374. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Sun-induced fluorescence: A new tool for precision farming. In Digital Imaging and Spectral Techniques: Application to Precision Agriculture and Crop Physiology; VanToai, T., Major, D., PMcDonald, M., Schepers, J., Tarpley, L., Eds.; American Society of Agronomy: Madison, WI, USA, 2003; pp. 209–222. [Google Scholar]
- Gomez-Chova, L.; Alonsso, L.; Amors-Lopez, J.; Vila-Francès, J.; del Valle-Tascon, S.; Calpe, J.; Moreno, J. Solar-induced fluorescence measurements using a field spectroradiometer. Earth observation for vegetation monitoring and water management. In Proceedings of the AIP Conference, Naples, Italy, 10–11 November 2006; Volume 852, pp. 274–281.
- Guanter, L.; Rossini, M.; Colombo, R.; Meroni, M.; Frankenberg, C.; Lee, J.E.; Joiner, J. Using field spectroscopy to assess the potential of statistical approaches for the retrieval of sun-induced chlorophyll fluorescence from ground and space. Remote Sens. Environ. 2013, 133, 52–61. [Google Scholar] [CrossRef]
- Guanter, L.; Alonso, L.; Gomez-Chova, L.; Meroni, M.; Preusker, R.; Fischer, J.; Moreno, J. Developments for vegetation fluorescence retrieval from spaceborne high-resolution spectrometry in the O-2-A and O-2-B absorption bands. J. Geophys. Res.-Atmos. 2010, 115, D19303. [Google Scholar] [CrossRef]
- Fournier, A. Influence de la Structure des Couverts Végétaux en Télédétection de la Fluorescence Chlorophyllienne. Ph.D. Thesis, Ecole polytechnique, Palaiseau, France, 2011. [Google Scholar]
- Cogliati, S.; Verhoef, W.; Kraft, S.; Sabater, N.; Alonso, L.; Vicent, J.; Moreno, J.; Drusch, M.; Colombo, R. Retrieval of sun-induced fluorescence using advanced spectral fitting methods. Remote Sens. Environ. 2015, 169, 344–357. [Google Scholar] [CrossRef]
- Fournier, A.; Daumard, F.; Champagne, S.; Ounis, A.; Moya, I.; Goulas, Y. Effects of vegetation directional reflectance on sun-induced fluorescence retrieval in the oxygen absorption bands. In Proceedings of the 5th International Workshop on Remote Sensing of Vegetation Fluorescence, Paris, France, 22–24 April 2014.
- Zarco-Tejada, P.J.; Berni, J.A.J.; Suarez, L.; Sepulcre-Canto, G.; Morales, F.; Miller, J.R. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ. 2009, 113, 1262–1275. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Catalina, A.; Gonzalez, M.R.; Martin, P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ. 2013, 136, 247–258. [Google Scholar] [CrossRef]
- Flexas, J.; Escalona, J.M.; Evain, S.; Gulias, J.; Moya, I.; Osmond, C.B.; Medrano, H. Steady-state chlorophyll fluorescence (Fs) measurements as a tool to follow variations of net CO2 assimilation and stomatal conductance during water-stress in C-3 plants. Physiol. Plant. 2002, 114, 231–240. [Google Scholar] [CrossRef] [PubMed]
- Moya, I.; Cartelat, A.; Cerovic, Z.; Ducruet, J.M.; Evain, S.; Flexas, F.; Goulas, Y.; Louis, J.; Meyer, S.; Moise, N.; et al. Possible approaches to remote sensing of photosynthetic activity. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium IGARSS ’03, Toulouse, France, 21–25 July 2003; Volume I, pp. 588–590.
- Middleton, E.; Cheng, Y.B.; Corp, L.; Huemmrich, K.F.; Campbell, P.K.E.; Zhang, Q.Y.; Kustas, W.P.; Russ, A.L. Diurnal and seasonal dynamics of canopy-level solar-induced chlorophyll fluorescence and spectral reflectance indices in a cornfield. In the Proceedings of the 6th EARSeL SIG Workshop on Imaging Spectroscopy, Tel-Aviv, Israël, 16–19 March 2009.
- Berry, J.; Frankenberg, C.; Wennberg, P.; Baker, I.; Bowman, K.; Castro-Contreas, S.; et al. New Methods for Measurements of Photosynthesis from Space. Available online: http://www.kis.caltech.edu/workshops/photosynthesis2012/NewMethod2.pdf (accessed on 22 February 2015).
- Joiner, J.; Yoshida, Y.; Vasilkov, A.; Schaefer, K.; Jung, M.; Guanter, L.; Zhang, Y.; Garrity, S.; Middleton, E.M.; Huemmrich, K.F.; et al. The seasonal cycle of satellite chlorophyll fluorescence observations and its relationship to vegetation phenology and ecosystem atmosphere carbon exchange. Remote Sens. Environ. 2014, 152, 375–391. [Google Scholar] [CrossRef]
- Hmimina, G.; Dufrene, E.; Soudani, K. Relationship between photochemical reflectance index and leaf ecophysiological and biochemical parameters under two different water statuses: Towards a rapid and efficient correction method using real-time measurements. Plant Cell Environ. 2014, 37, 473–487. [Google Scholar] [CrossRef] [PubMed]
- Merlier, E.; Hmimina, G.; Dufrene, E.; Soudani, K. Explaining the variability of the photochemical reflectance index (PRI) at the canopy-scale: Disentangling the effects of phenological and physiological changes. J. Photochem. Photobiol. B-Biol. 2015, 151, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.; Penuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Penuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Verhoef, W.; Van der Tol, C.; Middleton, E. Vegetation canopy fluorescence and reflectance retrieval by model inversion using optimization. In Proceedings of the 5th International Workshop on Remote Sensing of Vegetation Fluorescence, Paris, France, 22–24 April 2014.
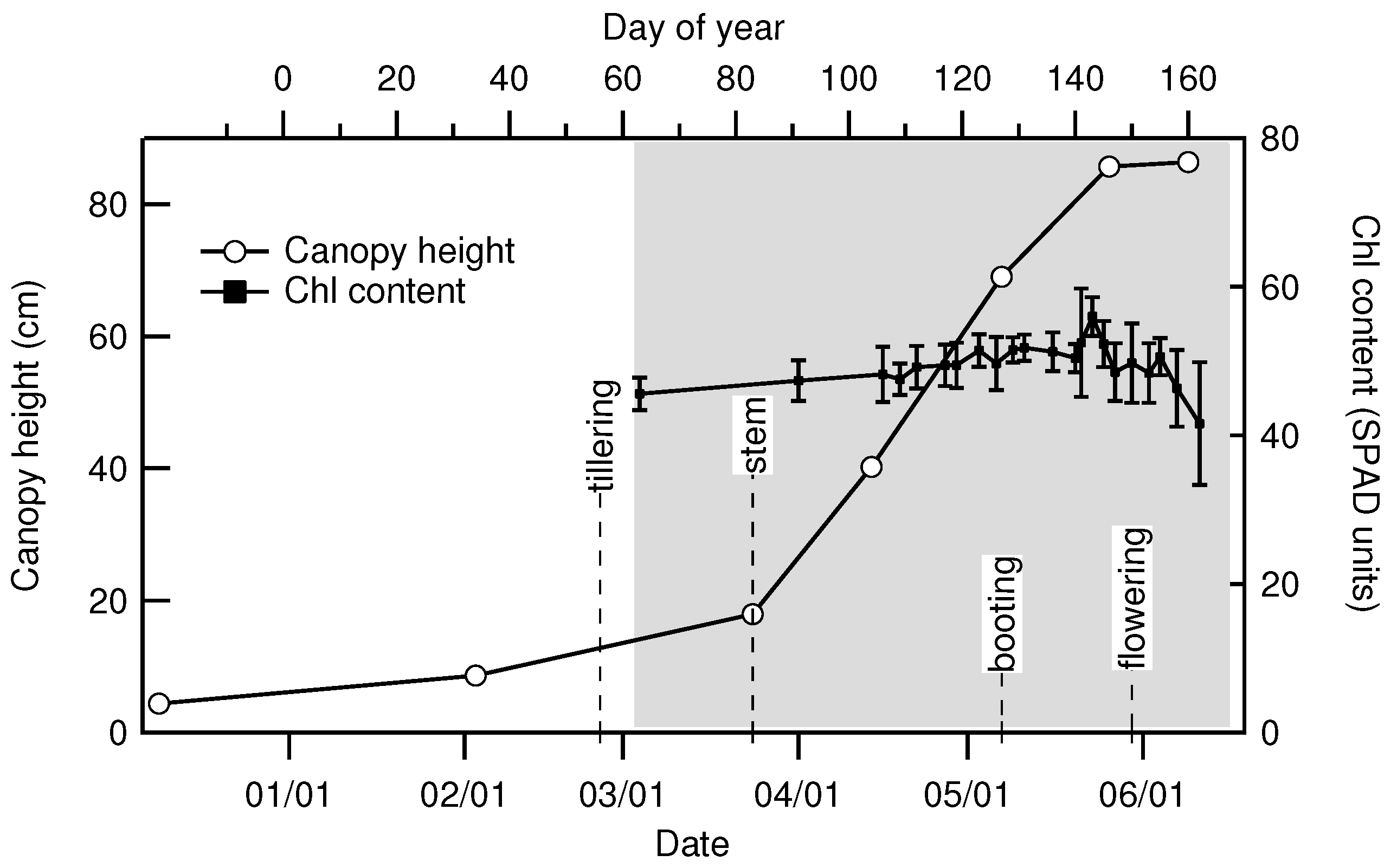


| Date | 2 March | 24 March | 14 April | 7 May | 26 May | 9 June |
|---|---|---|---|---|---|---|
| Day of Year | 34 | 83 | 104 | 127 | 146 | 160 |
| Height () | 8.6 | 18 | 40 | 69 | 86 | 86 |
| LAI () | 0.15 | 0.89 | 3.32 | 6.88 | 5.74 | 1.07 |
| Fresh biomass (kg) | 0.091 | 0.58 | 2.13 | 4.26 | 4.32 | 3.50 |
| Dry biomass (kg) | 0.018 | 0.116 | 0.384 | 1.02 | 1.51 | 1.67 |
| Date | PAR () | Fs (a.u.) | m (a.u.) | ASFY687 () | ASFY760 () | |
|---|---|---|---|---|---|---|
| 2010/04/29 (DOY 119) | (n = 20) | (n = 20) | (n = 20) | (n = 30) | (n = 30) | |
| morning | 1159 | 0.377 | 0.6 | 0.367 | 0.37 | 1.14 |
| Rel. var. noon/morning | −14% (***) | −25% (***) | −25% (***) | 12% (***) | −3% (***) | |
| 2010/05/13 (DOY 133) | (n = 20) | (n = 20) | (n = 20) | (n = 30) | (n = 30) | |
| morning | 1230 | 0.344 | 0.498 | 0.302 | 0.318 | 1.13 |
| Rel. var. noon/morning | −12% (*) | −16% (n.s.) | −12% (**) | 11% (***) | −11% (***) | |
| 2010/05/17 (DOY 137) | (n = 19) | (n = 19) | (n = 19) | (n = 30) | (n = 30) | |
| morning | 1257 | 0.359 | 0.534 | 0.328 | 0.325 | 1.08 |
| Rel. var. noon/morning | −15% (**) | −24% (***) | −25% (***) | 15% (***) | −3% (*) | |
| 2010/05/20 (DOY 140) | (n = 20) | (n = 20) | (n = 20) | (n = 30) | (n = 30) | |
| morning | 1288 | 0.347 | 0.513 | 0.321 | 0.341 | 1.12 |
| Rel. var. noon/morning | −17% (**) | −21% (n.s.) | −11% (***) | 12% (***) | −16% (***) | |
| 2010/05/22 (DOY 142) | (n = 17) | (n = 17) | (n = 17) | (n = 30) | (n = 30) | |
| morning | 1189 | 0.322 | 0.77 | 0.557 | 0.287 | 0.88 |
| Rel. var. noon/morning | −7% (n.s.) | −45% (***) | −47% (***) | 4% (***) | −10% (***) | |
| 2010/05/29 (DOY 149) | (n = 32) | (n = 32) | (n = 32) | (n = 30) | (n = 30) | |
| morning | 1327 | 0.194 | 0.387 | 0.474 | 0.345 | 1.04 |
| Rel. var. noon/morning | −10% (***) | −32% (***) | −30% (***) | 6% (***) | −5% (**) | |
| 2010/06/02 (DOY 153) | (n = 30) | (n = 30) | (n = 30) | (n = 30) | (n = 30) | |
| morning | 1289 | 0.196 | 0.443 | 0.526 | 0.3.=35 | 0.952 |
| Rel. var. noon/morning | −4% (n.s.) | −39% (***) | −45% (***) | 27% (***) | −4% (**) | |
| 2010/06/04 (DOY 155) | (n = 30) | (n = 30) | (n = 30) | (n = 30) | (n = 30) | |
| morning | 1291 | 0.194 | 0.367 | 0.44 | 0.307 | 0.822 |
| Rel. var. noon/morning | −13% (**) | −37% (***) | −44% (***) | 8% (***) | −16% (***) | |
| 2010/06/05 (DOY 156) | (n = 20) | (n = 20) | (n = 20) | (n = 30) | (n = 30) | |
| morning | 1299 | 0.189 | 0.307 | 0.368 | 0.308 | 0.751 |
| Rel. var. noon/morning | −20% (***) | −40% (***) | −52% (***) | 14% (***) | −10% (***) |
| Clear Sky | Overcast | |
|---|---|---|
| Diffuse fraction of PAR | ≤0.2 | ≥0.9 |
| n samples | 221 | 93 |
| Median PAR (mol) | 1620 | 494 |
| Median () | 6.1 | 9.3 |
| Median () | 18.7 | 21.1 |
| Integration Time | 30 min | 30 min | 30 min | 6.5 h | 6.5 h |
|---|---|---|---|---|---|
| Sky Conditions | All | Clear Sky | Clear Sky during the Whole Day | All | Clear Sky during the Whole Day |
| data points | 768 | 313 | 173 | 72 | 17 |
| SIF687 | |||||
| 0.25 | 0.16 | 0.33 | 0.34 | 0.58 | |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| t-statistics | 16.05 | 7.73 | 9.21 | 6.07 | 4.57 |
| SIF760 | |||||
| 0.58 | 0.52 | 0.61 | 0.83 | 0.88 | |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| t-statistics | 32.46 | 18.31 | 16.39 | 18.28 | 10.74 |
| GPP Integration Time | 30 min | 30 min | 30 min | 6.5 h | 6.5 h | 6.5 h |
|---|---|---|---|---|---|---|
| Sky Conditions | All | Clear Sky | Clear Sky during the Whole Day | All | Clear Sky | Clear Sky during the Whole Day |
| data points | 52 | 19 | 10 | 64 | 25 | 15 |
| SIF687 | ||||||
| 0.21 | 0.17 | 0.66 | 0.24 | 0.2 | 0.66 | |
| p-value | 0.001 | 0.08 | 0.004 | <0.001 | 0.02 | <0.001 |
| t-statistics | 3.66 | 1.84 | 3.91 | 4.41 | 2.42 | 5.01 |
| SIF760 | ||||||
| 0.56 | 0.56 | 0.75 | 0.76 | 0.78 | 0.93 | |
| p-value | <0.001 | <0.001 | 0.001 | <0.001 | <0.001 | <0.001 |
| t-statistics | 7.9 | 4.61 | 4.84 | 13.99 | 9.05 | 12.99 |
| Crop Stages | All | Without Senescence | Without Senescence |
|---|---|---|---|
| Sky Conditions | All | All | Clear Sky |
| Data points | 665 | 531 | 253 |
| 687 nm | |||
| 0.11 | 0.16 | 0.007 | |
| p-value | <0.0001 | <0.0001 | 0.19 |
| 760 nm | |||
| 0.10 | 0.006 | 0.05 | |
| p-value | <0.0001 | 0.06 | 0.0002 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goulas, Y.; Fournier, A.; Daumard, F.; Champagne, S.; Ounis, A.; Marloie, O.; Moya, I. Gross Primary Production of a Wheat Canopy Relates Stronger to Far Red Than to Red Solar-Induced Chlorophyll Fluorescence. Remote Sens. 2017, 9, 97. https://doi.org/10.3390/rs9010097
Goulas Y, Fournier A, Daumard F, Champagne S, Ounis A, Marloie O, Moya I. Gross Primary Production of a Wheat Canopy Relates Stronger to Far Red Than to Red Solar-Induced Chlorophyll Fluorescence. Remote Sensing. 2017; 9(1):97. https://doi.org/10.3390/rs9010097
Chicago/Turabian StyleGoulas, Yves, Antoine Fournier, Fabrice Daumard, Sébastien Champagne, Abderrahmane Ounis, Olivier Marloie, and Ismael Moya. 2017. "Gross Primary Production of a Wheat Canopy Relates Stronger to Far Red Than to Red Solar-Induced Chlorophyll Fluorescence" Remote Sensing 9, no. 1: 97. https://doi.org/10.3390/rs9010097
APA StyleGoulas, Y., Fournier, A., Daumard, F., Champagne, S., Ounis, A., Marloie, O., & Moya, I. (2017). Gross Primary Production of a Wheat Canopy Relates Stronger to Far Red Than to Red Solar-Induced Chlorophyll Fluorescence. Remote Sensing, 9(1), 97. https://doi.org/10.3390/rs9010097






