Refinement of Hyperspectral Image Classification with Segment-Tree Filtering
Abstract
:1. Introduction
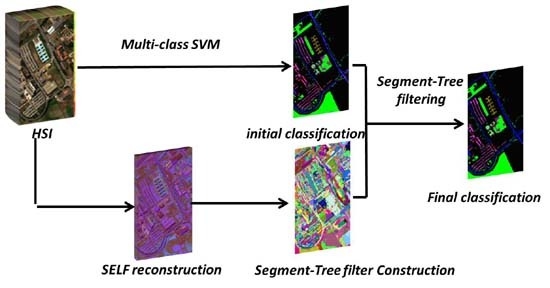
2. HSI Classification Refinement Using Segment-Tree Filtering
- Step 1: Construct the Segment-Tree Filter, which involves feature extraction using the SELF method followed by building a tree-structure filter for an HSI based on dimensionality reduction.
- Step 2: Use a Multi-class SVM method to obtain the initial classification map.
- Step3: Perform Segment-Tree Filtering based on the Multi-class SVM, pixel-based initial classification map. By combining this initial classification map and the Segment-Tree Filter, we can incorporate spatial information and spectral features, adaptively. Finally, the HSI classification map can be derived from the result of Segment-Tree Filtering.
2.1. Initial Classification
2.2. Semi-Supervised Local Fisher Discriminant Analysis
- Local scaling coefficient is pre-computed for each sample in the training set, which is equal to the Euclidean distance between the sample and its th nearest neighbor among all samples in both the training and test sets.
- Local between-class weight matrix and local within-class weight matrix are computed as Equations (4) and (5), respectively. In this step, if two samples have the same label in the training set, is used to scale the local geometric structure with heat kernel weighting.
- The local between-class scatter matrix and local, within-class scatter matrix are calculated by Equations (6) and (7):Note that is a unit column vector of size . Steps 1–3 are the same as those used in the LFDA procedure. In our procedure, only samples in the training set have been used at this point, and the statistical distribution of clusters has not been assessed or applied.
- The covariance matrix is computed based on all samples in both the training and test sets as below:where is the mean of all samples. Then, the regularized, local, between-class scatter matrix and the regularized, local, within-class scatter matrix are derived by Equations (9) and (10), respectively.is the trade-off parameter based on prior knowledge from the training set and the statistical distribution of clusters. Therefore, SELF maintains the advantages of LFDA and PCA. Note that is an identity matrix.
- Transformation matrix can be computed based on generalized eigenvalue decomposition. consists of weighted eigenvectors corresponding to the largest eigenvalues. After is determined, all the pixels in the HSI can be reprojected to a new low-dimensional space.
2.3. Segment-Tree Filter Construction
- All the edges are sorted in ascending order according to their weights. This step can be performed efficiently using a quicksort algorithm [31], even if the number of edges is very large.
- For each vertex, we initialize a tree .
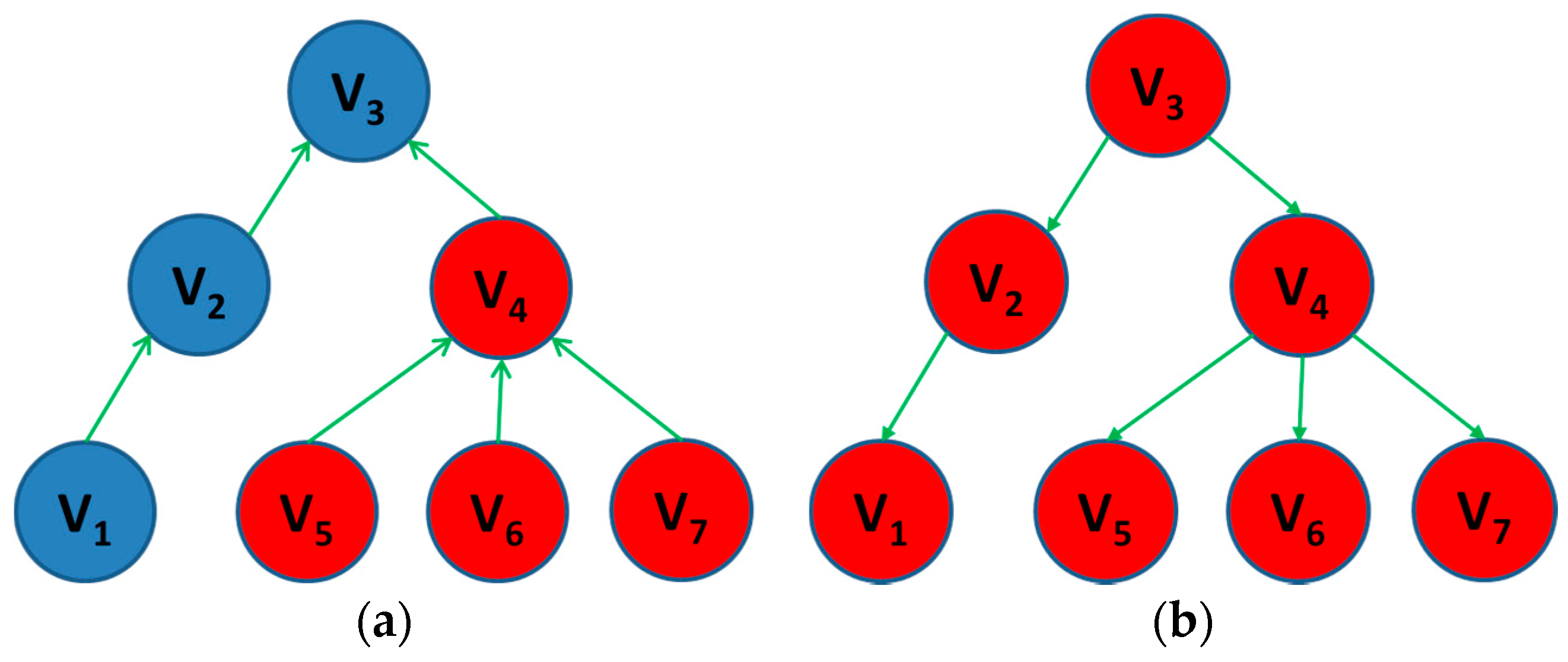
- A subtree is then built for each segment. Then, subtrees are merged based on the order of sorted edges. Segment-Tree Filtering is a variant of the conventional MST approach that considers an extra criterion to merge trees [22,32], as shown in Equation (11):where is the weight of the edge between subtrees and , is the number of vertices in the subtree , and is a constant. In our experiments, is set to five times the standard deviation of all weights in the graph. If criterion (3) is satisfied, subtrees and are merged. Criterion (3) establishes a trade-off between the edge weights and the numbers of pixels in the subtrees. Initially, merging subtrees is easy because the number of pixels in each subtree is small. As the number of pixels increases, the criterion becomes increasingly rigorous; therefore, it is adaptive.
- All the remaining edges that are not part of any subtree are sorted again. If the number of vertices in a subtree is smaller than a threshold , then the subtrees should be merged. In our experiment, . This processing step is based on the improvement presented in [23] to omit small fractions caused by noise. The obtained subtrees are illustrated in Figure 4, in which each color represents an obtained subtree. As shown, constructed subtrees can be used to segment HSIs adaptively.
- Finally, subtrees are merged until all vertices are included in the trees. For each tree, all the connected vertices exhibit the highest similarity and are within the shortest possible distance. As shown in Figure 5b, the edges of the final tree minimally cross the boundaries between two regions.
2.4. Segment-Tree Filtering
3. Experiments and Results
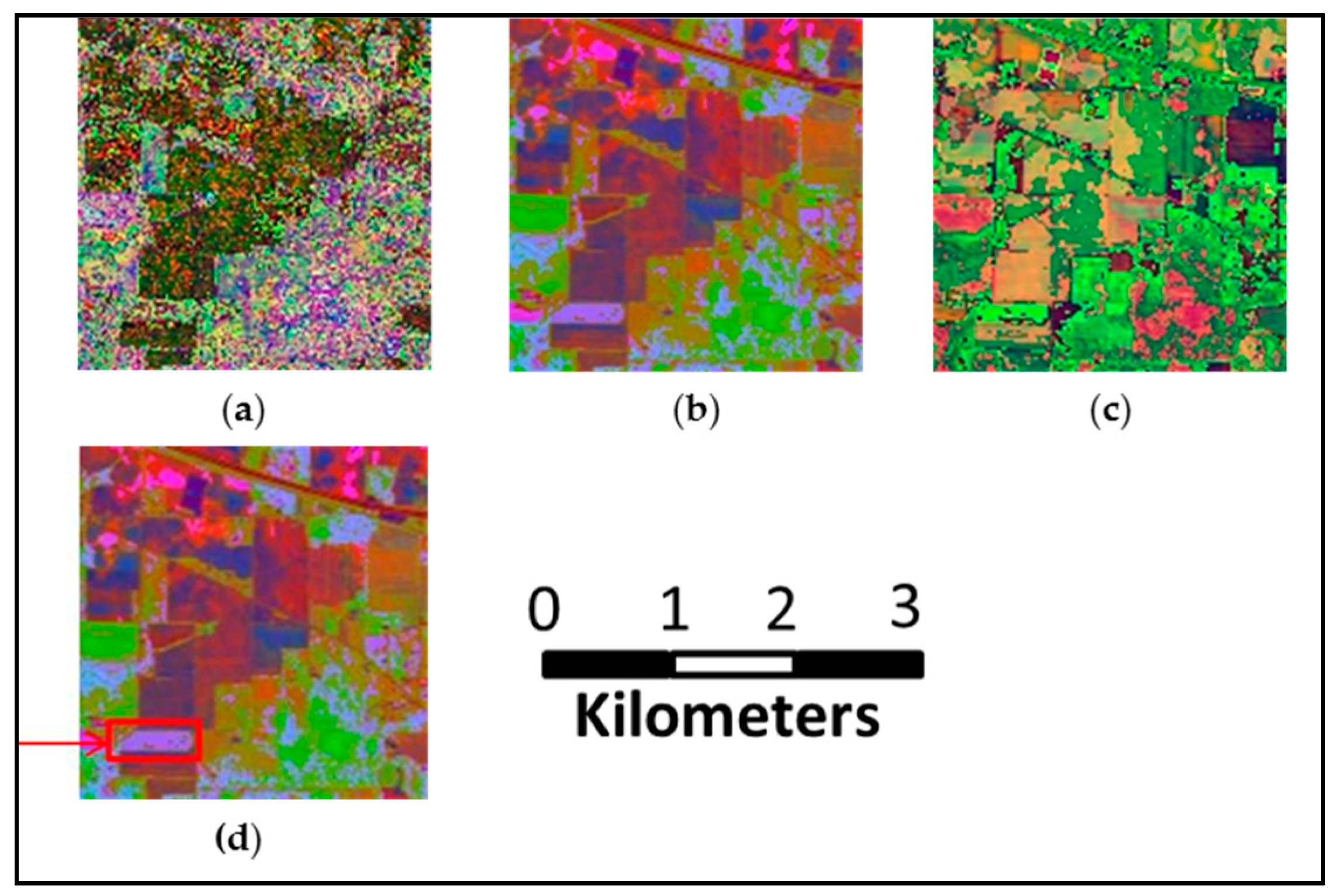
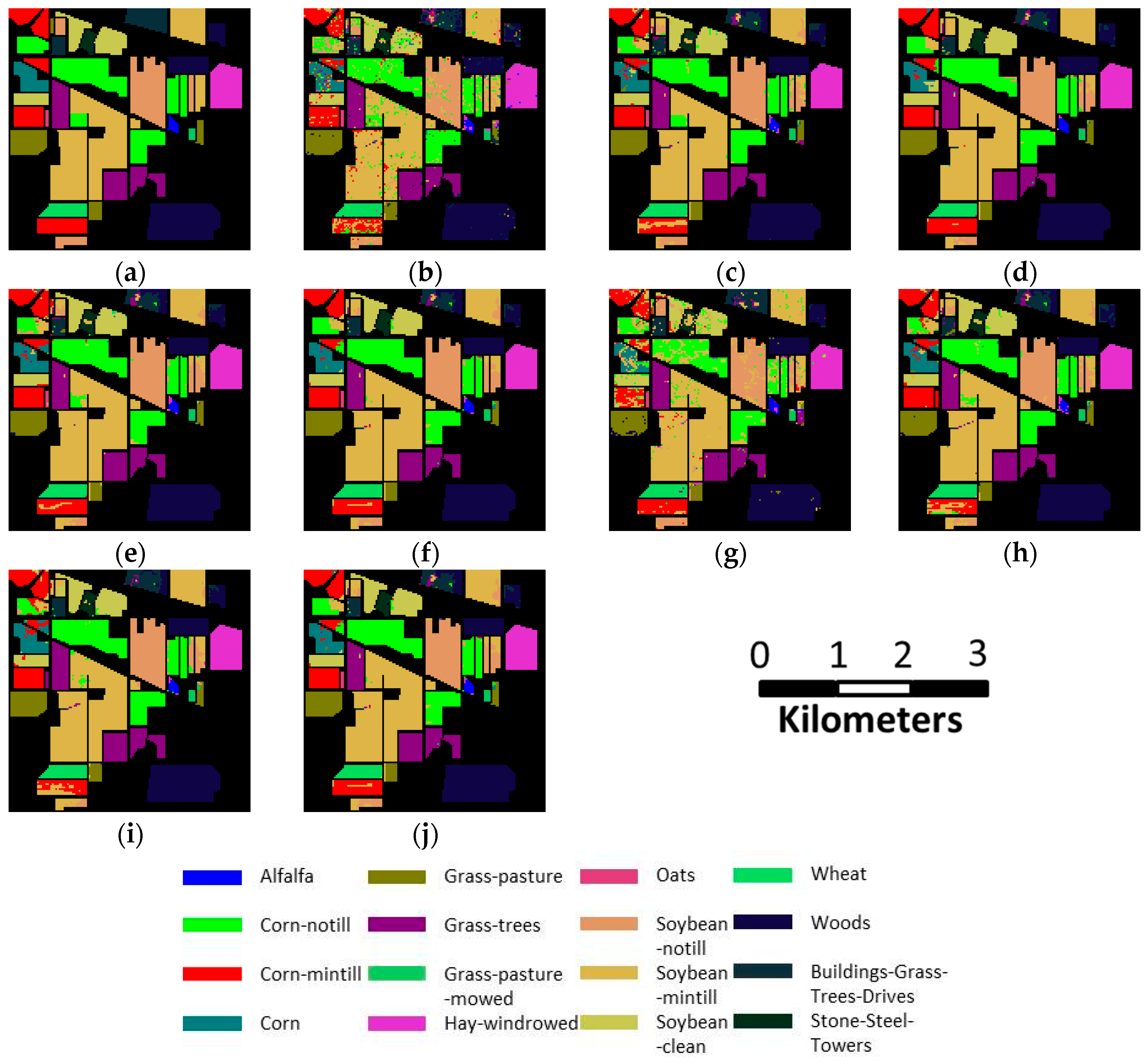
- The first HSI is a 2 × 2 mile portion of agricultural area over the Indian Pines region in Northwest Indiana, which was acquired by NASA’s Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor. This scene with a size of 145 × 145 pixels, comprises 202 spectral bands in the wavelength range from 0.4 to 2.5μm, with spatial resolution of 20 m. The ground truth of scene (see Figure 7a) contains 16 classes of interest and total 10,366 samples. Due to the imbalanced number of available labeled pixels and a large number of mixed pixels per class, this dataset creates a challenge in HSI classification.
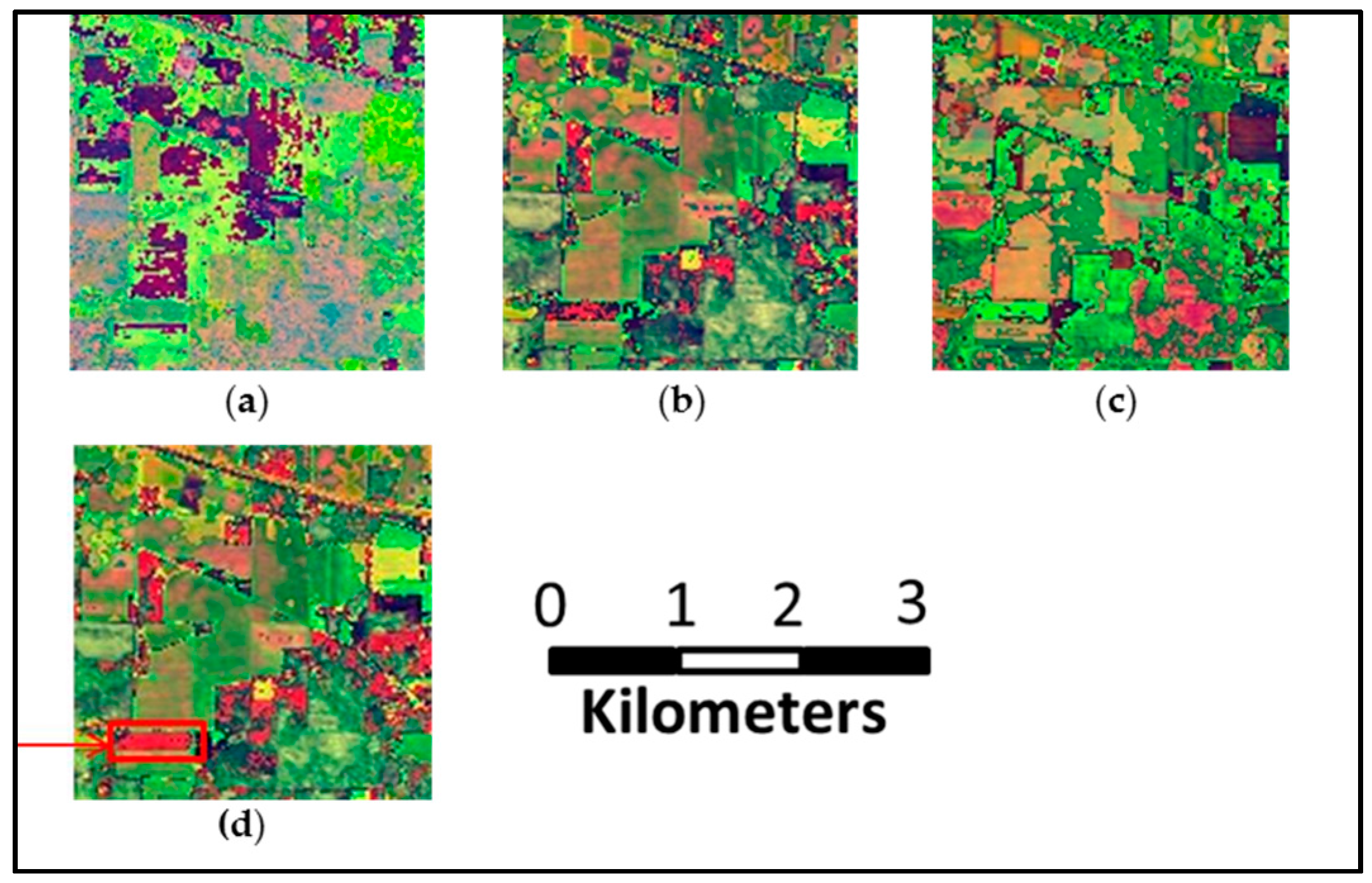
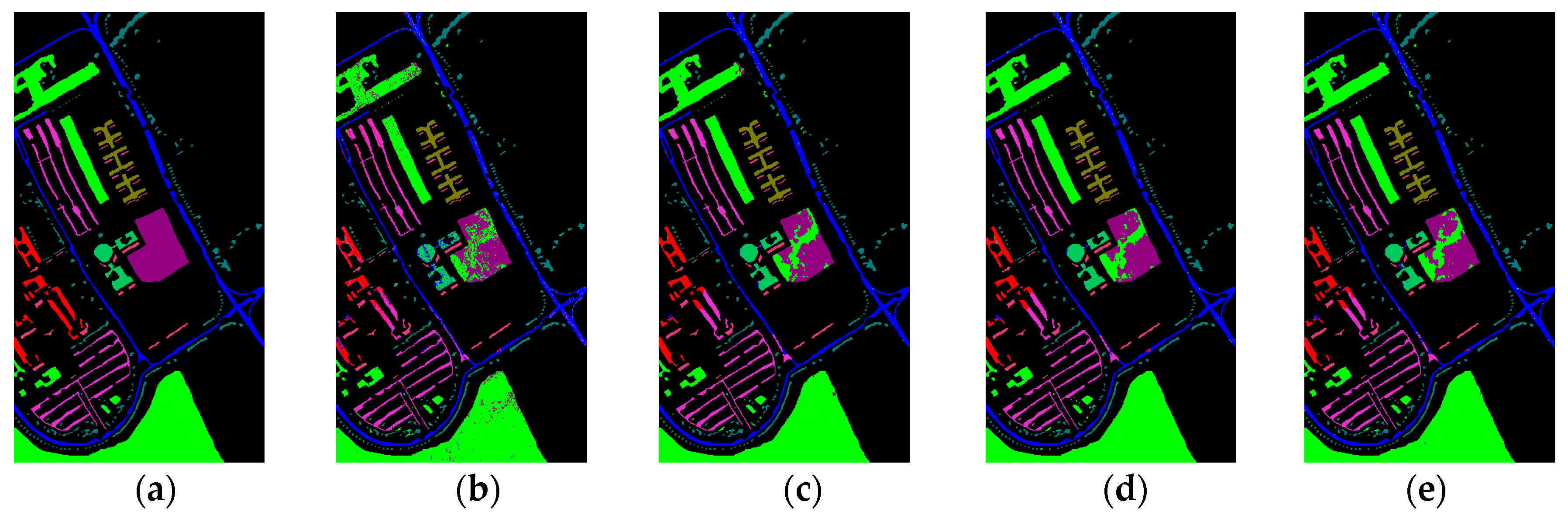
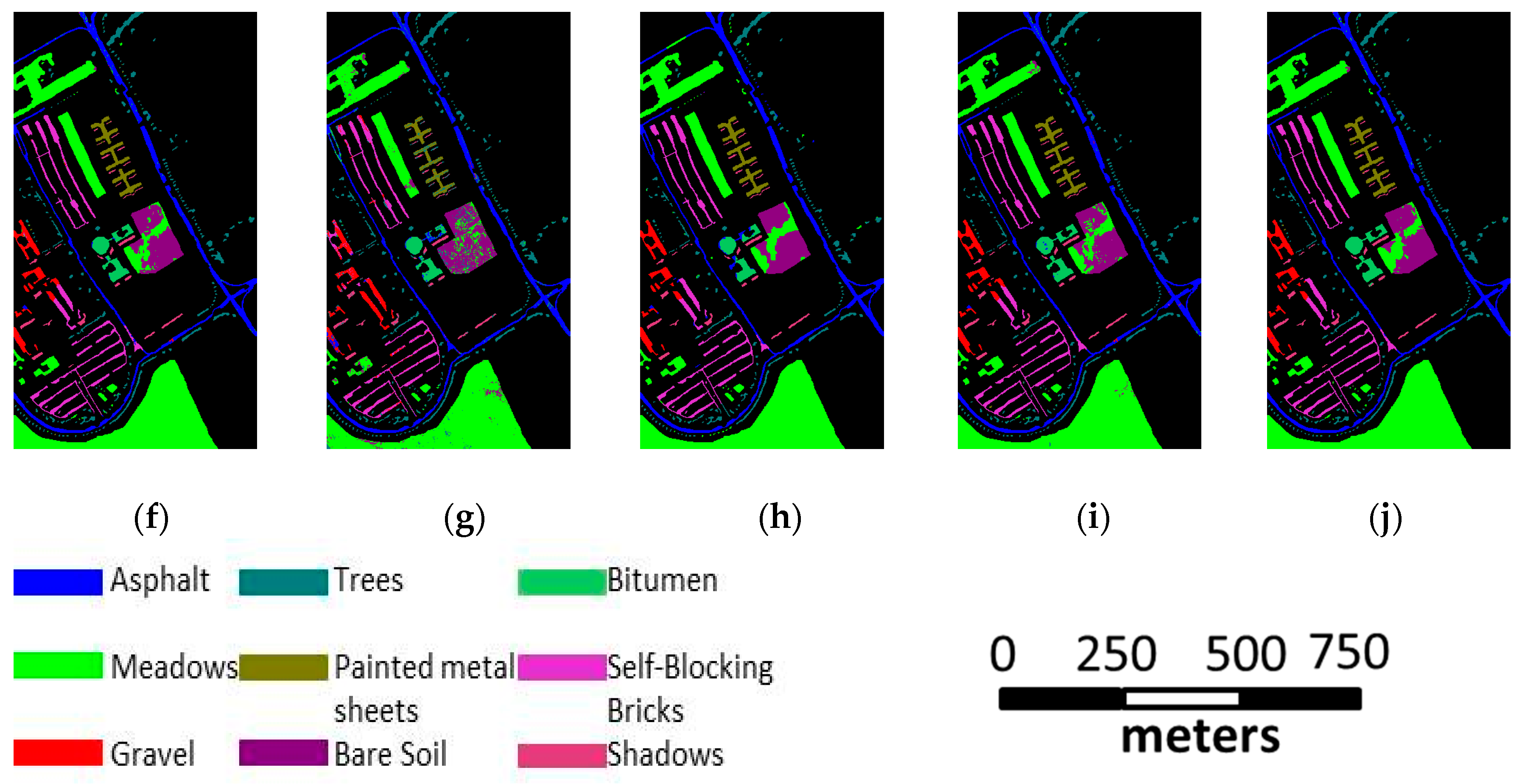
- The second HSI is a 103-band image acquired by Reflective Optics Spectrographic Image System (ROSIS-03) sensor over the urban area of the University of Pavia, Italy. The spatial resolution is 1.3 m and the scene contains 610 × 340 pixels and nine classes. The number of samples is 42,776 in total. The ground truth of the scene is shown in Figure 8a.
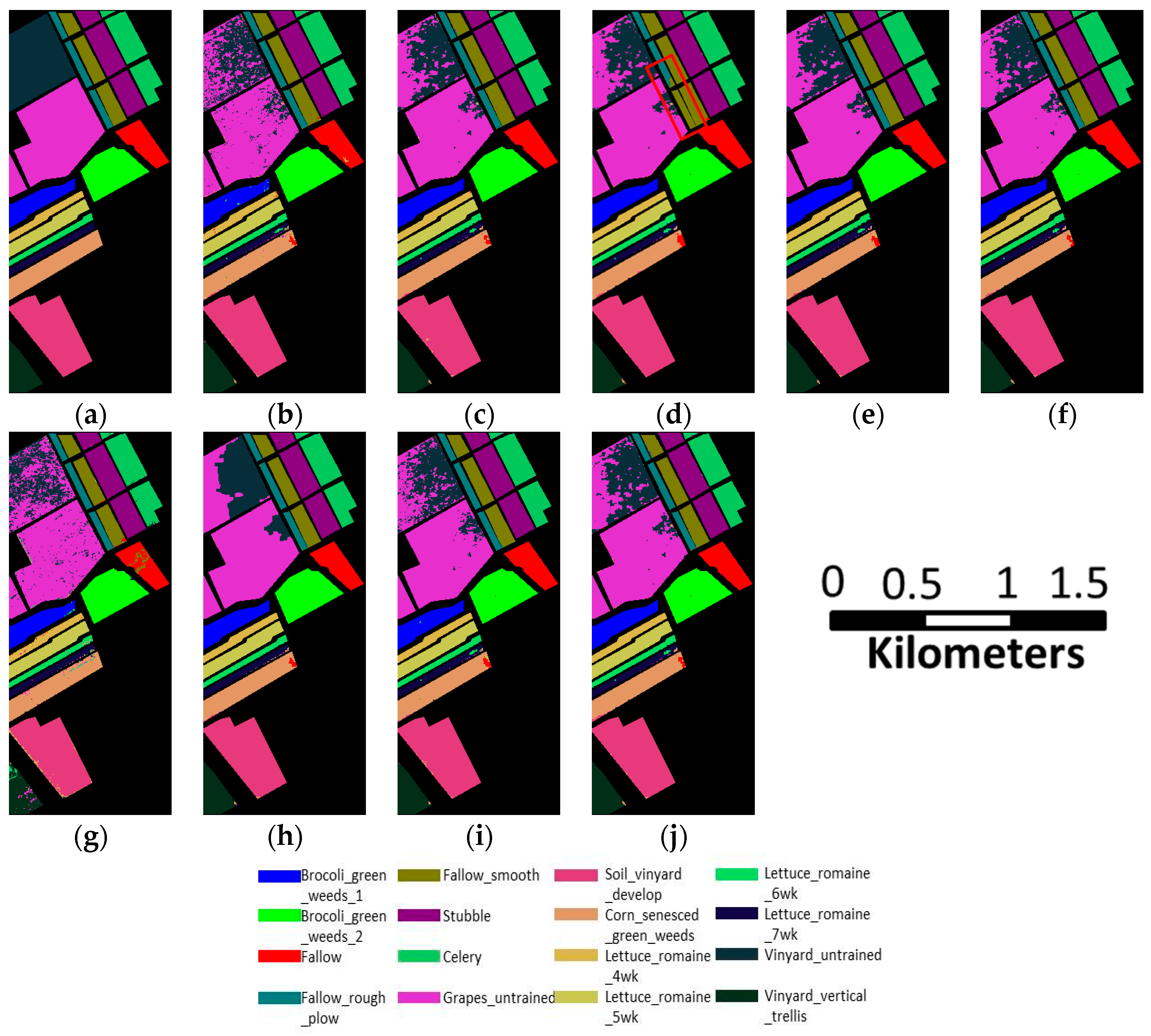
- The third HSI is also derived by AVIRIS sensor over Salinas Valley, California. This scene with a size of 512 × 217 pixels, and 204 spectral bands is used for classification. There are 16 classes in the ground truth image, which is shown in Figure 9a.
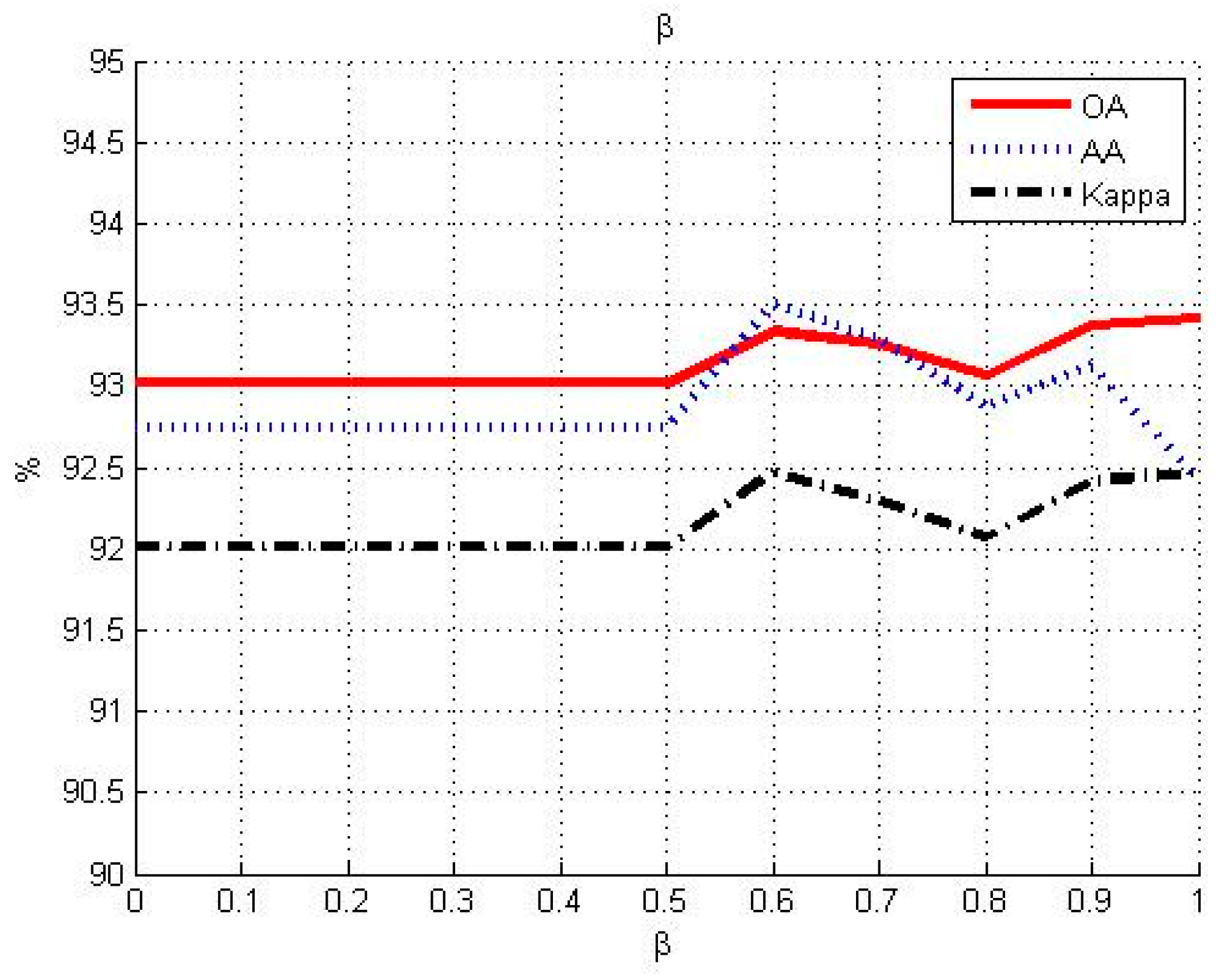
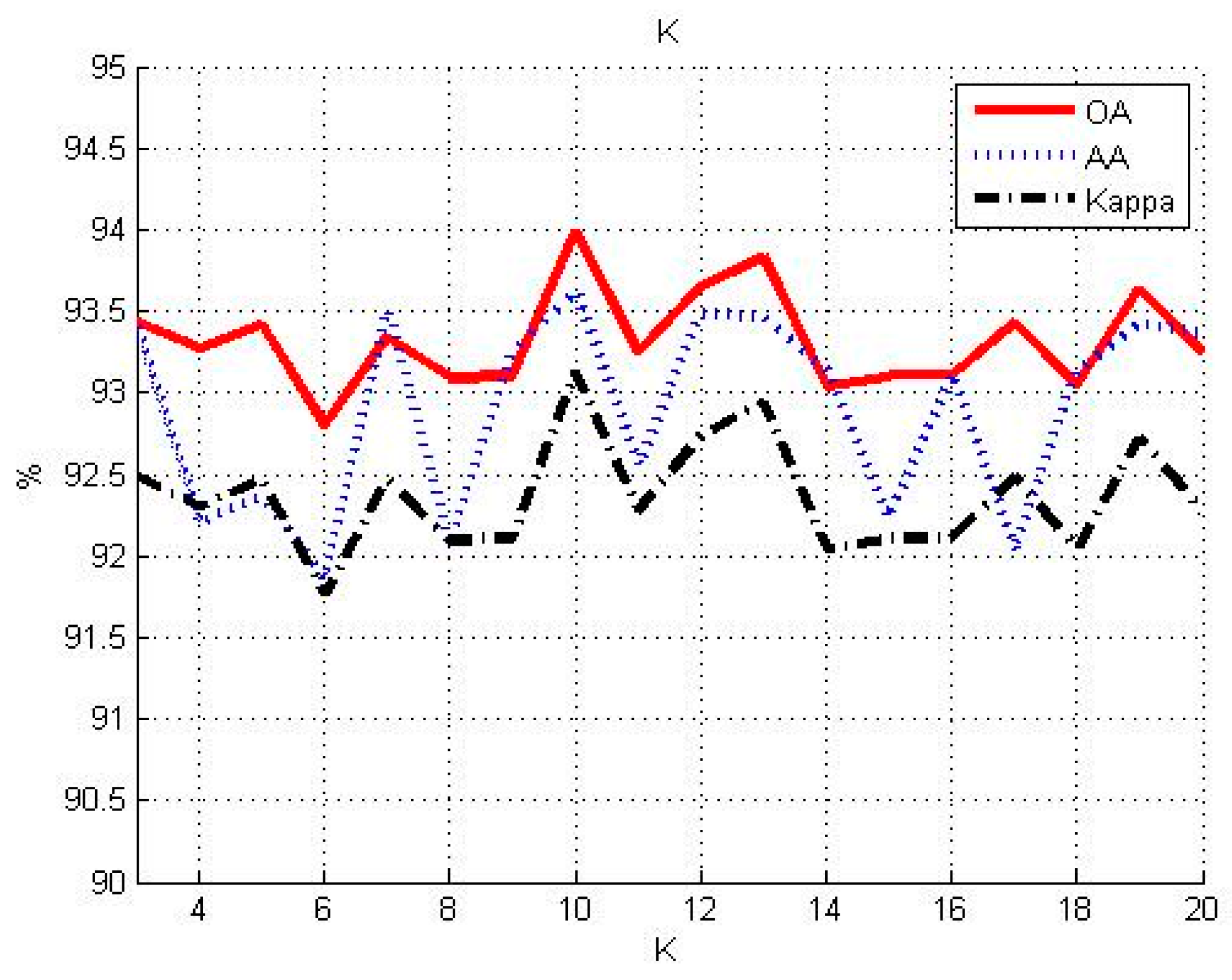
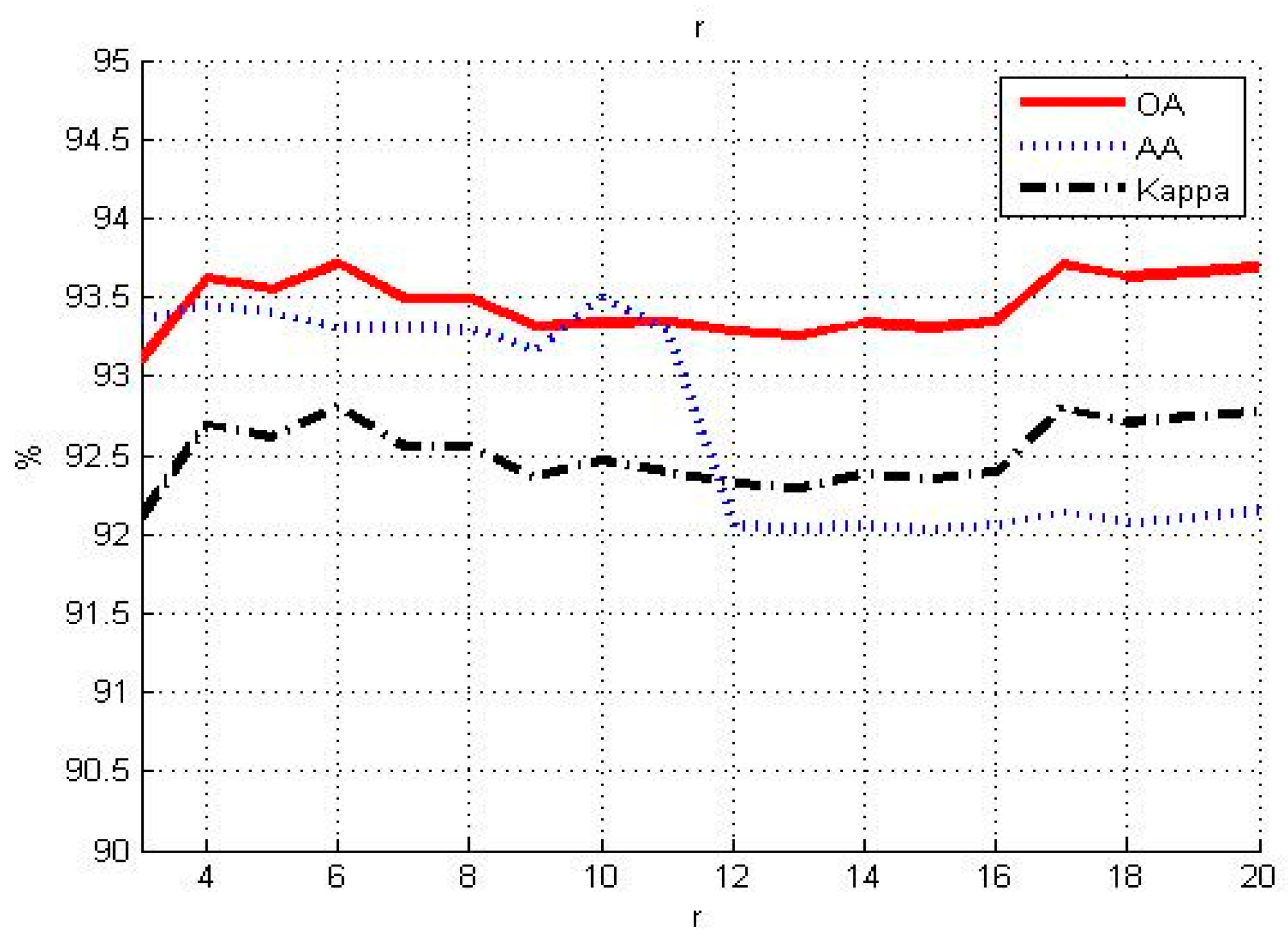
3.1. Influence of Different Parameters
3.2. Classification Accuracy Analysis
3.3. Influences of Different Techniques for Dimensionality Reduction
3.4. Comparison to Other Methods of Spectral-Spatial Classification
- The second approach uses MRFs [6] with Multi-class SVM, which is, to the best of our knowledge, the state of the art method for spatial-spectral image classification based on remote sensing. Multi-class SVM is used as the initial classifier, and the spatial optimization is performed using the max-flow/min-cut algorithms. In our experiment, -expansion is adopted, and the regularization coefficient is fixed to 0.5. The results of the SVM with MRFs are shown in Figure 7h, Figure 8h, and Figure 9h.
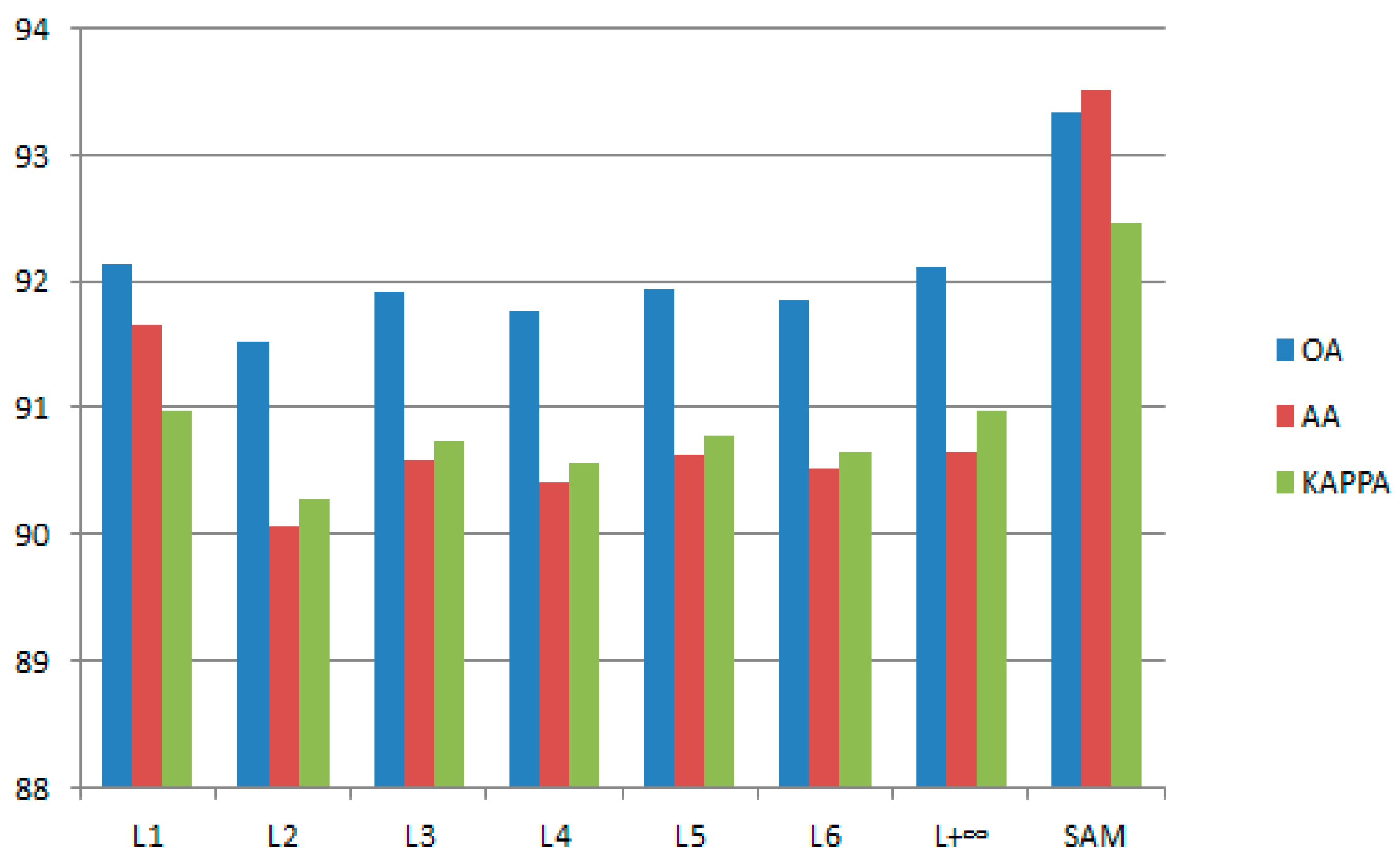
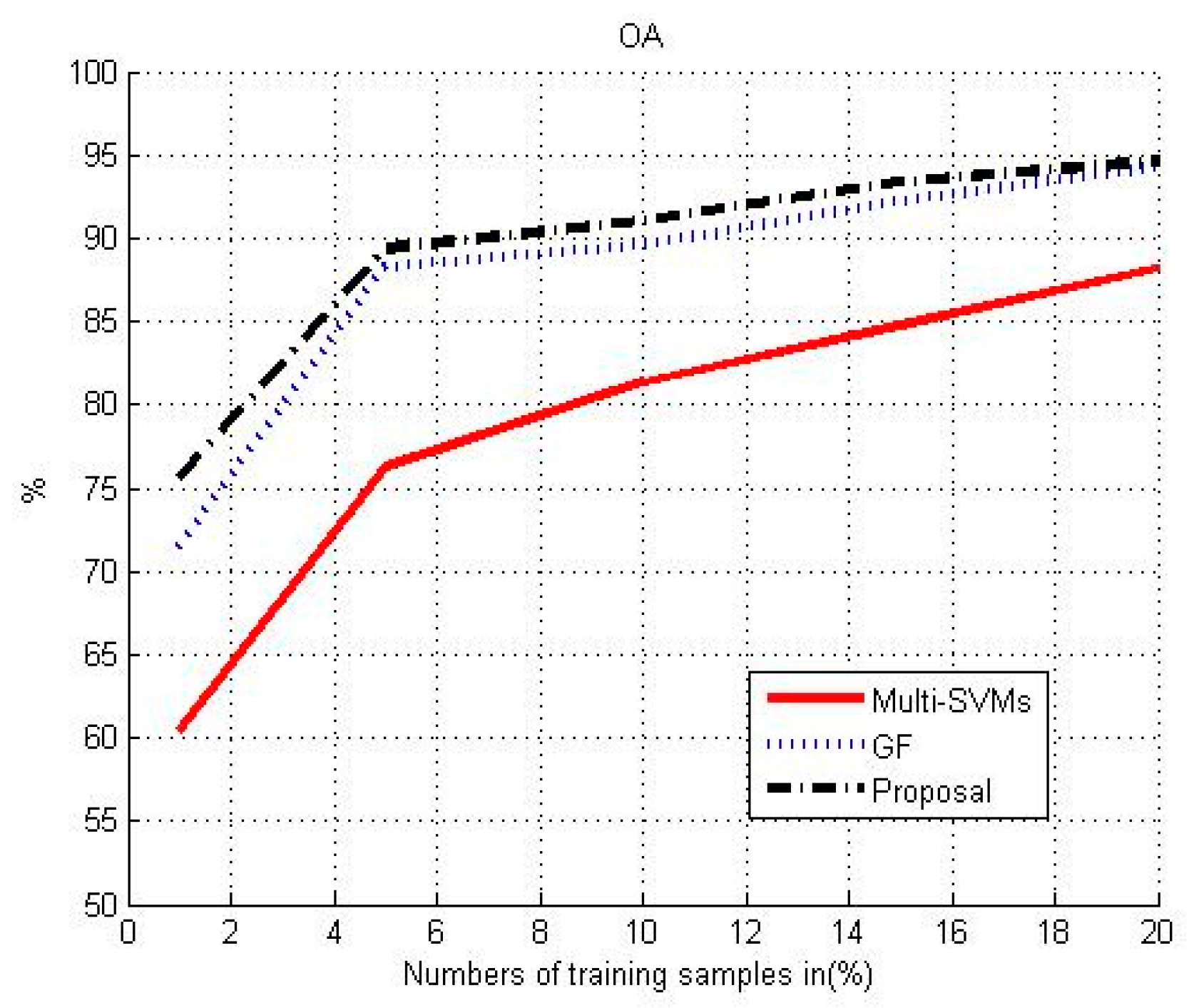
3.5. Effect of the Training Set on Classification
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Böhning, D. Multinomial logistic regression algorithm. Ann. Inst. Stat. Math. 1992, 44, 197–200. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.; Plaza, A. Semi-supervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar]
- Ratle, F.; Camps-Valls, G.; Weston, J. Semi-supervised neural networks for efficient hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2271–2282. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, E. Hyperspectral image classification using Gaussian mixture models and Markov random fields. IEEE Lett. Geosci. Remote Sens. 2014, 11, 153–157. [Google Scholar] [CrossRef]
- Li, J.; Bioucas, M.; Antonio, P. Spectral-spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Boykov, O.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Li, J.; Bioucas, M.; Antonio, P. Spectral-spatial classification of hyperspectral data using loopy belief propagation and active learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Benediktsson, A.; Palmason, A.; Sveinsson, R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Zortea, M.; de Martino, M.; Serpico, S. A SVM Ensemble approach for spectral-contextual classification of optical high spatial resolution imagery. In Proceeding of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Boston, MA, USA, 23–28 July 2007.
- Yuliya, T.; Jocelyn, C.; Jón Atli, B. Segmentation and classification of hyperspectral images using minimum spanning forest grown from automatically selected markers. IEEE Trans. Syst. Man Cybern. B Cybern. 2010, 40, 1267–1279. [Google Scholar] [CrossRef]
- Fu, W.; Li, S.; Fang, L. Spectral-spatial Hyperspectral image classification via superpixel merging and sparse representation. In Proceeding of the IEEE Proceedings on Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015.
- Duan, W.; Li, S.; Fang, L. Spectral-spatial hyperspectral image classification using superpixel and extreme learning machines. In Pattern Recognition, Proceedings the 6th Chinese Conference, Changsha, China, 17–19 November 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 483, pp. 159–167. [Google Scholar] [CrossRef]
- Weihua, S.; David, M. Trilateral filter on multispectral imagery for classification and segmentation. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Benediktsson, A.; Chanussot, J. Spectral-spatial classification of hyperspectral imagery based on partitional clustering techniques. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2973–2987. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W. Classification of hyperspectral images by exploiting spectral-spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6673. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Kang, X.; Li, s.; Jón Atli, B. Spectral-spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Hosni, A.; Rhemann, C.; Bleyer, M.; Rother, C.; Gelautz, M. Fast cost-volume filtering for visual correspondence and beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 504–511. [Google Scholar] [CrossRef] [PubMed]
- Hosni, A.; Rhemann, C.; Bleyer, M.; Gelautz, M. Temporally consistent disparity and optical flow via efficient spatio-temporal filtering. In Proceedings of the 5th Pacific Rim Symposium, Gwangju, Korea, 20–23 November 2011; Springer: Berlin, Germany, 2011; pp. 165–177. [Google Scholar]
- Shutao, L.; Xudong, K.; Jianwen, H. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar] [CrossRef] [PubMed]
- Felzenszwalb, F.; Huttenlocher, P. Efficient graph-based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Mei, X.; Sun, X.; Dong, W.; Wang, H.; Zhang, X. Segment-tree based cost aggregation for stereo matching. In Proceeding of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013.
- Yang, X. A Non-local cost aggregation method for stereo matching. In Proceeding of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012.
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Lin, J.; Wang, Q. Dual clustering based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Sugiyama, M.; Idé, T.; Nakajima, S.; Sese, J. Semi-supervised local Fisher discriminant analysis for dimensionality reduction. Mach. Learn. 2010, 78, 35–61. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Sugiyama, M. Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Huang, T.K.; Weng, R.C.; Lin, C.J. Generalized bradley-terry models and multi-class probability estimates. J. Mach. Learn. Res. 2006, 7, 85–115. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: London, UK, 2005; pp. 170–174. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]



| Class | Training/Test | SVM | ST | PCA + ST | LDA + ST | LFDA + ST | EMP | SVM + MRF | PCA + GF | Proposal |
|---|---|---|---|---|---|---|---|---|---|---|
| Alfalfa | 7/46 | 58.70 | 71.74 | 91.30 | 76.09 | 82.61 | 82.61 | 83.30 | 80.43 | 91.30 |
| Corn-N | 214/1428 | 81.65 | 92.86 | 89.22 | 90.68 | 89.64 | 71.57 | 88.51 | 89.29 | 92.37 |
| Corn-M | 125/830 | 75.90 | 83.25 | 96.51 | 91.81 | 92.65 | 76.99 | 80.84 | 81.20 | 92.16 |
| Corn | 36/237 | 64.56 | 85.23 | 76.79 | 91.56 | 93.67 | 62.87 | 87.34 | 89.87 | 88.61 |
| Grass-Pa | 73/483 | 89.23 | 90.89 | 92.75 | 91.10 | 92.13 | 78.05 | 91.72 | 93.17 | 93.37 |
| GrassT | 109/730 | 96.99 | 99.73 | 99.45 | 99.59 | 99.45 | 98.36 | 99.18 | 100 | 99.73 |
| GrassP | 5/28 | 89.29 | 96.43 | 92.85 | 100 | 96.42 | 89.29 | 96.43 | 96.43 | 96.43 |
| Hay-W | 72/478 | 98.74 | 99.79 | 100 | 100 | 100 | 98.95 | 100 | 100 | 100 |
| Oats | 5/20 | 75.00 | 100 | 100 | 90.00 | 100 | 90.00 | 0.00 | 0.00 | 100 |
| Soy-N | 146/972 | 82.10 | 89.20 | 86.31 | 88.17 | 88.16 | 84.77 | 87.14 | 84.26 | 88.17 |
| Soy-M | 368/2455 | 85.62 | 94.70 | 95.62 | 95.11 | 94.50 | 93.40 | 94.87 | 95.52 | 94.58 |
| Soy-C | 89/593 | 74.20 | 94.77 | 99.66 | 96.46 | 97.64 | 71.16 | 93.76 | 95.45 | 97.98 |
| Wheat | 31/205 | 96.59 | 99.51 | 99.51 | 99.51 | 99.51 | 97.56 | 99.51 | 100 | 99.51 |
| Woods | 190/1265 | 95.42 | 97.23 | 98.50 | 97.94 | 98.26 | 98.26 | 96.60 | 98.66 | 98.10 |
| Building | 58/386 | 61.14 | 59.07 | 60.62 | 58.55 | 60.33 | 85.23 | 62.79 | 76.42 | 64.88 |
| Stone-ST | 14/93 | 87.10 | 87.10 | 98.92 | 87.10 | 98.92 | 60.22 | 88.17 | 94.62 | 98.92 |
| OA | 84.78 | 92.11 | 93.32 | 92.83 | 93.01 | 70.48 | 91.22 | 92.20 | 93.34 | |
| AA | 82.01 | 90.09 | 92.44 | 90.85 | 92.74 | 67.26 | 89.07 | 85.96 | 93.50 | |
| Kappa | 82.60 | 90.97 | 92.47 | 91.80 | 92.00 | 67.28 | 90.11 | 91.08 | 92.47 |
| Class | Training/Test | SVM | ST | PCA + ST | LDA + ST | LFDA + ST | EMP | SVM + MRF | PCA + GF | Proposal |
|---|---|---|---|---|---|---|---|---|---|---|
| Asphalt | 995/6631 | 93.03 | 96.95 | 95.97 | 96.03 | 95.99 | 93.53 | 97.10 | 96.44 | 96.67 |
| Meadows | 2797/18,649 | 95.06 | 99.33 | 99.88 | 99.81 | 99.88 | 95.69 | 100 | 99.18 | 99.79 |
| Gravel | 315/2099 | 66.32 | 72.46 | 71.46 | 72.74 | 71.46 | 76.13 | 69.03 | 73.80 | 71.08 |
| Trees | 460/3064 | 93.05 | 94.65 | 94.39 | 94.09 | 94.45 | 98.63 | 90.31 | 97.03 | 93.79 |
| P-M-S | 202/1345 | 99.70 | 99.55 | 99.78 | 99.63 | 99.78 | 84.31 | 100 | 100 | 99.70 |
| Bare Soil | 754/5029 | 66.65 | 70.33 | 71.01 | 70.01 | 71.12 | 76.89 | 70.87 | 68.50 | 71.30 |
| Bitumen | 200/1330 | 77.21 | 96.99 | 97.07 | 95.78 | 97.74 | 84.81 | 83.38 | 97.22 | 99.92 |
| Self-B B | 552/3682 | 91.55 | 98.37 | 97.99 | 98.09 | 97.83 | 89.19 | 98.29 | 99.76 | 98.80 |
| Shadows | 142/947 | 100 | 98.94 | 96.09 | 91.12 | 96.09 | 77.82 | 98.10 | 100 | 98.32 |
| OA | 89.25 | 93.74 | 93.76 | 93.51 | 93.78 | 90.75 | 93.21 | 93.78 | 93.89 | |
| AA | 86.95 | 91.95 | 91.52 | 90.81 | 91.59 | 86.34 | 89.68 | 92.43 | 92.15 | |
| Kappa | 85.60 | 91.58 | 91.59 | 91.26 | 91.62 | 87.72 | 90.82 | 91.62 | 91.77 |
| Class | Training/Test | SVM | ST | PCA + ST | LDA + ST | LFDA + ST | EMP | SVM + MRF | PCA + GF | Proposal |
|---|---|---|---|---|---|---|---|---|---|---|
| g_w_1 | 301/2009 | 98.80 | 100 | 100 | 100 | 100 | 98.95 | 100 | 99.80 | 100 |
| g_w_2 | 491/3276 | 99.97 | 100 | 99.97 | 100 | 99.97 | 99.68 | 100 | 99.97 | 99.97 |
| Fallow | 296/1976 | 98.68 | 100 | 100 | 99.75 | 100 | 90.13 | 100 | 99.89 | 100 |
| Fallow_r_p | 209/1394 | 99.35 | 98.21 | 60.04 | 99.50 | 98.92 | 99.14 | 99.43 | 100 | 98.92 |
| Fallow_s | 401/2678 | 98.28 | 98.81 | 99.22 | 98.62 | 98.62 | 96.83 | 99.10 | 98.92 | 98.62 |
| Stubble | 593/3959 | 99.97 | 99.92 | 99.90 | 99.97 | 99.87 | 99.75 | 100 | 99.97 | 99.87 |
| Celery | 536/3579 | 99.35 | 99.61 | 99.66 | 99.52 | 99.64 | 98.46 | 99.89 | 99.78 | 99.64 |
| Grapes_u | 1690/11,271 | 92.11 | 95.03 | 95.20 | 95.16 | 95.51 | 95.40 | 94.58 | 95.11 | 95.52 |
| Soil_v_d | 930/6203 | 99.43 | 99.50 | 99.87 | 99.48 | 99.69 | 96.45 | 99.79 | 99.47 | 99.68 |
| C_s_g_w | 491/3278 | 93.62 | 96.06 | 94.63 | 95.18 | 95.79 | 94.97 | 96.86 | 95.73 | 95.64 |
| L_r_4 | 160/1068 | 96.44 | 99.25 | 96.72 | 97.94 | 99.63 | 94.66 | 98.69 | 99.25 | 99.63 |
| L_r_5 | 289/1927 | 99.53 | 100 | 95.69 | 100 | 100 | 99.79 | 100 | 100 | 100 |
| Le_r_6 | 137/916 | 98.03 | 97.82 | 98.25 | 97.49 | 98.14 | 95.09 | 98.25 | 98.80 | 98.14 |
| L_r_7 | 160/1070 | 92.05 | 93.74 | 93.74 | 93.93 | 93.48 | 96.07 | 96.26 | 93.64 | 93.49 |
| V_u | 1090/7268 | 56.89 | 57.33 | 56.70 | 56.84 | 57.75 | 50.30 | 57.04 | 57.66 | 57.85 |
| V_v | 271/1807 | 98.83 | 99.06 | 99.11 | 99.00 | 99.06 | 89.60 | 99.39 | 99.45 | 99.06 |
| OA | 91.56 | 92.59 | 91.35 | 92.49 | 92.77 | 90.32 | 92.76 | 92.72 | 92.78 | |
| AA | 95.08 | 95.89 | 93.05 | 95.77 | 96.00 | 93.45 | 96.17 | 96.09 | 96.00 | |
| Kappa | 90.57 | 91.73 | 90.33 | 91.60 | 91.91 | 89.17 | 91.92 | 91.85 | 91.92 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, C.; Chen, J.; Ma, J. Refinement of Hyperspectral Image Classification with Segment-Tree Filtering. Remote Sens. 2017, 9, 69. https://doi.org/10.3390/rs9010069
Li L, Wang C, Chen J, Ma J. Refinement of Hyperspectral Image Classification with Segment-Tree Filtering. Remote Sensing. 2017; 9(1):69. https://doi.org/10.3390/rs9010069
Chicago/Turabian StyleLi, Lu, Chengyi Wang, Jingbo Chen, and Jianglin Ma. 2017. "Refinement of Hyperspectral Image Classification with Segment-Tree Filtering" Remote Sensing 9, no. 1: 69. https://doi.org/10.3390/rs9010069
APA StyleLi, L., Wang, C., Chen, J., & Ma, J. (2017). Refinement of Hyperspectral Image Classification with Segment-Tree Filtering. Remote Sensing, 9(1), 69. https://doi.org/10.3390/rs9010069