Abstract
P-band radar remote sensing applied during the Airborne Microwave Observatory of Subcanopy and Subsurface (AirMOSS) mission has shown great potential for estimation of root zone soil moisture. When retrieving the soil moisture profile (SMP) from P-band radar observations, a mathematical function describing the vertical moisture distribution is required. Because only a limited number of observations are available, the number of free parameters of the mathematical model must not exceed the number of observed data. For this reason, an empirical quadratic function (second order polynomial) is currently applied in the AirMOSS inversion algorithm to retrieve the SMP. The three free parameters of the polynomial are retrieved for each AirMOSS pixel using three backscatter observations (i.e., one frequency at three polarizations of Horizontal-Horizontal, Vertical-Vertical and Horizontal-Vertical). In this paper, a more realistic, physically-based SMP model containing three free parameters is derived, based on a solution to Richards’ equation for unsaturated flow in soils. Evaluation of the new SMP model based on both numerical simulations and measured data revealed that it exhibits greater flexibility for fitting measured and simulated SMPs than the currently applied polynomial. It is also demonstrated that the new SMP model can be reduced to a second order polynomial at the expense of fitting accuracy.
1. Introduction
Soil moisture is a key state variable that controls all major processes and feedback loops within the climate system. Soil moisture impacts the water and energy cycles and the exchange of trace gases, including carbon dioxide, between land and atmosphere [1]. A number of comprehensive review articles published in recent years [1,2,3,4,5] highlight the crucial importance of spatial and temporal soil moisture information at various scales for virtually all hydrologic, atmospheric, and ecological processes.
Remote sensing (RS) has demonstrated great potential for large-scale monitoring of soil moisture utilizing various frequency bands of the electromagnetic spectrum such as shortwave infrared [6,7], thermal infrared [8,9,10], or microwave radiation [11,12]. Microwave RS techniques have shown greater promise for global monitoring of soil moisture variations [13], because in contrast to thermal and optical RS, they are not impacted by clouds and darkness and there is significant penetration into the soil and overlying vegetation at lower microwave frequencies [11].
Most of the existing microwave sensors operate within the X-band (e.g., AMSR-E; 10.65 and 18.7 GHz), C-band (e.g., AMSR-E; 6.9 GHz, ASCAT; 5.3 GHz), or L-band (e.g., SMOS and SMAP; 1.4 GHz), which only sense surface soil moisture (0–5 cm depth). However, the application of the low frequency P-band (0.42–0.44 GHz) in course of the National Aeronautics and Space Administration (NASA) Airborne Microwave Observatory of Subcanopy and Subsurface (AirMOSS) mission provides an unprecedented sensing depth of about 45 cm to directly retrieve root zone soil moisture under vegetation canopies [14].
The AirMOSS mission seeks to improve the estimates of the North American net ecosystem exchange via flying a P-band synthetic aperture radar (SAR) over nine regions representative of the major North American biomes. The SAR is able to penetrate vegetation and underlying soil to provide high-resolution maps of soil moisture profiles (SMPs). Past AirMOSS flights have covered areas of approximately 100 × 25 km2 with FLUXNET tower sites in regions ranging from boreal forests in Saskatchewan, Canada, to tropical forests in La Selva, Costa Rica. The radar snapshots are used to generate estimates of the SMPs via inversion of scattering models of vegetation overlying soils with variable soil moisture distributions. The retrieved SMPs are in turn assimilated or otherwise applied by hydrologists to estimate land surface model hydrological parameters over the nine biomes, generating a high-resolution time record of root zone soil moisture evolution. These hydrological parameters are ultimately integrated with an ecosystem demography model to predict the respiration and photosynthesis carbon fluxes [14].
When retrieving the soil moisture profile from P-band radar, a mathematical function describing the continuous SMP is required. Because inevitably only a limited number of observations is available, the number of free parameters of the mathematical model must not exceed the number of observed data to ensure unambiguous retrievals. For example, in the current AirMOSS retrieval algorithm a second order polynomial (hereinafter referred to as polynomial) with three free parameters is presumed and parameterized based on three backscatter observations provided by AirMOSS (i.e., one frequency at three polarizations of Horizontal-Horizontal, Vertical-Vertical and Horizontal-Vertical) [14]. To improve the AirMOSS SMP retrieval, we aimed to derive a more realistic and physically-based SMP model via solving Richards’ equation (RE) for unsaturated flow in soils [15] in this study.
Due to the highly nonlinear nature of flow processes in unsaturated soils, analytical solutions to the RE are commonly restricted to simple cases such as a linearized form of the RE [16,17,18] or steady-state Darcian flow [19,20,21,22]. However, these simplified cases rarely meet realistic soil and environmental conditions, where after wetting events (i.e., precipitation or irrigation) the most common flow scenario encompasses drying due to evaporation of water from the soil surface and gravity-driven movement of water to greater depths within the soil profile.
Existing analytical solutions to the RE for the abovementioned process are restricted to simplified cases. For example, solutions introduced by Gardner [23], Novak [24], and Suleiman and Ritchie [25] were obtained by reducing the RE to a diffusion-type partial differential equation neglecting gravity-driven flow. Analytical solutions of Warrick [16] and Teng et al. [26] were obtained by linearization of the RE based on the assumption of exponential saturation-pressure head and linear saturation-hydraulic conductivity relationships, which is rarely met under natural conditions.
Warrick et al. [27] based on the analysis of Broadbridge and White [28] introduced to our best knowledge the only analytical solution to the nonlinear RE for the case of evaporation and concurrent drainage. However, this solution (Equation (26) in [27]) is not applicable for AirMOSS SMP retrieval because it consists of more than three free parameters (considering time as a constant in the solution to fit snapshot observations at any given time).
Based on the hypothesis that a solution to RE with three free parameters is feasible, the objective of this study was to derive a physically-based alternative to the second-order polynomial SMP to advance the AirMOSS root zone soil moisture retrieval algorithm, adding physical significance to the model. In the following, a simple closed-form analytical solution to the nonlinear RE containing three free parameters is introduced. The solution is presented in a general form, without specifying distinct initial and boundary conditions. However, it will be demonstrated that the solution better suits the process of soil drying (i.e., concurrent evaporation and drainage). Theoretical aspects for derivation of the new solution and its validation based on measured and numerically simulated data are presented together with sample AirMOSS SMP retrievals with the modified inversion algorithm.
2. Mathematical Derivations
2.1. Richards’ Equation
The Richards’ equation (RE) [15] combines the Buckingham–Darcy law [29], q = K(∂h/∂z + 1), and the continuity principle, ∂θ/∂t = −∂q/∂z (conservation of mass):
where q [LT−1] is the water flux density, θ [L3L−3] is the soil water content, h [L] is the pressure head (absolute values are considered here for convenience), K [LT−1] is the unsaturated hydraulic conductivity, t [T] is time, and z [L] is soil depth assumed positive downward from the soil surface.
In an unsaturated soil, h and K are functions of θ, which are assumed to be invariant for a given soil, but may distinctly deviate for different soils. Various mathematical models exist for the soil hydraulic h(θ) and K(θ) functions (e.g., [30,31,32]) that are commonly parameterized via least-square fitting to measured h-θ and K-θ data for the soil of interest.
2.2. New Solution to Richards’ Equation
To obtain an analytical solution for Equation (1), the following soil hydraulic functions are assumed [33,34]:
where θs and θr are the saturated and residual volumetric water contents, respectively, Ks is the saturated hydraulic conductivity, P is an empirical parameter related to the soil pore size distribution, and hcM is the effective capillary drive introduced by Morel-Seytoux and Khanji [35]. As shown below in Equation (31), P is related to the van Genuchten parameter m. Assuming P = 1, the RE is reduced to a linearized form for which analytical solutions to various flow processes exist [16,17,18]. However, the assumption P = 1 is rarely met under realistic conditions; most soils exhibit a P significantly larger than 1 [33]. Thus, P is treated as a soil parameter in the following derivations, where the resulting nonlinear RE is solved analytically. Note that the soil hydraulic parameters θs, θr, P, Ks, and hcM are constant for a given soil and do not change with time. Therefore, they should be discerned from the so-called “free parameters”, which vary temporally to fit the SMP at any given time.
For convenience, variables are reduced to the following dimensionless forms:
Substituting Equation (4) to Equation (8) into Equation (1) yields a scaled form of the RE:
with the following scaled soil hydraulic functions:
Combining Equations (9)–(11) yields the scaled RE rearranged based on K*:
Assuming P >> 1 (i.e., 1 − 1/P ≈ 1) as is the case in many natural soils (see Table 1 in [33] as well as Table 1 in this paper), Equation (12) can be approximated as:

Table 1.
Average van Genuchten model parameters for the 12 soil textural classes of the United States Department of Agriculture classification scheme [40] as well as parameters for Equations (2) and (3) calculated with Equations (31) and (32).
To solve Equation (13), the method of separation of variables is applied:
Combining Equations (13) and (14) yields:
Thus, two ordinary differential equations are obtained:
Solutions to Equations (16) and (17) are:
where a1, a2, and a3 are the integral constants. Combining Equations (10), (11), (14), (18) and (19), and denoting the constants b1, b2, and b3, a simple closed-form solution is obtained:
Because AirMOSS observations are temporally not continuous but rather provide snapshots at specific times, time needs to be considered as a constant. This consideration, together with the assumption that θr is negligibly small, allows transformation of Equation (20) to the final SMP solution:
where c1, c2, and c3 are the combined constants or the final free parameters of the RE-based SMP model.
Equation (21) has been obtained without specifying boundary and initial conditions. This, however, should not imply that Equation (21) is applicable for all flow processes because the separation of variables method used to solve the RE only holds for a limited set of boundary and initial conditions. Equation (20) indicates that a given SMP at t = 0 will monotonically decrease with time. Therefore, it is expected that the solution works better for the drying process. Fortunately, soil drying is the most common flow process in nature that occurs after a wetting event (rainfall/irrigation) due to concurrent surface evaporation and internal drainage.
It should be noted that because of the exponential/power form of Equation (21), the derived SMP model is highly sensitive to variations of free model parameters. It can be analytically shown that the sensitivity of θ with respect to c1, c2, and c3 (i.e., ∂θ/∂c1, ∂θ/∂c2, and ∂θ/∂c3) is proportional to θ1−P that yields very large numbers for most cases. Therefore, small changes in c1, c2, and c3 can lead to a significant change of the SMP shape. This means that direct derivation of c1, c2, and c3 through inversion is not as straightforward as proposed in [14], for example, to find the optimum polynomial parameters. We resolve this problem by replacing the free model parameters (c1, c2, and c3) with soil moisture values at three arbitrary depths, θ1(z1), θ2(z2), and θ3(z3). Thereby we capitalize on both the physical significance of the free model parameters and the desirable sensitivity of the SMP, Equation (21), to variations of θ1, θ2, and θ3. Assuming that Equation (21) coincides with these three points, then c1, c2, and c3 can be calculated directly from θ1, θ2, and θ3 as follows:
where
2.3. Second Order Polynomial Approximation
As stated earlier, the parameter P is significantly larger than 1 for most soils. In the following it is demonstrated that the second order polynomial SMP can be derived from the new solution if P = 1, which highlights the limitation of the polynomial SMP when compared to the new solution. At the expense of fitting flexibility, Equation (21) can be simplified with the assumption that P = 1:
A Taylor series expansion yields:
For hcM larger than the maximum depth of interest (i.e., z/hcM < 1), all the terms with orders higher than 2 can be neglected. Hence Equation (26) can be reduced to the second order polynomial presumed in [14]:
Equation (28) implicates that the second order polynomial introduced in [14] based on empirical findings can be approximated based on the physics of unsaturated flow in soils. The accuracy of this approximation is dependent on the SMP shape, which is discussed in the following section.
3. Validation of the Proposed SMP Model
3.1. Numerical Data
To explore the flexibility of Equation (21) to match realistic SMPs, the original RE was solved numerically with the HYDRUS-1D model [36]. HYDRUS-1D is a software package for simulation of water, heat and solute movement in one-dimensional variably saturated porous media. The governing flow and transport equations in HYDRUS are solved numerically with a Galerkin-type linear finite element scheme. In this study HYDRUS was applied to simulate coupled liquid water and water vapor flows to account for the soil moisture vaporization plane recession during the second stage of the drying process [37].
The most common unsaturated flow scenario in nature, evaporation of water from the soil surface, was simulated concurrently with downward water redistribution along the soil profile after a wetting event (rainfall/irrigation). Therefore, free drainage at the bottom boundary (z = 50 cm in the presented simulations) and atmospheric conditions at the top boundary with a potential evaporation rate of 0.5 cm day−1 and atmospheric pressure head of −1000 m were assumed. To simulate the drying process after a wetting event, the initial soil profile was assumed to be saturated from z = 0 to 30 cm and air-dry from z = 30 to 50 cm. Hydraulic properties of three vastly different soil textures including sand, loam and clay were used to parameterize the HYDRUS simulations. The van Genuchten (VG) [30] soil hydraulic functions were applied with HYDRUS default soil hydraulic parameters listed in Table 1:
where α, n, and m are VG model parameters assuming m = 1 − 1/n.
Figure 1 (top row) depicts the HYDRUS simulation results for each of the three textures at three different drying times as well as the best fits of Equation (21). To find the optimum values of P and hcM for each soil (presented in each plot), first an initial guess was made. Then three arbitrary data points, θ1(z1), θ2(z2), and θ3(z3), from the Hydrus simulations were used to calculate c1, c2, and c3 with Equation (22) to Equation (25). Finally, P and hcM were optimized to visually best fit the simulation results.
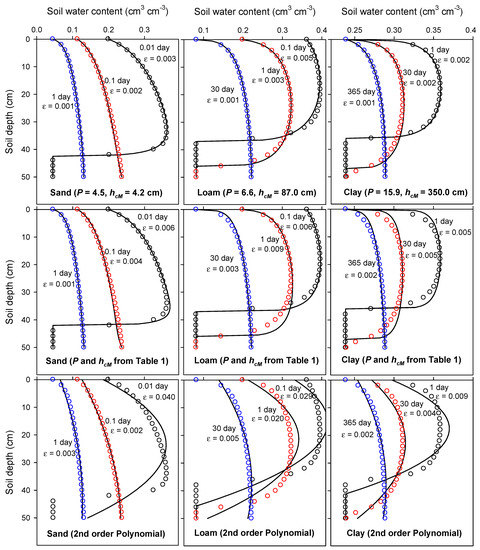
Figure 1.
The best fit of Equation (21) (solid lines) to HYDRUS-1D simulation results (circles) for simultaneous evaporation and drainage in three different soils. The soil parameters in Equation (21), P and hcM, were treated as fitting parameters (top row), taken from Table 1 (middle row), or were set to P = 1 and hcM >> 50 cm leading to the second order polynomial (bottom row). Data below the wetting front were not considered for least square fitting. The fitting accuracy is quantified with the mean absolute error, ε (cm3 cm−3).
Figure 1 (top row) illustrates how well the new SMP solution, Equation (21), fits numerical data. It is apparent that all assumptions that were required to derive the analytical SMP solution (e.g., soil hydraulic functions of Equations (2) and (3)) are suitable when Equation (21) is employed as a fitting curve rather than a predictive tool (e.g., common RE solutions to simulate SMP at different times along a specific initial/boundary value problem).
It should be noted that because the diffusivity function (D = Kdh/dθ) applied for the analytical solution yields zero at zero saturation, soil moisture vanishes at a finite depth termed “wetting front” at which the SMP is characterized by a “shock-type” front [38,39]. This means that the solution is only applicable for the dynamic zone of the profile (i.e., above the wetting front), but not for the dry region below the wetting front. Therefore, data below the wetting front were not considered for fitting. Additionally, it was assumed that the soil water content below the wetting front is the same as that of the wetting front. This assumption is similarly employed in the current AirMOSS algorithm, where soil moisture is assumed to be constant below a certain depth.
The SMP model, Equation (21), includes two soil parameters and three free parameters. Therefore, for application in the AirMOSS algorithm that only allows three free parameters, the soil parameters should be known. Determination of the soil hydraulic parameters (P and hcM) requires measurement of the soil hydraulic functions, which is impractical for large-scale applications. To avoid this complication, the following approximations for P and hcM from VG parameters is proposed:
Equations (31) and (32) were derived from equivalence of Equations (2) and (3) with Equations (29) and (30) such that they yield the same θ* at h = P × hcM and the same K at θ* = 0.5. These equations are introduced here because average VG parameters for various textures are well documented in the literature [40] (Table 1) and they can be approximated with pedotransfer functions from easy-to-measure textural properties (sand, silt and clay percentages) [41]. The calculated parameters P and hcM based on Equations (31) and (32) with VG parameters provided in [40] for the 12 soil textural classes of the United States Department of Agriculture (USDA) classification scheme are listed in Table 1.
Fitting of Equation (21) with values from Table 1 is also depicted in Figure 1 (middle row). It is evident that these values generally lead to a reasonable fit of Equation (21) to numerical data. Nonetheless, the parameters for the clay soil seem to be much higher than the best fitting parameters presented earlier. This is due to the fact that Equations (2) and (3) substantially deviate from the VG functions for clayey soils. Hence, for the two last soils of Table 1 (silty clay and clay) we recommend employing P = 15.9 and hcM = 350 cm (i.e., the optimum values obtained from HYDRUS-1D simulations shown in Figure 1) instead of the values listed in Table 1.
Figure 1 (bottom row) also depicts the polynomial, Equation (28), fitted to the numerical data. It is apparent that the polynomial does not capture numerical data at earlier stages of evaporation well, but it performs reasonably well at later times when the SMP is drier. The primary reason for this loss of fitting accuracy is due to the application of P = 1 and hcM >> 50 cm. Based on the values shown in Table 1, it is unlikely to find a natural soil which meets this condition, since P = 1 corresponds to an extremely coarse-textured soil and large hcM corresponds to a fine-textured soil. This mismatch highlights the advantage of applying the general model, Equation (21), rather than its reduced form, Equation (28), in the AirMOSS algorithm.
The free drainage bottom boundary condition considered in Figure 1 is common in arid and semi-arid environments. In more humid climates, the bottom boundary condition may be different due to the presence of a shallow water table. To evaluate how the model works under such condition, an evaporation process similar to the case presented in Figure 1, but with a shallow water table at z = 1 m was simulated with HYDRUS-1D. A uniformly saturated profile down to the water table was considered at t = 0. The results of this analysis that are depicted in Figure 2 indicate that the obtained SMP in the presence of a shallow water table is generally analogous to the late drying times in Figure 1, but distributed over a wider moisture range in some cases. From this analysis it can be concluded that the new SMP model exhibits sufficient flexibility to deal with varying water table depths that might influence the root zone moisture distribution.
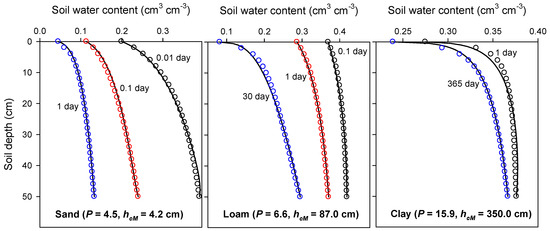
Figure 2.
The best fit of Equation (21) (solid lines) to HYDRUS-1D simulation results (circles) for evaporation in the presence of a shallow water table at z = 1 m for three different soil textures.
Another common flow scenario is water infiltration that occurs after a wetting event (rainfall or irrigation). Since the infiltration process commonly ceases a few hours after the wetting event, the SMPs established due to infiltration are not likely to be observed with RS techniques. Nonetheless, to evaluate the applicability of Equation (21) for soil wetting, a constant-flux (= 1 cm/h) of water infiltration into an initially air-dry loam soil was also simulated with HYDRUS-1D. Figure 3 depicts HYDRUS simulation results together with the best fit of Equation (21).
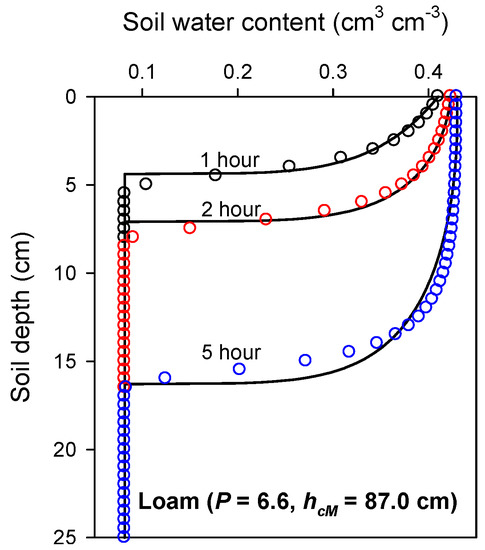
Figure 3.
The best fit of Equation (21) (lines) to HYDRUS-1D simulation results (circles) for a constant-flux (= 1 cm h−1) infiltration process into a loam soil with parameters given in Table 1.
It is evident that a reasonably good fit was achieved with the same soil parameters, P and hcM, as applied for the evaporation process shown in Figure 1 (top row). The small discrepancies are due to the nature of the analytical solution. According to Equation (20), an initial soil moisture profile dries with time if b1, b2 and b3 remain constant. This means that the constants of Equation (20) vary with time in the SMPs depicted in Figure 3. This time-dependency of constants contradicts the underlying assumption of the separation of variables method. Hence, while application of Equation (21) for a wetting process is possible in practice, it is theoretically not justifiable.
3.2. Measured Data
We also evaluated the proposed SMP model with real measurements from the Soil Climate Analysis Network (SCAN) [42]. As a first test case, SCAN site number 2078 in Madison, Alabama, which was also used in Mishra et al. [43] was considered. Mishra et al. [43] found the SCAN data to provide ideal test cases for evaluating fitting capabilities of their proposed SMP model. They indicated that two general shapes of soil moisture profiles are commonly observed in course of the drying process: (i) the “dynamic case”, which is analogous to earlier times of drying shown in Figure 1; and (ii) the “dry case”, which is similar to the late drying times in Figure 1.
Figure 4 compares the fitting capabilities of Equation (21) (new solution) and Equation (28) (polynomial) to measured soil moisture data exhibiting the dynamic case. Since the soil texture of the SCAN site is predominantly silty clay and clay, P = 15.9 and hcM = 350 cm were used for Equation (21). For both Equations (21) and (28), θ values measured at 5, 20 and 50 cm depths were applied for direct calculation of the three free model parameters. It was assumed that below the dynamic zone the water content is uniform and equal to that of the wetting front. It is well documented that at later evaporation stages, a dry zone develops close to the soil surface and the so-called drying front (or vaporization plane) recedes below the surface. In this case, the Buckingham–Darcy law is not applicable for modeling soil water content above the drying front without accounting for the vapor flow contribution, because the pressure head gradient approaches infinity at the drying front [44]. Therefore, it was assumed for Equation (21) that soil water content above the drying front (i.e., where Equation (21) intersects θ = 0) is zero.
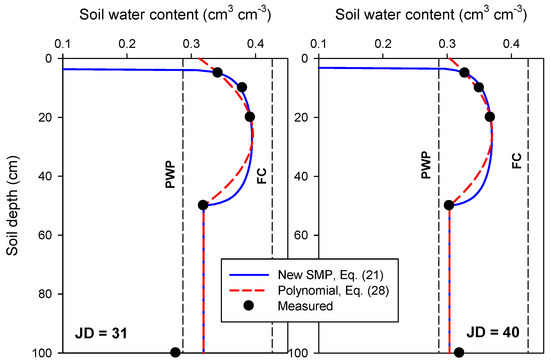
Figure 4.
Comparison of Equations (21) (new solution) and Equation (28) (second order polynomial) with measured soil moisture data from Soil Climate Analysis Network (SCAN) site number 2078 (Madison, Alabama) at Julian days (JD) 31 and 40, 2013. The clay soil parameters, P = 15.9 and hcM = 350 cm, were used in Equation (21). PWP: permanent wilting point; SMP: soil moisture profile.
With these assumptions, both models yielded reasonably good fits (Figure 4). When compared to Equation (21), the polynomial underestimates water content at intermediate depths. Conversely, the polynomial always shows a higher surface water content than Equation (21). It is obvious that there is uncertainty about the surface water content (i.e., θ exactly at z = 0) since there is no surface measurement available (Note: θ at 5 cm was used as one of the fitting points). In any case, the RE yields low values of surface θ in clay soils even at early stages of evaporation (see HYDRUS-1D simulations in Figure 1).
The comparisons for the dry case are shown in Figure 5, where θ values measured at 5, 20 and 100 cm depths were applied for direct calculation of the three free parameters of Equations (21) and (28). It is evident that the polynomial when compared with the RE solution overestimates water content at most depths, especially within the dry zone near the soil surface. Equation (21) predicts formation of a dry layer down to about 3–4 cm. This prediction is plausible, because the water content of the entire profile is close to the permanent wilting point (PWP; i.e., water content at h = −150 m).
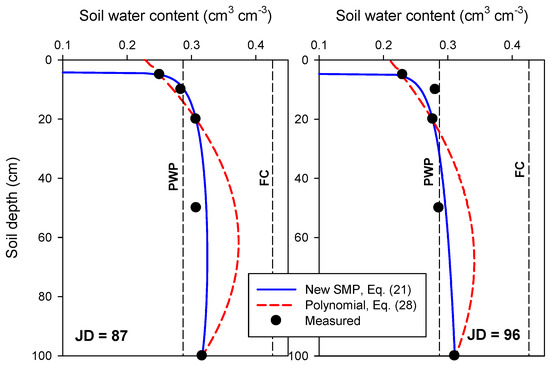
Figure 5.
Comparison of Equations (21), new solution, and Equation (28), second order polynomial, with measured soil moisture data from SCAN site number 2078 (Madison, Alabama) at Julian days (JD) 87 and 96, 2012. The clay soil parameters, P = 15.9 and hcM = 350 cm, were used in Equation (21).
The wetting front locations in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 were determined based on simulated and measured moisture data. However, for AirMOSS applications where in situ moisture measurements are not available for all pixels, determination of the wetting front location would be a challenging task. The AirMOSS radar senses the soil profile down to a depth of about 45 cm, where it may be assumed that no distinct wetting front exists. This assumption simplifies application of Equation (21) in the AirMOSS retrieval algorithm. In order to test the validity of this assumption, soil moisture data from SCAN site number 2026 in the Walnut Gulch watershed in Arizona were investigated. This site located within a USDA Agricultural Research Service (ARS) experimental watershed was selected because it was among the sites applied for AirMOSS evaluation in Tabatabaeenejad et al. [14] and it was also a validation site for other satellite missions (e.g., SMEX04, SMAPVEX15) [45].
To evaluate to what extent Equation (21) can capture SMP seasonal dynamics, biweekly data over one year were used for this analysis. The soil profile at this site is not uniform, consisting of various textures (loam, loamy sand, sandy loam) down to a depth of 1 m. Nonetheless, we evaluated Equation (21) assuming a uniform profile by applying the loam soil parameters, P = 6.6 and hcM = 87 cm. Equation (21) was visually fitted to measured data via varying θ1(z1), θ2(z2), and θ3(z3) in Equations (22)–(24).
The results depicted in Figure 6 verify that the wetting front is rarely located within the top 45 cm of the soil profile; hence, Equation (21) can be continuously used in the AirMOSS retrieval algorithm without truncation. Figure 6 also indicates that Equation (21) is able to adequately capture seasonal SMP dynamics, even with roughly approximated soil parameters for the heterogeneous soil profile. The estimated profiles could certainly be different from reality due to the lack of observations at the surface (z = 0) or missing information about the exact location of the wetting front. Nonetheless, the estimated dynamics are consistent with common observations (e.g., Figure 1) showing a similar pattern for damping the wetted zone formed after a wetting event (e.g., at Julian days, JD, of 32 and 214) over time. It is worth mentioning that the observation gaps can be potentially closed with a hydrological model calibrated with in situ soil moisture data, as for example demonstrated in Coopersmith et al. [46] for 160 SCAN sites distributed throughout the US.
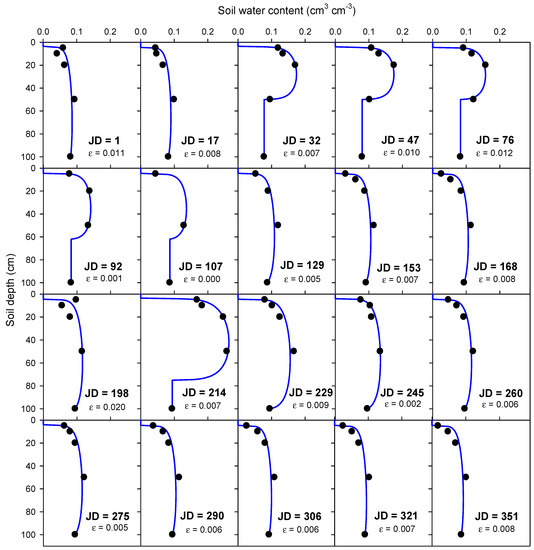
Figure 6.
The best fit of Equation (21) (lines) to measured soil moisture data (dots) from SCAN site number 2026 (Walnut Gulch, Arizona) at various dates during 2010. The loam soil parameters, P = 6.6 and hcM = 87 cm, were used for fitting Equation (21). The fitting accuracy is quantified with the mean absolute error, ε (cm3 cm−3).
4. AirMOSS Retrieval Algorithm
4.1. Background
To model the scattering of electromagnetic waves from a forested scene, AirMOSS used a discrete radar scattering model assuming a single-species forest with horizontal homogeneity within a radar pixel while allowing vertical heterogeneity by introducing a trunk layer and a canopy layer [47,48]. The trunk layer is represented by nearly vertical dielectric cylinders. The canopy layer contains randomly distributed large and small dielectric cylinders representing large and small branches. The canopy layer also contains leaves, which are randomly but uniformly distributed in the layer. Leaves are represented by disks or cylinders depending on the type of the forest (deciduous or coniferous). According to Equation (1) of Tabatabaeenejad et al. [14], the radar model calculates the total backscattered power as the sum of the powers from several contributing scatters; (1) scattering from crown layer; (2) scattering from trunks; (3) double-bounce scattering between crown layer and ground; (4) double-bounce scattering between trunks and ground; and (5) backscattering from the ground. The ground is modeled as a layer of homogenous soil. Figure 5 in Tabatabaeenejad et al. [14] shows the forest geometry. Interested readers are referred to Tabatabaeenejad et al. [14] for more details of the forward model.
In the AirMOSS retrieval algorithm, the SMP is assumed to be the only unknown, and all other parameters (i.e., soil texture, vegetation parameters, and structural information) are considered as known [14]. The SMP is retrieved from estimation of the free parameters a, b and c in Equation (28). A “simulated annealing” algorithm based on the work of Corana et al. [49] is used to minimize a cost function that is based on the difference between measured and calculated backscattering coefficients. Simulated annealing is a powerful global optimization technique that is capable of finding the global minimum hidden among many local minima and is insensitive to the initial guess of the free parameters [14]. At each iteration of a, b, and c in the inversion algorithm, soil moisture is calculated at all depths with Equation (28). Then the dielectric constant at each soil depth is calculated as a function of its moisture content, and finally the backscattering coefficient is calculated for each set of a, b and c coefficients. The optimum parameter set that minimizes the difference between measured and calculated backscattering coefficients is selected to yield the retrieved SMP from Equation (28).
The P-band retrieval algorithm of AirMOSS currently uses only the Horizontal-Horizontal and Vertical-Vertical channels due to calibration inaccuracy of the Horizontal-Vertical channel. Therefore, the corresponding inverse problem is ill-posed as three free parameters are retrieved with only two data points. Some regularization is thus necessary to overcome the effect of the ill-posedness. The method applied by Tabatabaeenejad et al. [14] is based on defining upper and lower bounds for each free parameter according to available in situ soil moisture data at each AirMOSS site. Considering the polynomial assumption, in situ measured soil moisture profiles at each site are fitted with a quadratic function and the free parameters are observed throughout the year. An upper and lower bound is empirically selected for each flight date based on the behavior of the free parameters within the time period encompassing the flight date. In addition to mathematical inaccuracies in the forward and inverse models, the physics of the problem (i.e., penetration depth of the electromagnetic waves) also imposes a limitation on retrieval accuracy. AirMOSS has assumed a validation depth of up to 45 cm in its retrieval algorithm. This depth makes the soil homogeneity assumption (underlying the new solution) valid should the presented new RE solution be used for similar future retrievals [14].
4.2. Considerations Regarding the New Model Application
When employing the new solution, Equation (21), in the AirMOSS algorithm, θ1, θ2 and θ3 at three arbitrary depths (z1, z2 and z3) are optimized instead of a, b and c. Therefore, the problem of finding the upper and lower bounds is more straightforward because of the physical meaning of θ1, θ2 and θ3 from which free parameters of Equation (21) can be directly calculated with Equations (22)–(24).
As discussed earlier, Equation (21) does not hold for any general initial and boundary conditions. Therefore, it may fail to fit some special SMPs occurring in nature. To better understand this point, three most likely arrangements of θ1, θ2 and θ3 shown in Figure 7 are discussed below.
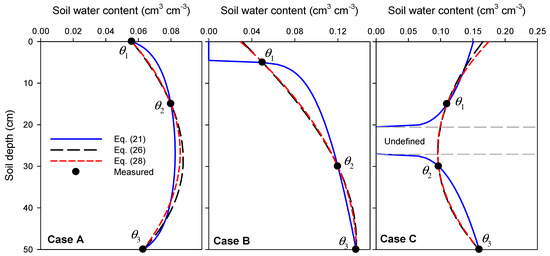
Figure 7.
Three possible arrangements of θ1, θ2 and θ3 (model parameters) throughout the drying process. Data were extracted from Figure 13a in Tabatabaeenejad et al. [14]; profile 2 (case A), profile 6 (case B) and profile 4 (case C). Values of P = 6.6 and hcM = 87 cm were assumed.
Case A is similar to early drying times for which θ2 > θ1 and θ3. Equation (21) is always valid for this case. Case B is similar to later drying times for which θ3 > θ2 > θ1. Equation (21) is valid for this case, unless θ3 is larger than a critical value θc. The critical value can be approximated with Equation (33) that ensures validity of Equation (21) in most cases:
The constraint of θ3 < θc is necessary for inversion from a mathematical point of view, although the condition θ3 > θc is rarely observed in natural settings. Therefore, the new solution can be easily applied to the profiles of cases A and B. These two cases can be merged into a single case when the two constraints of θ1 < θ2 and θ3 < θc are satisfied.
Case C for which θ2 < θ1 and θ3, however, cannot be predicted with Equation (21), as θ is undefined within part of the profile where c1z + c2 exp (z/hcM) + c3 is negative. For such a case, it is suggested to release the two constraints for cases A and B and rather assume P = 1 in order to replace Equation (21) with Equation (26), which is approximately the same as the polynomial, Equation (28), as indicated in Figure 7.
4.3. Preliminary Inversion Results
As a preliminary test of the new solution, we present sample inversion results from two AirMOSS flights; one flight over the Metolius site in Oregon on 21 August 2015 and one over the Boreal Ecosystem Research and Monitoring Site (BERMS) in Saskatchewan, Canada, on 28 September 2015 (for detailed information about AirMOSS flights, readers are referred to [50]). We observed that the behavior of one of the installed probes at each site could be categorized as case A or B for at least a 50-day period encompassing the flight dates. The AirMOSS observations for each site consisted of several hundred thousand pixels. However, in this preliminary analysis, we only inverted one pixel for each site for which in situ soil moisture measurements were available. Thus “Metolius pixel” and “BERMS pixel” in the following refer to the one inverted pixel at the respective sites.
As mentioned earlier, soil texture is considered as known information in the AirMOSS retrieval algorithm. Tabatabaeenejad et al. [14] used the Soil Survey Geographic (SSURGO) database to assign soil texture to each pixel. Hence, the additional soil parameters included in the new model, P and hcM, did not require extra information as they were directly estimated from soil texture (Table 1). The Metolius pixel exhibits a loamy sand soil with P = 5.52 and hcM = 2.94 cm, and the BERMS pixel a sandy loam soil with P = 6.73 and hcM = 5.70 cm.
We applied the inverse algorithm for the radar data for these two flights and compared the retrieval errors with those obtained from the current AirMOSS algorithm that is based on the polynomial function assumption (Figure 8). The depths z1, z2, and z3 have been chosen to coincide with 0, 20, and 45 cm. The applied inversion parameters are identical to the ones that had been previously used for these sites with the polynomial function assumption. The lower bounds for the unknowns, namely θ1, θ2 and θ3, are 0.01, 0.05, and 0.01 m3/m3, respectively, for both sites. Upper bounds for the unknowns are 0.10, 0.15, and 0.1 m3/m3, respectively, for both sites. These bounds were chosen based on in situ soil moisture data.
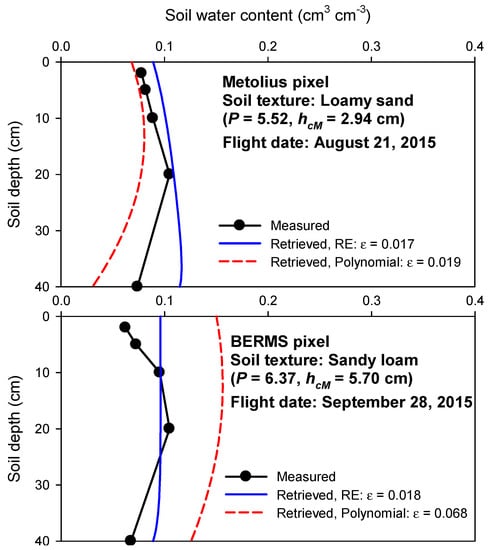
Figure 8.
AirMOSS retrieved soil moisture profiles using the new solution (RE) and second order polynomial for two flights over Metolius on 21 August 2015 and over BERMS on 28 September 2015. The inversion accuracy is quantified with the mean absolute error, ε (cm3 cm−3). BERMS: Boreal Ecosystem Research and Monitoring Site; RE: Richards’ equation.
As shown in Figure 8, the retrieval errors decreased, especially in the BERMS pixel, when representing the soil moisture profile with the new RE solution. The computational inversion time also decreased by about 20% for both cases. Nonetheless, the retrieved SMPs do not well resemble the measured SMPs. In addition to the retrieval errors (due to the scattering model, SMP model, etc.), soil heterogeneity could also affect the results, where point-scale measurements (in situ data) are compared with pixel-scale estimates with the resolution of 3 arcsec (~100 m).
Unless an extensive error comparison for several AirMOSS sites and several dates is performed, it is not possible to firmly claim that the error reduction (Figure 8) and computational time savings hold for all cases. However, for these two specific cases, we believe the error reduction can be attributed to two factors. Firstly, as discussed earlier, the sensitivity of the SMP function to variations of θ1, θ2 and θ3 is lower than the sensitivity of the polynomial to variations of a, b and c, which are in fact a special case of c1, c2 and c3. Secondly, the unknowns of the new solution are physical parameters. Therefore, the corresponding lower and upper bounds could be deduced with more confidence from in situ data when compared to the second order polynomial. Note that large dynamic ranges of the unknowns would result in inaccurate SMP retrievals, due to the limited length of the Markov chain in the simulated annealing method, discussed in [14], and the ill-posedness of the problem.
We acknowledge that this method has its own limitations when compared to the current AirMOSS method. One limitation is the requirement of a priori information about the SMP shape (i.e., whether it is case C or not). When there is no a priori information about the SMP shape (e.g., in situ observations), a possible solution to this limitation would be first to assume that the profile shape satisfies cases A or B, thus holding the required constraints (i.e., θ1 < θ2 and θ3 < θc). For the case that the error between measured and calculated backscattering coefficients cannot be satisfactorily minimized with these constrains, case C can then be assumed (i.e., P = 1).
These preliminary observations warrant an extensive study about the applicability and performance of this method for other AirMOSS sites and other flight dates, which is part of ongoing research.
5. Conclusions
Equation (21), a closed-form analytical solution to Richards’ equation, is proposed as an alternative to the second order polynomial that is currently employed in the Airborne Microwave Observatory of Subcanopy and Subsurface (AirMOSS) root zone soil moisture retrieval algorithm. It has been demonstrated that the second order polynomial is a special case of Equation (21) limited to P = 1. Evaluation of Equation (21) based on both numerical simulations and measured data revealed that it exhibits greater flexibility than the currently applied second order polynomial. Therefore, application of Equation (21) is recommended for more accurate retrieval of root zone moisture profiles from P-band radar remote sensing data. The results presented for two AirMOSS flights in 2015 demonstrate a reduction of the retrieval error with the new method. In conclusion, it should be noted that while the retrieval error and computational inversion time have improved for the two presented cases, a more extensive study is required to investigate the applicability, performance, and advantages of this method for AirMOSS root zone soil moisture retrievals.
Acknowledgments
We acknowledge funding from the National Science Foundation (NSF) grant No. 1521469 awarded to Utah State University and to the University of Arizona. Support of the National Aeronautics and Space Administration (NASA) AirMOSS EVS-1 mission under a contract to the University of Southern California is also gratefully acknowledged. Additional support was provided by the Utah Agricultural Experiment Station, Utah State University, Logan, Utah 84322-4810, approved as UAES journal paper No. 8888.
Author Contributions
M.S. derived the new analytical solution to RE and contributed to writing. S.B.J. and M.T. designed test cases, assisted with HYDRUS-1D simulations, and contributed to writing. M.M. and A.T. worked on the adaptation of the AirMOSS inversion algorithm for the new RE solution, tested the modified algorithm for two AirMOSS flights, and contributed to writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurements for ecological and hydrological watershed scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.; Cuenca, R.; Dorigo, W.; Draper, C.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Small, E.E.; Zreda, M. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Güntner, A.; Hübner, C.; Kusche, J.; Jonard, F.; Vey, S.; Vereecken, H. Emerging methods for noninvasive sensing of soil moisture dynamics from field to catchment scale: A review. Adv. Rev. 2015, 2, 635–647. [Google Scholar] [CrossRef]
- Whiting, M.L.; Li, L.; Ustin, S.L. Predicting water content using Gaussian model on soil spectra. Remote Sens. Environ. 2004, 89, 535–552. [Google Scholar] [CrossRef]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Veroustraete, F.; van der Sande, C.J.; Grootaers, I.; Feyen, J. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests. Remote Sens. Environ. 2006, 101, 299–314. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of surface soil moisture using high-resolution multi-spectral imagery and artificial neural networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef]
- Njoku, E.G.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, L.; Zhang, L.; Chen, K.S.; Wigneron, J.P.; Chanzy, A.; Jackson, T.J. Physically based estimation of bare-surface soil moisture with the passive radiometers. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3145–3152. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.-P.; Ducharne, A.; Kerr, Y.; de Rosnay, P.; de Jeue, R.; Govind, A.; Al Bitar, A.; Albergel, C.; Muñoz-Sabater, J.; et al. Global-scale evaluation of two satellite-based passive microwave soil moisture datasets (SMOS and AMSR-E) with respect to land data assimilation system estimates. Remote Sens. Environ. 2014, 149, 181–195. [Google Scholar] [CrossRef]
- Tabatabaeenejad, A.; Burgin, M.; Moghaddam, M. P-band radar retrieval of subcanopy and subsurface soil moisture profile as a second order polynomial: First AirMOSS results. IEEE Trans. Geosci. Remote Sens. 2015, 53, 645–658. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Warrick, A.W. Analytical solutions to the one-dimensional linearized moisture flow equation for arbitrary input. Soil Sci. 1975, 120, 79–84. [Google Scholar] [CrossRef]
- Chen, J.M.; Tan, Y.C.; Chen, C.H.; Parlange, J.Y. Analytical solutions for linearized Richards’ equation with arbitrary time-dependent surface fluxes. Water Resour. Res. 2001, 37, 1091–1093. [Google Scholar] [CrossRef]
- Tracy, F.T. Three-dimensional analytical solutions of Richards’ equation for a box-shaped soil sample with piecewise-constant head boundary conditions on the top. J. Hydrol. 2007, 336, 391–400. [Google Scholar] [CrossRef]
- Warrick, A.W. Additional solutions for steady-state evaporation from a shallow water table. Soil Sci. 1988, 146, 63–66. [Google Scholar] [CrossRef]
- Salvucci, G.D. An approximate solution for steady vertical flux of moisture through an unsaturated homogeneous soil. Water Resour. Res. 1993, 29, 3749–3753. [Google Scholar] [CrossRef]
- Sadeghi, M.; Shokri, N.; Jones, S.B. A novel analytical solution to steady-state evaporation from porous media. Water Resour. Res. 2012. [Google Scholar] [CrossRef]
- Hayek, M. An analytical model for steady vertical flux through unsaturated soils with special hydraulic properties. J. Hydrol. 2015, 527, 1153–1160. [Google Scholar] [CrossRef]
- Gardner, W.R. Solutions to the flow equation for the drying of soils and other porous media. Soil Sci. Soc. Am. Proc. 1959, 23, 183–187. [Google Scholar] [CrossRef]
- Novak, M.D. Quasi-analytical solutions of the soil water flow equation for problems of evaporation. Soil Sci. Soc. Am. J. 1988, 52, 916–924. [Google Scholar] [CrossRef]
- Suleiman, A.A.; Ritchie, J.T. Modeling soil water redistribution during second-stage evaporation. Soil Sci. Soc. Am. J. 2003, 67, 377–386. [Google Scholar] [CrossRef]
- Teng, J.; Yasufuku, N.; Liu, Q.; Liu, S. Analytical solution for soil water redistribution during evaporation process. Water Sci. Technol. 2013, 68, 2545–2551. [Google Scholar] [CrossRef] [PubMed]
- Warrick, A.W.; Lomen, D.O.; Islas, A. An analytical solution to Richards' equation for a draining soil profile. Water Resour. Res. 1990, 26, 253–258. [Google Scholar] [CrossRef]
- Broadbridge, P.; White, I. Constant rate rainfall infiltration: A versatile nonlinear mode1, l, analytical solution. Water Resour. Res. 1988, 24, 145–154. [Google Scholar] [CrossRef]
- Buckingham, E. Studies on the Movement of Soil Moisture; USDA, Bureau of Soils: Washington, DC, USA, 1907.
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media. Colo. State Univ. Hydrol. Pap. 1964, 3, 27. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Hydraulic conductivity of variably saturated porous media: Film and corner flow in angular pore space. Water Resour. Res. 2001, 37, 1257–1276. [Google Scholar] [CrossRef]
- Bakker, M.; Nieber, J.L. Damping of sinusoidal surface flux fluctuations with soil depth. Vadose Zone J. 2009, 8, 119–126. [Google Scholar] [CrossRef]
- Sadeghi, M.; Ghahraman, B.; Ziaei, A.N.; Davary, K.; Reichardt, K. Additional scaled solutions to Richards' equation for infiltration and drainage. Soil Tillage Res. 2012, 119, 60–69. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J.; Khanji, J. Derivation of an equation of infiltration. Water Resour. Res. 1974, 10, 795–800. [Google Scholar] [CrossRef]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Sakai, M.; Jones, S.B.; Tuller, M. Numerical evaluation of subsurface soil water evaporation derived from sensible heat balance. Water Resour. Res. 2011. [Google Scholar] [CrossRef]
- Hayek, M. Water pulse migration through semi-infinite vertical unsaturated porous column with special relative-permeability functions: Exact solutions. J. Hydrol. 2014, 517, 668–676. [Google Scholar] [CrossRef]
- Hayek, M. Analytical solution to transient Richards’ equation with realistic water profiles for vertical infiltration and parameter estimation. Water Resour. Res. 2016, 52, 4438–4457. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer function. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Natural Resources Conservation Service. Soil Climate Analysis Network (SCAN) Data & Products. Available online: http://www.wcc.nrcs.usda.gov/scan/ (accessed on 23 December 2016).
- Mishra, V.; Ellenburg, W.L.; Al-Hamdan, O.Z.; Bruce, J.; Cruise, J.F. Modeling soil moisture profiles in irrigated fields by the principle of maximum entropy. Entropy 2015, 17, 4454–4484. [Google Scholar] [CrossRef]
- Sadeghi, M.; Tuller, M.; Gohardoust, M.R.; Jones, S.B. Column-scale unsaturated hydraulic conductivity estimates in coarse-textured homogeneous and layered soils derived under steady-state evaporation from a water table. J. Hydrol. 2014, 519, 1238–1248. [Google Scholar] [CrossRef]
- Stillman, S.; Ninneman, J.; Zeng, X.; Franz, T.; Scott, R.L.; Shuttleworth, W.J.; Cummins, K. Summer soil moisture spatiotemporal variability in southeastern Arizona. J. Hydrometeor. 2014, 15, 1473–1485. [Google Scholar] [CrossRef]
- Coopersmith, E.J.; Bell, J.E.; Cosh, M.H. Extending the soil moisture data record of the US Climate Reference Network (USCRN) and Soil Climate Analysis Network (SCAN). Adv. Water Resour. 2015, 79, 80–90. [Google Scholar] [CrossRef]
- Durden, S.L.; Van Zyl, J.J.; Zebker, H.A. Modeling and observation of the radar polarization signature of forested areas. IEEE Trans. Geosci. Remote Sens. 1989, 27, 290–301. [Google Scholar] [CrossRef]
- Burgin, M.; Clewley, D.; Lucas, R.M.; Moghaddam, M. A generalized radar backscattering model based on wave theory for multilayer multispecies vegetation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4832–4845. [Google Scholar] [CrossRef]
- Corana, A.; Marchesi, M.; Martini, C.; Ridella, S. Minimizing multimodal functions of continuous variables with the ‘Simulated Annealing’ algorithm. ACM Trans. Math. Softw. 1987, 13, 262–280. [Google Scholar] [CrossRef]
- AirMOSS Science Team. AirMOSS: L1 S-0 Polarimetric Data from AirMOSS P-band SAR, Metolius, 2012–2015; ORNL DAAC: Oak Ridge, TN, USA, 2016. Available online: http://dx.doi.org/10.3334/ORNLDAAC/1412 (accessed on 23 December 2016).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).