Gap-Filling of Landsat 7 Imagery Using the Direct Sampling Method
Abstract
:1. Introduction
2. Materials and Methods
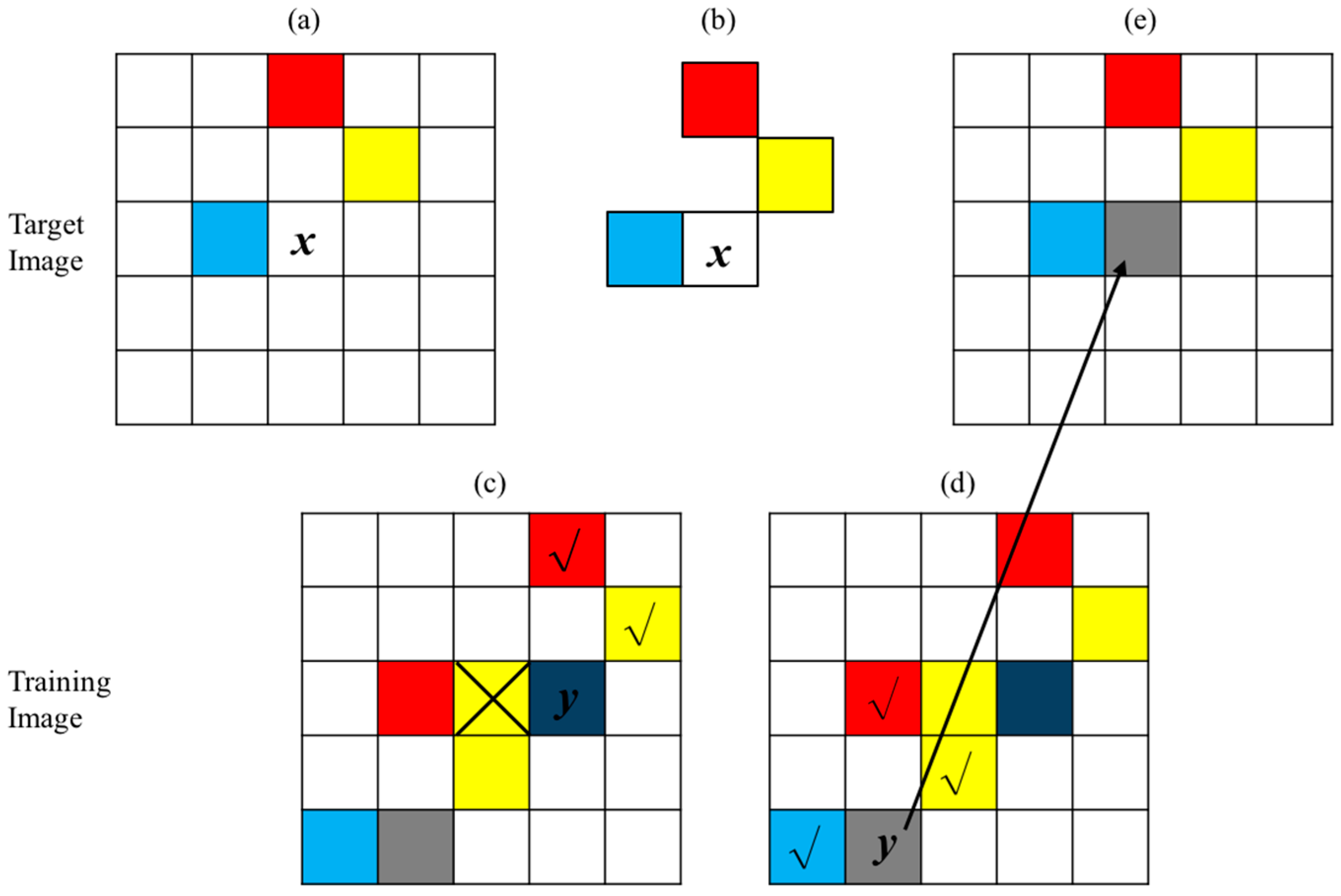
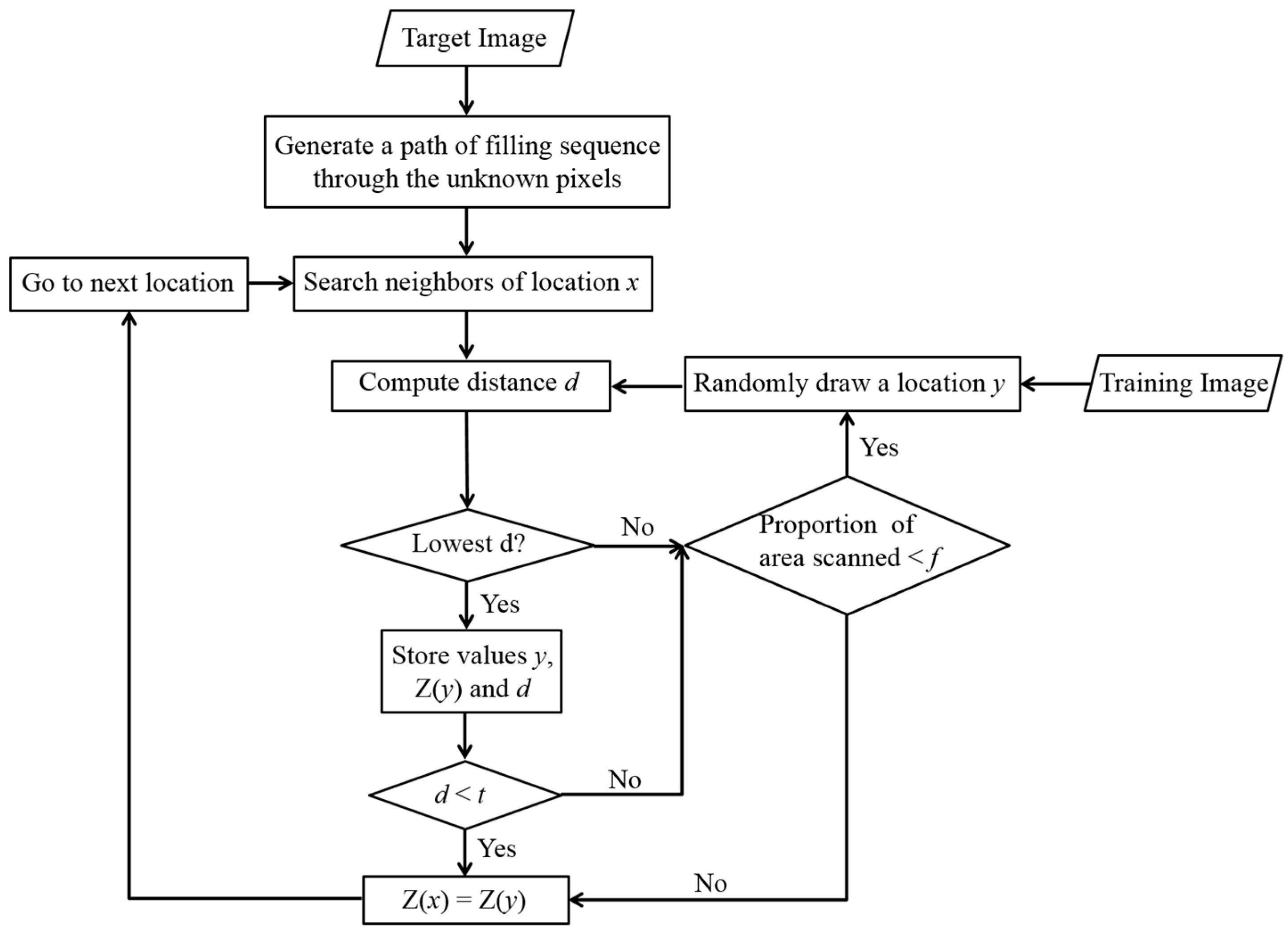
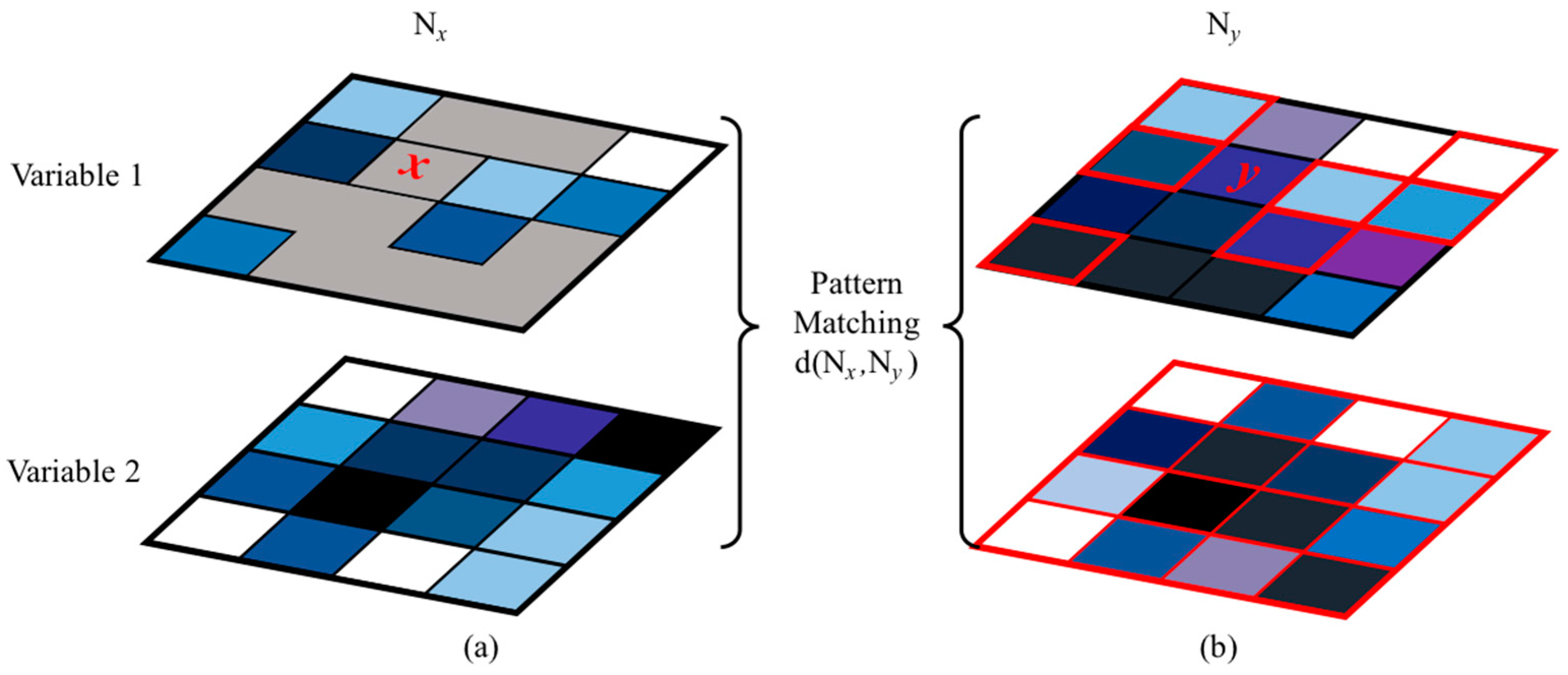
2.1. Direct Sampling Method
2.2. Experiment Design
2.3. Validation of Gap-Filling Results
- RMSE
- MSA
- rRMSE
- R2
- MdAPE
3. Results
3.1. Comparison of Univariate and Bivariate Simulations
3.2. Comparison of Multi-Temporal Influence of Training Imagery
3.3. Impact of Heterogeneity on Reconstructions
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Landsat; National Aeronautics and Space Administration (NASA). Landsat 7 Science Data Users Handbook. Available online: http://landsat.gsfc.nasa.gov/wp-content/uploads/2016/08/Landsat7_Handbook.pdf (accessed on 11 March 2011).
- United States Geological Survey (USGS). Landsat-A Global Land-Imaging Mission: Geological Survey Fact Sheet 2012-3072. Available online: https://pubs.usgs.gov/fs/2012/3072/ (accessed on 19 July 2012).
- United States Geological Survey (USGS). Preliminary Assessment of Landsat 7 ETM+ Data Following Scan Line Corrector Malfunction. Available online: https://landsat.usgs.gov/sites/default/files/documents/SLC_off_Scientific_Usability.pdf (accessed on 16 July 2003).
- Scaramuzza, P.; Micijevic, E.; Chander, G. SLC Gap-Filled Products Phase One Methodology. 2004. Available online: https://landsat.usgs.gov/sites/default/files/documents/SLC_Gap_Fill_Methodology.pdf (accessed on 18 March 2004). [Google Scholar]
- Scaramuzza, P.; Micijevic, E.; Chander, G. Phase 2 Gap-Fill Algorithm: SLC-off Gap-Filled Products Gap-Filled Algorithm Methodology. 2004. Available online: https://landsat.usgs.gov/sites/default/files/documents/L7SLCGapFilledMethod.pdf (accessed on 7 October 2004). [Google Scholar]
- Maxwell, S.K.; Schmidt, G.L.; Storey, J.C. A multi-scale segmentation approach to filling gaps in Landsat ETM+ SLC-off images. Int. J. Remote Sens. 2007, 28, 5339–5356. [Google Scholar] [CrossRef]
- Flanders, D.; Hall-Beyer, M.; Pereverzoff, J. Preliminary evaluation of eCognition object-based software for cut block delineation and feature extraction. Can. J. Remote Sens. 2003, 29, 441–452. [Google Scholar] [CrossRef]
- Pringle, M.J.; Schmidt, M.; Muir, J.S. Geostatistical interpolation of SLC-off Landsat ETM+ images. ISPRS J. Photogramm. Remote Sens. 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D.; Chen, J. A new geostatistical approach for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2012, 124, 49–60. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.; Zhang, L. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Guardiano, F.B.; Srivastava, R.M. Multivariate geostatistics: beyond bivariate moments. In Geostatistics Troia’92; Springer: Dordreche, The Netherlands, 1993; Volume 1, pp. 133–144. [Google Scholar]
- Mariethoz, G.; Caers, J. Multiple-Point Geostatistics: Stochastic Modeling with Training Images; Wiley Blackwell: Hoboken, NJ, USA, 2014. [Google Scholar]
- Strebelle, S. Conditional simulation of complex geological structures using multiple-point statistics. Math. Geol. 2002, 34, 1–21. [Google Scholar] [CrossRef]
- Arpat, G.B.; Caers, J. A multiple-scale, pattern-based approach to sequential simulation. In Geostatistics Banff 2004; Springer: Dordreche, The Netherlands, 2005; pp. 255–264. [Google Scholar]
- Daly, C. Higher order models using entropy, Markov random fields and sequential simulation. In Geostatistics Banff 2004; Springer: Dordreche, The Netherlands, 2005; pp. 215–224. [Google Scholar]
- Zhang, T.; Switzer, P.; Journel, A. Filter-based classification of training image patterns for spatial simulation. Math. Geol. 2006, 38, 63–80. [Google Scholar] [CrossRef]
- Hurley, N.F.; Zhang, T. Method to generate full-bore images using borehole images and multipoint statistics. SPE Reserv. Eval. Eng. 2011, 14, 204–214. [Google Scholar] [CrossRef]
- Okabe, H.; Blunt, M.J. Multiple-point statistics to generate pore space images. In Geostatistics Banff 2004; Springer: Dordreche, The Netherlands, 2005; pp. 763–768. [Google Scholar]
- Wu, J.; Boucher, A.; Zhang, T. A SGeMS code for pattern simulation of continuous and categorical variables: FILTERSIM. Comput. Geosci. 2008, 34, 1863–1876. [Google Scholar] [CrossRef]
- Tang, Y.; Atkinson, P.M.; Wardrop, N.A.; Zhang, J. Multiple-point geostatistical simulation for post-processing a remotely sensed land cover classification. Spat. Stat. 2013, 5, 69–84. [Google Scholar] [CrossRef]
- Yong, G.; Hexiang, B.; Qiuming, C. Solution of multiple-point statistics to extracting information from remotely sensed imagery. J. China Univ. Geosci. 2008, 19, 421–428. [Google Scholar] [CrossRef]
- Boucher, A. Sub-pixel mapping of coarse satellite remote sensing images with stochastic simulations from training images. Math. Geosci. 2009, 41, 265–290. [Google Scholar] [CrossRef]
- Tang, Y.; Atkinson, P.M.; Zhang, J. Downscaling remotely sensed imagery using area-to-point cokriging and multiple-point geostatistical simulation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 174–185. [Google Scholar] [CrossRef]
- Mariethoz, G.; McCabe, M.F.; Renard, P. Spatiotemporal reconstruction of gaps in multivariate fields using the direct sampling approach. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mariethoz, G.; Renard, P.; Straubhaar, J. The direct sampling method to perform multiple-point geostatistical simulations. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef]
- Jha, S.K.; Mariethoz, G.; Evans, J.; McCabe, M.F.; Sharma, A. A space and time scale-dependent nonlinear geostatistical approach for downscaling daily precipitation and temperature. Water Resour. Res. 2015, 51, 6244–6261. [Google Scholar] [CrossRef]
- Oriani, F.; Straubhaar, J.; Renard, P.; Mariethoz, G. Simulation of rainfall time series from different climatic regions using the direct sampling technique. Hydrol. Earth Syst. Sci. 2014, 18, 3015–3031. [Google Scholar] [CrossRef]
- Mariethoz, G.; Renard, P. Reconstruction of incomplete data sets or images using direct sampling. Math. Geosci. 2010, 42, 245–268. [Google Scholar] [CrossRef]
- Meerschman, E.; Pirot, G.; Mariethoz, G.; Straubhaar, J.; van Meirvenne, M.; Renard, P. A practical guide to performing multiple-point statistical simulations with the Direct Sampling algorithm. Comput. Geosci. 2013, 52, 307–324. [Google Scholar] [CrossRef]
- Teillet, P.M.; Barker, J.L.; Markham, B.L.; Irish, R.R.; Fedosejevs, G.; Storey, J.C. Radiometric cross-calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric cross calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 enhanced thematic mapper plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Mahmood, T.; Easson, G. Comparing aster and Landsat 7 ETM+ for change detection. In Proceedings of the Annual Conference of the American Society for Photogrammetry and Remote Sensing 2006: Prospecting for Geospatial Information Integration, Reno, NV, USA, 1–5 May 2006; pp. 828–839.
- Reza, M.M.; Ali, S.N. Using IRS products to recover 7ETM+ defective images. Am. J. Appl. Sci. 2008, 5, 618–625. [Google Scholar] [CrossRef]
- Chen, F.; Tang, L.; Qiu, Q. Exploitation of CBERS-02B as auxiliary data in recovering the Landsat7 ETM+ SLC-off image. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010.


| Landsat 7 | Wavelength (mm) | Resolution (m) |
|---|---|---|
| Band 1 | 0.45–0.52 | 30 |
| Band 2 | 0.52–0.60 | 30 |
| Band 3 | 0.63–0.69 | 30 |
| Band 4 | 0.77–0.90 | 30 |
| Band 5 | 1.55–1.75 | 30 |
| Band 7 | 2.09–2.35 | 30 |
| R1 | R2 | R3 | R4 | R5 | R6 | |
|---|---|---|---|---|---|---|
| Desert | Sparse Agricultural | Dense Farmland | Urban Area | Braided River | Coastal Area | |
| Path | 169 | 38 | 43 | 43 | 137 | 115 |
| Row | 40 | 37 | 34 | 34 | 44 | 78 |
| Target image | 28 August 2002 | 5 July 2002 | 8 July 2002 | 8 July 2002 | 31 October 2002 | 17 July 2002 |
| Date 1 | 13 September 2002 | 19 June 2002 | 24 July 2002 | 24 July 2002 | 16 November 2002 | 1 July 2002 |
| Date 2 | 29 September 2002 | 3 June 2002 | 9 August 2002 | 9 August 2002 | 2 December 2002 | 18 August 2002 |
| Date 3 | 15 October 2002 | 18 May 2002 | 25 August 2002 | 25 August 2002 | 18 December 2002 | 30 May 2002 |
| Date 4 | 6 April 2002 | 11 February 2002 | 2 March 2002 | 2 March 2002 | 5 March 2002 | 11 March 2002 |
| Case Name | Description |
|---|---|
| U-D1 | Univariate case with D1 (two-week distance) as training image |
| U-D2 | Univariate case with D2 (four-week distance) as training image |
| U-D3 | Univariate case with D3 (six-week distance) as training image |
| U-D4 | Univariate case with D4 (longer than four-month distance) as training image |
| U-D0 | Univariate case with non-gap area in target image as training image. No additional image introduced |
| B-D1 | Bivariate case, with one variable the reflectance value in the target image and another the reflectance value of D1 (two-week distance) |
| B-D2 | Bivariate case, with one variable the reflectance value in the target image and another the reflectance value of D2 (four-week distance) |
| B-D3 | Bivariate case, with one variable the reflectance value in the target image and another the reflectance value of D3 (six-week distance) |
| B-D4 | Bivariate case, with one variable the reflectance value in the target image and another the reflectance value of D4 (longer than four-month distance) |
| Univariate | Bivariate | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| U-D1 | U-D2 | U-D3 | U-D4 | U-D0 | B-D1 | B-D2 | B-D3 | B-D4 | ||
| RMSE | B1 | 0.0181 | 0.0174 | 0.0175 | 0.0189 | 0.0140 | 0.0096 | 0.0099 | 0.0104 | 0.0123 |
| B2 | 0.0235 | 0.0224 | 0.0228 | 0.0261 | 0.0177 | 0.0125 | 0.0129 | 0.0136 | 0.0162 | |
| B3 | 0.0315 | 0.0315 | 0.0323 | 0.0385 | 0.0282 | 0.0194 | 0.0196 | 0.0211 | 0.0265 | |
| B4 | 0.0496 | 0.0504 | 0.0504 | 0.0490 | 0.0431 | 0.0373 | 0.0341 | 0.0391 | 0.0398 | |
| B5 | 0.0463 | 0.0469 | 0.0474 | 0.0592 | 0.0447 | 0.0317 | 0.0307 | 0.0344 | 0.0390 | |
| B7 | 0.0458 | 0.0452 | 0.0464 | 0.0544 | 0.0403 | 0.0306 | 0.0307 | 0.0325 | 0.0381 | |
| MSA (°) | 7.7439 | 7.6745 | 7.6508 | 8.7928 | 6.0092 | 4.7069 | 4.5985 | 4.9973 | 5.6135 | |
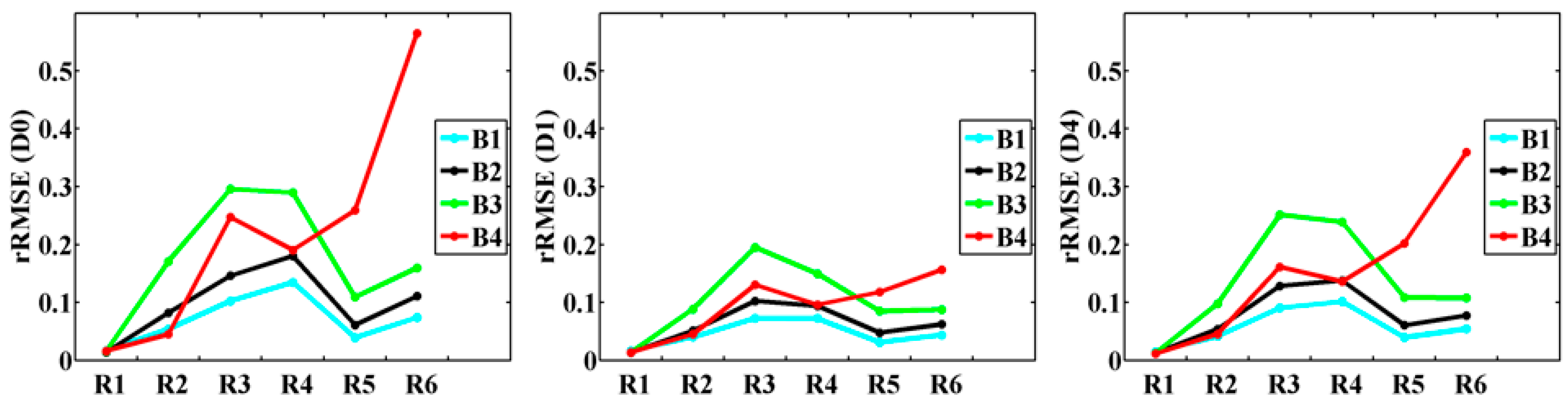
| rRMSE | B1 | 0.1348 | 0.1356 | 0.1323 | 0.1433 | 0.1026 | 0.0728 | 0.0737 | 0.0766 | 0.0904 |
| B2 | 0.1939 | 0.1868 | 0.1830 | 0.1965 | 0.1463 | 0.1027 | 0.1054 | 0.1108 | 0.1284 | |
| B3 | 0.3225 | 0.3245 | 0.3252 | 0.3295 | 0.2960 | 0.1950 | 0.1971 | 0.2041 | 0.2512 | |
| B4 | 0.2389 | 0.2651 | 0.2512 | 0.2458 | 0.2474 | 0.1303 | 0.1274 | 0.1411 | 0.1615 | |
| B5 | 0.9492 | 1.1717 | 1.3101 | 1.0687 | 2.2184 | 0.6958 | 0.7058 | 0.6629 | 0.7829 | |
| B7 | 9.7379 | 9.8900 | 10.2649 | 11.3710 | 7.5240 | 1.4503 | 2.3615 | 2.0421 | 1.9940 | |
| R2 | B1 | 0.3457 | 0.3797 | 0.3894 | 0.2675 | 0.5813 | 0.8064 | 0.7938 | 0.7748 | 0.6859 |
| B2 | 0.3627 | 0.4267 | 0.4345 | 0.3391 | 0.6158 | 0.8127 | 0.7990 | 0.7795 | 0.6895 | |
| B3 | 0.5708 | 0.5685 | 0.5556 | 0.4728 | 0.6428 | 0.8338 | 0.8288 | 0.8067 | 0.6910 | |
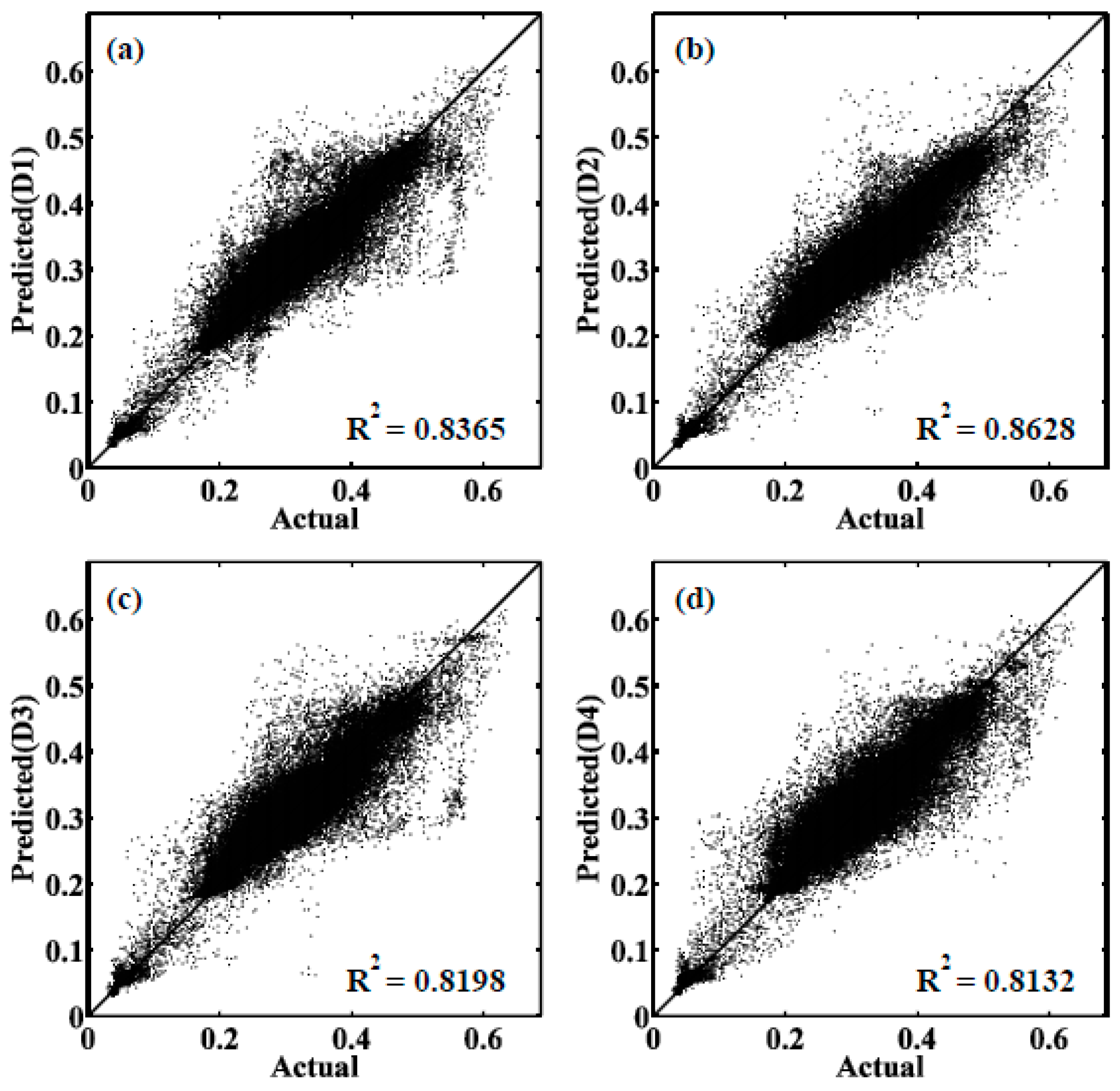
| B4 | 0.7134 | 0.7076 | 0.7105 | 0.7194 | 0.7811 | 0.8365 | 0.8628 | 0.8198 | 0.8132 | |
| B5 | 0.6544 | 0.6496 | 0.6462 | 0.5485 | 0.6642 | 0.8342 | 0.8438 | 0.8049 | 0.7470 | |
| B7 | 0.5777 | 0.5833 | 0.5694 | 0.4786 | 0.6576 | 0.8049 | 0.8044 | 0.7823 | 0.7000 | |
| MdAPE (%) | B1 | 9.9127 | 10.2607 | 9.9215 | 11.1535 | 4.7540 | 3.7660 | 3.6599 | 3.9347 | 4.3658 |
| B2 | 13.8214 | 13.2522 | 13.1244 | 15.0335 | 6.6289 | 5.2183 | 5.1734 | 5.6107 | 6.1724 | |
| B3 | 18.1135 | 18.3791 | 18.748 | 24.4024 | 11.7130 | 9.0637 | 9.0774 | 9.5551 | 11.3443 | |
| B4 | 9.0571 | 9.2563 | 9.4933 | 8.7362 | 5.9232 | 5.3764 | 5.4635 | 5.9204 | 6.4058 | |
| B5 | 11.9067 | 11.7296 | 12.0812 | 16.5120 | 8.0976 | 6.8696 | 6.5745 | 7.2466 | 7.9052 | |
| B7 | 20.8301 | 19.5497 | 20.8953 | 26.7857 | 13.8738 | 11.2427 | 11.0730 | 11.7867 | 13.3628 | |
| Case Name | Mean | St. Dev. | Skew | |
|---|---|---|---|---|
| Desert | Actual | 0.4891 | 0.0125 | −0.0980 |
| U-D0 | 0.4891 | 0.0116 | −0.2304 | |
| B-D1 | 0.4890 | 0.0117 | −0.1899 | |
| B-D4 | 0.4890 | 0.0119 | −0.1363 | |
| Sparse agricultural | Actual | 0.3782 | 0.0413 | 2.1496 |
| U-D0 | 0.3782 | 0.0400 | 2.2386 | |
| B-D1 | 0.3783 | 0.0402 | 2.2373 | |
| B-D4 | 0.3783 | 0.0404 | 2.2537 | |
| Dense farmland | Actual | 0.3132 | 0.0910 | −0.1222 |
| U-D0 | 0.3134 | 0.0879 | −0.1246 | |
| B-D1 | 0.3138 | 0.0891 | −0.2066 | |
| B-D4 | 0.3134 | 0.0886 | −0.1754 | |
| Urban area | Actual | 0.2714 | 0.0576 | 0.8012 |
| U-D0 | 0.2717 | 0.0530 | 0.8884 | |
| B-D1 | 0.2714 | 0.0553 | 0.8240 | |
| B-D4 | 0.2710 | 0.0538 | 0.8818 | |
| Braided river | Actual | 0.1854 | 0.0901 | −0.3713 |
| U-D0 | 0.1858 | 0.0887 | −0.4269 | |
| B-D1 | 0.1848 | 0.0888 | −0.4063 | |
| B-D4 | 0.1853 | 0.0889 | −0.4196 | |
| Coastal area | Actual | 0.1147 | 0.1267 | 0.6625 |
| U-D0 | 0.1150 | 0.1247 | 0.6331 | |
| B-D1 | 0.1145 | 0.1263 | 0.6482 | |
| B-D4 | 0.1153 | 0.1266 | 0.6347 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, G.; Mariethoz, G.; McCabe, M.F. Gap-Filling of Landsat 7 Imagery Using the Direct Sampling Method. Remote Sens. 2017, 9, 12. https://doi.org/10.3390/rs9010012
Yin G, Mariethoz G, McCabe MF. Gap-Filling of Landsat 7 Imagery Using the Direct Sampling Method. Remote Sensing. 2017; 9(1):12. https://doi.org/10.3390/rs9010012
Chicago/Turabian StyleYin, Gaohong, Gregoire Mariethoz, and Matthew F. McCabe. 2017. "Gap-Filling of Landsat 7 Imagery Using the Direct Sampling Method" Remote Sensing 9, no. 1: 12. https://doi.org/10.3390/rs9010012
APA StyleYin, G., Mariethoz, G., & McCabe, M. F. (2017). Gap-Filling of Landsat 7 Imagery Using the Direct Sampling Method. Remote Sensing, 9(1), 12. https://doi.org/10.3390/rs9010012









