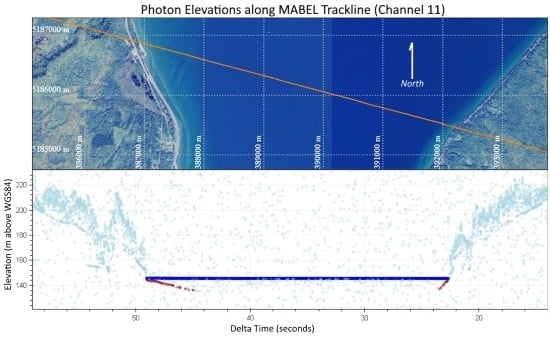
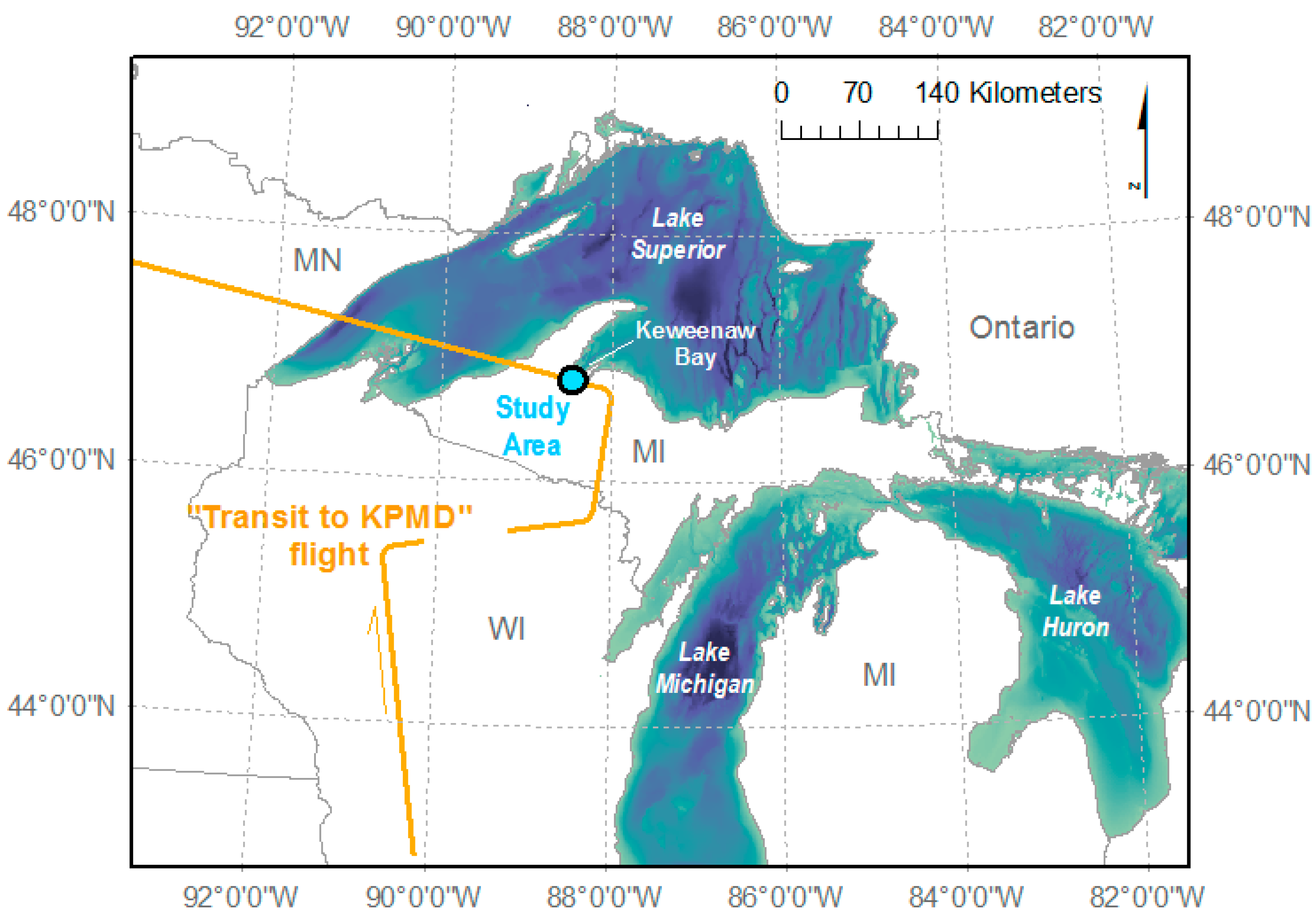
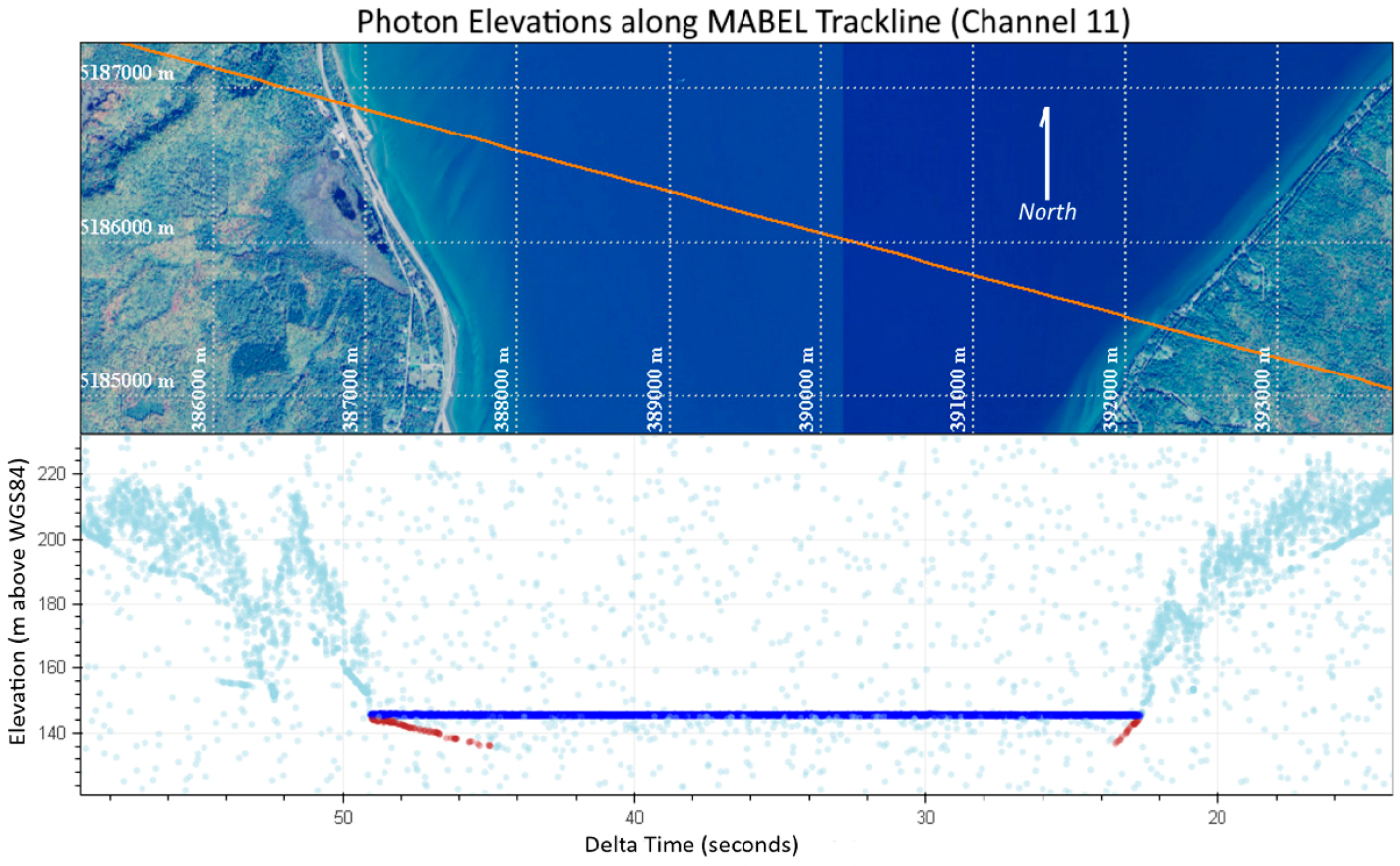
Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS
Abstract
:1. Introduction
1.1. Bathymetric Lidar Background
1.2. Lidar Equation
2. Materials and Methods
2.1. MABEL Data
2.2. Reference Data
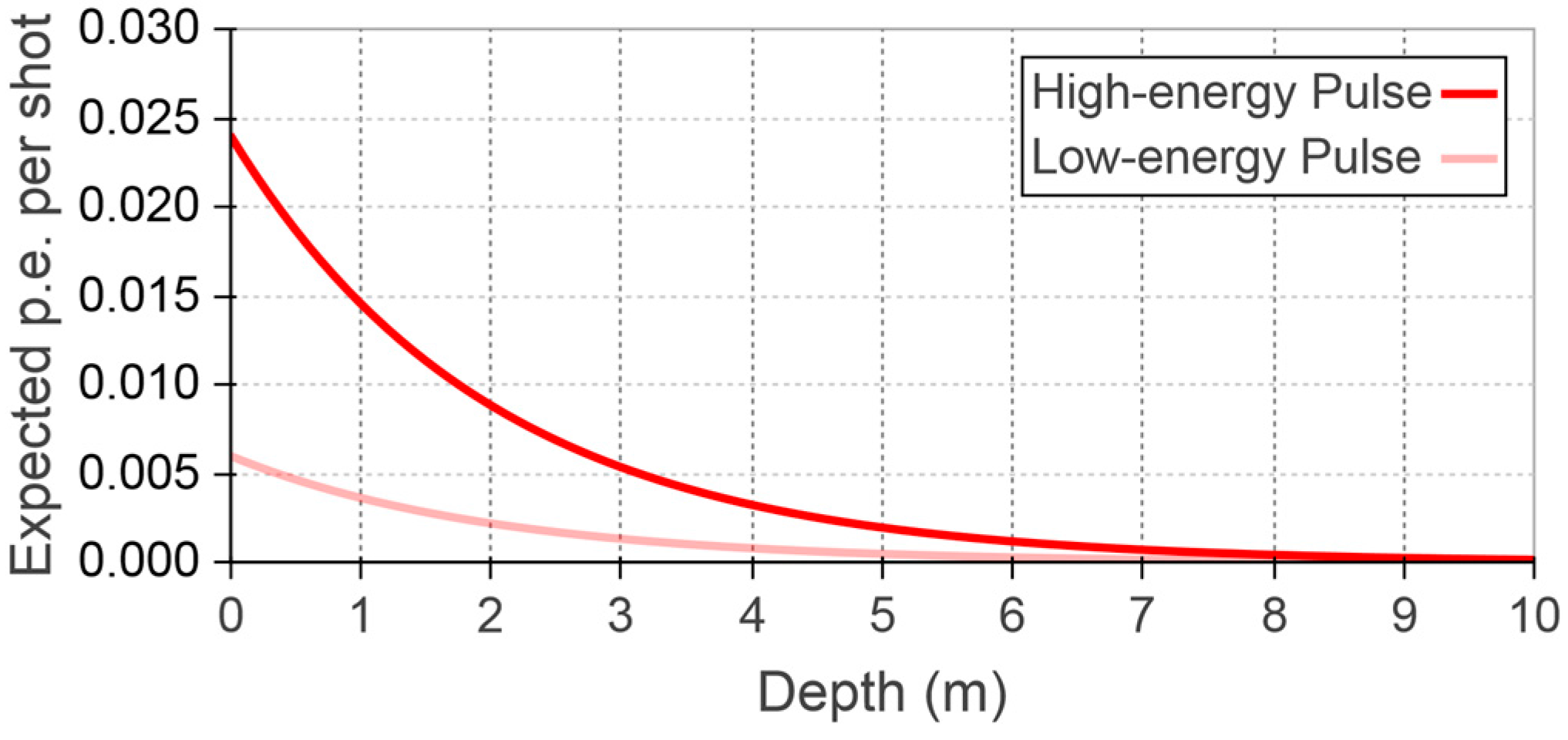
2.3. Predicted Number of Photoelectrons
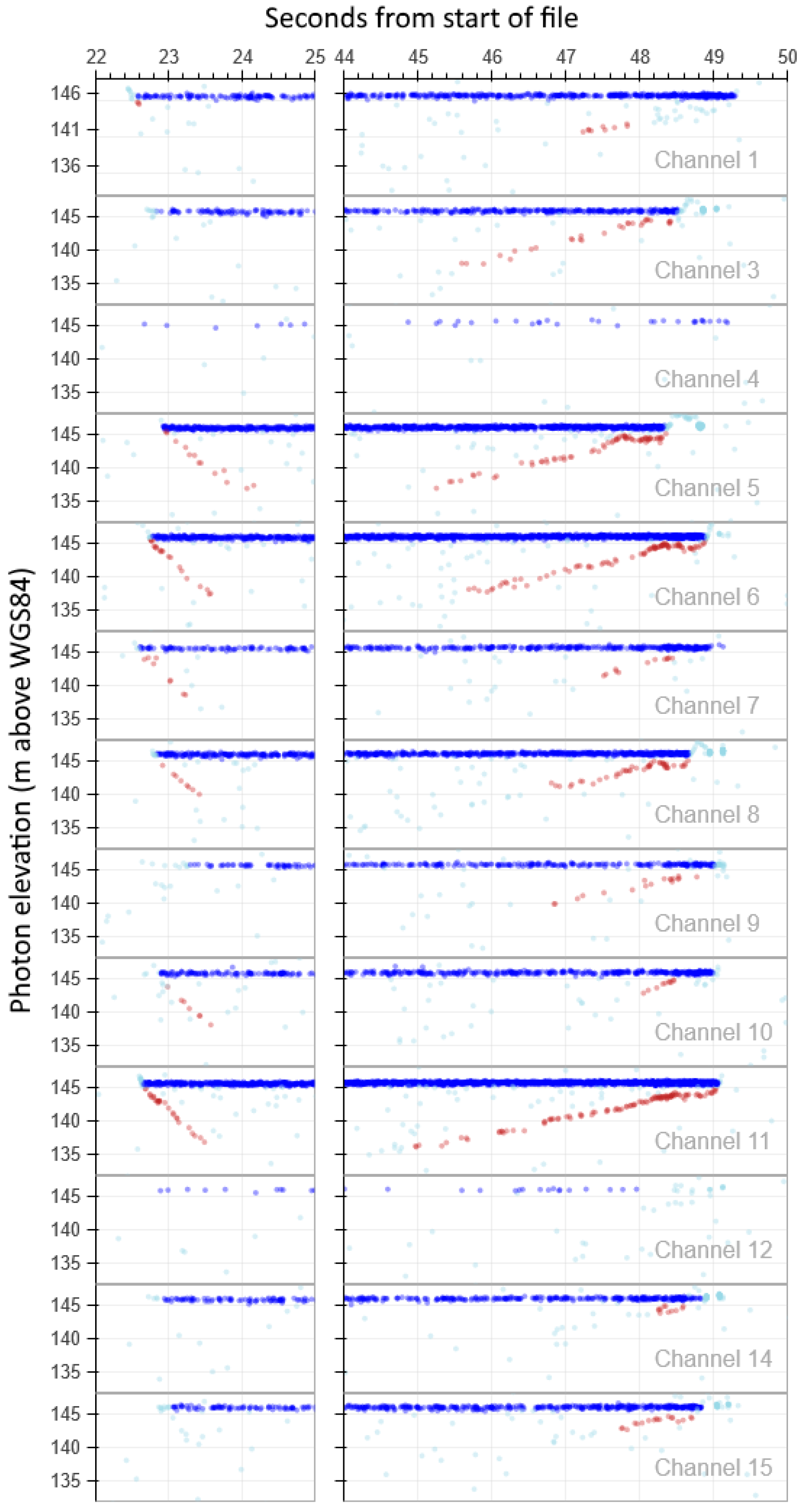
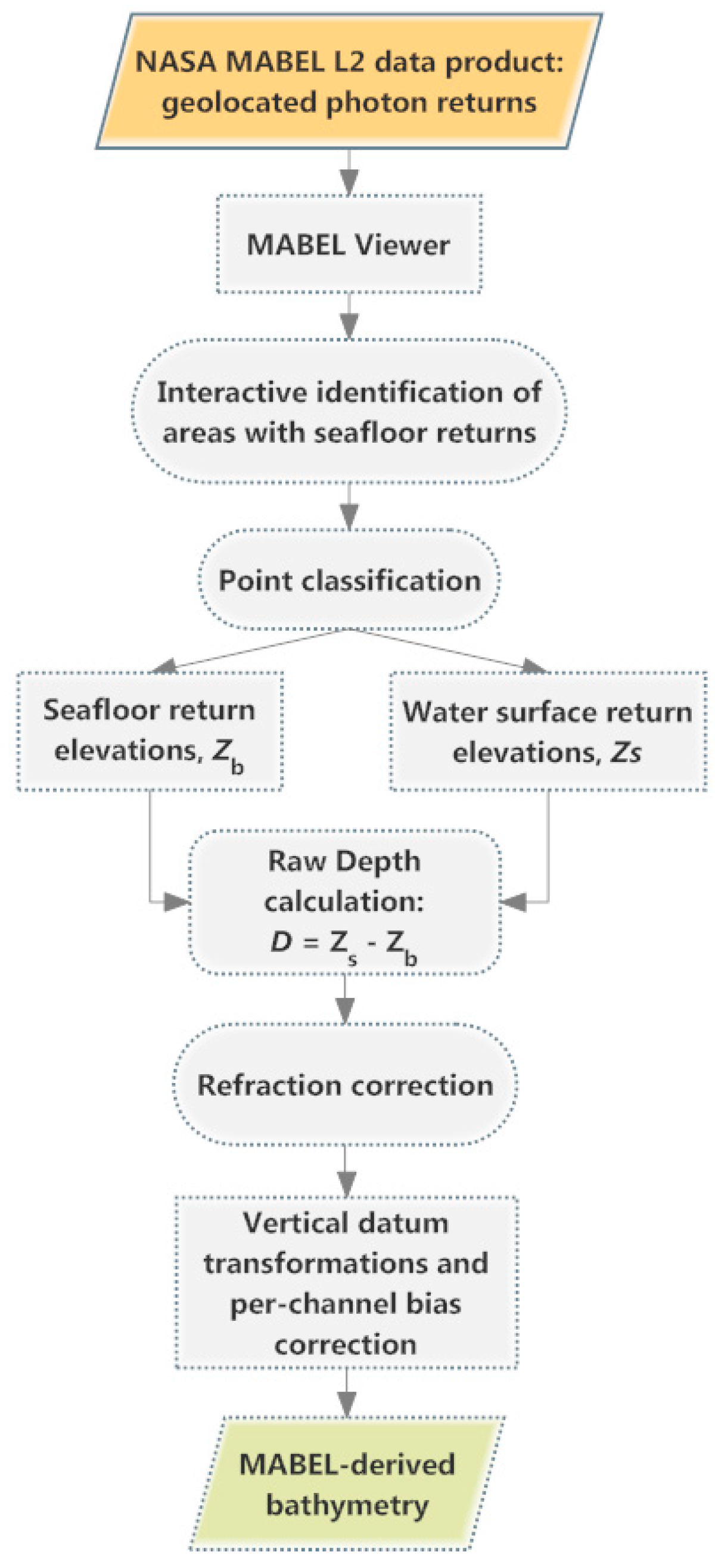
2.4. Deriving MABEL Bathymetry
2.4.1. Refraction Correction
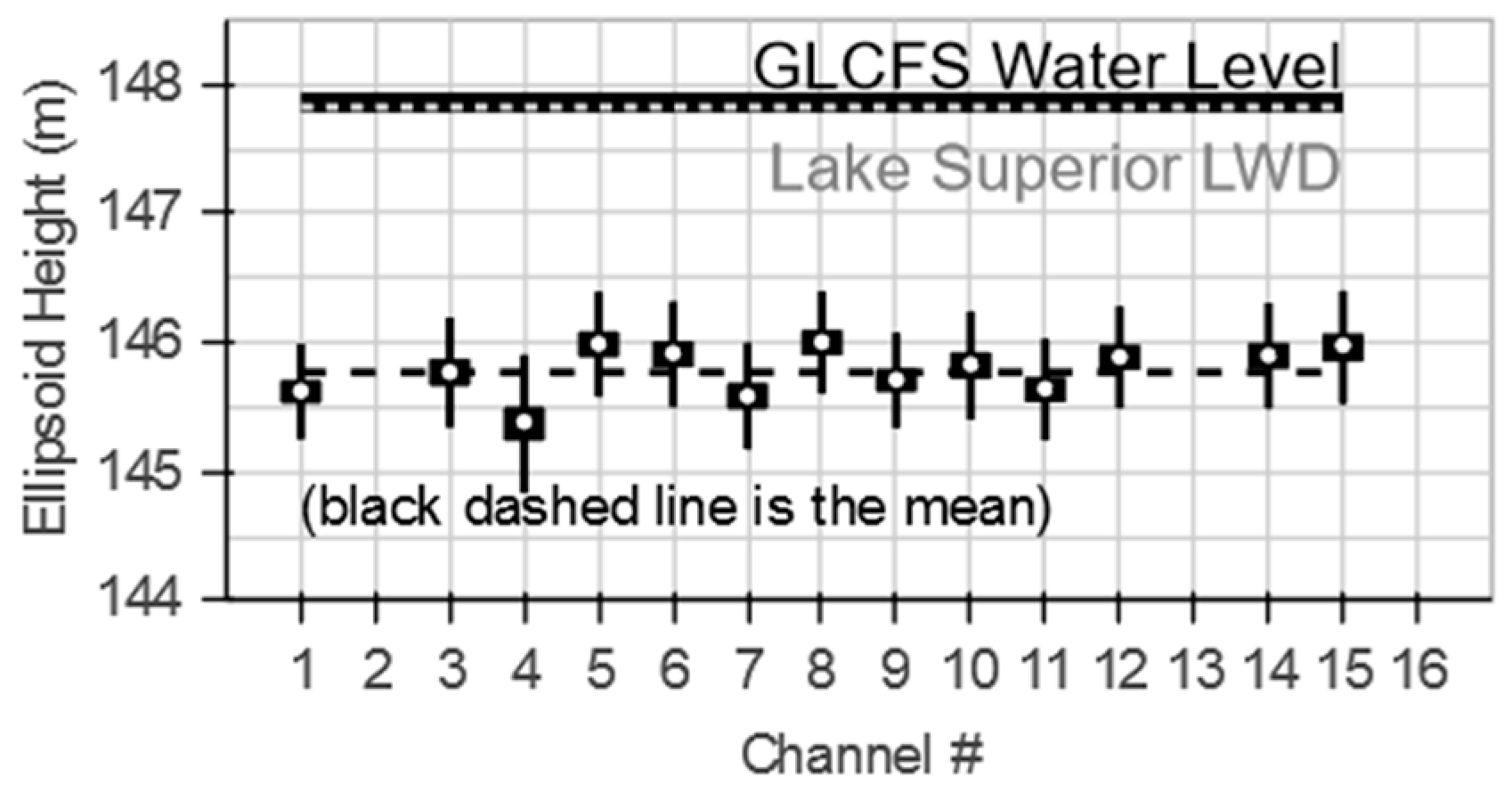
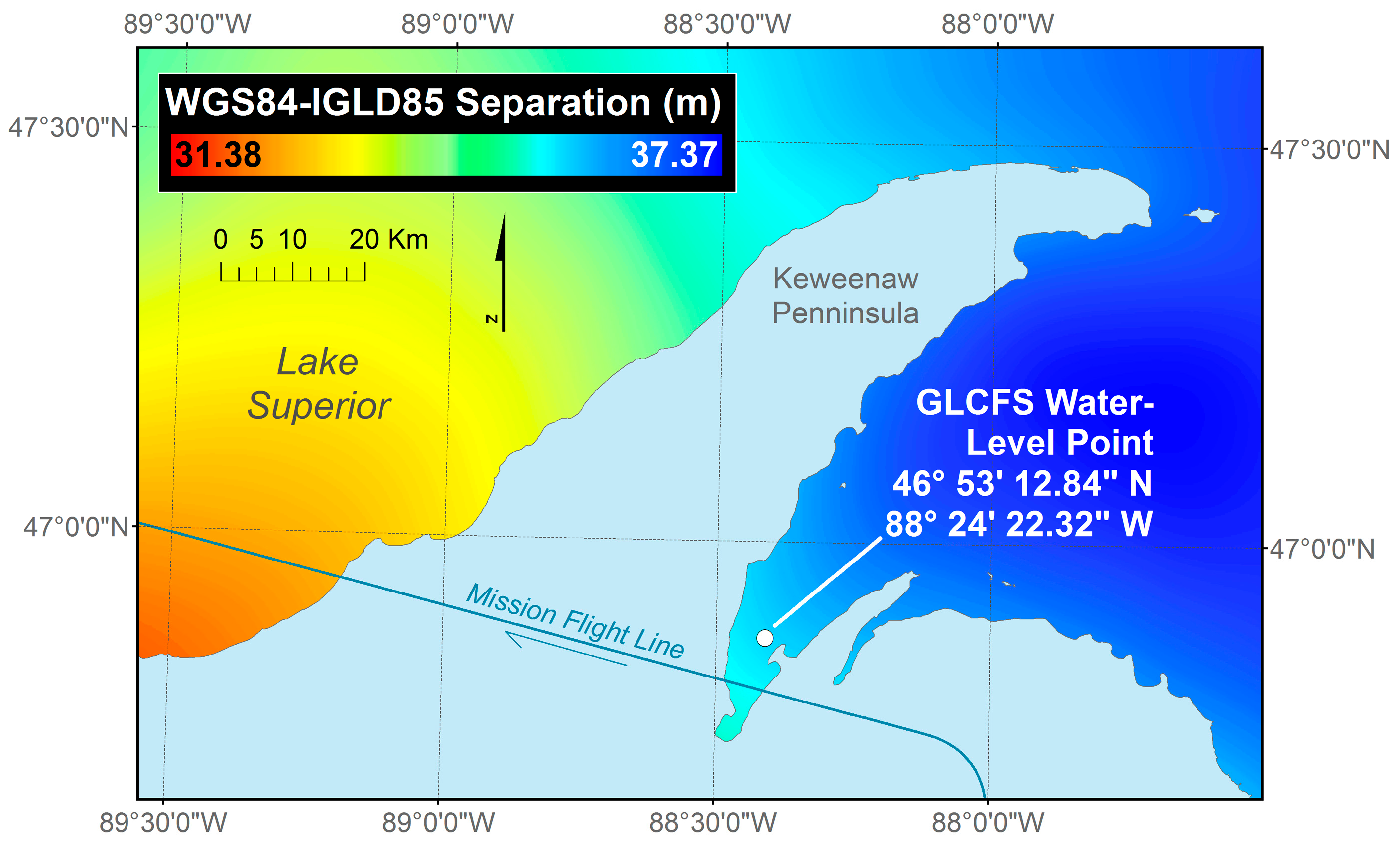
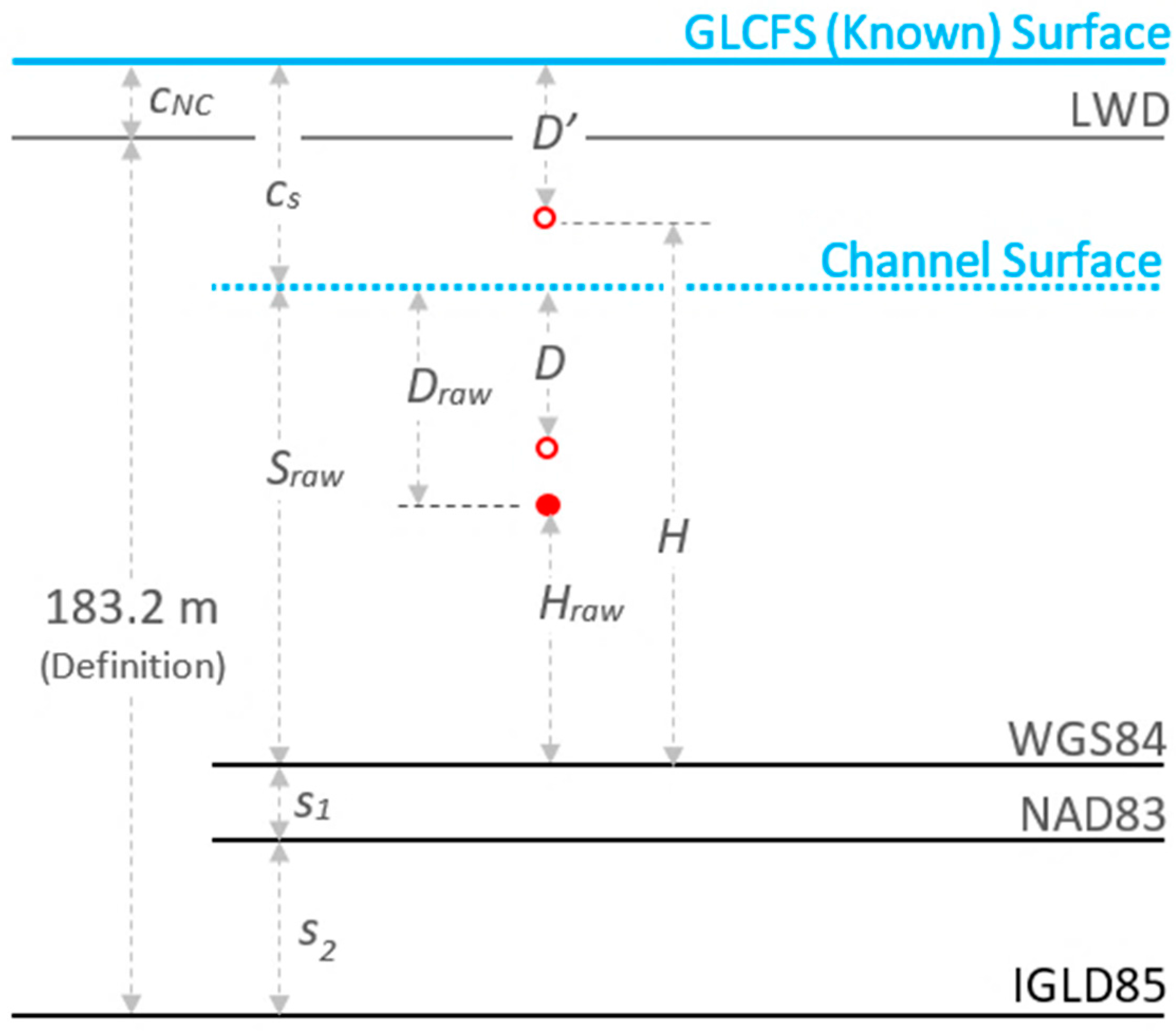
2.4.2. Vertical Datum Transformation
3. Results
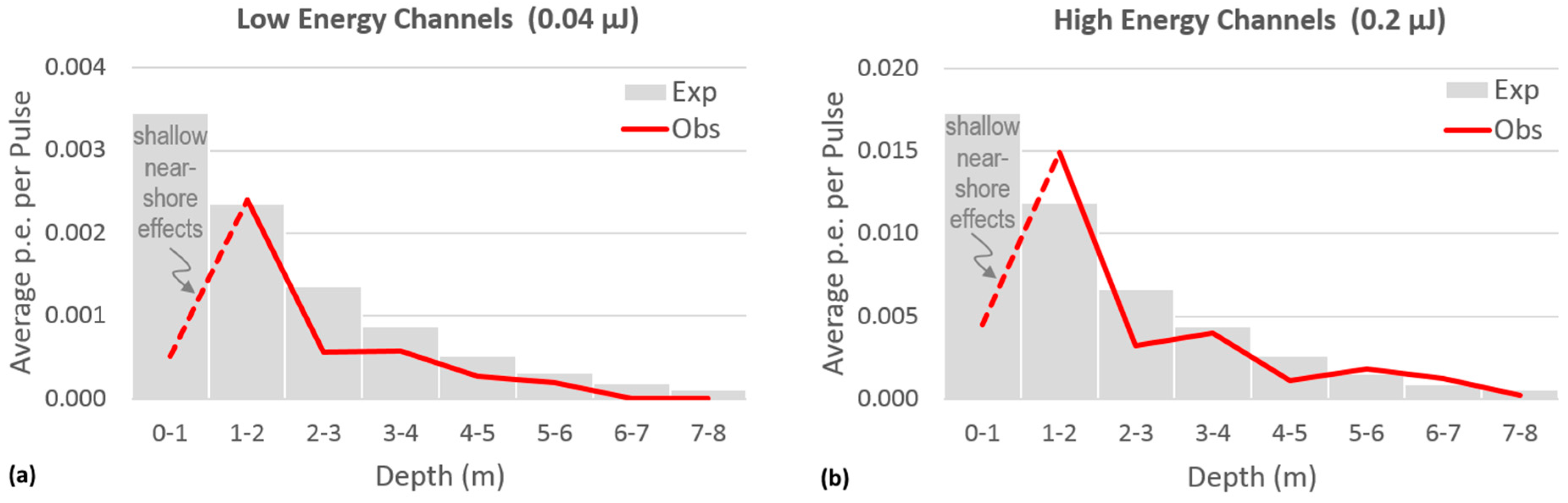
3.1. Predicted Photon Returns
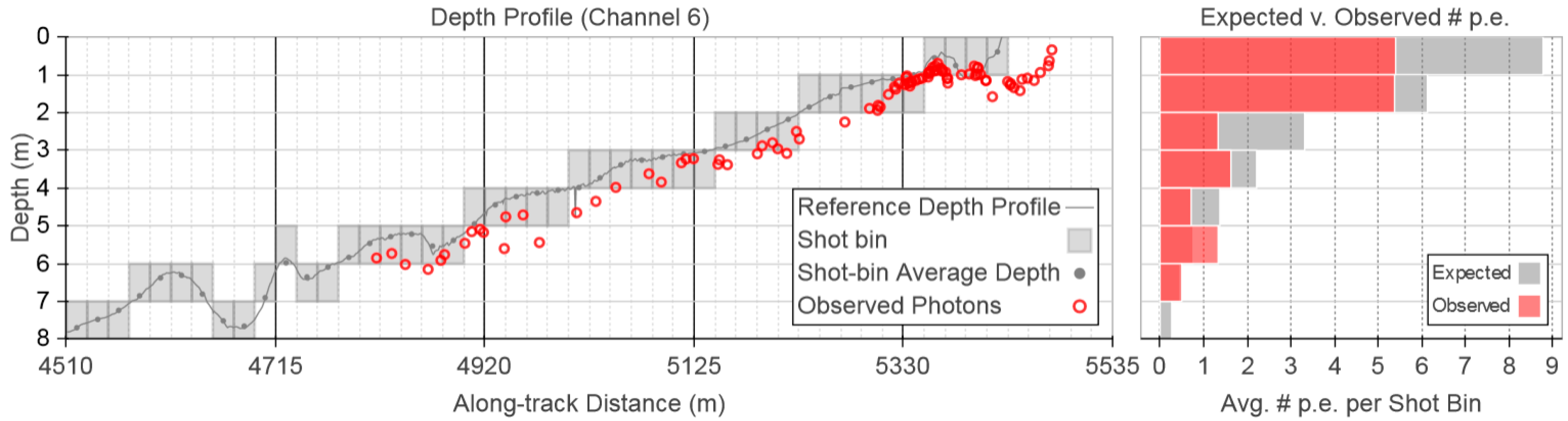
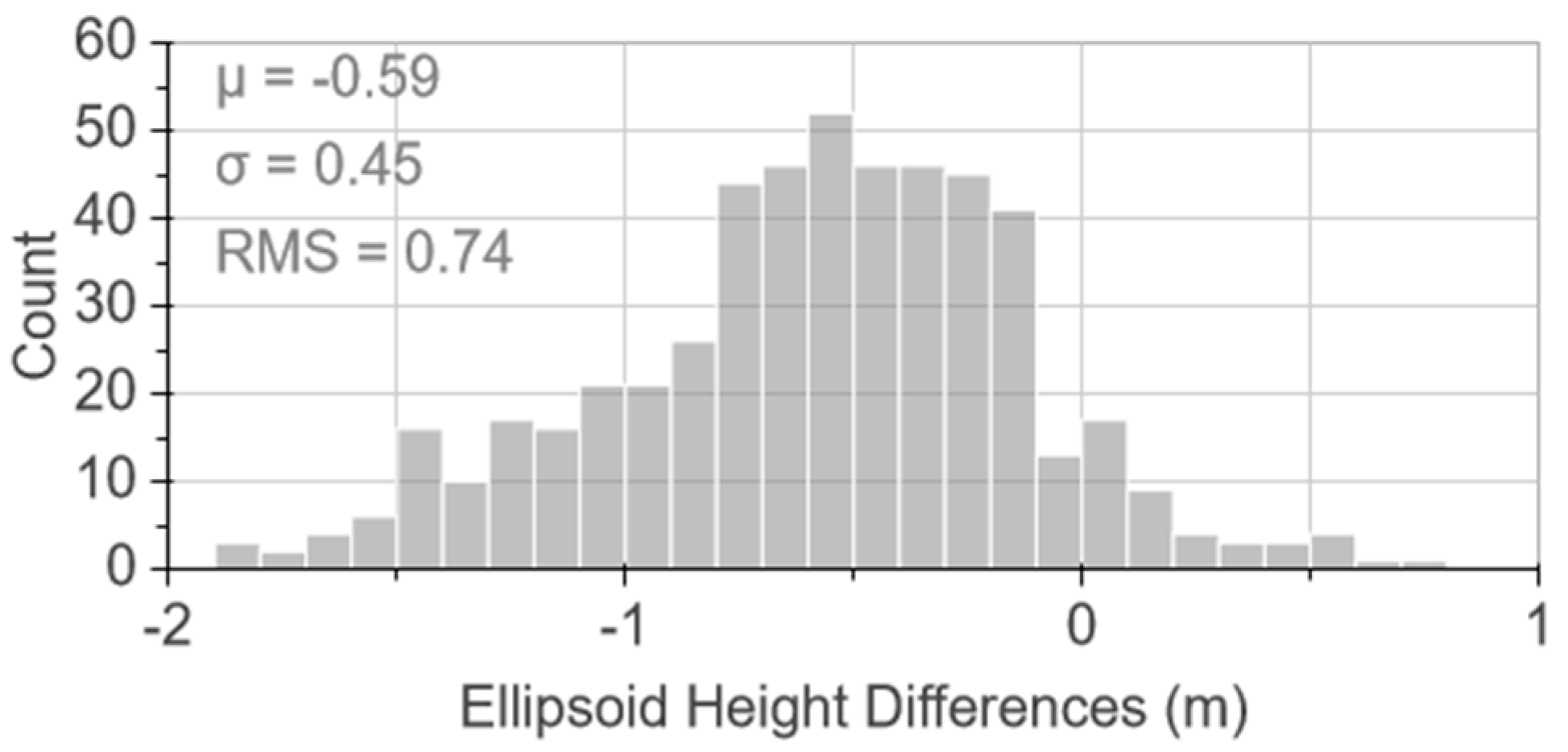
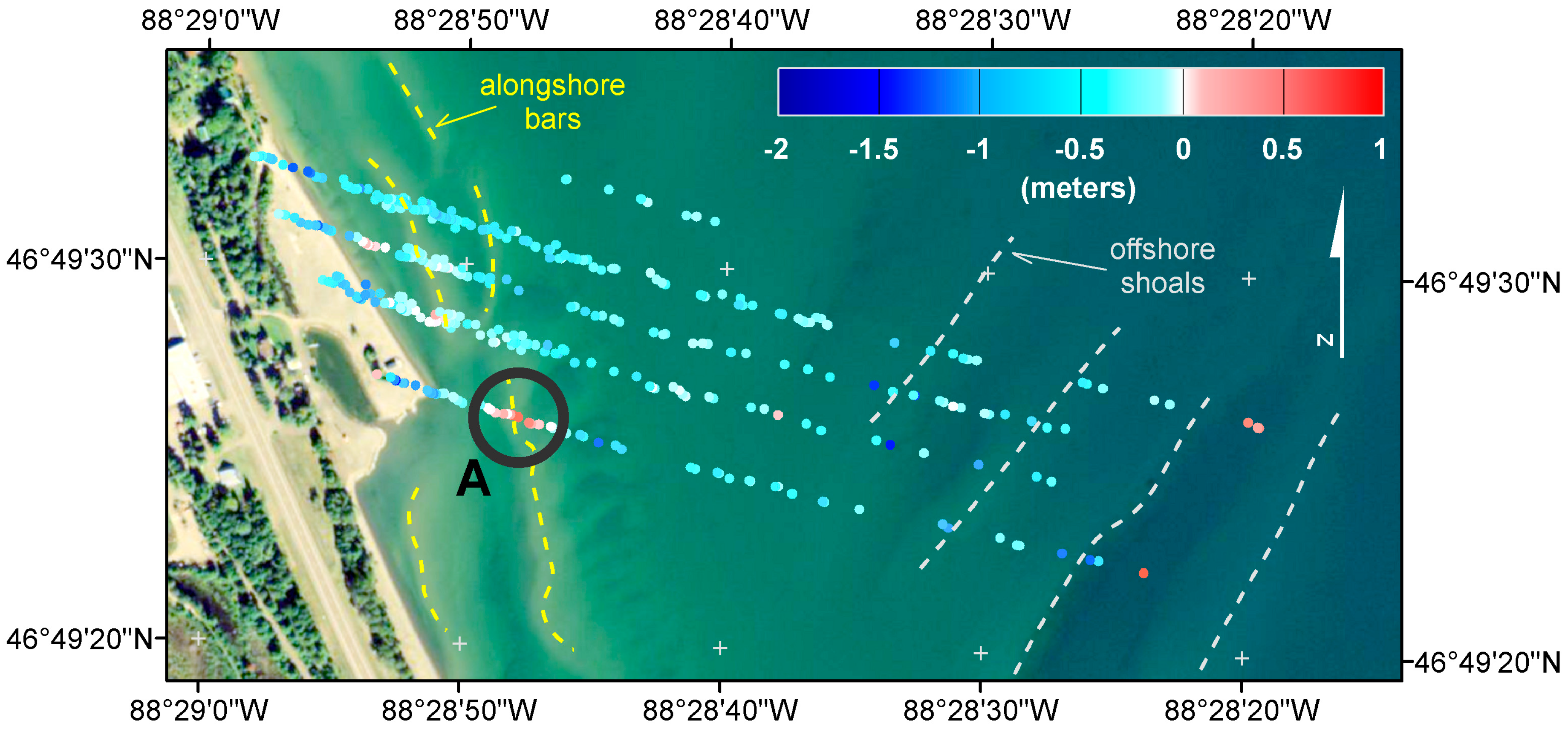
3.2. Bathymetry Accuracy Assessment
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 Laser Altimetry Mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- McGill, M.; Markus, T.; Scott, V.S.; Neumann, T. The Multiple Altimeter Beam Experimental Lidar (MABEL): An airborne simulator for the ICESat-2 Mission. J. Atmos. Ocean. Technol. 2013, 30, 345–352. [Google Scholar] [CrossRef]
- National Research Council (U.S.); Committee on National Needs for Coastal Mapping and Charting. A Geospatial Framework for the Coastal Zone: National Needs for Coastal Mapping and Charting; National Academies Press: Washington, DC, USA, 2004. [Google Scholar]
- Hamylton, S.; Hedley, J.; Beaman, R. Derivation of high-resolution bathymetry from multispectral satellite imagery: A comparison of empirical and optimisation methods through geographical error analysis. Remote Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef]
- Taramelli, A.; Valentini, E.; Innocenti, C.; Cappucci, S. FHYL: Field spectral libraries, airborne hyperspectral images and topographic and bathymetric LiDAR data for complex coastal mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 2270–2273.
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Pe’eri, S.; Azuike, C.; Parrish, C. Satellite-derived bathymetry a reconnaissance tool for hydrography. Hydro Int. 2013, 17, 16–19. [Google Scholar]
- Stewart, C.; Renga, A.; Gaffney, V.; Schiavon, G. Sentinel-1 bathymetry for North Sea palaeolandscape analysis. Int. J. Remote Sens. 2016, 37, 471–491. [Google Scholar] [CrossRef]
- Huang, W.; Fu, B. A spaceborne SAR technique for shallow water bathymetry surveys. J. Coast. Res. 2004, 43, 223–228. [Google Scholar]
- Calkoen, C.J.; Hesselmans, G.H.F.M.; Wensink, G.J.; Vogelzang, J. The Bathymetry Assessment System: Efficient depth mapping in shallow seas using radar images. Int. J. Remote Sens. 2001, 22, 2973–2998. [Google Scholar] [CrossRef]
- Ludeno, G.; Reale, F.; Dentale, F.; Carratelli, E.; Natale, A.; Soldovieri, F.; Serafino, F. An X-band radar system for bathymetry and wave field analysis in a Harbour area. Sensors 2015, 15, 1691–1707. [Google Scholar] [CrossRef] [PubMed]
- NASA Applied Sciences Program: Program Strategy; National Aeronautics and Space Administration: Washington, DC, USA, 2010.
- Yu, A.W.; Stephen, M.A.; Li, S.X.; Shaw, G.B.; Seas, A.; Dowdye, E.; Troupaki, E.; Liiva, P.; Poulios, D.; Mascetti, K. Space laser transmitter development for ICESat-2 mission. Proc. SPIE 2010, 7578, 757809-11. [Google Scholar]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Palm, S.; Yi, D.; Liiva, P. Geoscience Laser Altimeter System (GLAS) on the ICESat Mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Krainak, M.A.; Yu, A.W.; Yang, G.; Li, S.X.; Sun, X. Photon-counting detectors for space-based laser receivers. Proc. SPIE 2010, 7608, 760827-9. [Google Scholar]
- General Bathymetric Chart of the Oceans (GEBCO). Available online: http://www.gebco.net/ (accessed on 25 August 2016).
- International Hydrographic Organization/Organisation Hydrographique Internationale (IHO). Available online: http://www.iho.int/ (accessed on 25 August 2016).
- Intergovernmental Oceanographic Commission. Available online: http://ioc-unesco.org/ (accessed on 25 August 2016).
- US Department of Commerce. NOAA National Centers for Environmental Information (NCEI). Available online: https://www.ngdc.noaa.gov/ngdc.html (accessed on 29 August 2016).
- EMODNET Coastal Mapping. Available online: http://coastal-mapping.eu/ (accessed on 29 August 2016).
- Guenther, G.C. Airborne lidar bathymetry. In Digital Elevation Model Technologies and Applications: The DEM Users Manual; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007; pp. 253–320. [Google Scholar]
- Petrie, G.; Toth, C.K. Airborne and spaceborne laser profilers and scanners. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C.K., Eds.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2009; pp. 29–85. [Google Scholar]
- Hickman, G.D.; Hogg, J.E. Application of an airborne pulsed laser for near shore bathymetric measurements. Remote Sens. Environ. 1969, 1, 47–58. [Google Scholar] [CrossRef]
- Quadros, N.D. Unlocking the characteristics of Bathymetric Lidar sensors. LiDAR Mag. 2013, 3, 62–67. [Google Scholar]
- Pack, R.T.; Brooks, V.; Young, J.; Vilaca, N.; Vatslid, S.; Rindle, P.; Kurz, S.; Parrish, C.; Craig, R.; Smith, P.W. Chapter 2: An overview of ALS technology. In Manual of Airborne Topographic Lidar; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2012; pp. 7–97. [Google Scholar]
- Tulldahl, H.M.; Philipson, P.; Kautsky, H.; Wikström, S.A. Sea floor classification with satellite data and airborne lidar bathymetry. Proc. SPIE 2013, 8724, 87240B-16. [Google Scholar]
- Zavalas, R.; Ierodiaconou, D.; Ryan, D.; Rattray, A.; Monk, J. Habitat classification of temperate marine macroalgal communities using bathymetric LiDAR. Remote Sens. 2014, 6, 2154–2175. [Google Scholar] [CrossRef]
- Wedding, L.M.; Friedlander, A.M.; McGranaghan, M.; Yost, R.S.; Monaco, M.E. Using bathymetric lidar to define nearshore benthic habitat complexity: Implications for management of reef fish assemblages in Hawaii. Remote Sens. Environ. 2008, 112, 4159–4165. [Google Scholar] [CrossRef]
- Miller, A.D.; van Rooyen, A.; Rašić, G.; Ierodiaconou, D.A.; Gorfine, H.K.; Day, R.; Wong, C.; Hoffmann, A.A.; Weeks, A.R. Contrasting patterns of population connectivity between regions in a commercially important mollusc Haliotis rubra: Integrating population genetics, genomics and marine LiDAR data. Mol. Ecol. 2016, 25, 3845–3864. [Google Scholar] [CrossRef] [PubMed]
- Pe’eri, S.; Morgan, L.V.; Philpot, W.D.; Armstrong, A.A. Shoreline mapping resolved from airborne LIDAR bathymetry (ALB) waveforms. J. Coast. Res. Spec. Issue Appl. LIDAR Tech. 2011, 62, 75–85. [Google Scholar]
- Chamberlin, C.; Arcas, D. Modeling Tsunami Inundation for Hazard Mapping at Everett, Washington, from the Seattle Fault (NOAA Technical Memorandum OAR PMEL-147); National Oceanic and Atmospheric Administration, Pacific Marine Environmental Laboratory: Seattle, WA, USA, 2015.
- Mandlburger, G.; Hauer, C.; Wieser, M.; Pfeifer, N. Topo-bathymetric LiDAR for monitoring river morphodynamics and instream habitats—A case study at the Pielach River. Remote Sens. 2015, 7, 6160–6195. [Google Scholar] [CrossRef]
- McKean, J.; Tonina, D.; Bohn, C.; Wright, C.W. Effects of bathymetric lidar errors on flow properties predicted with a multi-dimensional hydraulic model. J. Geophys. Res. Earth Surf. 2014, 119, 644–664. [Google Scholar] [CrossRef]
- Kennedy, D.M.; Ierodiaconou, D.; Schimel, A. Granitic coastal geomorphology: Applying integrated terrestrial and bathymetric LiDAR with multibeam sonar to examine coastal landscape evolution. Earth Surf. Process. Landf. 2014, 39, 1663–1674. [Google Scholar] [CrossRef]
- Finkl, C.W.; Benedet, L.; Andrews, J.L. Interpretation of seabed geomorphology based on spatial analysis of high-density airborne laser bathymetry. J. Coast. Res. 2005, 501–514. [Google Scholar] [CrossRef]
- Houser, C.; Wernette, P.; Rentschlar, E.; Jones, H.; Hammond, B.; Trimble, S. Post-storm beach and dune recovery: Implications for barrier island resilience. Geomorphology 2015, 234, 54–63. [Google Scholar] [CrossRef]
- Irish, J.L.; Lillycrop, W.J. Scanning laser mapping of the coastal zone: the SHOALS system. ISPRS J. Photogramm. Remote Sens. 1999, 54, 123–129. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Wright, C.W.; Nelson, J.M.; Burman, A.R. Evaluation of an experimental LiDAR for surveying a shallow, braided, sand-bedded river. J. Hydraul. Eng. 2007, 133, 838–842. [Google Scholar] [CrossRef]
- Priedhorsky, W.C.; Smith, R.C.; Ho, C. Laser ranging and mapping with a photon-counting detector. Appl. Opt. 1996, 35, 441–452. [Google Scholar] [CrossRef] [PubMed]
- Degnan, J.J. Photon-counting multikilohertz microlaser altimeters for airborne and spaceborne topographic measurements. J. Geodyn. 2002, 34, 503–549. [Google Scholar] [CrossRef]
- Awadallah, M.; Ghannam, S.; Abbott, L.; Ghanem, A. A two-stage algorithm for extraction of ground and top of canopy in photon-counting profiling-LiDAR data in preparation for the ICESat-2 mission. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1353–1356.
- Herzfeld, U.C.; McDonald, B.W.; Wallin, B.F.; Neumann, T.A.; Markus, T.; Brenner, A.; Field, C. Algorithm for detection of ground and canopy cover in micropulse photon-counting lidar altimeter data in preparation for the ICESat-2 Mission. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2109–2125. [Google Scholar] [CrossRef]
- Moussavi, M.S.; Abdalati, W.; Scambos, T.; Neuenschwander, A. Applicability of an automatic surface detection approach to micro-pulse photon-counting lidar altimetry data: Implications for canopy height retrieval from future ICESat-2 data. Int. J. Remote Sens. 2014, 35, 5263–5279. [Google Scholar] [CrossRef]
- Farrell, S.L.; Markus, T.; Kwok, R.; Connor, L. Laser altimetry sampling strategies over sea ice. Ann. Glaciol. 2011, 52, 69–76. [Google Scholar] [CrossRef]
- Kwok, R.; Markus, T.; Morison, J.; Palm, S.P.; Neumann, T.A.; Brunt, K.M.; Cook, W.B.; Hancock, D.W.; Cunningham, G.F. Profiling sea ice with a Multiple Altimeter Beam Experimental Lidar (MABEL). J. Atmos. Ocean. Technol. 2014, 31, 1151–1168. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Walsh, K.M.; Markus, T. Determination of local slope on the Greenland ice sheet using a multibeam photon-counting lidar in preparation for the ICESat-2 Mission. IEEE Geosci. Remote Sens. Lett. 2014, 11, 935–939. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Amundson, J.M.; Kavanaugh, J.L.; Moussavi, M.S.; Walsh, K.M.; Cook, W.B.; Markus, T. MABEL photon-counting laser altimetry data in Alaska for ICESat-2 simulations and development. Cryosphere 2016, 10, 1707–1719. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Z.; Glennie, C. A novel noise filtering model for photon-counting laser altimeter data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 947–951. [Google Scholar] [CrossRef]
- Magruder, L.A.; Wharton, M.E.; Stout, K.D.; Neuenschwander, A.L. Noise filtering techniques for photon-counting ladar data. Proc. SPIE 2012, 8379. [Google Scholar] [CrossRef]
- Horan, K.H.; Kerekes, J.P. An automated statistical analysis approach to noise reduction for photon-counting lidar systems. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 4336–4339.
- Shrestha, K.Y.; Carter, W.E.; Slatton, K.C.; Cossio, T.K. Shallow bathymetric mapping via multistop single photoelectron sensitivity laser ranging. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4771–4790. [Google Scholar] [CrossRef]
- Jasinski, M.F.; Stoll, J.D.; Cook, W.B.; Ondrusek, M.; Stengel, E. Inland and near shore water profiles derived from high altitude, Multiple Altimeter Beam Experimental Lidar (MABEL). J. Coast. Res. 2016, in press. [Google Scholar]
- Cossio, T.; Slatton, K.C.; Carter, W.; Shrestha, K.; Harding, D. Predicting topographic and bathymetric measurement performance for low-SNR airborne lidar. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2298–2315. [Google Scholar] [CrossRef]
- Effler, S.W.; Perkins, M.; Peng, F.; Strait, C.; Weidemann, A.D.; Auer, M.T. Light-absorbing components in Lake Superior. J. Gt. Lakes Res. 2010, 36, 656–665. [Google Scholar] [CrossRef]
- Yousef, F.; Kerfoot, W.C.; Brooks, C.N.; Shuchman, R.; Sabol, B.; Graves, M. Using LiDAR to reconstruct the history of a coastal environment influenced by legacy mining. J. Gt. Lakes Res. 2013, 39, 205–216. [Google Scholar] [CrossRef]
- Kerfoot, W.C.; Yousef, F.; Green, S.A.; Regis, R.; Shuchman, R.; Brooks, C.N.; Sayers, M.; Sabol, B.; Graves, M. Light detection and ranging (LiDAR) and multispectral studies of disturbed Lake Superior coastal environments. Limnol. Oceanogr. 2012, 57, 749–771. [Google Scholar] [CrossRef]
- Biberhofer, J. Aquatic Substrate Mapping in Support of the Keweenaw Bay Indian Community’s Conservation Management Objectives; Environment Canada, National Water Research Institute: Burlington, ON, Canada, 2002. [Google Scholar]
- Cook, W.B.; NASA Goddard Space Flight Center, Greenbelt, MD, USA. Personal communication, 2016.
- Neumann, T.A.; NASA Goddard Space Flight Center, Greenbelt, MD, USA. Personal communication, 2016.
- Brunt, K.; Cryospheric Sciences Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, USA. Personal communication, 2016.
- National Oceanic and Atmospheric Administration, Coastal Services Center (NOAA CSC). Report of Survey, Lake Superior Bathymetric Lidar (Contract EA133C-05-CQ-1051); NOAA CSC: Charleston, SC, USA, 2011.
- Glennie, C.; National Center for Airborne Laser Mapping, University of Houston, Houston, TX, USA. Unpublished Data. 2016.
- Arroyo-Suarez, E.N.; Riley, J.L.; Glang, C.D.R.; Mabey, L.T. Evaluating a global differential GPS system for hydrographic surveying. In Proceedings of the MTS IEEE OCEANS, Washington, DC, USA, 18–23 September 2005; pp. 2557–2563.
- Dodd, D.; Mills, J. Ellipsoidally referenced surveys: Issues and solutions. Int. Hydrogr. Rev. 2011, 6, 19–30. [Google Scholar]
- Myers, E.; Wong, A.; Hess, K.; White, S.; Spargo, E.; Feyen, J.; Yang, Z.; Richardson, P.; Auer, C.; Sellars, J.; et al. Development of a National VDatum, and its application to sea level rise in North Carolina. In Proceedings of United States Hydrographic Conference, San Diego, CA, USA, 29–31 March 2005.
- Parker, B.; Hess, K.; Milbert, D.; Gill, S. A national vertical datum transformation tool. Sea Technol. 2003, 44, 10–15. [Google Scholar]
- NOAA NGS Great Lakes Low Water Datums. Available online: https://tidesandcurrents.noaa.gov/gldatums.html (accessed on 7 July 2016).
- Quadros, N.D.; Collier, P.A.; Fraser, C.S. Integration of bathymetric and topographic LiDAR: a preliminary investigation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 36, 1299–1304. [Google Scholar]
- Tuell, G.; Barbor, K.; Wozencraft, J. Overview of the coastal zone mapping and imaging lidar (CZMIL): A new multisensor airborne mapping system for the U.S. Army Corps of Engineers. Proc. SPIE 2010, 7695. [Google Scholar] [CrossRef]
- Pe’eri, S.; Philpot, W. Increasing the existence of very shallow-water LIDAR measurements using the red-channel waveforms. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1217–1223. [Google Scholar] [CrossRef]
- Guenther, G.C.; Cunningham, A.G.; LaRocque, P.E.; Reid, D.J. Meeting the accuracy challenge in airborne bathymetry. In Proceedings of EARSeL-SIG-Workshop LIDAR, Dresden, Germany, 16–17 June 2000.
- Ward, L.; University of New Hampshire, Department of Earth Sciences, Center for Coastal and Ocean Mapping. Personal communication, 2016.
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Brusch, S.; Held, P.; Lehner, S.; Rosenthal, W.; Pleskachevsky, A. Underwater bottom topography in coastal areas from TerraSAR-X data. Int. J. Remote Sens. 2011, 32, 4527–4543. [Google Scholar] [CrossRef]
- Hogrefe, K.R.; Wright, D.J.; Hochberg, E.J. Derivation and integration of shallow-water bathymetry: Implications for coastal terrain modeling and subsequent Analyses. Mar. Geod. 2008, 31, 299–317. [Google Scholar] [CrossRef]
- Chust, G.; Galparsoro, I.; Borja, Á.; Franco, J.; Uriarte, A. Coastal and estuarine habitat mapping, using LIDAR height and intensity and multi-spectral imagery. Estuar. Coast. Shelf Sci. 2008, 78, 633–643. [Google Scholar] [CrossRef]
- Deronde, B.; Houthuys, R.; Debruyn, W.; Fransaer, D.; Lancker, V.V.; Henriet, J.-P. Use of Airborne hyperspectral data and Laserscan data to study beach morphodynamics along the Belgian Coast. J. Coast. Res. 2006, 225, 1108–1117. [Google Scholar] [CrossRef]
- Elaksher, A.F. Fusion of hyperspectral images and lidar-based dems for coastal mapping. Opt. Lasers Eng. 2008, 46, 493–498. [Google Scholar] [CrossRef]
- Gilvear, D.; Tyler, A.; Davids, C. Detection of estuarine and tidal river hydromorphology using hyper-spectral and LiDAR data: Forth estuary, Scotland. Estuar. Coast. Shelf Sci. 2004, 61, 379–392. [Google Scholar] [CrossRef]
- Jones, T.G.; Coops, N.C.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest, Canada. Remote Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Lee, D.S.; Shan, J. Combining lidar elevation data and IKONOS multispectral imagery for coastal classification mapping. Mar. Geod. 2003, 26, 117–127. [Google Scholar] [CrossRef]
- Arsen, A.; Crétaux, J.-F.; Berge-Nguyen, M.; del Rio, R. Remote sensing-derived bathymetry of Lake Poopó. Remote Sens. 2013, 6, 407–420. [Google Scholar] [CrossRef]

| Green Channel | Energy Level (Metadata) | Energy Level (Reclassified) | Angle (Mrad) | Elevation (Mrad) |
|---|---|---|---|---|
| 1 | Low | Low | 5.0 | −1.5 |
| 3 | High | Low | −2.2 | −0.5 |
| 4 | High | Low | −0.2 | −0.5 |
| 5 | High | High | −5.0 | −1.5 |
| 6 | High | High | 0.0 | −1.5 |
| 7 | Low | Low | 1.8 | −0.5 |
| 8 | Low | High | −2.0 | −1.5 |
| 9 | Low | Low | 2.2 | −2.5 |
| 10 | High | Low | 0.2 | −2.5 |
| 11 | Low | High | 2.0 | −1.5 |
| 12 | High | Low | −1.9 | −2.0 |
| 14 | Low | Low | −2.1 | −1.0 |
| 15 | Low | Low | −1.8 | −2.5 |
| Variable | Value | Unit | Description |
|---|---|---|---|
| - | Detector quantum efficiency (Hamamatsu PMT H7260) | ||
| - | Receiver optical efficiency | ||
| - | Transmitter optical efficiency | ||
| 0.04 and 0.2 | µJ | Transmitted energy per channel pulse | |
| - | Bottom reflectance at laser wavelength, λ | ||
| 0.1 | rad | Incidence angle on lake bottom | |
| m2 | Collecting area of receiver aperture | ||
| m | Pulse travel distance in air | ||
| - | Reflectance of air-water interface | ||
| - | One-way atmospheric transmittance | ||
| m−1 | Effective total beam attenuation coefficient |
| Variable | Description |
|---|---|
| GLFCS water level (w.r.t. Lake Superior low water datum) | |
| Channel-specific water-level bias | |
| Lake Superior LWD–IGLD85 offset (183.2 m, by definition) | |
| Uncorrected channel water-surface ellipsoid height | |
| Raw depth (without index-of-refraction correction) | |
| Depth (with index-of-refraction correction) | |
| D adjusted vertically for | |
| Raw photon ellipsoid elevation | |
| Final photon ellipsoid elevation | |
| WGS84-NAD83 separation | |
| NAD84-IGLD85 separation | |
| Index of refraction for air | |
| Index of refraction for fresh water |
| Depth (m) | Low Energy Channels (0.04 µJ) | High Energy Channels (0.2 µJ) | ||||
|---|---|---|---|---|---|---|
| (1, 3, 4, 7, 9, 10, 12, 14, 15) | (5, 6, 8, 11) | |||||
| Expected | Observed | Difference | Expected | Observed | Difference | |
| 0–1 | 0.003 | 0.001 | −0.003 | 0.017 | 0.005 | −0.013 |
| 1–2 | 0.002 | 0.002 | 0.000 | 0.012 | 0.015 | 0.003 |
| 2–3 | 0.001 | 0.001 | −0.001 | 0.007 | 0.003 | −0.003 |
| 3–4 | 0.001 | 0.001 | 0.000 | 0.004 | 0.004 | 0.000 |
| 4–5 | 0.001 | 0.000 | 0.000 | 0.003 | 0.001 | −0.001 |
| 5–6 | 0.000 | 0.000 | 0.000 | 0.002 | 0.002 | 0.000 |
| 6–7 | 0.000 | 0.000 | 0.000 | 0.001 | 0.001 | 0.000 |
| 7–8 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 |
| Parameter | MABEL | ATLAS |
|---|---|---|
| Laser footprint () | 2 m (100 µrad) | 15 m (31 µrad) |
| Field of View | 4.2 m (210 µrad) | 41 m (83 µrad) |
| Laser pulse repetition freq. | 5–20 kHz | 10 kHz |
| Pulse energy | 5–7 µJ (0.04–0.2 J) | 41/160 µJ |
| Pulse pattern | 16 532-nm beams, 8 1054-nm beams | 6 beams (3 pairs of 2) |
| Swath width | 2 km (max) (variable) | 6 km |
| Wavelength | 532 and 1064 nm | 532 nm |
| Filter width | ~150/~400 pm (532/1064 nm) | 30 pm |
| Receiver aperture area | 0.013 m2 | 0.79 m2 |
| Operational altitude | 20 km | 500 km |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forfinski-Sarkozi, N.A.; Parrish, C.E. Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote Sens. 2016, 8, 772. https://doi.org/10.3390/rs8090772
Forfinski-Sarkozi NA, Parrish CE. Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote Sensing. 2016; 8(9):772. https://doi.org/10.3390/rs8090772
Chicago/Turabian StyleForfinski-Sarkozi, Nicholas A., and Christopher E. Parrish. 2016. "Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS" Remote Sensing 8, no. 9: 772. https://doi.org/10.3390/rs8090772
APA StyleForfinski-Sarkozi, N. A., & Parrish, C. E. (2016). Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote Sensing, 8(9), 772. https://doi.org/10.3390/rs8090772