A Simple Harmonic Model for FAPAR Temporal Dynamics in the Wetlands of the Volga-Akhtuba Floodplain
Abstract
:1. Introduction
1.1. Background
1.2. FAPAR Index
1.3. FAPAR Temporal Dynamics
1.4. Test Sites
2. Methodology and Data
2.1. General Considerations
2.2. Additional Constraints
2.3. Computing Harmonic Coefficients Using Reference Data and the Least Squares Method
2.4. Accuracy Assessment
2.5. Reference Data
3. Results
3.1. FAPAR Yearly Temporal Dynamics Model
- is Day Of Year;
- is the beginning of a growing season; for the Volga-Akhtuba floodplain, we assume (i.e., the beginning of March);
- is the end of a growing season; for the Volga-Akhtuba floodplain, we accept (i.e., the end of November);
- t is the relative (dimensionless) time within the growing season;
- n is the total number of harmonics; currently, we suppose n is in the range from 4–6; for all 15 test sites, the sixth harmonic has an amplitude of less than , which is definitely beyond the accuracy of the determination of the FAPAR index itself [26];
- j is the number of the harmonic terms;
- , , are the harmonic coefficients computed using an almost standard (except for some additional constraints and weighting described in Section 2) least squares methodology for the reference FAPAR time series;
- small f is used instead of just to clearly distinguish between the function of and the function of relative normalized time t;
- means modulo M operation, which is reasonable for regions where is greater than (e.g., in the Southern Hemisphere); in our case because 365 is the longest time interval between two different days within a year.
3.2. Model-Based Indicators
- , a yearly mean FAPAR value.
- , amplitude of the main harmonic and peak-to-peak amplitude (main harmonic overall span) :
- , maximum value of the FAPAR model function:
- , weighted active vegetation period (expressed in days), which is defined as the integral of a special weighting function, , over time. This function has two parameters, and , which are physically interpreted as the “FAPAR value of definitely low vegetation activity” and the “FAPAR value of definitely high vegetation activity,” respectively.For all days with a FAPAR value higher than , that is, the “high vegetation activity” threshold, just counts these days (since weighting function equals one). All days having a FAPAR value lower than , that is, the “low vegetation activity” threshold, are ignored (because the weighting function is zero). Finally, days with transition values of FAPAR between and are counted with weights proportional to the difference between the day’s FAPAR value and the threshold. This approach allows avoiding a leap between vegetation period estimates for FAPAR time series that are close to the threshold, but slightly lower or higher. Without weighting, given only one threshold parameter , a vegetation activity with FAPAR of on a 100-day period, for example, will be considered high for . However, the same vegetation activity with FAPAR will be considered low. Meanwhile, the accuracy of the FAPAR estimation is often off by several hundredths; thus, the practical difference between and is completely negligible. Therefore, weighting is required to obtain adequate estimates without leaps like those shown above. For the test sites under study, and are accepted as and , respectively.
- , the phase of the main harmonic,
- , the secondary harmonics’ intensity ratio (i.e., the ratio between the cumulative amplitude of all secondary harmonics and the amplitude of the main harmonic). It represents how “wobbly” the reference FAPAR curve is.
- , the day when the FAPAR model function reaches its maximum:
3.3. Application to Test Sites
4. Discussion
4.1. A Comparison of the Model with Reference Data and Vegetation Activity Observed in the Field
4.2. Model Accuracy and Limitations
- , weighted mean of residuals between the model and actual data, indicating whether the model is biased from the actual data. For all test sites, this value appeared to be effectively zero, as expected.
- , weighted root-mean-square deviation of residuals between the model and actual data, showing the degree of its consistency. appeared to be – in all cases, which corresponds well to the uncertainty of FAPAR observations themselves. Some evident examples of errors in reference FAPAR observations with the magnitude of – are seen in Figure 2a,b,d in winter (between Days of Year 0 and 50).
- , theoretically-estimated standard deviation of the model, based on the accuracy of reference data and observability properties of the estimation problem for harmonic coefficients. This measures the theoretical predictive power of the model for situations in which no significant anomalies are present, as compared to the reference dataset. Anyway, strongly depends on a priori estimated values for the uncertainty of FAPAR observations, which are typically not very accurate in the reference data. Thus, should be viewed a bit like an order-of-magnitude measure for what it is intended to indicate. These quantities turned out to be around –. In Figure 2, the estimated 2-σ corridors around the model are shown in yellow. They mean 95% probability to fit for the Gaussian distribution of errors.
5. Conclusions
- The designed model function matches well with actual data. All quality measures are consistent and acceptable. The predicted and validated accuracy of the model is at a level of several hundredths (typically –, compared to a full FAPAR range of one).
- Model-derived indicators can be used for plant cover and ecosystem type classification.
- Indicators can also serve as an objective measure of plant cover health and its seasonal and interannual dynamics. They allow quantitative description of anomalies, which is illustrated for the degradation of ecosystems in 2006, which was abnormally dry. The efficiency of runoff regulations can be estimated by comparison of model-derived quantities to reference values.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FAPAR | Fraction of absorbed photosynthetically-active radiation |
| DOY | Day of year |
| GIS | Geographic Information System |
| GRASS | Geographic Resources Analysis Support System |
| MERIS | MEdium-spectral Resolution Imaging Spectrometer |
| JRC | Joint Research Center of the European Commission |
| RMS | Root-mean-square |
| SeaWiFS | Sea-viewing Wide Field-of-view Sensor |
References
- Saadati, S.; Eslamian, S. Application of indicators of hydrologic alteration for evaluating environmental impacts of Dam operation during drought periods: A case study. In Proceedings of the 5th International Conference of Water Resources and Sustainable Development, Algiers, Algeria, 24–25 February 2013; pp. 727–734.
- Kozlova, M.V.; Gorelits, O.V.; Sapozhnikova, A.A.; Kozlov, A.V.; Zemlianov, I.V. Application of Spectral Indices Including Landsat Tasseled Cap Transformation to State Estimation of Wetlands under Natural and Regulated Hydrological Regime Changes and Direct Human Impact in Volga-Akhtuba Floodplain. Available online: https://istina.msu.ru/publications/article/11455210/ (accessed on 31 August 2016).
- Goss, K.F. Environmental flows, river salinity, and biodiversity conservation: Managing trade-offs in the Murray-Darling basin. Aust. J. Bot. 2003, 51, 619–625. [Google Scholar] [CrossRef]
- Catford, J.A.; Downes, J.B.; Gippel, C.J.; Peter, A.; Vesk, P.A. Flow regulation reduces native plant cover and facilitates exotic invasion in riparian wetlands. J. Appl. Ecol. 2011, 48, 432–442. [Google Scholar] [CrossRef]
- Gorelits, O.V.; Zemlianov, I.V.; Sapozhnikova, A.A. Inter-annual and seasonal variability of the basic hydrological parameters in Lower Volga at Volgograd station. In The Scientific and Practical Conference “Specially Protected Natural Areas of Lower Volga as the Essential for the Biodiversity Conservation: Results, Problems and Perspectives”; Astrakhan University Publishing: Astrakhan, Russia, 2010. (In Russian) [Google Scholar]
- Zemlianov, I.V.; Gorelits, O.V. The main tasks of the monitoring of water bodies in the Lower Volga. In Proceedings of Water Resources of the Volga. Present, Future Management Challenges, Astrakhan, Russia, 26–27 May 2008. (In Russian)
- Verstraete, M.M.; Scholes, R.J.; Smith, M.S. Climate and desertification: Looking at an old problem through new lenses. Front. Ecol. Environ. 2009, 7, 421–428. [Google Scholar] [CrossRef]
- Erwin, K.L. Wetlands and global climate change: The role of wetland restoration in a changing world. Wetl. Ecol. Manag. 2009, 17, 71–84. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soltani, S. Determination of water requirements of the Gavkhuni wetland, Iran: A hydrological approach. J. Arid. Environ. 2013, 98, 27–40. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Pittock, J.; Williams, J.; Jiang, Q.; Possingham, H.; Quiggin, J. Water planning and Hydro-Climatic Change in the Murray-Darling Basin, Australia. AMBIO 2014, 43, 1082–1092. [Google Scholar] [CrossRef] [PubMed]
- Semeraro, T.; Giannuzzi, C.; Beccarisi, L.; Aretano, R.; De Marco, A.; Pasimeni, M.R.; Zurlini, G.; Petrosillo, I. A constructed treatment wetland as an opportunity to enhance biodiversity and ecosystem services. Ecol. Eng. 2015, 82, 517–526. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Gobron, N.; Aussedat, O.; Robustelli, M.; Pinty, B.; Widlowski, J.-L.; Taberner, M. An automatic procedure to identify key vegetation phenology events using the JRC-FAPAR products. Adv. Space Res. 2008, 41, 1773–1783. [Google Scholar] [CrossRef]
- Baron, J.S.; Poff, L.; Angermeier, P.L.; Dahm, C.N.; Gleik, P.H.; Hairston, N.G., Jr.; Jackson, R.B.; Johnston, C.A.; Richter, B.D.; Steinman, A.D. Sustaining healthy freshwater ecosystems. Issues Ecol. 2003, 10, 1–16. [Google Scholar]
- Sadoddin, A.; Sheikh, V.; Mostafazadeh, R.; Halili, M.G. Analysis of vegetation-based management scenarios using MCDM in the Ramian watershed, Golestan, Iran. Int. J. Plant Prod. 2010, 4, 51–62. [Google Scholar]
- Acreman, M.; Dunbar, M.J. Defining environmental river flow requirements—A review. Hydrol. Earth Syst. Sci. 2004, 8, 861–876. [Google Scholar] [CrossRef]
- Starichkova, K.N.; Barmin, A.N.; Iolin, M.M.; Sharova, I.S.; Sorokin, A.N.; Nikolaychuk, L.F.; Golub, V.B. Estimate of vegetation dynamics along the transect in the northern part of the Volga-Akhtuba floodplain. Arid. Ecosyst. 2009, 15, 39–51. (In Russian) [Google Scholar]
- Sorokin, A.N.; Barmin, A.N.; Iolin, M.M.; Starichkova, K.A.; Nikolaychuk, L.F.; Golub, V.B. Indication of the environment change on transect in the Volga-Akhtuba flood-plain near Kapustin Yar village by using of Ramenskiy indicator values and DCA-ordination. Vestnik Volz. Univ. V.N. Tatischev 2010, 10, 12–15. (In Russian) [Google Scholar]
- Golub, V.B.; Bondareva, V.V.; Sorokin, A.N.; Barmin, A.N.; Iolin, M.M.; Nikolaychuk, L.F. Dynamics of meadow vegetation in the northern part of Volga-Akhtuba floodplain (1928–2009). Vestnik Volz. Univ. V.N. Tatischev 2011, 12, 52–65. (In Russian) [Google Scholar]
- Golub, V.B.; Barmin, A.N.; Iolin, M.M.; Starichkova, K.A.; Sorokin, A.N.; Sharova, I.S.; Nikolaychuk, L.F. Estimate of vegetation dynamics along the transect of the southern part of the Volga-Akhtuba floodplain near Hosheutovo village. Izv. Samar. Nauchnogo Tsentra Russ. Acad. Sci. 2011, 13, 107–113. (In Russian) [Google Scholar]
- Iolin, K.A.; Sorokin, A.N.; Iolin, M.M.; Starichkova, K.A.; Barmin, A.N.; Nikolaychuk, L.F.; Golub, V.B. Vegetation dynamics estimation along a transect in the Volga-Akhtuba floodplain near Kapustin Yar village. Povolz. Ekol. Zhurnal 2011, 4, 431–441. (In Russian) [Google Scholar]
- European Commission JRC FAPAR Algorithm. Available online: fapar.jrc.ec.europa.eu/WWW/Data/Pages/FAPAR_Algorithms/FAPAR_Algorithms_Fapar.php (accessed on 11 May 2016).
- Gorelits, O.V.; Zemlianov, I.V. Modern mechanism of flooding in the territories of the Volga-Akhtuba floodplain during flood (within Volgograd region). Sci. Potential Reg. Serv. Mod. Spec. Issue 2013, 2, 9–18. (In Russian) [Google Scholar]
- Kozlova, M.V.; Sapozhnikova, A.A.; Zemlianov, I.V.; Gorelits, O.V. The assessment of plant cover conditions at Volga-Akhtuba valley based on Remotely Sensed data and analysis of hydrological regime parameters during a period of regulated Volga runoff. 2015. (In Russian) [Google Scholar] [CrossRef]
- Summary Report of the Eleventh Session of the WMO-IOC-UNEP-ICSU, Steering Committee for GCOS, WMO/TD 1189; World Meteorological Organization: Melbourne, Australia, 2003.
- Pickett-Heaps, C.A.; Canadell, J.G.; Briggs, P.R.; Gobron, N.; Haverd, V.; Paget, M.J.; Pinty, B.; Raupach, M.R. Evaluation of six satellite-derived Fraction of Absorbed Photosynthetic Active Radiation (FAPAR) products across the Australian continent. Remote Sens. Environ. 2014, 140, 241–256. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Faber, O.; Mélin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS—Impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ. 2008, 112, 1871–1883. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussedat, O.; Chen, J.M.; Cohen, W.B.; Fensholt, R.; Gond, V.; Huemmrich, K.F.; Lavergne, T.; Mélin, F.; et al. Evaluation of fraction of absorbed photosynthetically active radiation products for different canopy radiation transfer regimes: Methodology and results using Joint Research Center products derived from SeaWiFS against ground-based estimations. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Govaerts, Y. A semidiscrete model for the scattering of light by vegetation. J. Geophys. Res. 1997, 102, 9431–9446. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. fAPAR (fraction of Absorbed Photosynthetically Active Radiation) estimates at various scale. In Proceedings of the 34th International Symposium on Remote Sensing of Environment, Sydney, Australia, 10–15 April 2011.
- Klisch, A.; Royer, A.; Lazar, C.; Baruth, B.; Genovese, G. Extraction of phenological parameters from temporally smoothed vegetation indices. In Proceedings of ISPRS WG VIII/10 Workshop: Remote Sensing Support to Crop Yield Forecast and Area Estimates, Stresa, Italy, 30 November–1 December 2006.
- European Commission JRC FAPAR Download Page. Available online: fapar.jrc.ec.europa.eu/WWW/Data/Pages/FAPAR_Download/FAPAR_Download.php (accessed on 11 May 2016).
- Pinty, B.; Gobron, N.; Mélin, F.; Verstraete, M.M. A Time Composite Algorithm for FAPAR Products. Theoretical Basis Document. Version 1.0; Institute for Environment and Sustainability Joint Research Centre: Ispra (VA), Italy, 2002. [Google Scholar]
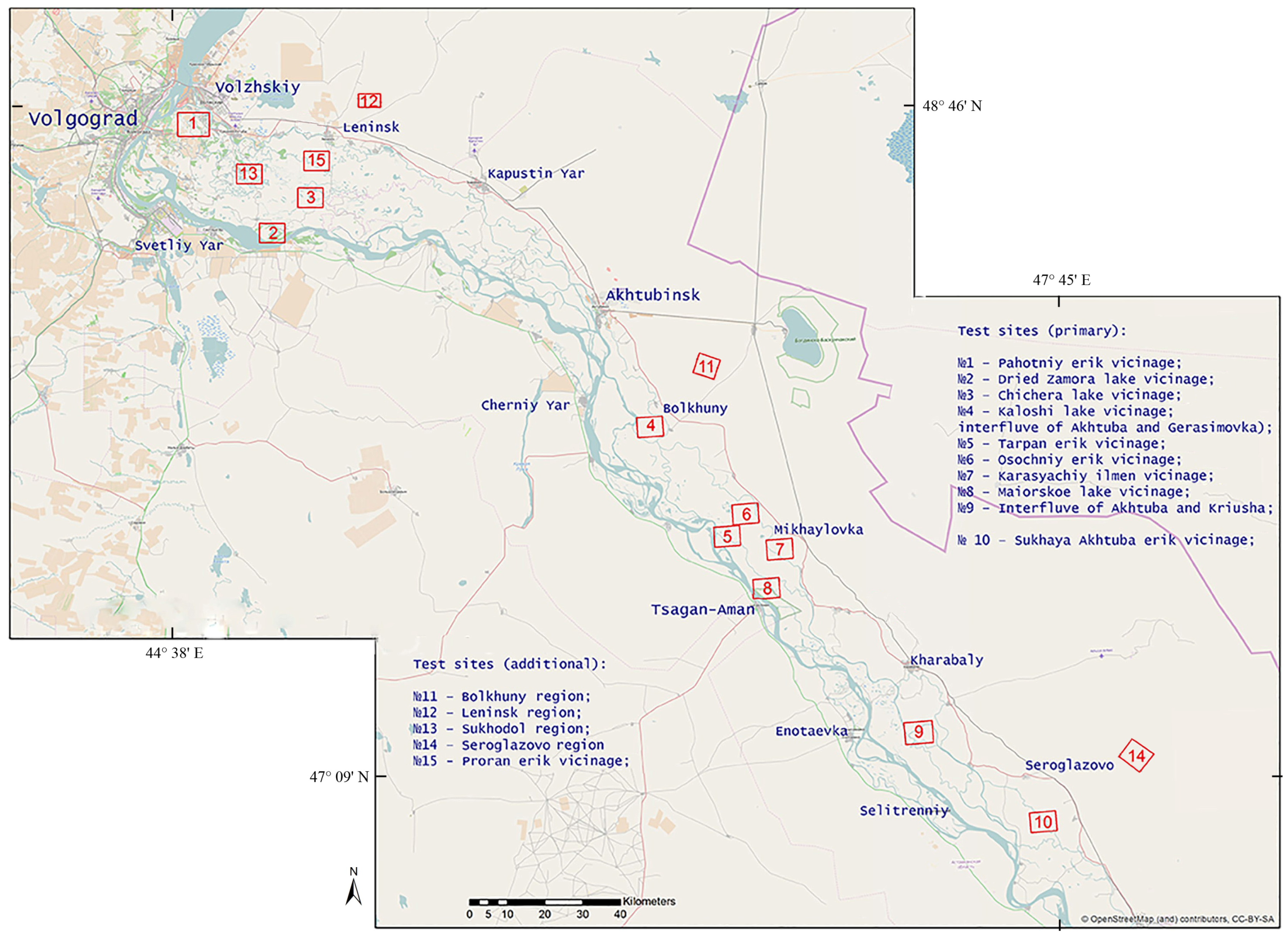

| Ref. No. | Site Name/Land Type | Location (N Latitude, E Longitude) | Prevailing Plant Cover Type |
|---|---|---|---|
| 1 | Pahotniy runnel vicinage | Woodlands (oakeries, black poplar and ash communities), abandoned agricultural lands | |
| 2 | Zamora/dried lake vicinage | Woodlands (black poplar and ash communities), secondary feather grass-sagebrush steppe | |
| 3 | Chichera lake vicinage | Steppe meadows and cereal meadows | |
| 4 | Kaloshi lake vicinage | Cereal meadows | |
| 5 | Tarpan runnel vicinage | Herb and cereal meadows temporally varying in proportions, partially overgrazed | |
| 6 | Osochniy runnel vicinage | Cereal and Glycyrrhiza glabra meadows, partially overgrazed | |
| 7 | Karasyachiy Ilmen vicinage | Cereal with Glycyrrhiza glabra meadows and steppe meadows | |
| 8 | Maiorskoe lake vicinage | Herb and cereal meadows temporally varying in proportions | |
| 9 | Akhtuba-Kriusha interfluve | Herb and cereal meadows with Glycyrrhiza glabra temporally varying in proportions | |
| 10 | Sukhaya Akhtuba runnel vicinage | Herb and cereal meadows temporally varying in proportions | |
| 11 | Bolkhuny desert | Desert, overgrazed | |
| 12 | Leninsk steppe | Dry steppe | |
| 13 | Sukhodol crop fields | Woodlands (ash and oleaster communities), settlements and abandoned agricultural lands | |
| 14 | Seroglazovo desert | Desert | |
| 15 | Proran runnel vicinage | Marshes |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlov, A.; Kozlova, M.; Skorik, N. A Simple Harmonic Model for FAPAR Temporal Dynamics in the Wetlands of the Volga-Akhtuba Floodplain. Remote Sens. 2016, 8, 762. https://doi.org/10.3390/rs8090762
Kozlov A, Kozlova M, Skorik N. A Simple Harmonic Model for FAPAR Temporal Dynamics in the Wetlands of the Volga-Akhtuba Floodplain. Remote Sensing. 2016; 8(9):762. https://doi.org/10.3390/rs8090762
Chicago/Turabian StyleKozlov, Alexander, Maria Kozlova, and Nikolai Skorik. 2016. "A Simple Harmonic Model for FAPAR Temporal Dynamics in the Wetlands of the Volga-Akhtuba Floodplain" Remote Sensing 8, no. 9: 762. https://doi.org/10.3390/rs8090762
APA StyleKozlov, A., Kozlova, M., & Skorik, N. (2016). A Simple Harmonic Model for FAPAR Temporal Dynamics in the Wetlands of the Volga-Akhtuba Floodplain. Remote Sensing, 8(9), 762. https://doi.org/10.3390/rs8090762






