The algorithm performance and accuracy were tested on two MLS datasets from RoamerR2. The datasets contain points from a 2.1 km road section of the Ring III road that gives access to the Finnish Geospatial Research Institute (FGI), in Masala, Southern Finland. It is a non-straight interurban stretch of road, whose asphalt/road edge is not always very clear, as in some sections it is leveled or almost leveled with compact terrain. Cracks and different asphalt patches occur frequently on the road surface.
3.1. MLS System and Point Cloud Dataset Description
The RoamerR2 system consists of a GNSS-IMU positioning system and FARO Focus 3D 120S laser scanner (FARO Focus3D Features, Benefits & Technical Specifications, Lake Mary, FL, USA) for cross-track profiling of the road environment. The data acquisition and positioning sensors, NovAtel Flexpak6 GNSS receiver, 702GG antenna, and UIMU-LCI IMU (NovAtel Inc., Calgary, AB, Canada), are mounted on a single integration plate that could be mounted on any imaginable support structure, as shown in
Figure 7.
In the RoamerR2 installation for this study the scanner was mounted on top of a car at 3.4 m elevation from the road surface below. Laser data was acquired at 95 Hz scan frequency and 244 kHz point measurement rate (scanner setting 1/16 at 3× noise compression) resulting in 2.4 mrad angular resolution of the data (i.e., 8 mm point spacing at nadir on the road surface). The LiDAR data was recorded on the scanner SD card, while the 200 Hz positioning data was stored on a tablet computer used to control the positioning system. The positioning data was post-processed with virtual GNSS reference base station data from Trimnet Service by Geotrim Oy, Finland, for accurate 3D trajectory of the system. Georeferenced point cloud data was then generated with proprietary tools using sensor bore-sight calibration and time stamp information.
The test dataset consist of two different point clouds: (i) Dataset 1, with 38 million points, and obtained with the vehicle moving from south to north; and (ii) Dataset 2, with 33 million points, and obtained with the vehicle moving in the opposite direction. The distance between consecutive points along the sweeps ranges between 8 mm and more than 20 cm, and the distance between sweeps along the trajectory is, on average, 10 cm.
3.5. Results
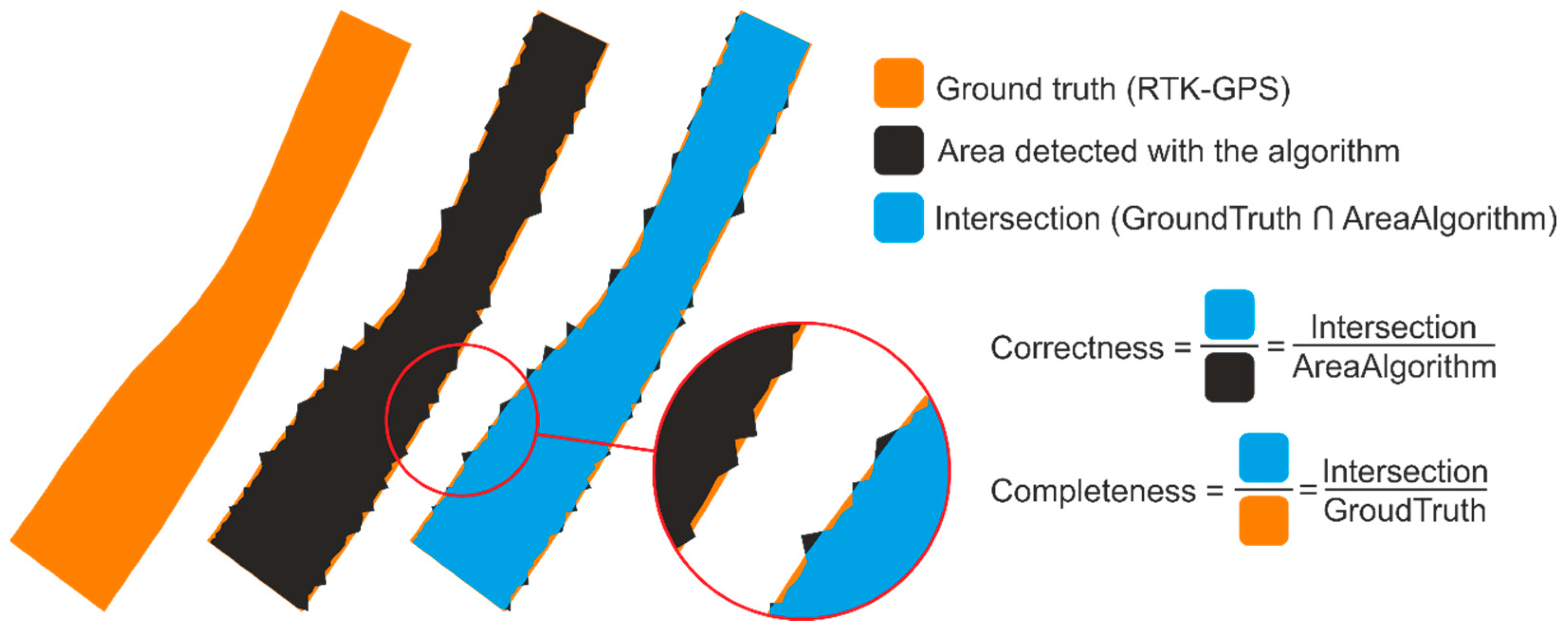
Correctness, completeness, and the distances along the perpendicular lines were calculated for (i) Dataset 1; (ii) Dataset 2; and (iii) the union of both datasets (i.e., the union of the polygons obtained from Dataset 1 and Dataset 2).
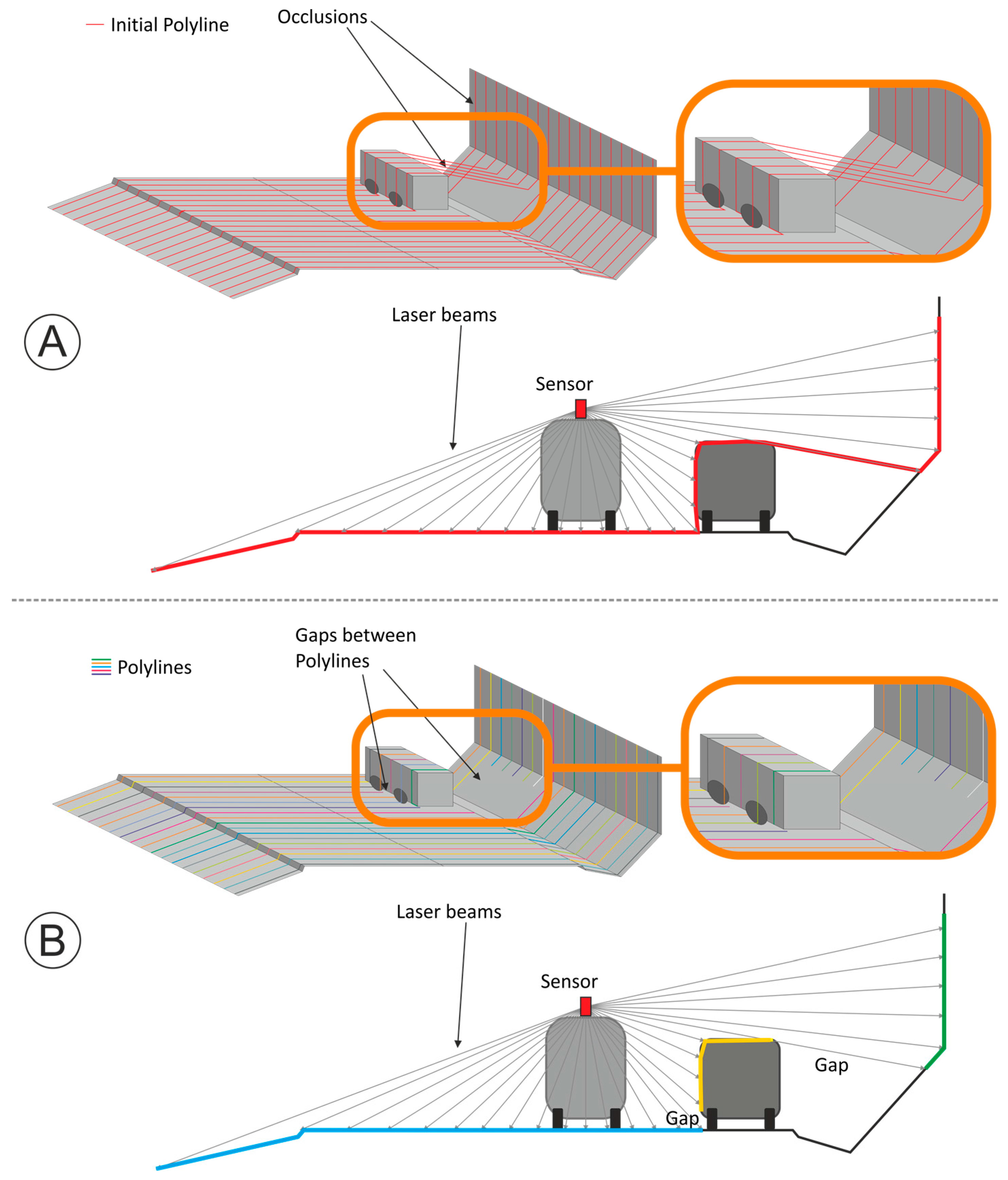
Figure 10 shows a portion of the line cloud, the smoothed polyline and the RTK-GNSS line of a small road patch.
Figure 11 shows the smoothed polyline from the two test datasets and the union of them for three different sections (A, B, and C) of the test road.
The three sections in
Figure 11 are examples with some particularities: there is a sudden gauge widening in the left margin of A. In B, there is a smoothed widening in the right margin. The polyline from Dataset 1 in C reflects the presence of a compact terrain surface, which is almost leveled to the asphalt on the road. The polyline from Dataset 2 is affected by the presence of two vehicles moving in the opposite direction while the MLS was registering data.
The correctness and completeness values of the three polygons (i.e., Dataset 1 (D1), Dataset 2 (D2), and the union of (D1) and (D2)) are shown in the first two lines of
Table 2.
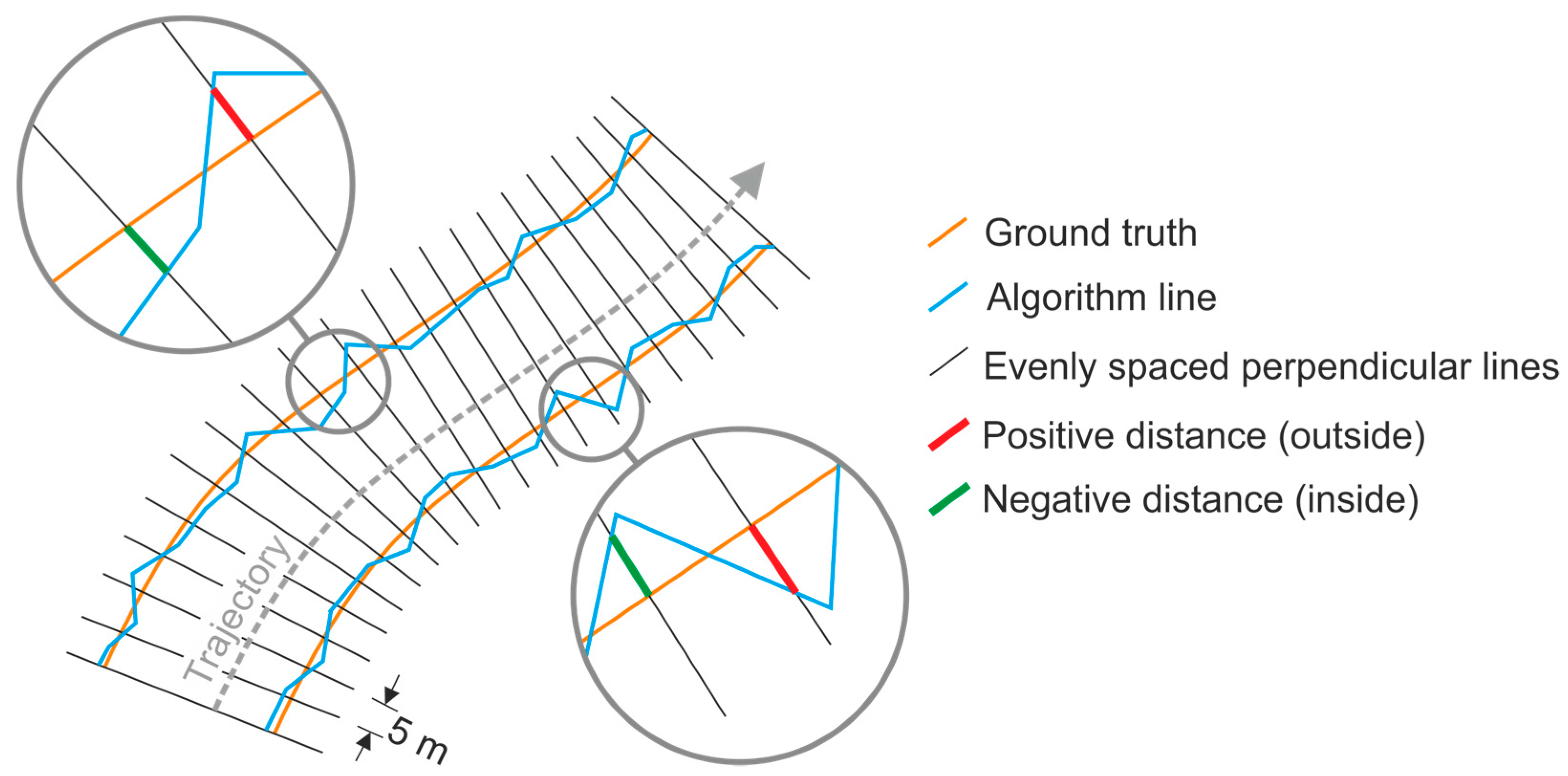
The distances between the RTK-GNSS polyline and the algorithm lines were computed from the measurements on the 426 perpendicular lines. The last two rows from
Table 2 show the average and median distances in both sides of the stretch of road. In order to compare the distribution of the distances in the test datasets, the boxplots are shown in
Figure 12.
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8 show the incidence of single or multiple parameter variations on correctness and completeness. These sensitivity tests were performed on a 300 m long stretch of the test road section.
For evaluating the effect of the variation of several (or all) parameters at the same time, 1000 sets of random values for all the variables (varying up to ±30% from the standard values) were created and used on the same 300 m long road section. This joint variation of all the parameters in ±30% did not produce completeness values below 95.1%, nor correctness values below 99.1%.
3.6. Discussion
The test results show that 99% of the area effectively detected by the algorithm was correct (i.e., corresponds to the actual surface), and that 97% of the road surface was correctly detected by the algorithm. If the union of the two datasets that register data from the same section (but with the MLS moving in the opposite direction) is used, both the proportion of correctly detected surface (correctness) and the proportion of the actual surface that was detected (completeness) go to 98%. See
Table 2.
On the other hand, the algorithm tends to place the line around 10 cm to the inside of the road when using a single dataset, and 5–6 cm on average if using the union of the two datasets. This distance is larger on the most distant border from the trajectory (i.e., the west border when the MLS is moving from south to north [Dataset 1], and the east border in Dataset 2), see
Table 2 and
Figure 12. The difference between the two roadsides may be due to the effect of the lower incidence angle that produces a larger gap between consecutive points on the furthest road border. Moreover, the fact that the detected lines are, on average, 10 cm away from the RTK-GNSS line (when using a single dataset) could be fully explained by (i) the distance between points on a sweep, and (ii) the curvature of the asphalt border immediately before the edge.
Using the MLS configuration described in
Section 3.1, the distance between consecutive points on the same sweep ranges between 1.5 and 7–8 cm at the road border. These distances are most often 2 cm at the closest road edge and 4–5 cm at the furthest one, and depend on the slant distance to the sensor and the tilt angle of the surface. This explains part of the displacement of the edge line towards the center line of the road (i.e., from a few millimeters to several centimeters).
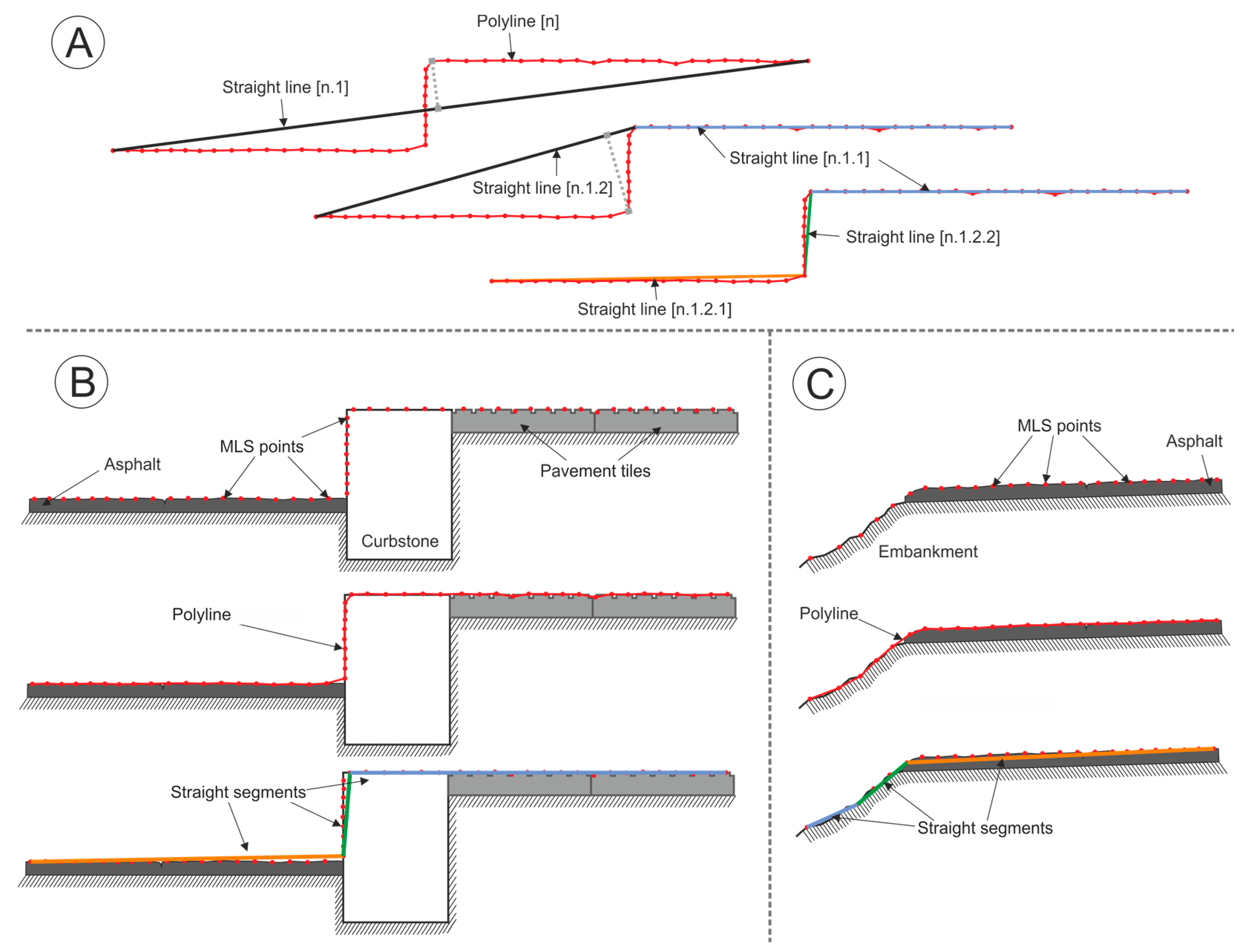
The asphalt edge is not completely clear/sharp, but there is certain curvature on the asphalt profile immediately before the road edge. See
Figure 2C. Using small Douglas Peucker tolerances (e.g., 1 cm, as the one used for the test), it is usual that the break of the line is produced towards the inside of the road. This effect could be reduced by using a larger Douglas Peucker tolerance, but this would lead to errors in shallow borders, as no break would be detected in the lines.
The surface misdetection (i.e., surface from the actual road that is not detected by the algorithm: (100%)–(completeness)) could be explained by the joint effect of (i) the fact that the detected road edge tends to be some centimeters inwards of the road; and (ii) the presence of some vehicles on the road while registering data (e.g., the two vehicles shown in
Figure 11C). When using the union of two datasets, the completeness rises to 98%, as (i) the effect of the moving vehicles is eliminated (e.g., the gaps produced by the two vehicles in
Figure 11 (C, Dataset 2) are removed when using the union of the two datasets); and (ii) the displacement of the detected line to the inside of the road is partially mitigated, as the polygon whose border stands out prevails. See
Table 2.
The surface over-detection (i.e., surface detected by the algorithm that does not belong to the actual road: (100%)–(correctness)) is due to the absence of a clear/sharp asphalt edge in relatively long sections of the road side. These sections correspond to surfaces of compact terrain that are leveled, or almost leveled to the asphalt, such as the leveled surface in
Figure 11.
The surface in
Figure 11 is completely joined to the road polygon from Dataset 1, whereas in Dataset 2, a much smaller patch was joined. In this case, the surface is not completely leveled to the road, and the subtle step is only detected by the algorithm from Dataset 2, in which the west boundary is closer to the trajectory, and the gap between consecutive points is smaller. Using the data from Dataset 1, the step is too shallow if compared with the gap between points, thus, no break in the lines is detected there. The correctness of the union of the two datasets is slightly smaller than the one from Dataset 1 and 2 separately, as the leveled surfaces ‘over-detected’ in only one of them are added to the union.
It is also to be noted that decreasing the angular resolution (i.e., higher point measurement rate of 488 kHz or 970 kHz, or lower scan frequency) of the MLS system may improve the edge detection accuracy. A higher point density along the scanning lines could lead to better results in terms of (i) distances from the road edge polyline to the ground truth and (ii) completeness, as the displacement of the edge line to the inside of the road would be reduced. Nevertheless, there is no apparent reason for expecting different results with a different distance between lines along the trajectory, unless the road edge shape is very intricate, and the distance between sweeps is very large (e.g., 1 m). This may produce an over-smoothing of the road edge polyline, and the misdetection of some complex shapes or features.
The algorithm parameters are configurable, and their values directly affect the results and performance of the algorithm. In this study, a set of standard parameters are proposed for general use, and applied for the test; however, different values could be used for specific datasets and environments. Most of the values of the standard parameters could be modified individually by 40% or 50% without significant variations on the performance, as it is shown in
Table 3,
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8. In some cases, like the polyline split threshold (PST), larger variations in the parameter values could lead to larger misdetections or over-detections (see
Table 4). The distance between consecutive points on the scan lines (i.e., sweeps) must be taken into account when setting up the polyline split threshold, as, if the PST is larger than the gap between points, they cannot be transformed into lines. For this reason, the PST must be larger than the maximum distance between consecutive points expected on the road surface. Nevertheless, individual large variations in most of the parameters are barely noticeable in terms of completeness and correctness. Douglas Peucker tolerance (DPT) is one of the most sensitive parameters, as it directly affects the configuration of the line cloud that is the basis for the rest of processes. A DPT value smaller than the irregularities on the road surface would produce over-segmentation of the line cloud and, therefore, would result in more misdetections (i.e., DPT values below 6 mm in
Table 3), whereas a DPT larger than the height of the road edge step would avoid the line break needed for its identification and produce over-detection (e.g., DPT values above 2 cm in
Table 3). On the other hand, single variations of the parameters that control the length of the lines, their parallelism, the minimum size of the groups, or the threshold for rejecting a node during the smoothing processes barely affect the performance of the algorithm (see
Table 5,
Table 6,
Table 7 and
Table 8).
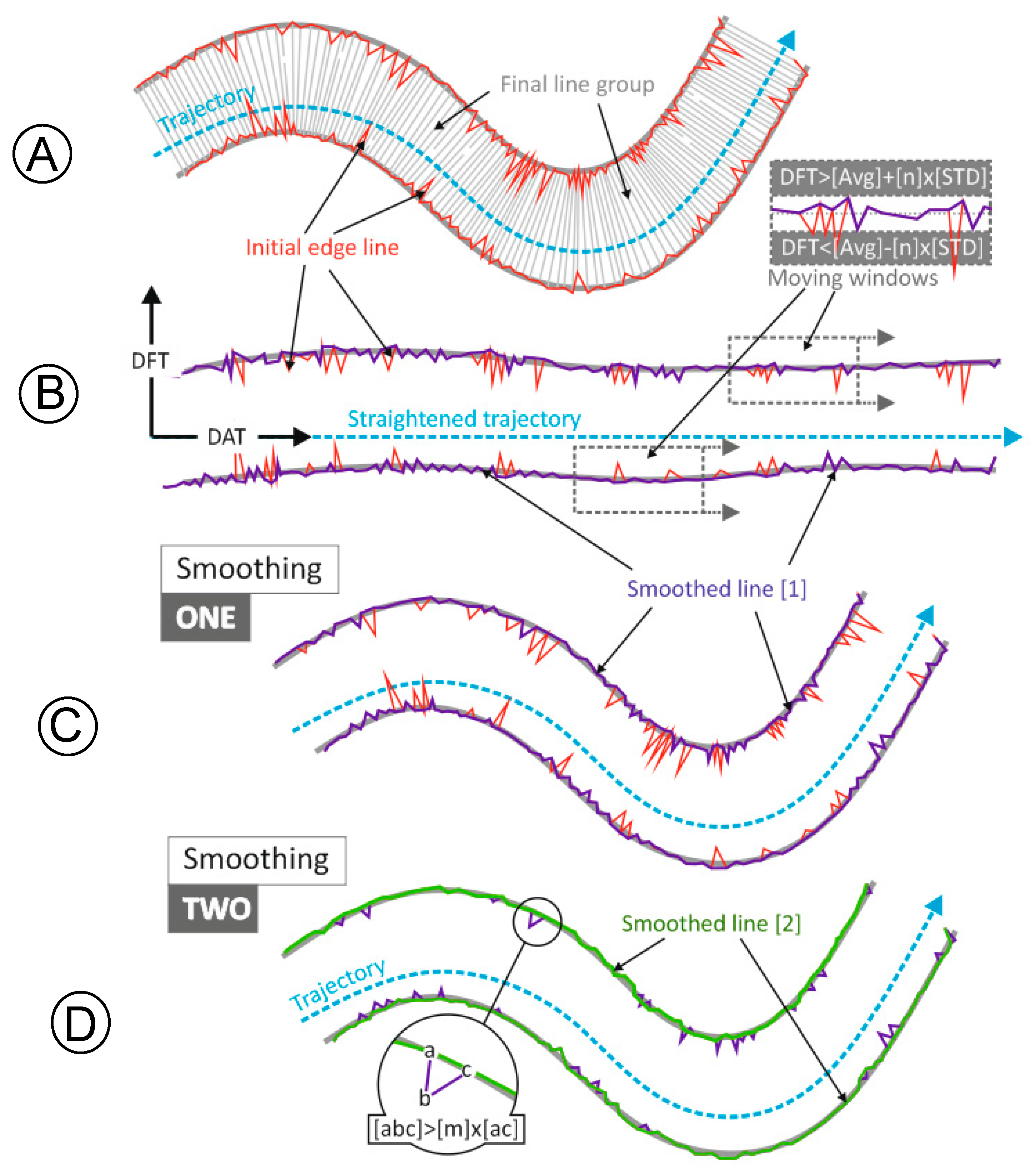
The parameters that control Smoothing 1 are specially interrelated. The window width controls the size of the irregularities in the polyline that the filter smooths, but the rest of the parameters must be set off accordingly (especially the scroll forward step and the threshold for a node to be labeled as an outlier). The (m) value from Smoothing 2 (see
Section 2.4.2 and
Table 1) controls the shape of the irregularities that are removed from the polyline. Using the standard value (i.e., √2) sharp peaks whose angle is smaller than 90° are removed when the distances (ab) and (bc) are similar, see
Figure 6.
Moderate variations of several (or all) parameters at the same time (i.e., up to 30%), do not produce a significant variation of the performance of the algorithm, as completeness and correctness values do not decrease more than 1.3% and 0.7%, respectively, in any case.
Although there are several articles presenting new methods for automatically defining the shape of roads/streets from MLS data, comparing the results of the present study with previous work is not straightforward. For instance, some studies [
6,
24,
31] focus on the extraction of road markings and, even though some of them report their performance in terms of completeness and correctness, these values are not comparable to the ones obtained in this study, as they do not try to detect the road edge. Several other studies present algorithms for automatic detection of curbs [
15,
22,
23,
25,
32,
34], and most of them assess completeness and correctness, but these refer to the length of the curbs detected. In contrast, Zhao et al. [
28], Smadja et al. [
29] and Guan et al. [
35] show methods for automatically identifying road points from MLS data, but their performance is not assessed. Boyko and Funkhouser, and Bin et al. [
26,
30] are focused on the detection of the road surface, but limited to the presence of curbs. Misdetections and over-detections on the street surface are evaluated in Bin et al. [
30], however, they are calculated based on the detection of points, rather than based on the surfaces. Completeness and correctness are reported in Boyko and Funkhouser [
26] in a similar way to this study, although a 0.5 m × 0.5 m grid is used for surface comparisons. Completeness is 94%, and correctness is 86%. Kumar et al. [
36] presented a method for road edge detection from MLS data, where elevation, reflectance/intensity, and pulse width, along with the trajectory, were used. The algorithm was tested in three small road sections, and the distances from the detected edges to the actual road edge were checked. In their experiments, the mean distances from the detected road edge to the ground truth ranged between 2 cm and 38 cm, depending on the type of road edge, the point density, the side of the road (i.e., closest or furthest border to the trajectory), and the kind and quality of the data available in each test dataset (i.e., elevation, reflectance/intensity, and pulse width).