Ocean Wave Parameters Retrieval from Sentinel-1 SAR Imagery
Abstract
:1. Introduction
2. Data Description
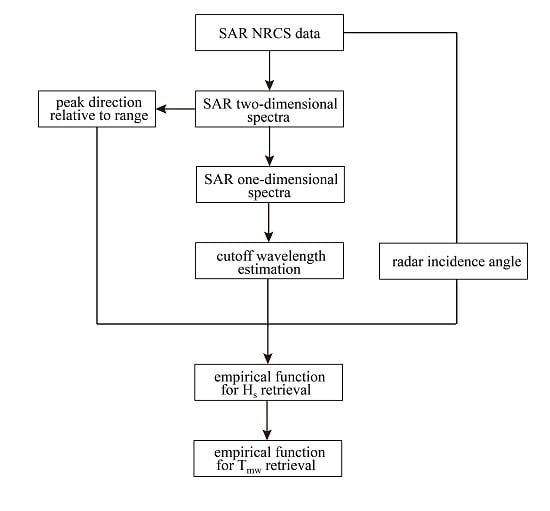
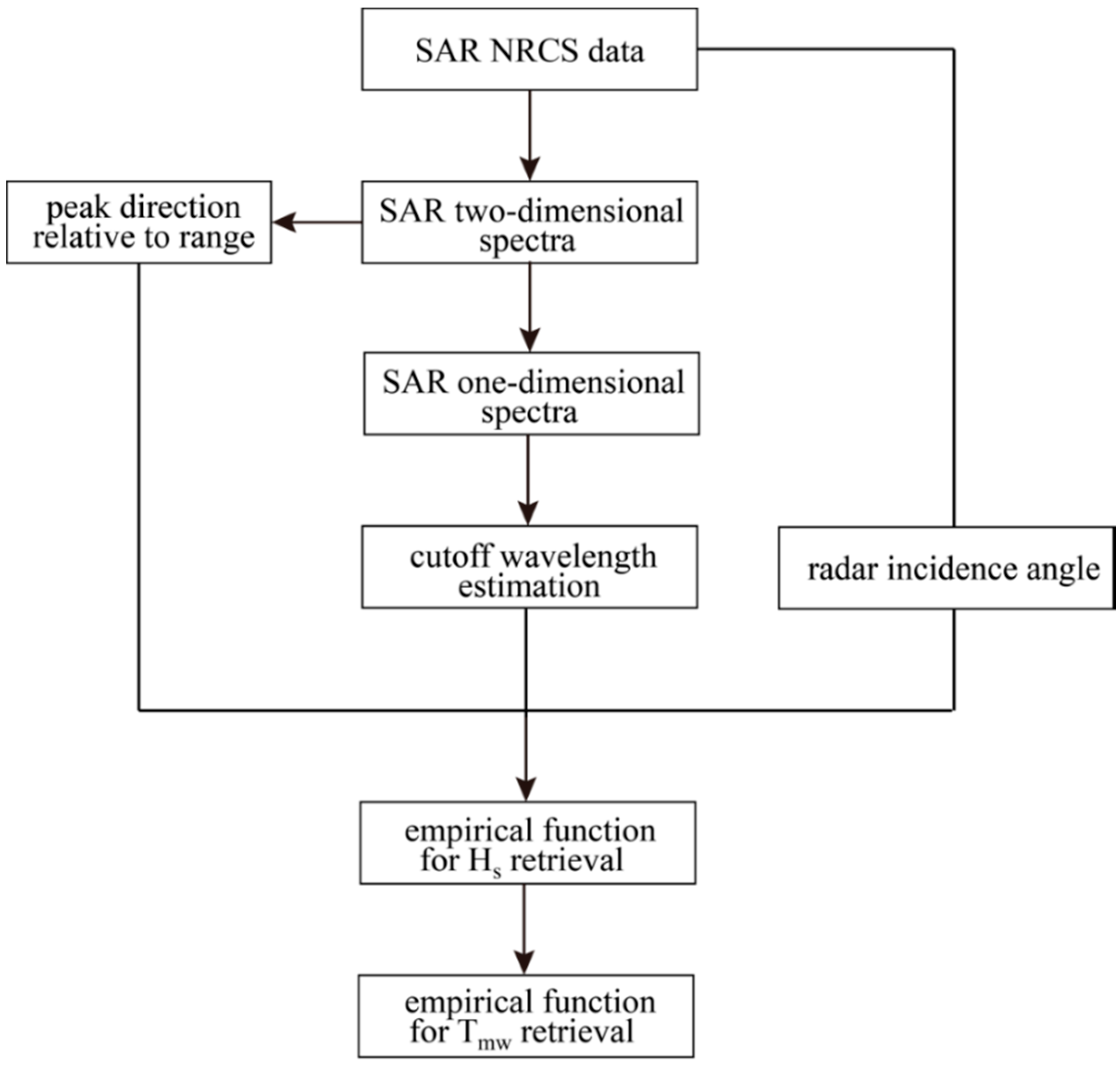
3. Methodology
3.1. A Semi-Empirical Model for Hs Retrieval
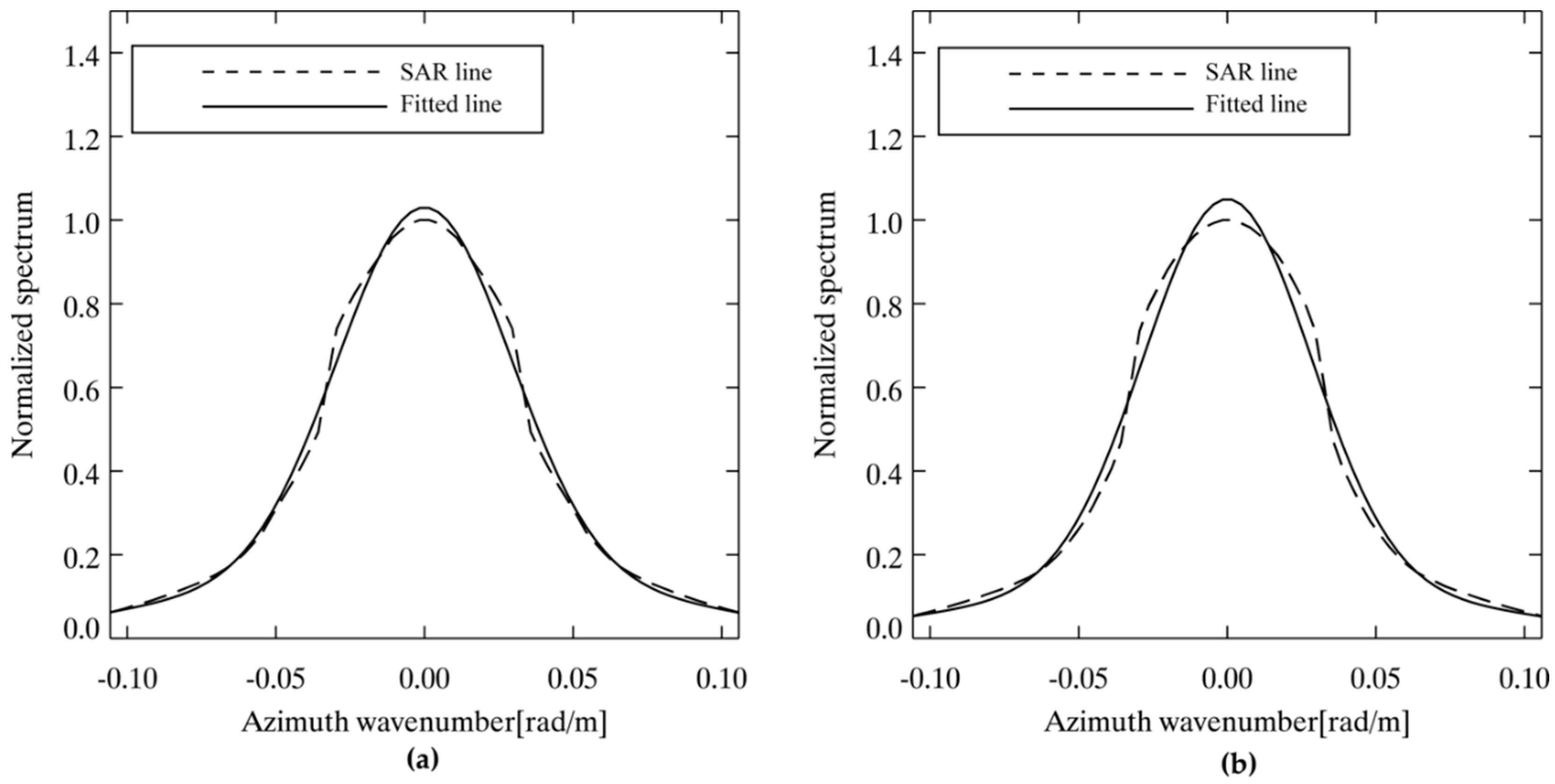
3.2. An Empirical Model for Tmw Retrieval
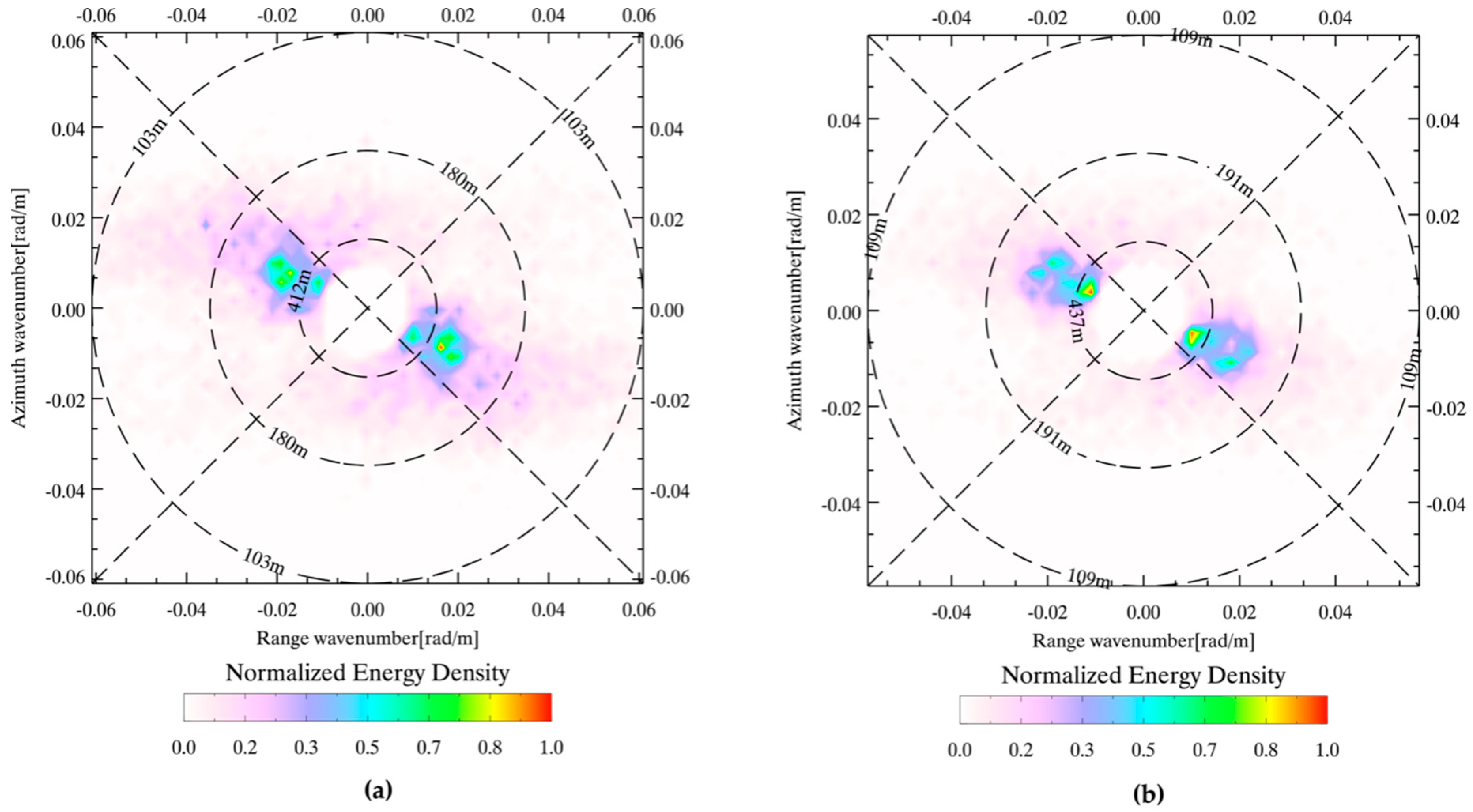
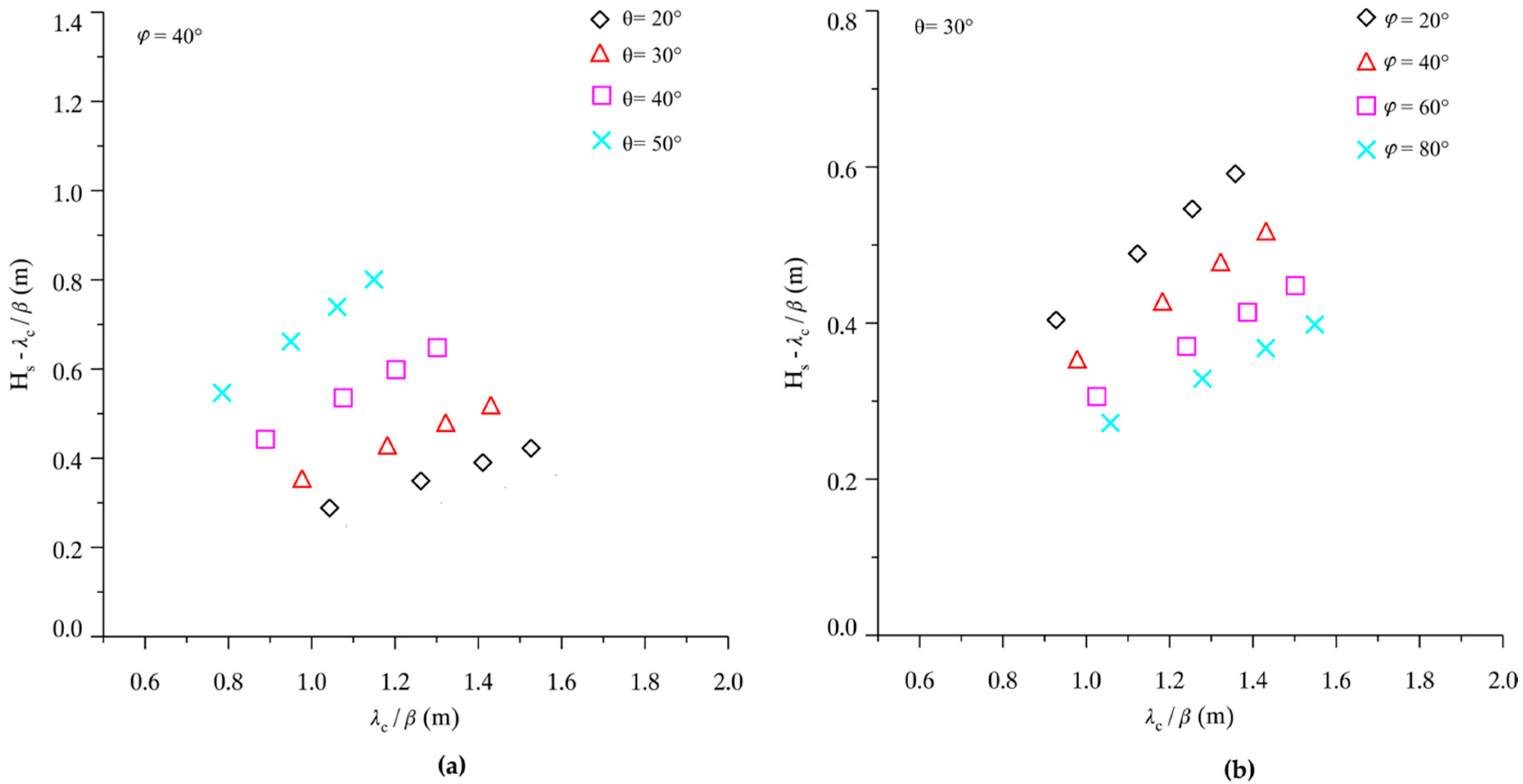
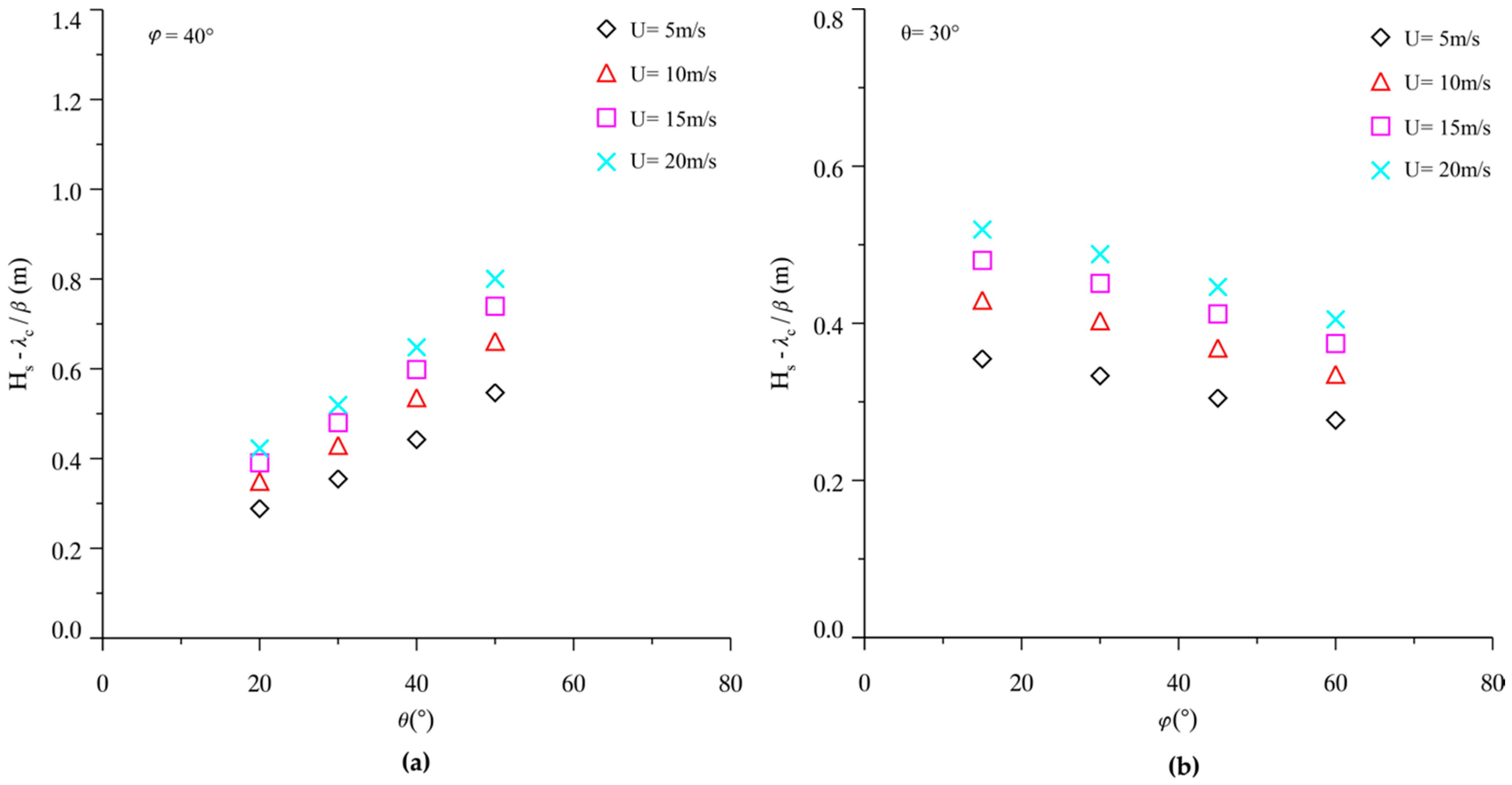
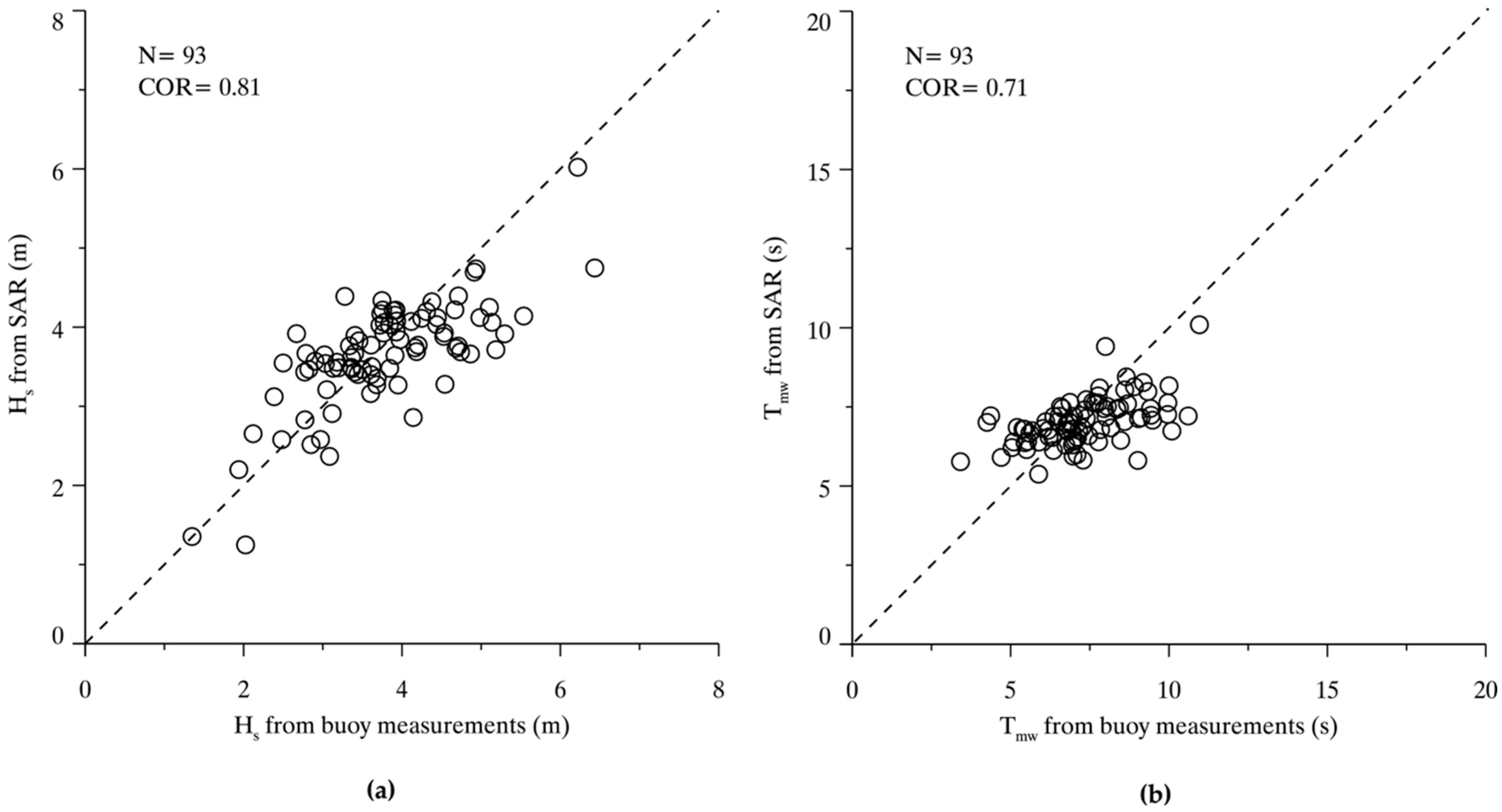
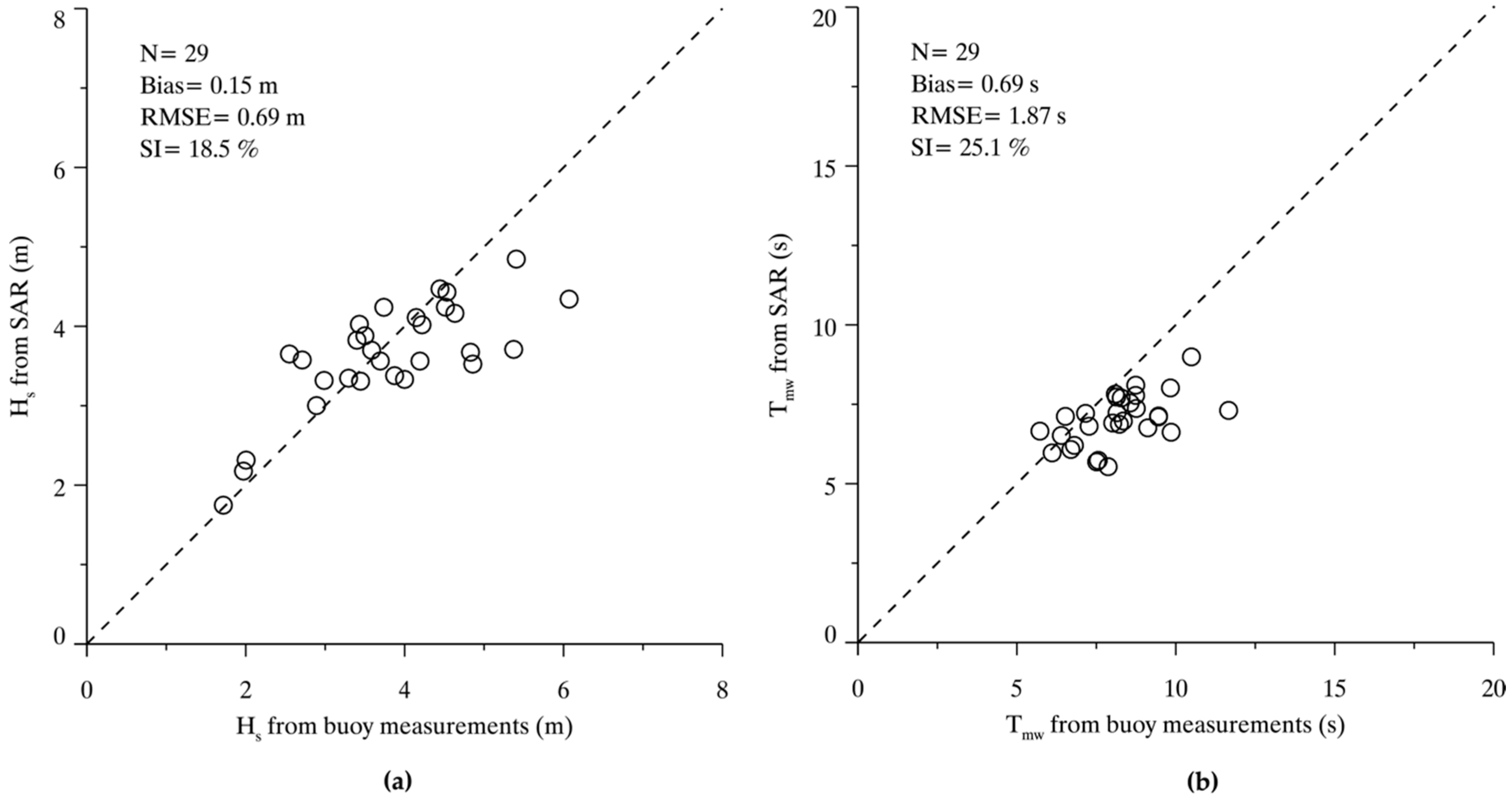
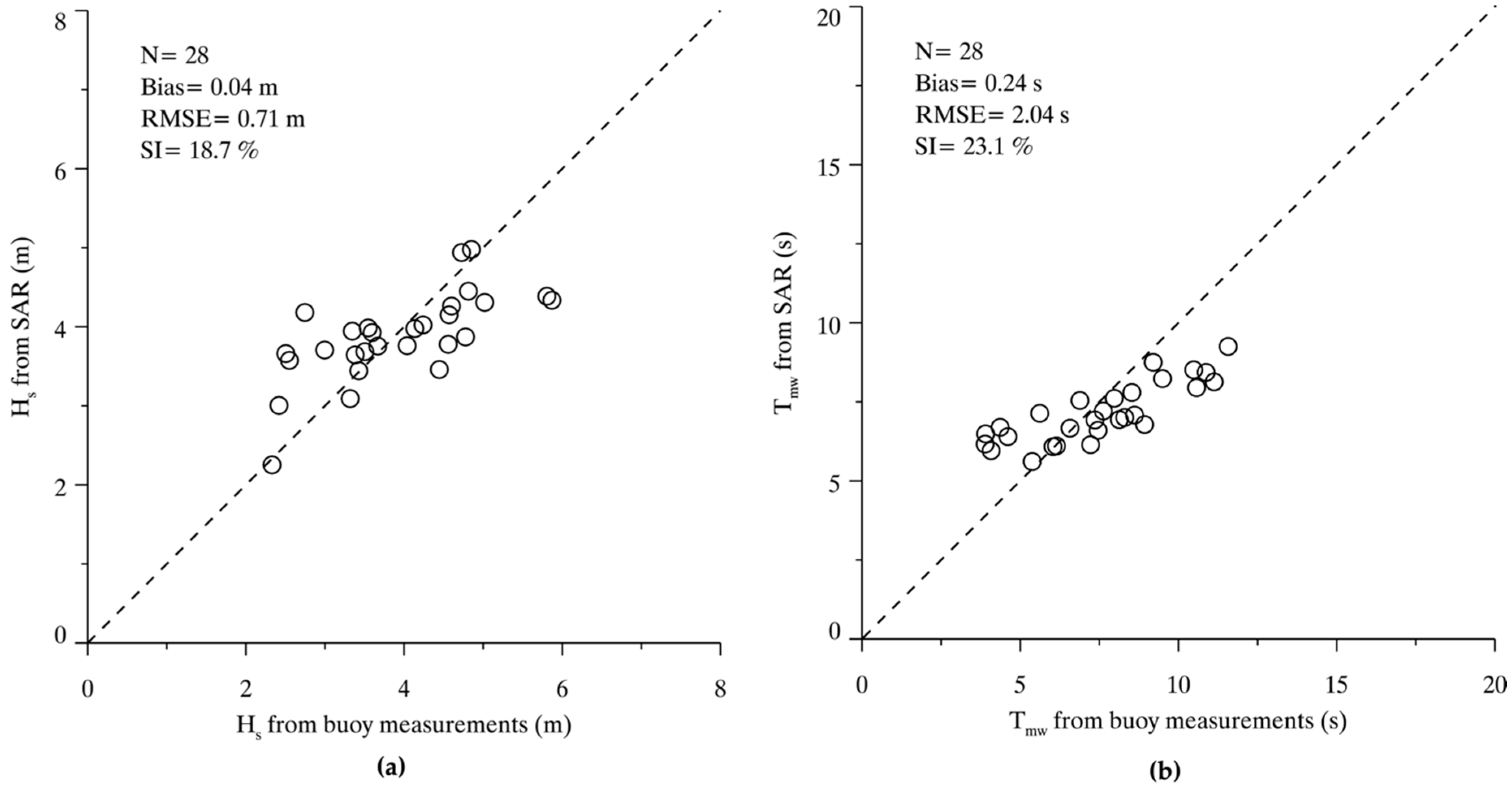
4. Tuning the Algorithm
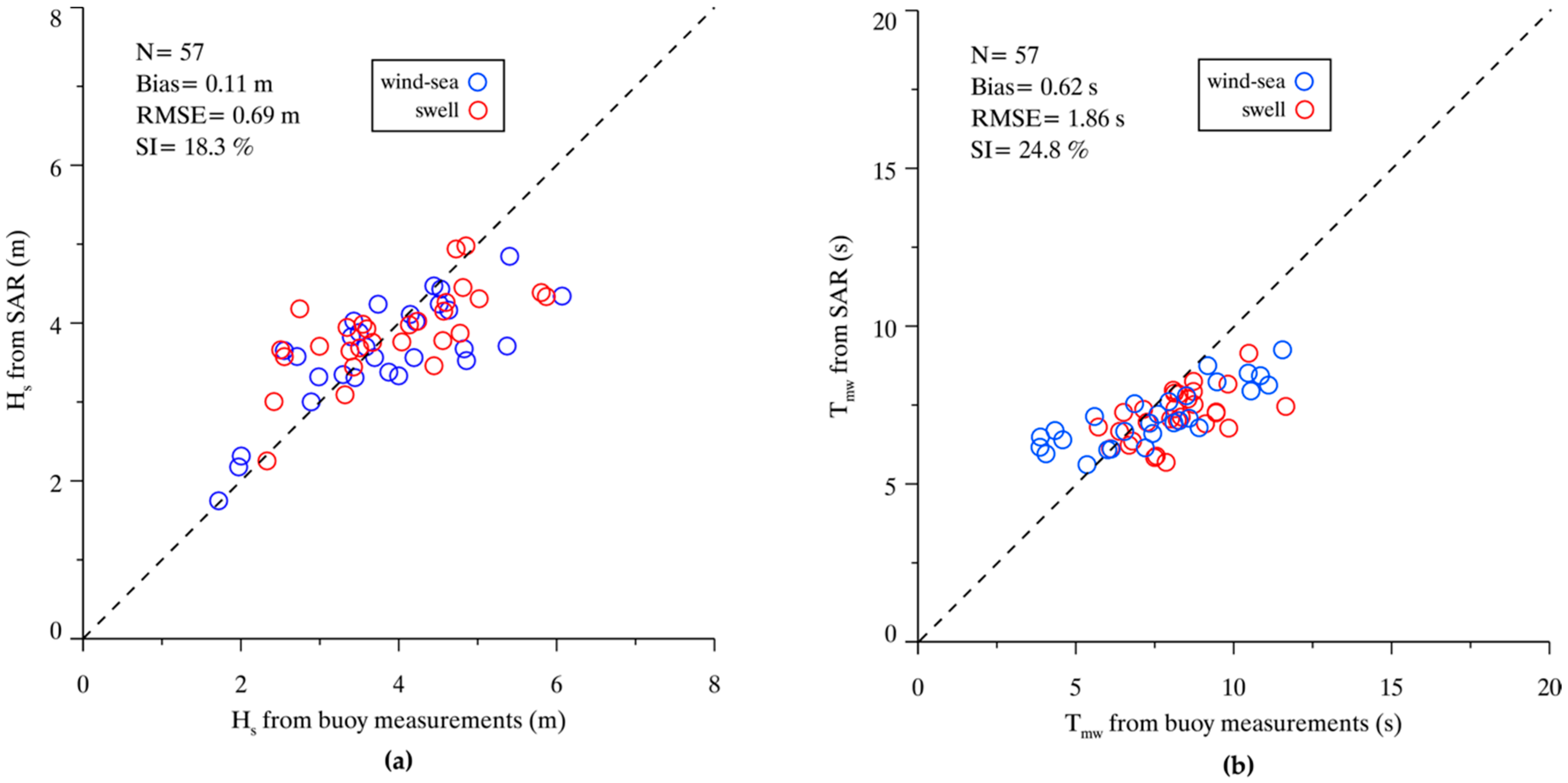
5. Discussions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chapron, B.; Johnsen, H.; Garello, R. Wave and wind retrieval from SAR images of the ocean. Ann. Telecommun. 2001, 56, 682–699. [Google Scholar]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound-Lay Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Alpers, W.; Ross, D.B.; Rufenach, C.L. On the detectability of ocean surface waves by real and synthetic radar. J. Geophys. Res. 1981, 86, 10529–10546. [Google Scholar] [CrossRef]
- Alpers, W.; Bruning, C. On the relative importance of motion-related contributions to SAR imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens. 1986, 24, 873–885. [Google Scholar] [CrossRef]
- Li, X.F.; Pichel, W.; He, M.X.; Wu, S.; Friedman, K.; Clemente-Colon, P.; Zhao, C. Observation of hurricane-generated ocean swell refraction at the Gulf Stream North Wall with the RADARSAT-1 synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2131–2142. [Google Scholar]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum. J. Geophys. Res. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Hasselmann, S.; Bruning, C.; Hasselmann, K. An improved algorithm for the retrieval of ocean wave spectra from synthetic aperture radar image spectra. J. Geophys. Res. 1996, 101, 6615–6629. [Google Scholar] [CrossRef]
- Mastenbroek, C.; de Valk, C.F. A semi-parametric algorithm to retrieve ocean wave spectra from synthetic aperture radar. J. Geophys. Res. 2000, 105, 3497–3516. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.F.; Perrie, W.; He, Y.J. Synergistic measurements of ocean winds and waves from SAR. J. Geophys. Res. 2015, 120, 6164–6184. [Google Scholar] [CrossRef]
- Sun, J.; Guan, C.L. Parameterized first-guess spectrum method for retrieving directional spectrum of swell-dominated waves and huge waves from SAR images. Chin. J. Oceanol. Limn. 2006, 24, 12–20. [Google Scholar]
- Sun, J.; Kawamura, H. Retrieval of surface wave parameters from SAR images and their validation in the coastal seas around Japan. J. Oceanogr. 2009, 65, 567–577. [Google Scholar] [CrossRef]
- Shao, W.Z.; Li, X.F.; Sun, J. Ocean wave parameters retrieval from TerraSAR-X images validated against buoy measurements and model results. Remote Sens. 2015, 7, 12815–12828. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S.; Hoja, D. A parametric scheme for the retrieval of two-dimensional ocean wave spectra from synthetic aperture radar look cross spectra. J. Geophys. Res. 2005, 110, 297–314. [Google Scholar] [CrossRef]
- Li, X.M.; Konig, T.; Schulz-Stellenfleth, J.; Lehner, S. Validation and intercomparison of ocean wave spectra inversion schemes using ASAR wave mode data. Int. J. Remote Sens. 2010, 31, 4969–4993. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Schulz-Stellenfleth, J.; Konig, T.; Lehner, S. An empirical approach for the retrieval of integral ocean wave parameters from synthetic aperture radar data. J. Geophys. Res. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Li, X.M.; Lehner, S.; Bruns, T. Ocean wave integral parameter measurements using Envisat ASAR wave mode data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 155–174. [Google Scholar] [CrossRef]
- Romeiser, R.; Graber, H.C.; Caruso, M.J.; Jensen, R.E.; Walker, D.T.; Cox, A.T. A new approach to ocean wave parameter estimates from C-band ScanSAR images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1320–1345. [Google Scholar] [CrossRef]
- The Wamdi Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Pottier, E. Measurement of ocean surface slopes and wave spectra using polarimetric SAR image data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- He, Y.J.; Shen, H.; Perrie, W. Remote sensing of ocean waves by polarimetric SAR. J. Atmos. Oceanic Techno. 2006, 23, 1768. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; He, Y.J. Validation of RADARSAT-2 fully polarimetric SAR measurements of ocean surface waves. J. Geophys. Res. 2010, 115, 302–315. [Google Scholar] [CrossRef]
- Kerbaol, V.; Chapron, B.; Vachon, P.W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. J. Geophys. Res. 1998, 115, 7833–7846. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Collard, F.; Chapron, B. Estimating wave orbital velocities through the azimuth cut-off from space borne satellites. J. Geophys. Res. 2015, 120, 7616–7634. [Google Scholar] [CrossRef]
- Vachon, P.W.; Krogstad, H.E.; Paterson, J.S. Airborne and spaceborne synthetic aperture radar observations of ocean waves. Atmos. Ocean 1994, 32, 83–112. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, J.; Yang, J.S. A semi-empirical algorithm for SAR wave height retrieval and its validation using Envisat ASAR wave mode data. Acta Oceanol. Sin. 2012, 31, 59–66. [Google Scholar]
- Ren, L.; Yang, J.S.; Zheng, G.; Wang, J. Significant wave height estimation using azimuth cutoff of C-band RADARSAT-2 single-polarization SAR images. Acta Oceanol. Sin. 2015, 12, 1–9. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Kozai, K.; Hasager, C.B.; Badger, M. Comparison of geophysical model functions for SAR wind speed retrieval in Japanese coastal waters. Remote Sens. 2013, 5, 1956–1973. [Google Scholar] [CrossRef]
- Yang, X.F.; Li, X.F.; Zheng, Q.A.; Gu, X.F.; Pichel, W.G.; Li, Z. Comparison of ocean-surface winds retrieved from Quikscat scatterometer and Radarsat-1 SAR in offshore waters of the U.S. west coast. IEEE Geosci. Remote Sens. 2011, 8, 163–167. [Google Scholar] [CrossRef]
- Hersbach, H. Comparison of C-Band scatterometer CMOD5.N equivalent neutral winds with ECMWF. J. Atmos. Ocean Tech. 2010, 27, 721–736. [Google Scholar] [CrossRef]
- Yang, X.F.; Li, X.F.; Pichel, W.G.; Li, Z. Comparison of ocean surface winds from Envisat ASAR, Metop Ascat scatterometer, buoy measurements, and NOGAPS model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Shao, W.Z.; Sun, J.; Guan, C.L.; Sun, Z.F. A method for sea surface wind field retrieval from SAR image mode data. J. Ocean Univ. China 2014, 13, 198–204. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: derivation of the transfer function, CMOD4. J. Geophys. Res. 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; Haan, S.D. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. 2007, 112, C03006. [Google Scholar] [CrossRef]
- Marghany, M.; Ibrahim, Z.; Genderen, J.V. Azimuth cut-off model for significant wave height investigation along coastal water of Kuala Terengganu, Malaysia. Int. J. Appl. Earth Obs. 2002, 4, 147–160. [Google Scholar] [CrossRef]
- Wen, S.C.; Guo, P.F.; Zhang, D.C.; Guan, C.L.; Zhan, H.G. Analytically derived wind-wave directional spectrum part 2. characteristics, comparison and verification of spectrum. J. Oceanogr. 1993, 49, 149–172. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Longuet-Higinns, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floating buoy. In Proceedings of the a conference on Ocean Wave Spectra, Easton, Maryland, 1–4 May 1963; pp. 111–136.



| 0.48 | 0.26 | 0.27 | 0.22 |
| 1.65 | 5.60 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, W.; Zhang, Z.; Li, X.; Li, H. Ocean Wave Parameters Retrieval from Sentinel-1 SAR Imagery. Remote Sens. 2016, 8, 707. https://doi.org/10.3390/rs8090707
Shao W, Zhang Z, Li X, Li H. Ocean Wave Parameters Retrieval from Sentinel-1 SAR Imagery. Remote Sensing. 2016; 8(9):707. https://doi.org/10.3390/rs8090707
Chicago/Turabian StyleShao, Weizeng, Zheng Zhang, Xiaofeng Li, and Huan Li. 2016. "Ocean Wave Parameters Retrieval from Sentinel-1 SAR Imagery" Remote Sensing 8, no. 9: 707. https://doi.org/10.3390/rs8090707
APA StyleShao, W., Zhang, Z., Li, X., & Li, H. (2016). Ocean Wave Parameters Retrieval from Sentinel-1 SAR Imagery. Remote Sensing, 8(9), 707. https://doi.org/10.3390/rs8090707