Highlighting Biome-Specific Sensitivity of Fire Size Distributions to Time-Gap Parameter Using a New Algorithm for Fire Event Individuation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fire Data
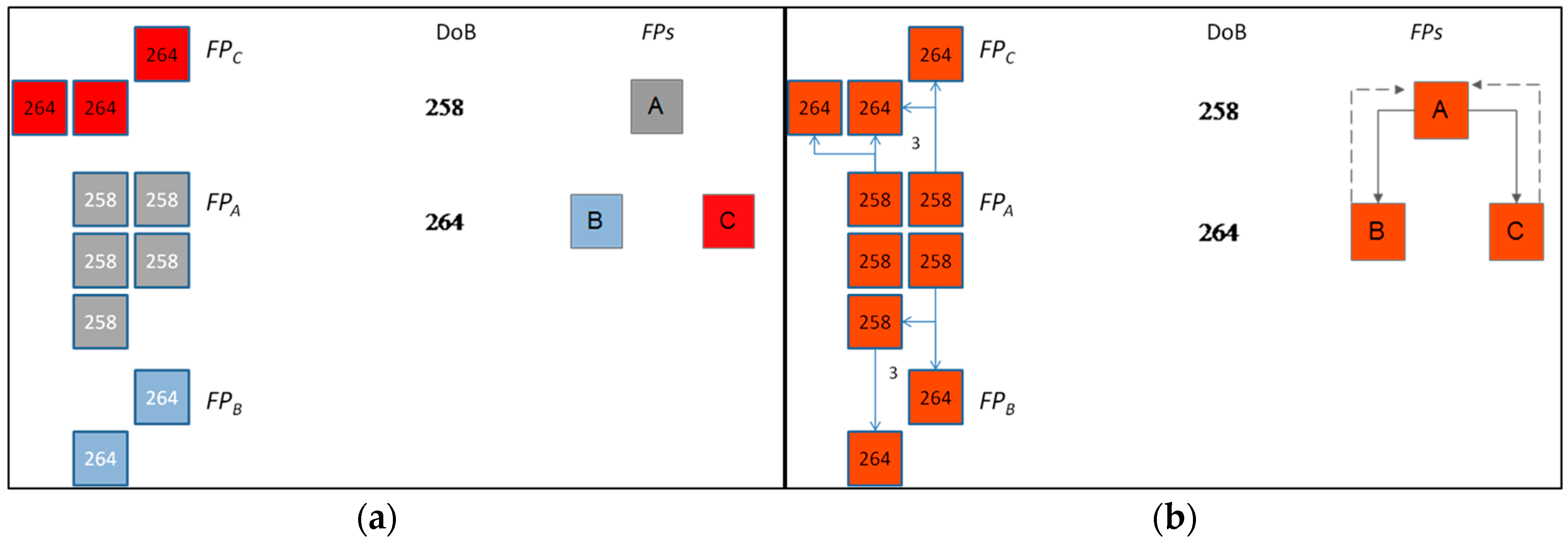
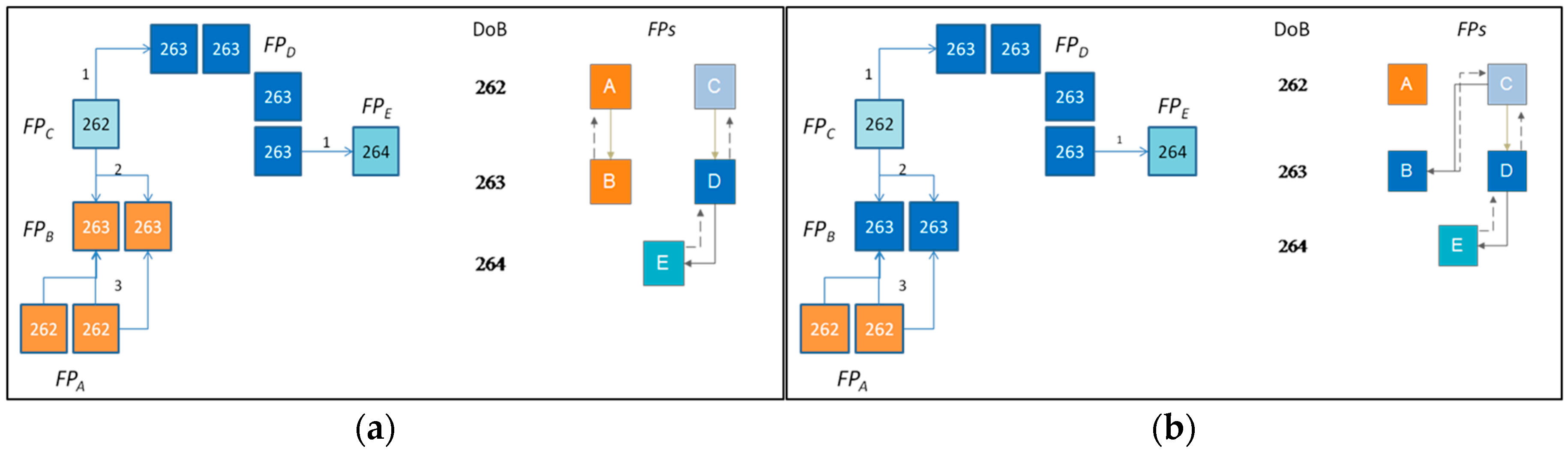
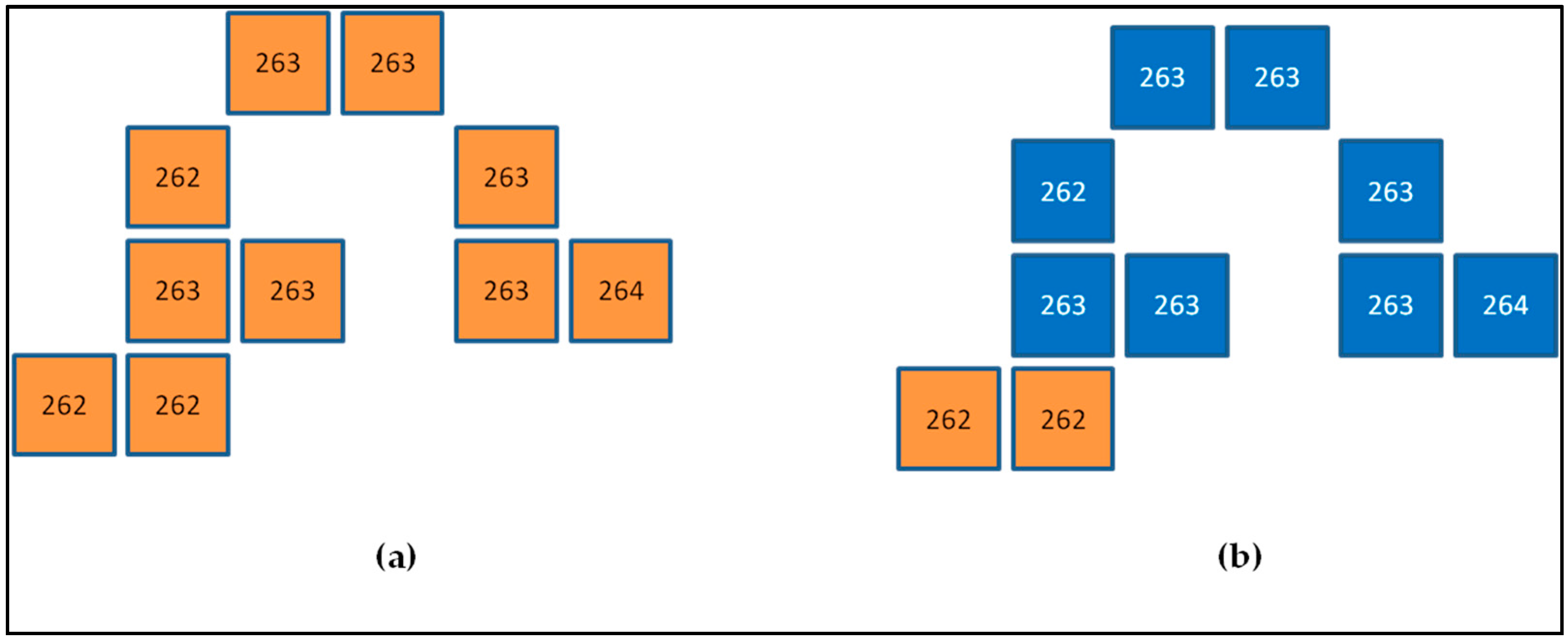
2.2. Active Fire Clusters Individuation Algorithm
2.3. Sensitivity of Fire Size Distributions to the Time-Gap Parameter
3. Results
3.1. Sensitivity of Fire Size Distributions to the Time-gap Parameter
3.2. Performance of the Active Fire Clusters Individuation Algorithm
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| FSD | Fire size distributions |
| FP | Fire Patch Unit |
References and Note
- Archibald, S.; Lehmann, C.E.; Gómez-Dans, J.L.; Bradstock, R.A. Defining pyromes and global syndromes of fire regimes. Proc. Natl. Acad. Sci. USA 2013, 110, 6442–6447. [Google Scholar] [PubMed]
- Kasischke, E.S.; Turetsky, M.R. Recent changes in the fire regime across the North American boreal regional: Spatial and temporal patterns of burning across Canada and Alaska. Geophys. Res. Lett. 2006, 33. [Google Scholar]
- Van Wagtendonk, J.; Lutz, J. Fire regime attributes of wildland fires in Yosemite National Park, USA. Fire Ecol. 2007, 3, 34–52. [Google Scholar] [CrossRef]
- Cui, W.; Perera, A.H. What do we know about forest fire size distribution, and why is this knowledge useful for forest management? Int. J. Wildland Fire 2008, 17, 234–244. [Google Scholar] [CrossRef]
- Haire, S.L.; McGarigal, K.; Miller, C. Wilderness shapes contemporary fire size distributions across landscapes of the Western United States. Ecosphere 2013, 4, 1–20. [Google Scholar] [CrossRef]
- Barclay, H.J.; Li, C.; Hawkes, B.; Benson, L. Effects of fire size and frequency and habitat heterogeneity on forest age distribution. Ecol. Model. 2006, 197, 207–220. [Google Scholar] [CrossRef]
- Hantson, S.; Pueyo, S.; Chuvieco, E. Global fire size distribution is driven by human impact and climate. Glob. Ecol. Biogeogr. 2014, 24, 77–86. [Google Scholar] [CrossRef]
- Pausas, J.G.; Fernández-Muñoz, S. Fire regime changes in the western Mediterranean basin: From fuel-limited to drought-driven fire regime. Clim. Chang. 2012, 110, 215–226. [Google Scholar] [CrossRef] [Green Version]
- Justice, C.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The modis fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Arino, O.; Rosaz, J. 1997 and 1998 world ATSR fire ATLAS using ERS-2 ATSR-2 data. In Proceedings of the Joint Fire Science Conference and Workshop, Boise, ID, USA, 15–17 June 1999; pp. 177–182.
- Laris, P. Burning the seasonal mosaic: Preventative burning strategies in the wooded savanna of Southern Mali. Hum. Ecol. 2002, 30, 155–186. [Google Scholar] [CrossRef]
- Loboda, T.; Csiszar, I. Reconstruction of fire spread within wildland fire events in Northern Eurasia from the MODIS active fire product. Glob. Planet. Chang. 2007, 56, 258–273. [Google Scholar] [CrossRef]
- Ichoku, C.; Kaufman, Y.; Giglio, L.; Li, Z.; Fraser, R.; Jin, J.-Z.; Park, W. Comparative analysis of daytime fire detection algorithms using AVHRR data for the 1995 fire season in Canada: Perspective for MODIS. Int. J. Remote Sens. 2003, 24, 1669–1690. [Google Scholar] [CrossRef]
- Archibald, S.; Scholes, R.; Roy, D.; Roberts, G.; Boschetti, L. Southern African fire regimes as revealed by remote sensing. Int. J. Wildland Fire 2010, 19, 861–878. [Google Scholar]
- Hantson, S.; Lasslop, G.; Kloster, S.; Chuvieco, E. Anthropogenic effects on global mean fire size. Int. J. Wildland Fire 2015, 24, 589–596. [Google Scholar] [CrossRef]
- Archibald, S.; Roy, D. Identifying individual fires from satellite-derived burned area data. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. 160–163.
- Ellis, E.C.; Klein Goldewijk, K.; Siebert, S.; Lightman, D.; Ramankutty, N. Anthropogenic transformation of the biomes, 1700 to 2000. Glob. Ecol. Biogeogr. 2010, 19, 589–606. [Google Scholar] [CrossRef]
- Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.; Underwood, E.C.; D’amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C. Terrestrial ecoregions of the world: A new map of life on earth a new global map of terrestrial ecoregions provides an innovative tool for conserving biodiversity. BioScience 2001, 51, 933–938. [Google Scholar] [CrossRef]
- Giglio, L.; Descloitres, J.; Justice, C.O.; Kaufman, Y.J. An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ. 2003, 87, 273–282. [Google Scholar] [CrossRef]
- Oom, D.; Pereira, J. Exploratory spatial data analysis of global MODIS active fire data. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 326–340. [Google Scholar] [CrossRef]
- Tarjan, R. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Gini, C.W. Variability and mutability, contribution to the study of statistical distribution and relations. Studi Economico-Giuricici della R. Universita de Cagliari, 1912. [Google Scholar] Reviewed in Light, R.J.; Margolin, B.H. An analysis of variance for categorical data. J. Amer. Stat. Assoc. 1971, 66, 534–544. [Google Scholar]
- Sharma, A.R.; Kharol, S.K.; Badarinath, K.; Singh, D. Impact of agriculture crop residue burning on atmospheric aerosol loading—A study over Punjab state, India. Ann. Geophys. 2010, 28, 367–379. [Google Scholar] [CrossRef]
- Tarimo, B.; Dick, Ã.Y.B.; Gobakken, T.; Totland, Ã.R. Spatial distribution of temporal dynamics in anthropogenic fires in miombo savanna woodlands of Tanzania. Carbon Balance Manag. 2015, 10, 1–15. [Google Scholar]
- Archibald, S.; Staver, A.C.; Levin, S.A. Evolution of human-driven fire regimes in Africa. Proc. Natl. Acad. Sci. USA 2012, 109, 847–852. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Kim, J.E.; Kim, Y.J.; Kim, J.; Von Hoyningen-Huene, W. Impact of the smoke aerosol from Russian forest fires on the atmospheric environment over Korea during May 2003. Atmos. Environ. 2005, 39, 85–99. [Google Scholar] [CrossRef]
- Laris, P.S. Spatiotemporal problems with detecting and mapping mosaic fire regimes with coarse-resolution satellite data in savanna environments. Remote Sens. Environ. 2005, 99, 412–424. [Google Scholar] [CrossRef]
- Csiszar, I.A.; Morisette, J.T.; Giglio, L. Validation of active fire detection from moderate-resolution satellite sensors: The MODIS example in northern eurasia. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1757–1764. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L.; Justice, C.O.; Ju, J. The collection 5 MODIS burned area product—Global evaluation by comparison with the MODIS active fire product. Remote Sens. Environ. 2008, 112, 3690–3707. [Google Scholar] [CrossRef]
- Boschetti, L.; Roy, D.P.; Justice, C.O.; Giglio, L. Global assessment of the temporal reporting accuracy and precision of the MODIS burned area product. Int. J. Wildland Fire 2010, 19, 705–709. [Google Scholar] [CrossRef]
- Van Wilgen, B.W.; Govender, N.; MacFadyen, S. An assessment of the implementation and outcomes of recent changes to fire management in the Kruger National Park. Koedoe 2008, 50, 22–31. [Google Scholar] [CrossRef]
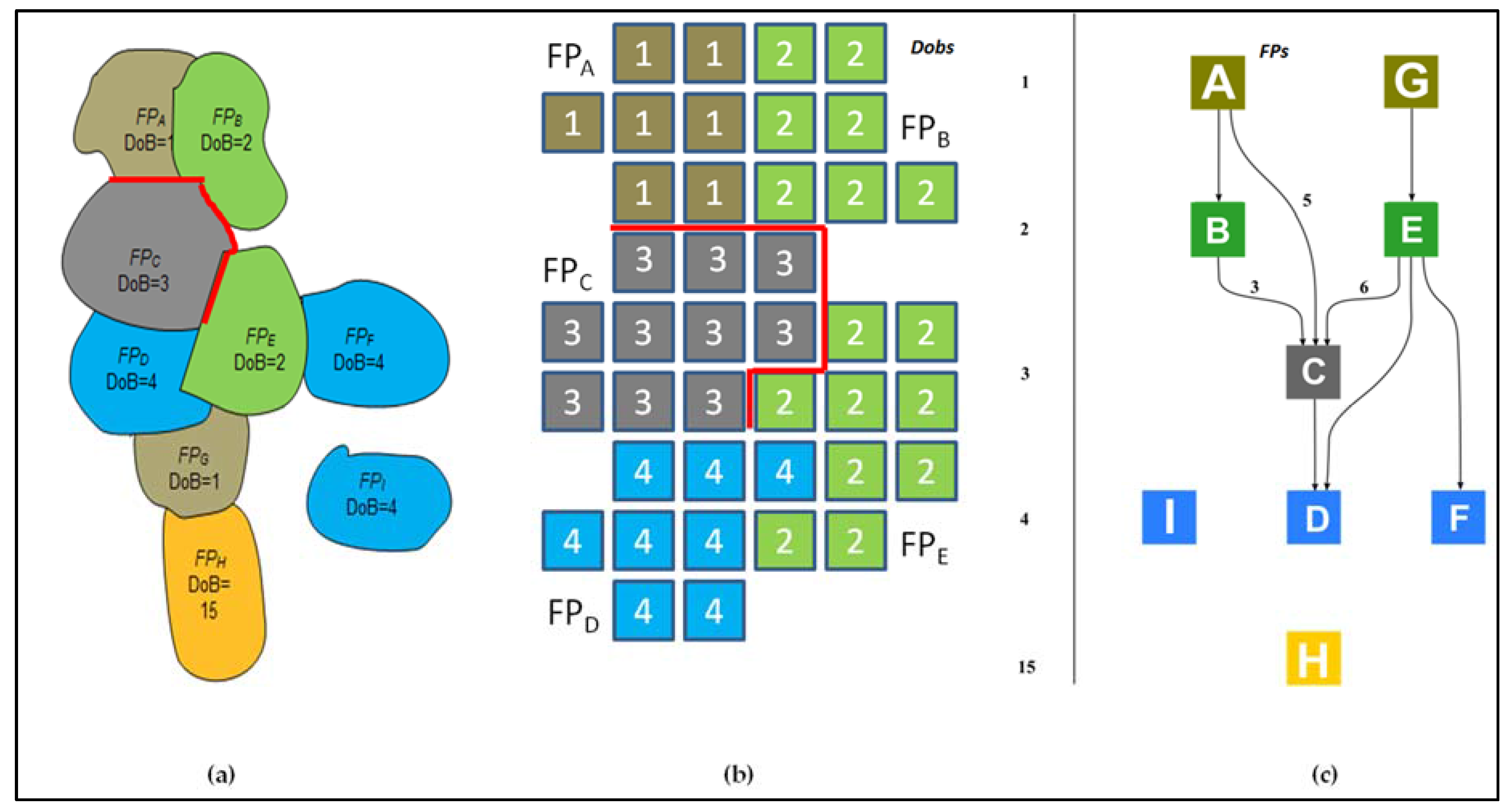

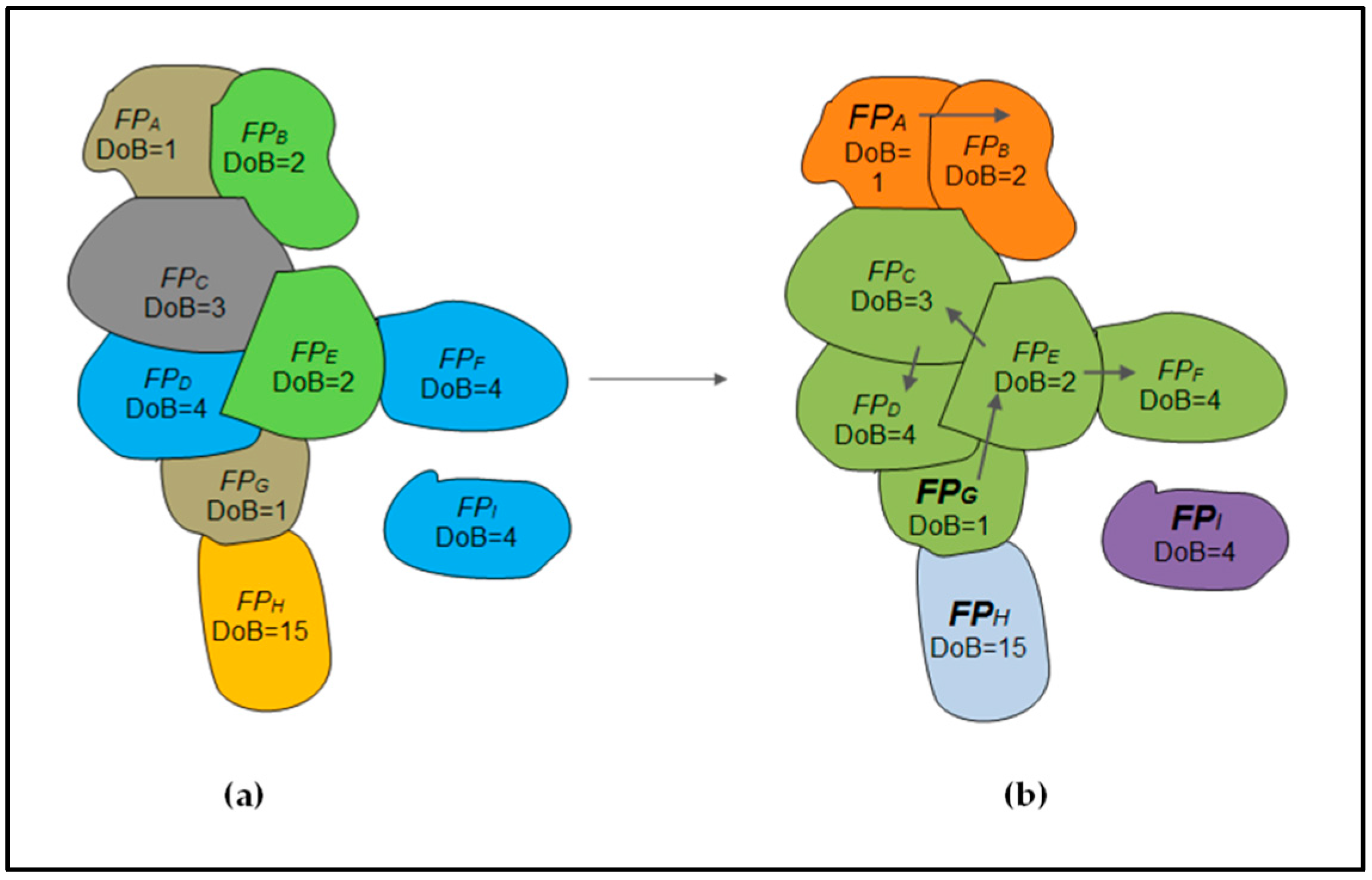
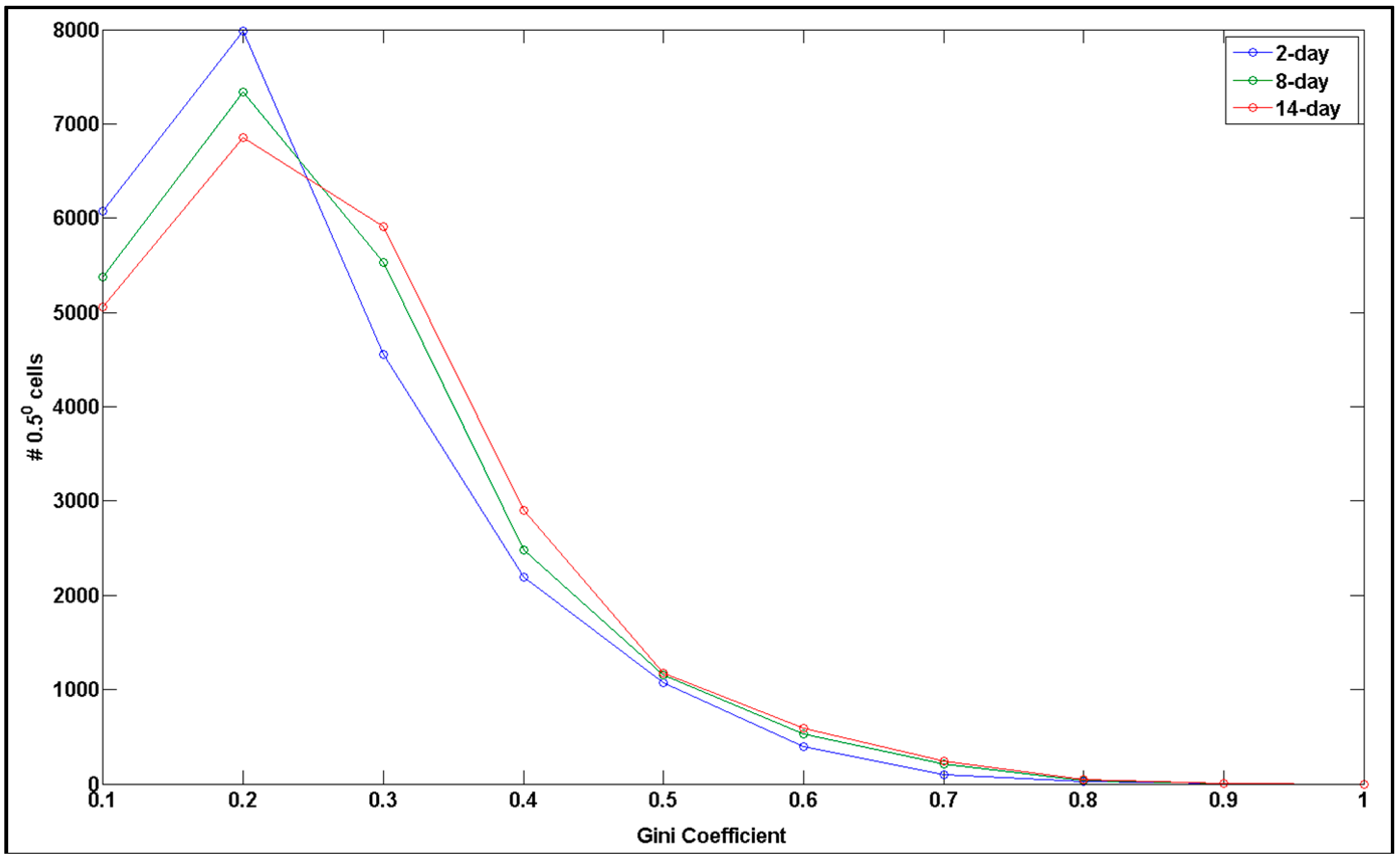
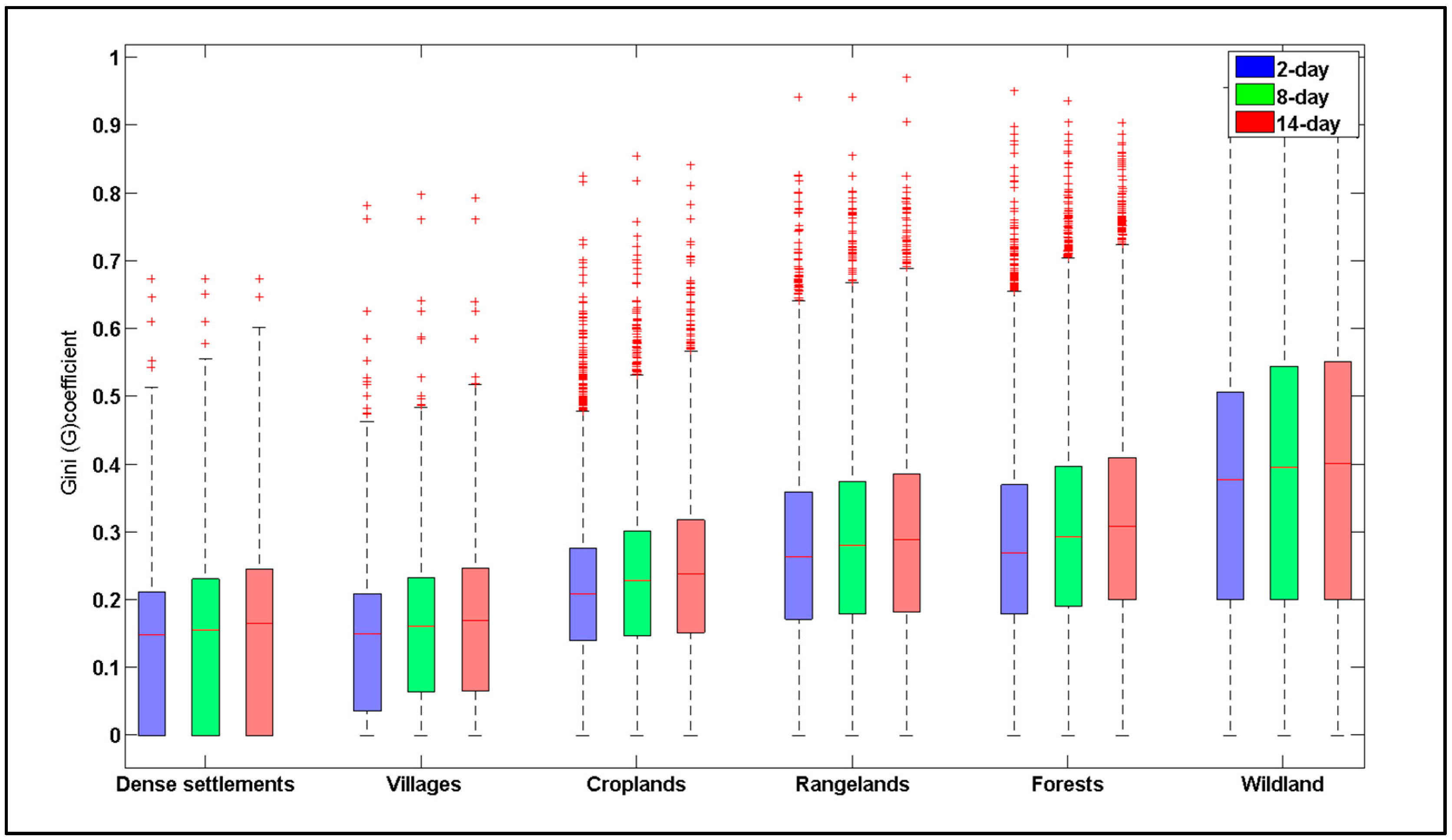
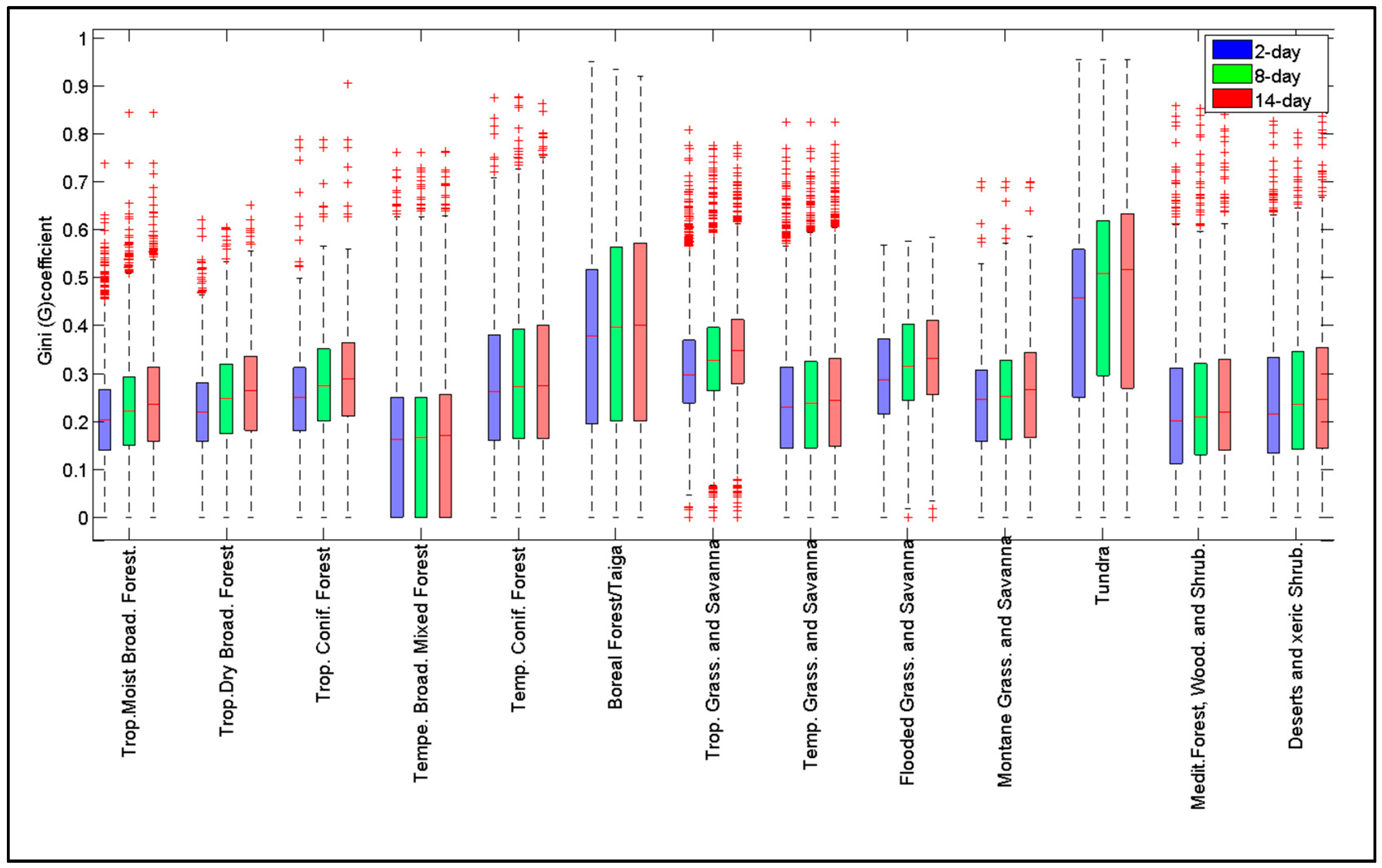
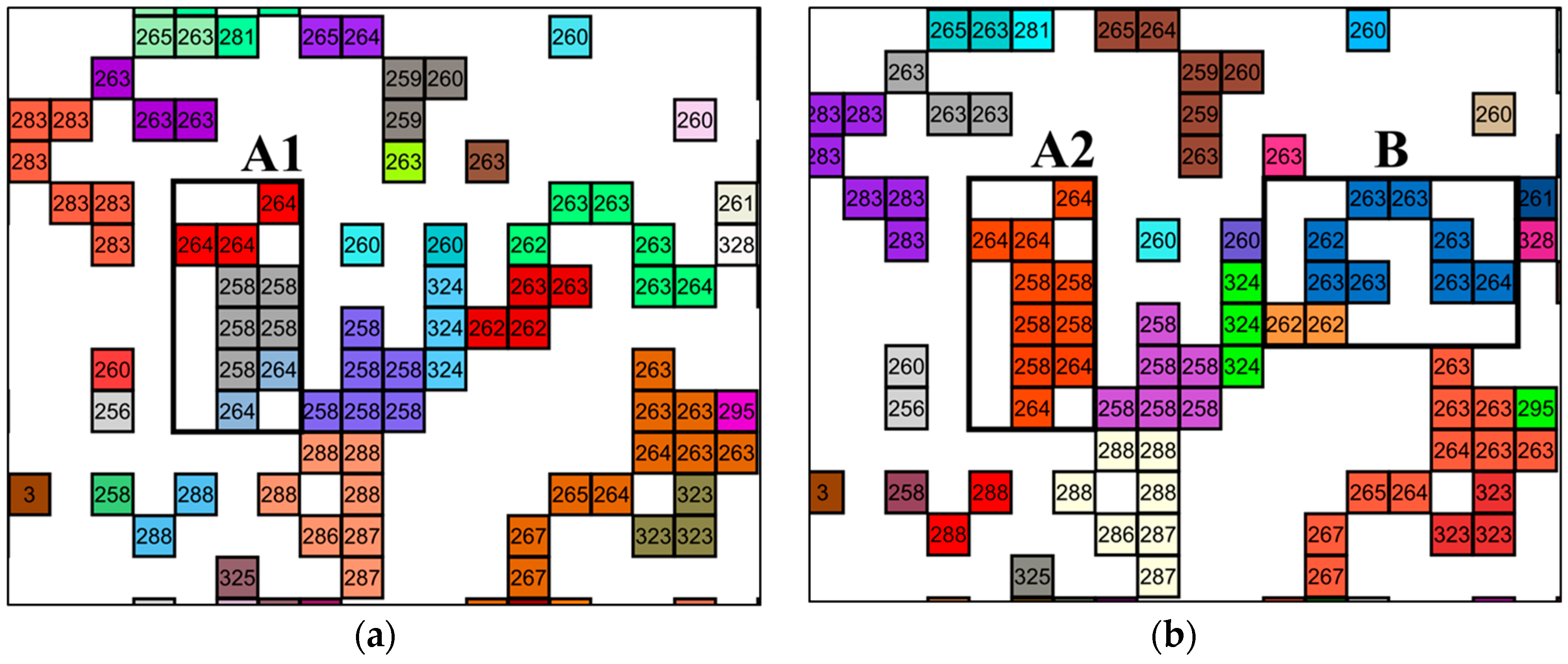
| Time-Gap (Days) | Number of Active Fire Clusters | Fire Size Classes (km2) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1–5 | 5–10 | 10–20 | 20–50 | >50 | ||
| 2 | 2,101,171 | 65.86 | 31.09 | 2.27 | 0.60 | 0.16 | 0.02 |
| 8 | 1,900,092 | 62.15 | 33.50 | 3.24 | 0.86 | 0.22 | 0.03 |
| 14 | 1,764,628 | 59.48 | 34.98 | 4.10 | 1.13 | 0.27 | 0.04 |
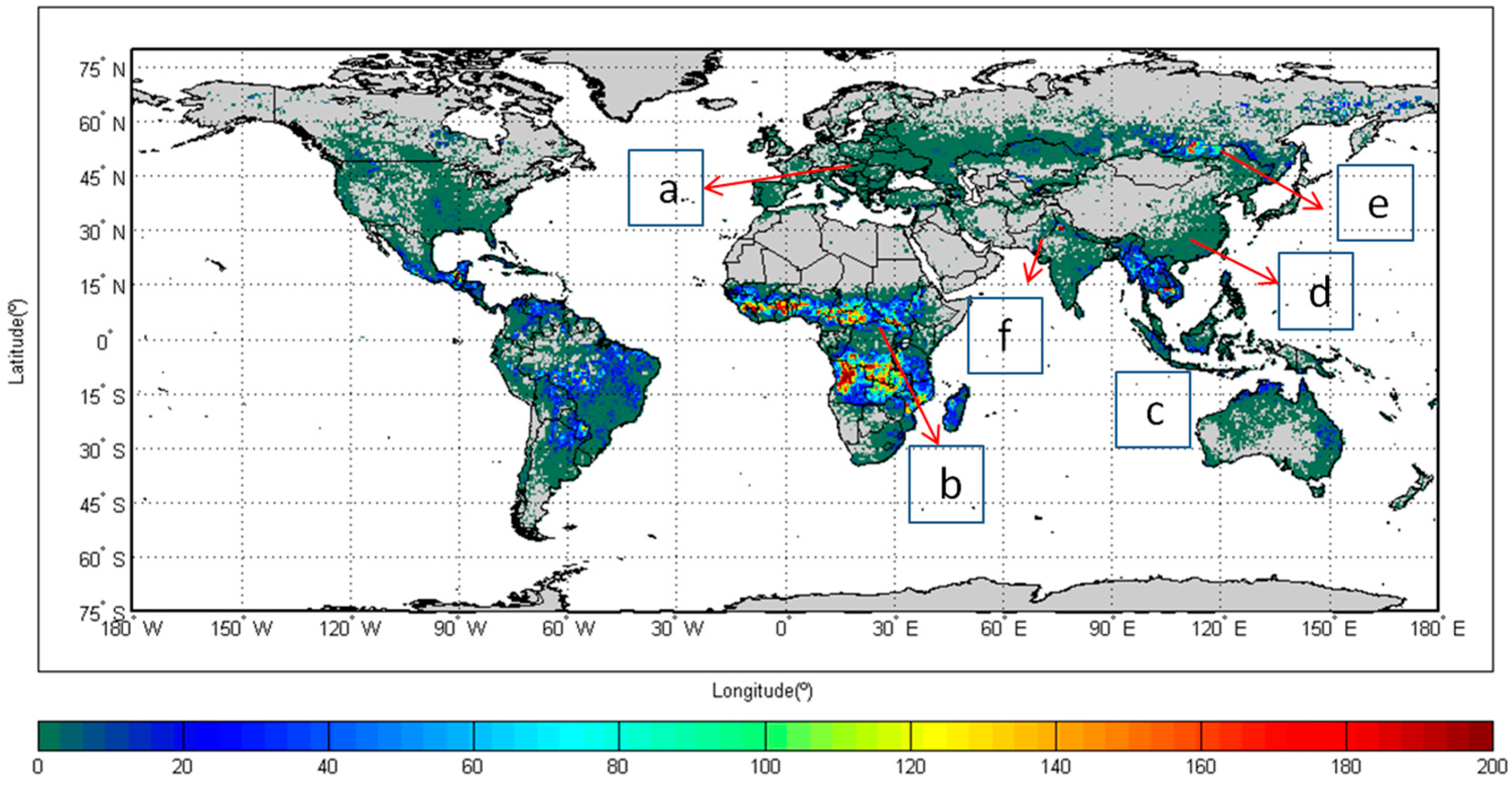
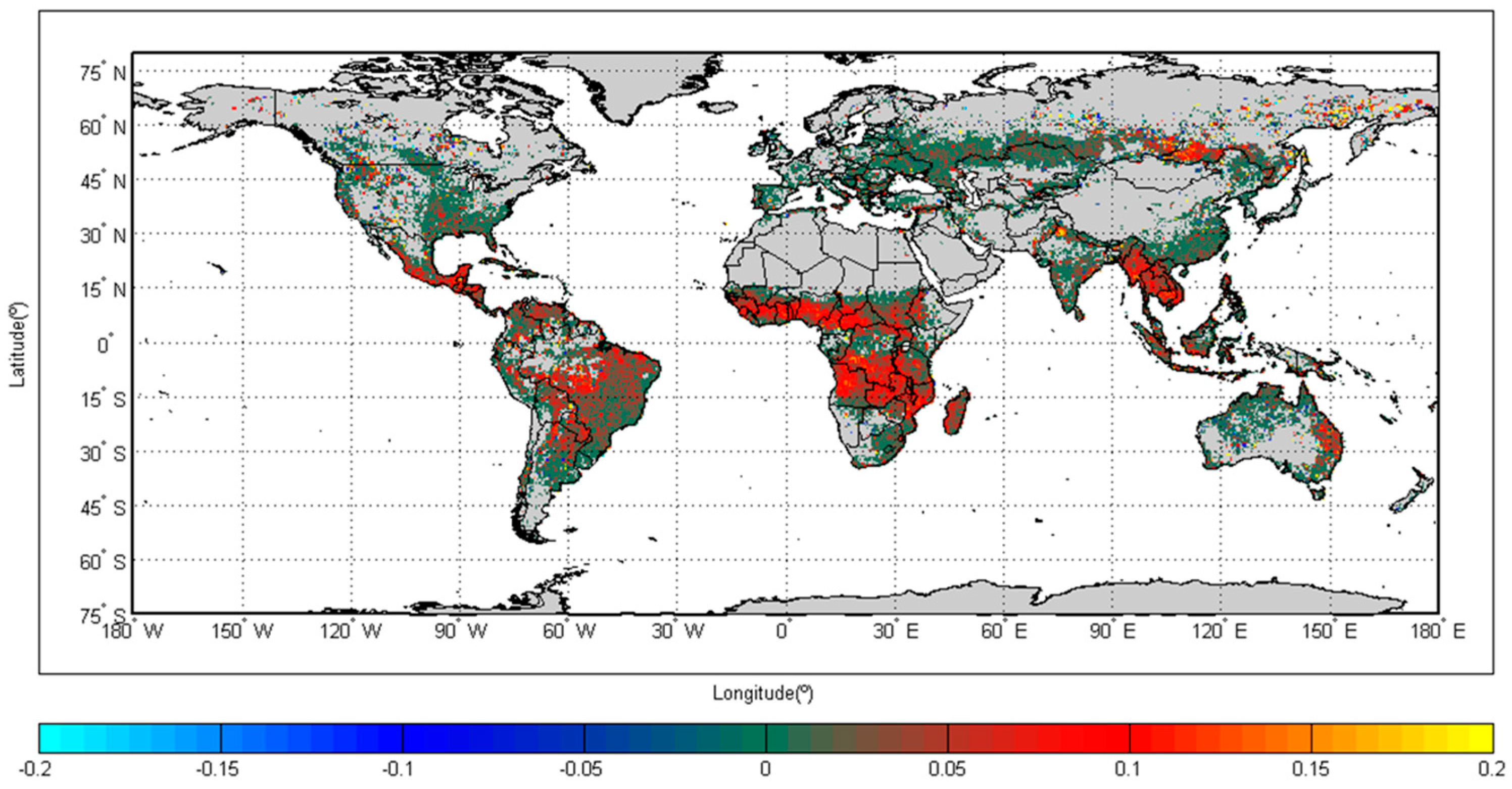
| Case Study | Country | Anthrome Class | Time-Gap (Days) | ||
|---|---|---|---|---|---|
| 2 | 8 | 14 | |||
| (a) | Ukraine | Cropland | 46 | 44 | 44 |
| (0.21) | (0.21) | (0.21) | |||
| (b) | Sudan | Rangeland | 470 | 423 | 409 |
| (0.35) | (0.37) | (0.39) | |||
| (c) | Cambodja | Forests | 472 | 397 | 319 |
| (0.25) | (0.32) | (0.38) | |||
| (d) | China | Villages | 32 | 31 | 31 |
| (0.15) | (0.16) | (0.16) | |||
| (e) | Russia | Wildland | 129 | 56 | 56 |
| (0.7) | (0.71) | (0.71) | |||
| (f) | India (Punjab district) | Dense settlements | 774 | 480 | 401 |
| (0.26) | (0.42) | (0.44) | |||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oom, D.; Silva, P.C.; Bistinas, I.; Pereira, J.M.C. Highlighting Biome-Specific Sensitivity of Fire Size Distributions to Time-Gap Parameter Using a New Algorithm for Fire Event Individuation. Remote Sens. 2016, 8, 663. https://doi.org/10.3390/rs8080663
Oom D, Silva PC, Bistinas I, Pereira JMC. Highlighting Biome-Specific Sensitivity of Fire Size Distributions to Time-Gap Parameter Using a New Algorithm for Fire Event Individuation. Remote Sensing. 2016; 8(8):663. https://doi.org/10.3390/rs8080663
Chicago/Turabian StyleOom, Duarte, Pedro C. Silva, Ioannis Bistinas, and José M. C. Pereira. 2016. "Highlighting Biome-Specific Sensitivity of Fire Size Distributions to Time-Gap Parameter Using a New Algorithm for Fire Event Individuation" Remote Sensing 8, no. 8: 663. https://doi.org/10.3390/rs8080663







