A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
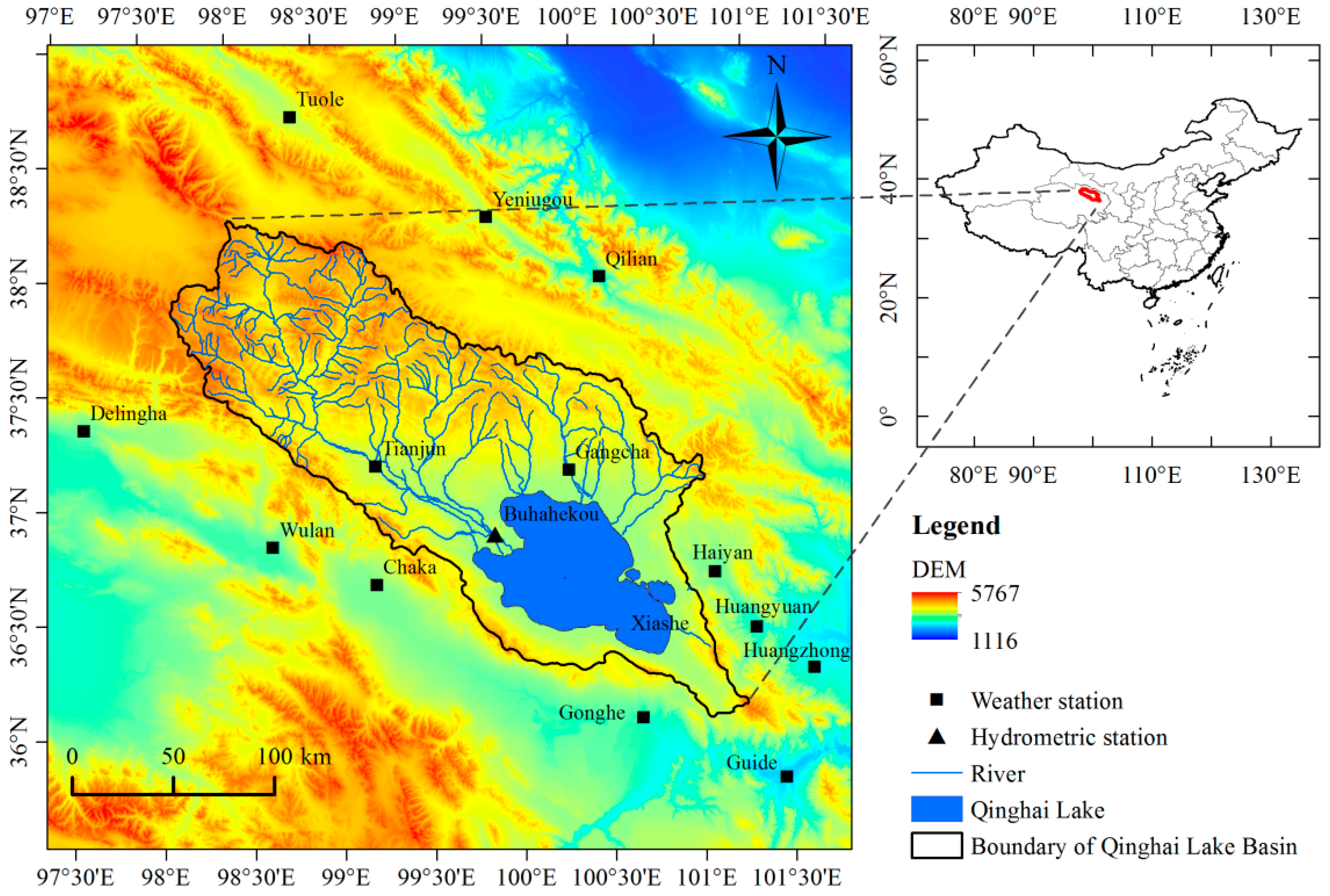
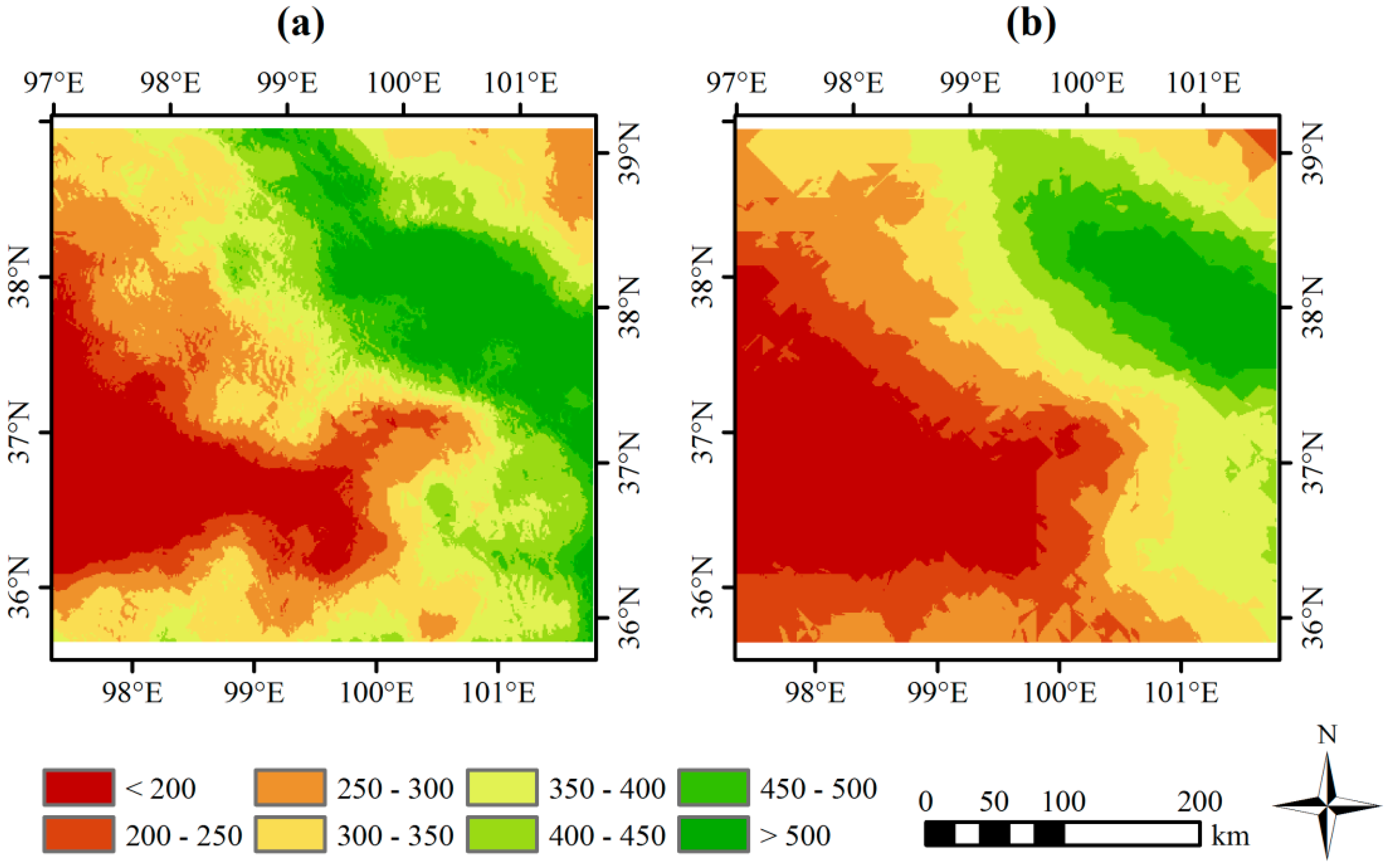
2.1.1. The Qinghai Lake Basin
2.1.2. Datasets
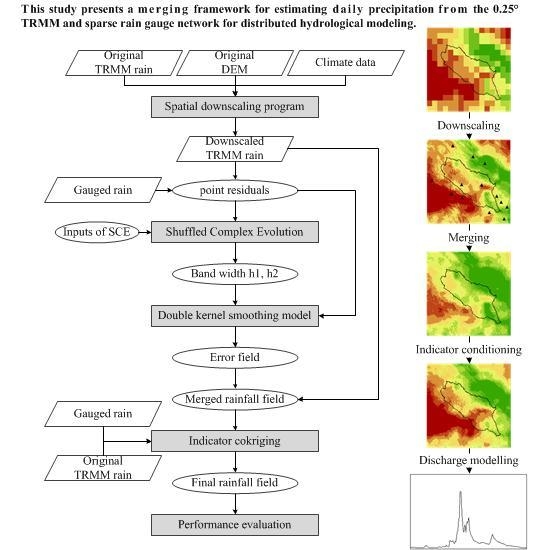
2.2. Merging Framework
2.2.1. Spatial Downscaling of TRMM
2.2.2. The Double Kernel Smoothing Technique
- Estimating the point residuals at each gauge location si:where XB, XO, and D denote the background (satellite), observed, and residual fields, respectively.
- Performing a first level interpolation of point residuals to generate gridded pseudo-residuals with a grid size of 25 km:where K is a kernel function satisfying (i) K(u) ≥ 0; (ii) K(u) = K(−u); and (iii) K(u)du = 1, is the Euclidean distance, and h is the bandwidth.
- Applying a second level of interpolation on both the observed point residuals D and the gridded pseudo-residuals to generate the error field µB on each grid of the 1 km downscaled satellite data:
- 4.
- Estimating the merged field XM by subtracting the error field µB from the background field XB:
2.2.3. Bandwidth Estimation
2.2.4. Accounting for Spatial Intermittency
- Convert the 25 km gridded daily TRMM rainfall values into point features and append the rain gauges with their rainfall values to the TRMM-derived point file. This ensures TRMM and gauge rainfall values are considered in the indicator field generation.
- Transform the rainfall values generated from the previous step to create a binary variable indicating where the rainfall value is zero (0) or nonzero (1).
- Under the assumption that the binary variable is stationary and autocorrelated, generate a soft indicator field at 1 km resolution, presenting the probability of rainfall occurrence by using ordinary kriging with a Gaussion model fitting its semi-variogram.
- Produce a hard indicator field by assigning a probability threshold to the soft indicator field (0.5 in this study).
- Estimate the final rainfall field by multiplying the merged rainfall field by the hard indicator field.
2.3. Evaluation Statistics
2.3.1. Performance Indicators
2.3.2. Hydrological Evaluation
3. Results
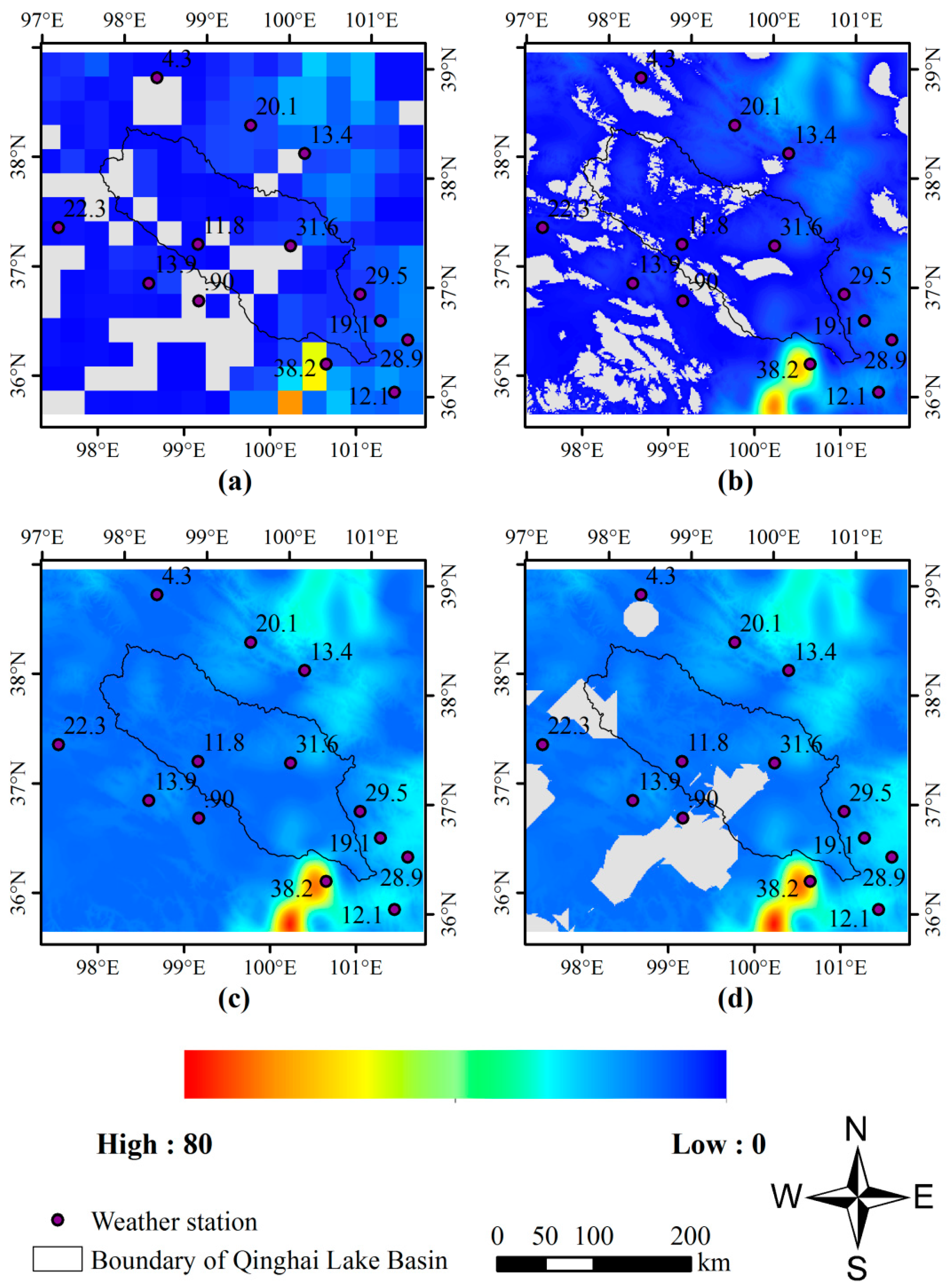
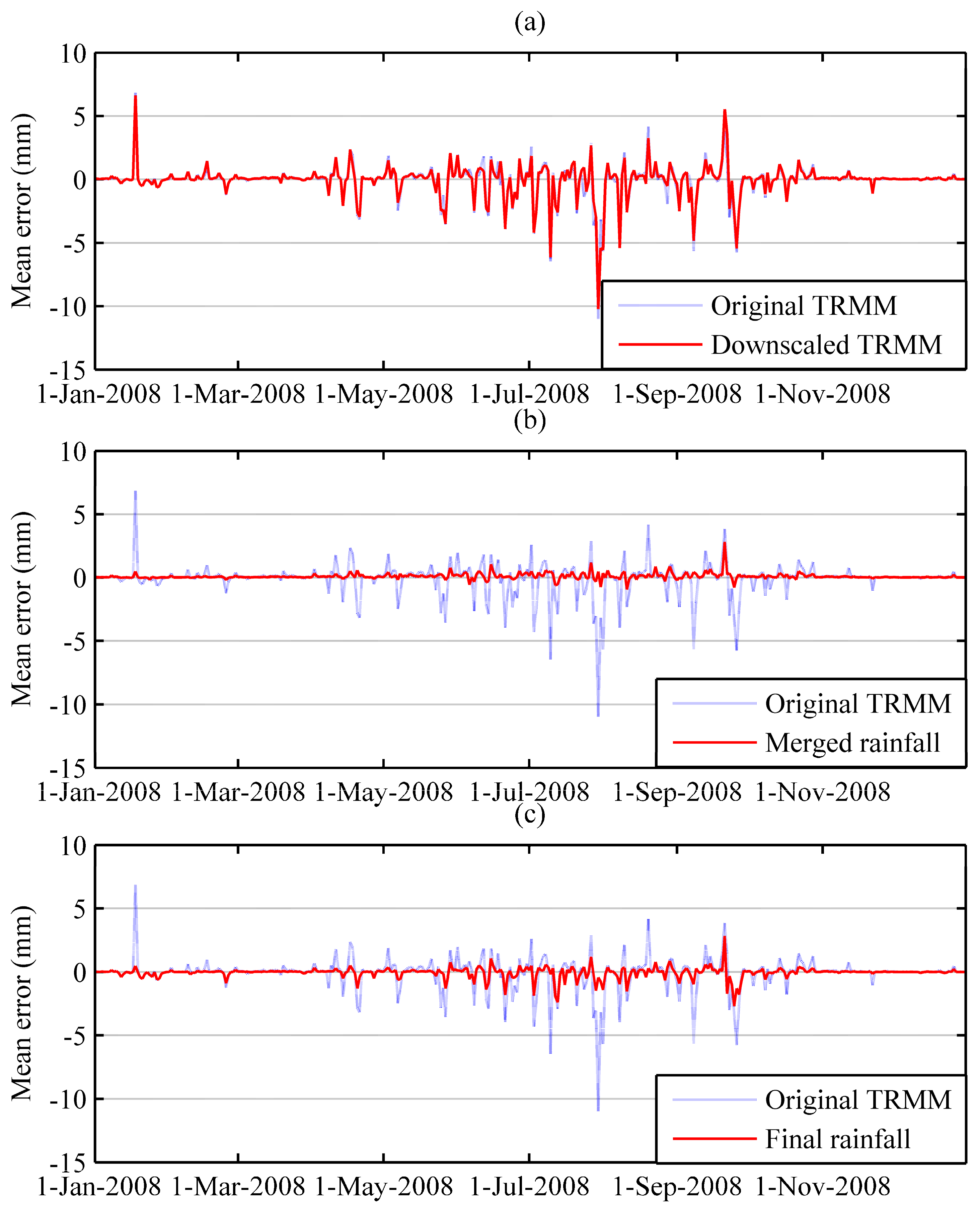
3.1. Merging Process
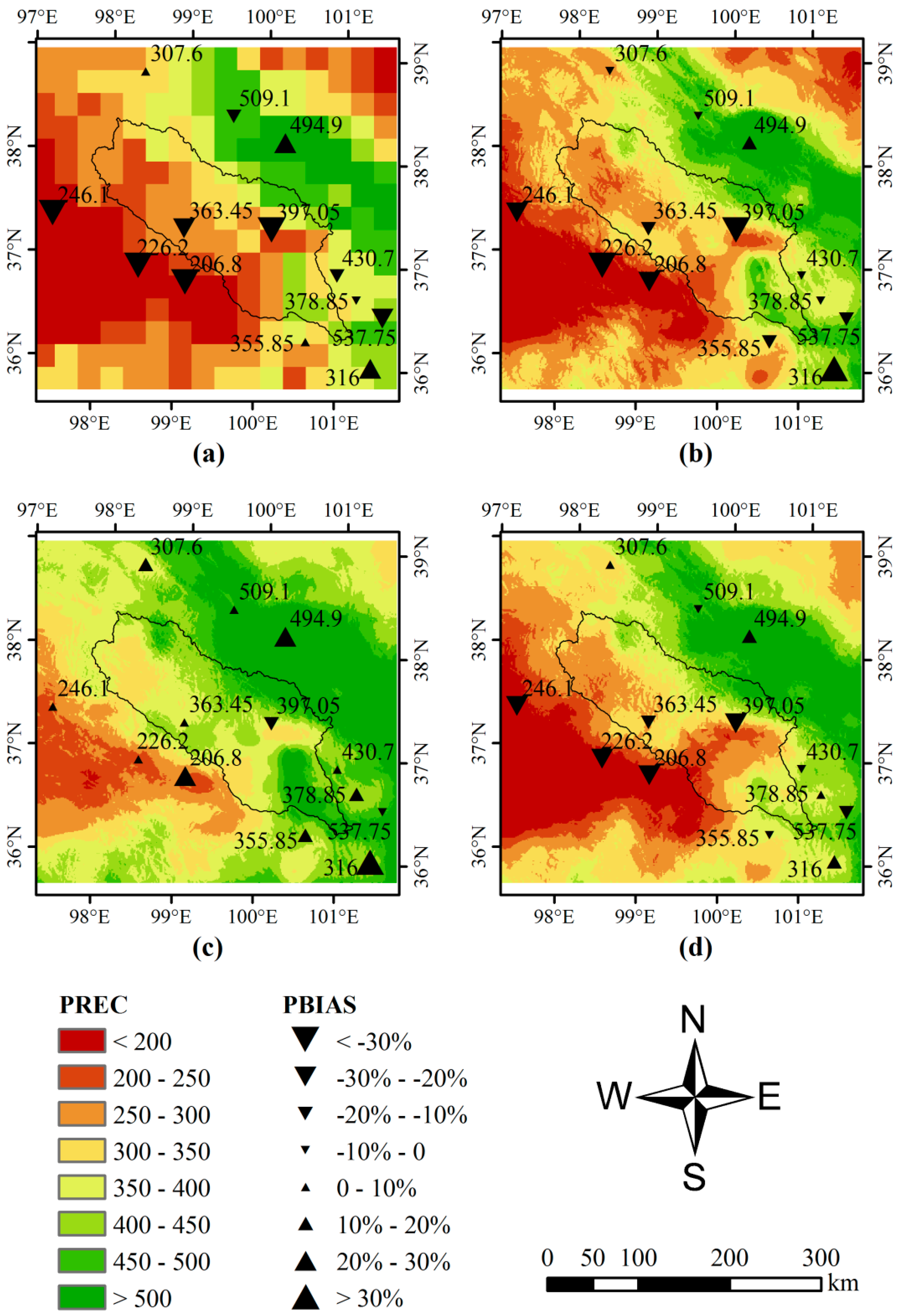
3.2. Performance of Estimation
3.2.1. Overall Performance
3.2.2. Performance at the Tianjun Station
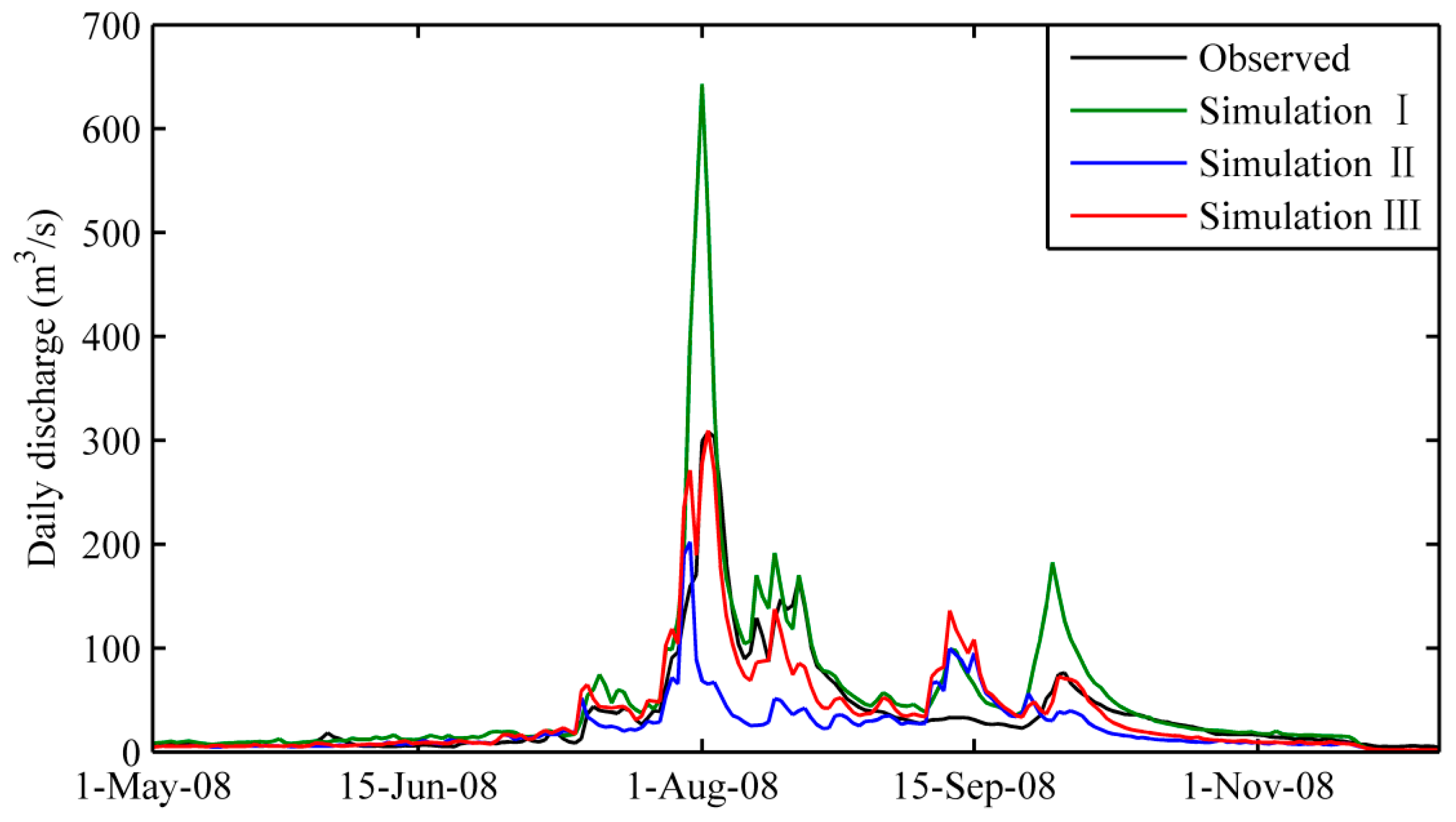
3.2.3. Hydrological Evaluation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jatho, N.; Pluntke, T.; Kurbjuhn, C.; Bernhofer, C. An approach to combine radar and gauge based rainfall data under consideration of their qualities in low mountain ranges of saxony. Nat. Hazards Earth Syst. Sci. 2010, 10, 429–446. [Google Scholar] [CrossRef]
- Mercogliano, P.; Segoni, S.; Rossi, G.; Sikorsky, B. Brief communication “a prototype forecasting chain for rainfall induced shallow landslides”. Nat. Hazards Earth Syst. Sci. 2013, 13, 771–777. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 2. Application. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Salamon, P.; Feyen, L. Assessing parameter, precipitation, and predictive uncertainty in a distributed hydrological model using sequential data assimilation with the particle filter. J. Hydrol. 2009, 376, 428–442. [Google Scholar] [CrossRef]
- Syed, T.H.; Lakshmi, V.; Paleologos, E.; Lohmann, D.; Mitchell, K.; Famiglietti, J.S. Analysis of process controls in land surface hydrological cycle over the continental united states. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Rudari, R.; Pulvirenti, L.; Boni, G.; Fascetti, F.; Pierdicca, N.; et al. Impact of different satellite soil moisture products on the predictions of a continuous distributed hydrological model. Int. J. Appl. Earth Obs. Geoinform. 2016, 48, 131–145. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sivakumar, B.; Sharma, A. Merging gauge and satellite rainfall with specification of associated uncertainty across australia. J. Hydrol. 2013, 499, 167–176. [Google Scholar] [CrossRef]
- Martens, B.; Cabus, P.; De Jongh, I.; Verhoest, N. Merging weather radar observations with ground-based measurements of rainfall using an adaptive multiquadric surface fitting algorithm. J. Hydrol. 2013, 500, 84–96. [Google Scholar] [CrossRef]
- Krajewski, W.F. Cokriging radar-rainfall and rain gage data. J. Geophys. Res. Atmos. 1987, 92, 9571–9580. [Google Scholar] [CrossRef]
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating geostatistical methods of blending satellite and gauge data to estimate near real-time daily rainfall for australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Grimes, D.; Pardo-Iguzquiza, E.; Bonifacio, R. Optimal areal rainfall estimation using raingauges and satellite data. J. Hydrol. 1999, 222, 93–108. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; de Goncalves, L.G.G.; Vila, D.A. Combining TRMM and surface observations of precipitation: Technique and validation over south america. Weather Forecast. 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q.X. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Nerini, D.; Zulkafli, Z.; Wang, L.-P.; Onof, C.; Buytaert, W.; Lavado, W.; Guyot, J.-L. A comparative analysis of TRMM-rain gauge data merging techniques at the daily time scale for distributed rainfall-runoff modelling applications. J. Hydrometeorol. 2015. [Google Scholar] [CrossRef]
- Rahman, S.; Bagtzoglou, A.C.; Hossain, F.; Tang, L.; Yarbrough, L.D.; Easson, G. Investigating spatial downscaling of satellite rainfall data for streamflow simulation in a medium-sized basin. J. Hydrometeorol. 2009, 10, 1063–1079. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and dem in the qaidam basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Fang, J.; Du, J.; Xu, W.; Shi, P.J.; Li, M.; Ming, X.D. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area. Adv. Water Resour. 2013, 61, 42–50. [Google Scholar] [CrossRef]
- Shi, Y.L.; Song, L.; Xia, Z.; Lin, Y.R.; Myneni, R.B.; Choi, S.H.; Wang, L.; Ni, X.L.; Lao, C.L.; Yang, F.K. Mapping annual precipitation across mainland China in the period 2001–2010 from TRMM3B43 product using spatial downscaling approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]
- Barancourt, C.; Creutin, J.D.; Rivoirard, J. A method for delineating and estimating rainfall fields. Water Resour. Res. 1992, 28, 1133–1144. [Google Scholar] [CrossRef]
- Grimes, D.I.F.; Pardo-Iguzquiza, E. Geostatistical analysis of rainfall. Geogr. Anal. 2010, 42, 136–160. [Google Scholar] [CrossRef]
- Li, X.-Y.; Xu, H.-Y.; Sun, Y.-L.; Zhang, D.-S.; Yang, Z.-P. Lake-level change and water balance analysis at lake Qinghai, west China during recent decades. Water Resour. Manag. 2007, 21, 1505–1516. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Zhang, L.; Hao, Z. Tibetan plateau precipitation as depicted by gauge observations, reanalyses and satellite retrievals. Int. J. Climatol. 2014, 34, 265–285. [Google Scholar] [CrossRef]
- Yang, K.; Guo, X.; He, J.; Qin, J.; Koike, T. On the climatology and trend of the atmospheric heat source over the Tibetan plateau: An experiments-supported revisit. J. Clim. 2010, 24, 1525–1541. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. A terrain ruggedness index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 1–4. [Google Scholar]
- Prudhomme, C.; Reed, D.W. Relationships between extreme daily precipitation and topography in a mountainous region: A case study in Scotland. Int. J. Climatol. 1998, 18, 1439–1453. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, Y.; Zhao, G.; Yan, P.; Li, Q.; LI, R. The uncertainty in meteorological and hydrological processes modeled by using swat model—A case study in the buhachu river basin. J. Glaciol. Geocryol. 2012, 34, 660–667. [Google Scholar]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Gasser, T.; Muller, H.G.; Mammitzsch, V. Kernels for nonparametric curve estimation. J. R. Stat. Soc. B Methodol. 1985, 47, 238–252. [Google Scholar]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Yang, D.; Oki, T.; Herath, S.; Musiake, K.; Singh, V.; Frevert, D. A geomorphology-based hydrological model and its applications. Math. Models Small Watershed Hydrol. Appl. 2002, 259–300. [Google Scholar]
- Yang, D.; Herath, S.; Musiake, K. A hillslope-based hydrological model using catchment area and width functions. Hydrol. Sci. J. 2002, 47, 49–65. [Google Scholar] [CrossRef]
- Yang, D. Distributed hydrologic Model Using Hillslope Discretization Based on Catchment Area Function: Development and Applications; University of Tokyo: Tokyo, Japan, 1998. [Google Scholar]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Zhuang, D.; Zhang, Z.; Deng, X. Study on spatial pattern of land-use change in china during 1995–2000. Sci. China 2003, 46, 373–384. [Google Scholar]
- Shi, X.; Yu, D.; Pan, X.; Sun, W.; Gong, Z.; Warner, E.; Petersen, G. A Framework for the 1:1,000,000 Soil Database of China. In Proceedings of the 17th World Congress of Soil Science, Bangkok, Thailand, 14–21 August 2002.
- NASA LP DAAC. Nasa Eosdis Land Processes Daac, Usgs Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota. Available online: https://lpdaac.Usgs.Gov/dataset_discovery/modis/modis_products_table/mcd15a3 (accessed on 4 November 2014).
- NASA LP DAAC. Nasa Eosdis Land Processes Daac, Usgs Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota. Available online: https://lpdaac.Usgs.Gov/dataset_discovery/modis/modis_products_table/mcd13q1 (accessed on 9 January 2015).
- Zhang, G.Q.; Xie, H.J.; Yao, T.D.; Li, H.Y.; Duan, S.Q. Quantitative water resources assessment of Qinghai Lake basin using snowmelt runoff model (SRM). J. Hydrol. 2014, 519, 976–987. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; Germann, U. Real-time radar-rain-gauge merging using spatio-temporal co-kriging with external drift in the alpine terrain of Switzerland. Q. J. R. Meteorol. Soc. 2013, 140, 1097–1111. [Google Scholar] [CrossRef]

| Item | Source |
|---|---|
| DEM | STRM V4.0 [28] |
| Landuse | the 1:100,000 land use map of China [40] |
| Soil parameters | the 1:1,000,000 soil database of China [41] |
| LAI | MODIS MCD15A3 [42] |
| NDVI | MODIS MOD13Q1 [43] |
| Downscaling | Regression Model | r2 | p |
| y = 0.001ELE + 1.042TEM − 13.230 | 0.173 | <0.05 | |
| DS Merging | h1 (km) | h2 (km) | CV (mm) |
| 30.609 | 548.255 | 1596.1 | |
| Indicator Kriging | Range (km) | Nugget | Sill |
| 81.953 | 0.101 | 0.048 |
| Spatial Averaged Precipitation (mm) | ME | PBIAS | RMSE | NSE | |
|---|---|---|---|---|---|
| Original TRMM | 1.90 | −10.99 | −58.05% | 15.32 | −1.11 |
| Downscaled TRMM | 1.89 | −10.22 | −53.99% | 14.52 | −0.89 |
| Merged Rainfall | 12.54 | 0.46 | 2.42% | 10.34 | 0.04 |
| Final Rainfall | 11.40 | −0.44 | −2.33% | 9.90 | 0.12 |
| Spatial Average Precipitation (mm) | ME | PBIAS | RMSE | NSE | |
|---|---|---|---|---|---|
| Original TRMM | 305.39 | −0.13 | −12.64% | 2.89 | 0.13 |
| Downscaled TRMM | 332.95 | −0.09 | −9.23% | 2.71 | 0.24 |
| Merged Rainfall | 416.20 | 0.08 | 8.44% | 1.71 | 0.70 |
| Final Rainfall | 330.27 | −0.07 | −6.72% | 1.88 | 0.63 |
| ME | PBIAS | RMSE | NSE | |
|---|---|---|---|---|
| Original TRMM | −0.29 | −29.44% | 2.33 | 0.46 |
| Downscaled TRMM | −0.17 | −17.09% | 2.13 | 0.55 |
| Merged Rainfall | 0.06 | 6.17% | 1.87 | 0.65 |
| Final Rainfall | −0.19 | −18.77% | 2.04 | 0.59 |
| NSE | R2 | PBIAS | RSR | |
|---|---|---|---|---|
| Simulation I | 0.33 | 0.84 | 41.02% | 0.82 |
| Simulation II | 0.37 | 0.42 | −35.87% | 0.79 |
| Simulation III | 0.82 | 0.83 | 0.85% | 0.43 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, Y.; Zhang, Y.; Ma, Q. A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area. Remote Sens. 2016, 8, 599. https://doi.org/10.3390/rs8070599
Long Y, Zhang Y, Ma Q. A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area. Remote Sensing. 2016; 8(7):599. https://doi.org/10.3390/rs8070599
Chicago/Turabian StyleLong, Yinping, Yaonan Zhang, and Qimin Ma. 2016. "A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area" Remote Sensing 8, no. 7: 599. https://doi.org/10.3390/rs8070599
APA StyleLong, Y., Zhang, Y., & Ma, Q. (2016). A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area. Remote Sensing, 8(7), 599. https://doi.org/10.3390/rs8070599