Pansharpening by Convolutional Neural Networks
Abstract
:1. Introduction
2. Background
2.1. Deep Learning and Convolutional Neural Networks
2.2. CNN-Based Super-Resolution
| , | ||
| , | ||
| , |
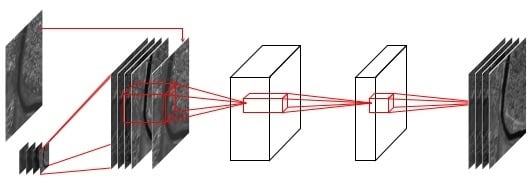
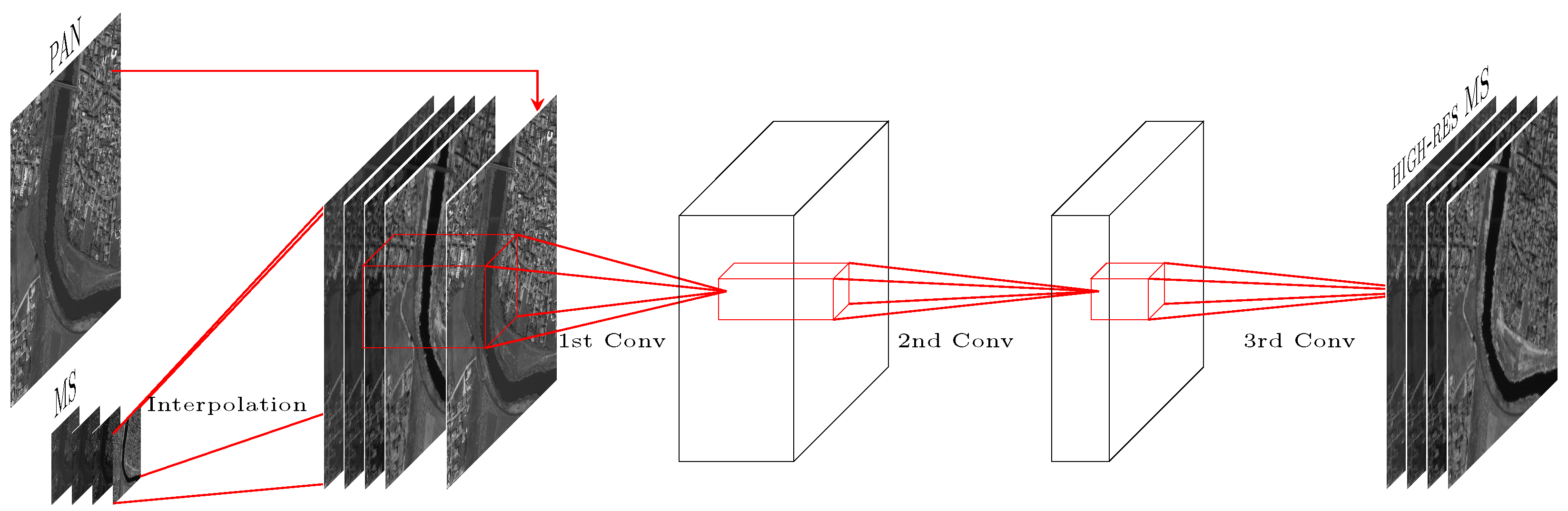
3. Proposed CNN-Based Pansharpening
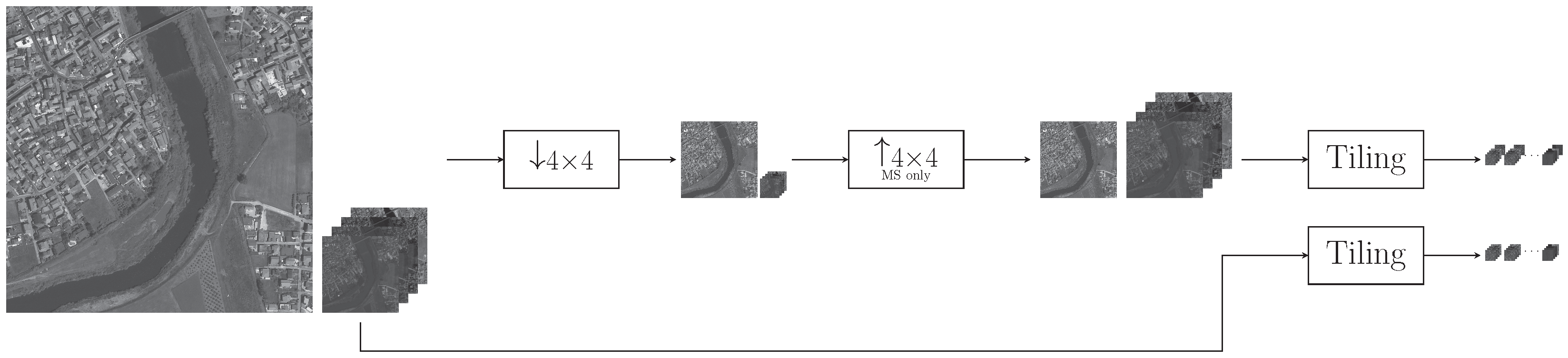
3.1. Datasets
3.2. Basic Architecture
3.3. Remote-Sensing Specific Architecture
- Normalized Difference Water Index:
- Normalized Difference Vegetation Index:
- Normalized Difference Soil Index (applies to WorldView-2 only):
- Non-Homogeneous Feature Difference (applies to WorldView-2 only):
4. Results and Discussion
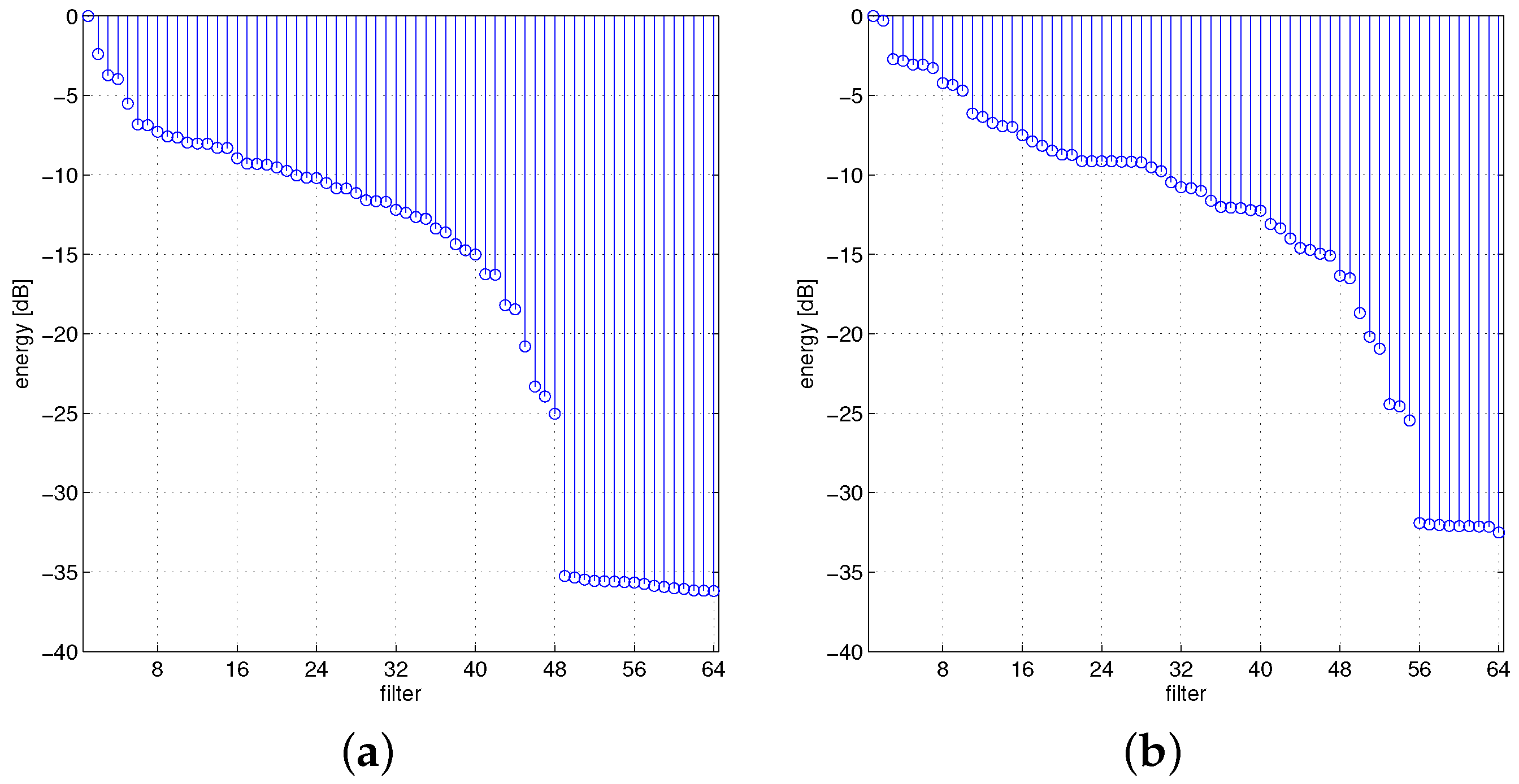
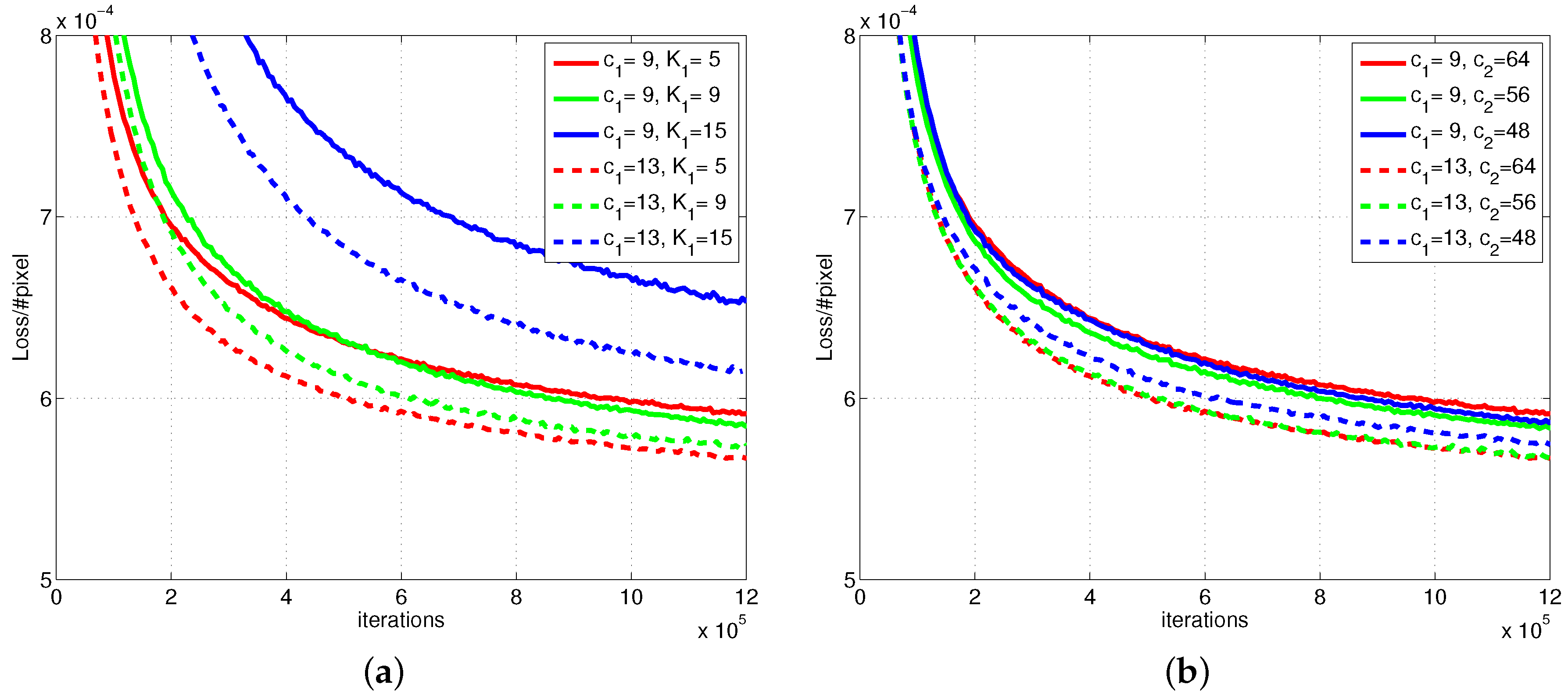
4.1. Comparing Different Networks
4.2. Comparison with the State of the Art
- PRACS: Partial Replacement Adaptive Component Substitution [10];
- Indusion: Decimated Wavelet Transform using an additive injection model [18];
- ATWT-M3: A Trous Wavelet Transform with the injection Model 3 proposed in [15];
- MTF-GLP-HPM: Generalized Laplacian Pyramid with MTF-matched filter and multiplicative injection model [16];
- BDSD: Band-Dependent Spatial-Detail with local parameter estimation [25];
- C-BDSD: A non-local extension of BDSD, proposed in [26].
4.3. Visual Inspection
4.4. Implementation Details
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ATWT/ATWT-M3 | À Trous Wavelet transform/ATWT with injection Model 3 |
| AWL/AWLP | Additive Wavelet Luminance/AWL Proportional |
| BDSD | Band-Dependent Spatial-Detail with local parameter estimation |
| C-BDSD | Non-local extension of BDSD |
| BT | Brovey transorm |
| CNN | Convolutional Neural Networks |
| CS | Component Substitution |
| ERGAS | Erreur Relative Globale Adimensionnelle de Synthèse |
| GPU | Graphics Processing Unit |
| GS | Gram-Schmidt |
| IHS/GIHS | Intensity-Hue-Saturation/Generalized IHS |
| LP | Laplacian Pyramid |
| MMSE | Minimum mean-square-error |
| MS | Multispectral |
| MRA | Multi Resolution Analysis |
| MT | Modulation Transfer Function |
| MTF-GLP-HPM | Generalized Laplacian Pyramid with MTF-matched filter and multiplicative injection model |
| NDSI | Normalized Difference Soil Index |
| NDVI | Normalized Difference Vegetation Index |
| NDWI | Normalized Difference Water Index |
| NHFD | Non-Homogeneous Feature Difference |
| NIR | Near-Infrared |
| PAN | Panchromatic |
| PCA | Principal Component Analysis |
| PNN | CNN-based Pansharpening (proposed method) |
| PRACS | Partial Replacement Adaptive Component Substitution |
| Q/Qx | Universal Image Quality Index/x-band extension of Q |
| QNR | Quality with no-reference |
| ReLU | Rectified Linear Unit |
| SAM | Spectral Angle Mapper |
| SCC | Spacial Correlation Coefficient |
| SFIM | Smoothing-filter-based Intensity Modulation |
| SRCNN | Super-resolution CNN |
Appendix
References
- Gaetano, R.; Masi, G.; Poggi, G.; Verdoliva, L.; Giuseppe, S. Marker controlled watershed based segmentation of multi-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1987–3004. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Shettigara, V. A generalized component substitution technique for spatial enhancement of multispectral images using a higher resolution data set. Photogramm. Eng. Remote Sens. 1992, 58, 561–567. [Google Scholar]
- Tu, T.M.; Su, S.C.; Shyu, H.C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A fast intensity hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Chavez, P.; Kwarteng, A. Extracting spectral contrast in Landsat thematic mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Laben., C.; Brower, B. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Choi, J.; Yu, K.; Kim, Y. A new adaptive component-substitution-based satellite image fusion by using partial replacement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 295–309. [Google Scholar] [CrossRef]
- Chavez, P.; Anderson, J. Comparison of three different methods to merge multiresolution and multispectral data: Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Yocky, D. Multiresolution wavelet decomposition image merger of Landsat Thematic Mapper and SPOT panchromatic data. Photogramm. Eng. Remote Sens. 1996, 62, 1067–1074. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. Remote sensing image fusion using the curvelet transform. Inf. Fusion 2007, 8, 143–156. [Google Scholar]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. An MTF-based spectral distortion minimizing model for pan-sharpening of very high resolution multispectral images of urban areas. In Proceedings of the 2nd GRSS/ISPRS Joint Workshop on Remote Sensing and Data Fusion over Urban Areas, Berlin, Germany, 22–23 May 2003.
- Liu, J. Smoothing filter based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Khan, M.; Chanussot, J.; Condat, L.; Montanvert, A. Indusion: Fusion of multispectral and panchromatic images using the induction scaling technique. IEEE Geosci. Remote Sens. Lett. 2008, 5, 98–102. [Google Scholar] [CrossRef]
- Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
- Otazu, X.; Gonzalez-Audicana, M.; Fors, O.; Nunez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Mura, M.D.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. Fast and efficient panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2010, 48, 155–163. [Google Scholar]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Garzelli, A. Pansharpening of multispectral images based on nonlocal parameter optimization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2096–2107. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.; Ulfarsson, M. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. A new pan-sharpening method using a compressed sensing technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 738–746. [Google Scholar] [CrossRef]
- Li, S.; Yin, H.; Fang, L. Remote sensing image fusion via sparse representations over learned dictionaries. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4779–4789. [Google Scholar] [CrossRef]
- Zhu, X.; Bamler, R. A sparse image fusion algorithm with application to pan-sharpening. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2827–2836. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, C.; Li, J. Sparse representation based pansharpening using trained dictionary. IEEE Geosci. Remote Sens. Lett. 2014, 11, 293–297. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, L.; Wei, Z.; Liu, H.; Tang, S. A new pan-sharpening method with deep neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1037–1041. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Xu, F.; Jin, Y.Q. Application of deep learning algorithms to MSTAR data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015.
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks. Available online: http://arxiv.org/abs/1508.00092 (accessed on 13 July 2016).
- Dong, C.; Loy, C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2012. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on CVPR 2009, Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009.
- Ouyang, W.; Wang, X. Joint deep learning for pedestrian detection. In Proceedings fo the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 3–6 December 2013.
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolution: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. Available online: http://arxiv.org/abs/1312.6034 (accessed on 13 July 2016).
- Nouri, H.; Beecham, S.; Anderson, S.; Nagler, P. High spatial resolution worldview-2 imagery for mapping NDVI and Its relationship to temporal urban landscape evapotranspiration factors. Remote Sens. 2014, 6, 580–602. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the Spectral AngleMapper (SAM) algorithm. In Summaries of the Third Annual JPL Airborne Geoscience Workshop; AVIRIS Workshop: Pasadena, CA, USA, 1992; pp. 147–149. [Google Scholar]
- Wald, L. Data Fusion: Definitions and Architectures–Fusion of Images of Different Spatial Resolutions; Presses des Mines: Paris, France, 2002. [Google Scholar]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Open Remote Sensing. Available online: http://openremotesensing.net/ (accessed on 13 July 2016).
- Image Processing Research Group. Available online: http://www.grip.unina.it (accessed on 13 July 2016).
- Caffe. Available online: http://caffe.berkeleyvision.org (accessed on 13 July 2016).
- MatConvNet: CNNs for MATLAB. Available online: http://www.vlfeat.org/matconvnet (accessed on 13 July 2016).
- Gaetano, R.; Scarpa, G.; Poggi, G. Recursive texture fragmentation and reconstruction segmentation algorithm applied to VHR images. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009.
- Gaetano, R.; Masi, G.; Scarpa, G.; Poggi, G. A marker-controlled watershed segmentation: Edge, mark and fill. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012.









| PAN | MS | |
|---|---|---|
| Ikonos | 0.82 m GSD at nadir | 3.28 m GSD at nadir |
| GeoEye-1 | 0.46 m GSD at nadir | 1.84 m GSD at nadir |
| WorldView-2 | 0.46 m GSD at nadir | 1.84 m GSD at nadir |
| PAN | Coastal | Blue | Green | Yellow | Red | Red Edge | Nir | Nir 2 | |
|---|---|---|---|---|---|---|---|---|---|
| Ikonos | 526–929 | no | 445–516 | 506–595 | no | 632–698 | no | 757–853 | no |
| GeoEye-1 | 450–900 | no | 450–520 | 520–600 | no | 625–695 | no | 760–900 | no |
| WorldView-2 | 450–800 | 400–450 | 450–510 | 510–580 | 585–625 | 630–690 | 705–745 | 770–895 | 860–1040 |
| 5 | ReLU | 64 | ReLU | 32 | x | 4 |
| Sensor | B | ||||
|---|---|---|---|---|---|
| Ikonos, GeoEye-1 | 4 | ||||
| WorldView-2 | 8 |
| Training | Validation | Test | |
|---|---|---|---|
| Ikonos | |||
| GeoEye-1 | |||
| WorldWiew-2 |
| full reference | SAM | Spectral Angle Mapper [45] |
| ERGAS | Erreur Relative Globale Adimensionnelle de Synthèse [46] | |
| SCC | Spatial Correlation Coefficient [47] | |
| Q | Universal Image Quality index [48] averaged over the bands | |
| Qx | x-band extension of Q [49] | |
| no reference | QNR | Quality with no-Reference index [44] |
| Spectral component of QNR | ||
| Spatial component of QNR |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 5 | 48 | 0.8518 | 0.9445 | 2.5750 | 1.6031 | 0.9405 | 0.0190 | 0.0551 | 0.9269 |
| 56 | 0.8519 | 0.9446 | 2.5754 | 1.6028 | 0.9403 | 0.0198 | 0.0557 | 0.9256 | ||
| 64 | 0.8514 | 0.9440 | 2.5867 | 1.6055 | 0.9402 | 0.0192 | 0.0552 | 0.9267 | ||
| 9 | 48 | 0.8500 | 0.9438 | 2.6034 | 1.6147 | 0.9402 | 0.0209 | 0.0522 | 0.9280 | |
| 56 | 0.8515 | 0.9441 | 2.5851 | 1.6045 | 0.9403 | 0.0206 | 0.0522 | 0.9283 | ||
| 64 | 0.8520 | 0.9445 | 2.5703 | 1.6016 | 0.9403 | 0.0199 | 0.0532 | 0.9280 | ||
| 15 | 64 | 0.8448 | 0.9413 | 2.6671 | 1.6615 | 0.9370 | 0.0232 | 0.0534 | 0.9248 | |
| 13 | 5 | 48 | 0.8528 | 0.9449 | 2.5483 | 1.5844 | 0.9413 | 0.0200 | 0.0523 | 0.9287 |
| 56 | 0.8537 | 0.9449 | 2.5454 | 1.5783 | 0.9418 | 0.0181 | 0.0525 | 0.9303 | ||
| 64 | 0.8539 | 0.9452 | 2.5390 | 1.5792 | 0.9419 | 0.0181 | 0.0521 | 0.9308 | ||
| 9 | 48 | 0.8511 | 0.9442 | 2.5767 | 1.6029 | 0.9392 | 0.0199 | 0.0485 | 0.9326 | |
| 56 | 0.8527 | 0.9450 | 2.5570 | 1.5898 | 0.9412 | 0.0194 | 0.0497 | 0.9319 | ||
| 64 | 0.8525 | 0.9448 | 2.5585 | 1.5899 | 0.9414 | 0.0186 | 0.0508 | 0.9316 | ||
| 15 | 64 | 0.8472 | 0.9425 | 2.6263 | 1.6413 | 0.9392 | 0.0213 | 0.0508 | 0.9290 |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 48 | 0.7557 | 0.8970 | 2.3199 | 1.6693 | 0.9384 | 0.0569 | 0.0768 | 0.8713 |
| 56 | 0.7565 | 0.8974 | 2.3170 | 1.6681 | 0.9386 | 0.0547 | 0.0791 | 0.8712 | ||
| 64 | 0.7562 | 0.8970 | 2.3223 | 1.6629 | 0.9386 | 0.0538 | 0.0798 | 0.8713 | ||
| 9 | 48 | 0.7565 | 0.8970 | 2.3149 | 1.6569 | 0.9401 | 0.0602 | 0.0725 | 0.8719 | |
| 56 | 0.7575 | 0.8979 | 2.3071 | 1.6521 | 0.9404 | 0.0613 | 0.0768 | 0.8672 | ||
| 64 | 0.7581 | 0.8981 | 2.3068 | 1.6537 | 0.9404 | 0.0617 | 0.0764 | 0.8672 | ||
| 7 | 5 | 48 | 0.7609 | 0.9006 | 2.2831 | 1.6634 | 0.9411 | 0.0514 | 0.0731 | 0.8796 |
| 56 | 0.7607 | 0.9003 | 2.2774 | 1.6547 | 0.9413 | 0.0527 | 0.0733 | 0.8782 | ||
| 64 | 0.7611 | 0.9005 | 2.2737 | 1.6544 | 0.9409 | 0.0525 | 0.0731 | 0.8786 | ||
| 9 | 48 | 0.7613 | 0.8997 | 2.2743 | 1.6380 | 0.9422 | 0.0568 | 0.0720 | 0.8757 | |
| 56 | 0.7616 | 0.9003 | 2.2645 | 1.6339 | 0.9427 | 0.0589 | 0.0737 | 0.8722 | ||
| 64 | 0.7616 | 0.9004 | 2.2658 | 1.6335 | 0.9425 | 0.0573 | 0.0733 | 0.8740 |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 48 | 0.8090 | 0.9395 | 2.1582 | 1.5953 | 0.9117 | 0.0354 | 0.0700 | 0.8974 |
| 56 | 0.8065 | 0.9388 | 2.1658 | 1.6052 | 0.9106 | 0.0377 | 0.0682 | 0.8970 | ||
| 64 | 0.8089 | 0.9398 | 2.1562 | 1.5994 | 0.9116 | 0.0365 | 0.0683 | 0.8979 | ||
| 9 | 48 | 0.8089 | 0.9394 | 2.1597 | 1.5836 | 0.9134 | 0.0394 | 0.0672 | 0.8964 | |
| 56 | 0.8097 | 0.9403 | 2.1416 | 1.5688 | 0.9147 | 0.0377 | 0.0663 | 0.8988 | ||
| 64 | 0.8094 | 0.9398 | 2.1494 | 1.5742 | 0.9145 | 0.0346 | 0.0652 | 0.9028 | ||
| 7 | 5 | 48 | 0.8112 | 0.9401 | 2.1249 | 1.5689 | 0.9167 | 0.0340 | 0.0650 | 0.9034 |
| 56 | 0.8089 | 0.9398 | 2.1360 | 1.5889 | 0.9146 | 0.0337 | 0.0648 | 0.9040 | ||
| 64 | 0.8088 | 0.9401 | 2.1296 | 1.5843 | 0.9154 | 0.0344 | 0.0663 | 0.9018 | ||
| 9 | 48 | 0.8094 | 0.9402 | 2.1311 | 1.5661 | 0.9152 | 0.0327 | 0.0611 | 0.9084 | |
| 56 | 0.8112 | 0.9403 | 2.1299 | 1.5598 | 0.9153 | 0.0333 | 0.0626 | 0.9065 | ||
| 64 | 0.8103 | 0.9400 | 2.1364 | 1.5605 | 0.9151 | 0.0345 | 0.0603 | 0.9075 |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||
|---|---|---|---|---|---|---|---|---|
| PRACS | 0.7908 | 0.8789 | 3.6995 | 2.4102 | 0.8522 | 0.0234 | 0.0734 | 0.9050 |
| Indusion | 0.6928 | 0.8373 | 3.7261 | 3.2022 | 0.8401 | 0.0552 | 0.0649 | 0.8839 |
| AWLP | 0.8127 | 0.9043 | 3.4182 | 2.2560 | 0.8974 | 0.0665 | 0.0849 | 0.8549 |
| ATWT-M3 | 0.7039 | 0.8186 | 4.0655 | 3.1609 | 0.8398 | 0.0675 | 0.0748 | 0.8628 |
| MTF-GLP-HPM | 0.8242 | 0.9083 | 3.4497 | 2.0918 | 0.9019 | 0.0755 | 0.0953 | 0.8373 |
| BDSD | 0.8110 | 0.9052 | 3.7449 | 2.2644 | 0.8919 | 0.0483 | 0.0382 | 0.9156 |
| C-BDSD | 0.8004 | 0.8948 | 3.9891 | 2.6363 | 0.8940 | 0.0251 | 0.0458 | 0.9304 |
| PNN | 0.8511 | 0.9442 | 2.5767 | 1.6029 | 0.9392 | 0.0199 | 0.0485 | 0.9326 |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||
|---|---|---|---|---|---|---|---|---|
| PRACS | 0.6597 | 0.8021 | 2.9938 | 2.3597 | 0.8735 | 0.0493 | 0.1148 | 0.8424 |
| Indusion | 0.5928 | 0.7660 | 3.2800 | 2.7961 | 0.8506 | 0.1264 | 0.1619 | 0.7340 |
| AWLP | 0.7143 | 0.8389 | 2.8426 | 2.1126 | 0.9069 | 0.1384 | 0.1955 | 0.6951 |
| ATWT-M3 | 0.5579 | 0.7249 | 3.5807 | 3.0327 | 0.8183 | 0.1244 | 0.1452 | 0.7490 |
| MTF-GLP-HPM | 0.7178 | 0.8422 | 2.8820 | 2.0550 | 0.9072 | 0.1524 | 0.2186 | 0.6646 |
| BDSD | 0.7199 | 0.8576 | 2.9147 | 1.9852 | 0.9084 | 0.0395 | 0.0884 | 0.8761 |
| C-BDSD | 0.7204 | 0.8569 | 2.9101 | 2.0553 | 0.9164 | 0.0710 | 0.1218 | 0.8173 |
| PNN | 0.7609 | 0.9006 | 2.2831 | 1.6634 | 0.9411 | 0.0514 | 0.0731 | 0.8796 |
| Q4 | Q | SAM | ERGAS | SCC | QNR | |||
|---|---|---|---|---|---|---|---|---|
| PRACS | 0.6995 | 0.8568 | 3.2364 | 2.4296 | 0.8113 | 0.0470 | 0.0877 | 0.8698 |
| Indusion | 0.5743 | 0.7771 | 3.5361 | 3.5480 | 0.7600 | 0.1270 | 0.1262 | 0.7651 |
| AWLP | 0.7175 | 0.8615 | 3.6297 | 2.6134 | 0.7878 | 0.1247 | 0.1521 | 0.7436 |
| ATWT-M3 | 0.6008 | 0.7907 | 3.5546 | 3.0729 | 0.7944 | 0.0712 | 0.0710 | 0.8633 |
| MTF-GLP-HPM | 0.7359 | 0.8718 | 3.2205 | 5.0344 | 0.7887 | 0.1526 | 0.1815 | 0.6956 |
| BDSD | 0.7399 | 0.8832 | 3.3384 | 2.2342 | 0.8526 | 0.0490 | 0.0994 | 0.8572 |
| C-BDSD | 0.7391 | 0.8784 | 3.4817 | 2.4370 | 0.8591 | 0.0832 | 0.1342 | 0.7953 |
| PNN | 0.8094 | 0.9402 | 2.1311 | 1.5661 | 0.9152 | 0.0327 | 0.0611 | 0.9084 |
| WorldView-2 | Ikonos | GeoEye-1 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Q4 | SAM | QNR | Q4 | SAM | QNR | Q4 | SAM | QNR | |
| PRACS | 5.0 | 4.3 | 3.7 | 5.8 | 4.2 | 3.0 | 5.6 | 3.5 | 3.1 |
| Indusion | 7.6 | 4.2 | 4.5 | 7.0 | 4.9 | 5.6 | 7.6 | 4.9 | 5.9 |
| AWLP3.7 | 3.8 | 2.6 | 6.5 | 3.7 | 2.2 | 6.7 | 4.8 | 3.0 | 6.7 |
| ATWT-M3 | 7.4 | 6.0 | 6.4 | 7.8 | 7.0 | 5.3 | 7.3 | 5.9 | 2.9 |
| MTF-GLP-HPM | 2.5 | 2.8 | 7.7 | 3.2 | 2.8 | 8.0 | 3.1 | 3.1 | 8.0 |
| BDSD | 3.7 | 8.0 | 3.3 | 3.7 | 6.5 | 2.1 | 3.1 | 7.8 | 3.0 |
| C-BDSD | 5.0 | 7.0 | 2.0 | 3.4 | 7.2 | 3.4 | 3.5 | 6.8 | 5.0 |
| PNN | 1.0 | 1.2 | 1.9 | 1.2 | 1.0 | 1.9 | 1.0 | 1.0 | 1.4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by Convolutional Neural Networks. Remote Sens. 2016, 8, 594. https://doi.org/10.3390/rs8070594
Masi G, Cozzolino D, Verdoliva L, Scarpa G. Pansharpening by Convolutional Neural Networks. Remote Sensing. 2016; 8(7):594. https://doi.org/10.3390/rs8070594
Chicago/Turabian StyleMasi, Giuseppe, Davide Cozzolino, Luisa Verdoliva, and Giuseppe Scarpa. 2016. "Pansharpening by Convolutional Neural Networks" Remote Sensing 8, no. 7: 594. https://doi.org/10.3390/rs8070594
APA StyleMasi, G., Cozzolino, D., Verdoliva, L., & Scarpa, G. (2016). Pansharpening by Convolutional Neural Networks. Remote Sensing, 8(7), 594. https://doi.org/10.3390/rs8070594