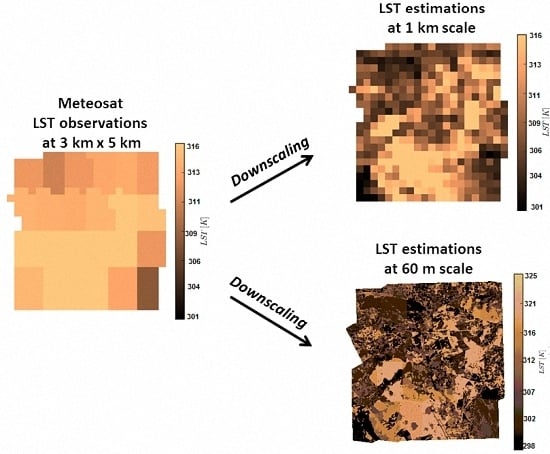
Downscaling Meteosat Land Surface Temperature over a Heterogeneous Landscape Using a Data Assimilation Approach
Abstract
:1. Introduction
2. Methodology and Data
2.1. GPS Downscaling Methodology
2.1.1. Data Assimilation Approach
2.1.2. Implementation of the GPS
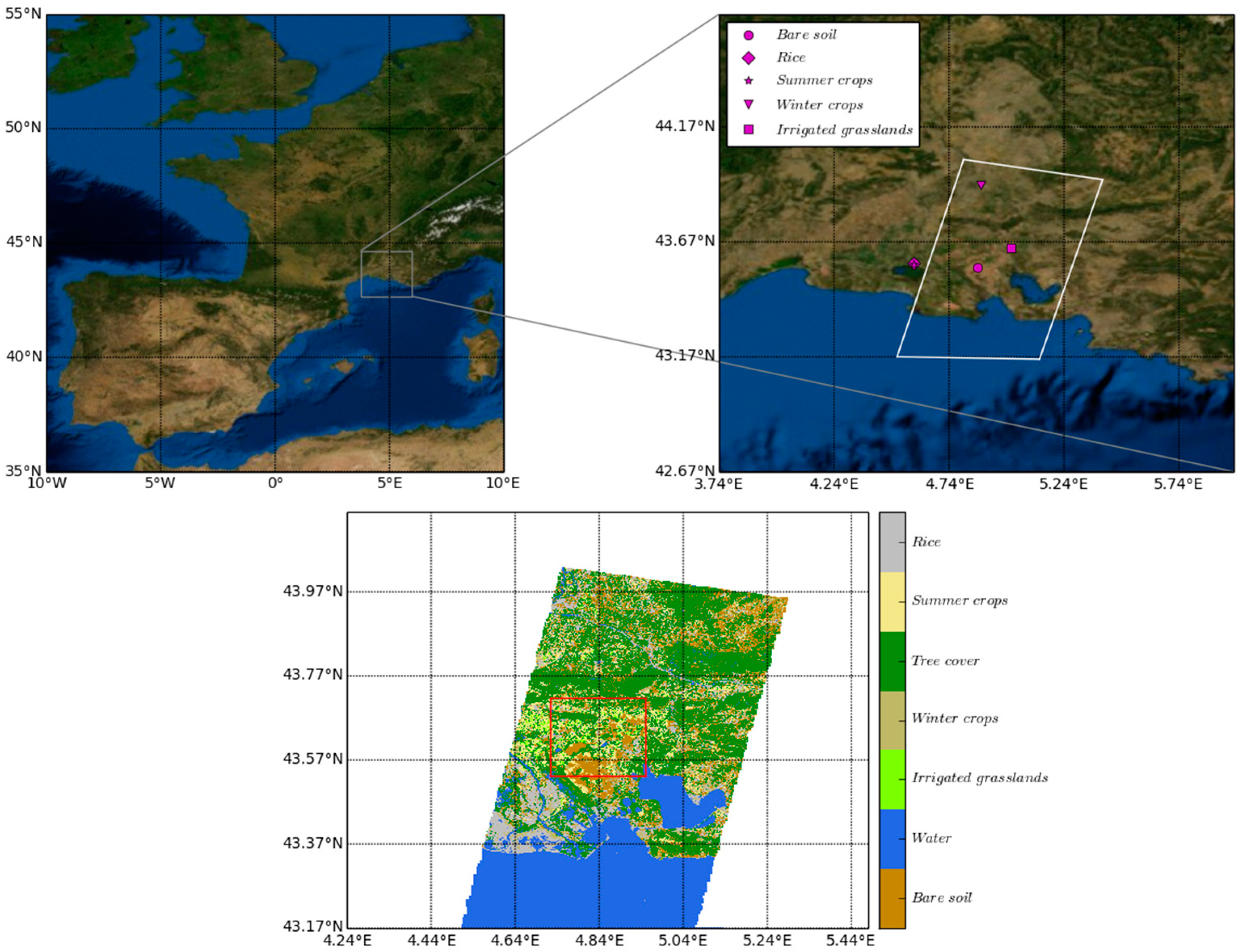
2.2. Study Area and Forcing Data
2.3. Satellite Data
2.3.1. Meteosat 8 SEVIRI Data
2.3.2. MODIS LST Data
2.3.3. Landsat 7 Data
3. Downscaling Application and Results
3.1. Particle Definition
3.2. Downscaling Experiments
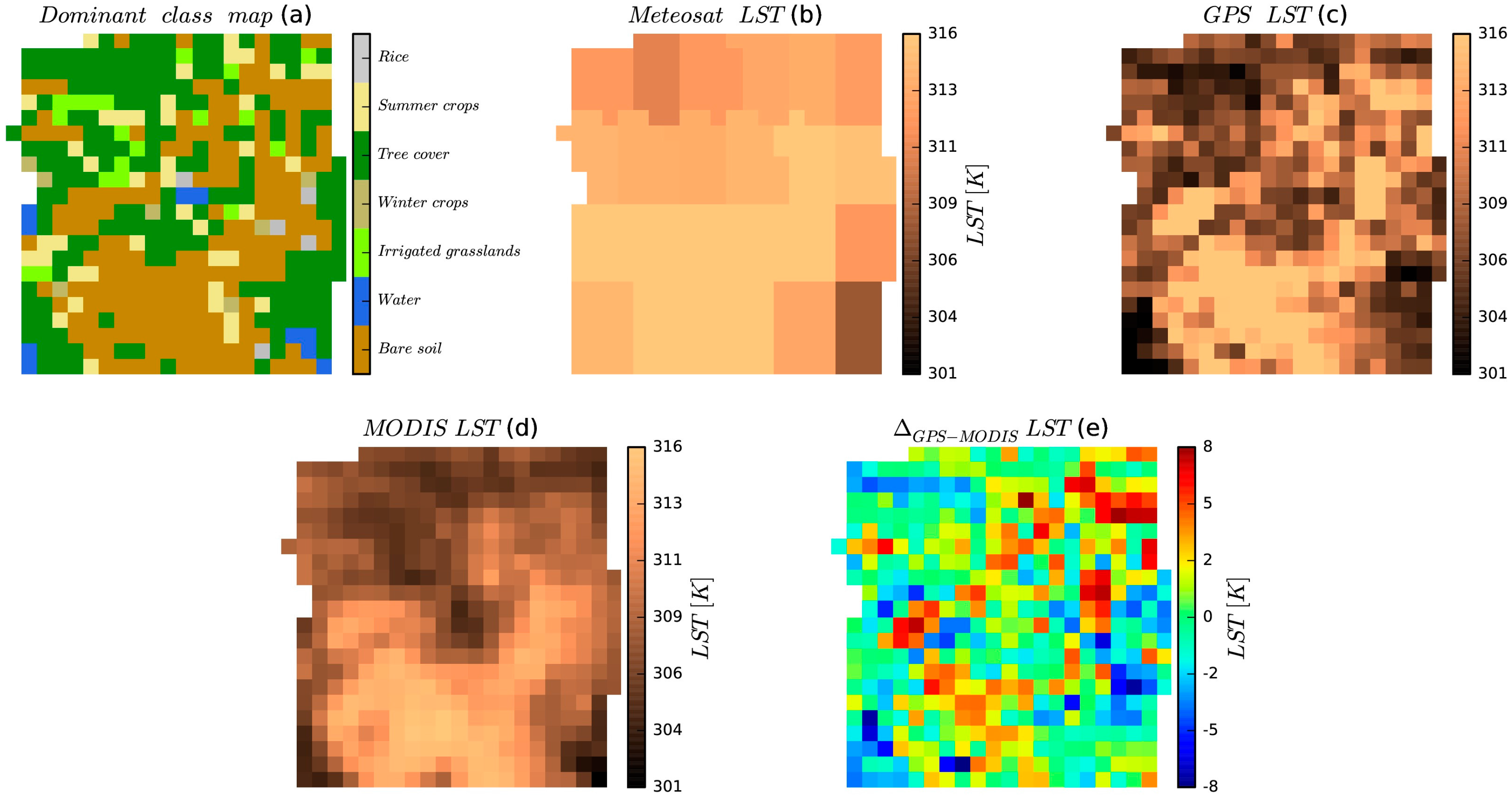
3.3. GPS Downscaling LST Evaluation at 1 km Scale
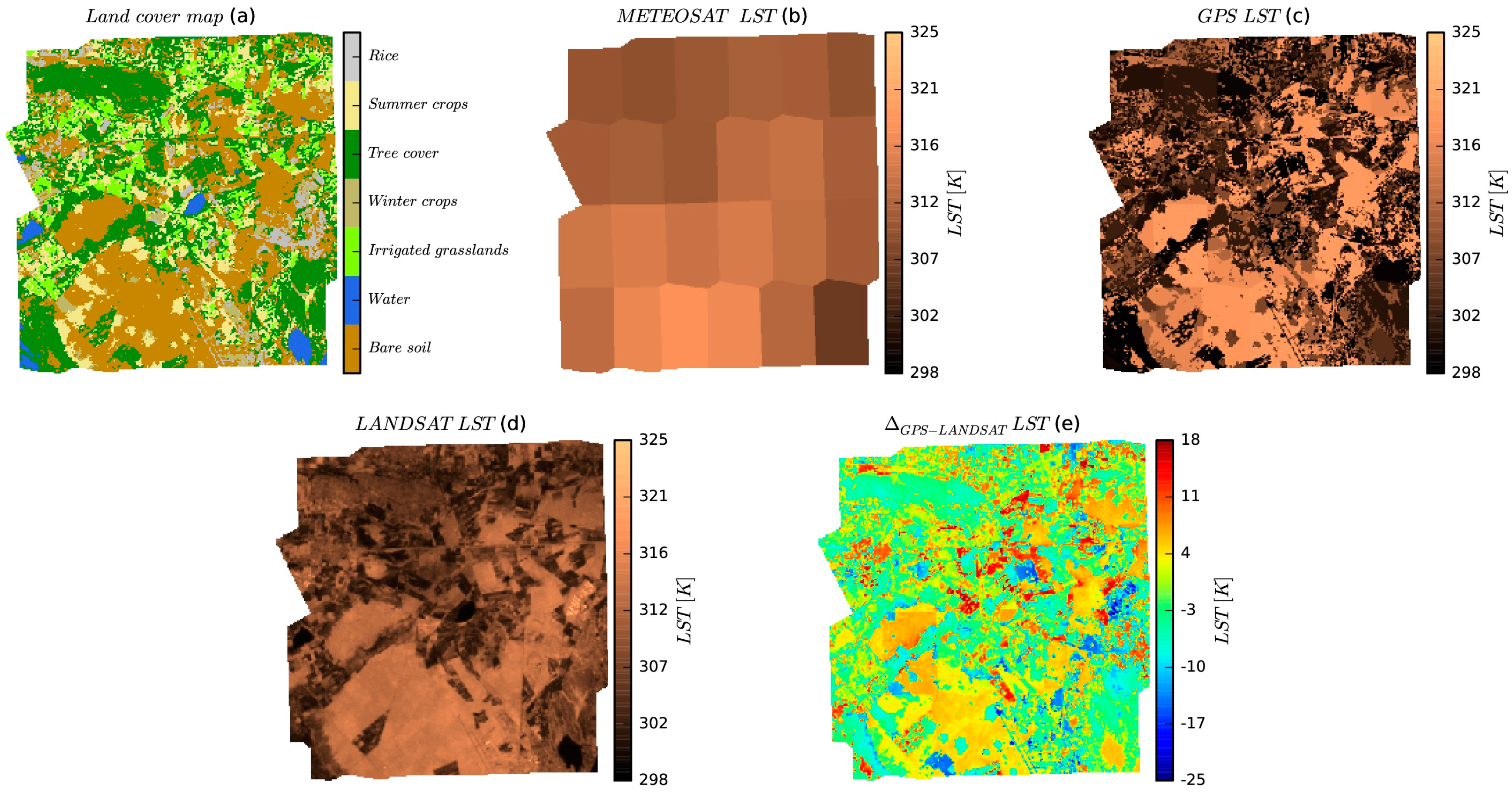
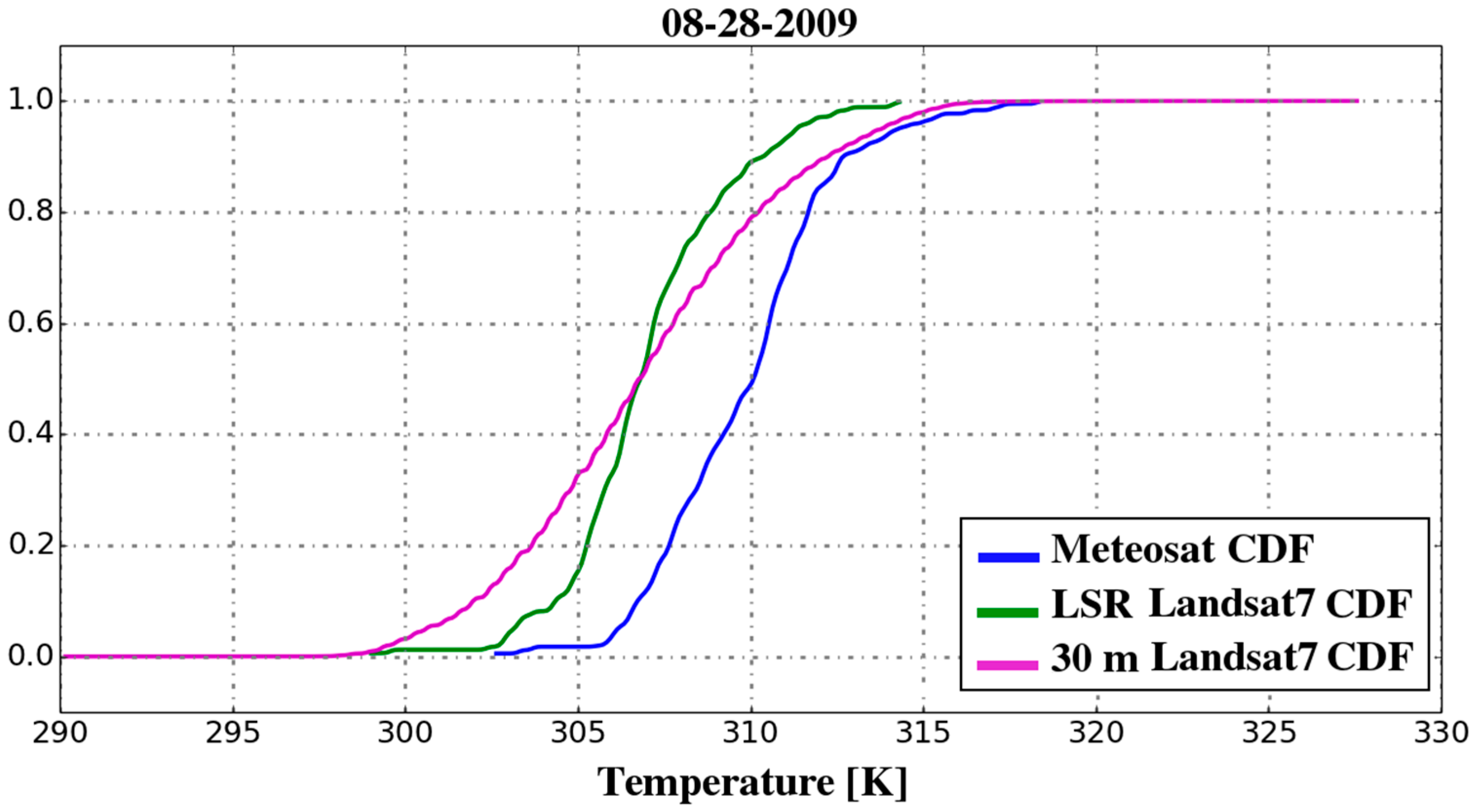
3.4. GPS Downscaling Approach Validation at 60 m Scale
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Particle Filter and Smoother Presentation
Appendix A.1. The Particle Filter
Appendix A.2. The Particle Smoother
References
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Zakšek, K.; Oštir, K. Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ. 2012, 117, 114–124. [Google Scholar] [CrossRef]
- Dennison, P.E.; Matheson, D.S. Comparison of fire temperature and fractional area modeled from SWIR, MIR, and TIR multispectral and SWIR hyperspectral airborne data. Remote Sens. Environ. 2011, 115, 876–886. [Google Scholar] [CrossRef]
- Diak, G.R.; Mecikalski, J.R.; Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Torn, R.D.; DeWolf, R.L. Estimating Land Surface Energy Budgets From Space: Review and Current Efforts at the University of Wisconsin—Madison and USDA–ARS. Bull. Am. Meteorol. Soc. 2004, 85, 65–78. [Google Scholar] [CrossRef]
- Coudert, B.; Ottlé, C.; Briottet, X. Monitoring land surface processes with thermal infrared data: Calibration of SVAT parameters based on the optimisation of diurnal surface temperature cycling features. Remote Sens. Environ. 2008, 112, 872–887. [Google Scholar] [CrossRef]
- Quattrochi, D.; Luvall, J. Thermal Remote Sensing in Land Surface Processes; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Karnieli, A.; Bayasgalan, M.; Bayarjargal, Y.; Agam, N.; Khudulmur, S.; Tucker, C.J. Comments on the use of the Vegetation Health Index over Mongolia. Int. J. Remote Sens. 2006, 27, 2014–2017. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Colaizzi, P.D. Utility of thermal image sharpening for monitoring field-scale evapotranspiration over rainfed and irrigated agricultural regions. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Coudert, B.; Ottlé, C.; Boudevillain, B.; Guillevic, P.; Demarty, J. Multi-objective calibration of a dual source SVAT model: Contribution of thermal infrared remote sensing data. J. Hydrometeorol. 2006, 7, 404–420. [Google Scholar] [CrossRef]
- Coudert, B.; Ottlé, C. An improved SVAT model calibration strategy based on the optimization of surface temperature temporal dynamics. Geophys. Res. Lett. 2007, 34, L04402. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Colaizzi, P.D. Utility of thermal sharpening over Texas high plains irrigated agricultural fields. J. Geophys. Res. D Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Kallel, A.; Ottlé, C.; Le Hegarat-Mascle, S.; Maignan, F.; Courault, D. Surface Temperature Downscaling from Multiresolution Instruments Based on Markov Models. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1588–1612. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Ottlé, C.; Kallel, A.; Monteil, G.; LeHegarat, S.; Coudert, B. Subpixel Temperature Estimation from Low Resolution Thermal Infrared Remote Sensing. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008.
- Montzka, C.; Pauwels, V.R.N.; Franssen, H.J.H.; Han, X.; Vereecken, H. Multivariate and multiscale data assimilation in terrestrial systems: A review. Sensors 2012, 12, 16291–16333. [Google Scholar] [CrossRef] [PubMed]
- Mechri, R.; Ottlé, C.; Pannekoucke, O.; Kallel, A. Genetic particle filter application to land surface temperature downscaling. J. Geophys. Res. Atmos. 2014, 119, 131–146. [Google Scholar] [CrossRef]
- Jeganathan, C.; Hamm, N.; Mukherjee, S.; Atkinson, P.; Raju, P.; Dadhwal, V. Evaluating a thermal image sharpening model over a mixed agricultural landscape in India. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 178–191. [Google Scholar] [CrossRef]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Dedieu, G.; Garatuza, J.; Kerr, Y. Disaggregation of MODIS surface temperature over an agricultural area using a time series of Formosat-2 images. Remote Sens. Environ. 2010, 114, 2500–2512. [Google Scholar] [CrossRef]
- Ottlé, C.; Stoll, M. Effect of atmospheric absorption and surface emissivity on the determination of land surface temperature from infrared satellite data. Int. J. Remote Sens. 1993, 14. [Google Scholar] [CrossRef]
- Inamdar, A.K.; French, A. Disaggregation of GOES land surface temperatures using surface emissivity. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. Examining the impacts of urban biophysical compositions on surface urban heat island: A spectral unmixing and thermal mixing approach. Remote Sens. Environ. 2013, 131, 262–274. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Decharme, B.; André, C.; Zribi, M.; Perrier, A.; Coudert, B.; Boulain, N.; Cappelaere, B.; Descroix, L.; et al. Water and energy budgets simulation over the AMMA-Niger super-site spatially constrained with remote sensing data. J. Hydrol. 2009, 375, 287–295. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Perrier, A.; Decharme, B.; Coudert, B.; Zribi, M.; Boulain, N.; Cappelaere, B.; Ramier, D. SEtHyS_Savannah: A multiple source land surface model applied to Sahelian landscapes. Agric. For. Meteorol. 2009, 149, 1421–1432. [Google Scholar] [CrossRef]
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-de Coca, F.; Carrer, D.; Freitas, S.C.; García-Haro, J.; et al. The Satellite Application Facility for Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F.; McLaughlin, D.B.; Entekhabi, D.; Luo, L. A Multiscale Ensemble Filtering System for Hydrologic Data Assimilation. Part I: Implementation and Synthetic Experiment. J. Hydrometeorol. 2009, 10, 794–806. [Google Scholar] [CrossRef]
- Quaife, T.; Lewis, P.; De Kauwe, M.; Williams, M.; Law, B.; Disney, M.; Bowyer, P. Assimilating canopy reflectance data into an ecosystem model with an Ensemble Kalman Filter. Remote Sens. Environ. 2008, 112, 1347–1364. [Google Scholar] [CrossRef]
- Gordon, N.; Salmond, D.; Smith, A. Novel approach to nonlinear/non-gaussian bayesian state estimator. IEE Proc. F Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J. Nonlinear data assimilation in geosciences: An extremely efficient particle filter. Q. J. R. Meteorol. Soc. 2010, 136, 1991–1999. [Google Scholar] [CrossRef]
- Hill, T.C.; Quaife, T.; Williams, M. A data assimilation method for using low-resolution Earth observation data in heterogeneous ecosystems. J. Geophys. Res. 2011, 116, D08117. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Wilson, T.B.; Meyers, T.P. Determining vegetation indices from solar and photosynthetically active radiation fluxes. Agric. For. Meteorol. 2007, 144, 160–179. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; et al. Albedo and LAI estimates from FORMOSAT-2 data for crop monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Bioucas-Dias, J.M.; Göttsche, F.M. Quantifying the uncertainty of land surface temperature retrievals from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN5: 2006 Update. Proc. SPIE 2006, 6233, 62331F. [Google Scholar]
- Mira, M.; Olioso, A.; Gallego-Elvira, B.; Courault, D.; Garrigues, S.; Marloie, O.; Hagolle, O.; Guillevic, P.; Boulet, G. Uncertainty assessment of surface net radiation derived from Landsat image. Remote Sens. Environ. 2016, 175, 251–270. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Bork-Unkelbach, A.; Gottsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.-P.; Olesen, F.S.; Privette, J.L. Directional Viewing Effects on Satellite Land Surface Temperature Products over Sparse Vegetation Canopies—A Multisensor Analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Inglada, J.; Arias, M.; Tardy, B.; Hagolle, O.; Valero, S.; Morin, D.; Dedieu, G.; Sepulcre, G.; Bontemps, S.; Defourny, P.; et al. Assessment of an Operational System for Crop Type Map Production Using High Temporal and Spatial Resolution Satellite Optical Imagery. Remote Sens. 2015, 7, 12356–12379. [Google Scholar] [CrossRef]
- Quintana-Seguí, P.; Le Moigne, P.; Durand, Y.; Martin, E.; Habets, F.; Baillon, M.; Canellas, C.; Franchisteguy, L.; Morel, S. Analysis of Near-Surface Atmospheric Variables: Validation of the SAFRAN Analysis over France. J. Appl. Meteorl. Climatol. 2008, 47, 92–107. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory (Mathematics in Science and Engineering); Academic Press Inc.: Cambridge, MA, USA, 1970; Volume 64, pp. iii–ix. [Google Scholar]
- Del Moral, P.; Feynman-Kac, F. Genealogical and Interacting Particle Systems with Applications; Springer: New York, NY, USA, 2004. [Google Scholar]
- Rémy, S.; Pannekoucke, O.; Bergot, T.; Baehr, C. Adaptation of a particle filtering method for data assimilation in a 1D numerical model used for fog forecasting. Q. J. R. Meteorol. Soc. 2012, 138, 536–551. [Google Scholar] [CrossRef]
| Class | Selected Parameters | Definition | Variation Ranges |
|---|---|---|---|
| Bare soil | Facttherm | Factor controlling soil heat capacity | [0.7, 2.2] |
| Alb | Surface albedo | [0.25, 0.45] | |
| Water | Facttherm | Factor controlling soil heat capacity | [1.7, 3.2] |
| Alb | Surface albedo | [0.25, 0.45] | |
| es | Surface emissivity | [0.93, 0.97] | |
| wsat | Saturation volumetric soil moisture (m3·m−3) | [0.4, 0.5] | |
| Irrigated grasslands | Facttherm | Factor controlling soil heat capacity | [0.6, 2.1] |
| Alb | Surface albedo | [0.2, 0.4] | |
| Vmax | Vegetation photosynthetic capacity | [20.0, 80.0] | |
| Albg | Vegetation albedo | [0.1, 0.26] | |
| eg | Vegetation emissivity | [0.92, 1.0] | |
| Summer crops | Facttherm | Factor controlling soil heat capacity | [0.75, 2.25] |
| Alb | Surface albedo | [0.2, 0.4] | |
| Tree cover (including a grass understory layer) | Facttherm | Factor controlling soil heat capacity | [1.53, 3.03] |
| Albt | Tree albedo | [0.15, 0.33] | |
| lft | Tree leaf width (m) | [0.005, 0.015] | |
| eg | Understory emissivity | [0.92, 1.0] | |
| et | Tree emissivity | [0.92, 1.0] | |
| Winter crops | Facttherm | Factor controlling soil heat capacity | [0.75, 2.25] |
| Alb | Soil albedo | [0.2, 0.4] | |
| Vmax | Vegetation photosynthetic capacity | [20.0, 80.0] | |
| lfg | Vegetation leaf width (m) | [0.009, 0.1] | |
| eg | Vegetation emissivity | [0.92, 1.0] | |
| Rice | Facttherm | Factor controlling soil heat capacity | [1.75, 23.25] |
| Alb | Surface albedo | [0.2, 0.4] | |
| wsat | Saturation volumetric soil moisture (m3·m−3) | [0.4, 0.5] | |
| Vmax | Vegetation photosynthetic capacity | [20.0, 80.0] | |
| eg | Vegetation emissivity | [0.92, 1.0] |
| Common Settings | |
|---|---|
| Number of classes | Q = 7 |
| Number of parameters/class | K = 5 |
| Assimilation starting day | DOY 60 (21 March 2009) |
| Particle ensemble size | N = 100 |
| Observation window | 07:45 a.m. → 06:00 p.m. |
| Specific settings: assimilation window size | |
| 1 day | Experiment 1: Uncertainties on air temperature (±1 K) |
| Experiment 2: No uncertainty on forcing data | |
| 3 days | Experiment 3: No uncertainty on forcing data |
| 7 days | Experiment 4: No uncertainty on forcing data |
| Prior | Scenario 1 (1 Day) | Scenario 2 (3 Days) Exp 3 | Scenario 3 (7 Days) Exp 4 | ||
|---|---|---|---|---|---|
| Exp 1 | Exp 2 | ||||
| RMSE (K) | 4.0 | 2.7 | 2.8 | 2.9 | 2.9 |
| Bias (K) | −2.3 | 0.1 | 0.3 | 0.4 | 0.3 |
| Eff (%) | - | 32.5 | 30 | 27.5 | 27.5 |
| Scenario 1 (1 Day) | Scenario 2 (3 Days) | Scenario 3 (7 Days) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Land Cover Types | No. Pixels | Prior | Exp 1 | Exp 2 | Exp 3 | Exp 4 | |||||||||
| RMSE (K) | Bias (K) | RMSE (K) | Bias (K) | Eff % | RMSE (K) | Bias (K) | Eff % | RMSE (K) | Bias (K) | Eff % | RMSE (K) | Bias (K) | Eff % | ||
| Tree Cover | 1315 | 2.4 | −1.4 | 1.3 | −0.1 | 46 | 1.3 | 0.1 | 46 | 1.3 | 0.2 | 46 | 1.3 | 0.1 | 46 |
| Bare soil | 309 | 4.6 | −3.4 | 1.7 | 0.6 | 63 | 1.9 | 0.6 | 59 | 1.9 | 0.7 | 59 | 1.9 | 0.7 | 59 |
| Water | 255 | 3.7 | 3 | 2.6 | 2.3 | 30 | 2.8 | 2.5 | 24 | 3 | 2.4 | 19 | 3 | 2.1 | 19 |
| Rice | 71 | 3.4 | −2.8 | 1.4 | −0.2 | 59 | 1.5 | 0 | 56 | 1.5 | 0 | 56 | 1.5 | −0.2 | 56 |
| Win. crops | 17 | 5.3 | −4.7 | 2.7 | −2 | 49 | 2.6 | −1.9 | 51 | 2.4 | −1.9 | 55 | 2.6 | −2.1 | 51 |
| Sum. crops | 10 | 5.3 | −4.5 | 2.1 | −1.2 | 60 | 1.9 | −1 | 64 | 1.6 | −0.7 | 70 | 1.8 | −1.1 | 66 |
| Grasslands | 5 | 4 | −3.7 | 1.3 | 0.4 | 67 | 1.3 | 0.7 | 67 | 2.2 | 1.5 | 45 | 1.4 | 0.7 | 65 |
| Prior | Scenario 1 (1 Day) | Scenario 2 (3 Days) Exp 3 | Scenario 3 (7 Days) Exp 4 | ||
|---|---|---|---|---|---|
| Exp 1 | Exp 2 | ||||
| RMSE (K) | 4.5 | 4.9 | 4.9 | 5.2 | 5.4 |
| Bias (K) | 0.0 | 1.3 | 1.5 | 1.7 | 1.6 |
| Eff (%) | - | −8.9 | −8.9 | −15.6 | −20. |
| Land Cover Types | Prior | Exp 1 | |||
|---|---|---|---|---|---|
| RMSE (K) | Bias (K) | RMSE (K) | Eff % | Bias (K) | |
| Tree cover | 3.4 | −0.5 | 3.8 | −11.8 | −0.3 |
| Bare soil | 4.5 | 2.9 | 7 | −55.6 | 5.3 |
| Water | 6.6 | 6.1 | 5.8 | 12.1 | 5 |
| Rice | 5.4 | −2.2 | 4.9 | 9.3 | −0.7 |
| Winter crops | 5.2 | −3.3 | 4.4 | 15.4 | 1.4 |
| Summer crops | 4.3 | −2.9 | 3.6 | 16.3 | 0.8 |
| Grasslands | 3 | −1.2 | 3.1 | −3.3 | 0.9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mechri, R.; Ottlé, C.; Pannekoucke, O.; Kallel, A.; Maignan, F.; Courault, D.; Trigo, I.F. Downscaling Meteosat Land Surface Temperature over a Heterogeneous Landscape Using a Data Assimilation Approach. Remote Sens. 2016, 8, 586. https://doi.org/10.3390/rs8070586
Mechri R, Ottlé C, Pannekoucke O, Kallel A, Maignan F, Courault D, Trigo IF. Downscaling Meteosat Land Surface Temperature over a Heterogeneous Landscape Using a Data Assimilation Approach. Remote Sensing. 2016; 8(7):586. https://doi.org/10.3390/rs8070586
Chicago/Turabian StyleMechri, Rihab, Catherine Ottlé, Olivier Pannekoucke, Abdelaziz Kallel, Fabienne Maignan, Dominique Courault, and Isabel F. Trigo. 2016. "Downscaling Meteosat Land Surface Temperature over a Heterogeneous Landscape Using a Data Assimilation Approach" Remote Sensing 8, no. 7: 586. https://doi.org/10.3390/rs8070586
APA StyleMechri, R., Ottlé, C., Pannekoucke, O., Kallel, A., Maignan, F., Courault, D., & Trigo, I. F. (2016). Downscaling Meteosat Land Surface Temperature over a Heterogeneous Landscape Using a Data Assimilation Approach. Remote Sensing, 8(7), 586. https://doi.org/10.3390/rs8070586