Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics
Abstract
:1. Introduction
2. Methodology
2.1. The Diagnostic of Desroziers et al. (2005)
2.2. The Met Office UKV Model and 3D Variational Assimilation Scheme
2.3. SEVIRI Observations
3. Experimental Design
4. Results
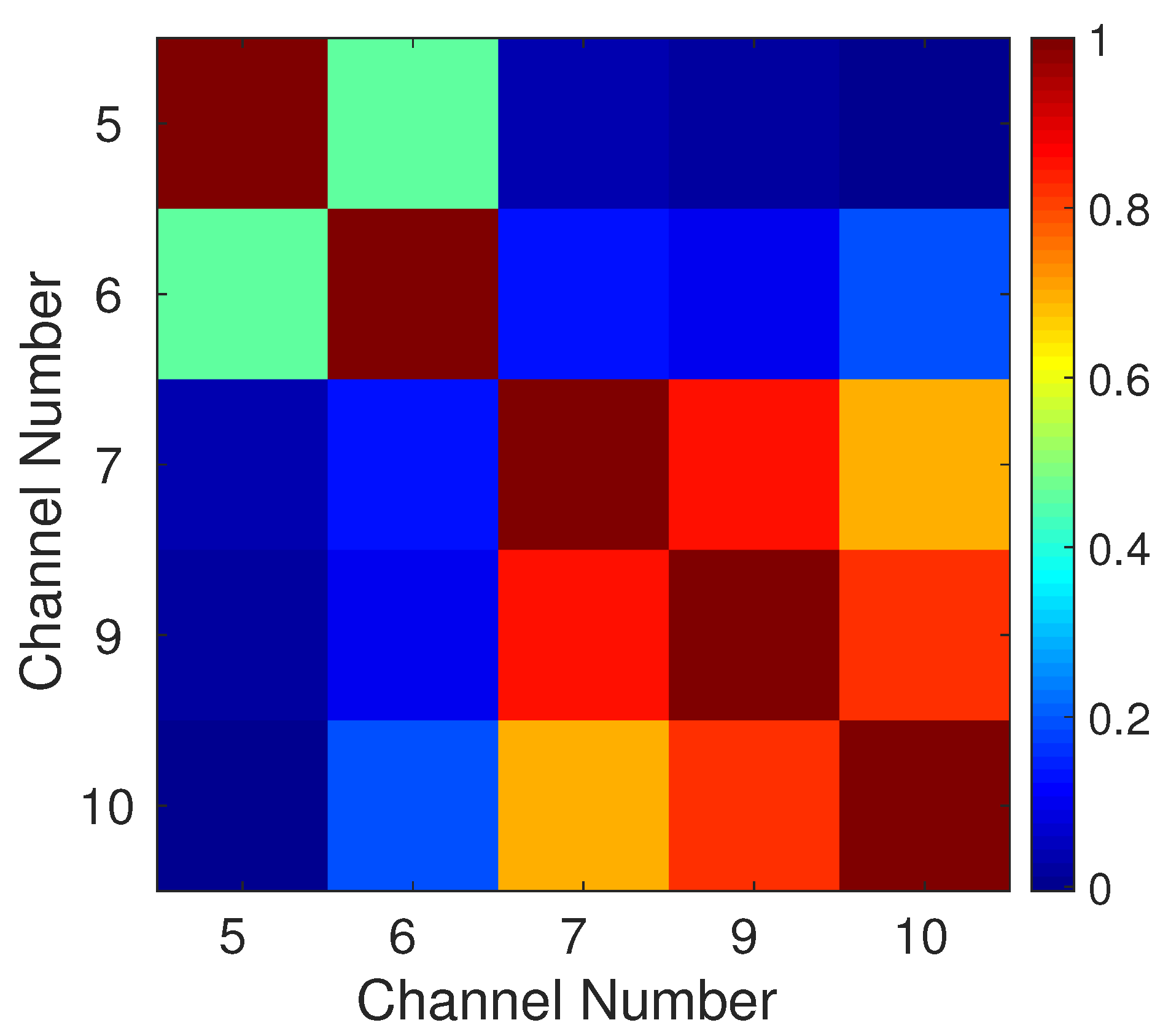
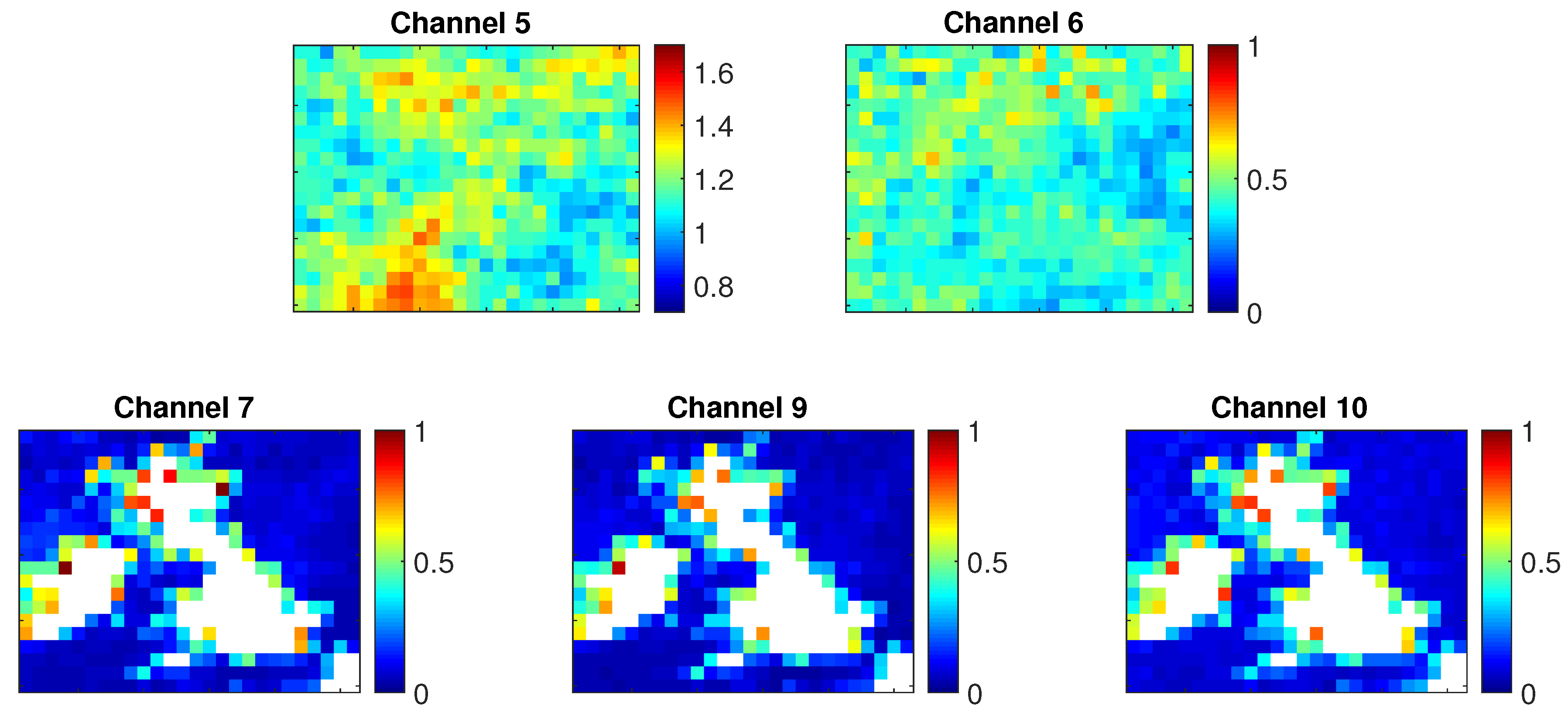
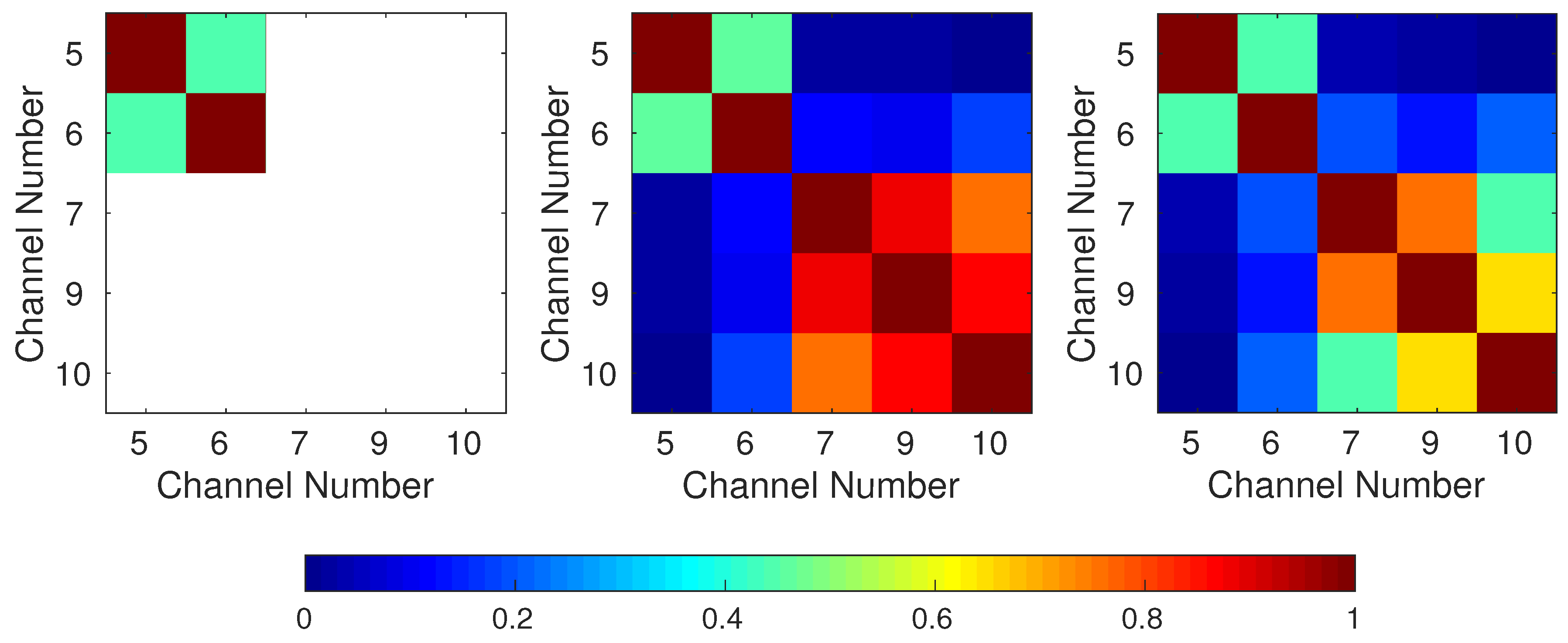
4.1. Inter-Channel Correlations
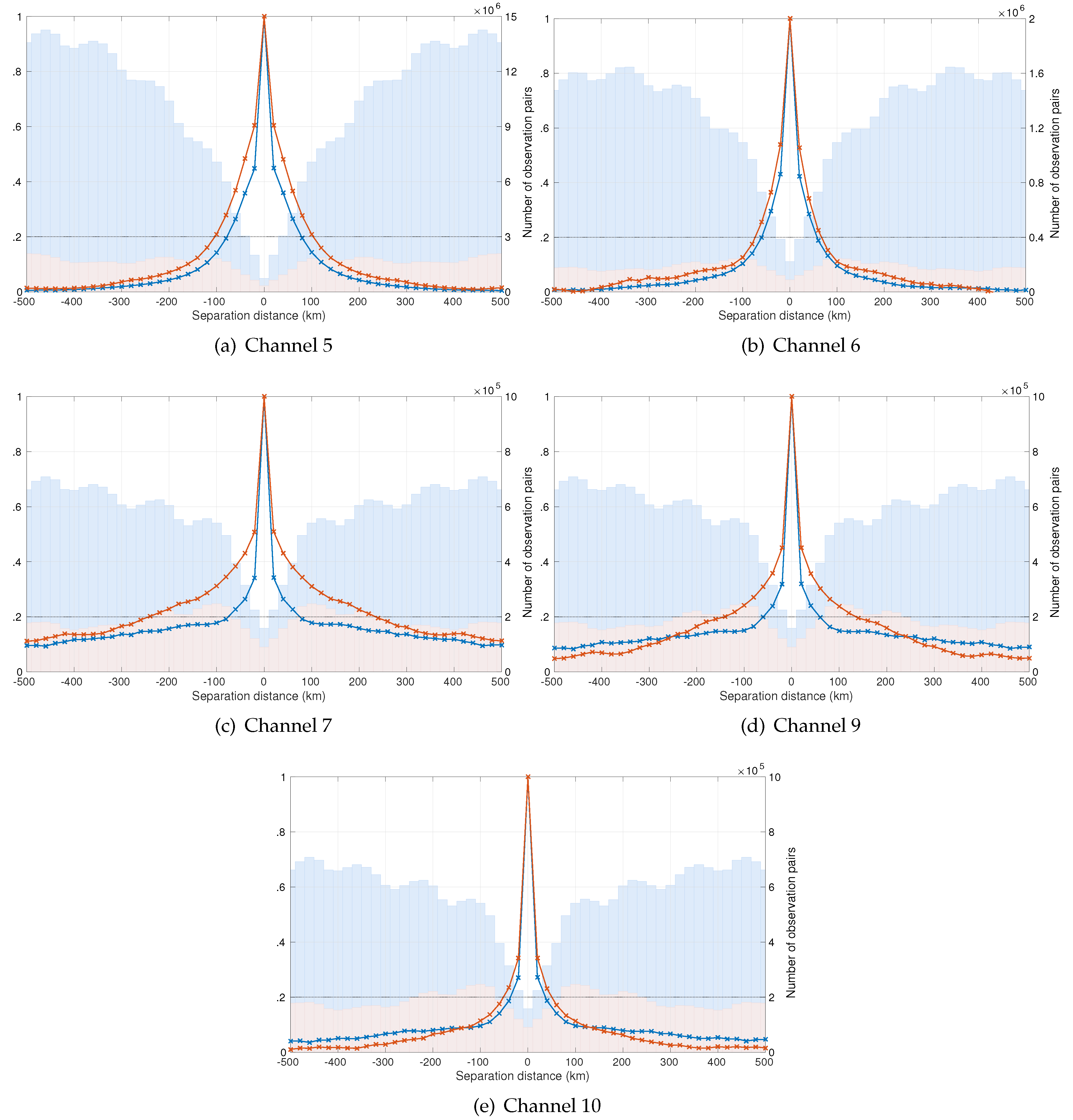
4.2. Horizontal Correlations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Janjic, T.; Cohn, S.E. Treatment of Observation Error due to Unresolved Scales in Atmospheric Data Assimilation. Mon. Weather Rev. 2006, 134, 2900–2915. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Lawless, A.S.; Nichols, N.K.; Eyre, J.R. Representativity error for temperature and humidity using the Met Office high-resolution model. Q. J. R. Meteorol. Soc. 2014, 140, 1189–1197. [Google Scholar] [CrossRef]
- Sherlock, V.; Collard, A.; Hannon, S.; Saunders, R. The Gastropod Fast Radiative Transfer Model for Advanced Infrared Sounders and Characterization of Its Errors for Radiance Assimilation. J. Appl. Meteorol. 2003, 42, 1731–1747. [Google Scholar] [CrossRef]
- Matricardi, M. Technical Note: An assessment of the accuracy of the RTTOV fast radiative transfer model using IASI data. Atmos. Chem. Phys. 2009, 9, 6899–6913. [Google Scholar] [CrossRef]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Stewart, L.M. Correlated Observation Errors in Data Assimilation. Ph.D Thesis, University of Reading, 2010. Available online: http://www.reading.ac.uk/maths-and-stats/research/theses/maths-phdtheses.aspx (accessed on 24 March 2016). [Google Scholar]
- Li, H.; Kalnay, E.; Miyoshi, T. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter. Q. J. R. Meteorol. Soc. 2009, 128, 1367–1386. [Google Scholar] [CrossRef]
- Miyoshi, T.; Kalnay, E.; Li, H. Estimating and including observation-error correlations in data assimilation. Inverse Probl. Sci. Eng. 2013, 21, 387–398. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Lawless, A.S.; Nichols, N.K. Estimating correlated observation error statistics using an ensemble transform Kalman filter. Tellus A 2014, 66, 23294. [Google Scholar] [CrossRef]
- Waller, J.A.; Dance, S.L.; Nichols, N.K. Theoretical insight into diagnosing observation error correlations using observation-minus-background and observation-minus-analysis statistics. Q. J. R. Meteorol. Soc. 2016, 142, 418–431. [Google Scholar] [CrossRef]
- Ménard, R. Error covariance estimation methods based on analysis residuals: theoretical foundation and convergence properties derived from simplified observation networks. Q. J. R. Meteorol. Soc. 2016, 142, 257–273. [Google Scholar] [CrossRef]
- Stewart, L.M.; Cameron, J.; Dance, S.L.; English, S.; Eyre, J.R.; Nichols, N.K. Observation Error Correlations in IASI Radiance Data. Technical Report. Mathematics Reports Series; University of Reading, 2009. Available online: www.reading.ac.uk/web/FILES/maths/obs_error_IASI_radiance.pdf (accessed on 24 March 2016).
- Stewart, L.M.; Dance, S.L.; Nichols, N.K.; Eyre, J.R.; Cameron, J. Estimating interchannel observation-error correlations for IASI radiance data in the Met Office system. Q. J. R. Meteorol. Soc. 2014, 140, 1236–1244. [Google Scholar] [CrossRef]
- Bormann, N.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. I: Methods and application to ATOVS data. Q. J. R. Meteorol. Soc. 2010, 136, 1036–1050. [Google Scholar] [CrossRef]
- Bormann, N.; Collard, A.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. II: Application to AIRS and IASI data. Q. J. R. Meteorol. Soc. 2010, 136, 1051–1063. [Google Scholar] [CrossRef]
- Weston, P.P.; Bell, W.; Eyre, J.R. Accounting for correlated error in the assimilation of high-resolution sounder data. Q. J. R. Meteorol. Soc. 2014, 140, 2420–2429. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K. Data assimilation with correlated observation errors: Experiments with a 1-D shallow water model. Tellus A 2013, 65, 19546. [Google Scholar] [CrossRef]
- Healy, S.B.; White, A.A. Use of discrete Fourier transforms in the 1D-Var retrieval problem. Q. J. R. Meteorol. Soc. 2005, 131, 63–72. [Google Scholar] [CrossRef]
- Stewart, L.M.; Dance, S.L.; Nichols, N.K. Correlated observation errors in data assimilation. Int. J. Numer. Methods Fluids 2008, 56, 1521–1527. [Google Scholar] [CrossRef]
- Schmid, J. The SEVIRI instrument. In Proceedings of the 2000 EUMETSAT Meteorological Satellite Data User’s Conference, Bologna, Italy, 29 May–2 June 2000.
- Waller, J.A.; Simonin, D.; Dance, S.L.; Nichols, N.K.; Ballard, S.P. Diagnosing observation error correlations for Doppler radar radial winds in the Met Office UKV model using observation-minus-background and observation-minus-analysis statistics. AMS 2015. [Google Scholar] [CrossRef]
- Lean, H.; Clark, P.; Dixon, M.; Roberts, N.; Fitch, A.; Forbes, R.; Halliwell, C. Charictaristics of high-resolution versions of the Met Office Unified Model for forecasting convection over the United Kingdom. Monthly Waether Rev. 2008, 136, 3408–3424. [Google Scholar] [CrossRef]
- Tang, Y.; Lean, H.W.; Bornemann, J. The benefits of the Met Office variable resolution NWP model for forecasting convection. Meteorol. Appl. 2013, 20, 417–426. [Google Scholar] [CrossRef]
- Ballard, S.P.; Li, Z.; Simonin, D.; Caron, J.F. Performance of 4D-Var NWP-based nowcasting of precipitation at the Met Office for summer 2012. Q. J. R. Meteorol. Soc. 2016, 144, 472–487. [Google Scholar] [CrossRef]
- Clark, P.; Roberts, N.; Lean, H.; Ballard, S.; Charlton-Perez, C. Convection-permitting models: A step-change in rainfall forecasting. Met. Apps. 2015, 23, 165–181. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Met. Office global three-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Rawlins, F.; Ballard, S.P.; Bovis, K.J.; Clayton, A.M.; Li, D.; Inverarity, G.W.; Lorenc, A.C.; Payne, T.J. The Met Office global four-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2007, 133, 347–362. [Google Scholar] [CrossRef]
- Courtier, P.; Thepaut, J.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Piccolo, C.; Cullen, M. Adaptive mesh method in the Met Office variational data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 631–640. [Google Scholar] [CrossRef]
- Piccolo, C.; Cullen, M. A new implementation of the adaptive mesh transform in the Met Office 3D-Var system. Q. J. R. Meteorol. Soc. 2012, 138, 1560–1570. [Google Scholar] [CrossRef]
- Parish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An Introduction to Meteosat Second Generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Kelly, G. Preparations and Experiments to Assimilate Satellite Image Data into High Resolution NWP; Technical Report No. 522; Met Office: Exeter, UK, 2008. [Google Scholar]
- Tubbs, R.; Kelly, G. Assimilation into the Met Office 1.5 km Grid UKV NWP Model of Water Vapour Radiances from Areas with Low Cloud. 2013 EUMETSAT Meteorological Satellite Conference, 2013. Available online: https://www.eumetsat.int/website/wcm/idc/idcplg?IdcService=GET_FILE&dDocName=PDF_CONF_P_S7_09_TUBBS_V&RevisionSelectionMethod=LatestReleased&Rendition=Web (accessed on 24 March 2016).
- Saunders, R.; Francis, R.; Francis, P.; Crawford, J.; Smith, A.; Brown, I.; Taylor, R.; Forsythe, M.; Doutriaux-Boucher, M.; Millington, S. The exploitation of METOSAT SECOND GENERATION data in the Met Office. In Proceedings of the 2006 EUMETSAT Meteorological Satellite Conference, Helsinki, Finland, 12–16 June 2006.
- Francis, P.; Capacci, D.; Saunders, R. Improving the Nimrod nowcasting system’s satellite precipitation estimates by introducing the new SEVIRI channels. In Proceedings of the 2006 EUMETSAT Meteorological Satellite Conference, Helsinki, Finland, 12–16 June 2006.
- Harris, B.; Kelly, G. A satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Saunders, R.; Andersson, E.; Brunel, P.; Chevallier, F.; Deblonde, G.; English, S.; Matricardi, M.; Rayer, P.; Sherlock, V. RTTOV-7 Science and Validation Report; Technical Report; NWP SAF: Exeter, UK, 2002. [Google Scholar]
- Tubbs, R.; Kelly, G. Assimilation of Infrared Meteosat Data into High-resolution NWP and Nowcasting Models. Available online: https://ams.confex.com/ams/91Annual/webprogram/Manuscript/Paper180505/rntubbs_ams_ext_abs.pdf (accessed on 24 March 2016).
- Garand, L.; Turner, D.S.; Larocque, M.; Bates, J.; Boukabara, S.; Brunel, P.; Chevallier, F.; Deblonde, G.; Engelen, R.; Hollingshead, M.; et al. Radiance and Jacobian intercomparison of radiative transfer models applied to HIRS and AMSU channels. J. Geophys. Res. Atmos. 2001, 106, 24017–24031. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Rabier, F. The interaction between model resolution observation resolution and observation density in data assimilation: A one dimensional study. Q. J. R. Meteorol. Soc. 2002, 128, 1367–1386. [Google Scholar] [CrossRef]

| Channel | Channel | Channel | Assimilated over |
|---|---|---|---|
| Number | Wavelength (μm) | Description | Land/Sea/Low Cloud |
| 5 | 6.2 | Upper level water vapour (humidity) | ✔/✔/✔ |
| 6 | 7.3 | Upper level water vapour (humidity) | ✔/✔/✘ |
| 7 | 8.7 | Surface (temperature) | ✘/✔/✘ |
| 9 | 10.8 | Surface (temperature) | ✘/✔/✘ |
| 10 | 12.0 | Surface (temperature) | ✘/✔/✘ |
| Case | Channel 5 | Channel 6 | Channel 7 | Channel 9 | Channel 10 |
|---|---|---|---|---|---|
| Operational | 4.00 | 4.00 | 1.00 | 1.00 | 1.00 |
| Inter-Channel Full Domain | 1.19 | 0.40 | 0.19 | 0.16 | 0.20 |
| Inter-Channel Land | 1.17 | 0.44 | - | - | - |
| Inter-Channel Coast | 1.18 | 0.44 | 0.34 | 0.29 | 0.34 |
| Inter-Channel Sea | 1.19 | 0.39 | 0.07 | 0.06 | 0.09 |
| Horizontal Full Domain | 1.19 | 0.40 | 0.19 | 0.16 | 0.20 |
| Horizontal Sea | 1.19 | 0.39 | 0.07 | 0.06 | 0.09 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waller, J.A.; Ballard, S.P.; Dance, S.L.; Kelly, G.; Nichols, N.K.; Simonin, D. Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics. Remote Sens. 2016, 8, 581. https://doi.org/10.3390/rs8070581
Waller JA, Ballard SP, Dance SL, Kelly G, Nichols NK, Simonin D. Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics. Remote Sensing. 2016; 8(7):581. https://doi.org/10.3390/rs8070581
Chicago/Turabian StyleWaller, Joanne A., Susan P. Ballard, Sarah L. Dance, Graeme Kelly, Nancy K. Nichols, and David Simonin. 2016. "Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics" Remote Sensing 8, no. 7: 581. https://doi.org/10.3390/rs8070581
APA StyleWaller, J. A., Ballard, S. P., Dance, S. L., Kelly, G., Nichols, N. K., & Simonin, D. (2016). Diagnosing Horizontal and Inter-Channel Observation Error Correlations for SEVIRI Observations Using Observation-Minus-Background and Observation-Minus-Analysis Statistics. Remote Sensing, 8(7), 581. https://doi.org/10.3390/rs8070581








