Integrating Crowdsourced Data with a Land Cover Product: A Bayesian Data Fusion Approach
Abstract
:1. Introduction
2. Theory and Methods
2.1. Recoding Volunteers Opinions When Lacking Information about Their Performance
2.2. Accounting for Information about Volunteers’ Performance
2.3. Bayesian Data Fusion to Combine Multiple Volunteers’ Opinions at the Same Location
2.4. Bayesian Maximum Entropy to Interpolate the Fused Volunteers Opinions
2.5. Bayesian Data Fusion to Combine the Interpolated Map with the Land Cover
3. Results and Discussion
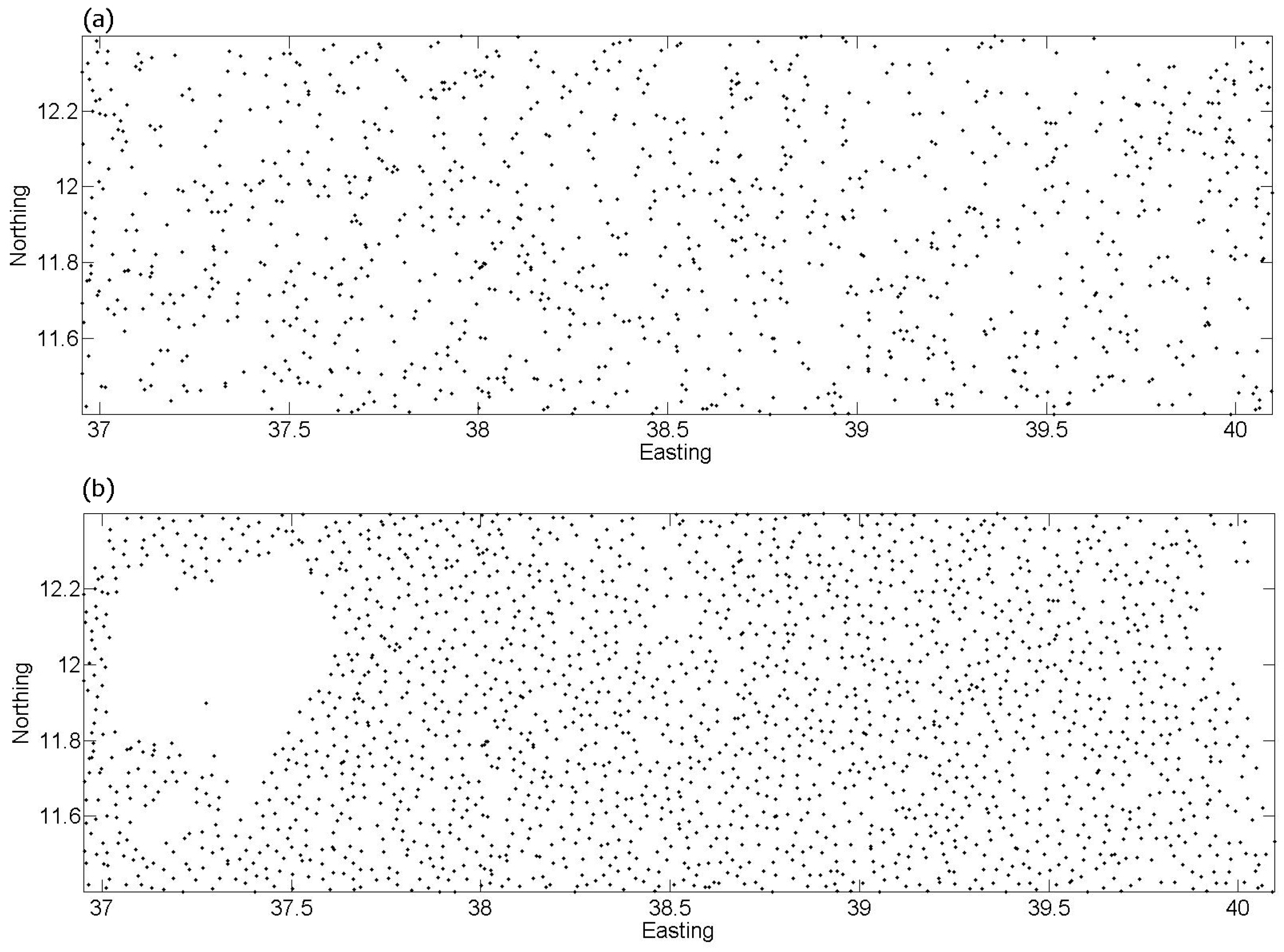
3.1. Recoding Crowdsourced Data
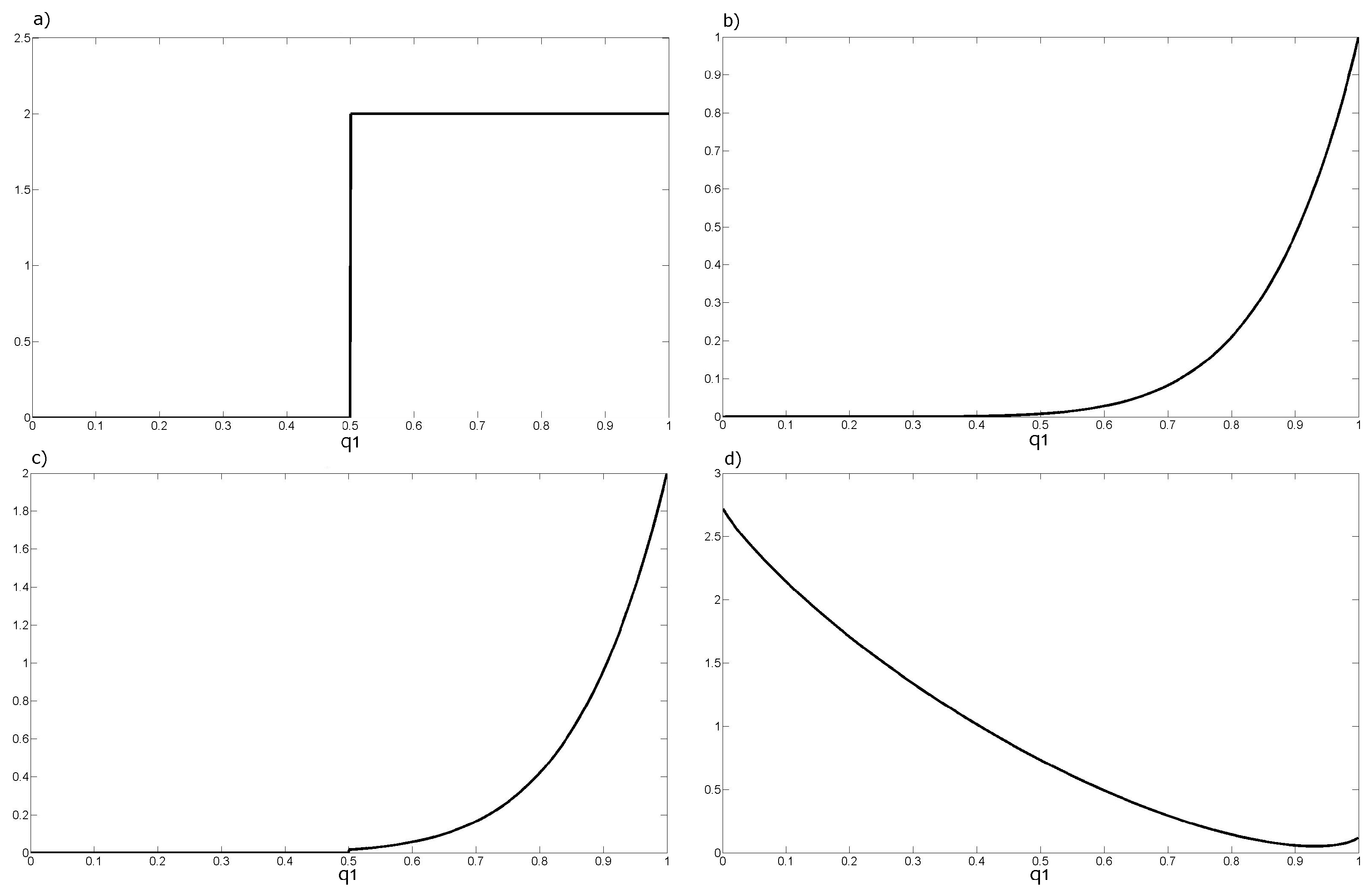
3.2. Fusion of Multiple Contributions at a Specific Location
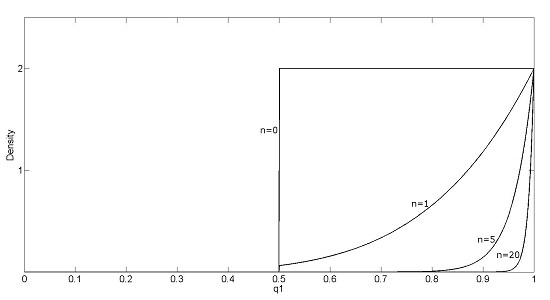
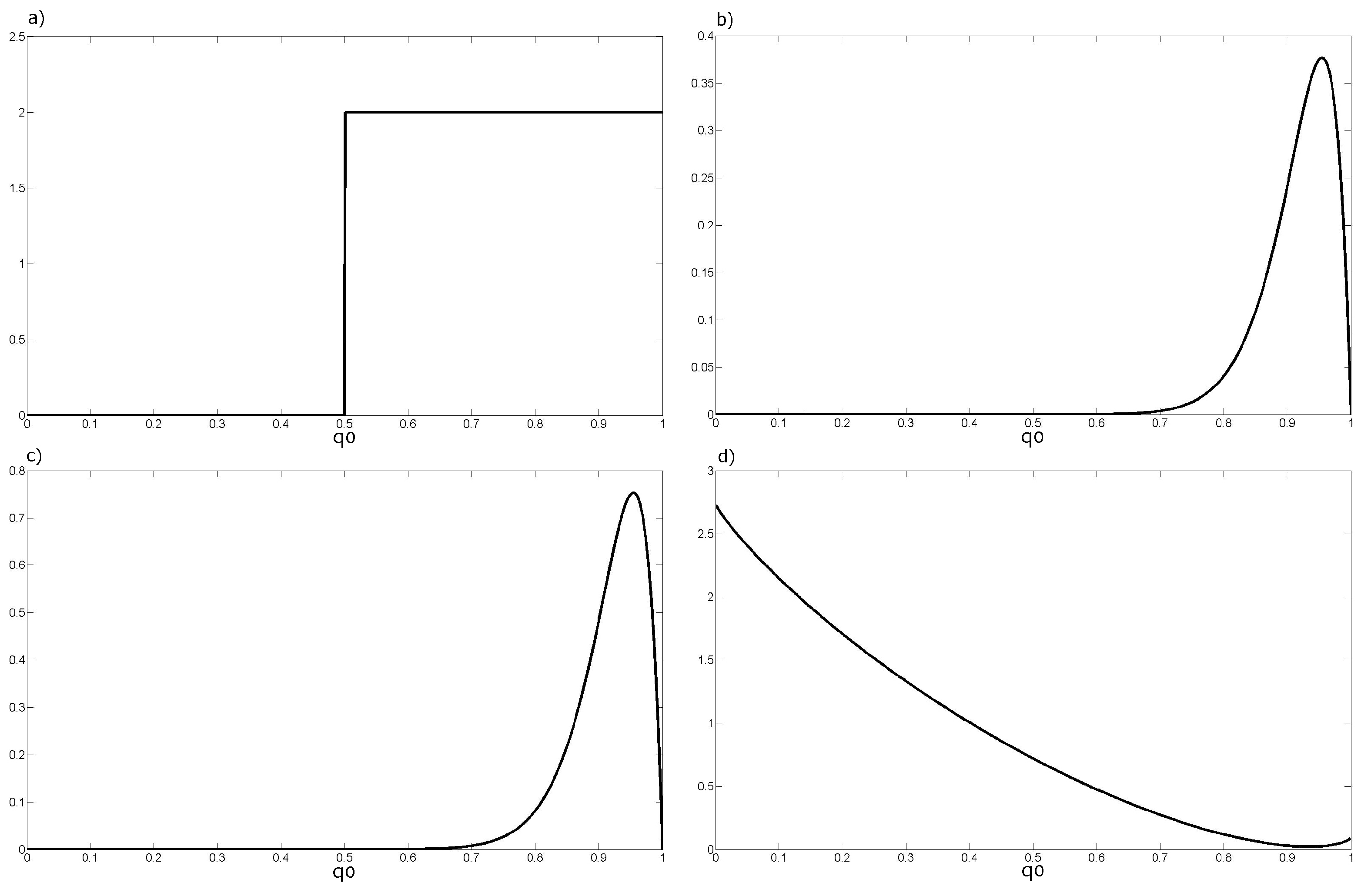
3.3. Fused Opinions Interpolation
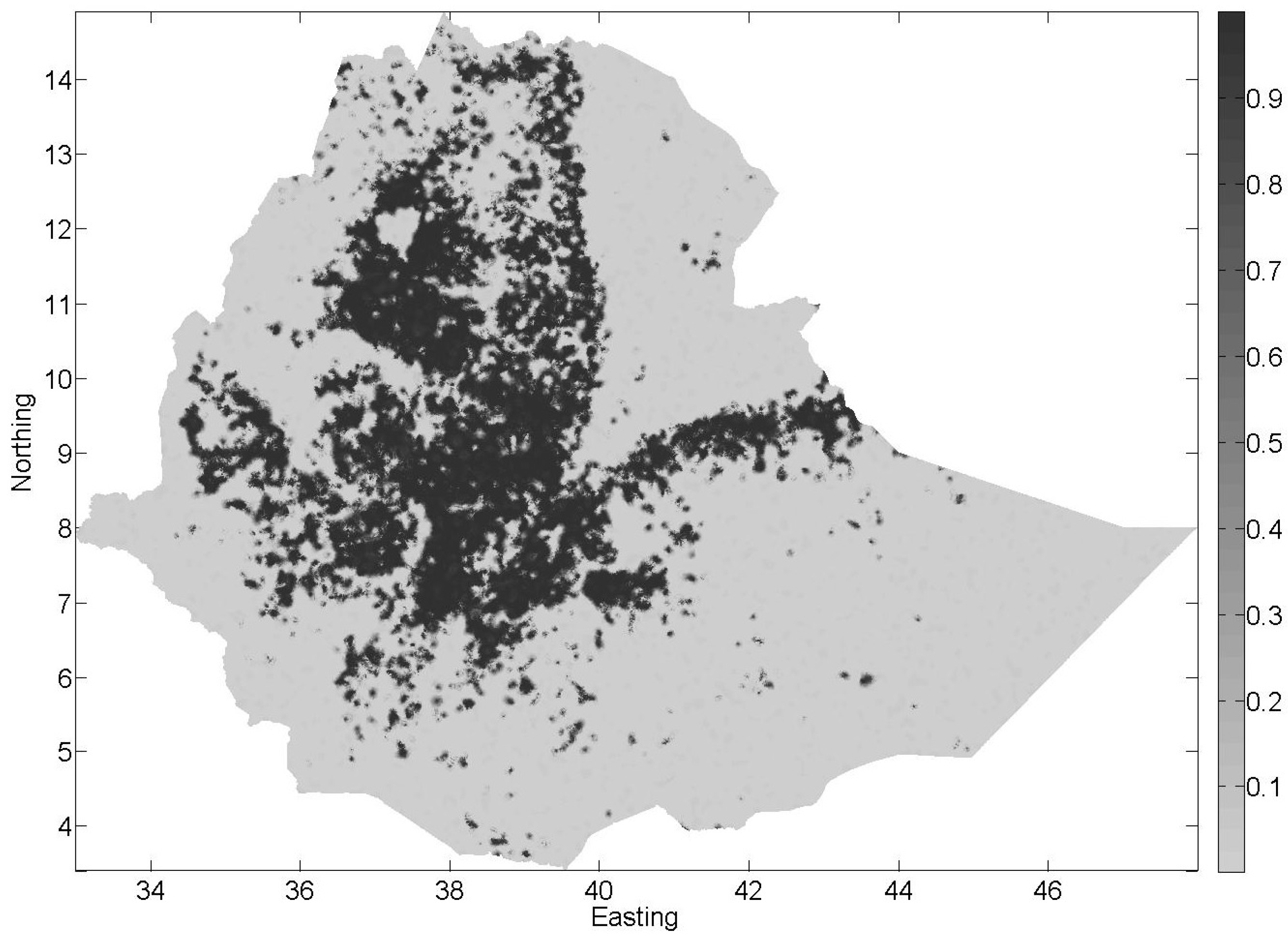
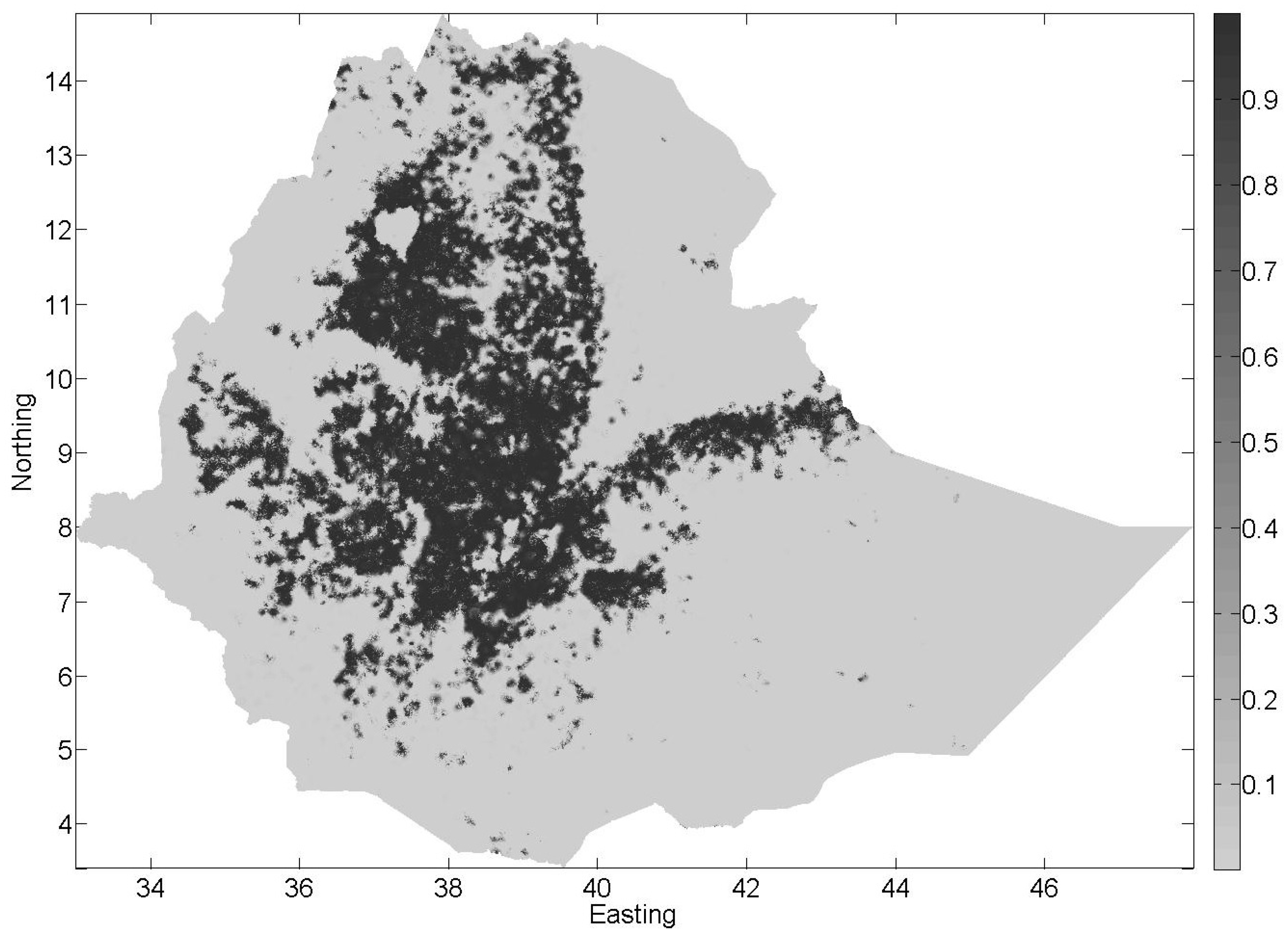
3.4. Combining the Interpolated Map with the CCI-LC Product Using BDF
3.5. Comparison of the Three Land Cover Maps
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; Grillmayer, R.; Achard, F.; Kraxner, F.; Obersteiner, M. Geo-Wiki.Org: The use of crowdsourcing to improve global land cover. Remote Sens. 2009, 1, 345–354. [Google Scholar] [CrossRef]
- Fritz, S.; You, L.; Bun, A.; See, L.; McCallum, I.; Schill, C.; Perger, C.; Liu, J.; Hansen, M.; Obersteiner, M. Cropland for sub-Saharan Africa: A synergistic approach using five land cover data sets. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- See, L.; McCallum, I.; Fritz, S.; Perger, C.; Kraxner, F.; Obersteiner, M.; Baruah, U.D.; Mili, N.; Kalita, N.R. Mapping cropland in Ethiopia using crowdsourcing. Int. J. Geosci. 2013, 4, 6–13. [Google Scholar] [CrossRef]
- See, L.; Fritz, S.; You, L.; Ramankutty, N.; Herrero, M.; Justice, C.; Becker-Reshef, I.; Thornton, P.; Erb, K.; Gong, P.; et al. Improved global cropland data as an essential ingredient for food security. Glob. Food Secur. 2015, 4, 37–45. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Jung, M.; Henkel, K.; Herold, M.; Churkina, G. Exploiting synergies of global land cover products for carbon cycle modeling. Remote Sens. Environ. 2006, 101, 534–553. [Google Scholar]
- Pérez-Hoyos, A.; García-Haro, F.; San-Miguel-Ayanz, J. A methodology to generate a synergetic land-cover map by fusion of different land-cover products. Int. J. Appl. Earth Observ. Geoinf. 2012, 19, 72–87. [Google Scholar]
- See, L.; Fritz, S. A method to compare and improve land cover datasets: Application to the GLC-2000 and MODIS land cover products. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1740–1746. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, H.; Chen, B.; Zhang, H.; Yan, J.; Chen, J.; Che, M.; Lin, X.; Dou, X. A bayesian based method to generate a synergetic land-cover map from existing land-cover products. Remote Sens. 2014, 6, 5589–5613. [Google Scholar] [CrossRef]
- Cardille, J.A. Characterizing Patterns of Agricultural Land Use in Amazonia By Merging Satellite Imagery and Census Data. Ph.D. Thesis, University of Wisconsin-Madison, Madiso, WM, USA, 2002. [Google Scholar]
- Cardille, J.A.; Clayton, M.K. A regression tree-based method for integrating land-cover and land-use data collected at multiple scales. Environ. Ecol. Stat. 2007, 14, 161–179. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Rosentrater, L.; Frolking, S.; Moore, B. Linking remote-sensing estimates of land cover and census statistics on land use to produce maps of land use of the conterminous United states. Glob. Biogeochem. Cycl. 2001, 15, 673–685. [Google Scholar] [CrossRef]
- Fonte, C.C.; Bastin, L.; See, L.; Foody, G.; Lupia, F. Usability of VGI for validation of land cover maps. Int. J. Geogr. Inf. Sci. 2015, 29, 1269–1291. [Google Scholar] [CrossRef]
- Muller, C.; Chapman, L.; Johnston, S.; Kidd, C.; Illingworth, S.; Foody, G.; Overeem, A.; Leigh, R. Crowdsourcing for climate and atmospheric sciences: Current status and future potential. Int. J. Climatol. 2015, 35, 3185–3203. [Google Scholar] [CrossRef]
- Poser, K.; Dransch, D. Volunteered Geographic Information for Disaster Management with Application to Rapid Flood Damage Estimation. Geomatica 2010, 64, 89–98. [Google Scholar]
- Roche, S.; Propeck-Zimmermann, E.; Mericskay, B. GeoWeb and crisis management: issues and perspectives of volunteered geographic information. GeoJournal 2011, 78, 21–40. [Google Scholar] [CrossRef]
- Zook, M.; Graham, M.; Shelton, T.; Gorman, S. Volunteered geographic information and crowdsourcing disaster relief: A case study of the Haitian Earthquake. World Med. Health Policy 2010, 2, 6–32. [Google Scholar] [CrossRef]
- Coleman, D.J.; Sabone, B.; Nkhwanana, N. Volunteering geographic information to authoritative databases: Linking contributor motivations to program effectiveness. Geomatica 2013, 64, 383–396. [Google Scholar]
- Sui, D.; Elwood, S.; Goodchild, M. Crowdsourcing Geographic Knowledge; Springer: Berlin, Germany, 2013. [Google Scholar]
- Goodchild, M.F.; Glennon, J.A. Crowdsourcing geographic information for disaster response: A research frontier. Int. J. Digit. Earth 2010, 3, 231–241. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spatial Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Hunter, J.; Alabri, A.; Ingen, C.V. Assessing the quality and trustworthiness of citizen science data. Concurr. Comput. Pract. Exp. 2013, 25, 454–466. [Google Scholar] [CrossRef]
- Comber, A.; See, L.; Fritz, S.; Van der Velde, M.; Perger, C.; Foody, G. Using control data to determine the reliability of volunteered geographic information about land cover. Int. J. Appl. Earth Observ. Geoinf. 2013, 23, 37–48. [Google Scholar] [CrossRef]
- Bogaert, P.; Gengler, S. MinNorm approximation of MaxEnt/MinDiv problems for probability tables. In Proceedings of the Bayesian Inference and Maximum Entropy Methods in Science and Engineering MaxEnt 2014, Amboise, France, 21–26 September 2014; pp. 287–296.
- Gengler, S.; Bogaert, P. Bayesian data fusion for spatial prediction of categorical variables in environmental sciences. In Proceedings of the Bayesian Inference and Maximum Entropy Methods in Science and Engineering MaxEnt 2013, Canberra, Australia, 15–20 September 2013; pp. 88–93.
- Gengler, S.; Bogaert, P. Bayesian data fusion applied to soil drainage classes spatial mapping. Math. Geosci. 2015, 48, 79–88. [Google Scholar] [CrossRef]
- Negash, M.; Swinnen, J.F. Biofuels and food security: Micro-evidence from Ethiopia. Energy Policy 2013, 61, 963–976. [Google Scholar] [CrossRef]
- Waldner, F.; Fritz, S.; Di Gregorio, A.; Defourny, P. Mapping priorities to focus cropland mapping activities: Fitness assessment of existing global, regional and national cropland maps. Remote Sens. 2015, 7, 7959–7986. [Google Scholar] [CrossRef]
- Tang, W.; Lease, M. Semi-supervised consensus labeling for crowdsourcing. In Proceedings of the SIGIR 2011 Workshop on Crowdsourcing for Information Retrieval, Beijing, China, 28 July 2011; pp. 36–41.
- Wahyudi, A.; Bartzke, M.; Küster, E.; Bogaert, P. Maximum entropy estimation of a Benzene contaminated plume using ecotoxicological assays. Environ. Pollut. 2013, 172, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Bogaert, P.; Fasbender, D. Bayesian data fusion in a spatial prediction context: A general formulation. Stoch. Environ. Res. Risk Assess. 2007, 21, 695–709. [Google Scholar] [CrossRef]
- Fasbender, D.; Peeters, L.; Bogaert, P.; Dassargues, A. Bayesian data fusion applied to water table spatial mapping. Water Resour. Res. 2008, 44, w12422. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- D’Or, D.; Bogaert, P. Continous-valued map reconstruction with the Bayesian Maximum Entropy. Geoderma 2003, 112, 169–178. [Google Scholar] [CrossRef]
- D’Or, D.; Bogaert, P. Combining categorical information with the Bayesian Maximum Entropy approach. In geoENV IV—Geostatistics for Environmental Applications; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Defourny, P.; Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C.; Schlerf, M.; Santoro, M. Land Cover CCI : Product User Guide Version 2. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-PUG-v2.5.pdf (accessed on 28 January 2016).
- Haklay, M.; Basiouka, S.; Antoniou, V.; Ather, A. How many volunteers does it take to map an area well? The validity of Linus’ Law to volunteered geographic information. Cartogr. J. 2010, 47, 315–322. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Bakillah, M. Exploiting volunteered geographic information to ease land use mapping of an urban landscape. Int. Arch. Photogram. Remote Sens. Spatial Inf. Sci. 2013, 1, 51–55. [Google Scholar] [CrossRef]
- Johnson, B.A.; Iizuka, K. Integrating OpenStreetMap crowdsourced data and Landsat time-series imagery for rapid land use/land cover (LULC) mapping: Case study of the laguna Bay area of the Philippines. Appl. Geogr. 2016, 67, 140–149. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Biometry; Freeman and Company: San Francisco, CA, USA, 1969. [Google Scholar]
- Foody, G.M. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogram. Eng. Remote Sens. 2004, 7, 627–633. [Google Scholar] [CrossRef]

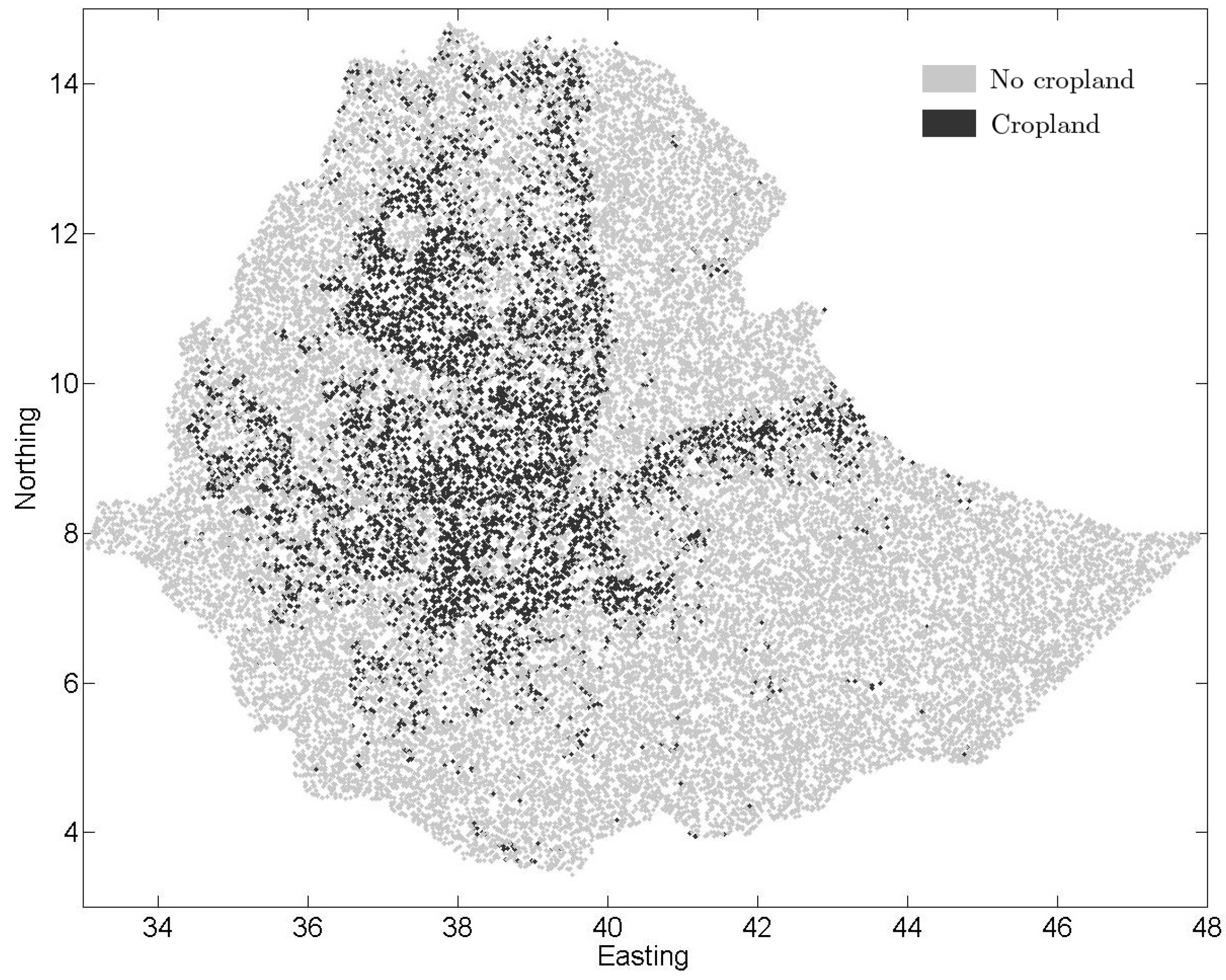
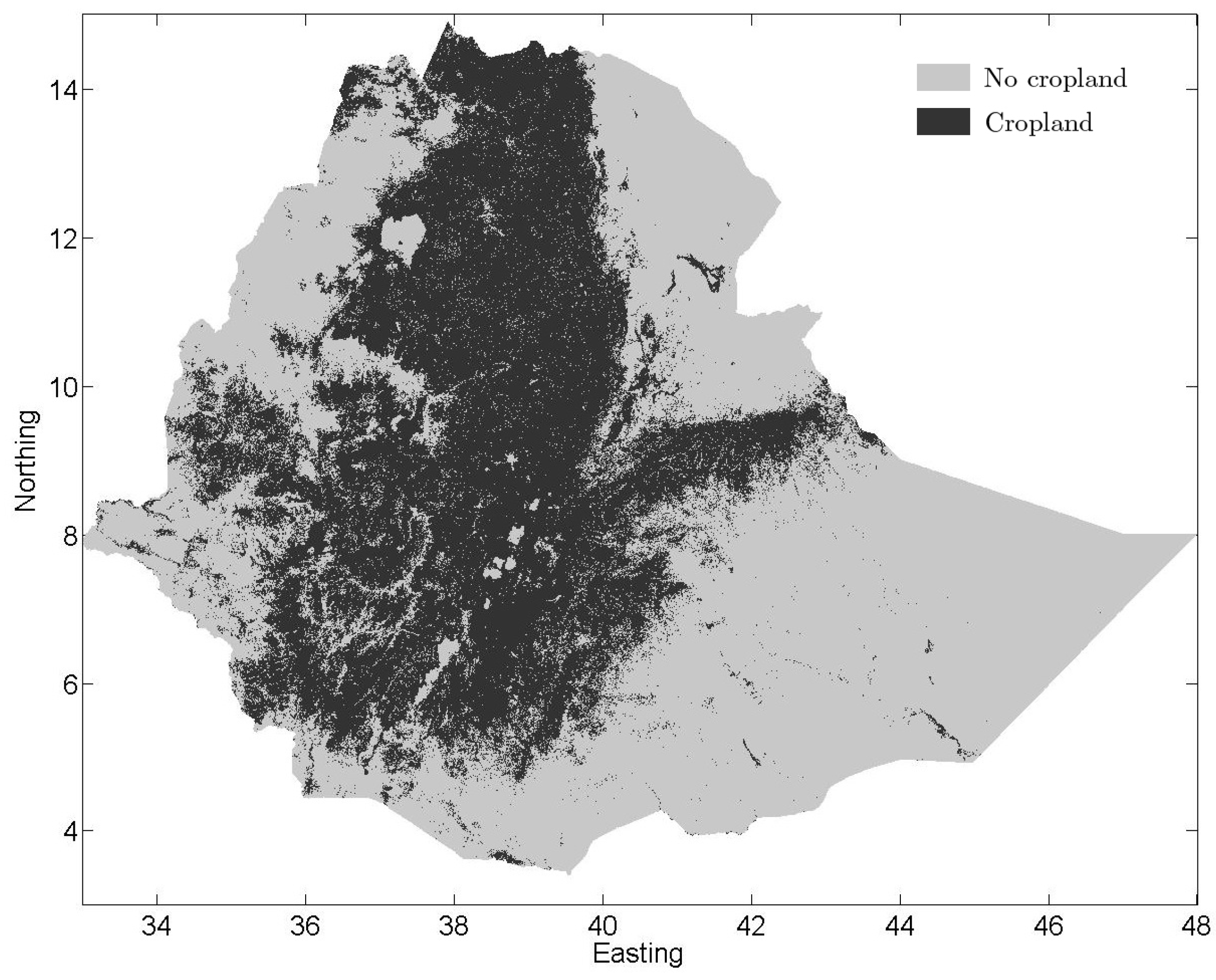
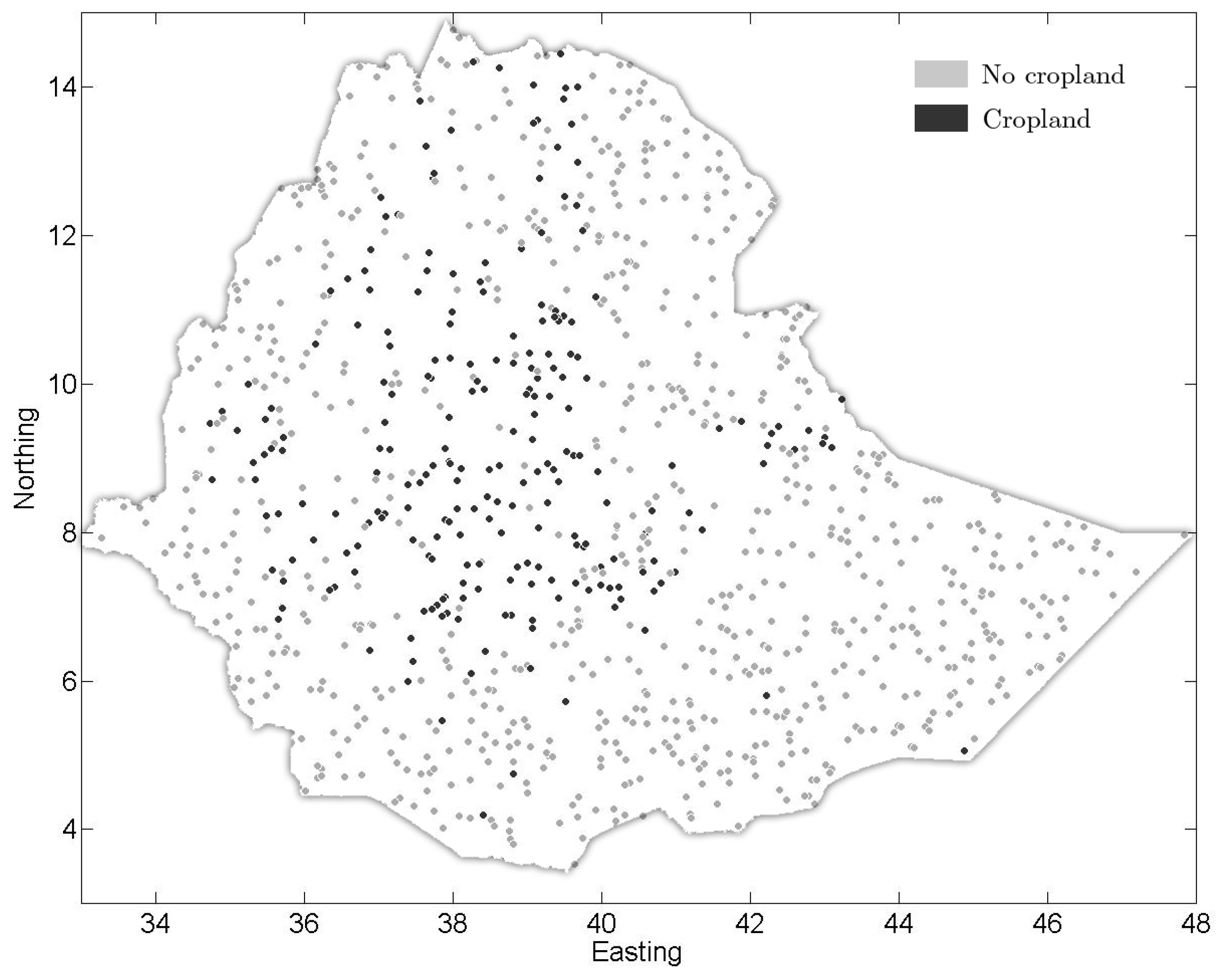


| Contributor ID | Number of Contributions | Number of Validation Points |
|---|---|---|
| #1 | 20,497 | 279 |
| #2 | 20,311 | 317 |
| #3 | 19,238 | 284 |
| #4 | 5575 | 83 |
| #5 | 3311 | 49 |
| #6 | 1536 | 29 |
| #7 | 1534 | 16 |
| #8 | 1427 | 11 |
| #9 | 901 | 10 |
| #10 | 659 | 10 |
| CCI-LC | ||||
|---|---|---|---|---|
| Crop | No Crop | Producer’s Accuracy (%) | ||
| Validation | Crop | 110 | 14 | 88.71 |
| No crop | 102 | 274 | 72.87 | |
| User’s Accuracy (%) | 51.89 | 95.14 | 76.80 | |
| Contributor ID | E = 1 | E = 0 | ||
|---|---|---|---|---|
| #1 | P(Z = 1 | E) | 0.992 | 0.017 | |
| P(Z = 0 | E) | 0.008 | 0.983 | ||
| #2 | P(Z = 1 | E) | 0.990 | 0.044 | |
| P(Z = 0 | E) | 0.010 | 0.956 | ||
| #3 | P(Z = 1 | E) | 0.992 | 0.034 | |
| P(Z = 0 | E) | 0.008 | 0.966 | ||
| #4 | P(Z = 1 | E) | 0.831 | 0.089 | |
| P(Z = 0 | E) | 0.169 | 0.911 | ||
| #5 | P(Z = 1 | E) | 0.969 | 0.017 | |
| P(Z = 0 | E) | 0.031 | 0.983 | ||
| #6 | P(Z = 1 | E) | 0.931 | 0.066 | |
| P(Z = 0 | E) | 0.069 | 0.934 | ||
| #7 | P(Z = 1 | E) | 0.911 | 0.046 | |
| P(Z = 0 | E) | 0.089 | 0.954 | ||
| #8 | P(Z = 1 | E) | 0.931 | 0.103 | |
| P(Z = 0 | E) | 0.069 | 0.897 | ||
| #9 | P(Z = 1 | E) | 0.922 | 0.103 | |
| P(Z = 0 | E) | 0.078 | 0.897 | ||
| #10 | P(Z = 1 | E) | 0.857 | 0.164 | |
| P(Z = 0 | E) | 0.143 | 0.836 |
| Interpolation Crowdsourcing | ||||
|---|---|---|---|---|
| Crop | No Crop | Producer’s Accuracy (%) | ||
| Validation | Crop | 95 | 29 | 76.61 |
| No crop | 21 | 355 | 94.41 | |
| User’s Accuracy (%) | 81.90 | 92.45 | 98.00 | |
| Fusion CCI-LC-Crowdsourcing | ||||
|---|---|---|---|---|
| Crop | No Crop | Producer’s Accuracy (%) | ||
| Validation | Crop | 94 | 30 | 75.81 |
| No crop | 20 | 356 | 94.68 | |
| User’s Accuracy (%) | 82.46 | 92.23 | 98.00 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gengler, S.; Bogaert, P. Integrating Crowdsourced Data with a Land Cover Product: A Bayesian Data Fusion Approach. Remote Sens. 2016, 8, 545. https://doi.org/10.3390/rs8070545
Gengler S, Bogaert P. Integrating Crowdsourced Data with a Land Cover Product: A Bayesian Data Fusion Approach. Remote Sensing. 2016; 8(7):545. https://doi.org/10.3390/rs8070545
Chicago/Turabian StyleGengler, Sarah, and Patrick Bogaert. 2016. "Integrating Crowdsourced Data with a Land Cover Product: A Bayesian Data Fusion Approach" Remote Sensing 8, no. 7: 545. https://doi.org/10.3390/rs8070545
APA StyleGengler, S., & Bogaert, P. (2016). Integrating Crowdsourced Data with a Land Cover Product: A Bayesian Data Fusion Approach. Remote Sensing, 8(7), 545. https://doi.org/10.3390/rs8070545