Posterior Probability Modeling and Image Classification for Archaeological Site Prospection: Building a Survey Efficacy Model for Identifying Neolithic Felsite Workshops in the Shetland Islands
Abstract
:1. Introduction
1.1. The Shetland Islands
1.2. The North Roe Felsite Project (NRFP)
“These rocks occur in Shetland only in the small area…, but material from them has been found throughout the main island in the shape of stone axes and flensing knives. For such implements the toughness and durability of the rock and its capacity to take a clean, sharp edge render it pre-eminently suitable and former inhabitants of the island have evidently been well aware of its source.”
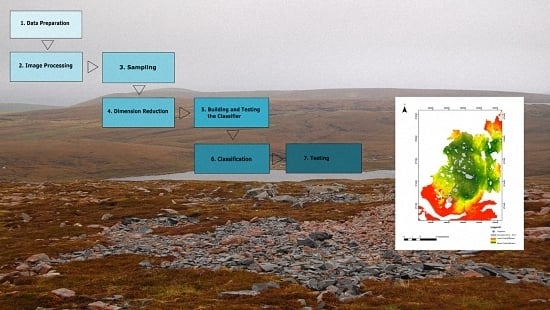
2. Materials and Methods
2.1. Archaeological Predictive Modelling and Direct Detection Protocols
2.2. Project Datasets
2.3. Image Processing Techniques
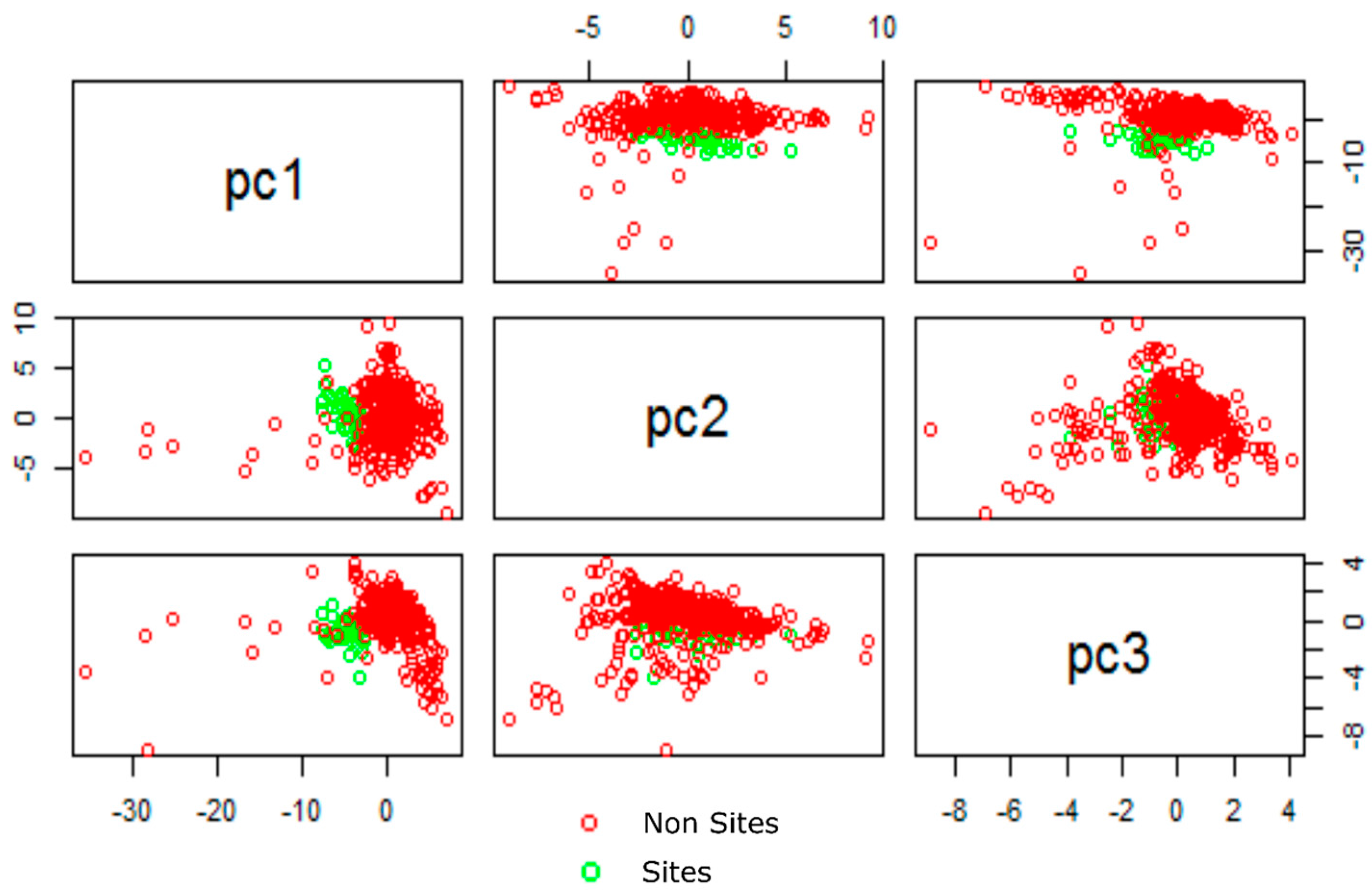
2.4. Image Classification
2.5. Understanding Access: The Least-Cost Approach
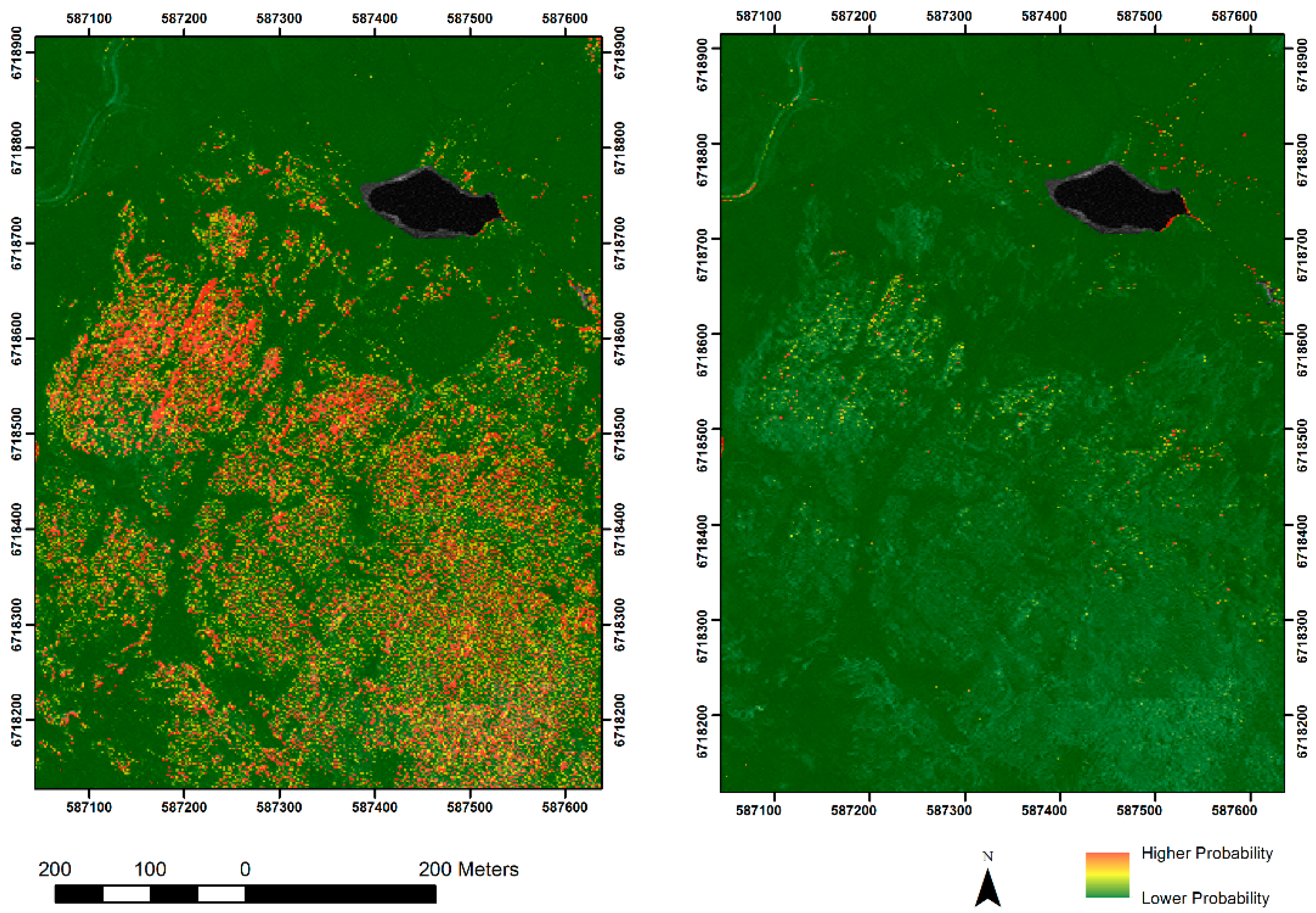
3. Results
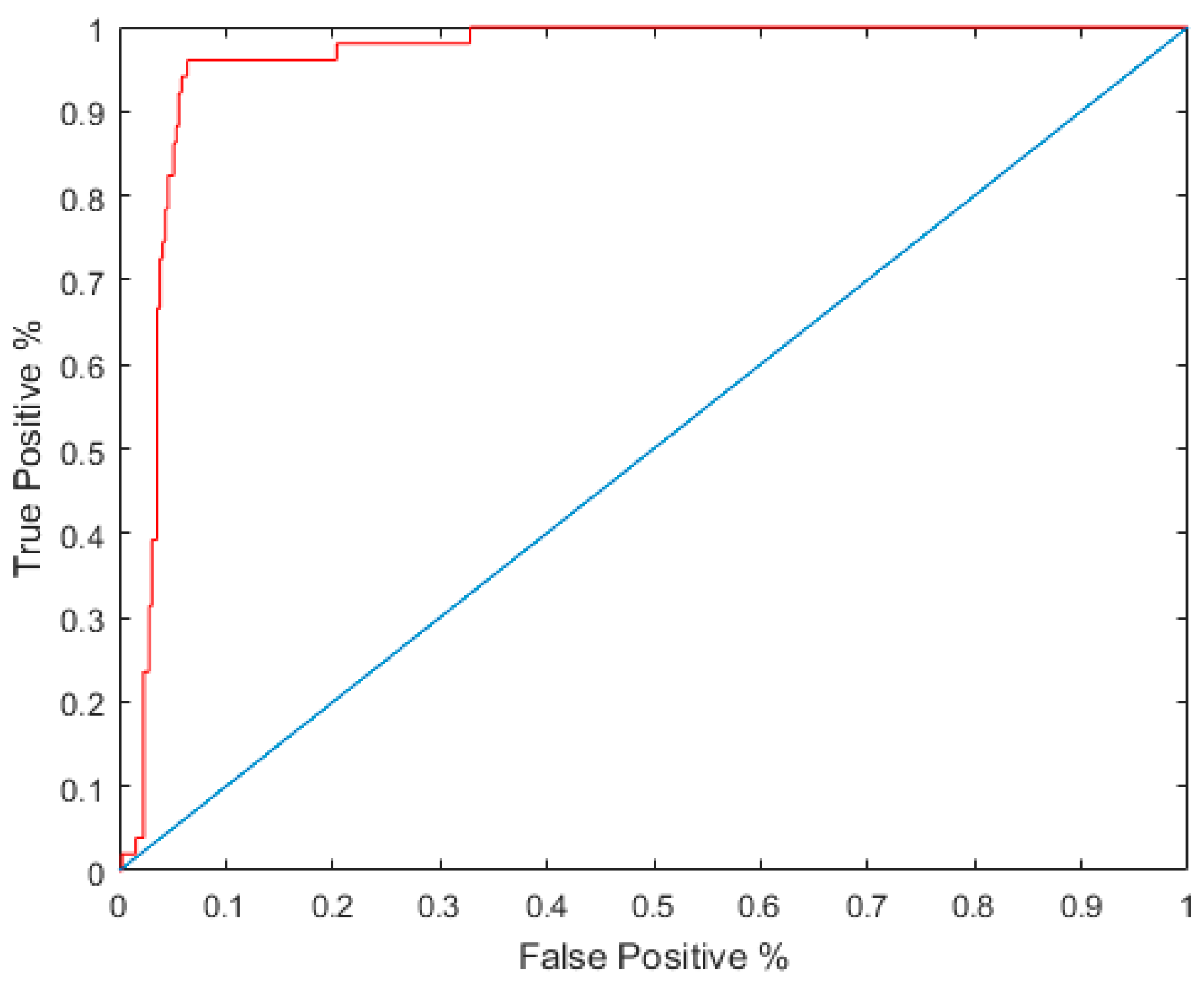
3.1. Assessing the Models
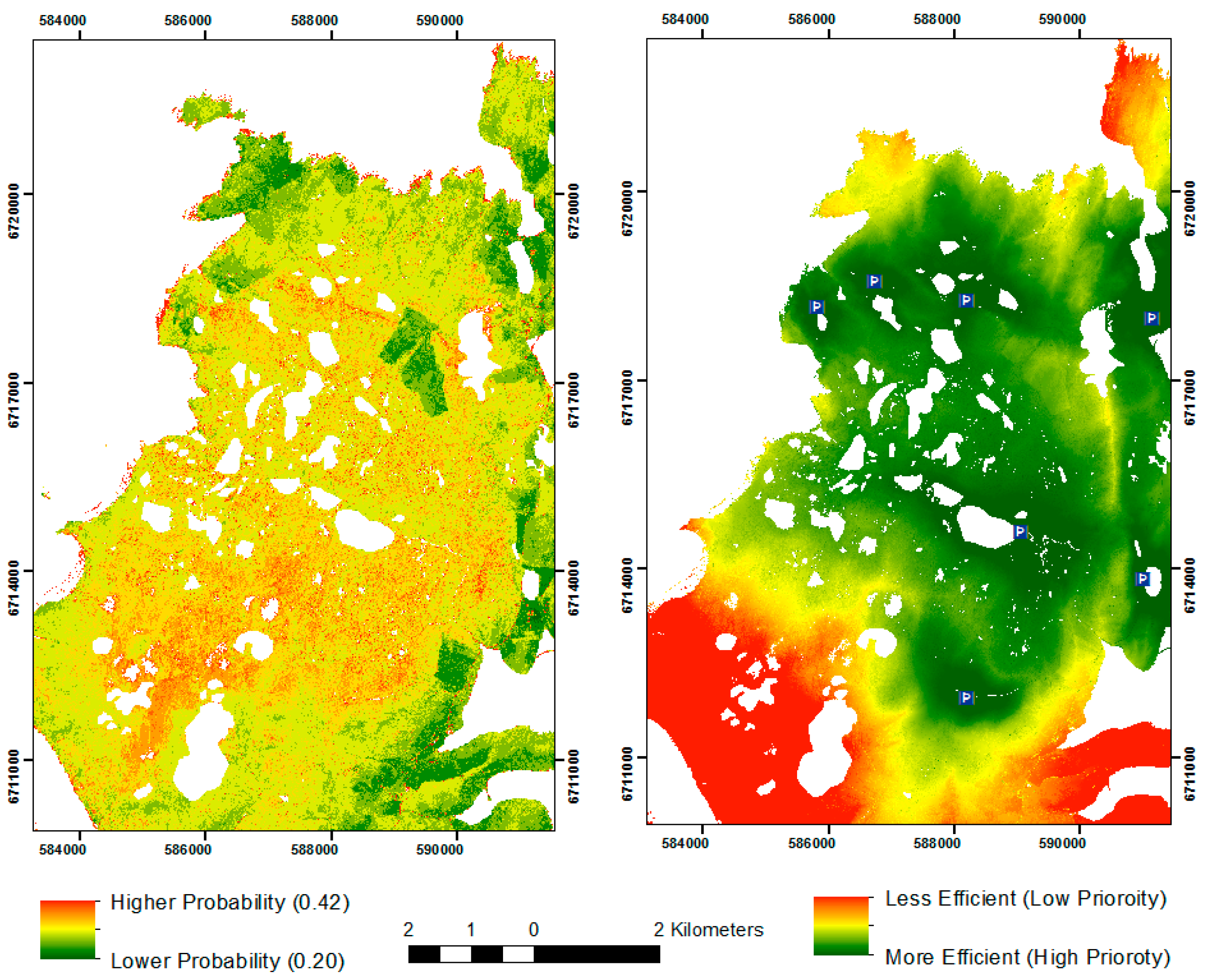
3.2. Assessing the Cost-Efficacy of the Study
3.3. Integrating the PPM with Least-Cost Surfaces
4. Discussion
4.1. Posterior Probability Modelling and Archaeological Field Survey
4.2. Imagery and Topography
4.3. PPM and Scale
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interests
References
- Sheridan, A. Neolithic Shetland: A view from the “mainland”. In The Border of Farming and the Cultural Markers—Short Papers from the Network Meeting in Lerwick, Shetland, September 5th–9th 2011; Mahler, D.L.D., Ed.; Nationalmuseet: Copenhagen, Denmark, 2012; pp. 6–36. [Google Scholar]
- Mahler, D.L.D. Farming on the Edge: Cultural Landscapes of the North; Nationalmuseet: Copenhagen, Denmark, 2011. [Google Scholar]
- Ballin, T.B. The distribution of worked felsites—Within and outwith neolithic Shetland. In The Border of Farming and the Cultural Markers—Short Papers from the Network Meeting in Lerwick, Shetland, September 5th–9th 2011; Mahler, D.L.D., Ed.; Nationalmuseet: Copenhagen, Denmark, 2012; pp. 62–79. [Google Scholar]
- Ballin, T.B. The felsite quarries of North Roes, Shetland—An overview. In Stone Axe Studies III; Davis, V., Edmonds, M., Eds.; Oxbow Books: Oxford, UK, 2011; pp. 121–130. [Google Scholar]
- Melton, N.D. Shells, seals and ceramics: An evaluation of a midden at West Voe, Sumburgh, Shetland, 2004–2005. In Mesolithic Horizons: Papers Presented at the Seventh International Conference on the Mesolithic in Europe, Belfast; McCartan, S., Schulting, R., Warren, G., Woodman, P., Eds.; Oxbow Books: Oxford, UK, 2009; pp. 184–189. [Google Scholar]
- Ballin, T.B. Felsite axehead reduction—The flow from quarry pit to discard/deposition. In The Border of Farming Shetland and Scandinavia: Neolithic and Bronze Age Farming—Short Papers from the Symposium in Copenhagen, September 19th—21th 2012; Mahler, D.L.D., Ed.; Nationalmuseet: Copenhagen, Denmark, 2013; pp. 73–92. [Google Scholar]
- Ballin, T. Making and Island World: Neolithic Shetland. Felsite Polished Axeheads/Adzes and Shetland Knives in Shetland Museum, Characterization and Interpretation of the Collection; UCD School of Archaeology: Dublin, Ireland, 2015. [Google Scholar]
- Phemister, J.; Harvey, C.O.; Sabine, P.A. The riebeckite-bearing dikes of Shetland. Mineral. Mag. 1950, 29, 359–373. [Google Scholar] [CrossRef]
- Ritchie, R. Stone axeheads and cushion maceheads from Orkney and Shetland: Some similarities and contrasts. In Vessels for the Ancestors: Essays on the Neolithic of Britain and Ireland in Honour of Audrey Henshall; Sharples, N.M., Sheridan, J.A., Eds.; Edinburgh University Press: Edinburgh, UK, 1992; pp. 213–220. [Google Scholar]
- Cooney, G.; Ballin, T.; Davis, V.; Sheridan, A.; Megarry, W. Making an Island World: Neolithic Shetland. 2013 Field Season Report; UCD School of Archaeology: Dublin, Ireland, 2013. [Google Scholar]
- Practical Applications of GIS for Archaeologists. A Predictive Modeling Kit; Wescott, K.L.; Brandon, R.J. (Eds.) Taylor & Francis: London, UK, 2000.
- Harrower, M.J. Methods, concepts and challenges in archaeological site detection. In Mapping Archaeological Landscapes from Space; Comer, D.C., Harrower, M.J., Eds.; Springer: New York, NY, USA, 2013; pp. 213–218. [Google Scholar]
- Kvamme, K. Determining empirical relationships between the natural environment and prehistoric site locations. In For Concordance in Archaeological Analysis: Bridging Data Structure, Quantitative Technique, and Theory; Carr, C., Ed.; Westport Publishers: Kansas City, MO, USA, 1985; pp. 208–239. [Google Scholar]
- Chen, L.; Priebe, C.E.; Sussman, D.L.; Comer, D.C.; Megarry, W.P.; Tilton, J.C. Enhanced Archaeological Predictive Modelling in Space Archaeology. 2013. Available online: http://arxiv.org/abs/1301.2738 (accessed on 15 January 2016).
- Chen, L.; Comer, D.C.; Priebe, C.E.; Sussman, D.; Tilton, J.C. Refinement of a method for identifying probable archaeological sites from remotely sensed data. In Mapping Archaeological Landscapes from Space; Comer, D.C., Harrower, M.J., Eds.; Springer: New York, NY, USA, 2013; pp. 251–258. [Google Scholar]
- Comer, D. Institutionalizing Protocols for Wide-Area Inventory of Archaeological Sites by Analysis of Aerial and Satellite Imagery, Project Number (11–158); Department of Defense Program Office: Washington, DC, USA, 2011. [Google Scholar]
- Tilton, J.C.; Comer, D.C. Identifying probable archaeological sites on Santa Catalina island, California using SAR and IKONOS data. In Mapping Archaeological Landscapes from Space; Comer, D.C., Harrower, M.J., Eds.; Springer: New York, NY, USA, 2013; pp. 241–249. [Google Scholar]
- Comer, D.C.; Blom, R.G. Detection and identification of archaeological sites and features using Synthetic Aperture Radar (SAR) data collected from airborne platforms. In Remote Sensing in Archaeology: Interdisciplinary Contributions To Archaeology; Springer: New York, NY, USA, 2006; pp. 103–136. [Google Scholar]
- Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S. Quick Atmospheric Correction Code: Algorithm Description and Recent Upgrades. Opt. Eng. 2012, 51, 111719:1–111719:11. [Google Scholar] [CrossRef]
- Doneus, M.; Verhoeven, G.; Atzberger, C.; Wess, M.; Ruš, M. New ways to extract archaeological information from hyperspectral pixels. J. Archaeol. Sci. 2014, 52, 84–96. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4. [Google Scholar] [CrossRef]
- Verhoeven, G.J.J.; Doneus, M. Balancing on the borderline e a low-cost approach to visualize the red-edge shift for the benefit of aerial archaeology. Archaeol. Prospect. 2011, 18, 267–278. [Google Scholar] [CrossRef]
- Marchisio, G.; Padwick, C.; Pacifici, F. Evidence of improved vegetation discrimination and urban mapping using worlview-2 multi-spectral imagery. In Proceedings of the ASPRS 2011 Annual Conference, Milwaukee, WI, USA, 1–5 May 2011.
- Llobera, M. Building past landscape perception with GIS: Understanding topographic prominence. J. Archaeol. Sci. 2001, 28, 1005–1014. [Google Scholar] [CrossRef]
- Žiga, K.; Klemen, Z.; Oštir, K. Application of sky-view factor for the visualization of historic landscape features in LiDAR-derived relief models. Antiquity 2011, 85, 263–273. [Google Scholar]
- Klemen, Z.; Oštir, K.; Žiga, K. Sky-View factor as a relief visualization technique. Remote Sens. 2011, 3, 398–415. [Google Scholar]
- Atzberger, C.; Wess, M.; Doneus, M.; Verhoeven, G. ARCTIS—A MATLAB® Toolbox for archaeological imaging spectroscopy. Remote Sens. 2014, 6, 8617–8638. [Google Scholar] [CrossRef]
- Traviglia, A. Archaeological usability of hyperspectral images: Successes and failures of image processing techniques. In From Space to Place. Proceedings of the 2nd International Conference on Remote Sensing in Archaeology, CNR, Rome, Italy. December 2–4; Archaeopress: Oxford, UK, 2006; pp. 123–130. [Google Scholar]
- Gareth, J.; Witten, D.; Hastie, T.; Tibshirani, R. Classification. In An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; pp. 127–168. [Google Scholar]
- Langmuir, E. Mountaincraft and Leadership; The Scottish Sports Council/MLTB: Cordee, Leicester, UK, 1984. [Google Scholar]
- Kvamme, K.L. Development and testing of quantitative models. In Quantifying the Present and Predicting the Past: Theory, Methods, and Applications of Archaeological Predictive Modeling; Judge, W.J., Sebastian, L., Eds.; US Department of Interior, Bureau of Land Management Service Center: Denver, CO, USA, 1988; pp. 325–428. [Google Scholar]



| Band | Lower Band Edge (nm) | Upper Band Edge (nm) | Centre Wavelength |
|---|---|---|---|
| Coastal Blue | 396 | 458 | 427 |
| Blue | 442 | 515 | 478 |
| Green | 506 | 586 | 546 |
| Yellow | 584 | 632 | 608 |
| Red | 624 | 694 | 659 |
| Red Edge | 699 | 749 | 724 |
| Near Infrared I | 765 | 901 | 833 |
| Near Infrared II | 856 | 1043 | 949 |
| Dataset | No. Bands | Source | Resolution |
|---|---|---|---|
| WV-2 | 8 | Digitalglobe Foundation | 2 m |
| BDR | 28 | Using Data from Digitalglobe Foundation | 2 m |
| Slope | 1 | Elevation Model from Ordnance Survey | 2 m * |
| Skyview | 1 | Elevation Model from Ordnance Survey | 2 m * |
| Aspect | 1 | Elevation Model from Ordnance Survey | 2 m * |
| Model | No. Bands | Statistic | Datasets |
|---|---|---|---|
| 1 | 8 | Mean | WV-2 |
| 2 | 8 | Median | WV-2 |
| 3 | 11 | Mean | WV-2 and Topography |
| 4 | 11 | Median | WV-2 and Topography |
| 5 | 28 | Mean | WV-2 BDR |
| 6 | 28 | Median | WV-2 BDR |
| 7 | 31 | Mean | WV-2 BDR and Topography |
| 8 | 31 | Median | WV-2 BDR and Topography |
| 9 | 36 | Mean | WV-2, WV-2 BDR |
| 10 | 39 | Mean | WV-2, WV-2 BDR and Topography |
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| AUC | 0.9562 | 0.9497 | 0.9562 | 0.9590 | 0.9511 | 0.9520 | 0.9611 | 0.9536 | 0.0576 | 0.9511 |
| Model | Statistic | Datasets | KS p-Value | Gain | Gain Area % |
|---|---|---|---|---|---|
| 1 | Mean | WV-2 | 4.2501 × 10−27 | 0.8312 | 5% |
| 2 | Median | WV-2 | 1.3669 × 10−25 | 0.8786 | 5% |
| 3 | Mean | WV-2 and Topography | 0.0010 | 0.5202 | 38% |
| 4 | Median | WV-2 and Topography | 0.0004 | 0.5306 | 32% |
| 5 | Mean | WV-2 BDR | 1.7723 × 10−23 | 0.8688 | 5% |
| 6 | Median | WV-2 BDR | 2.5351 × 10−23 | 0.8788 | 6% |
| 7 | Mean | WV-2 BDR and Topography | 0.0660 | 0.6877 | 28% |
| 8 | Median | WV-2 BDR and Topography | 0.0590 | 0.7039 | 25% |
| 9 | Mean and Median | WV-2 and WV-2 BDR | 0.0080 | 0.9365 | 5% |
| 10 | Mean and Median | WV-2, WV-2 BDR and Topography | 0.0023 | 0.8890 | 5% |
| Model | KS p-Value | Gain Statistic |
|---|---|---|
| Model 9 | 0.0080 | 0.9365 |
| Maximum Likelihood | 3.6672 × 10−32 | 0.8383 |
| Random Forests (1000) | 1.2831 × 10−05 | 0.8438 |
| Random Forests (1000): Top 5 Parameters | 0.0186 | 0.8871 |
| Random Forests (1000): Top 5 Parameters and Topography | 0.0221 | 0.8833 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megarry, W.P.; Cooney, G.; Comer, D.C.; Priebe, C.E. Posterior Probability Modeling and Image Classification for Archaeological Site Prospection: Building a Survey Efficacy Model for Identifying Neolithic Felsite Workshops in the Shetland Islands. Remote Sens. 2016, 8, 529. https://doi.org/10.3390/rs8060529
Megarry WP, Cooney G, Comer DC, Priebe CE. Posterior Probability Modeling and Image Classification for Archaeological Site Prospection: Building a Survey Efficacy Model for Identifying Neolithic Felsite Workshops in the Shetland Islands. Remote Sensing. 2016; 8(6):529. https://doi.org/10.3390/rs8060529
Chicago/Turabian StyleMegarry, William P., Gabriel Cooney, Douglas C. Comer, and Carey E. Priebe. 2016. "Posterior Probability Modeling and Image Classification for Archaeological Site Prospection: Building a Survey Efficacy Model for Identifying Neolithic Felsite Workshops in the Shetland Islands" Remote Sensing 8, no. 6: 529. https://doi.org/10.3390/rs8060529
APA StyleMegarry, W. P., Cooney, G., Comer, D. C., & Priebe, C. E. (2016). Posterior Probability Modeling and Image Classification for Archaeological Site Prospection: Building a Survey Efficacy Model for Identifying Neolithic Felsite Workshops in the Shetland Islands. Remote Sensing, 8(6), 529. https://doi.org/10.3390/rs8060529