1. Introduction
Moderate spatial resolution satellite data from the similar polar-orbiting sun-synchronous Landsat-8 and Sentinel-2 sensors together provide the opportunity for improved mapping and monitoring of the Earth’s surface [
1]. Landsat-8 carries the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIRS) that sense 11 spectral bands including eight 30 m reflective wavelength bands, one 15 m panchromatic band, and two 100 m thermal wavelength bands [
2]. The Landsat-8 swath is approximately 185 km (15° field of view from an altitude of 705 km) and provides a global coverage of the Earth’s surface every 16 days [
2]. Sentinel-2A carries the Multi Spectral Instrument (MSI) that has 13 spectral bands ranging from 0.433 μm to 2.19 μm, including four 10 m visible and near-infrared bands, six 20 m red edge, near-infrared and short wave infrared bands, and three 60 m bands [
3]. The Sentinel-2A swath is approximately 290 km (20.6° field of view from an altitude of 786 km) and provides a global coverage every 10 days and with the planned launch of a follow on identical Sentinel-2B sensor will provide 5-day global coverage [
3]. Combined, the Sentinel-2 and Landsat-8 sensors will provide 10 m to 30 m multi-spectral reflective wavelength global coverage approximately every 3 days.
This paper describes the automated registration of Landsat-8 and Sentinel-2A reflectance data into the same common coordinate system. The geometrically corrected sensor data are available for Sentinel-2A as L1C top-of-atmosphere (TOA) tiles [
4,
5] and for Landsat-8 as L1T TOA images defined in a Worldwide Reference System (WRS) path/row coordinate system [
6,
7]. The geolocation performance specification for Sentinel-2A is 12.5 m (3σ) [
8] and for Landsat-8 is 12 m (90% circular error) [
9]. However, the Sentinel-2A L1C and Landsat-8 L1T data are currently misaligned relative to each other by more than several 10 m pixels [
10]. This is because although both sensor geolocation systems use parametric approaches, whereby information concerning the sensing geometry is modeled and the sensor exterior orientation parameters (attitude and position) are measured, they use different ground control and digital elevation models to refine the geolocation [
8,
9]. The Landsat geolocation uses a global sample of ground control points derived from the Global Land Survey (GLS) cloud-free single-date Landsat images that are defined for each WRS path/row for different decades [
11,
12]. The Sentinel-2A geolocation will be improved by using a global reference image derived from an orthorectified set of Sentinel-2A cloud-free images [
13,
14]. Unfortunately, a relative misalignment of the Landsat-8 L1T and Sentinel-2A L1C data has been observed that varies among Landsat WRS path/row locations due primarily to variable GLS path/row locational accuracies [
9]. Consequently, the GLS data are being reprocessed to provide a better match with the ground control used for operational geolocation of the Sentinel-2A data [
10]. A more detailed description of the causes of the sensor misregistration is provided in [
15].
A large body of research has been published concerning the registration of satellite images [
16]. Methods are divided broadly into area-based matching methods, whereby a small region of one image is moved systematically across the other image and the location that provides the highest reflectance correlation provides a tie-point, and feature-based methods where tie-points are found by locating the positions of high-contrast features common to both images [
17]. Given a sufficient number of tie-points, a transformation function, usually expressed as two polynomial functions that map the x and the y pixel locations of one image to the other image, is derived, often by least-squares regression analysis. For highly distorted data such as airborne imagery, local transformation functions are needed [
18,
19,
20]. Different satellite data registration methods have been refined and proposed, for example, with respect to the initial knowledge of the relative orientation and scale of the images, to include computational efficiencies required to improve the matching speed, and to robustly handle cloud occlusion, land surface changes and differences between sensors [
16].
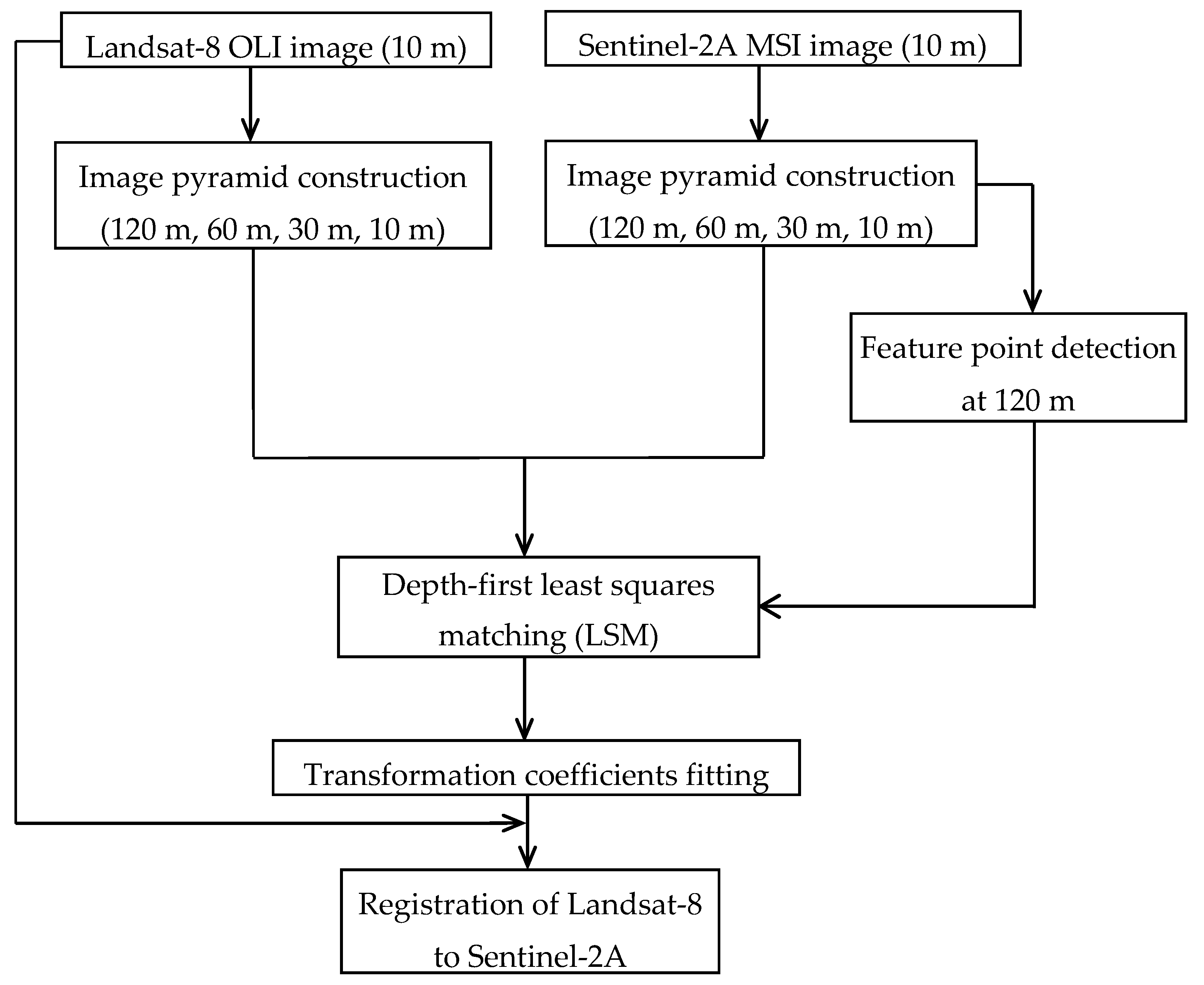
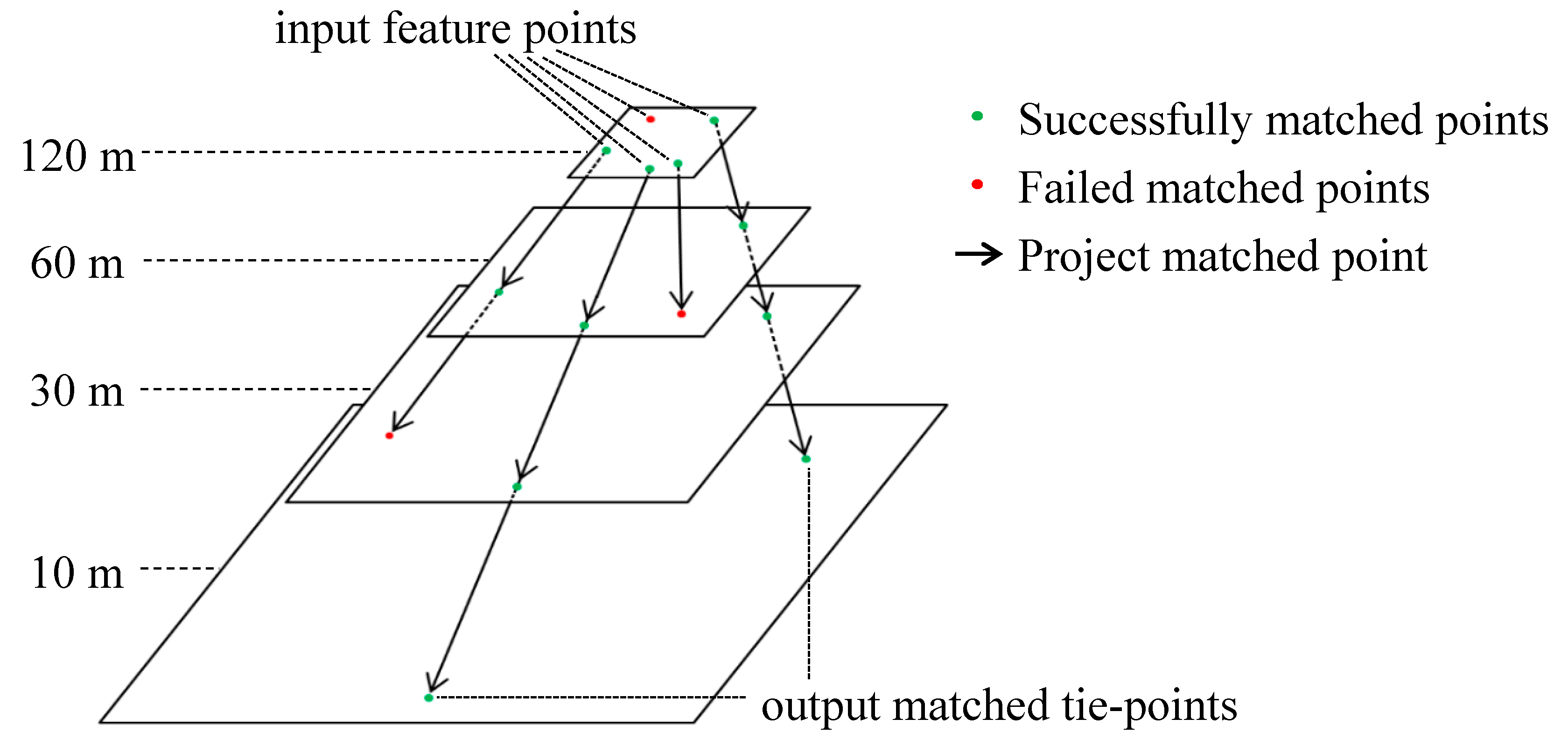
In this study, a hierarchical image matching approach, which was originally developed for registration of High-Resolution Imaging Science Experiment (HiRISE) single-band stereo images to derive digital elevation models of Mars [
21], was refined for registration of Landsat-8 L1T and Sentinel-2A L1C data. This approach was adopted because it has been proven for operational automated processing. Moreover, it uses an efficient feature- and area-based matching approach, is robust to noise, generates a large number of dense matches in a computationally efficient manner, and works well when the relative orientation and location of the images to be registered are known approximately. In this study, the approach was refined and applied to the 10 m Sentinel-2A near-infrared (NIR) and the 30 m Landsat-8 NIR bands. The NIR bands were selected because NIR reflectance has a greater range over soil, vegetation, and water, than visible wavelengths [
22], and so usually the NIR provides high spatial contrast suitable for area- and feature-based matching of images acquired with similar dates (as in this study). In addition, the NIR is less sensitive to atmospheric contamination than at visible wavelengths [
23]. We note that the NIR is commonly used for registration of moderate and high spatial resolution satellite data [
17,
24,
25]. The Landsat-8 15 m panchromatic band, which covers predominantly the green and red wavelengths (503 to 676 nm) [
26], was not used in this study because there is no spectrally similar Sentinel-2A band.
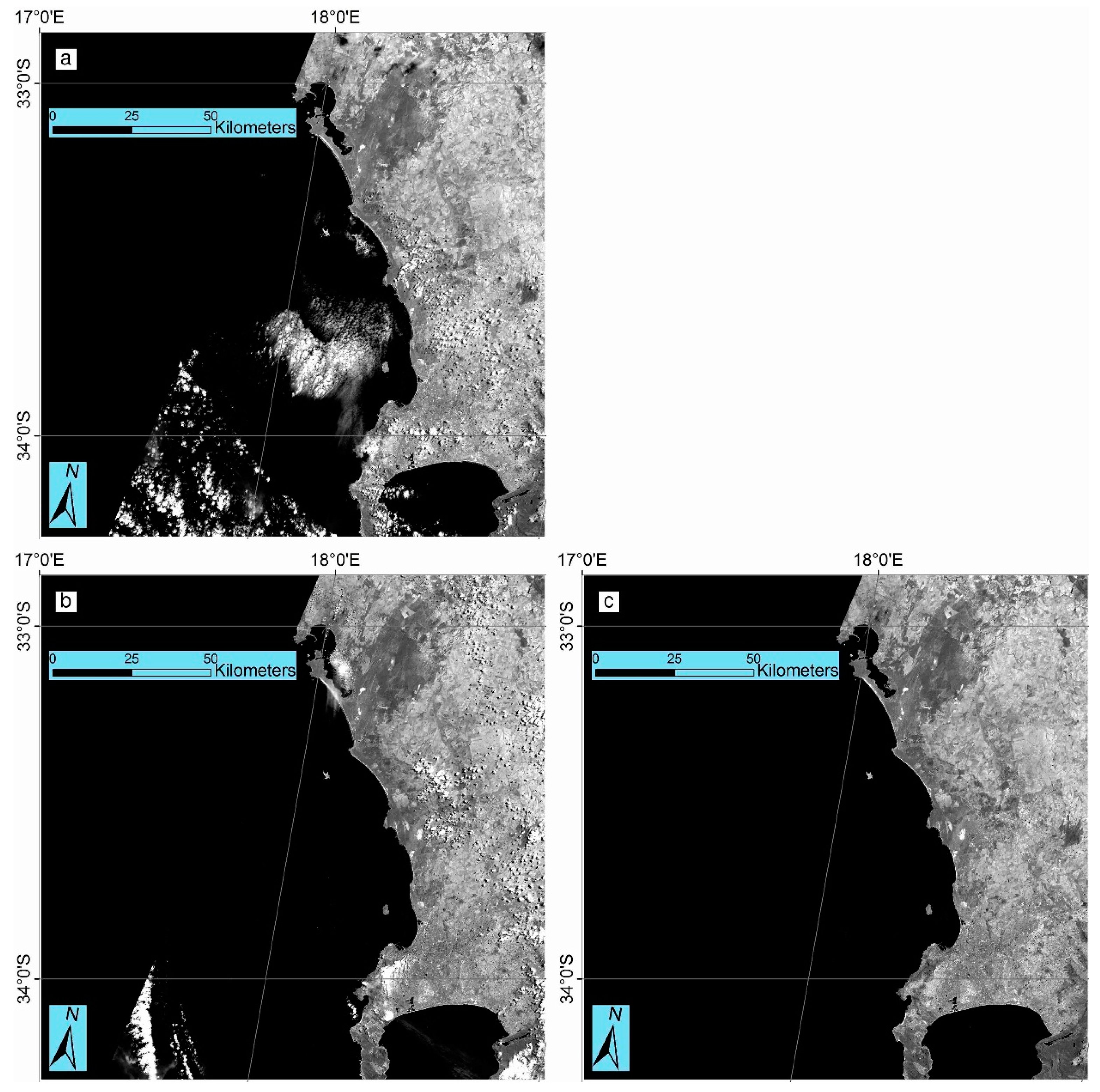
The paper is organized as follows. First, the Sentinel-2A L1C and Landsat-8 L1T geometric data characteristics and the common projection and tiling scheme used to reproject the data are described and illustrated for the test data that are selected in South Africa where approximately contemporaneous Sentinel-2A and Landsat-8 were available. The registration methodology and assessment approach are then described. Quantitative and qualitative results are presented to illustrate the registration performance and examples of the misregistration between Landsat-8 and Sentinel-2A data. The paper concludes with a discussion on the results and implications for combined Landsat-8 and Sentinel-2A data applications.
6. Discussion
Registration of satellite data to sub-pixel precision is a pre-requisite for meaningful data comparison and surface change detection [
54,
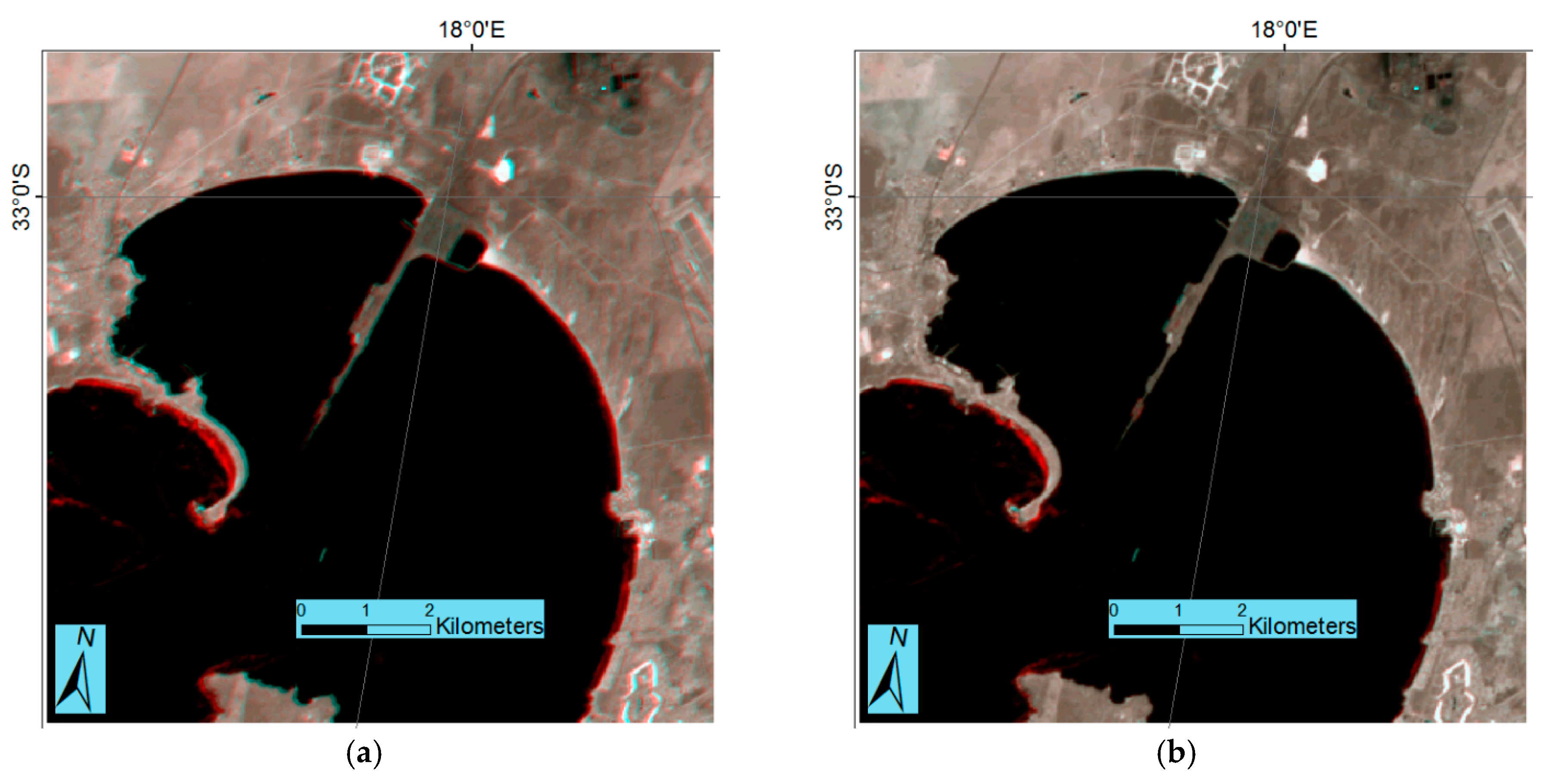
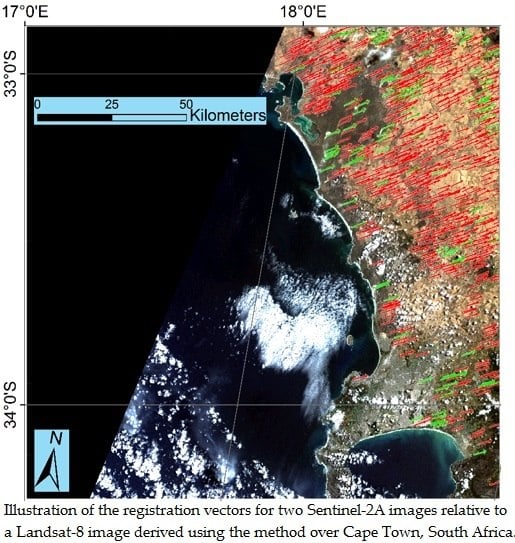
55]. The registration tie-points were derived by least squares matching, which provides sub-pixel location precision and handles the sensor spectral band differences and the non-linear geometric distortions present between the Landsat-8 and Sentinel-2A data. The tie-points were used to fit translation, affine and second order polynomial transformation functions, and for the three pairs of sensor data (different dates and locations), the translation transformation was less accurate with RMSE fit values greater than 0.5 pixels and greater dense-matching prediction errors. The affine and second order polynomial transformations had RMSE fit values of approximately 0.3 pixels and dense-matching prediction errors of similar magnitude. However, the tie-points derived from the two Sentinel-2A Cape Town images and the same Landsat-8 Cape Town image (
Figure 5) provided less stable transformations relative to each other when the second order polynomial rather than the affine transformation was used. This is likely because of the greater sensitivity of the polynomial model to the different numbers and spatial distributions of tie-points [
18,
56] (
Figure 5). These results suggest that an affine transformation is sufficient to register Landsat-8 L1T and Sentinel-2A L1C data when there are considerably more tie-points than transformation coefficients.
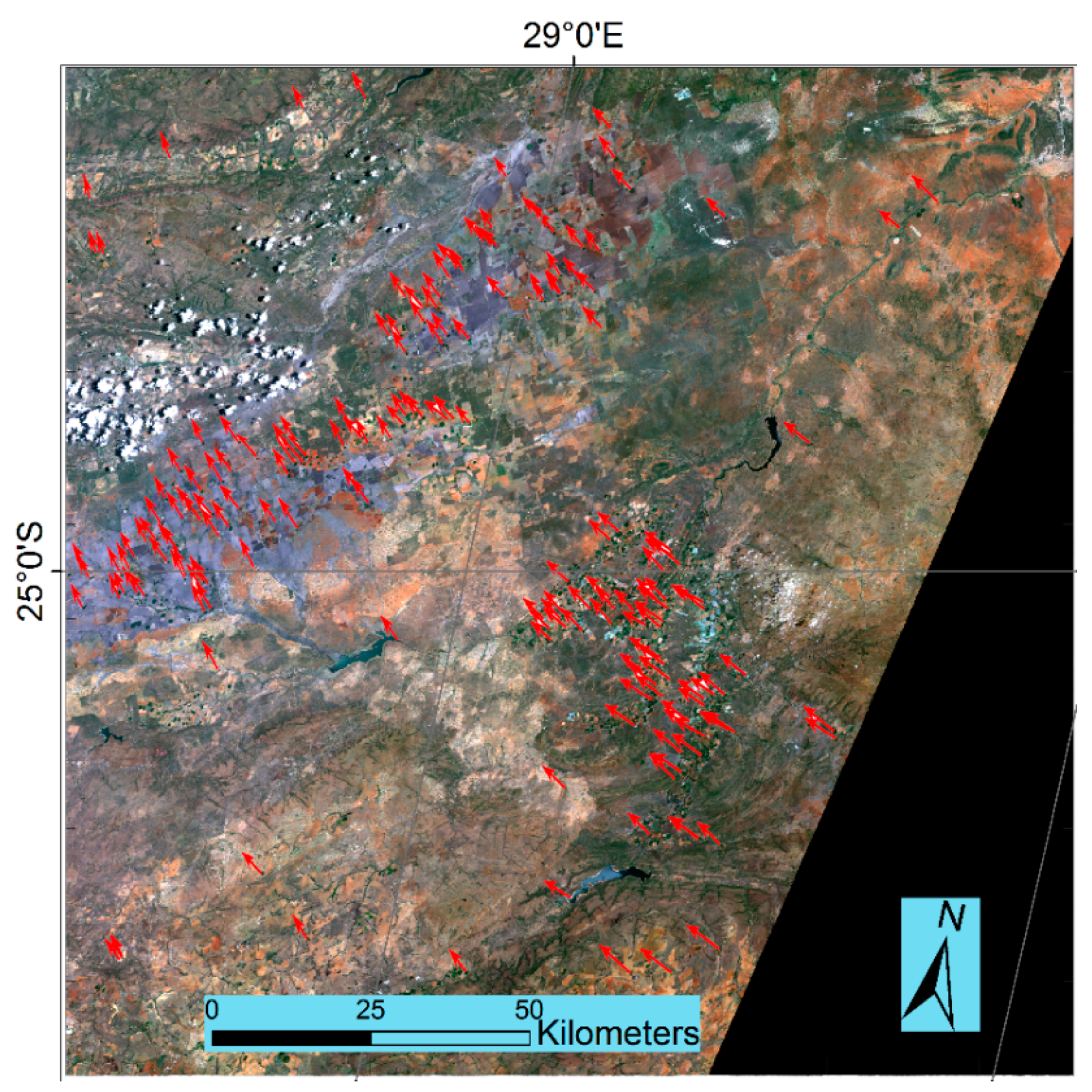
The causes of the observed sensor misregistration are complex. For both Cape Town image pairs, the Landsat-8 image was misaligned in a similar south-west direction relative to the Sentinel-2A images, and for the Limpopo image pair, the Landsat-8 misalignment was in a relative south-east direction. The relatively constant geographical pattern of tie-point-characterized sensor misregistration (
Figure 5 and
Figure 6) supports the hypothesis that the misregistration is due primarily to Landsat GLS path/row specific locational errors [
9,
15]. However, other sources of error may be present, including, for example, geometric relief distortion imposed by digital elevation model inaccuracies, although we observed no elevation related shifts, and inadequate knowledge and/or modeling of the sensor interior and exterior orientation. The detailed study on these error sources is beyond the scope of this paper.
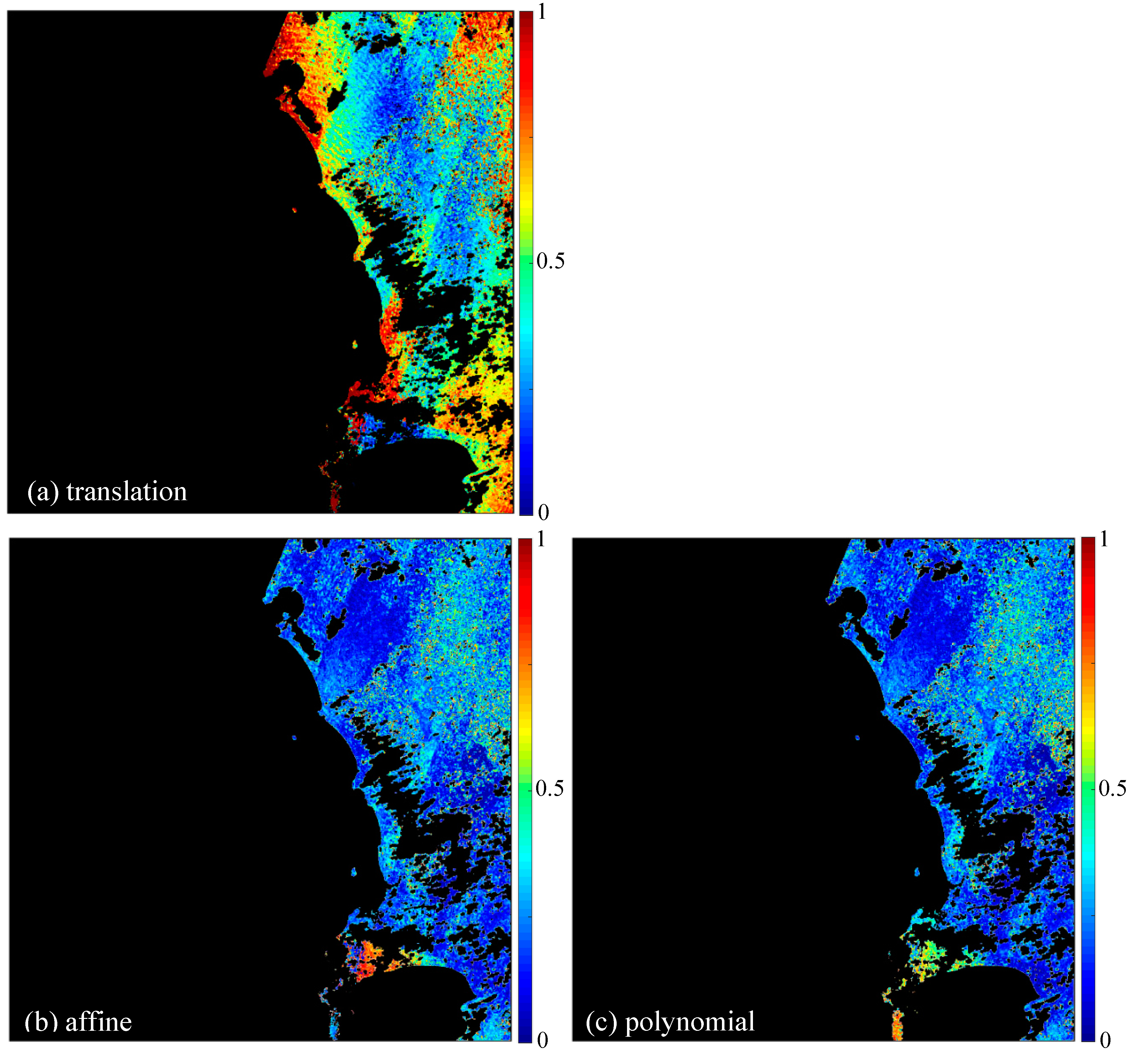
The dense-matching prediction-error maps (
Figure 7 and
Figure 9) exhibited stripes that are aligned approximately parallel to the Sentinel-2A and Landsat-8 track directions. To investigate this further, maps of the x and y axis shifts used to compute the dense-matching prediction errors (Equation (7)) were generated. The results revealed similar patterns for all the study data.
Figure 10a,b show the dense-matching x and y shifts for the Limpopo image pair. The mean
x-shift and
y-shift values were −1.592 and −1.674 pixels, respectively, which is a similar magnitude to the fitted translation transformation coefficients (
Table 7). However, the shifts were unevenly distributed across the tile, with
x-shift and
y-shift standard deviations of 0.473 and 0.237 pixels, respectively. This illustrates why the translation transformation had larger errors than the other transformation types.
Figure 10c shows the Sentinel-2A L1C tile and detector boundaries and
Figure 10d shows the Landsat-8 L1T image boundaries. The dense-matching x and y axis shift maps have apparent zones with edges aligned approximately parallel to the detector and image boundaries. The x and y shifts across the zone boundaries are quite small however, usually less than 0.35 pixels (manually measured). Their cause is likely due to a combination of factors. Small geometric misalignments and/or radiometric calibration differences between the detector banks combined with directional reflectance affects may result in least squares matching differences between the sensor data that will be pronounced along the detector bank boundaries. Along scan directional reflectance variations of several percent are present in 15° field of view Landsat data [
57] and are expected to be greater in wider field of view (20.5°) Sentinel-2 data. Consequently, different sensor viewing geometry and forward and backward scatter sensing conditions may introduce along scan reflectance variations that cause small least squares matching shifts. However, we note that for the data considered, the solar zenith angles were only a few degrees different and the images were sensed in the same scattering direction. The along track shifts evident at the bottom left of
Figure 10 are coincident with the Landsat-8 L1T boundary, evident in
Figure 10d, and may be caused by a different set of Landsat ground controls being used.
Finally, as with all registration methods, the accuracy will be dependent upon the availability of tie-points which will be limited in regions of unstructured terrain and where there are clouds and shadows. However, if the sensor misregistration is predominantly constant for each Landsat WRS path/row location,
i.e., due primarily to GLS path/row locational errors [
9,
15], then tie-points extracted from matching many pairs of approximately contemporaneous Landsat-8 and Sentinel-2A data through time may provide a reliable set of tie-points, from either a “good” pair or a combination of multiple pairs. This will require further assessment on sensor’s multi-temporal intra-misregistration.