Vegetation Indices for Mapping Canopy Foliar Nitrogen in a Mixed Temperate Forest
Abstract
:1. Introduction
2. Materials and Methods
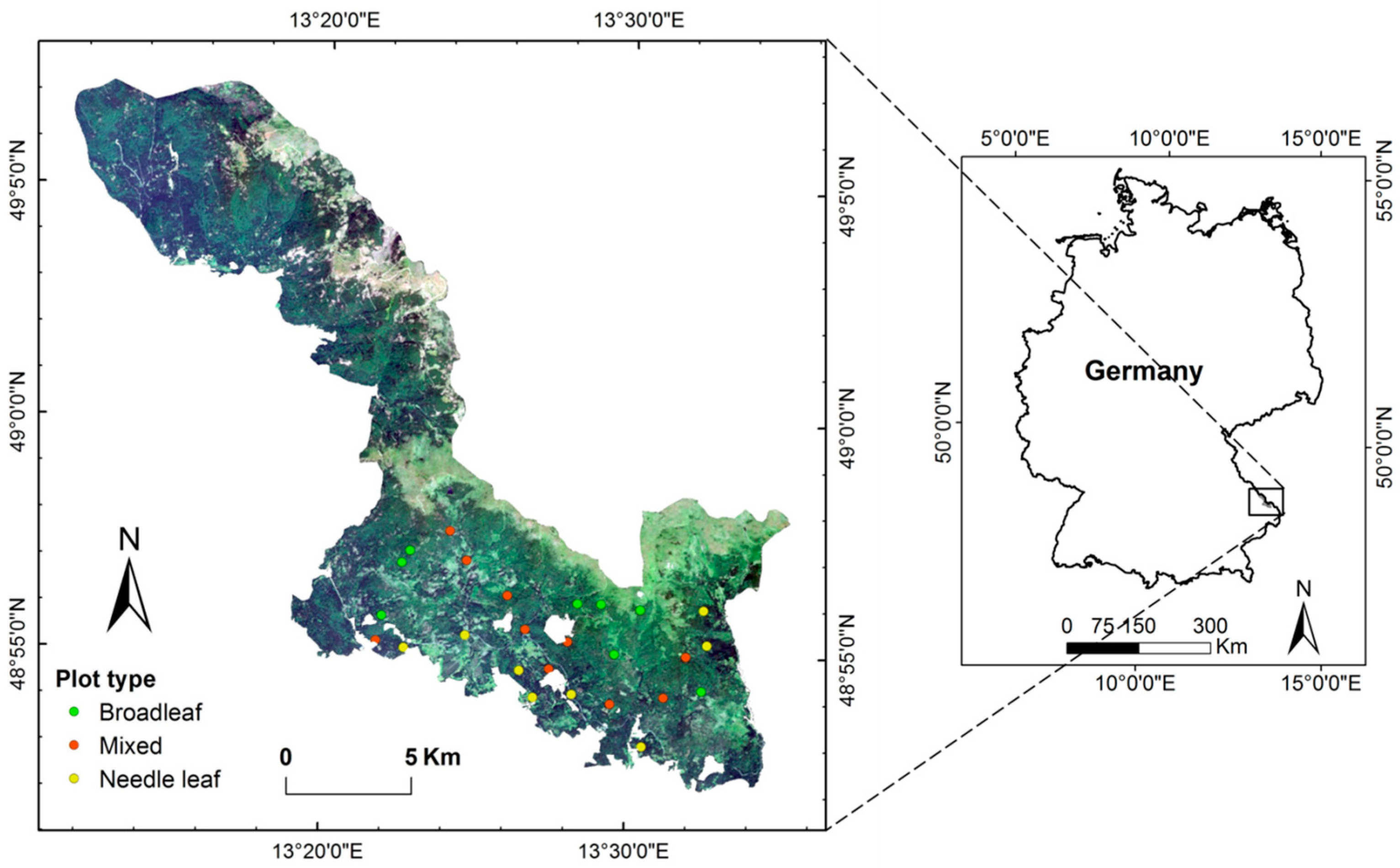
2.1. Study Area and Field Data
2.2. Airborne Hyperspectral Data Collection and Processing
2.3. Vegetation Indices Calculation
2.3.1. Vegetation Indices Related to Nitrogen
2.3.2. Vegetation Indices Related to Structural Parameters
2.3.3. Vegetation Indices Related to Chlorophyll
2.4. Statistical Analysis
3. Results
3.1. Characteristics of in Situ Canopy Foliar Nitrogen and LAI
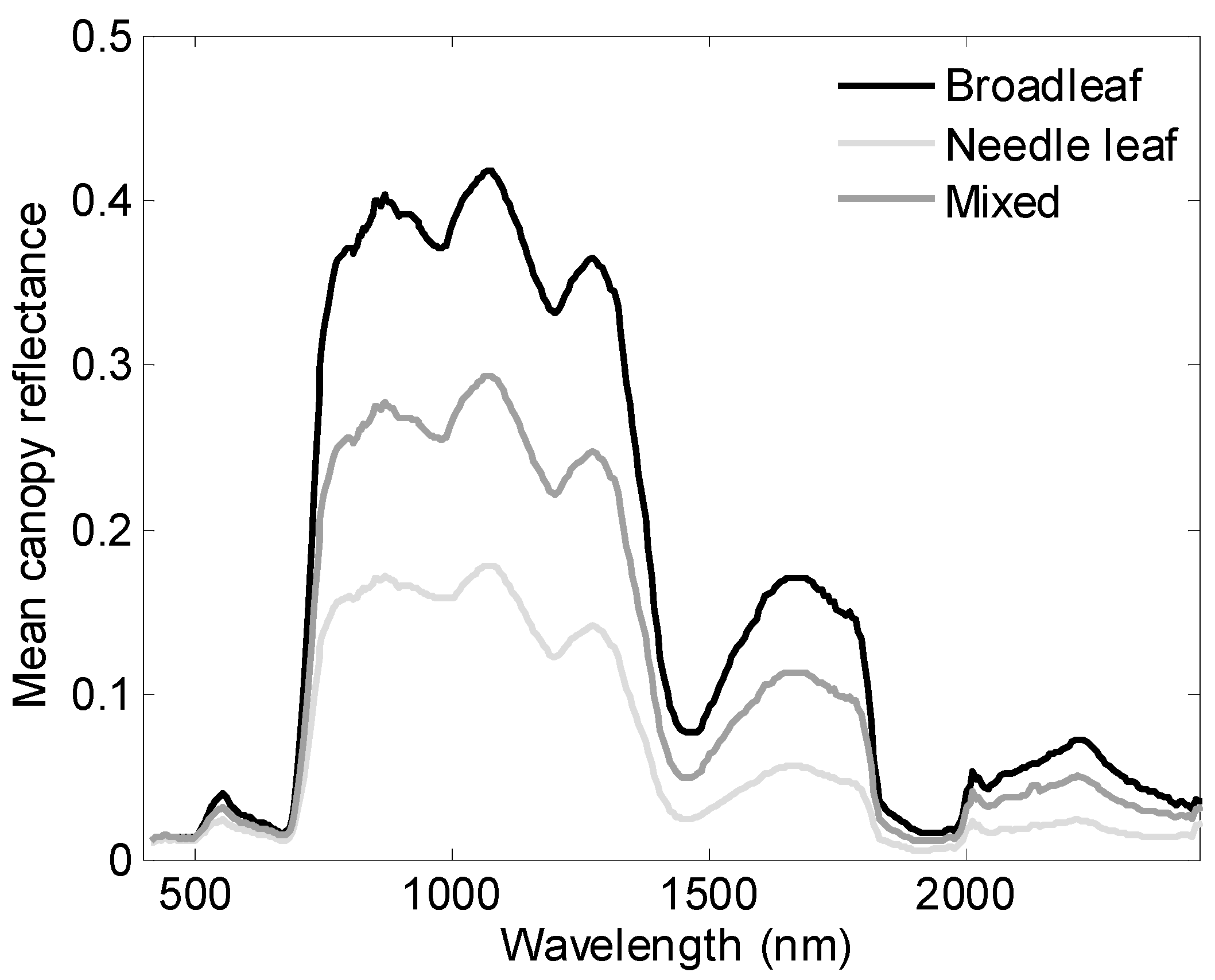
3.2. Variance of Nitrogen by Species and Functional Type
3.3. Performance of Vegetation Indices in %N Estimation
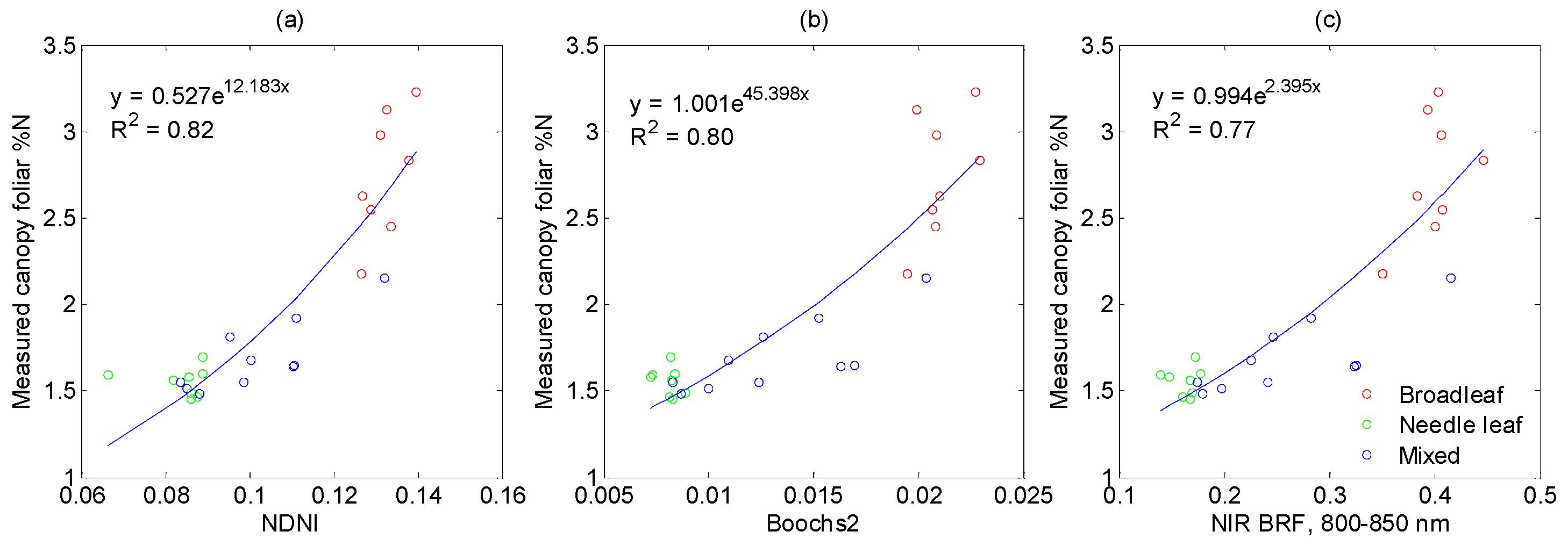
3.3.1. Vegetation Indices Related to Nitrogen
3.3.2. Vegetation Indices Related to Structural Parameters
3.3.3. Vegetation Indices Related to Chlorophyll
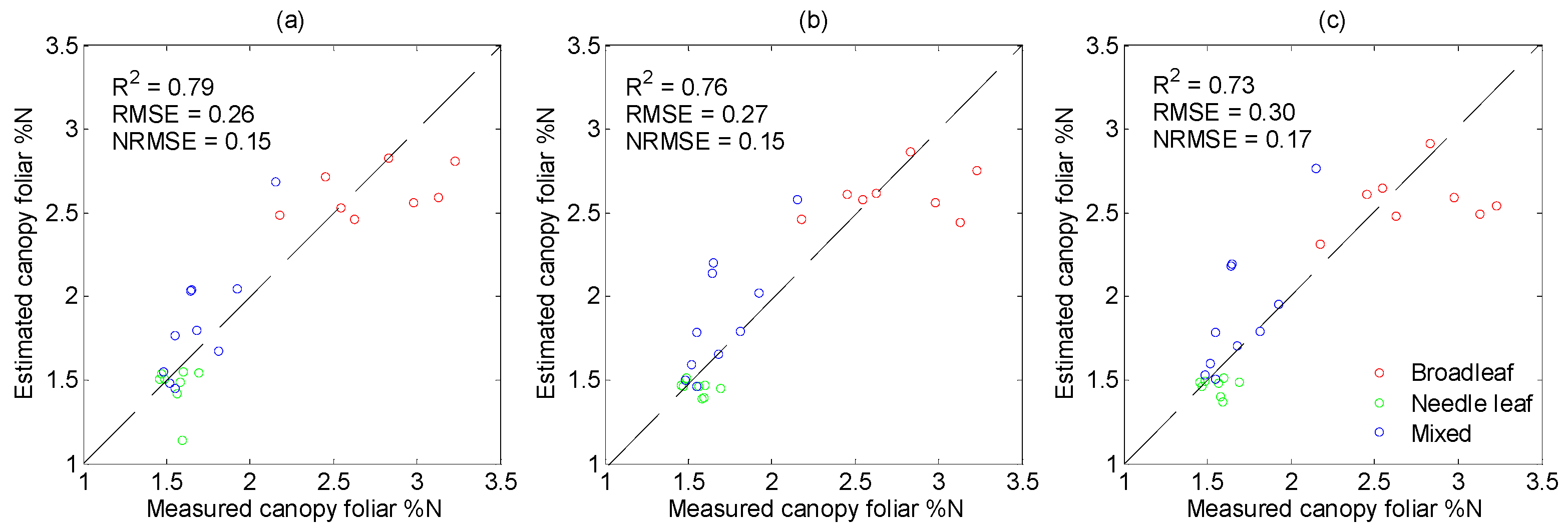
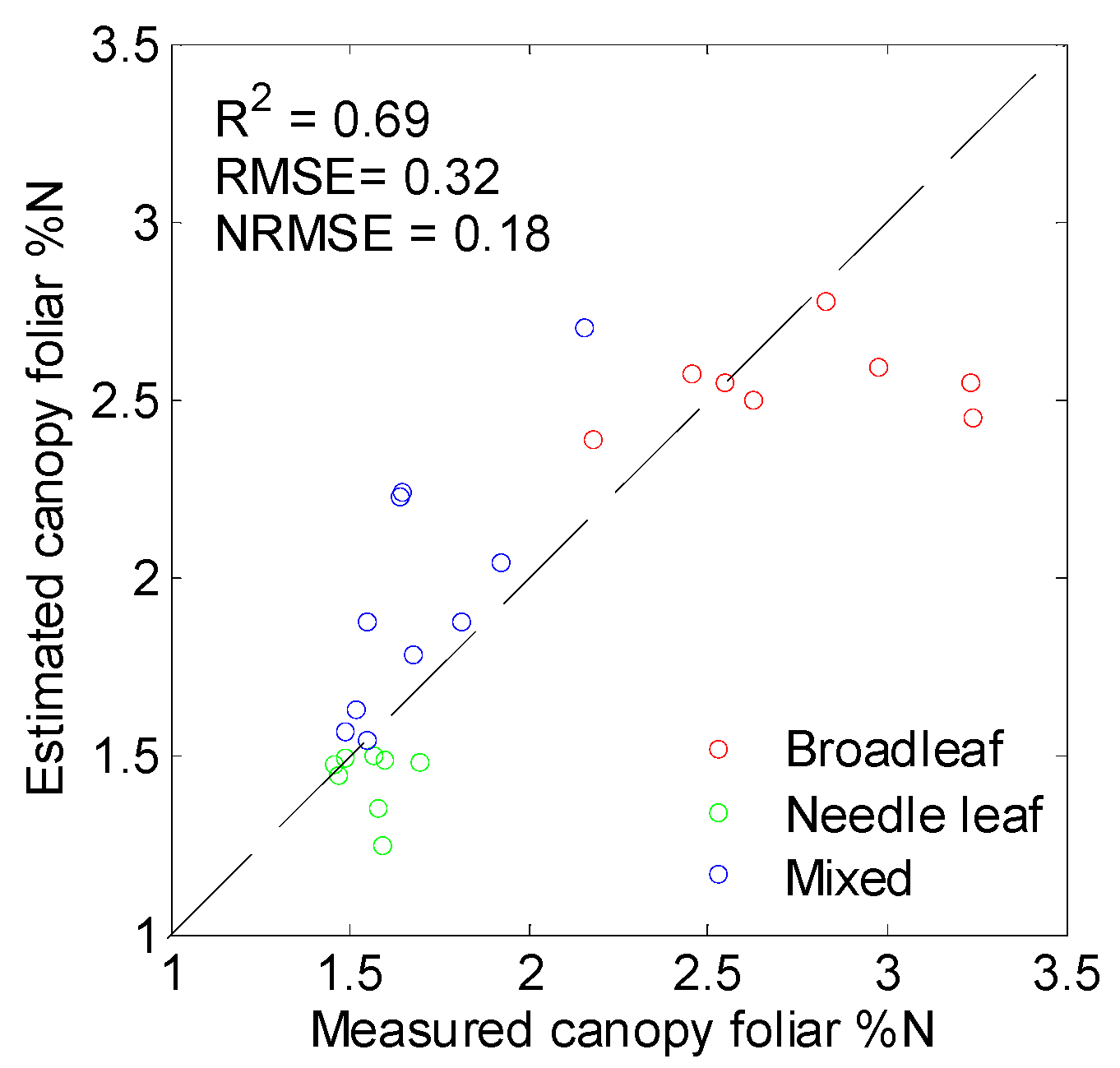
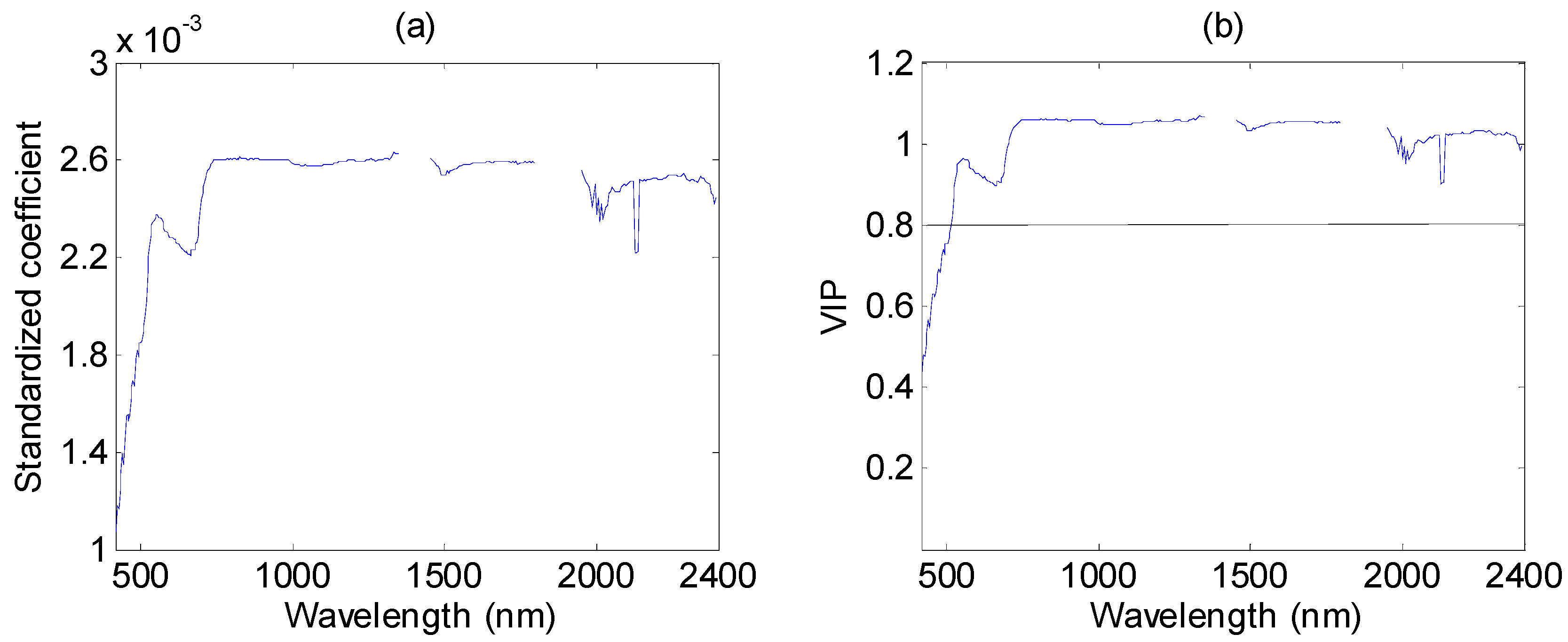
3.4. Performance of PLSR in %N Estimation
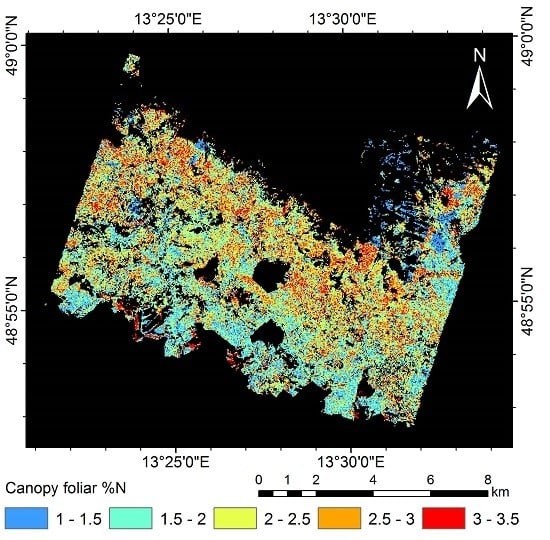
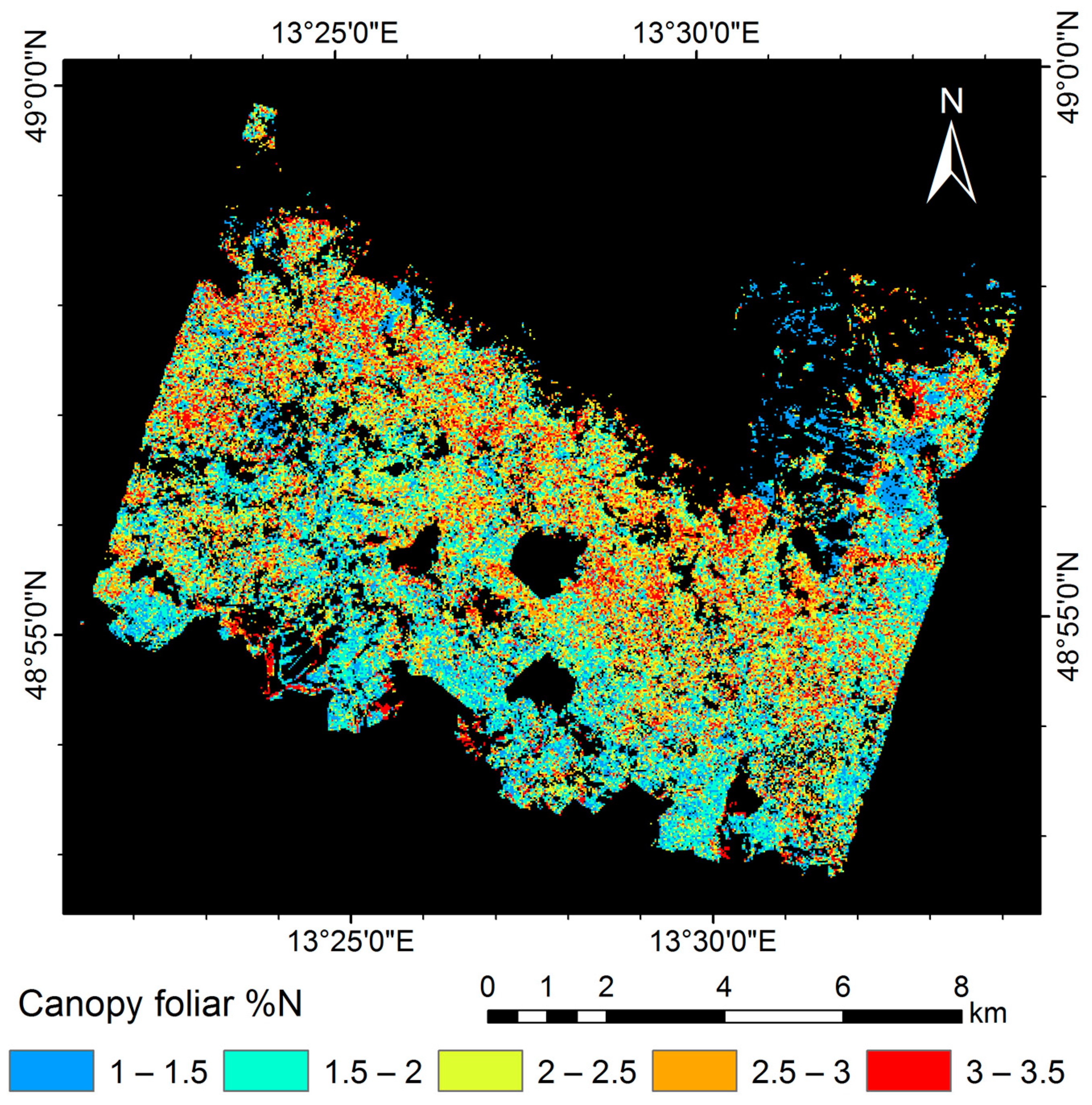
3.5. Mapping Canopy Foliar Nitrogen
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Field, C.; Mooney, H.A. The photosynthesis-nitrogen relationship in wild plants. In On the Economy of Plant Form and Function; Givnish, T.J., Ed.; Cambridge University Press: Cambridge, UK, 1986; pp. 25–55. [Google Scholar]
- Evans, J. Photosynthesis and nitrogen relationships in leaves of C3 plants. Oecologia 1989, 78, 9–19. [Google Scholar] [CrossRef]
- Reich, P.B.; Ellsworth, D.S.; Walters, M.B. Leaf structure (specific leaf area) modulates photosynthesis–nitrogen relations: Evidence from within and across species and functional groups. Funct. Ecol. 1998, 12, 948–958. [Google Scholar] [CrossRef]
- Smith, M.L.; Ollinger, S.V.; Martin, M.E.; Aber, J.D.; Hallett, R.A.; Goodale, C.L. Direct estimation of aboveground forest productivity through hyperspectral remote sensing of canopy nitrogen. Ecol. Appl. 2002, 12, 1286–1302. [Google Scholar] [CrossRef]
- Green, D.S.; Erickson, J.E.; Kruger, E.L. Foliar morphology and canopy nitrogen as predictors of light-use efficiency in terrestrial vegetation. Agric. For. Meteorol. 2003, 115, 163–171. [Google Scholar] [CrossRef]
- Ollinger, S.V.; Smith, M.L. Net primary production and canopy nitrogen in a temperate forest landscape: An analysis using imaging spectroscopy, modeling and field data. Ecosystems 2005, 8, 760–778. [Google Scholar] [CrossRef]
- Ollinger, S.V.; Richardson, A.D.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R.; et al. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [PubMed]
- Sievering, H.; Fernandez, I.; Lee, J.; Hom, J.; Rustad, L. Forest canopy uptake of atmospheric nitrogen deposition at eastern US conifer sites: Carbon storage implications? Glob. Biogeochem. Cycles 2000, 14, 1153–1159. [Google Scholar] [CrossRef]
- Lamarque, J.F.; Kiehl, J.T.; Brasseur, G.P.; Butler, T.; Cameron-Smith, P.; Collins, W.D.; Collins, W.J.; Granier, C.; Hauglustaine, D.; Hess, P.G.; et al. Assessing future nitrogen deposition and carbon cycle feedback using a multimodel approach: Analysis of nitrogen deposition. J. Geophys. Res. Atmos. 2005, 110, 1–21. [Google Scholar] [CrossRef]
- Plummer, S.E. Perspectives on combining ecological process models and remotely sensed data. Ecol. Model. 2000, 129, 169–186. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.; Chen, X.; Luo, G.; Li, L.; Li, X.; Yan, Y.; Shao, H. A spatial-explicit dynamic vegetation model that couples carbon, water, and nitrogen processes for arid and semiarid ecosystems. J. Arid Land 2013, 5, 102–117. [Google Scholar] [CrossRef]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential biodiversity variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental science: Agree on biodiversity metrics to track from space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef] [PubMed]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornellssen, J.H.C.; Diemer, M.; et al. The worldwide leaf economics spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef] [PubMed]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Martin, M.E.; Plourde, L.C.; Ollinger, S.V.; Smith, M.L.; McNeil, B.E. A generalizable method for remote sensing of canopy nitrogen across a wide range of forest ecosystems. Remote Sens. Environ. 2008, 112, 3511–3519. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F. On spectral estimates of fresh leaf biochemistry. Int. J. Remote Sens. 1998, 19, 1283–1297. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-up and model inversion methods with narrowband optical indices for chlorophyll content estimation in closed forest canopies with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400–2500 nm) at leaf and canopy scales. Remote Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Coops, N.C.; Smith, M.L.; Martin, M.E.; Ollinger, S.V. Prediction of eucalypt foliage nitrogen content from satellite-derived hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1338–1346. [Google Scholar] [CrossRef]
- Huang, Z.; Turner, B.J.; Dury, S.J.; Wallis, I.R.; Foley, W.J. Estimating foliage nitrogen concentration from HYMAP data using continuum removal analysis. Remote Sens. Environ. 2004, 93, 18–29. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J.; Buddenbaum, H.; Werner, W.; Schueler, G. Retrieval of chlorophyll and nitrogen in Norway spruce (Picea abies L. Karst.) using imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 17–26. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Schlerf, M.; Mathieu, R.; Heitkönig, I.M.A. Water-removed spectra increase the retrieval accuracy when estimating savanna grass nitrogen and phosphorus concentrations. ISPRS J. Photogramm. Remote Sens. 2011, 66, 408–417. [Google Scholar] [CrossRef]
- Ferwerda, J.G.; Jones, S.D. Continuous wavelet transformations for hyperspectral feature detection. In Progress in Spatial Data Handling; Riedl, A., Kainz, W., Elmes, G.A., Eds.; Springer-Berlin: Heidelberg, Germany, 2006; pp. 167–178. [Google Scholar]
- Asner, G.P.; Martin, R.E. Airborne spectranomics: Mapping canopy chemical and taxonomic diversity in tropical forests. Front. Ecol. Environ. 2008, 7, 269–276. [Google Scholar] [CrossRef]
- Gökkaya, K.; Thomas, V.; Noland, T.L.; McCaughey, H.; Morrison, I.; Treitz, P. Prediction of macronutrients at the canopy level using spaceborne imaging spectroscopy and LiDAR data in a mixedwood boreal forest. Remote Sens. 2015, 7, 9045–9069. [Google Scholar] [CrossRef]
- Singh, A.; Serbin, S.P.; McNeil, B.E.; Kingdon, C.C.; Townsend, P.A. Imaging spectroscopy algorithms for mapping canopy foliar chemical and morphological traits and their uncertainties. Ecol. Appl. 2015, 25, 2180–2197. [Google Scholar] [CrossRef] [PubMed]
- Mutanga, O.; Skidmore, A.K.; Prins, H.H.T. Predicting in situ pasture quality in the Kruger National Park, South Africa, using continuum-removed absorption features. Remote Sens. Environ. 2004, 89, 393–408. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Ferwerda, J.G.; Mutanga, O.; Van Wieren, S.E.; Peel, M.; Grant, R.C.; Prins, H.H.T.; Balcik, F.B.; Venus, V. Forage quality of savannas—Simultaneously mapping foliar protein and polyphenols for trees and grass using hyperspectral imagery. Remote Sens. Environ. 2010, 114, 64–72. [Google Scholar] [CrossRef]
- Pellissier, P.A.; Ollinger, S.V.; Lepine, L.C.; Palace, M.W.; McDowell, W.H. Remote sensing of foliar nitrogen in cultivated grasslands of human dominated landscapes. Remote Sens. Environ. 2015, 167, 88–97. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crops Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Yao, X.; Huang, Y.; Shang, G.; Zhou, C.; Cheng, T.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of six algorithms to monitor wheat leaf nitrogen concentration. Remote Sens. 2015, 7, 14939–14966. [Google Scholar] [CrossRef]
- Miphokasap, P.; Honda, K.; Vaiphasa, C.; Souris, M.; Nagai, M. Estimating canopy nitrogen concentration in sugarcane using field imaging spectroscopy. Remote Sens. 2012, 4, 1651–1670. [Google Scholar] [CrossRef]
- Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral analysis of mangrove foliar chemistry using PLSR and support vector regression. Int. J. Remote Sens. 2013, 34, 1724–1743. [Google Scholar] [CrossRef]
- Zhao, K.; Valle, D.; Popescu, S.; Zhang, X.; Mallick, B. Hyperspectral remote sensing of plant biochemistry using Bayesian model averaging with variable and band selection. Remote Sens. Environ. 2013, 132, 102–119. [Google Scholar] [CrossRef]
- Homolova, L.; Maenovsky, Z.; Clevers, J.; Garcia-Santos, G.; Schaeprnan, M.E. Review of optical-based remote sensing for plant trait mapping. Ecol. Complex. 2013, 15, 1–16. [Google Scholar] [CrossRef]
- Le Maire, G.; Francois, C.; Soudani, K.; Berveiller, D.; Pontailler, J.Y.; Breda, N.; Genet, H.; Davi, H.; Dufrene, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Le Maire, G.; Francois, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Tian, Y.C.; Yao, X.; Yang, J.; Cao, W.X.; Hannaway, D.B.; Zhu, Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground- and space-based hyperspectral reflectance. Field Crops Res. 2011, 120, 299–310. [Google Scholar] [CrossRef]
- Wang, W.; Yao, X.; Yao, X.; Tian, Y.; Liu, X.; Ni, J.; Cao, W.; Zhu, Y. Estimating leaf nitrogen concentration with three-band vegetation indices in rice and wheat. Field Crops Res. 2012, 129, 90–98. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Serrano, L.; Peñuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data: Decomposing biochemical from structural signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mottus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Latorre Carmona, P.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed]
- Ollinger, S.V.; Reich, P.B.; Frolking, S.; Lepine, L.C.; Hollinger, D.Y.; Richardson, A.D. Nitrogen cycling, forest canopy reflectance, and emergent properties of ecosystems. Proc. Natl. Acad. Sci. USA 2013, 110, E2437–E2437. [Google Scholar] [CrossRef] [PubMed]
- Townsend, P.A.; Serbin, S.P.; Kruger, E.L.; Gamon, J.A. Disentangling the contribution of biological and physical properties of leaves and canopies in imaging spectroscopy data. Proc. Natl. Acad. Sci. USA 2013, 110, E1074. [Google Scholar] [CrossRef] [PubMed]
- Ollinger, S. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Martin, R.E.; Ford, A.J.; Metcalfe, D.J.; Liddell, M.J. Leaf chemical and spectral diversity in Australian tropical forests. Ecol. Appl. 2009, 19, 236–253. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Martin, R.E.; Suhaili, A.B. Sources of canopy chemical and spectral diversity in lowland Bornean forest. Ecosystems 2012, 15, 504–517. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Tupayachi, R.; Anderson, C.B.; Sinca, F.; Carranza-Jiménez, L.; Martinez, P. Amazonian functional diversity from forest canopy chemical assembly. Proc. Natl. Acad. Sci. USA 2014. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy vs. field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- McNeil, B.E.; Read, J.M.; Sullivan, T.J.; McDonnell, T.C.; Fernandez, I.J.; Driscoll, C.T. The spatial pattern of nitrogen cycling in the Adirondack Park, New York. Ecol. Appl. 2008, 18, 438–452. [Google Scholar] [CrossRef] [PubMed]
- Gökkaya, K.; Thomas, V.; Noland, T.; McCaughey, H.; Morrison, I.; Treitz, P. Mapping continuous forest type variation by means of correlating remotely sensed metrics to canopy N:P ratio in a boreal mixedwood forest. Appl. Veg. Sci. 2015, 18, 143–157. [Google Scholar] [CrossRef]
- Dahlin, K.M.; Asner, G.P.; Field, C.B. Environmental and community controls on plant canopy chemistry in a Mediterranean-type ecosystem. Proc. Natl. Acad. Sci. USA 2013, 110, 6895–6900. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Walters, M.B.; Ellsworth, D.S. From tropics to tundra: Global convergence in plant functioning. Proc. Natl. Acad. Sci. USA 1997, 94, 13730–13734. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Li, B. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Heurich, M.; Beudert, B.; Rall, H.; Křenová, Z. National parks as model regions for interdisciplinary long-term ecological research: The Bavarian Forest and Šumavá national parks underway to transboundary ecosystem research. In Long-Term Ecological Research; Müller, F., Baessler, C., Schubert, H., Klotz, S., Eds.; Springer Science & Business Media: New York, NY, USA, 2010; pp. 327–344. [Google Scholar]
- Lausch, A.; Heurich, M.; Fahse, L. Spatio-temporal infestation patterns of Ips typographus (L.) in the Bavarian Forest National Park, Germany. Ecol. Indic. 2013, 31, 73–81. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Heiden, U.; Heurich, M.; Wang, T. Leaf nitrogen content indirectly estimated by leaf traits derived from the PROSPECT model. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3172–3182. [Google Scholar] [CrossRef]
- Gower, S.T.; Reich, P.B.; Son, Y. Canopy dynamics and aboveground production of five tree species with different leaf longevities. Tree Physiol. 1993, 12, 327–345. [Google Scholar] [CrossRef] [PubMed]
- Widlowski, J.-L.; Verstraete, M.; Pinty, B.; Gobron, N. Allometric Relationships of Selected European Tree Species: Parametrizations of Tree Architecture for the Purpose of 3-D Canopy Reflectance Models Used in the Interpretation of Remote Sensing: Betula pubescens, Fagus sylvatica, Larix decidua, Picea abies, Pinus sylvestris; EC Joint Research Centre: Ispra, Italy, 2003. [Google Scholar]
- Woodgate, W.; Jones, S.D.; Suarez, L.; Hill, M.J.; Armston, J.D.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. Understanding the variability in ground-based methods for retrieving canopy openness, gap fraction, and leaf area index in diverse forest systems. Agric. For. Meteorol. 2015, 205, 83–95. [Google Scholar] [CrossRef]
- Macfarlane, C. Classification method of mixed pixels does not affect canopy metrics from digital images of forest overstorey. Agric. For. Meteorol. 2011, 151, 833–840. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M.; Fernandes, R.; Deering, D.W.; Conley, A. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agric. For. Meteorol. 2005, 129, 187–207. [Google Scholar] [CrossRef]
- Richter, R.; Schlaepfer, D. Atmospheric/Topographic Correction for Airborne Imagery: ATCOR-4 User Guide; DLR IB 565-02/16; Wessling, Germany, 2016. [Google Scholar]
- Rogge, D.M.; Rivard, B. Iterative spatial filtering for reducing intra-class spectral variability and noise. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010; pp. 1–4.
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R. Spectral polishing of high resolution imaging spectroscopy data. In Proceedings of the 7th SIG-IS Workshop on Imaging Spectroscopy, Edinburgh, UK, 11–13 April 2011; pp. 1–7.
- Ferwerda, J.G.; Skidmore, A.K.; Mutanga, O. Nitrogen detection with hyperspectral normalized ratio indices across multiple plant species. Int. J. Remote Sens. 2005, 26, 4083–4095. [Google Scholar] [CrossRef]
- Mobasheri, M.R.; Rahimzadegan, M. Introduction to protein absorption lines index for relative assessment of green leaves protein content using EO-1 Hyperion datasets. J. Agric. Sci. Technol. 2011, 14, 135–147. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Boochs, F.; Kupfer, G.; Dockter, K.; KÜHbauch, W. Shape of the red edge as vitality indicator for plants. Int. J. Remote Sens. 1990, 11, 1741–1753. [Google Scholar] [CrossRef]
- Smith, R.; Adams, J.; Stephens, D.; Hick, P. Forecasting wheat yield in a Mediterranean-type environment from the NOAA satellite. Aust. J. Agric. Res. 1995, 46, 113–125. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. Angular Dependence of Maize and Sugar Beet VIs from Directional CHRIS/Proba Data; ESRIN: Frascati, Italy, 2006. [Google Scholar]
- Elvidge, C.D.; Chen, Z. Comparison of broad-band and narrow-band red and near-infrared vegetation indices. Remote Sens. Environ. 1995, 54, 38–48. [Google Scholar] [CrossRef]
- Li, P.; Wang, Q. Developing and validating novel hyperspectral indices for leaf area index estimation: Effect of canopy vertical heterogeneity. Ecol. Indic. 2013, 32, 123–130. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K.; van Wieren, S. Discriminating tropical grass (Cenchrus ciliaris) canopies grown under different nitrogen treatments using spectroradiometry. ISPRS J. Photogramm. Remote Sens. 2003, 57, 263–272. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Lepine, L.C.; Ollinger, S.V.; Ouimette, A.P.; Martin, M.E. Examining spectral reflectance features related to foliar nitrogen in forests: Implications for broad-scale nitrogen mapping. Remote Sens. Environ. 2016, 173, 174–186. [Google Scholar] [CrossRef]
- Wold, S. PLS for multivariate linear modeling. In Chemometric Methods in Molecular Design (Methods and Principles in Medicinal Chemistry); de Vaterbeemd, H., Ed.; Verlag-Chemie: Weinheim, Germany, 1984; pp. 195–218. [Google Scholar]
- Clevers, J.G.P.W.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Schlemmer, M.; Gitelson, A.A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Wang, T.; Darvishzadeh, R.; Hearne, J. Applicability of the PROSPECT model for estimating protein and cellulose + lignin in fresh leaves. Remote Sens. Environ. 2015, 168, 205–218. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Omari, K.; White, H.P.; Staenz, K.; King, D.J. Retrieval of forest canopy parameters by inversion of the PROFLAIR leaf-canopy reflectance model using the lut approach. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 715–723. [Google Scholar] [CrossRef]
| Index | Formula | Reference |
|---|---|---|
| 1. Nitrogen Index | ||
| NDNI1510 | [log10(1/R1510) − log10(1/R1680)]/[log10(1/R1510) + log10(1/R1680)] | Serrano et al. [49] |
| NI_Tian | R705/(R717 + R491) | Tian et al. [46] |
| NI_Wang | (R924 − R703 + 2R423)/(R924 + R703 − 2R423) | Wang et al. [47] |
| NI_Ferwerda | (R693 − R1770)/(R693 + R1770) | Ferwerda et al. [75] |
| PALI | Mobasheri and Rahimzadegan [76] | |
| Modified PALI | This study | |
| 2. Structural Index | ||
| NDVI | (R800 − R670)/(R800 + R670) | Tucker [77] |
| RVI | R800/R670 | Jordan [78] |
| TVI | 0.5 [120(R750 − R550) − 200(R670 + R550)] | Broge and Leblanc [79] |
| RDVI | (R800 − R670)/(SQRT(R800 + R670)) | Roujean and Breon [80] |
| MSAVI | 0.5 (2R800 +1 − SQRT((2R800 + 1)2 – 8 (R800 − R670))) | Qi et al. [81] |
| DLAI | R1725 − R970 | le Maire et al. [41] |
| DASF | See Knyazikhin et al. (2013) | Knyazikhin et al. [50] |
| NIR Reflectance | Mean reflectance in the near infrared (800–850 nm) spectral range | Ollinger et al. [7] |
| 3. Canopy Chlorophyll Index | ||
| Boochs | D703 | Boochs et al. [82] |
| Boochs2 | D720 | Boochs et al. [82] |
| DDn | 2R710 − R(710 − ∆) − R(710 + ∆) | le Maire et al. [41] |
| GI (Green Index) | R554/R677 | Smith et al. [83] |
| Green NDVI | (R800 − R550)/(R800 + R550) | Gitelson et al. [84] |
| OSAVI | (1 + 0.16)(R800 − R670)/(R800 + R670 + 0.16) | Rondeaux et al. [85] |
| OSAVI[705,750] | (1 + 0.16)(R750 − R705/(R750 + R705 + 0.16) | Wu et al. [42] |
| MCARI | ((R700 − R670) − 0.2(R700 − R550))(R700/R670) | Daughtry et al. [86] |
| MCARI/OSAVI | MCARI/OSAVI | Haboudane et al. [87] |
| MCARI[705,750] | ((R750 − R705) − 0.2(R750 − R550))(R750/R705) | Wu et al. [42] |
| MCARI/OSAVI[705,750] | MCARI[705,750]/OSAVI[705,750] | Wu et al. [42] |
| TCARI | 3((R700 − R670) − 0.2(R700 − R550)(R700/R670)) | Haboudane et al. [87] |
| TCARI[705,750] | 3((R750 − R705) − 0.2(R750 − R550)(R750/R705)) | Wu et al. [42] |
| TCARI/OSAVI | TCARI/OSAVI | Haboudane et al. [87] |
| TCARI/OSAVI[705,750] | TCARI[705,750]/OSAVI[705,750] | Wu et al. [42] |
| MTCI | (R754 − R709)/(R709 − R681) | Dash and Curran [88] |
| SPVI | 0.4 × 3.7(R800 − R670) − 1.2SQRT((R530 − R670)2 | Vincini et al. [89] |
| Sum_Dr1 | Sum of first derivative reflectance between R625 and R795 | Elvidge and Chen [90] |
| Canopy Foliar %N | LAI | |||||
|---|---|---|---|---|---|---|
| Needle Leaf | Broadleaf | Mixed | Needle Leaf | Broadleaf | Mixed | |
| Min | 1.45 | 2.18 | 1.48 | 3.61 | 2.85 | 2.79 |
| Max | 1.69 | 3.29 | 2.15 | 5.14 | 3.24 | 4.55 |
| Mean | 1.55 | 2.77 | 1.69 | 4.21 | 3.00 | 3.63 |
| SD | 0.09 | 0.39 | 0.20 | 0.46 | 0.14 | 0.39 |
| CV | 0.06 | 0.14 | 0.12 | 0.11 | 0.05 | 0.11 |
| Range | 0.24 | 1.11 | 0.67 | 1.53 | 0.39 | 1.76 |
| Variance (%) | Significance | |
|---|---|---|
| 1. Foliar level | ||
| Species | 91 | p < 0.0001 |
| Functional type | 98 | p < 0.0001 |
| 2. Plot level | ||
| Functional type | 98 | p < 0.0001 |
| Index | R2CV | RMSECV | NRMSECV |
|---|---|---|---|
| 1. Nitrogen index | |||
| NDNI1510 | 0.79 | 0.26 | 0.15 |
| NI_Tian | 0.05 | 0.55 | 0.31 |
| NI_Wang | 0.08 | 0.54 | 0.30 |
| NI_Ferwerda | 0.49 | 0.40 | 0.23 |
| PALI | 0.14 | 0.52 | 0.29 |
| Modified PALI | 0.68 | 0.32 | 0.18 |
| 2. Structural index | |||
| NDVI | 0.57 | 0.37 | 0.21 |
| RVI | 0.59 | 0.36 | 0.20 |
| TVI | 0.62 | 0.35 | 0.19 |
| RDVI | 0.71 | 0.31 | 0.17 |
| MSAVI | 0.71 | 0.30 | 0.17 |
| DLAI | 0.65 | 0.33 | 0.19 |
| DASF | 0.55 | 0.38 | 0.21 |
| NIR Reflectance | 0.73 | 0.30 | 0.17 |
| 3. Canopy chlorophyll index | |||
| Boochs | 0.66 | 0.33 | 0.19 |
| Boochs2 | 0.76 | 0.27 | 0.15 |
| DDn | 0.72 | 0.30 | 0.17 |
| GI (Green Index) | 0.16 | 0.52 | 0.29 |
| Green NDVI | 0.56 | 0.38 | 0.21 |
| OSAVI | 0.67 | 0.32 | 0.18 |
| OSAVI[705,750] | 0.65 | 0.33 | 0.19 |
| MCARI | 0.51 | 0.39 | 0.22 |
| MCARI/OSAVI | 0.38 | 0.45 | 0.25 |
| MCARI[705,750] | 0.67 | 0.32 | 0.18 |
| MCARI/OSAVI[705,750] | 0.68 | 0.32 | 0.18 |
| TCARI | 0.58 | 0.37 | 0.21 |
| TCARI[705,750] | 0.13 | 0.53 | 0.30 |
| TCARI/OSAVI | 0.37 | 0.45 | 0.25 |
| TCARI/OSAVI[705,750] | 0.23 | 0.49 | 0.28 |
| MTCI | 0.03 | 0.56 | 0.31 |
| SPVI | 0.73 | 0.29 | 0.17 |
| Sum_Dr1 | 0.73 | 0.30 | 0.17 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, T.; Darvishzadeh, R.; Skidmore, A.K.; Jones, S.; Suarez, L.; Woodgate, W.; Heiden, U.; Heurich, M.; Hearne, J. Vegetation Indices for Mapping Canopy Foliar Nitrogen in a Mixed Temperate Forest. Remote Sens. 2016, 8, 491. https://doi.org/10.3390/rs8060491
Wang Z, Wang T, Darvishzadeh R, Skidmore AK, Jones S, Suarez L, Woodgate W, Heiden U, Heurich M, Hearne J. Vegetation Indices for Mapping Canopy Foliar Nitrogen in a Mixed Temperate Forest. Remote Sensing. 2016; 8(6):491. https://doi.org/10.3390/rs8060491
Chicago/Turabian StyleWang, Zhihui, Tiejun Wang, Roshanak Darvishzadeh, Andrew K. Skidmore, Simon Jones, Lola Suarez, William Woodgate, Uta Heiden, Marco Heurich, and John Hearne. 2016. "Vegetation Indices for Mapping Canopy Foliar Nitrogen in a Mixed Temperate Forest" Remote Sensing 8, no. 6: 491. https://doi.org/10.3390/rs8060491
APA StyleWang, Z., Wang, T., Darvishzadeh, R., Skidmore, A. K., Jones, S., Suarez, L., Woodgate, W., Heiden, U., Heurich, M., & Hearne, J. (2016). Vegetation Indices for Mapping Canopy Foliar Nitrogen in a Mixed Temperate Forest. Remote Sensing, 8(6), 491. https://doi.org/10.3390/rs8060491