1. Introduction and Background
Multi-temporal images acquired by optical [
1] or radar remote sensing sensors [
2] are routinely applied to the detection of changes on the Earth’s surface. As both of these two sensor types have their own imaging and sensitivity characteristics, their performance in change detection varies with the properties of the changing surface features [
3]. In recent years, synthetic aperture radar (SAR) data have gained increasing importance in change detection applications, because SAR is an active sensor, operating without regard to weather, smoke, cloud cover, or daylight [
4]. So SAR has shown to be a valuable data source for the detection of changes related to river ice breakup [
5], earthquake damage [
6], oil spill detection [
7], flood [
8], and forest growth assessment [
9].
In this paper we are interested in developing an unsupervised change detection method from series of SAR images. Despite extensive research that was dedicated to this topic throughout the last decade [
7], automation and robust change detection from a series of SAR images remains difficult for the following reasons: (A) Due to the complicated nature of the surface backscatter response in SAR data, most SAR-based change detection methods require repeated acquisitions from near-identical vantage points. These repeated acquisitions provide a static background against which surface change can be identified with reasonable performance [
10]. This requirement severely limits the temporal sampling that can be achieved with modern SAR sensors with revisit times in the order of tens of days, and strongly limits the relevance of the method for many dynamic phenomena; (B) The multiplicative speckle statistic associated with SAR images limits the change detection performance because it renders the identification of a suitable detection threshold difficult and it adds noise to the detection result; (C) The lack of automatic and adaptive techniques for the definition of change detection thresholds has hindered the development of a fully automatic change detection approach. Finally; (D) the lack of accuracy in delineating the boundary of changed regions has limited the performance of SAR data for applications that require high location accuracy of change information.
Most of the recently proposed SAR-based change detection techniques utilize the concept of ratio or difference images for suppressing background information and enhancing change information. Published methods differ in their approach to extracting a final binary change detection map from the image ratio or difference data. In [
1], two automatic unsupervised approaches based on Bayesian inferencing were proposed for the analysis of the difference image data. The first approach aims to select an adaptive decision threshold to minimize the overall change detection error, using the assumption that the pixels of the change map are spatially independent and that the gray value probability density function (PDF) of the difference image map is composed of two Gaussian distributions representing a change and a no-change class. This approach was further extended in [
11,
12] by adding an expectation-maximization (EM) algorithm to estimate the statistical parameters of the two Gaussian components. The second approach in [
1], which utilizes a Markov random field (MRF) model, is taking into account contextual information when analyzing the change map.
In [
13], an MRF is used to model noiseless images for an optimal change image using the maximum
a posteriori probability computation and the simulated annealing (SA) algorithm. The SA algorithm generates a random sequence of change images, such that a new configuration is established, which depends only on the previous change image and observed images by using the Gibbs sampling procedure [
13].
A computationally efficient approach for unsupervised change detection is proposed in [
14]. The approach initially start by generating an h × h non-overlapping image block from the difference image. Eigenvector space is created using Principal Component Analysis (PCA) on the h × h non-overlapping image blocks. In addition, a feature vector space over the entire difference image is created by projecting overlapping h × h data blocks around each pixel onto eigenvector space. Furthermore, a k-means algorithm is employed to cluster the feature vector space into two clusters and assigns each pixel in the final change detection map to the cluster that minimizes the Euclidean distance between the pixel’s feature vector and the mean feature vector of clusters [
14].
Several recent publications have utilized wavelet techniques for change detection from SAR. Analyzing an image in the wavelet domain helps to reduce the problems caused by the speckle noise. Wavelet domain analysis has been applied to unsupervised change detection for SAR images [
15,
16,
17,
18]. In [
15], a two-dimensional discrete stationary wavelet transform (2D-SWT) was applied to decompose SAR ratio images into different scale-dependent images, each of which is characterized by a tradeoff between speckle noise suppression and preservation of image details. The undecimated discrete wavelet transform (UDWT) was proposed by [
16] to decompose the difference image. For each pixel in the difference image, a feature vector is extracted by locally sampling the data from the multiresolution representation of the difference image [
16]. The final change detection map is obtained using a binary k-means algorithm to cluster the multi-scale feature vectors, while obtaining two disjoint classes: change and no-change. Individual decompositions of each input image using the dual-tree complex wavelet transform (DT-CWT) are used in [
17]. Each input image is decomposed into a single low-pass band and six directionally-oriented high-pass bands at each level of decomposition. The DT-CWT coefficient difference resulting from the comparison of the six high-pass bands of each input image determines classification of either change or no-change classes, creating a binary change detection map for each band. These detection maps are then merged into a final change detection map using inter-scale and intra-scale fusion. The number of decomposition scales (levels) for this method must be determined in advance. This method boasts high performance and robust results, but has a high computational cost. In [
18], a region-based active contour model with UDWT was applied to a SAR difference image for segmenting the difference image into change and no-change classes. More recently, [
19] used a curvelet-based change detection algorithm to automatically extract changes from SAR difference images.
Even though these papers have provided a solution to a subset of the limitations highlighted above, not all the limitations are solved in a single paper. The work done by [
1,
11,
12] does not provide an effective way to select the number of scales needed for the EM algorithm in order to avoid over- or under-estimation of the classification. Also, the noise filtering methods employed do not preserve the detailed outline of a change feature. The disadvantages of the method in [
13] are its high computational complexity and reduced performance in the presence of speckle noise. Although the method in [
14] achieves a good result with low computational cost, the performance of the employed PCA algorithm decreases when the data is highly nonlinear. While [
15,
16,
17,
18,
19] provided promising results in a heterogeneous image, the various methods have several disadvantages. They do not consider image acquisitions from multiple geometry, are not fully preserving the outline of the changed regions, and require manual selection of detection thresholds.
To improve upon previous work, we developed a change detection approach that is automatic, more robust in detecting surface change across a range of spatial scales, and efficiently preserves the boundaries of change regions. In response to the previously identified limitation (A), we utilize modern methods for radiometric terrain correction (RTC) [
10,
20,
21] to mitigate radiometric differences between SAR images acquired from different geometries (e.g., from neighboring tracks). We show in this paper that the application of RTC technology allows combining multi-geometry SAR data into joint change detection procedures with little reduction in performance. Thus, we show that the addition of RTC results in improved temporal sampling with change detection information and in an increased relevance of SAR for monitoring dynamic phenomena.
To reduce the effects of speckle on image classification (limitation (B)), we integrate several recent image processing developments in our approach: We use modern non-local filtering methods [
22] to effectively suppress noise while preserving most relevant image details. Similarly, we perform a multi-scale decomposition of the input images to generate image instances with varying resolutions and signal-to-noise ratios. We use a 2D-SWT in our approach to conduct this decomposition.
To fully automate the classification operations required in the multi-scale change detection approach (limitation (C)), we model the probability density function of the change map at each resolution level as a sum of two or more Gaussian distributions (similar to [
11]). We developed an automatic method to identify the number of Gaussian processes that make up our data and then use probabilistic Bayesian inferencing with EM algorithm and mathematical morphology to optimally separate these processes.
Finally, to accurately delineate the boundary of the changed region (limitation (D)), we utilize measurement level fusion techniques. These techniques used the posterior probability of each class at each multi-scale image to compose a final change detection map. Here we tested five different techniques including (i) product rule fusion; (ii) sum rule fusion; (iii) max rule fusion; (iv) min rule fusion; and (v) majority voting rule fusion.
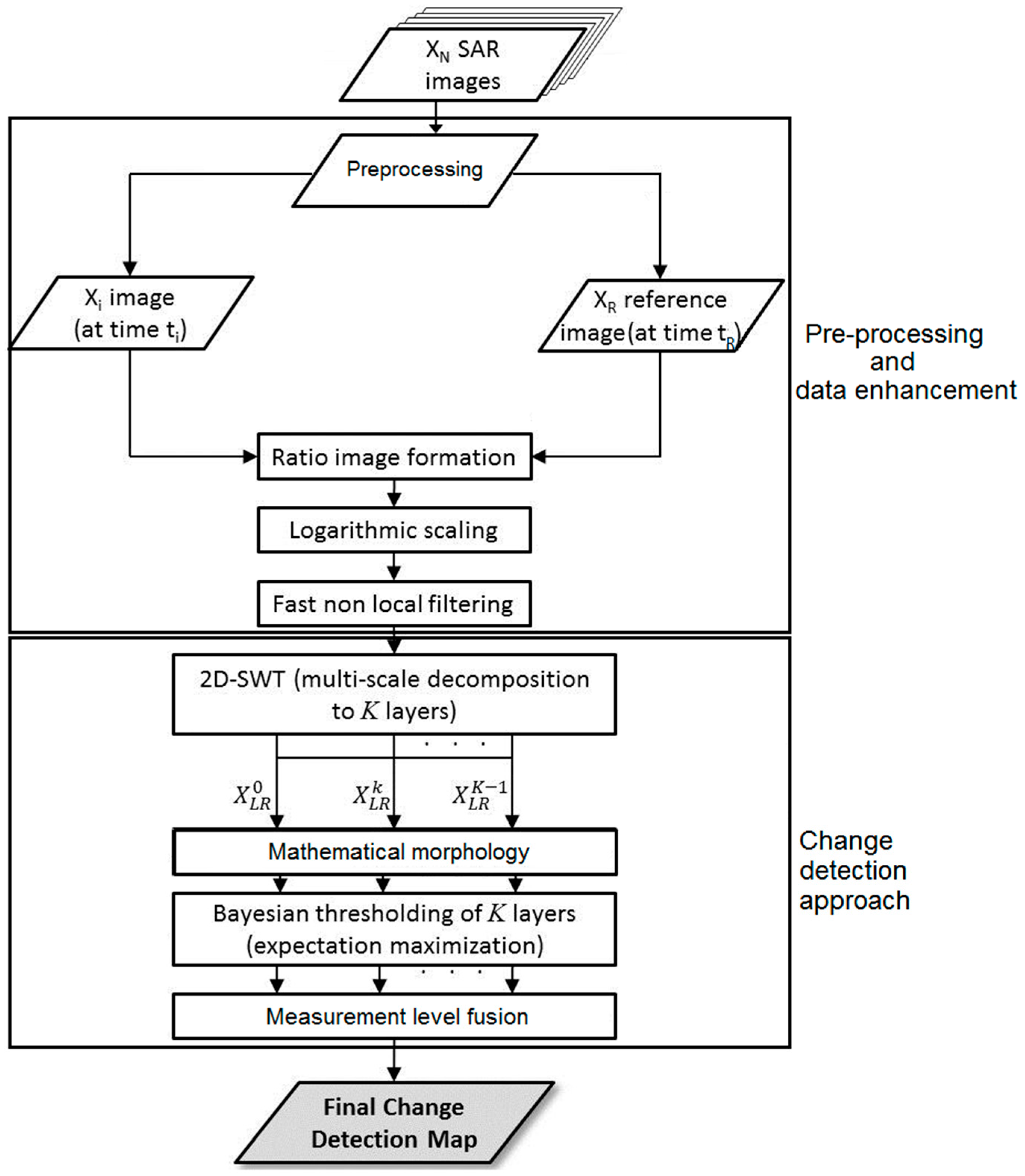
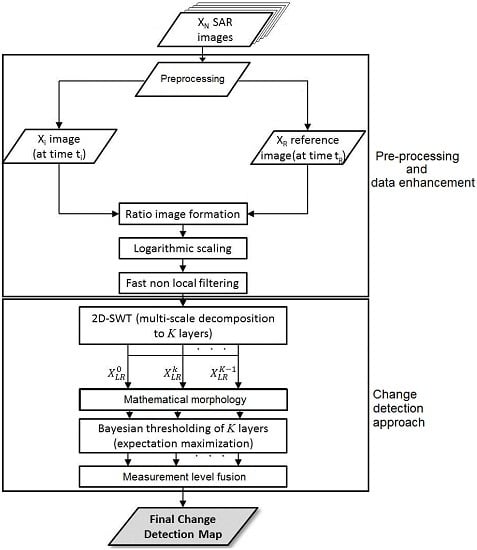
These individual methods are combined in a multi-step change detection approach consisting of a pre-processing step, a data enhancement and filtering step, and the application of the multi-scale change detection algorithm. The details of the proposed approach are described in
Section 2. A performance assessment using a synthetic dataset and an application to wildfire mapping is shown in
Section 3 and
Section 4, respectively. A summary of the presented work is shown in
Section 5.
2. Change Detection Methodology
The work presented here is motivated by the challenges associated with change detection and the desire to develop an improved algorithm for unsupervised change detection in SAR images that can provide change information at high temporal sampling rates. We aim at using information at different resolution levels to obtain high accuracy change detection maps in both heterogeneous and homogeneous regions, contributing to a change detection method that is applicable to a wide range of change situations. To achieve this goal, a multi-step processing workflow was developed that is presented in
Figure 1. The overall contribution of our methodology has two components. First, we developed a set of new techniques that are utilized within our change detection workflow to streamline processing and improve detection performance. As part of these techniques we (1) developed an efficient way to improve classification performance by combining EM algorithms with mathematical morphology—this is a novel contribution to this field of research; (2) we integrated a low computational complexity way to achieve high accuracy in preserving the boundary of changed regions using measurement level fusion techniques; and (3) we combine modern non-local filtering and 2D-SWT to provide robustness against noise. The second contribution comes from a novel way of combining our own technology with other published processing procedures to arrive at a new, efficient and highly flexible change detection workflow that can be applied to a wide range of change detection problems.
It is worth mentioning that the automatic process of our approach requires some parameters to be set beforehand. The parameters that need to be set include (i) the neighborhood size of the filtering step; (ii) the number of multi-scale decomposition levels; (iii) the structuring element of the morphological filter; and, finally, (iv) the maximum number of allowed change classes. Please note that while we identified optimal settings for these parameters, we found that the performance of our algorithm does not critically depend on the exact choice for these variables. This is true for the following reasons: (i) as non-local means filtering is conducted very early in the workflow, the impact of changes in the neighborhood size is mitigated by subsequent processing steps such as multi-scale decomposition and the application of mathematical morphology. Hence, we found that varying the neighborhood size from its optimal value changed system performance only slowly; (ii) in empirical tests it was found that using six decomposition levels was a good compromise between processing speed and classification accuracy. Adding additional levels (beyond six) did not result in significant performance improvement but added computational cost. Reducing the number of layers leads to a slow decrease of change detection performance, yet this reduction of performance does not become significant unless the number of bands drops below four; (iii) from an analysis of a broad range of data from different change detection projects we found (1) that a 20 × 20 pixel-sized structuring element of the morphological filter led to the most consistent results; and (2) that change detection performance changed slowly with deviation from the 20 pixel setting. Hence, while 20 pixels was found to be optimal, the exact choice of the window size is not critical for change detection success; finally, (iv) the maximum number of allowable change classes is a very uncritical variable as it merely sets an upper bound for a subsequent algorithm that automatically determines the number of distinguishable classes in a data set (see
Section 2.3.3). By presetting this variable to 20 classes we ensure that almost all real life change detection scenarios are captured. There is no need to change this variable unless unusually complex change detection situations with more than 20 radiometrically distinguishable change features are expected
2.1. SAR Data Pre-Processing
The ultimate goal of the pre-processing step is to perform image normalization,
i.e., to suppress all image signals other than surface change that may introduce radiometric differences between the acquisitions used in the change detection analysis. Such signals are largely related to (i) seasonal growth or (ii) topographic effects such as terrain undulation that arise if images were not acquired from near-identical vantage points. In order to enable a joint change detection analysis of SAR amplitude images acquired from different observation geometries, we attempt to mitigate relative geometric and radiometric distortions. In a calibrated SAR image, the radar cross-section (RCS) of a pixel can be modeled as [
4]:
where
is the (incidence angle–dependent) surface area covered by a pixel,
is the local incidence angle, and
is the normalized RCS. According to (1), images acquired from different geometries will differ due to the look angle dependence of both
and
.
In areas that are dominated by rough surface scattering and for moderate differences
of observation geometries, we can often assume that
[
4]. Under these conditions, the geometric dependence of
can largely be removed by correcting for
. This correction is called radiometric terrain correction [
20], which is completed by the following steps:
In the first step, geometric image distortions related to the non-nadir image geometry are removed by applying a “geometric terrain correction” step [
10] using a digital elevation model (DEM).
Secondly, to remove radiometric differences between images, we use radiometric terrain normalization [
10]. This normalization also utilizes a DEM to estimate, pixel by pixel, and compensate
, for the radiometric distortions.
In areas dominated by rough surface scattering, the application of RTC allows for combining SAR data acquired from moderately different incidence angles into joint change detection procedures with little reduction in performance. Hence, it can lead to significant improvements in the temporal sampling with change detection data.
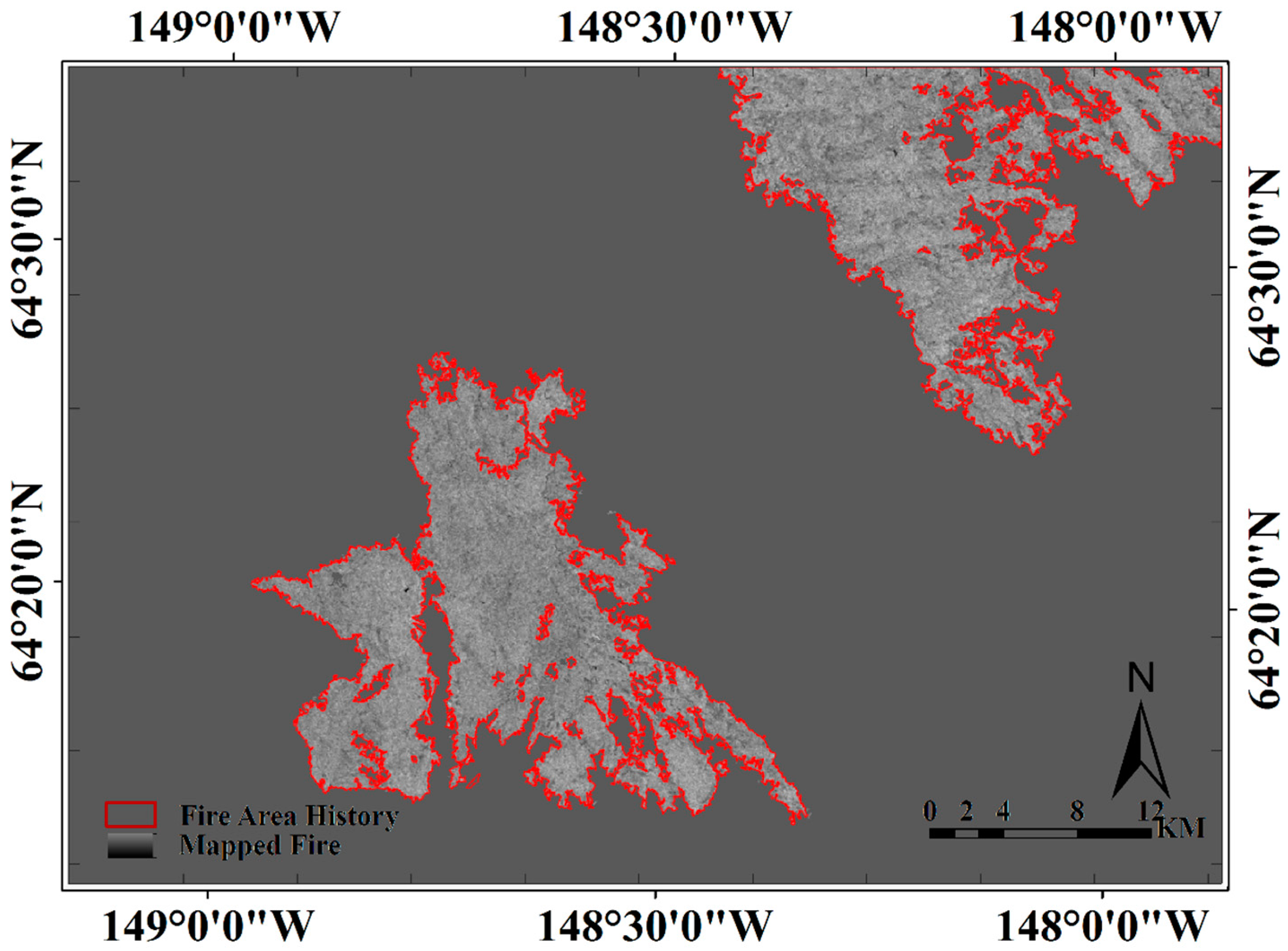
An example of the effect of geometric and radiometric terrain correction is shown in
Figure 2.
Figure 2a shows an original ALOS PALSAR image over the Tanana Flats region in Alaska while the image after geometric and radiometric terrain correction is presented in
Figure 2b. The normalized data is now largely free of geometric influences, reducing differences between images acquired from different geometries and enhancing the performance of change detection from multi-geometry data.
It is worth mentioning that the RTC utilized in our approach is most effective when dealing with natural environments that are dominated by rough surface scattering. For these target types, the surface scattering properties change slowly with incidence angle and differences in measured radar brightness are dominated by geometric effects. However, RTC will be less useful for areas dominated by targets with very oriented scattering characteristics (e.g., urban environments). For these regions, RTC correction may not lead to significant reduction of radiometric differences between images from different incidence angles. Furthermore, limitations exist for regions with complex small-scale topography, if this topography is not sufficiently captured in the available DEM.
2.2. Data Enhancement
2.2.1. Logarithmic Scaling and Ratio Image Formation
To suppress image background structure and improve the detectability of potential surface changes from SAR data, a ratio image is formed between a newly acquired image
Xi and a reference image
XR. Using ratio images in change detection was first suggested by [
3] and has since been the basis of many change detection methods [
12,
23,
24]. The reference image
XR and image
Xi are selected such that the effects of seasonal variations as well as spurious changes of surface reflectivity on the change detection product are minimized. Before ratio image formation, all data are geometrically and radiometrically calibrated following the approach in
Section 2.1. The resulting ratio image can then be modeled as [
3]:
where
is the observed intensity ratio,
is a multiplicative speckle contribution, and
is the underlying true intensity ratio. The observed intensity ratio image has the disadvantage that the multiplicative noise is difficult to remove. Therefore, a logarithmic scaling is applied to
, resulting in:
The application of logarithmic scaling and ratio image formation helps to transform our data into a near normal distribution which closely resembles a Gaussian distribution. To suppress the now-additive noise in the log-scaled ratio image , we applied a fast non-local means filtering procedure.
2.2.2. Fast Non-Local Means Filtering Approach
As we are interested in developing a flexible change detection method that can be applied to a wide range of change situations, we are interested in preserving the original image resolution when filtering the data. Non-local means filters are ideal for this task as they identify similar image patches in a dataset and use those patches to optimally suppress noise without sacrificing image resolution. The non-local means concept was first published in [
25]. The algorithm uses redundant information to reduce noise, and restores the original noise-free image by performing a weighted average of pixel values, considering the spatial and intensity similarities between pixels [
22]. Given the log-ratio image
(see
Section 2.2), we interpret its noisy content over a discrete regular grid,
.
The restored image content
at pixel
is then computed as a weighted average of all of the pixels in the image, according to:
The weight
measures the similarities between two pixels
and
and is given by:
where
controls the amount of filtering,
is the normalization constant, and
is the weighted Euclidean distance (gray-value distance) of two neighborhood pixels (
and
) that are of equal size. According to [
25], the similarity between two neighborhood pixels (
and
) is based on the similarity of their intensity gray level. Neighborhoods having similar gray-level pixels will have larger weights in the average. To compute the similarity of the intensity gray level, we estimated
as follow:
The standard deviation of the Gaussian kernel is denoted as . To ensure that the averaging in Equations (5)–(7) is more robust, we set the neighborhood size for weight computation to 5 × 5 pixels and the size of the searching region to 13 × 13 pixels. We referred to as the searching window. The optimal neighborhood sizes were determined in empirical tests. These tests also showed that the choice of neighborhood size does not critically affect the filtering performance. We implemented the modern non-local filtering methods to effectively suppress the noise while preserving most relevant details in the image.
2.3. Change Detection Approach
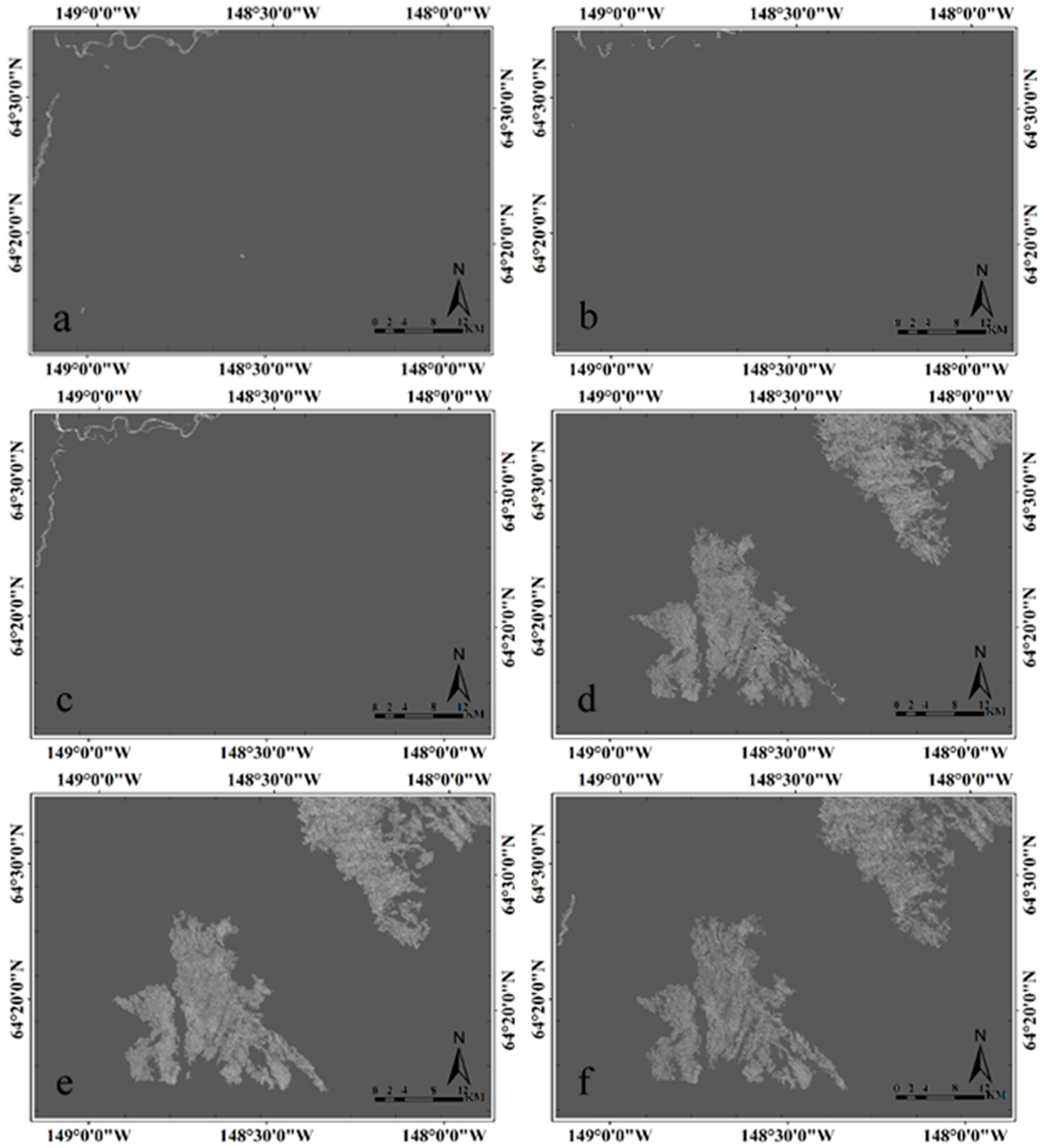
The workflow of our change detection approach is shown in the lower frame of the sketch in
Figure 1 and includes three key elements. In an initial step, a multi-scale decomposition of the input ratio images is conducted using a 2D-SWT and resulting in
image instances. Secondly, a multi-scale classification is performed at each of the
levels, resulting in
classification results per pixel. In our approach, the classifications are performed automatically and adaptively using an EM algorithm with mathematical morphology. Finally, in a third step, we conduct a measurement level fusion of the classification results to enhance the performance of our change detection.
2.3.1. Multi-Scale Decomposition
As previously mentioned, often our ability to detect change in SAR images is limited by substantial noise in full resolution SAR data. Here, we utilize multi-scale decomposition of our input images to generate image instances with varying resolutions and signal-to-noise ratios, and also to further reduce residual noise that remains after an initial non-local means filtering algorithm (
Section 2.2) was applied.
Multi-scale decomposition is an elegant way to optimize noise reduction while preserving the desired geometric detail [
2]. In our approach, 2D-SWTs are used to decompose the log-ratio images [
26].
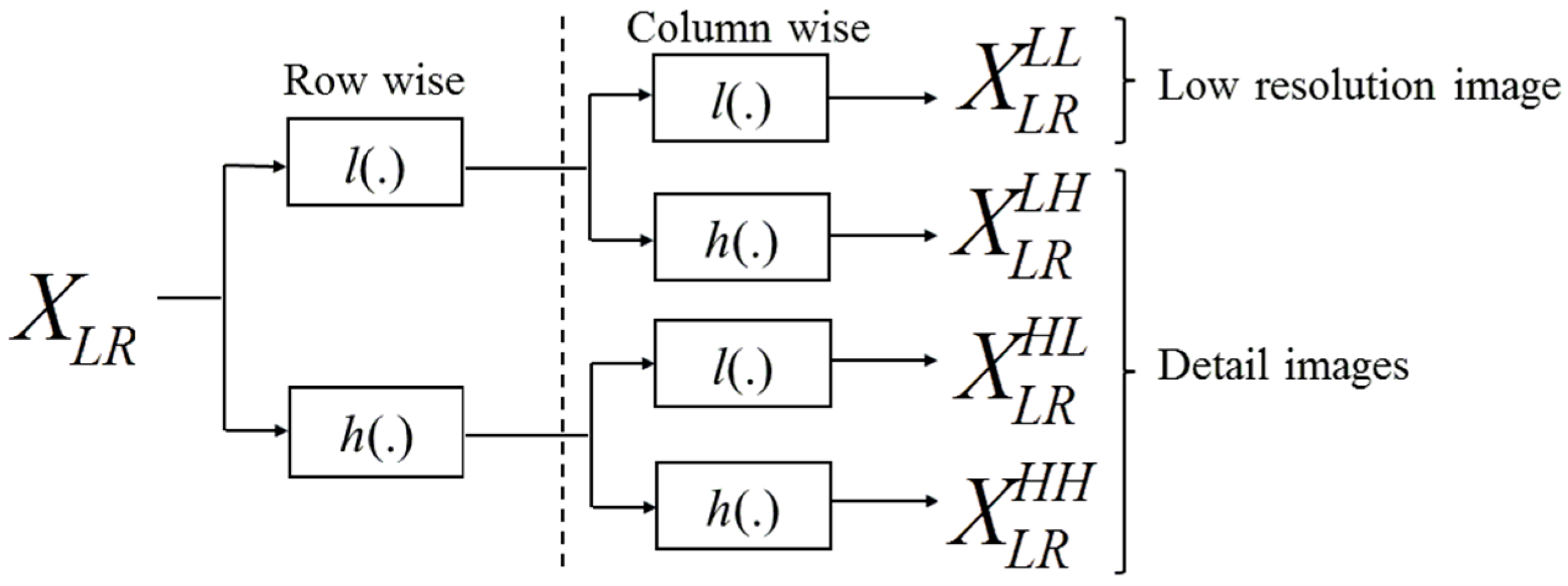
Figure 3 shows that in our implementation of the wavelet decomposition we apply a set of high-pass and low-pass filters first to the rows and then to the columns of an input image at resolution level
, resulting in four decomposition images at resolution level
. The four decomposition images include (1) a lower resolution image
and (2) three high-frequency detail images (
,
, and
), where the superscripts
,
,
,
indicate in which order low-pass (
) and high-pass (
) filters were applied.
We chose the discrete stationary wavelet transform () over the discrete wavelet transform (), as the is computationally more efficient, shift invariant, and un-decimated ( adjusts the filters (up-sampling) at each level by padding them with zero in order to preserve the image size). To gain a greater flexibility in the construction of wavelet bases, we select a wavelet decomposition filter from the biorthogonal wavelet family. The biorthogonal wavelet was selected because of its symmetric capabilities, which is often desirable since it exhibits the property of linear phase, which is needed for image reconstruction. Another reason for using the biorthogonal wavelet was that, rather than having one wavelet and one scaling function, biorthogonal wavelets have two different wavelet functions and two scaling functions that may produce different multiresolution analyses. In addition, the biorthogonal wavelet has good compact support, smoothness and good localization. We choose the fifth-order filter, which has a filter length of 12. The fifth-order filter was selected to avoid distortions along the image boundary. Using , the log-ratio image is recursively decomposed into six resolution levels. Empirical analysis suggested six to be the optimum level for multi-scale decomposition.
To reduce computation time, we focused only on the lower resolution images
per decomposition level. Discarding the detail images is allowed as the information contents at a certain resolution level are recovered at a higher level. Hence, the exclusion of the detail images does not affect the change detection approach. The final multi-scale decomposition
image stack then contains the lower resolution images at each level, as below:
2.3.2. Classification by Expectation-Maximization (EM) Algorithm with Mathematical Morphology
After the multi-scale decomposition, each decomposed image is inserted into a mathematical morphology framework. Mathematical morphology defines a family of morphological filters, which are nonlinear operators that aim at emphasizing spatial structures in a gray-level image. For more details on mathematical morphology the reader is referred to [
27]. Morphological filters are defined by a structuring element
, which is based on a moving window of a given size and shape centered on a pixel
. In image processing, erosion
and dilation
are the basic operators used, and are defined as follows [
27]:
The two morphological filters used are opening
and closing
, and they are the concatenation of erosion and dilation. They are defined as follows:
The effect of opening on a gray-level image tends to suppress regions that are brighter than the surroundings while closing suppresses regions that are darker than the surroundings. In order to preserve the spatial structures of our original image, opening by reconstruction followed with closing by reconstruction was applied. The sequence of first doing opening by reconstruction followed by closing by reconstruction is particularly designed to reduce noise in detection masks without incurring loss of details in mask outlines [
27]. Hence, it is relevant for achieving boundary preservation. The method requires an original image and a marker
image. If the marker image is obtained after erosion has been initially applied to the original image
, and the original image is reconstructed by a series of iterative dilations of
, then the resulting filter is opening by reconstruction
:
Moreover, closing by reconstruction
initially applies dilation to the original image, then reconstructs the original image by applying a series of iterative erosion. The resulting filter is:
Both filtering processes stop when
. It is worth mentioning that in this paper, we used a fixed square shape
with a size of 20 × 20 pixels. From an analysis of a broad range of data from different change detection projects, we found (1) that most consistent results were achieved with a 20 pixel window; and (2) that change detection performance changed slowly with deviation from the 20 pixel setting. Hence, while 20 pixels was found to be optimal, the exact choice of the window size is not critical for change detection success. The new multi-scale decomposition
stack now contains morphological filtered images at each level in
, as below:
The importance of opening and closing by reconstruction is that it filters out darker and brighter elements smaller than
, while preserving the original boundaries of structures in our image. Note that morphological filtering leads to a quantization of the gray-value space such that each image in
can be normalized into the gray-value range of [0, 255] without loss of information. At the k
th level in
, a lossless normalization is applied, leading to a float value between 0 and 255, such that:
After the mathematical morphology step, we calculate the posterior probability of one “no-change” and potentially several “change” classes at every one of the
resolution levels, resulting in
posterior probabilities per pixel. The various classes are assumed to be a mixture of Gaussian density distributions. While an approximation, assuming Gaussian characteristics for SAR log-ratio data is not uncommon. Previous research [
3] has found that the statistical distribution of log-ratio data is near normal and closely resembles a Gaussian distribution. Hence, our assumption of Gaussian characteristics is only weakly affecting the performance of our change detection approach. Still, we are currently assessing the benefits of using non-Gaussian descriptions in these processing steps and, depending on the results of this study, may modify our approach in the future. To automate the calculation of the posterior probabilities, we employ an EM approach. The importance of integrating mathematical morphology into our EM algorithm framework is to suppress the effect of background clutter that may constitute false positives after applying the EM algorithm.
The EM algorithm focuses on discrimination between the posterior probability of one no-change
and potentially several change classes
. For each level in
, we model the probability density function
of the normalized image series
as a mixture of
density distributions. This mixture contains the probability density functions, denoted
and
, and the prior probability,
and
. At the
kth level in
, the probability density function (PDF) is modeled as:
The first summand in Equation (17) (
represents the mixture of
change PDFs described by their respective likelihood
and prior probabilities
, while the second summand describes the PDF of a single no-change class. It is worth noting that all PDFs in Equation (17) are assumed to be of Gaussian nature, such that the mean
and variance
are sufficient to define the density function associated with the change classes
, and mean
and variance
can be used to describe the density function related with the no-change classes
. The parameters in Equation (17) are estimated using an EM algorithm. Given
is the
kth level image in
, we inferred which class
each pixel in
belongs to, using
which is our current (best) estimate for the full distribution, and
as our improved estimate. The expectation step at the
iteration is calculated by the conditional expectation:
The maximization step maximizes
to acquire the next estimate:
The iterations cease when the absolute differences between the previous and current variables are below a tolerance value (
ɛ). In our paper, we empirically set the tolerance value
ɛ to 10
−6. Once the iterations cease, the final optimal
is used to calculate the posterior probability using Bayes’ formula. The
algorithm (see algorithm 1) is applied separately to all
levels of the multi-scale decomposition series,
, resulting in a stack of posterior probability maps
of depth
where each map contains the posterior probability of change and no-change classes, respectively. Our EM algorithm is illustrated as follows:
| Algorithm 1. (Expectation-Maximization) |
| Begin initialize Ɵ°, ε, s = 0 |
| do s ← s + 1 |
| E step: compute Q(Ɵ|Ɵs) |
| M step: Ɵs+1 ← argmax Q(Ɵ|Ɵs) |
| until Q(Ɵs+1|Ɵs) − Q(Ɵs|Ɵs−1) ≤ ε |
| return Ӫ ← Ɵs+1 |
| end |
2.3.3. Selection of Number of Change Classes
In order to execute the expectation maximization algorithm from
Section 2.3, the number of change classes that are present in an image has to be known. Selection of classes is a difficult task, and care should be taken to avoid over- or under-classifying the data. Various methods have been proposed for selecting the number of classes
to best fit the data, and examples include the penalty method [
28], the cross-validation method [
29] and the minimum description length approach [
30]. In our paper, we developed a selection approach that identifies the number of required classes
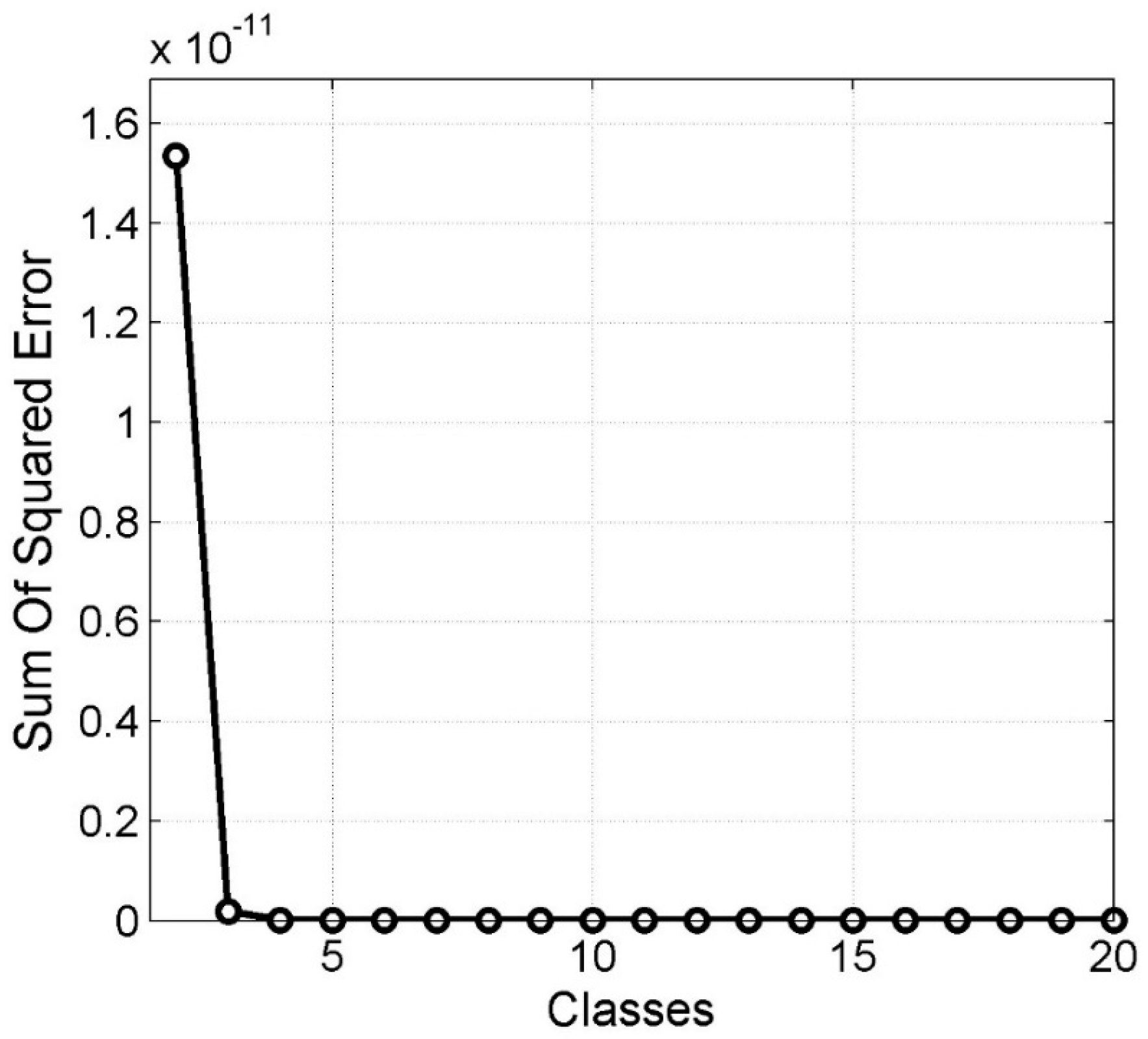
using a sum of square error (SSE) approach. The SSE approach utilized the measured data PDF, which is the statistical distribution of the highest decomposition level image, and the estimated PDF, which is the statistical distribution estimated after applying the EM algorithm to the highest decomposition level image. The highest decomposition level image was used because at this level, most of the noise in the image was filtered out. This approach seeks to minimize the sum of the square of the differences between the measured data PDF and the estimated PDF, as follows:
where
is the overall number of classes,
is the original measured PDF and
is the estimated PDF. An example of the dependence of
on the number of classes used in
is shown in
Figure 4. Initially, we start with two classes (one change and one no-change class) and calculate the SSE. For each extra class that is added into the procedure, its corresponding SSE is estimated. Plotting each class sequentially against its corresponding SSE leads to a continuous decrease of approximation error as NN gets larger.
The data from
Section 4 is used in this example and SSE was carried out using a maximum of 20 classes, with each classes being added sequentially. The knee point on the curve in
Figure 4 suggests that
is a good candidate for
.
2.3.4. Measurement Level Fusion
We developed a measurement level fusion technique to accurately delineate the boundary of the changed region by using the posterior probability of each class at each multi-scale image to compose a final change detection map (
). We developed and tested five measurement level fusion methods that are briefly explained below:
Product rule fusion: This fusion method assumes conditionally statistical independence, and each pixel is assigned to the class that maximizes the posterior conditional probability, creating a change detection map. Each pixel is assigned to the class such that
Sum rule fusion: This method is very useful when there is a high level of noise leading to uncertainty in the classification process. This fusion method assumes each posterior probability map in
does not deviate much from its corresponding prior probabilities. Each pixel is assigned to the class such that
Max rule fusion: Approximating the sum in Equation (22) by the maximum of the posterior probability, we obtain
Min rule fusion: This method is derived by bounding the product of posterior probability. Each pixel is assigned to the class such that
Majority voting rule fusion: This method assigns a class to the pixel that carries the highest number of votes. Each pixel in each posterior probability map
is converted to binary,
i.e.,
The measurement level fusion with the lowest overall error, highest accuracy, and highest kappa coefficient is selected as the best fusion method and is used as our final change detection map. The next section shows how the best fusion method was selected.
5. Conclusions
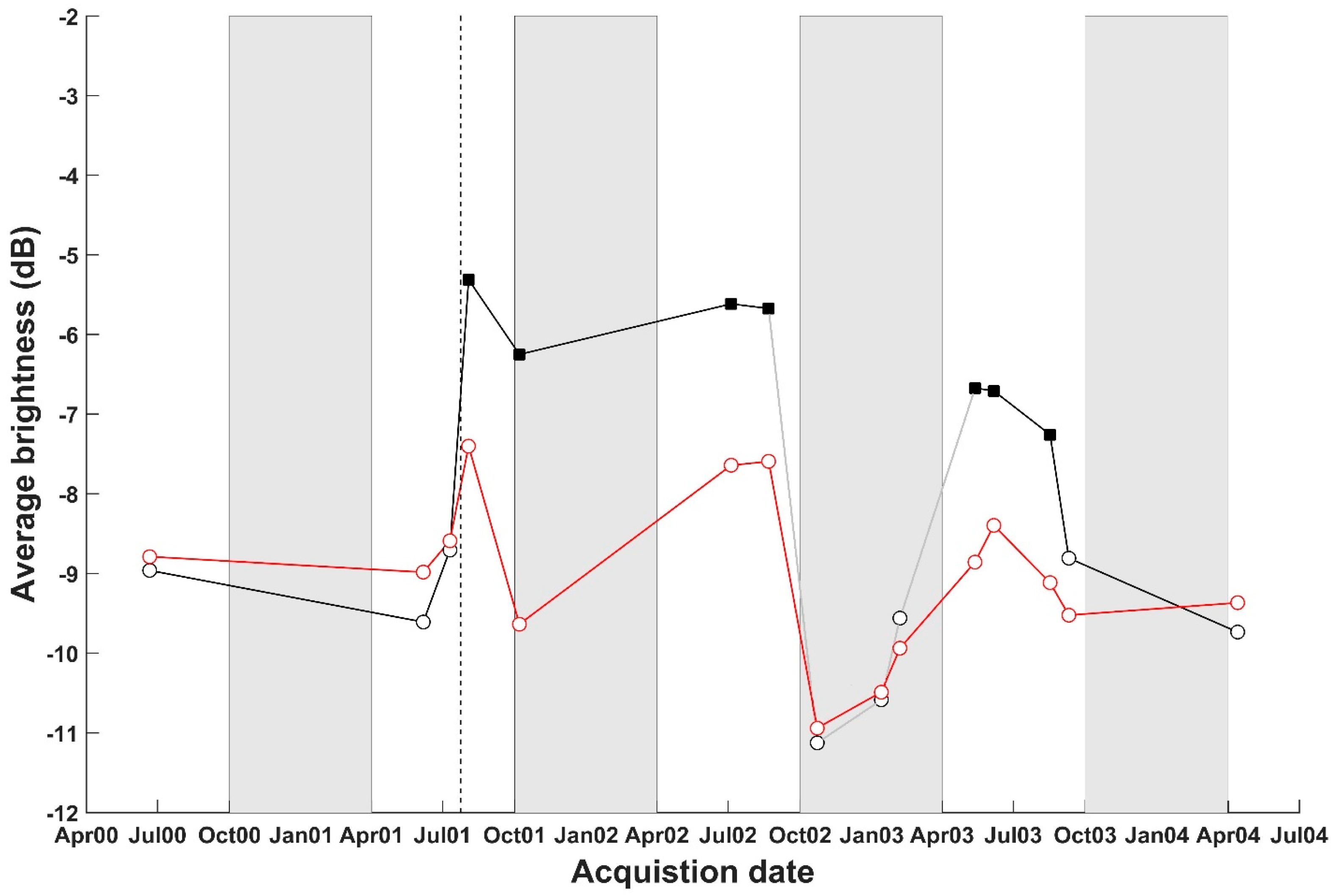
A flexible and automatic change detection method was presented that is effective at identifying change signatures from pairs of SAR images. The proposed approach removes radiometric differences between SAR images acquired from different geometries by utilizing radiometric terrain correction (RTC) which enables change detection from different image geometries and, hence, improves the temporal sampling of surface change that can be achieved from a given database. Suppressing background information and enhancing change information by performing log-ratio operations, our approach displayed high detection performance while preserving change signature details. The integration of modern non-local filtering and 2D-SWT techniques provided robustness against noise. The classification performance, increased by integrating an EM algorithm with mathematical morphology and preservation of the geometric details in the border regions, was shown when product rule fusion was employed. Moreover, our approach gave a very high overall accuracy. In addition to analyzing the performance of our approach on synthetic data, we used our algorithm to conduct change detection in an area affected by wildfires. From this change detection analysis, we found that a fire scar could be detected with high accuracy from the available data. In addition to accurately detecting the location and extent of the burn scar, an analysis of the image information within the detected scar revealed slow changes in image amplitudes over time, most likely related to the regrowth of forest within the burned area.
Comparison of our approach to selected recent methods showed that (1) our approach performed with a high overall accuracy and high geometric preservation; (2) neglecting any of the steps in our approach will result in an inferior change detection capability.
The main drawbacks of the proposed approach are: (1) the assumption that the image is a mixture of Gaussian distribution; and (2) that the approach does not take full advantage of all the information present in the speckle. Future work will explore using Gamma distribution for fitting the EM algorithm rather than the assumed Gaussian distribution. Non-uniform geometric and radiometric properties for all the areas of change in the synthetic image will be pursued as well. Images with high varying geometry will be considered and analyzed. In addition, the development of the advanced approach for selecting the number of changed classes will be pursued.