Abstract
Increased sophistication of high spatial resolution multispectral satellite sensors provides enhanced bathymetric mapping capability. However, the enhancements are counter-acted by per-pixel variability in sunglint, atmospheric path length and directional effects. This case-study highlights retrieval errors from images acquired at non-optimal geometrical combinations. The effects of variations in the environmental noise on water surface reflectance and the accuracy of environmental variable retrievals were quantified. Two WorldView-2 satellite images were acquired, within one minute of each other, with Image 1 placed in a near-optimal sun-sensor geometric configuration and Image 2 placed close to the specular point of the Bidirectional Reflectance Distribution Function (BRDF). Image 2 had higher total environmental noise due to increased surface glint and higher atmospheric path-scattering. Generally, depths were under-estimated from Image 2, compared to Image 1. A partial improvement in retrieval error after glint correction of Image 2 resulted in an increase of the maximum depth to which accurate depth estimations were returned. This case-study indicates that critical analysis of individual images, accounting for the entire sun elevation and azimuth and satellite sensor pointing and geometry as well as anticipated wave height and direction, is required to ensure an image is fit for purpose for aquatic data analysis.
1. Introduction
Satellite-derived bathymetry (SDB) using optical satellite data has been increasingly implemented as an alternative to traditional bathymetric surveying techniques. Acoustic surveying methods are difficult to conduct in shallow coastal waters because their coverage is limited to where a vessel can safely navigate. Coastal areas often have high population density, heavy maritime traffic and vulnerable ecosystems, such as salt marshes, mangroves, lagoons, and coral reefs. Due to erosion and sedimentation processes, as well as potential changes in sea level, many coastal regions need periodic bathymetry updates. SDB offers a practical means of regularly mapping and monitoring these environments, where the substratum reflectance contains a measureable spectral response compared to that of an optically deep water column, at local and continental scales [1].
SDB can be implemented photogrammetrically, empirically, or analytically. Each implementation has its own strengths and limitations.
Photogrammetric approaches rely on multiple images acquired over the same target area. Bathymetry can be derived from multiple images by computing wave heights and tracking their motion [2,3]. Shallow water bathymetry, where the substratum is visible, can also be determined implementing photogrammetric methods on stereo pairs of images, collected at multiple viewing angles [2,4,5].
Empirical approaches, using spectral information to derive water depth from satellite data, have been implemented for over 30 years [6,7,8]. A drawback of these methods is that they require in situ depth information to retrieve accurate depths or rely on the presumption that a homogenous water column and a simplified benthic substratum. Thus, although they are computationally fast and easy to use, these methodologies are often site and/or scene specific, hampering continental-scale SDB implementation.
Analytical approaches rely on radiative transfer theory and modelling of water column bio-optical properties and may implement spectral optimization [9,10,11,12,13] or lookup tables [14] to derive water depth. All analytical models require accurate radiometric calibrations to account for atmospheric effects [15,16]. Although the analytical implementation is more complex than the empirical approach, it offers the advantage of being temporally and spatially transferable across most relevant sensors [17].
Satellite remote sensing can characterize optically shallow waters by bathymetric estimation, benthic habitat mapping, and water quality assessment. With increases in spatial resolution, multispectral satellite sensors can retrieve more accurate information in optically shallow environments. The capability of any high-resolution satellite optical sensor to estimate water column, bathymetry, and benthic information is determined by its spectral, spatial, and radiometric resolution. However, noise introduced by environmental factors, such as atmospheric and air-water interface effects, may reduce their performance if not fully corrected for [18].
1.1. Factors Affecting Image Quality
This section will discuss spectral, spatial, and radiometric resolution. Then, the in-space pointing capability of modern satellite sensors will be discussed in more detail, focusing on SDB and benthic mapping.
Higher spectral resolution satellite data enhances substratum separability [19], leading to more accurate bathymetric and substratum retrieval [20]. In coastal waters [21] found that sensors with 20 nm contiguous bands in the 400–800 nm spectral region provide better results than sensors with a limited number of broader multispectral bands with regard to bathymetric depth retrieval. They suggested a minimum of 15 bands within the 400–800 nm spectral range are required for water column, bathymetry and benthic coastal remote-sensing applications.
Most high spatial resolution satellite sensors have three to four spectral bands in the spectral region where the water column is transparent. These bands are often highly correlated, thus offering limited information per band. Additional bands in the visible spectrum enhances the ability to retrieve bathymetry, benthic, and water quality characteristics [19,22,23,24,25,26,27].
When considering spatial resolution requirements for coastal mapping, the pixel size relative to the size of the features within the water bodies determines the mapping ability. High spatial resolution sensors permit fine-scale mapping in spatially-heterogeneous coastal and reef environments. High spatial resolution mapping in these environments does introduce some factors to consider:
- Inter-pixel heterogeneity; and
- Intra-pixel effects caused by glint off individual wave facets or atmospheric adjacency effects.
The radiometric resolution is a function of pixel size (equates to photons received from the surface area imaged), integration time, sensor sensitivity, and signal registration capability. For aquatic applications, the sensor should have a high signal to noise ratio (SNR) to ensure sufficient signal to capture spectral features ranging from relatively dark water bodies to bright targets in the intertidal zone. The WV2 sensor, for example, has a SNR of over 300 in shallow water that tapers off to 200 in optically deeper water [2].
The pointing capability of some high spatial resolution satellite sensors to acquire images by pointing the sensor away from nadir has both positive and negative consequences. Numerous nearly-simultaneous images can be captured across the same area from different view angles, thus increasing the probability of acquiring good quality images that are not affected by sunglint. However, the acquisition of off-nadir images may also increase surface glint, introduce angular effects and increase atmospheric path radiance. Without understanding these factors, end-users may acquire seemingly useful cloud free images, only to find sunglint and other noise-inducing environmental variables rendering the image data unsuitable for aquatic analysis.
The bidirectional reflectance function of a target, measured by a satellite sensor, is strongly dependent on the geometric relationship of illumination and observation at the time of image acquisition. For example, substratum separability is enhanced by higher solar zenith angles [20], while the probability of sunglint in the image is enhanced by clear skies, shallow waters, high spatial resolution, and wide sensor field of view (FOV) [28,29]. This may lead to the signal from the target being saturated. Optimal sun-sensor-target geometry over water includes solar zenith angles of 30° to 60° and sensor azimuth angles of 0° or 180° with respect to the solar azimuth [27].
Multiple images across a single target will result in variations in image quality, requiring an understanding of the effect of noise within each image. The enhanced pointing capability, in all directions, of the recent versatile high spatial resolution satellite sensors results in variable sun-sensor-target geometry combinations. The analysis of multi-angle data provides us with an opportunity to examine and quantify the effect of image quality, caused by variations in sun-sensor-target geometry, on bathymetric retrievals.
Water-leaving radiance is often small, compared to the reflected radiance from other sources, such as atmospheric and water surface scattering [26,30]. It is, thus, important to be aware of all of the environmental noise factors that can impact the precision and accuracy with which desired environmental variables can be retrieved from a satellite image. The total environmental noise for the entire sensor–atmosphere–air–water interface system can be quantified by the environmental noise-equivalent difference (NEΔrsE) [1,31].
The factors that affect the magnitude of the NEΔrsE in any given scene can be broadly divided into sensor-specific effects and scene-specific effects. The sensor-specific factors are dependent on sensor design and calibration, and are generally invariant, or change slowly, over time due to instrument degradation.
Factors that add environmental noise to individual scenes includes atmospheric variability, the water surface state (with swell-, wave-, and wavelet-induced reflections), and refraction of diffuse and direct sky and sunlight [1].
In addition to the atmosphere attenuating the energy to the target and reflected off a target (e.g., a shallow benthic environment), the atmosphere also adds a scattered path radiance into the signal of the target detected by the sensor. The signal detected for any given pixel can, thus, be expressed:
where Ltotal is the at-sensor radiance for surface reflectance ρ, E is the irradiance on the object, τ the total atmospheric transmittance (downwelling and upwelling path) and Lpath is the path radiance [32,33].
The Lpath component of Ltotal, does not include any relevant information about target reflectance. Atmospheric conditions contributing to Lpath includes Rayleigh scattering, Mie scattering, and clouds. Rayleigh scatter, induced by atmospheric molecules, is strongly wavelength-dependent and has a larger effect in the shorter wavelengths. This effect is always present in the atmosphere and is influenced by solar elevation angle. Mie scattering is induced by larger particles in the atmosphere, such as dust and water droplets. This scattering is weakly dependent or independent of wavelength. Both clouds and large atmospheric particles contribute to directional scattering and are also a factor in differential scattering due to anisotropic distribution of particles in the atmosphere.
Larger off-nadir view angles result in higher path-scattering due to a longer path-length. Rayleigh scattering, which is more pronounced in the shorter wavelengths, increases with a longer path-length, caused by a larger off-nadir view angle.
As accurate as possible atmospheric correction during image pre-processing is important for reliable water column composition, benthic, and bathymetric information retrieval [18,26].
Water-surface conditions, such as wind- and wave-induced sunglint can introduce a significant amount of noise to an image. Wind-induced waves roughen the water surface, which then acts as a non-Lambertian reflector, causing significant forward scattering. A rough surface generally has the effect of widening the solid angle through which light will penetrate the water column by rapidly changing the direction in which light rays are refracted at the sea surface [27]. Additionally, wave-induced sunglint broadens the reflectance cone of the specular point [34], increasing the likelihood of sunglint contaminating the image. As a result of sunglint, a reflected sunlight radiation component is added to the signal, measured by the sensor, that does not carry any information about the water column and which may be higher than the water-leaving signal depending on wavelength and view angle. The pointing capability of high spatial resolution sensors can avoid or exacerbate this effect by pointing into or away from the sun.
1.2. Objectives
Multiple images taken near-simultaneously with variable sun-sensor-target geometry combinations across a single target will result in variations in image quality, requiring an understanding of the effect of the multiple sources of environmental noise within each image. The analysis of such a pair of multi-angle data provides us with an opportunity to examine and quantify the effect of image quality, caused by variations in sun-sensor-target geometry, on bathymetric retrievals. This analysis will help to establish retrieval error guidelines for images acquired at non-optimal geometrical combinations. This is relevant for applications where rapid image acquisition is required, such as during extreme events, or where cloud-free images are rare, such as in the tropics. These images would be opportunistically acquired, which would limit the choice of viewing geometry and seastate. Quantifying the effects of non-optimal image quality, will help with making more informed decisions when considering which images to acquire for analysis.
Previous studies reported bathymetric retrievals from WV2 data (e.g., [5,25,26,35]). However, with the exception of [35], all of these studies report results from single images, selected for the most optimal conditions available. This may lead to the false belief that that merely ordering cloud free images is sufficient for obtaining useful images for shallow coastal water assessment purposes. In actual fact the entire sun elevation and azimuth and satellite sensor pointing and geometry as well as anticipated wave height and direction must all be taken into account. Unlike other studies focusing on multiple images, such as [35,36], the main aim of this work is to help individuals make more informed decisions when acquiring high-resolution image data for aquatic analysis.
This case study focuses on two WV2 satellite images of a shallow coastal lagoon. The images were acquired one minute apart. Variation in acquisition angles placed one image in an optimal sun-sensor geometric configuration and the second image close to the specular point of the Bidirectional Reflectance Distribution Function (BRDF) (worst-case scenario, glinted image). This presented us with the opportunity to quantify the effects of variations in NE∆rsE on Ltotal, rrs and the accuracy of environmental variable retrievals from a good image, a glint-affected image, and a glint-corrected image of the same lagoonal area, acquired almost simultaneously.
2. Materials and Methods
2.1. Data
Two WV2 satellite images of a shallow coastal lagoon in Tasmania, Australia (42.8211°S, 147.5508°E) were acquired one minute apart on 22 October 2011. The position of the sun, relative to the target, was constant (φsun = 40°, θsun = 52°) while the position of the sensor, relative to the target, changed (Image 1: φview = 106°, θview = 77°; Image 2: φview = 175°, θview = 57°; Figure 1). The images were acquired during an outgoing tide with a gentle (16 km/h) south-easterly breeze. The WV2 image data consists of 2 m spatial resolution data in eight spectral bands: coastal (400–450 nm), blue (450–510 nm), green (510–580 nm), yellow (585–625 nm), red (630–690 nm), red-edge (705–745 nm), and two bands in the near-infrared portion of the spectrum (770–895 nm and 860–1040 nm).
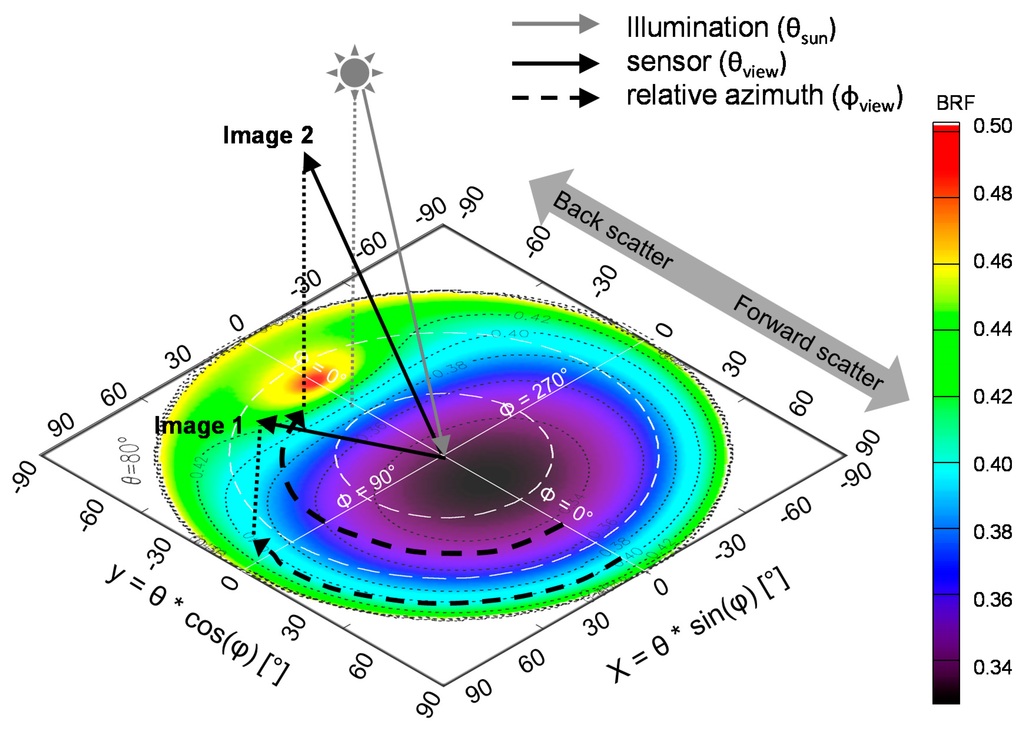
Figure 1.
Graphic representation of the geometric relationship between the sun and satellite sensor, relative to the target, for the two image acquisitions: (1) Image 1: φview = 106°, θview = 77° and (2) Image 2: φview = 175°, θview = 57° (BRF field in the figure was generated using [37]).
2.2. Pre-Processing
Both images were corrected with a standardized atmospheric and air/water interface correction [1] to retrieve subsurface irradiance reflectance (rrs). The “coastal Water and Ocean MODTRAN-4 Based ATmospheric correction” (“c-WOMBAT-c”) atmospheric correction procedure combines an atmospheric inversion from at-sensor-radiance to above water reflectance [38,39] with an inversion of the air-water interface from above water reflectance to subsurface reflectance [39].
A full MODTRAN-4 atmosphere parameterization and characterization is implemented in c-WOMBAT-c to retrieve rrs. The atmospheric parameterization is listed in Table 1. Adjacency effects from photons transferring from adjacent pixels to the one being sampled are corrected for by using an averaged surface radiance for the surrounding region. This spatially-weighted image is generated by convolving the input radiance imagery with a one square kilometer spatial weighting function [38].

Table 1.
Atmospheric correction parameters.
The acquisition geometry of Image 2 places the sensor close to the specular point in the backscattering direction (Figure 1), thus exacerbating the effect of sunglint within this image (Figure 2). The atmospherically-corrected Image 2 was, therefore, corrected for glint effects, implementing the method revised by [28] after [29]. This method assumes negligible water reflectance in the near-infrared (NIR) band. However, this assumption is only useful where the water leaving reflectance is not affected by the bottom reflectance within a shallow water column. To maintain the non-negligible NIR reflectance in pixels over shallow water, the glint correction algorithm considers both the spectral shape of a glint-affected pixel and the magnitude of the glint in each pixel [43].

Figure 2.
Subset of (a) Image 1 (φview = 106°, θview = 77°) and (b) Image 2 (φview = 175°, θview = 57°), acquired one minute apart on 22 October 2011 during an outgoing tide with a gentle (16 km/h) south-easterly breeze. Gray mask: exposed land area; 1: location of the in situ depth observations (red dots) collected on 22 August 2013; 2: location of the least glint-affected image segment, selected for atmospheric correction inter-comparison; 3: location of an as homogenous as possible area of water that is as optically deep as possible, selected for NEΔrsE computation.
To estimate the spectral shape of glint within an image, a relatively homogenous optically deep area of interest (AOI) is selected. Within the homogenous area, the inter-pixel reflectance difference is due to the difference of glint reflectance. The spectral shape of the sunglint is obtained by averaging the spectra over the AOI and then normalizing at a NIR band. This glint spectral shape function is applied for the entire image.
The magnitude of the glint in each image pixel is determined within a 3 × 3 moving kernel. Within this kernel, the pixel of minimum reflectance is assumed to be glint-free. The magnitude of glint in each pixel is estimated by subtracting the minimum kernel reflectance from the reflectance of the pixel. Finally, by multiplying the glint spectral shape function described above, the glint reflectance spectrum for each pixel is computed and is subtracted from the measured spectrum.
Glint correction of the WV2 images is complicated by the sensor design where two sensor arrays collect four spectral bands each (creating the total of eight spectral bands) with offsets in both the location of the sensor array and in the time of collection [26,36,44]. Due to the reliance of the glint-correction method on near infrared (NIR) reflectance, the glint correction algorithm has to be applied separately on the image bands that were collected with each individual sensor array [45]. Fortunately each of the two arrays has three optical bands and one NIR band. This ensures that the changes in surface glint that occurs in microseconds are appropriately accounted for. Implementing glint correction on all eight bands across the two sensor arrays simultaneously results in the addition of noise to the image instead of reducing the effects of glint (data not presented).
2.3. SAMBUCA
Similar to the approach outlined by [13], SAMBUCA, an enhanced implementation of the inversion/optimization approach by [11], was applied to the atmospherically-corrected satellite imagery. In the SAMBUCA inversion/optimization scheme, the modelled rrs () is compared to the rrs obtained from each image pixel (). The set of variables that minimizes the difference between and is used to retrieve bathymetry, benthic composition, and concentrations of the optically-active constituents of the water column.
The SAMBUCA model uses the optical properties of the water column and substratum albedo (magnitude of reflectance) to estimate the total rrs. In This study, the optical parameterization was based on water column optical properties adapted from a coastal water column, representative of Cockburn Sound, Australia [46], and a substratum spectral reflectance library of three benthos (sand, sea grass, and brown algae) [47].
In addition to estimates of bathymetry, benthic composition, and concentrations of the optically-active constituents of the water column, output from SAMBUCA also includes the following model accuracy estimates: the optimization residuum (∆) and the substratum detectability index (SDI).
The ∆ is an estimation of the accuracy between the modelled spectra and the image spectra. This measure is based on the spectral magnitude and -shape difference of the modelled and measured spectra:
where α is the spectral angle between reference spectra and the spectra under consideration as defined in the Spectral Angle Mapper (SAM, [48]) and LSQ is the Euclidean Minimum Distance [13]. By defining a threshold for ∆, it is possible to identify pixels with a good (smaller ∆) or poor (larger ∆) spectral match from the model inversion.
The SDI is a measure of the contribution of the reflectance of the substratum () to the total rrs. By incorporating a measure of SNR in the imagery, in this case the NEΔrsE, it can estimate how well the is measured in the rrs. The SDI is defined for the spectral band of maximum penetration (i.e., the band with the highest value for ) as:
The NEΔrsE is defined as the standard deviation in each band over an as homogenous as possible area of optically deep water (i.e., where the contribution of to the total rrs is negligible) within the image, as outlined by [1,31]. The size of the uniform area can be determined by increasing the size of the kernel (1, 3 × 3, 5 × 5, 7 × 7, etc.) until the standard deviation reaches a first asymptotic limit. The assumption of homogeneity over a kernel of pixels ensures that the standard deviation returned by the NEΔrsE calculation predominantly variations in sea surface state. In this study, NEΔrsE was computed in a portion of the images where the water that was both as homogenous and as optically deep as possible (Figure 2).
When the water column is considered optically deep (), the SDI will be zero. Very low values for SDI denotes a negligible contribution of to total rrs and can be considered quasi-optically deep [13], while increasing SDI values denotes an increasing contribution of to total rrs, resulting in more accurate retrievals of bathymetry and benthic cover.
2.4. In Situ Data
An in situ dataset of water depth (measured z) was collected for selected transects within the lagoon (transect 1, Figure 2) with a Humminbird 998C SI echo sounder (Eufaula, AL, USA) on 22 August 2013. The transducer was installed at a draft of 10 cm (which was accounted for in the processing). Each individual dataset was reduced for tide using a local tidal reference. Determination of the bottom return was performed by hand on the raw sonar data resulting in a water depth determination accuracy of 1–4 cm.
The depth measurements (6655 data points) were collected over a two hour period (not coincident with the images but almost two years later) along a transect that captured a range of depths across the lagoon. Due to the geometry of the lagoon and a lack of a nearby tidal gauge, we could only do an approximate tidal correction for the in situ measurements.
Analysis of the image data and depth retrieval accuracy was done as follows:
- Model-derived depth was compared with in situ depth measurements.
- The frequency of the absolute relative error between the in situ depth observations and image-derived depth () was determined.
- Comparison between SDI values returned for the two images
3. Results
Figure 2 shows the pseudo true color composites of the satellite images and the locations where spectral data were collected for the analyses presented in this section. These locations can be summarized as: (1) the location where the in situ depth observations were collected on 22 August 2013; (2) the least glint-affected image segment, located in the lee of a cliff, selected for atmospheric correction inter-comparison; and (3) the location of an area of water that was as homogenous and as optically deep as possible, used for the NEΔrsE computation.
3.1. Atmospheric Conditions
The atmospheric correction inter-comparison between Image 1 and Image 2 was done using spectral data collected over a short transect in shallow water over a homogenous sandy bottom in an image segment that was relatively unaffected by glint in both Image 1 and Image 2 (area 2 in Figure 2). Figure 3 and Table 2 compares the atmospheric correction of Image 1 to Image 2 in the visible spectrum. All bands were strongly correlated (R2 > 93%). For visible wavelengths beyond 545 nm, the atmospheric correction produced very similar rrs (bias < 0.008, MAPD < 10%). However, the coastal (400–450 nm) and the blue bands (450–510 nm) showed negative bias (bias of −0.0302 and −0.0156) as well as large MAPD values (MAPD of 104.6% and 16.5% for coastal and blue bands, respectively). This is likely due to overcorrection by the atmospheric correction method as a result of the longer atmospheric path length (~100 km more than Image 1), caused by the acute off-nadir view angle of Image 2. The coastal, the blue and, to some extent, the green (510–580 nm) bands are significantly different from each other, as described by the non-parametric Kruskal-Willis H test (Table 2).
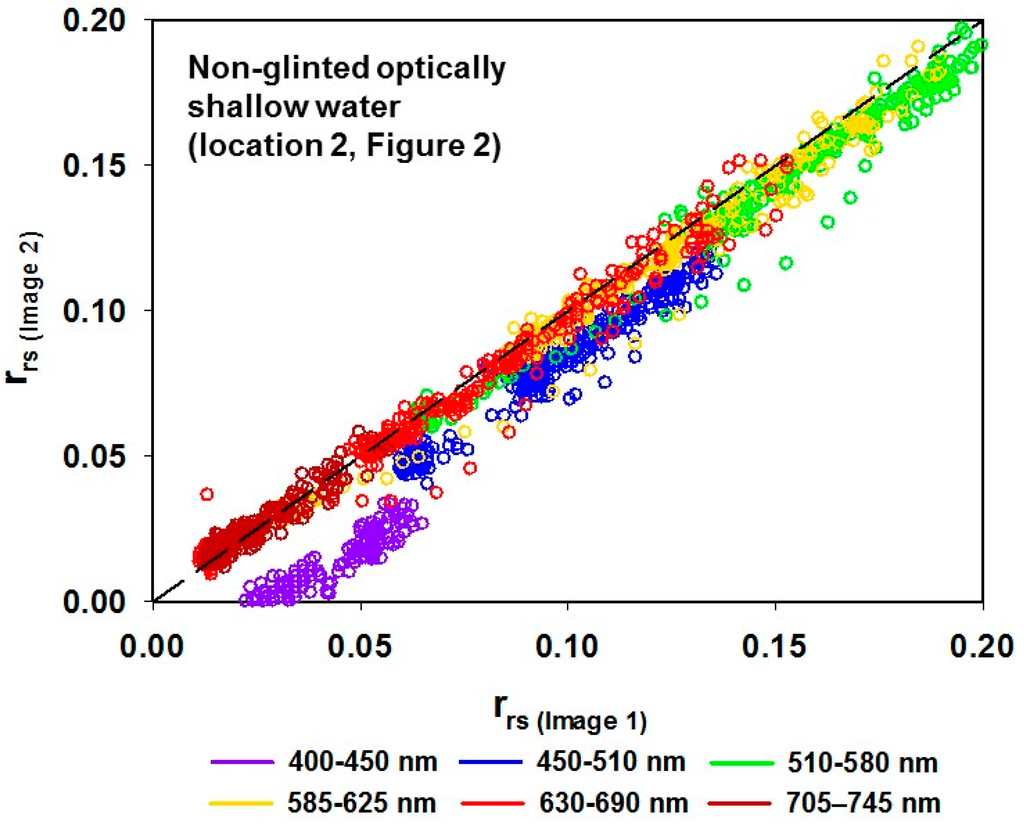
Figure 3.
Comparison of atmospherically-corrected rrs spectra of the first six WoldView-2 spectral bands, of a cross-track sample of a shallow water over sandy bottom in an image segment that is least affected by glint in both Image 1 and Image 2 (dashed line represents 1:1 relationship).

Table 2.
Band specific bias, RMSE, RMSD, and R2, as well as Kruskal-Wallis H test computed for atmospherically-corrected rrs spectra of the WoldView-2 spectral bands, of a cross-track sample of a shallow water over sandy bottom in an image segment that is least affected by glint in both Image 1 and Image 2 (n = 319).
3.2. Sun-Sensor-View Geometry
The acquisition geometry of Image 2 places the sensor close to the specular point in the backscattering direction (Figure 1), thus exacerbating the effect of sunglint within this image, as observed in Figure 2. The NEΔrsE of each image was computed on a kernel of 35 × 35 pixels collected over an as homogenous as possible area of optically deep water (location 3, Figure 2). Figure 4 shows that the NEΔrsE of Image 2 is significantly higher than that of Image 1 prior to glint correction and still much higher after glint correction. The glint removal removed about half of the additional noise due to the adverse sun-sensor-target geometry. The coastal band (400−450 nm) has the largest NEΔrsE in all three images, while the green band (510−580 nm) has the lowest NEΔrsE.
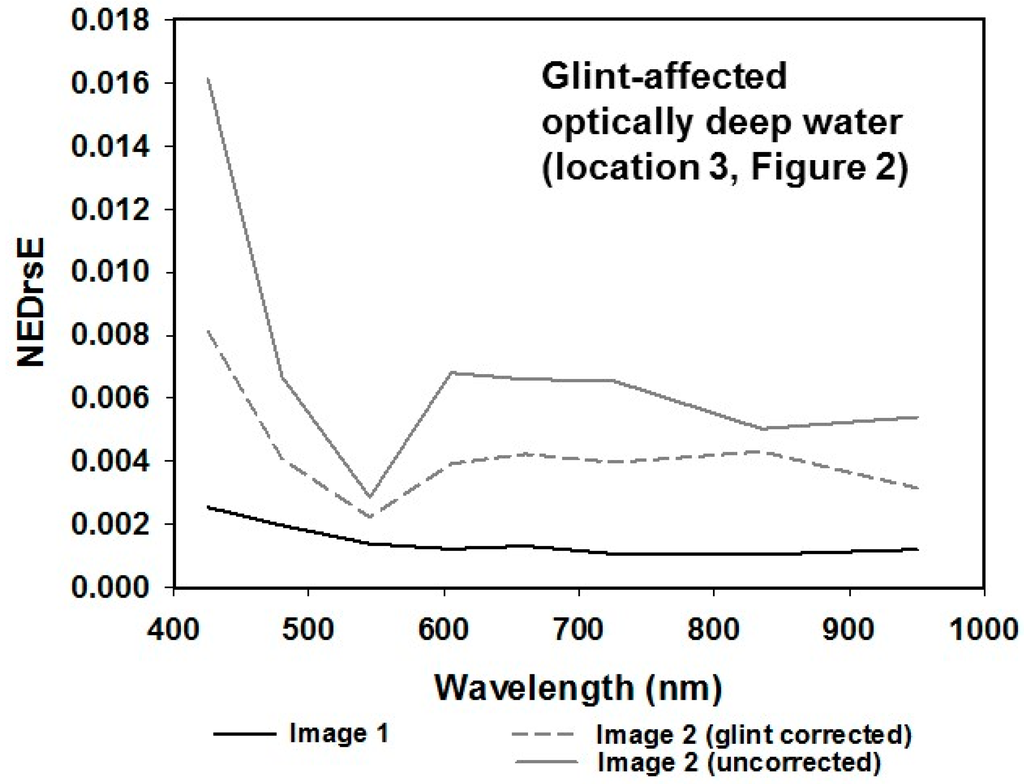
Figure 4.
NEΔrsE, a standard deviation computed on a kernel of 35 × 35 pixels collected over an as homogenous as possible area of optically deep water, from Image 1 and Image 2, illustrating the effects of environmental factors due to sunglint and related sun-sensor target geometry on the inherent noise of each individual image.
To illustrate the effects of the total environmental noise within each image on rrs, a spectral profile was collected from each image at the locations where the in situ depth samples were collected (location 3, Figure 2). This transect represents a range of water depths and severity of glint affecting individual pixels within an optically complex lagoonal area. The location of this transect was selected to represent a relatively homogenous sandy substratum with variable water depths and water column properties. The median and 5th and 95th percentiles rrs in each band of the collected spectral profiles for each of the images is presented in Figure 5. The median was selected for this representation because of the non-normal distribution of the collected spectral data. In general, Image 2, both before and after glint correction, has higher reflectance than Image 1 in most bands in transect 1 (Figure 2). The exception being the coastal band (400–450 nm) that has lower rrs in Image 2, compared to Image 1, when all the data in transect 1 is considered. However, when the data points collected in transect 1 (Figure 2) are separated into optically shallow water (z < 1 m) and pseudo-optically deep water (z > 1 m), the median rrs in bands two and three is lower in Image 2, compared to Image 1 in optically shallow water, whilst the bands with longer wavelengths have similar rrs than Image 1. In pseudo-optically deep water, the coastal band has lower median rrs in Image 2, compared to Image 1.
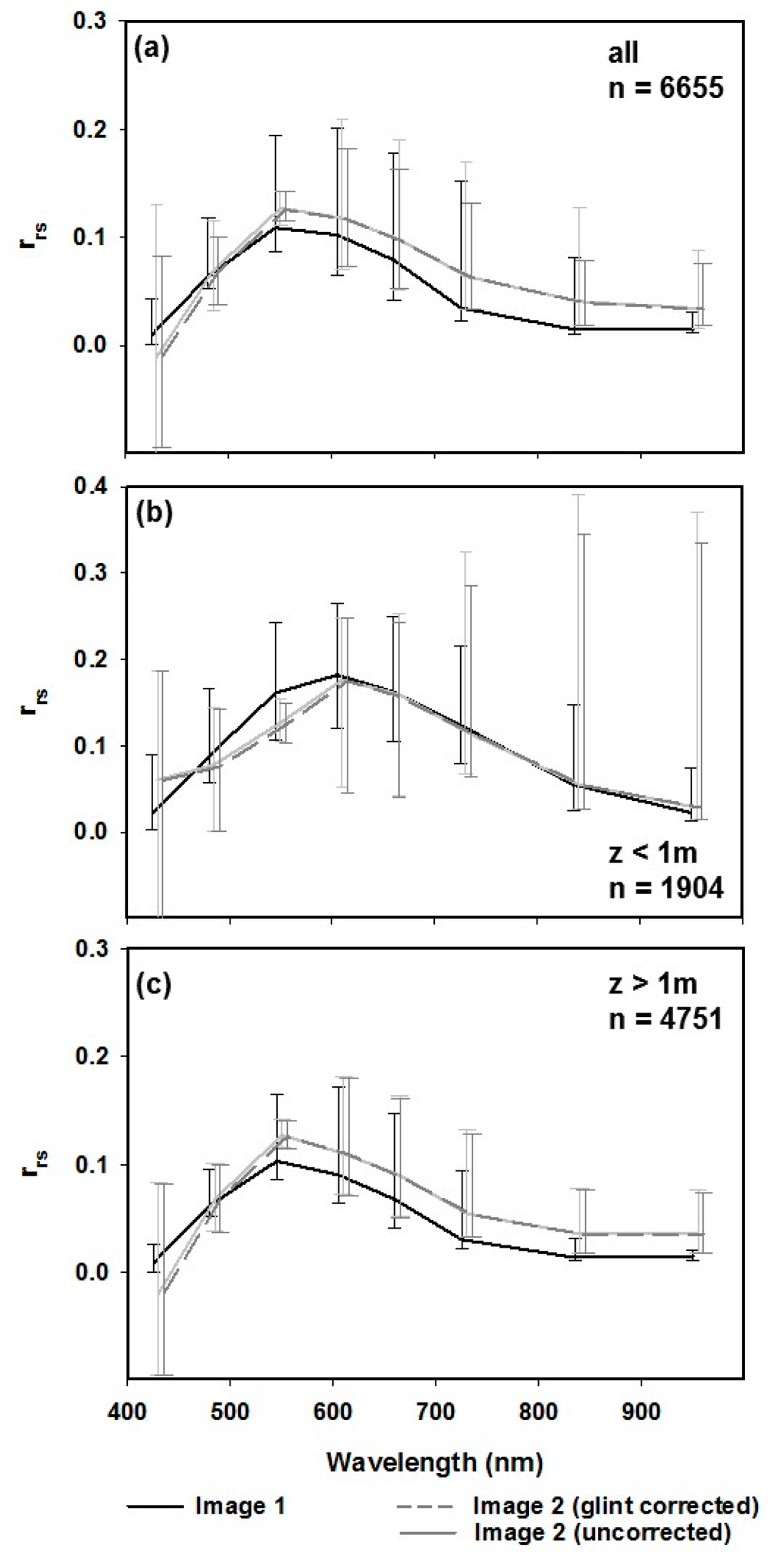
Figure 5.
(a) Median and 5th and 95th percentiles rrs in each spectral band of a cross-track spectral profile, collected from each image (Image 1, Image 2 (uncorrected), and Image 2 (GC: glint corrected)) where in situ depth observations were collected (transect 1, Figure 2); (b) median and 5th and 95th percentiles rrs in each spectral band of all optically shallow (<1 m water depth) observations; and (c) mMedian and the 5th and 95th percentiles rrs in each spectral band of all optically deep (>1 m water depth) observations.
The glint-correction applied to the image did not significantly change the shape of the median spectral response curve of Image 2 as can be seen in the overlap between the two curves in Figure 5. However, the effect of the glint-correction can be observed in the lower 95th percentile rrs in the glint-corrected Image 2, particularly when all the data points are considered (Figure 5a) and in optically shallow water (Figure 5b).
3.3. Depth Retrieval
The model retrieved environmental parameters for each pixel were evaluated for accuracy using the ∆ and SDI model outputs. An in situ dataset of water depth (measured z) was collected for selected transects within the lagoon (transect 1, Figure 2) with a Humminbird 998C SI echo sounder on 22 August 2013. The location of this transect was selected to represent a relatively homogenous sandy substratum with variable water depths and water column properties. Although the SAMBUCA model retrieves both depth and substratum type, only depth was considered for further analysis due to the homogeneity of the substratum and the lag between satellite and in situ data acquisitions. Only pixels with a good (smaller ∆) spectral match from the model inversion that were identified as optically shallow (SDI > 0) were considered for the assessment of depth retrieval.
Figure 6a–c presents the scatter-plot of the depth estimated from WV2 Image 1, Image 2, and the glint-corrected Image 2, respectively, versus the in situ depth observations. Figure 6d–f presents the distribution of the relative difference between the depths as estimated from Image 1 and Image 2, respectively, and the in situ depth observations.
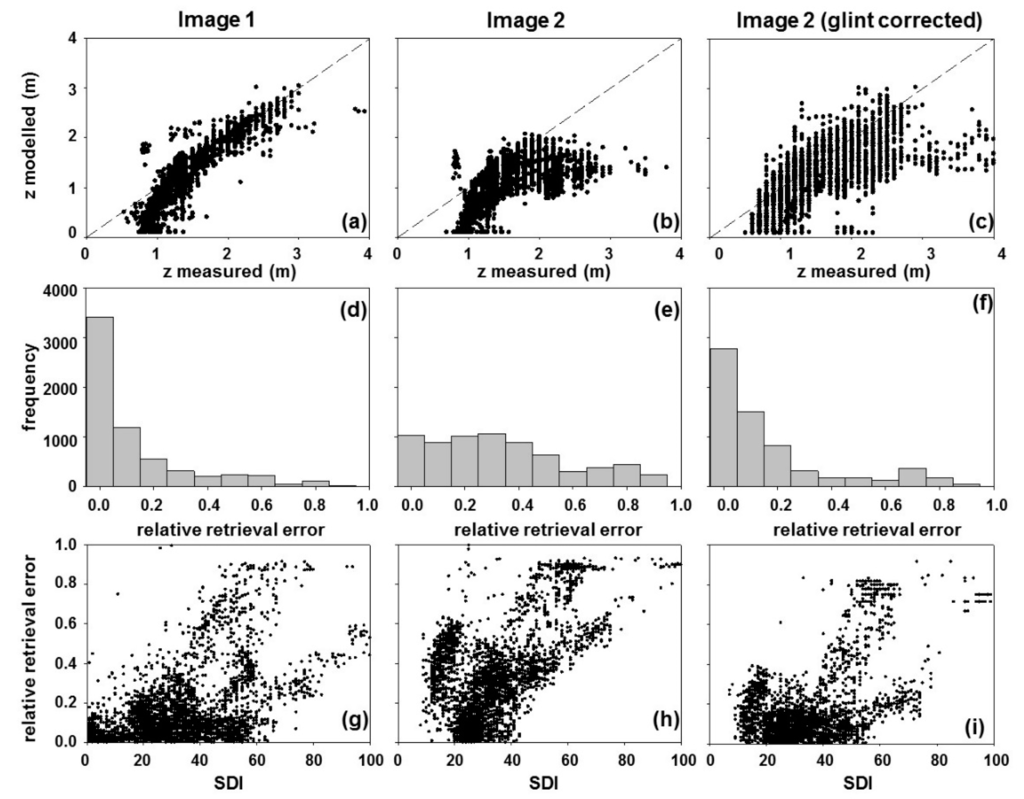
Figure 6.
Analysis of depth retrieval: scatterplot of the model-estimated depth versus in situ depth observations retrieved from (a) Image 1; (b) Image 2 and (c) Image 2 after glint correction (dashed line represents 1:1 relationship). Histogram of the frequency of absolute relative depth errors (), retrieved from (d) Image 1; (e) Image 2; and (f) Image 2 after glint correction. Scatterplot of relative depth error versus SDI retrieved from (g) Image 1; (h) Image 2; and (i) Image 2 after glint correction.
Depths derived from Image 1 (Figure 6a) shows the relationship between measured- and image-derived depths to be close to the 1:1 line. In this study, the accuracy of the depth retrievals was strongly dependent on the total environmental noise associated with the individual images. Depths retrieved from Image 1 had an overall lower retrieval error than those retrieved from Image 2.
After glint correction of Image 2 an improvement was observed in the maximum depth to which accurate depth estimations were returned (Figure 6c). The percentage of model depth estimates with an absolute relative retrieval error of less than 0.2 improved from 30% to 42% for Image 2 after glint-correction.
Due to the time difference between image acquisition and the acquisition of the in situ dataset, an inter-comparison was done between the depths derived from the each image. Figure 7a,b presents the scatterplot of the depth estimated from WV2 Image 1 (x-axis) versus the depth estimated from Image 2 and the glint-corrected Image 2 (y-axis), respectively. Figure 7c,d presents the scatter-plot of the relative difference between the model derived depths and in situ depth observations, estimated from WV2 Image 1 (x-axis) versus the relative difference between the model derived depths and in situ depth observations estimated from Image 2 and the glint-corrected Image 2 (y-axis), respectively. For this analysis, Image 1 was chosen as a reference as it lead to more accurate depth retrieval when compared to the in situ data (Figure 6a,d,g).
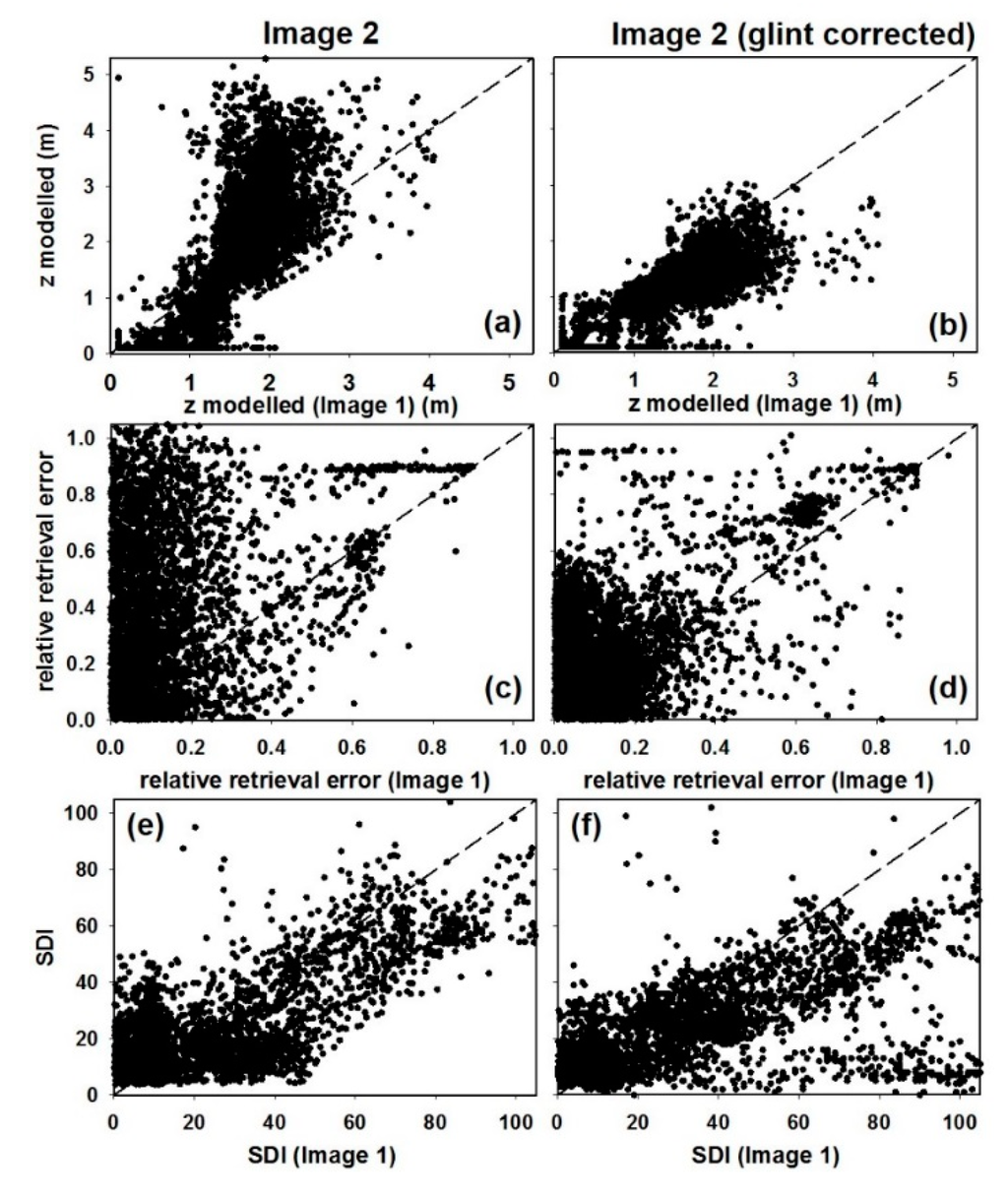
Figure 7.
Relative comparison of depth retrieval: scatterplot of the model-estimated depth retrieved from Image 1 versus model–estimated depth retrieved from (a) Image 2 and (b) Image 2 after glint correction (dashed line represents 1:1 relationship). Scatterplot of absolute relative depth errors (), retrieved from Image 1 versus absolute relative depth errors retrieved from (c) Image 2 and (d) Image 2 after glint correction. Scatterplot of SDI retrieved from Image 1 versus SDI retrieved from (e) Image 2 and (f) Image 2 after glint correction.
Compared to Image 1, depths derived from Image 2 (Figure 7a,c) there were a larger number of pixels where depth was estimated with a large degree of inaccuracy (large relative retrieval error, compared to Image 1). After glint correction, the large overestimation in depth were corrected for (Figure 7b,d), as was also shown when compared with in situ data (Figure 6c,f,i).
3.4. SDI
Figure 6g–i presents a scatterplot of the relative difference between the model-derived depths and in situ depth observations, versus the SDI as estimated from Image 1, Image 2 and the glint-corrected Image 2, respectively. The point cloud density in Figure 6g–i need to be interpreted with the aid of the frequency distribution of the relative retrieval error in Figure 6d–f. When the SDI value approaches zero, the model attributes most of the rrs to the water column, while increasing SDI values indicates an increasing contribution to the total rrs observed. Image 1 has a higher number of model depth estimates with an absolute relative retrieval error of less than 0.2 than Image 2 (62% and 30%, respectively), supporting the observations in Figure 6a,b. It is also evident from Figure 6h that, for Image 2, the model returned fewer correct estimates with low SDI than for Image 1. Compared to Image 1, SDI derived from Image 2 (Figure 7e,f) were generally lower. After glint correction, more pixels returned a higher SDI. However, compared to Image 1, the SDI was still slightly lower. The lack of SDI values below 10 in Image 2 can be attributed to the increased surface reflectance caused by glint. The model interprets the higher albedo to a larger contribution. This resulted in a poorer spectral match (∆) between modeled and measured spectra and were removed prior to the evaluation retrieval accuracy.
4. Discussion
Due to a lack of concurrent in situ spectral observations, the atmospheric correction of the satellite images could only be assessed through our knowledge of what the spectral response in this environment should look like. The atmospheric correction of the two images, relative to each other, were assessed using spectra collected from an image segment that was relatively unaffected by glint in both images (transect 2, Figure 2). This ensured that most of the variation between the two sets of spectra can be attributed to atmospheric effects. In general, the atmospheric correction of the two images appear to be similar, as would be expected from the same atmospheric parameterization. The lower rrs in the bands with shorter wavelengths of Image 2 (Figure 3) may be partially due to the atmospheric correction over-compensating for the longer atmospheric path-length by estimating a too high path-scattering. Rayleigh scattering in the atmosphere is more pronounced in the shorter wavelengths and increases with a longer path-length. The larger off-nadir view angle of Image 2 added an additional ~100 km to the path-length, compared to Image 1. The assumption of homogenous path scattering may not have held true, leading to overcorrection in the shorter wavelengths by the atmospheric correction model.
Sunglint is exacerbated by the acquisition geometry of Image 2 which places the sensor close to the specular point in the backscattering direction. This explains the higher NEΔrsE within Image 2, compared to Image 1. The glint correction applied to Image 2 was partially successful, as indicated by the lower NEΔrsE of the glint-corrected Image 2. This indicates that the water-leaving radiance component of these glint-affected pixels is partly (30% to 50% removal) recoverable in areas where the pixels remain radiometrically unsaturated within each spectral band.
Atmospheric effects, such as Rayleigh scattering, also affected noise observed in the images, particularly in the coastal band (400–450 nm), as this band is the most sensitive to Rayleigh scattering [2,32]. Sensor SNR also contributed to the observed patterns in the NEΔrsE. For example, the green band (510–580 nm) has the highest observed SNR in shallow waters (z < 5 m) [2], which can explain the lower NEΔrsE observed in this band (Figure 4).
The influence of the total environmental noise within each image on rrs, was examined using a cross-track spectral profile. This profile was collected over a range of water-column depths and substratum types, representing pixels that ranged between not glint-affected to severely glint-affected to the point of being saturated by surface reflectance (transect 1, Figure 2).
The effects of the placement of Image 2 close to the specular point in the backscattering direction is clear in the higher median reflectance across most bands, compared to Image 1. Very shallow water (z < 1 m, Figure 3b), presents spectral responses that differ significantly from deeper water. Water-leaving radiance in this environment is affected by a complex combination of multiple scattering from the substratum, wave lensing, shadowing, and exposure. The available data for this study is not sufficient to quantify the contribution of each factor to the overall spectral signal measured by the sensor.
There is no significant difference in the shape of the median spectral response curve of the uncorrected and glint-corrected spectra, collected from Image 2 at location 1. It is most likely that due to the number of observations (n = 6655), the influence of sunglinted and shaded wave facets are averaged across the entire sample. However, the effects of glint correction can be observed in the lower NEΔrsE of the glint corrected Image 2 and the lower 95th percentile rrs values in the glint-corrected Image 2, particularly in the longer wavelengths.
The apparent under estimation of depth in areas shallower than one meter can be attributed to a combination of factors. The in situ depth data may be incorrect due to the operational limitations of the echo sounder in very shallow waters and/or changes in the bathymetry in the period between image acquisition and in situ observations. The assumption by the SAMBUCA model that the rrs is approximated as a sum of contributions from the water column and the substratum [11,13] might also not adequately account for light reflecting multiple times between the bottom and surface, thus skewing the depth retrievals.
Generally, depths were under-estimated from Image 2 due to the higher surface signal, introduced by sunglint. Due to this higher surface signal, the SAMBUCA model assumed a stronger substratum signal, usually associated with shallow water, which contributed to the higher retrieval error in this image. A partial improvement in retrieval error after glint correction of Image 2 resulted in an increase to the maximum depth to which accurate depth estimations were returned. Goodman [18] concluded that careful pre-processing of sub-optimal images has a significant influence on model output. Although the best available de-glinting algorithm for multispectral imagery was implemented, this procedure was only partially successful due to the severity of the glint affecting a large number of the image pixels.
The higher reflectance component of the signal, introduced by the prevalent glint in Image 2, was translated by the SAMBUCA model as a larger contribution to total larger rrs. This resulted in a poorer spectral match between modeled and measured spectra and were removed prior to the evaluation retrieval accuracy. This explains the lack of SDI values below 10 in Image 2.
Glint-correction improved bathymetric retrieval accuracy significantly in shallow water where the signal makes a considerable contribution to rrs. This explains the general decrease in relative retrieval error at SDI values between 60 and 80 as well as the fact that the SDI of the glint-corrected pixels are relatively more similar to that of Image 1, compared to before glint correction. The removal of the glint component from the rrs recorded within those pixels, resulted in an improvement in the capability of the model to retrieve accurate depths.
5. Conclusions
Increased sophistication of high spatial resolution multispectral satellite sensors and their ability to point the sensor in multiple off-nadir directions, provides enhanced bathymetric and benthic mapping capability. However, water-leaving radiance is a low signal in a noisy environment and the enhancements are counteracted by per-pixel variability in sunglint, atmospheric path length, and directional effects.
Although, optimal image acquisition conditions increases the likelihood of accurate bathymetric retrieval from multispectral satellite images, the reality of many applications of high spatial resolution satellite imagery on shallow coastal and coral reef environments is that the water-surface state will seldom be ideal. In cases where urgent image capture is required, such as during or just after extreme events, or in pervasively cloudy environments, such as the tropics, non-optimal image acquisition geometries will occur. Thus, for practical applications it is necessary to understand the sensitivity to sun-sensor-target angles, especially with the versatile pointing capabilities of these sensors. This study quantifies these effects for two near-simultaneous acquisitions.
In the case study presented here, with two WV images acquired one minute from each other, one of which was acquired at a sub-optimal sun-sensor-target geometry which exacerbated the spectral effects of wind induced waves and sunglint, it was still possible to achieve sufficiently relevant results. Glint-correction algorithms improved the retrieval accuracy from the sub-optimal image data. However, pixels with a high amount of glint may saturate the sensor to such an extent that the contribution of is irretrievable.
Increased sophistication in satellite sensor design, particularly the capability of pointing in multiple off-nadir directions, increases the likelihood of acquiring multiple images at high spatial resolution. However, this case-study indicates that merely ordering cloud-free images is insufficient for obtaining useful images for shallow coastal water assessment purposes. In actual fact, the entire sun elevation and azimuth and satellite sensor pointing and geometry, as well as anticipated wave height and direction, must all be taken into account. Critical analysis of each collected image using all of the above-mentioned criteria is required to ensure an image is fit for purpose for aquatic data analysis.
Acknowledgments
This work was supported by the CSIRO Wealth from Oceans Flagship Program, the CSIRO Earth Observation and Informatics Future Science Platform, the European Union (under FP7-People—Co-funding of Regional, National and International Programs, GA n. 600407) and the CNR RITMARE Flagship Project. We are grateful to Simon Allen, skipper of the RK SCRAP, for acquiring the in situ depth estimates.
Author Contributions
Elizabeth Botha and Vittorio Brando conceived and designed the image analysis. Elizabeth Botha contributed to algorithm implementation, data preparation, and results generation. Vittorio Brando and Arnold Dekker supported and contributed to all phases of the research. All authors contributed to manuscript writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Miecznik, G.; Grabowska, D. WorldView-2 bathymetric capabilities. Proc. SPIE 2012, 8390. [Google Scholar] [CrossRef]
- Mancini, S.; Olsen, R.C.; Abileah, R.R.; Lee, K.R. Automating nearshore bathymetry extraction from wave motion in satellite optical imagery. Proc. SPIE 2012, 8390. [Google Scholar] [CrossRef]
- Collings, S.; Botha, E.J.; Anstee, J.M.; Campbell, N. Depth from satellite images: Fusion of physics based depth retrieval and stereo. Unpublished work. 2016. [Google Scholar]
- Deidda, M.; Sanna, G. Bathymetric extraction using WorldView-2 high resolution images. In Proceedings of the XXII ISPRS Congress International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XXXIX-B8, Melbourne, VIC, Australia, 25 August–1 September 2012; pp. 153–157.
- Clark, R.K.; Fay, T.H.; Walker, C.L. Bathymetry calculations with Landsat 4 TM imagery under a generalized ratio assumption. Appl. Opt. 1987, 26, 4036–4038. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- Adler-Golden, S.M.; Acharya, P.K.; Berk, A.; Matthew, M.W.; Gorodetzky, D. Remote Bathymetry of the Littoral Zone From AVIRIS, LASH, and QuickBird Imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 337–347. [Google Scholar] [CrossRef]
- Albert, A.; Gege, P. Inversion of irradiance and remote sensing reflectance in shallow water between 400 and 800 nm for calculations of water and bottom properties. Appl. Opt. 2006, 45, 2331–2343. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.F. Hyperspectral remote sensing for shallow waters: 2. deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Kendall, L.C.; Chen, R.F.; Peacock, T.G. Properties of the water column and bottom derived from Airborne Visible Imaging Spectrometer (AVIRIS) data. J. Geophys. Res. Ocean. 2001, 106, 11639–11651. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bisset, W.P.; Kohler, D.D.R.; Reid, R.P.; et al. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Digital Analysis of Remotely Sensed Imagery; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
- Andrefouet, S. Coral reef habitat mapping using remote sensing: A user vs. producer perspective. Implications for research, management and capacity building. J. Spat. Sci. 2008, 53, 113–129. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.; Anstee, J.M.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.D.; Klonowski, W.M.; Lee, Z.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Goodman, J.A.; Lee, Z.; Ustin, S.L. Influence of atmospheric and sea-surface corrections on retrieval of bottom depth and reflectance using a semi-analytical model: A case study in Kaneohe Bay, Hawaii. Appl. Opt. 2008, 47, F1–F11. [Google Scholar] [CrossRef] [PubMed]
- Botha, E.J.; Brando, V.E.; Dekker, A.G.; Anstee, J.M.; Sagar, S. Increased spectral resolution enhances coral detection under varying water conditions. Remote Sens. Environ. 2013, 131, 247–261. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Phinn, S.R.; Mumby, P.J. Environmental and sensor limitations in optical remote sensing of coral reefs: Implications for monitoring and sensor design. Remote Sens. 2012, 4, 271–302. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K. Effect of spectral band numbers on the retrieval of water column and bottom properties from ocean color data. Appl. Opt. 2002, 41, 1291–2201. [Google Scholar] [CrossRef]
- Anstee, J.M.; Dekker, A.G.; Botha, E.J.; Park, Y.J.; Brando, V.E.; Williams, R.J. Comparing and quantifying the impact of increased spectral resolution of WorldView2 satellite data for monitoring of shallow coastal waters. In Proceedings of the Geospatial World Forum, Hyderabad, India, 18–21 January 2011.
- Collin, A.; Hench, J.L. Towards deeper measurements of tropical reefscape structure using the WorldView-2 spaceborne sensor. Remote Sens. 2012, 4, 1425–1447. [Google Scholar] [CrossRef]
- Reshitnyk, L.; Costa, M.; Robinson, C.; Dearden, P. Evaluation of WorldView-2 and acoustic remote sensing for mapping benthic habitats in temperate coastal Pacific waters. Remote Sens. Environ. 2014, 153, 7–23. [Google Scholar] [CrossRef]
- Yuzugullu, O.; Aksoy, A. Generation of the bathymetry of a eutrophic shallow lake using WorldView-2 imagery. J. Hydroinform. 2014, 16, 50–59. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-Resolution Maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Dekker, A.G.; Brando, V.E.; Anstee, J.M.; Pinnel, T.; Kuster, H.; Hoogenboom, H.J.; Pasterkamp, S.W.M.; Peters, R.J.; Vos, O.C.; Malthus, T.J. Chapter 11: Imaging spectrometry of water. In Imaging Spectrometry: Basic Principles and Prospective Applications: Remote Sensing and Digital Image Processing; Van der Meer, F.D., De Jong, S.M., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Hedley, D.; Harborne, A.R.; Mumby, P.J. Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Andrefouet, S.; Tyler, M.R. Sea surface correction of high spatial resolution IKONOS images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Concha, J.; Gerace, A. Atmospheric compensation for WV2 Satellite and in-water component retrieval. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012.
- Wettle, M.; Brando, V.E.; Dekker, A.G. A methodology for retrieval of environmental noise equivalent spectra applied to four Hyperion scenes of the same tropical coral reef. Remote Sens. Environ. 2004, 93, 188–197. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 4th ed.; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- De Haan, J.F.; Kokke, J.M.M.; Hoogenboom, H.J.; Dekker, A.G. An integrated toolbox for processing and analysis of remote sensing data of inland and coastal waters-atmospheric correction. In Proceedings of the Fourth International Conference: Remote Sensing for Marine and Coastal Environments, Orlando, FL, USA, 17–19 March 1997.
- Lee, K.R.; Olsen, R.C.; Kruse, F.A.; Kim, A.M. Using multi-angle WorldView-2 imagery to determine bathymetry near Oahu, Hawaii. Proc. SPIE 2013, 8743. [Google Scholar] [CrossRef]
- Patterson, K.W.; Lamela, G. Impact of specular reflection on bottom type retrieved from World View-2 images. Proc. SPIE 2013, 8743. [Google Scholar] [CrossRef]
- Vogt, P.; Verstraete, M.M. AnisView. 2009. Available online: http://forest.jrc.ec.europa.eu/download/software/anisview/ (accessed on 1 March 2013).
- Cox, C.; Munk, W. Slopes of the Sea Surface Deduced from Photographs of Sun Glitter; Bulletin of the Scripps Institution of Oceanography; University of California Press: Berkeley and Los Angeles, CA, USA, 1956; pp. 401–488. [Google Scholar]
- Adler-Golden, S.M.; Bernstein, L.S.; Richtsmeier, S.C. FLAASH, a MODTRAN4 atmospheric correction package for hyperspectral data retrievals and simulations. In Proceedings of the AVIRIS Airborne Geoscience Workshop, Pasadena, CA, USA, 12–16 January 1998.
- Atmospheric Soundings. Available online: http://weather.uwyo.edu/upperair/sounding.html (accessed on 1 July 2013).
- NASA Goddard Ozone & Air Quality. Available online: http://ozoneaq.gsfc.nasa.gov/ (accessed on 1 July 2013).
- Australian Government. Available online: http://www.bom.gov.au/ (accessed on 1 July 2013).
- Botha, E.J.; Dekker, A.G.; Park, Y.J.; Anstee, J.M.; Cherukuru, N.; Clementson, L. Remote Sensing for Mapping and Change Detection in Tropical Commonwealth Marine Protected Areas: Phase 2; CSIRO Wealth from Oceans Flagship report prepared for: The Department of Environment, Water, Heritage and the Arts; CSIRO Land and Water and Wealth from Oceans: Canberra, Australia, 2010. [Google Scholar]
- Martin, J.; Eugenio, F.; Marcello, J.; Medina, A. Automatic sun glint removal of multispectral high-resolution WorldView-2 imagery for retrieving coastal shallow water parameters. Remote Sens. 2016. [Google Scholar] [CrossRef]
- Doxani, G.; Papadopoulou, M.; Lafazani, P.; Pikridas, C.; Tsakiri-Strati, M. Shallow-water bathymetry over variable bottom types using multispectral WorldView-2 image. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; Shortis, M., Shimoda, H., Cho, K., Eds.; pp. 159–164.
- IMOS. SRS Bio Optical Database. Available online: http://imos.aodn.org.au/imos/ (accessed on 1 October 2013).
- Anstee, J.M.; Botha, E.J.; Williams, R.J.; Dekker, A.G.; Brando, V.E. Optimizing classification accuracy of estuarine macrophytes: By combining spatial and physics-based image analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1367–1370.
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebreche, K.B.; Shapiro, A.B.; Barloo, P.J.; Goetz, A.F.H. The Spectral ImagProcessing System (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).