MERIS Phytoplankton Time Series Products from the SW Iberian Peninsula (Sagres) Using Seasonal-Trend Decomposition Based on Loess
Abstract
:1. Introduction
- Will stl.fit() better capture the dynamics of the time series of the study area?
- How can stl.fit() be used to describe and explain the variability of the study area?
2. Data and Methods
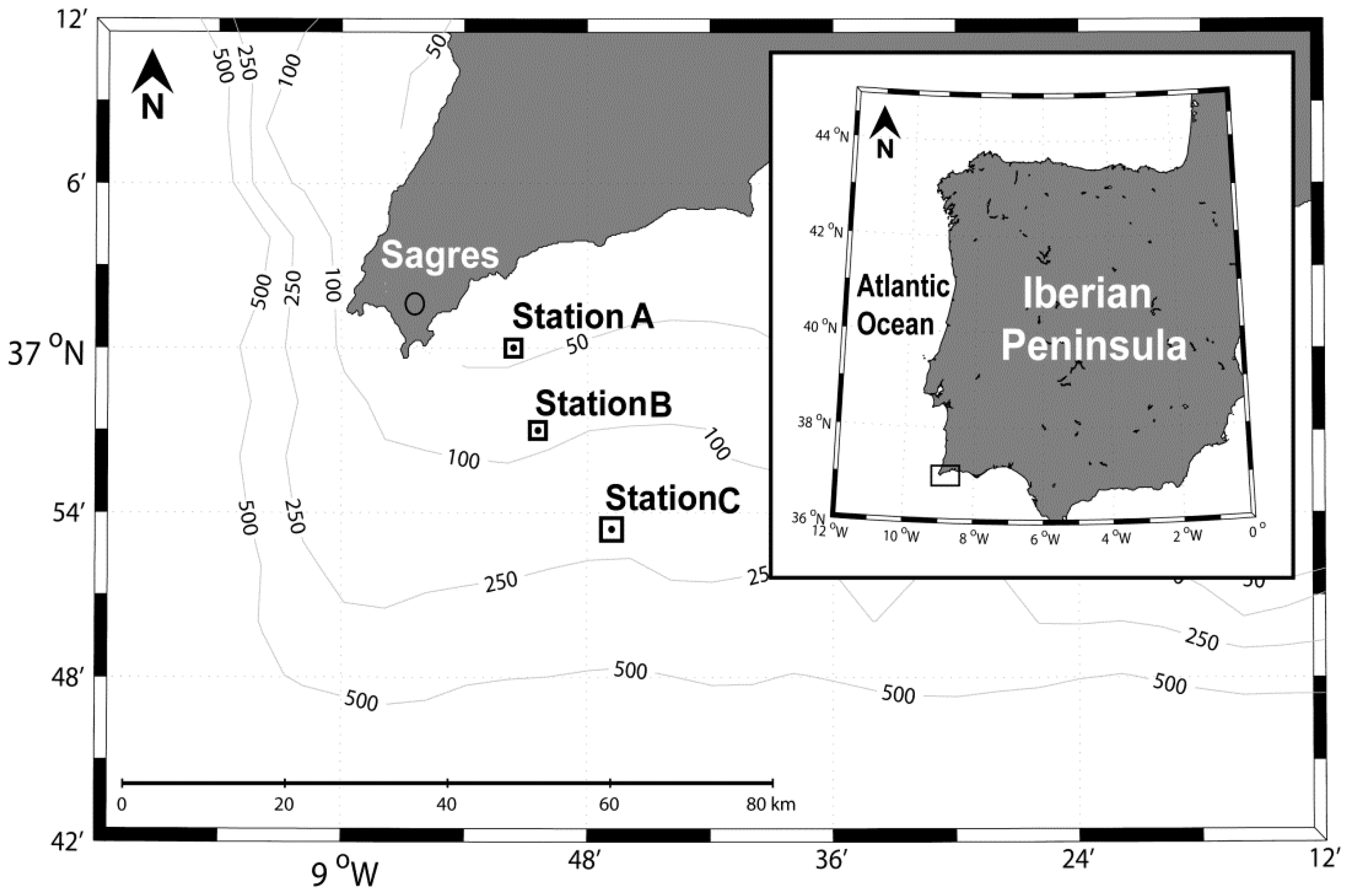
2.1. Study Area
2.2. Earth Observation
2.3. Time Series Decomposition
2.3.1. STL Decomposition
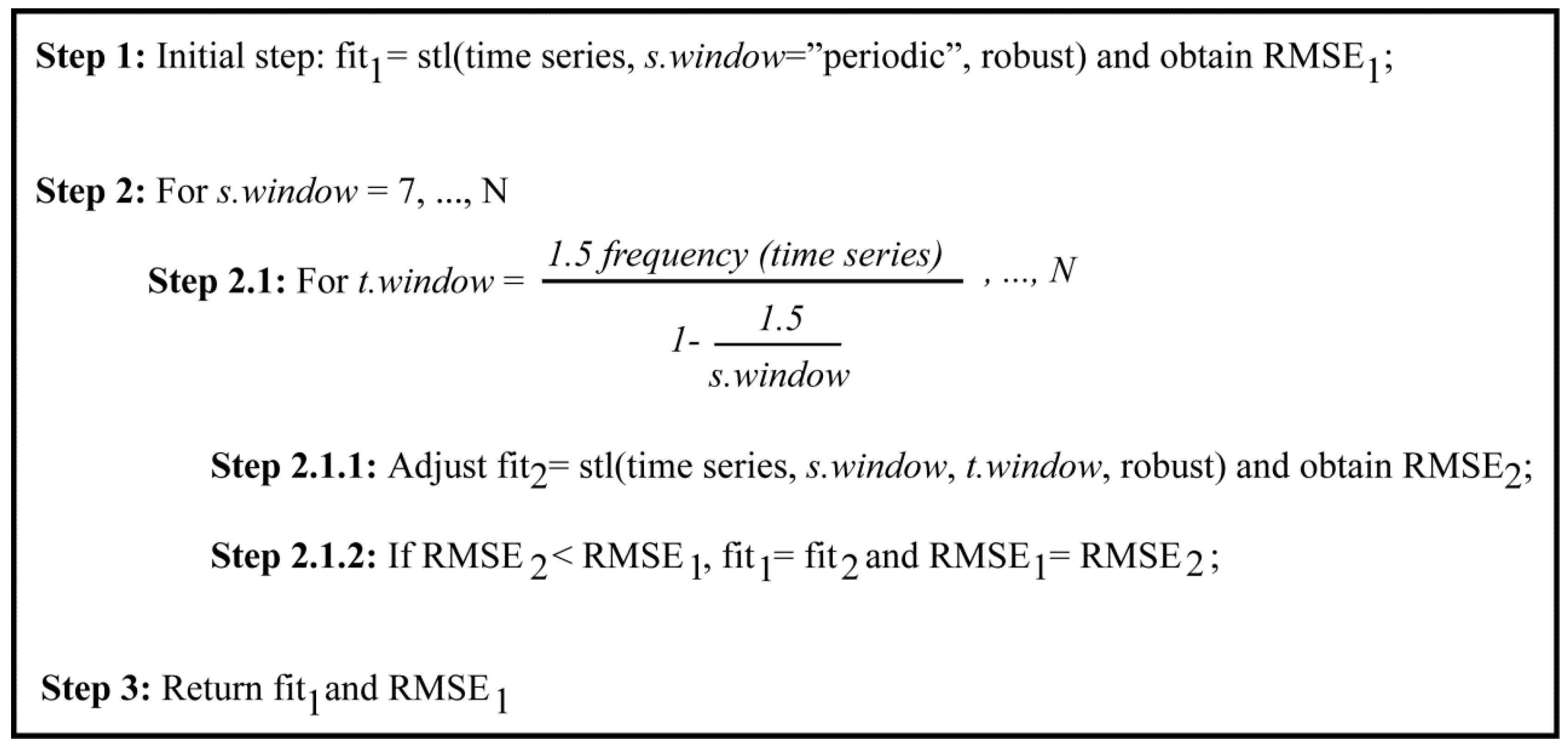
2.3.2. The stl.fit() Procedure
3. Results
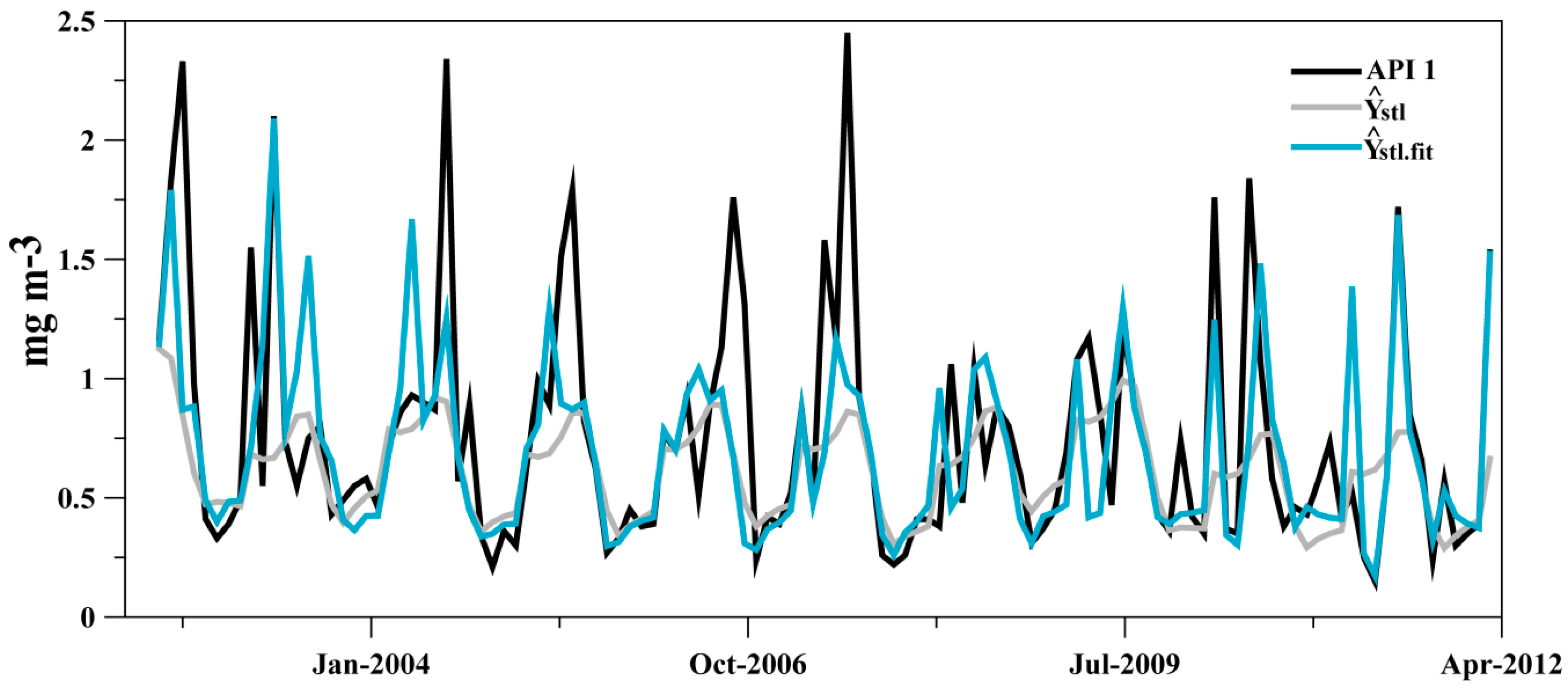
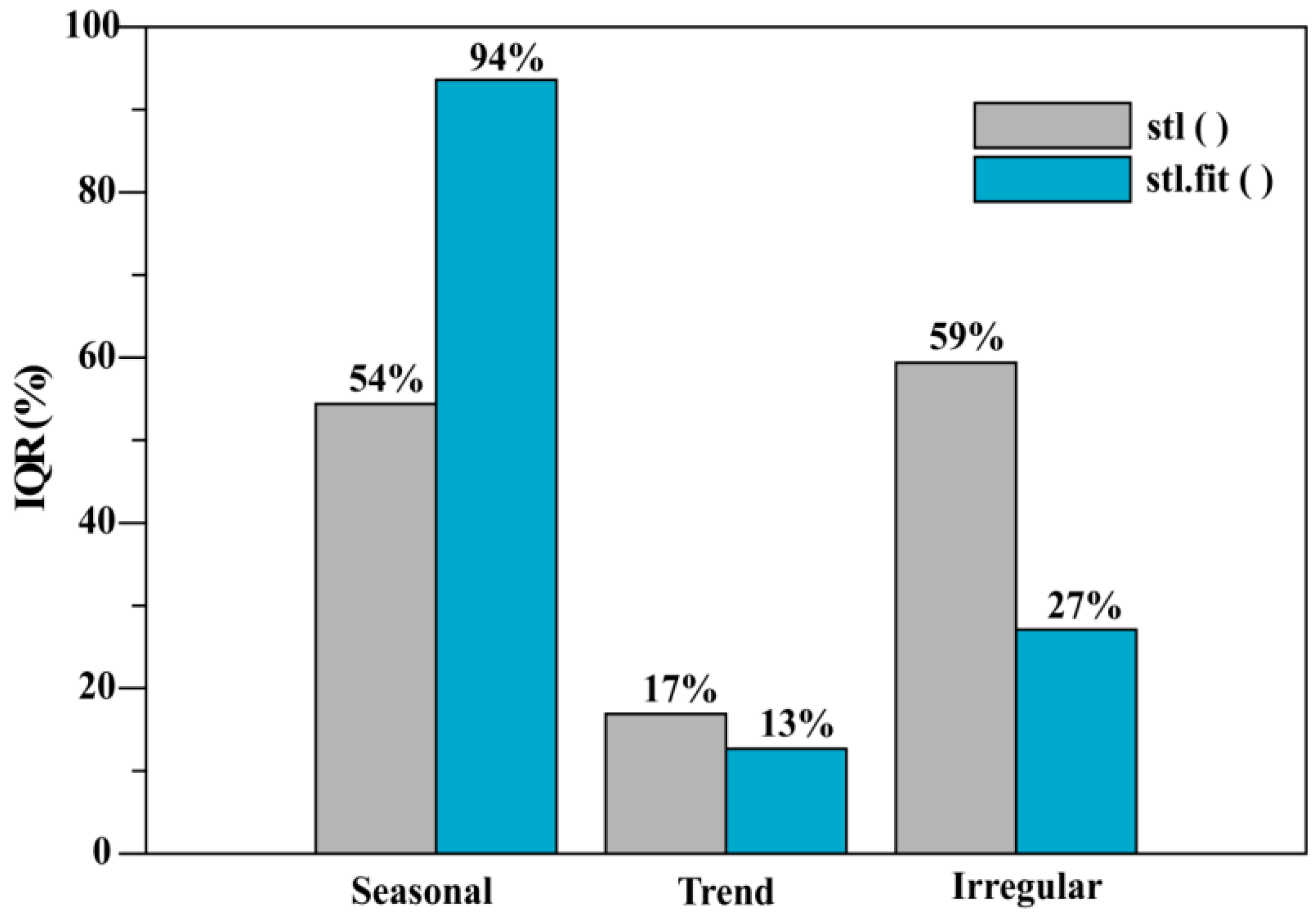
3.1. Comparison of stl.fit() to the Standard Approach
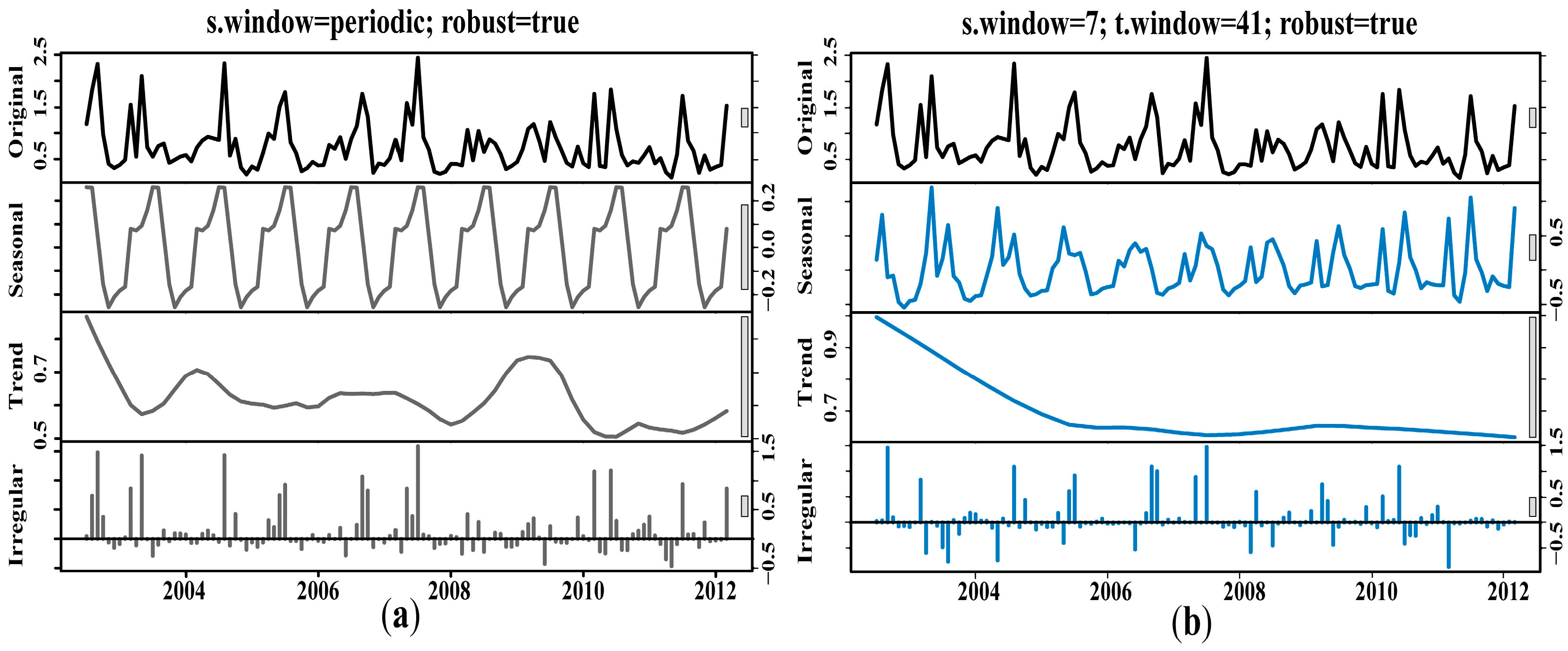
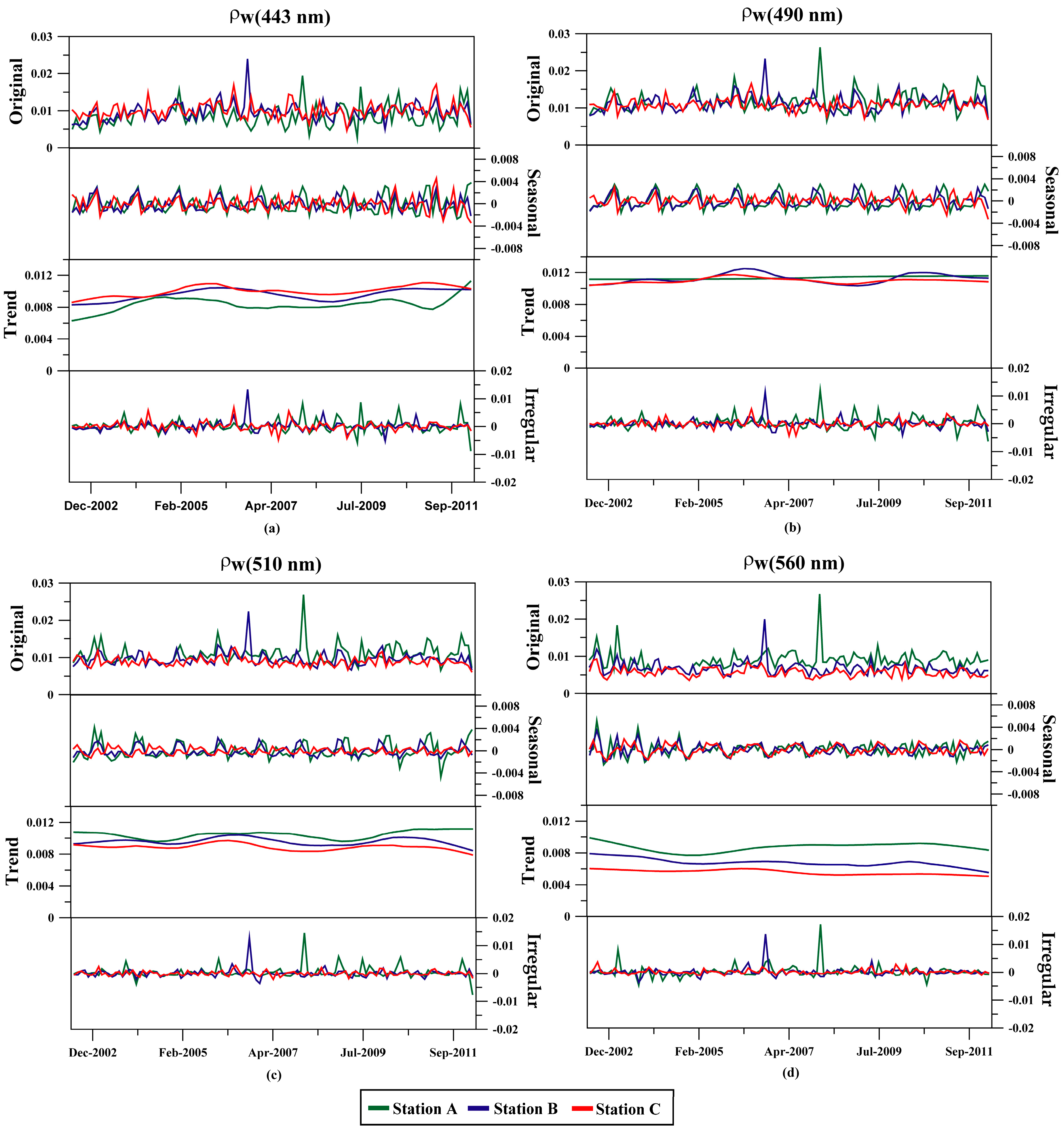
3.2. Analysis of the Decomposition of a MERIS Time Series
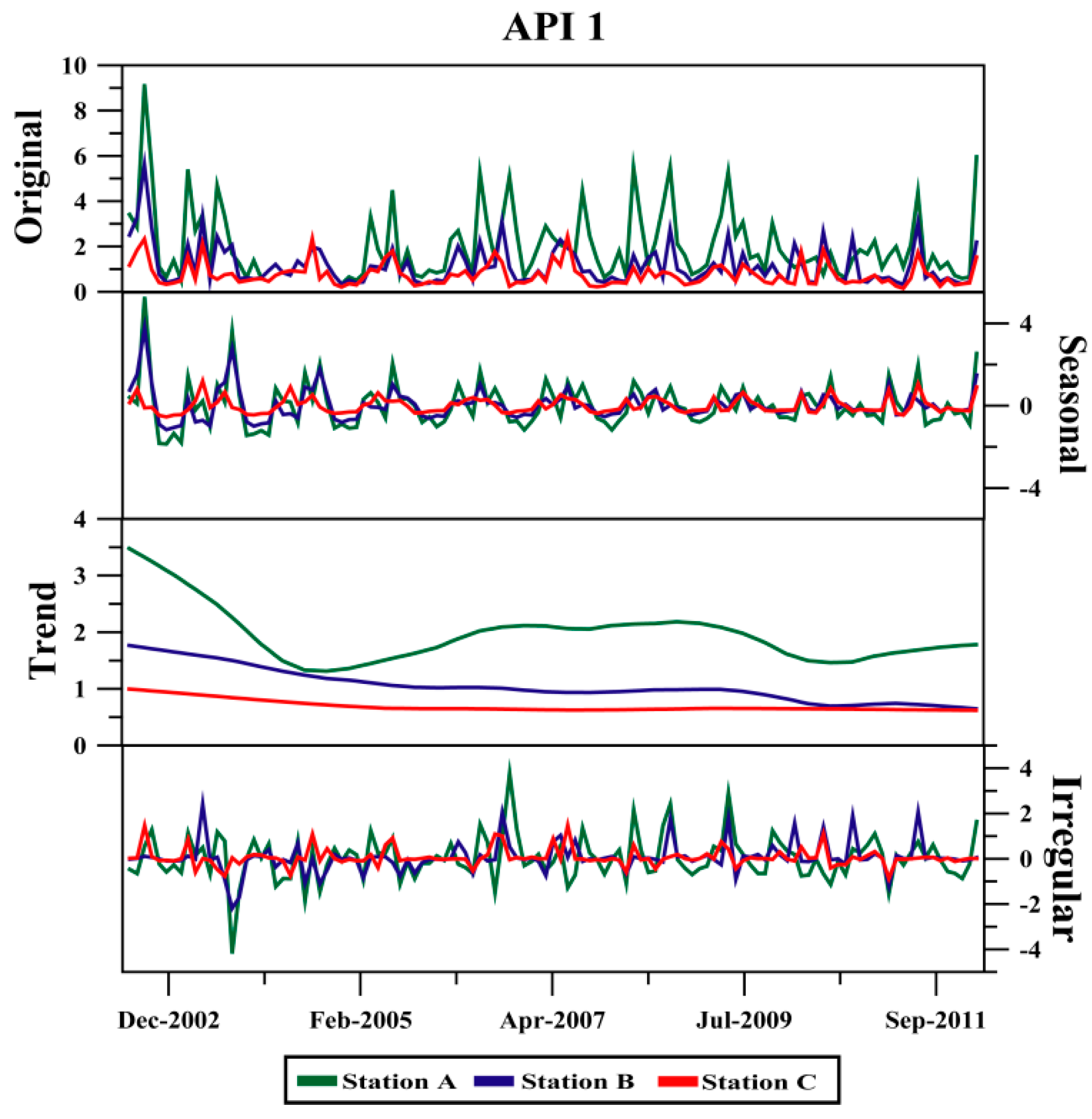
3.3. Modelling with stl.fit()
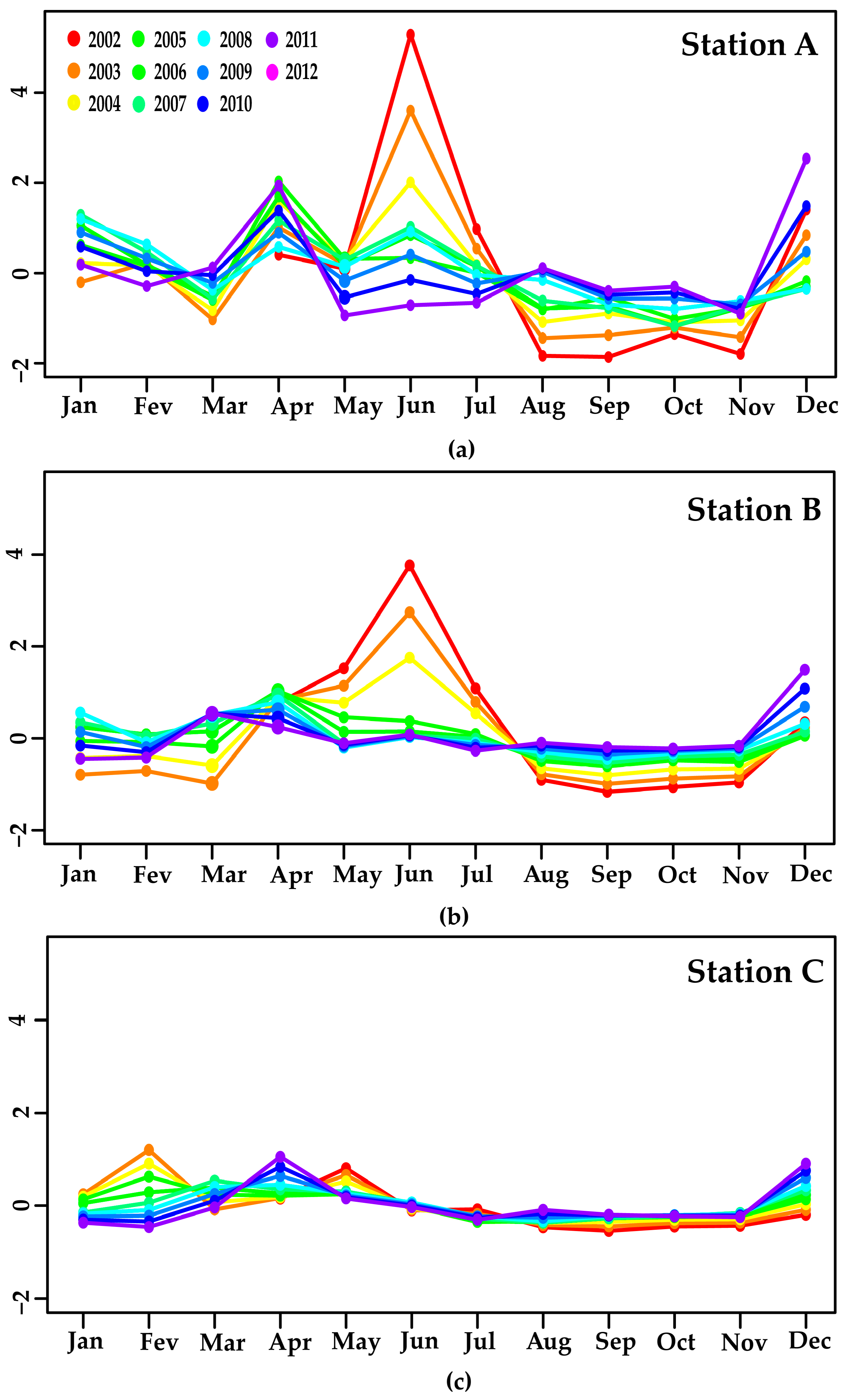
3.4. Inter-Annual Variability of the Seasonal Component of MERIS API 1
4. Discussion
4.1. The stl.fit() Approach
4.2. MERIS Time Series
- (1)
- Will stl.fit() capture the dynamics of the time series of the study area better?
- (2)
- How can stl.fit() be used to describe and explain the variability of the study area?
5. Conclusions
- This study has analyzed the MERIS time series for the products, water leaving reflectance ρw(λ) and the Algal Pigment Index 1 (API 1) at Sagres on the SW coast of Iberia. The optical characteristics of this area are well characterized from in situ validation of MERIS between 2008 and 2012.
- The variation in the MERIS time series has been decomposed into components representing seasonal (), trend () and irregular () fluctuations using the Seasonal-Trend decomposition (STL) based on Loess. The advantages of STL is that it can identify a seasonal component that changes over time, it is responsive to nonlinear trends, and it is robust in the presence of outliers. It is also available within the R software through the stl() function.
- One of the novelties in this study is the development of stl.fit() which has the advantages of the STL but also allows an automatic selection of the best model, by varying the values of the smoothing parameters, based on minimizing the error measure.
- After decomposing the MERIS products time series into seasonal, trend and irregular components, the interquartile range is taken into account. The ρw(λ) product is dominated by both the seasonal and irregular components, whilst the API 1 product is dominated mainly by the seasonal component, with an increasing effect from inshore to offshore.
- The comparison of the seasonal components between the ρw(λ) and the API 1 product at Sagres site, shows that the variations during the 10 years of monthly observations decrease along this period .
- A more detailed study of the inter-annual seasonal variation for API 1 shows the influence of upwelling events, and in which month(s) of the year these occur at each of the three stations at Sagres. Most of the inter-annual seasonal variability of MERIS products can be explained by the optically significant constituents of these waters. Nevertheless, future studies should also take into account the physical and climatic variables that are related to and influence the ρw(λ) and API 1 off Sagres.
- This study, demonstrates how stl.fit() procedure is a good option for any remote sensing study of time series, particularly those addressing inter-annual seasonal variations. This procedure will be made available in R software, so that it is accessible to a wider community, including other fields of research.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zibordi, G.; Berthon, J.-F.; Mélin, F.; D’Alimonte, D. Cross-site consistent in situ measurements for satellite ocean color applications: The BiOMaP radiometric dataset. Remote Sens. Environ. 2011, 115, 2104–2115. [Google Scholar] [CrossRef]
- Kirchgässner, G.; Wolters, J.; Hassler, U. Introduction to Modern Time Series Analysis; Springer-Verlag: Berlin, Germany; Heidelberg, Germany, 2008. [Google Scholar]
- Vantrepotte, V.; Mélin, F. Temporal variability in SeaWiFS derived apparent optical properties in European seas. Cont. Shelf Res. 2010, 30, 319–334. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Mélin, F. Inter-annual variations in the SeaWiFS global chlorophyll a concentration (1997–2007). Deep Sea Res. Part I 2011, 58, 429–441. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Clerici, M.; D’Alimonte, D.; Zibordi, G.; Berthon, J.F.; Canuti, E. Multi-sensor satellite time series of optical properties and chlorophyll-a concentration in the Adriatic Sea. Prog. Oceanogr. 2011, 91, 229–244. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.-F. Intra-annual variations of biases in remote sensing primary ocean color products at a coastal site. Remote Sens. Environ. 2012, 124, 627–636. [Google Scholar] [CrossRef]
- Alikas, K.; Kangro, K.; Randoja, R.; Philipson, P.; Asukull, E.; Pisek, J.; Reinart, A. Satellite-based products for monitoring optically complex inland waters in support of EU Water Framework Directive. Int. J. Remote Sens. 2015, 36, 4446–4468. [Google Scholar] [CrossRef]
- Bisgaard, S.; Kulahci, M. Time series model selection. In Book Time Series Analysis and Forecasting by Example, 1st ed.; Shewhart, W.A., Wilks, S.S., Eds.; John Wiley & Sons, Inc. Publication: Hoboken, NJ, USA, 2011; pp. 155–175. [Google Scholar]
- Loisel, H.; Mangin, A.; Vantrepotte, V.; Dessailly, D.; Dinh, D.N.; Garnesson, P.; Ouillon, S.; Lefebvre, J.-P.; Mériaux, X.; Phan, T.M. Variability of suspended particulate matter concentration in coastal waters under the Mekong’s influence from ocean color (MERIS) remote sensing over the last decade. Remote Sens. Environ. 2014, 150, 218–230. [Google Scholar]
- Volpe, G.; Colella, S.; Forneris, V.; Tronconi, C.; Santoleri, R. The mediterranean ocean colour observing system—System development and product validation. Ocean Sci. 2012, 8, 869–883. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice. Available online: http://otexts.org/fpp/ (accessed on 8 September 2015).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Ndungu, J.; Monger, B.C.; Augustijn, D.C.; Hulscher, S.J.; Kitaka, N.; Mathooko, J.M. Evaluation of spatio-temporal variations in chlorophyll-a in Lake Naivasha, Kenya: Remote-sensing approach. Int. J. Remote Sens. 2013, 34, 8142–8155. [Google Scholar] [CrossRef]
- Lu, H.; Li, Y.; Clilverd, M.A.; Jarvis, M.J. Trend and abrupt changes in long-term geomagnetic indices. J. Geophy. Res. Space 2012, 117, 1–14. [Google Scholar] [CrossRef]
- Petropavlovskikh, I.; Evans, R.; McConville, G.; Manney, G.L.; Rieder, H.E. The influence of the North Atlantic Oscillation and El Niño-Southern Oscillation on mean and extreme values of column ozone over the United States. Atmos. Chem. Phys. 2015, 15, 1585–1598. [Google Scholar] [CrossRef]
- Brown, C.W.; Uz, S.S.; Corliss, B.H. Seasonality of oceanic primary production and its interannual variability from 1998 to 2007. Deep Sea Res. Part I 2014, 90, 166–175. [Google Scholar] [CrossRef]
- Novoa, S.; Chust, G.; Sagarminaga, Y.; Revilla, M.; Borja, A.; Franco, J. Water quality assessment using satellite-derived chlorophyll-a within the European directives, in the southeastern Bay of Biscay. Mar. Pollut. Bull. 2012, 64, 739–750. [Google Scholar] [CrossRef] [PubMed]
- Cristina, S.; Icely, J.; Goela, P.C.; DelValls, T.A.; Newton, A. Using remote sensing as a support to the implementation of the European Marine Strategy Framework Directive in SW Portugal. Cont. Shelf Res. 2015, 108, 169–177. [Google Scholar] [CrossRef]
- Kratzer, S.; Harvey, E.T.; Philipson, P. The use of ocean color remote sensing in integrated coastal zone management—A case study from Himmerfjärden, Sweden. Mar. Policy 2014, 43, 29–39. [Google Scholar] [CrossRef]
- Harvey, E.T.; Kratzer, S.; Philipson, P. Satellite-based water quality monitoring for improved spatial and temporal retrieval of chlorophyll-a in coastal waters. Remote Sens. Environ. 2015, 158, 417–430. [Google Scholar] [CrossRef]
- Cristina, S.C.V.; Moore, G.F.; Goela, P.R.F.C.; Icely, J.D.; Newton, A. In situ validation of MERIS marine reflectance off the southwest Iberian Peninsula: Assessment of vicarious adjustment and corrections for near-land adjacency. Int. J. Remote Sens. 2014, 35, 2347–2377. [Google Scholar]
- Cristina, S.V.; Goela, P.; Icely, J.D.; Newton, A.; Fragoso, B. Assessment of water-leaving reflectances of oceanic and coastal waters using MERIS satellite products off the southwest coast of Portugal. J. Coast. Res. 2009, 56, 1479–1483. [Google Scholar]
- Goela, P.C.; Icely, J.; Cristina, S.; Newton, A.; Moore, G.; Cordeiro, C. Specific absorption coefficient of phytoplankton off the southwest coast of the Iberian Peninsula: A contribution to algorithm development for ocean colour remote sensing. Cont. Shelf Res. 2013, 52, 119–132. [Google Scholar] [CrossRef]
- Goela, P.C.; Icely, J.; Cristina, S.; Danchenko, S.; DelValls, T.; Newton, A. Using bio-optical parameters as a tool for detecting changes in the phytoplankton community (SW Portugal). Estuar. Coast. Shelf Sci. 2015, 167, 125–137. [Google Scholar] [CrossRef]
- Goela, P.; Danchenko, S.; Icely, J.; Lubián, L.; Cristina, S.; Newton, A. Using CHEMTAX to evaluate seasonal and interannual dynamics of the phytoplankton community off the South-west Coast of Portugal. Estuar. Coast. Shelf Sci. 2014, 151, 112–123. [Google Scholar] [CrossRef]
- Goela, P.; Newton, A.; Cristina, S.; Fragoso, B. Water framework directive implementation: Intercalibration exercise for biological quality elements—A case study for the south coast of Portugal. J. Coast. Res. 2009, 56, 1214–1218. [Google Scholar]
- Loureiro, S.; Icely, J.; Newton, A. Enrichment experiments and primary production at Sagres (SW Portugal). J. Exp. Mar. Biol. Ecol. 2008, 359, 118–125. [Google Scholar] [CrossRef]
- Loureiro, S.; Reñé, A.; Garcés, E.; Camp, J.; Vaqué, D. Harmful algal blooms (HABs), dissolved organic matter (DOM), and planktonic microbial community dynamics at a near-shore and a harbour station influenced by upwelling (SW Iberian Peninsula). J. Sea Res. 2011, 65, 401–413. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D. Mesoscale patterns in the Cape São Vicente (Iberian Peninsula) upwelling region. J. Geophys. Res. Oceans 2002, 107, 28:1–28:23. [Google Scholar] [CrossRef]
- Loureiro, S.; Newton, A.; Icely, J.D. Microplankton composition, production and upwelling dynamics in Sagres (SW Portugal) during the summer of 2001. Sci. Mar. 2005, 69, 323–341. [Google Scholar]
- Ramos, A.M.; Pires, A.C.; Sousa, P.M.; Trigo, R.M. The use of circulation weather types to predict upwelling activity along the western Iberian Peninsula coast. Cont. Shelf Res. 2013, 69, 38–51. [Google Scholar] [CrossRef]
- Basic ERS & ENVISAT (A) ATSR and MERIS Toolbox (BEAM Version 4.11). Available online: http://www.brockmann-consult.de/cms/web/beam/ (accessed on 1 September 2015).
- Optical Data Processor of the European Space Agency (ODESA). Available online: http://www.odesa-info.eu/process_basic/basic.php (accessed on 1 September 2015).
- MERIS Quality Working Group (QWG). MERIS 3rd Data Reprocessing—Software and ADF Updated, Technical Document Ref. A879.NT.008.ACRI-ST. 27 June 2011. Available online: https://earth.esa.int/web/guest/-/meris-3rd-data-reprocessing-software-and-adf-updates-7929 (accessed on 30 September 2015).
- Morel, A.; Antoine, D. Pigment Index Retrieval in Case 1 Waters, Algorithm Theoretical Basis Document PO-TN-MEL-GS-0005. 2007. Available online: https://earth.esa.int/documents/700255/2042855/MERIS_ATBD_2.9_v4.3+-+2011.pdf (accessed on 30 September 2015).
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Brockmann, C. Limitations of the application of the MERIS atmospheric correction. In Proceedings of the Second Working Meeting on MERIS and AATSR Calibration and Geophysical Validation, Frascati, Italy, 20–24 March 2006.
- ESA. MERIS Product Handbook Issue 3.0. Available online: https://earth.esa.int/handbooks/meris/CNTR.html (accessed on 7 September 2015).
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.E.; Bernard, S.; O’Donoghue, S. The assessment of optimal MERIS ocean colour products in the shelf waters of the KwaZulu-Natal Bight, South Africa. Remote Sens. Environ. 2013, 137, 124–138. [Google Scholar] [CrossRef]
- Hyndman, R.J. Forecast: Forecasting Functions for Time Series and Linear Models, R Package Version 6.2. Available online: http://github.com/robjhyndman/forecast (accessed on 30 October 2015).
- Qian, S.S.; Borsuk, M.E.; Stow, C.A. Seasonal and long-term nutrient trend decomposition along a spatial gradient in the Neuse River watershed. Environ. Sci. Technol. 2000, 34, 4474–4482. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Wang, J.; Xiao, Z. Modeling MODIS LAI time series using three statistical methods. Remote Sens. Environ. 2010, 114, 1432–1444. [Google Scholar] [CrossRef]
- Pezzulli, S.; Stephenson, D.B.; Hannachi, A. The variability of seasonality. J. Clim. 2005, 18, 71–88. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Mélin, F. Temporal variability of 10-year global SeaWiFS time-series of phytoplankton chlorophyll-a concentration. ICES J. Mar. Sci. 2009, 66, 1547–1556. [Google Scholar] [CrossRef]
- Cardeira, S.; Rita, F.; Relvas, P.; Cravo, A. Chlorophyll a and chemical signatures during an upwelling event off the South Portuguese coast (SW Iberia). Cont. Shelf Res. 2013, 52, 149. [Google Scholar] [CrossRef]
- Goela, P.C.; Cordeiro, C.; Danchenko, S.; Icely Cristina, S.; Newton, A. Time series analysis of data for Sea Surface Temperature and Upwelling components from the Southwest Coast of Portugal. J. Mar. Syst. 2016. under review. [Google Scholar]
| A | B | C | ||||
|---|---|---|---|---|---|---|
| stl() | stl.fit() | stl() | stl.fit() | stl() | stl.fit() | |
| ρw(443) | 0.0024 | 0.0023 (12, 21) | 0.0021 | 0.0019 (7, 32) | 0.0019 | 0.0016 (7, 23) |
| ρw(490) | 0.0023 | 0.0023 (116,116) | 0.0018 | 0.0017 (7, 23) | 0.0014 | 0.0013 (8, 26) |
| ρw(510) | 0.0022 | 0.0021 (7, 23) | 0.0016 | 0.0016 (7, 23) | 0.0009 | 0.0009 (22, 21) |
| ρw(560) | 0.0023 | 0.0022 (7, 36) | 0.0017 | 0.0016 (7, 24) | 0.0009 | 0.0008 (14, 36) |
| API 1 | 1.3259 | 0.9813 (7, 26) | 0.7722 | 0.6529 (7, 23) | 0.4325 | 0.3900 (7, 41) |
| A | B | C | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Seasonal | Trend | Irregular | Seasonal | Trend | Irregular | Seasonal | Trend | Irregular | |
| ρw (443) | 62.9 | 26.9 | 52.4 | 47.1 | 39.9 | 58.1 | 67.9 | 35.9 | 51.2 |
| ρw (490) | 75.2 | 10.3 | 59.6 | 62.1 | 39.8 | 77.1 | 56.8 | 20.5 | 73.8 |
| ρw (510) | 59.0 | 27.1 | 45.7 | 55.3 | 35.6 | 73.0 | 65.6 | 27.9 | 90.6 |
| ρw (560) | 68.1 | 30.2 | 60.4 | 63.8 | 20.7 | 59.2 | 59.1 | 28.2 | 40.0 |
| API 1 | 75.1 | 33.9 | 76.1 | 75.3 | 27.0 | 19.6 | 93.6 | 12.7 | 27.1 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cristina, S.; Cordeiro, C.; Lavender, S.; Costa Goela, P.; Icely, J.; Newton, A. MERIS Phytoplankton Time Series Products from the SW Iberian Peninsula (Sagres) Using Seasonal-Trend Decomposition Based on Loess. Remote Sens. 2016, 8, 449. https://doi.org/10.3390/rs8060449
Cristina S, Cordeiro C, Lavender S, Costa Goela P, Icely J, Newton A. MERIS Phytoplankton Time Series Products from the SW Iberian Peninsula (Sagres) Using Seasonal-Trend Decomposition Based on Loess. Remote Sensing. 2016; 8(6):449. https://doi.org/10.3390/rs8060449
Chicago/Turabian StyleCristina, Sónia, Clara Cordeiro, Samantha Lavender, Priscila Costa Goela, John Icely, and Alice Newton. 2016. "MERIS Phytoplankton Time Series Products from the SW Iberian Peninsula (Sagres) Using Seasonal-Trend Decomposition Based on Loess" Remote Sensing 8, no. 6: 449. https://doi.org/10.3390/rs8060449
APA StyleCristina, S., Cordeiro, C., Lavender, S., Costa Goela, P., Icely, J., & Newton, A. (2016). MERIS Phytoplankton Time Series Products from the SW Iberian Peninsula (Sagres) Using Seasonal-Trend Decomposition Based on Loess. Remote Sensing, 8(6), 449. https://doi.org/10.3390/rs8060449








