Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers
Abstract
:1. Introduction
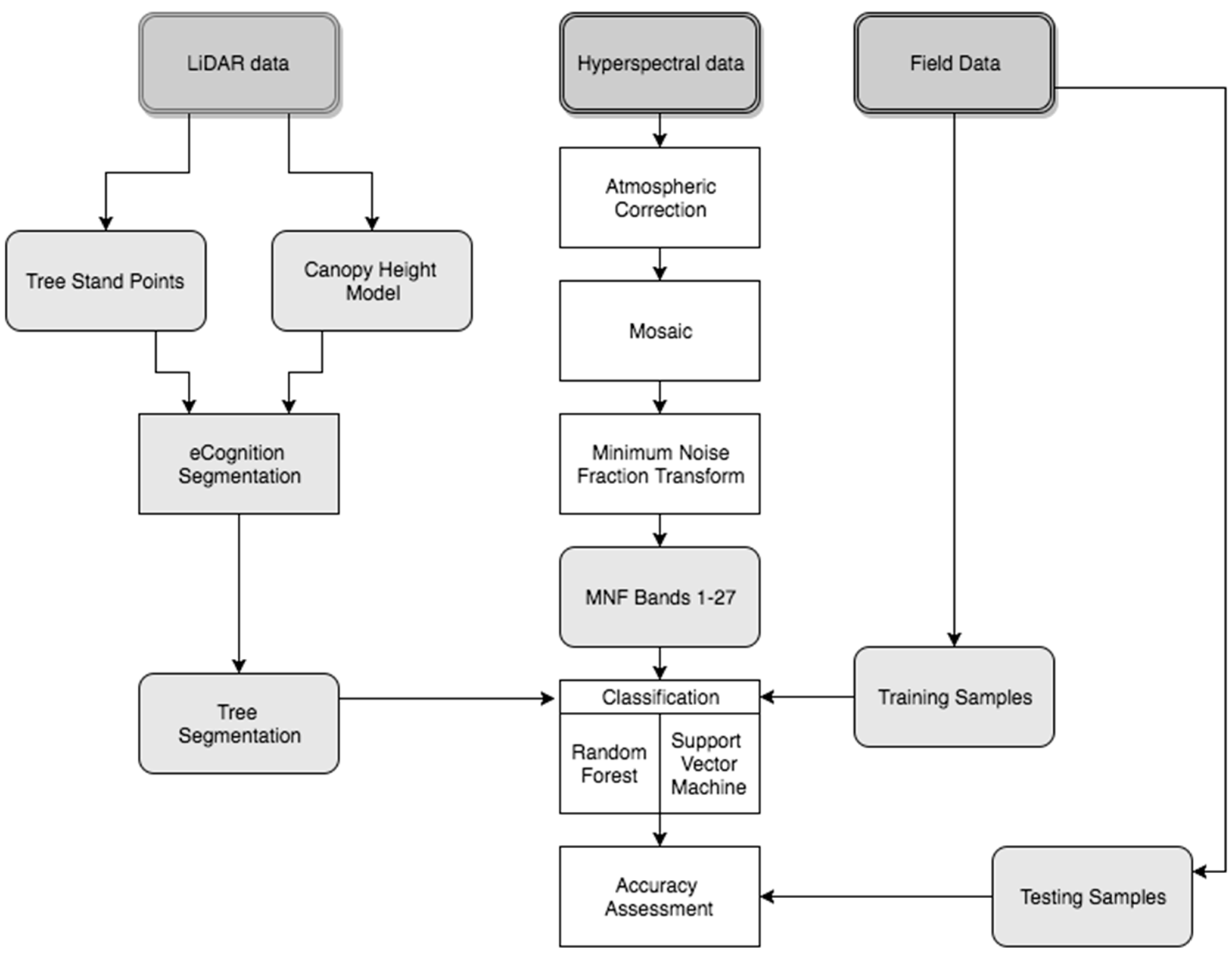
2. Materials and Methods
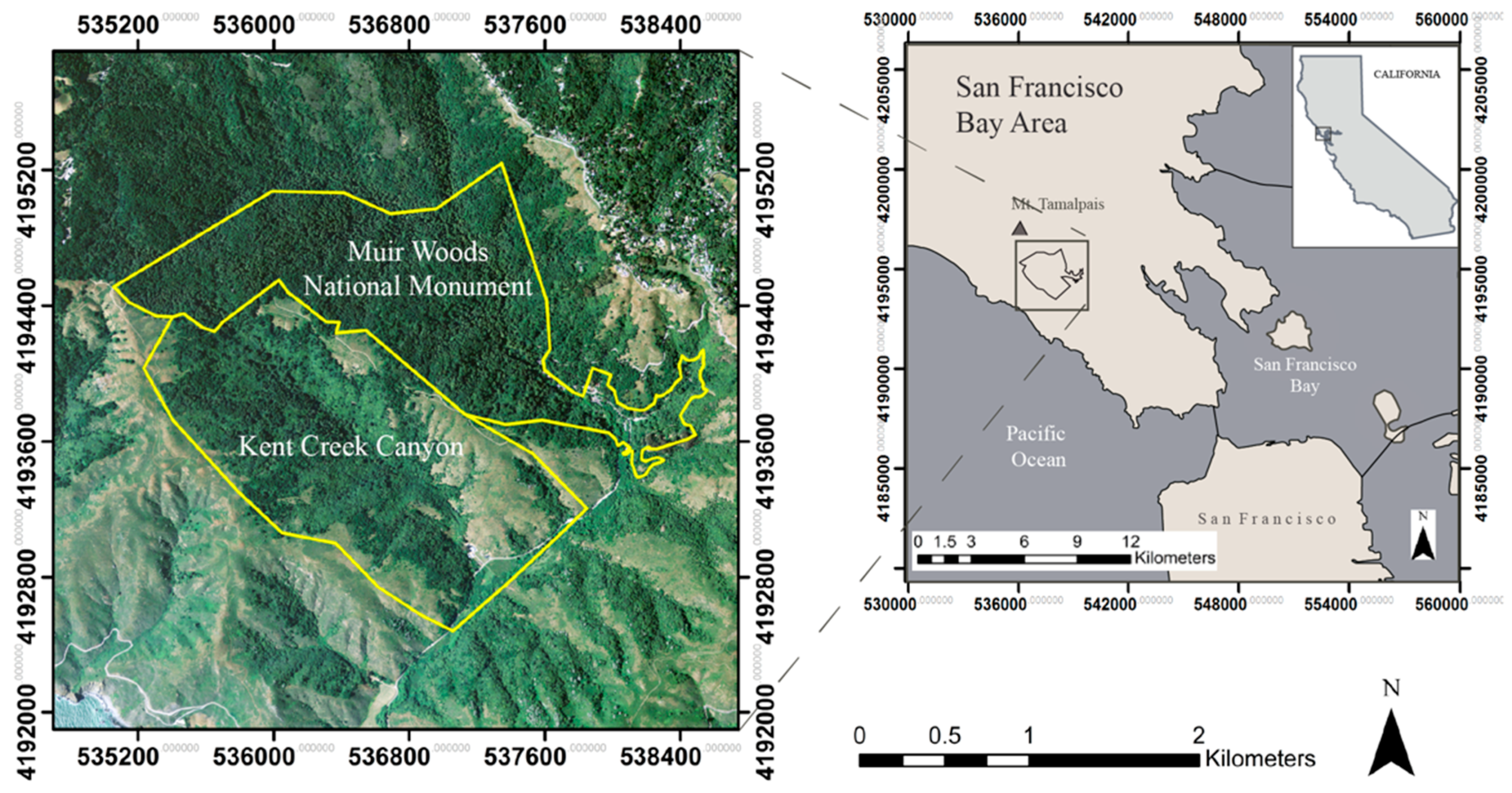
2.1. Study Area
2.2. Remote Sensing Data
2.3. Pre-Processing
2.4. Masking
2.5. Object-Based Tree Segmentation
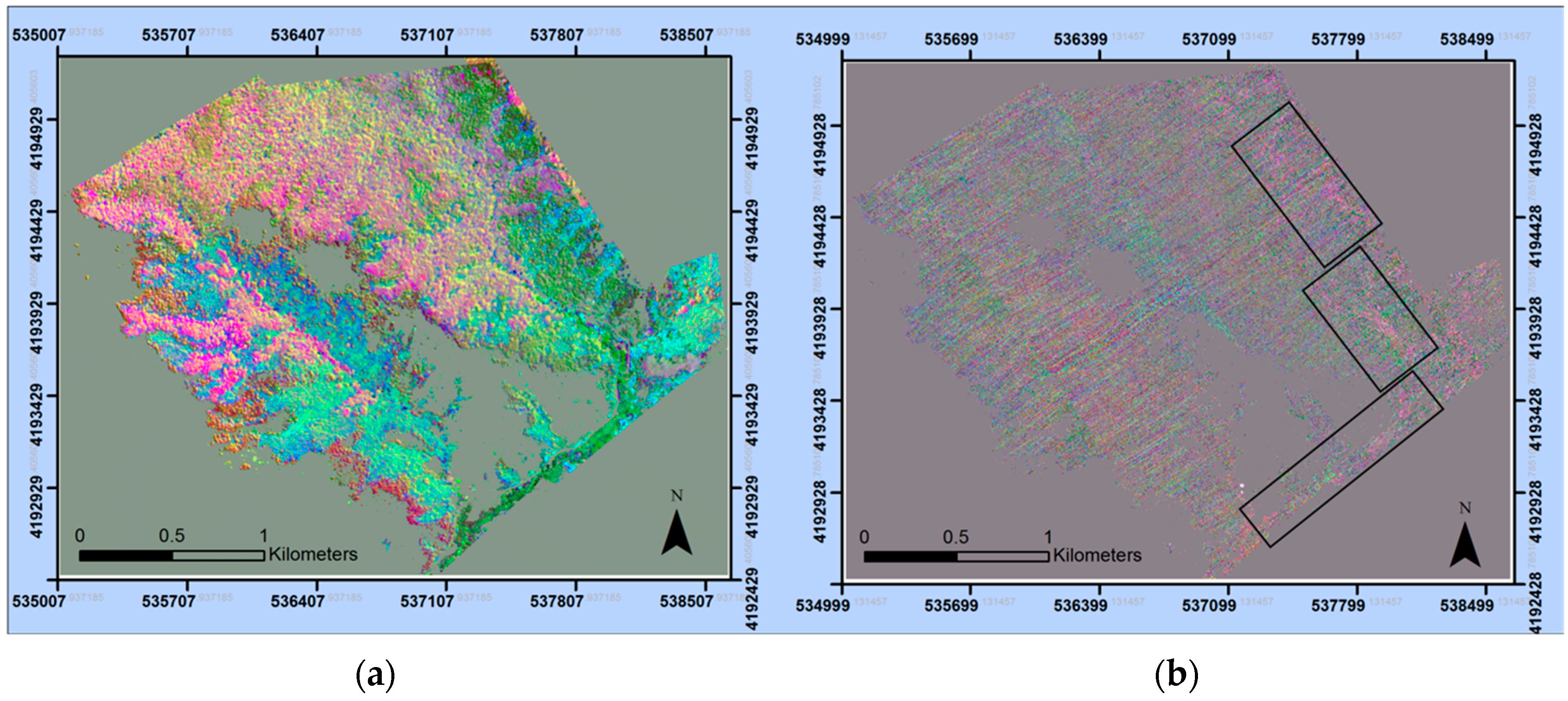
2.6. Data Reduction and Feature Selection
2.7. Sample Data
2.8. Classification
2.9. Accuracy Assessment
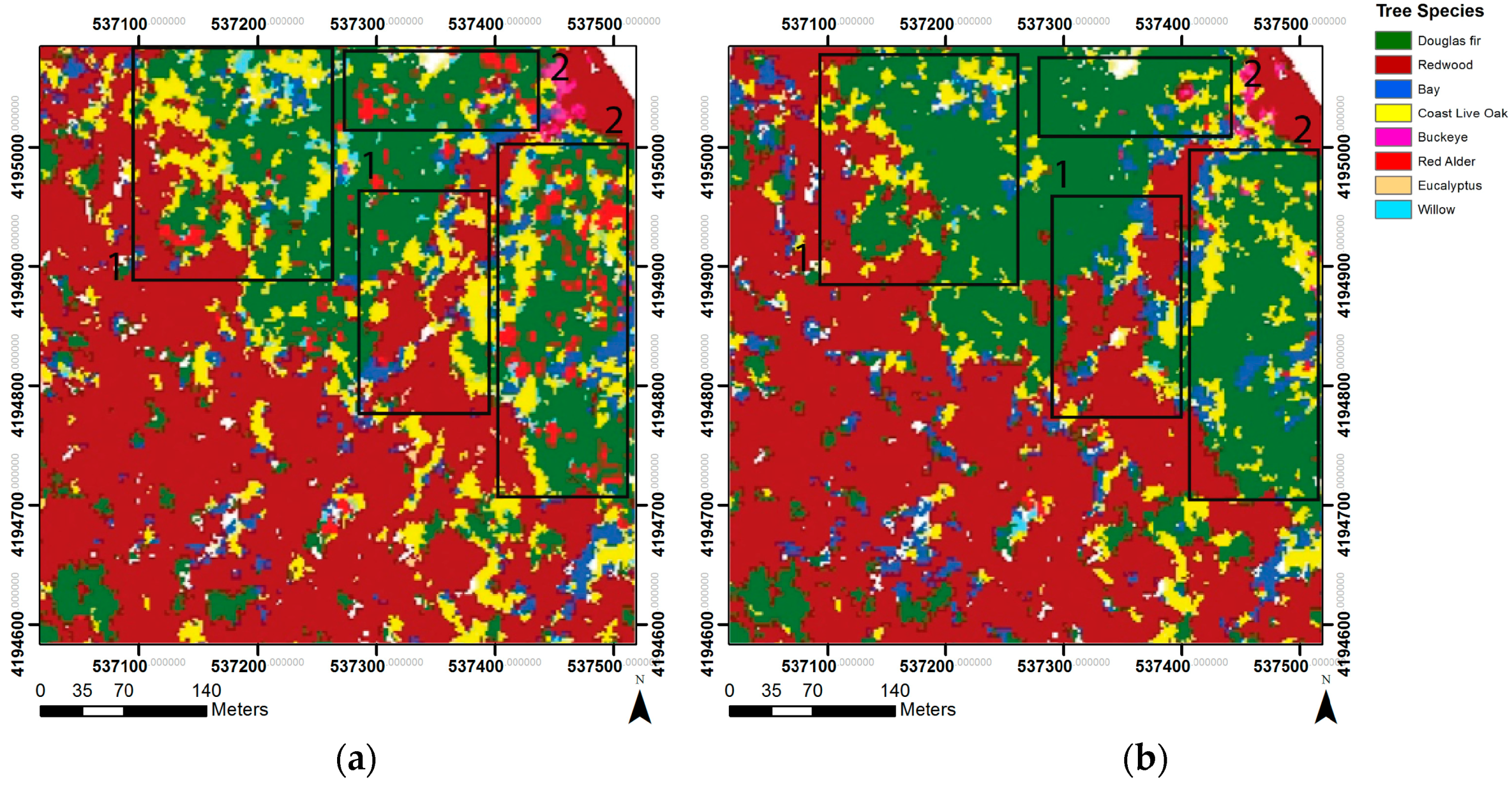
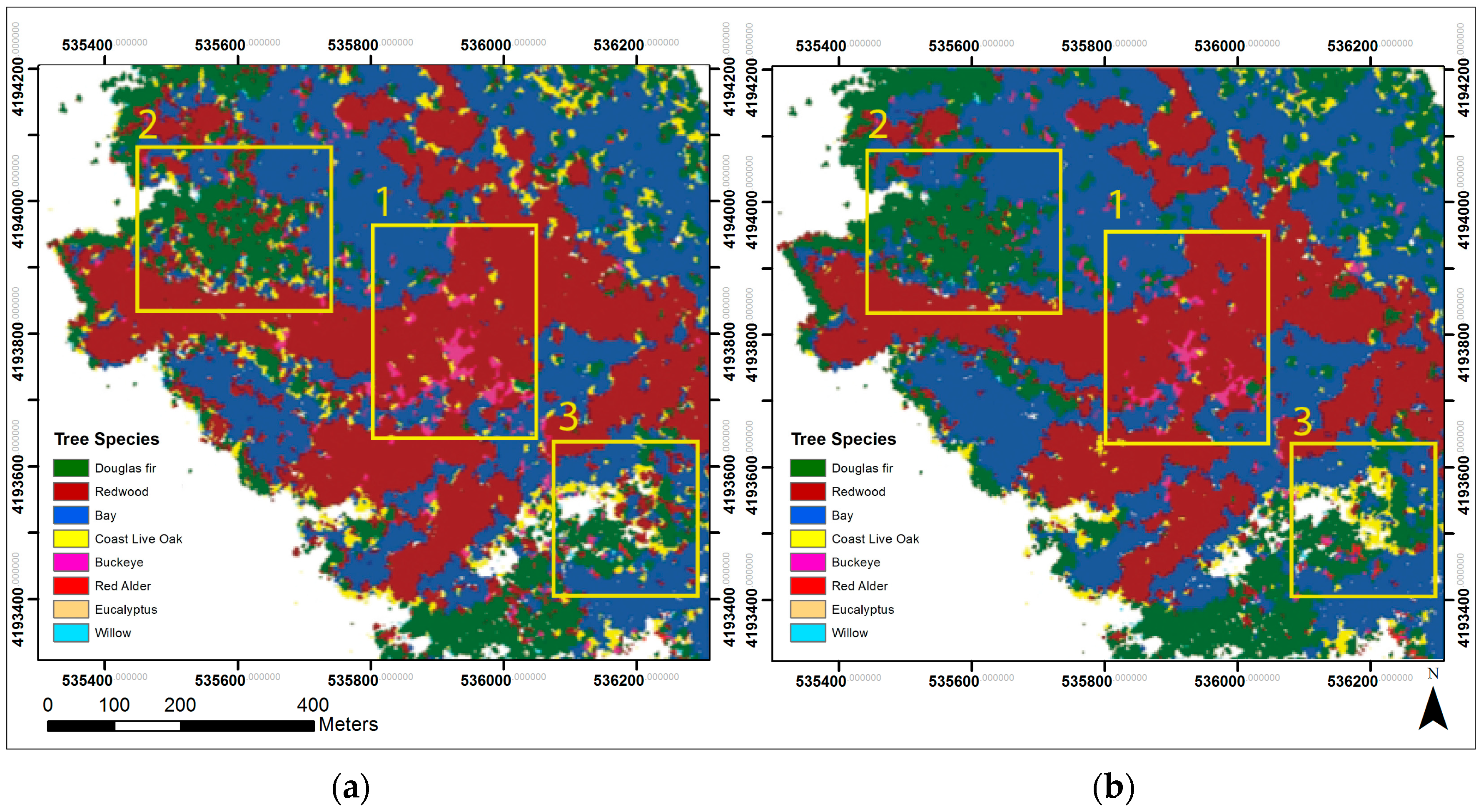
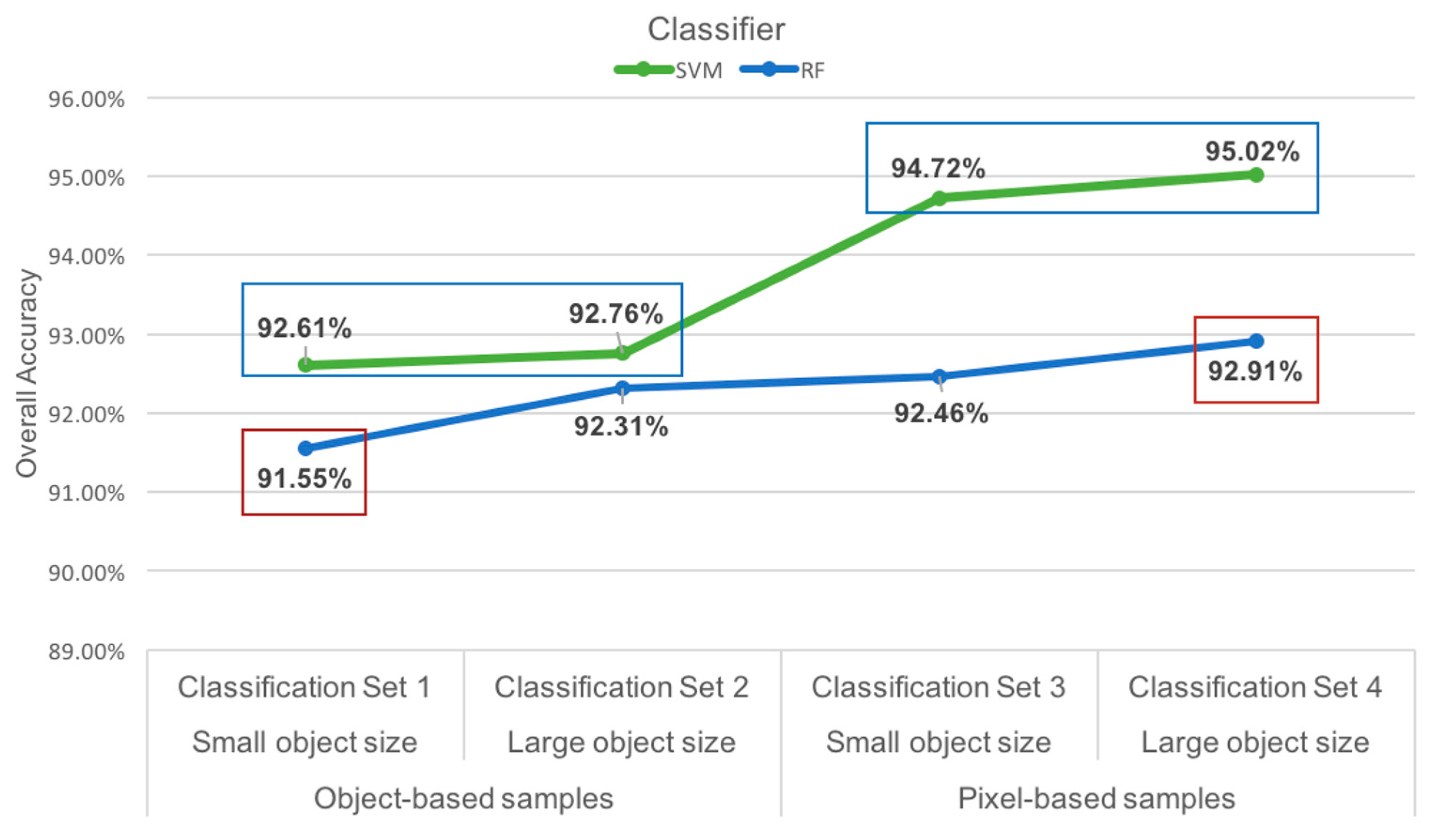
3. Results
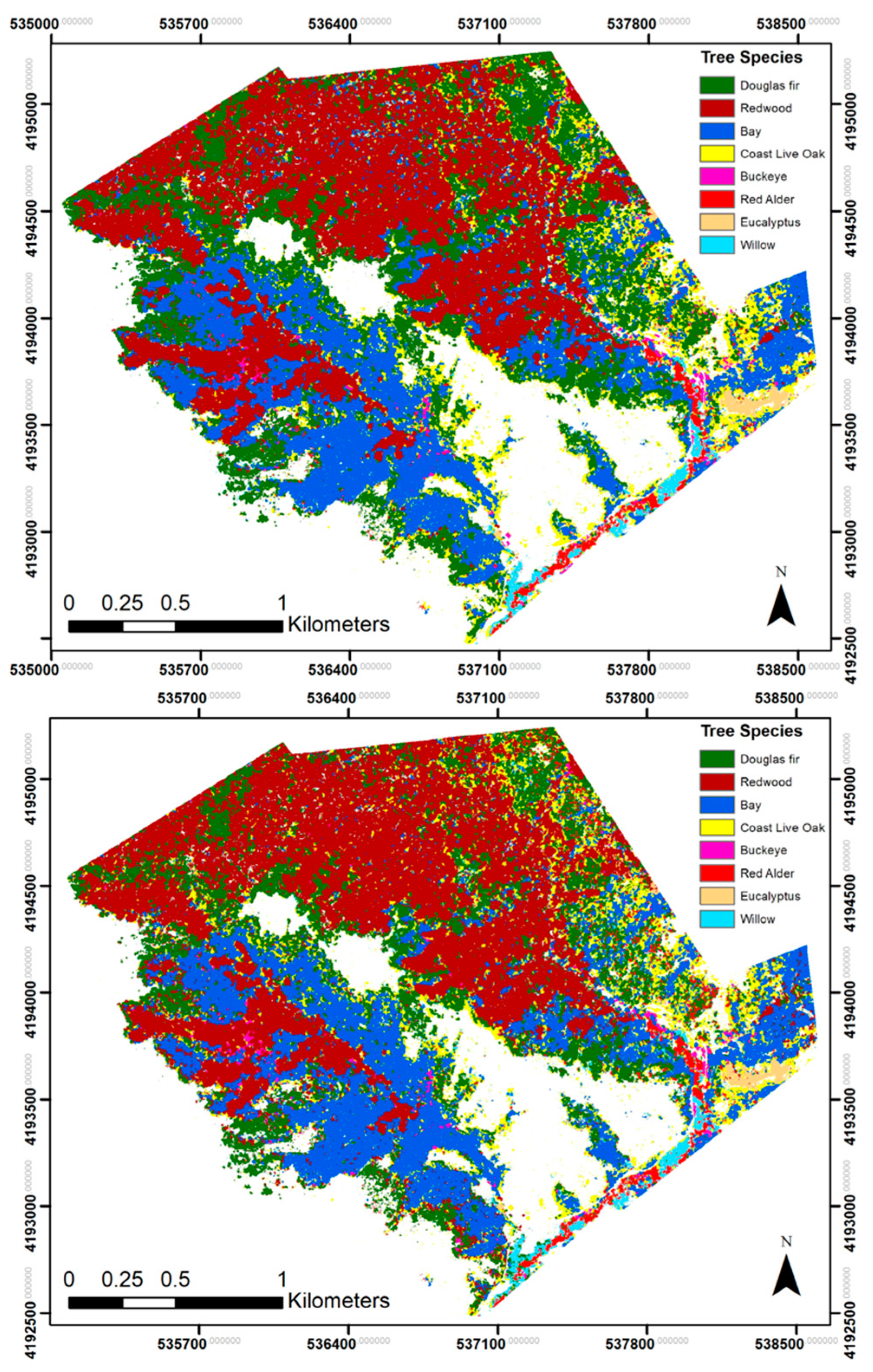
3.1. Overall Classification Results
3.2. Best Performance: Classification Set 4
3.3. Individual Classifier Performance
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DEM | digital elevation model |
| CHM | canopy height model |
| SVM | support vector machine |
| RBF | radial basis function |
| RF | random forest |
| MNF | minimum noise fraction |
References
- Leckie, D.G.; Tinis, S.; Nelson, T.; Burnett, C.; Gougeon, F.A.; Cloney, E.; Paradine, D. Issues in species classification of trees in old growth conifer stands. Can. J. Remote Sens. 2005, 31, 175–190. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LIDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Commercial tree species discrimination using airborne AISA Eagle hyperspectral imagery and partial least squares discriminant analysis (PLS-DA) in KwaZulu–Natal, South Africa. ISPRS J. Photogramm. Remote Sens. 2013, 79, 19–28. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinform. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Franklin, S.E. Remote Sensing for Sustainable Forest Management; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Dale, V.; Joyce, L.; McNulty, S.; Neilson, R.; Ayres, M.; Flannigan, M.; Hanson, R.; Irland, L.; Lugo, A.; Peterson, C.; et al. Climate Change and Forest Disturbances. BioScience 2001, 51, 723–734. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral Image Data Analysis as a High Dimensional Signal Processing Problem. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Van Aardt, J.A.N.; Wynne, R.H. Examining pine spectral separability using hyperspectral data from an airborne sensor: An extension of field-based results. Int. J. Remote Sens. 2007, 28, 431–436. [Google Scholar] [CrossRef]
- Martin, M.E.; Newman, S.D.; Aber, J.D.; Congalton, R.G. Determining forest species composition using high spectral resolution remote sensing data. Remote Sens. Environ. 1998, 65, 249–254. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Akar, Ö.; Güngör, O. Classification of multispectral images using Random Forest algorithm. J. Geod. Geoinform. 2012, 1, 105–112. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, A.; Söderman, U. Species identification of individual trees by combining high resolution LiDAR data with multi-spectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Tree species classification in the Southern Alps based on the fusion of very high geometrical resolution multispectral/hyperspectral images and LiDAR data. Remote Sens. Environ. 2012, 123, 258–270. [Google Scholar] [CrossRef]
- Key, T.; Warner, T.A.; McGraw, J.B.; Fajvan, M.A. A comparison of multispectral and multitemporal information in high spatial resolution imagery for classification of individual tree species in a temperate hardwood forest. Remote Sens. Environ. 2001, 75, 100–112. [Google Scholar] [CrossRef]
- Franklin, S.E.; Hall, R.J.; Moskal, L.M.; Maudie, A.J.; Lavigne, M.B. Incorporating texture into classification of forest species composition from airborne multispectral images. Int. J. Remote Sens. 2000, 21, 61–79. [Google Scholar] [CrossRef]
- Shippert, P. Why use hyperspectral imagery? Photogramm. Eng. Remote Sens. 2004, 70, 377–396. [Google Scholar]
- Heinzel, J.; Koch, B. Investigating multiple data sources for tree species classification in temperate forest and use for single tree delineation. Int. J. Appl. Earth Obs. Geoinform. 2012, 18, 101–110. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognit. 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
- Jones, T.G.; Coops, N.C.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest, Canada. Remote Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Hughes, G.F. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inform. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Rojas, M.; Dópido, I.; Plaza, A.; Gamba, P. Comparison of support vector machine-based processing chains for hyperspectral image classification. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Voss, M.; Sugumaran, R. Seasonal effect on tree species classification in an urban environment using hyperspectral data, LiDAR, and an object-oriented approach. Sensors 2008, 8, 3020–3036. [Google Scholar] [CrossRef]
- Buddenbaum, H.; Schlerf, M.; Hill, J. Classification of coniferous tree species and age classes using hyperspectral data and geostatistical methods. Int. J. Remote Sens. 2005, 26, 5453–5465. [Google Scholar] [CrossRef]
- Denghui, Z.; Le, Y. Support vector machine based classification for hyperspectral remote sensing images after minimum noise fraction rotation transformation. In Proceedings of the 2011 International Conference on Internet Computing & Information Services (ICICIS), Hong Kong, China, 17–18 September 2011.
- Exelis Visual Information Solutions. ENVI Help; Exelis Visual Information Solutions: Boulder, CO, USA, 2013. [Google Scholar]
- Xiao, Q.; Ustin, S.L.; McPherson, E.G. Using AVIRIS data and multiple-masking techniques to map urban forest tree species. Int. J. Remote Sens. 2004, 25, 5637–5654. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Naesset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- MacLean, M.G.; Congalton, R. Map accuracy assessment issues when using an object-oriented approach. In Proceedings of the American Society for Photogrammetry and Remote Sensing 2012 Annual Conference, Sacramento, CA, USA, 19–23 March 2012.
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Schoenherr, A.A. A Natural History of California; University of California Press: Berkeley, CA, USA, 1992. [Google Scholar]
- National Parks Conservation Association. State of the Parks, Muir Woods National Monument: A Resource Assessment. 2011. Available online: http://www.npca.org/about-us/center-for-parkresearch/stateoftheparks/muir_woods/MuirWoods.pdf (accessed on 22 October 2014).
- National Park Service. Annual Park Recreation Visitation (1904—Last Calendar Year) Muir Woods NM (MUWO) Reports. 2014. Available online: https://irma.nps.gov/Stats/Reports/Park/MUWO (accessed on 6 October 2015). [Google Scholar]
- National Park Service. Muir Woods: 100th Anniversary 2008; 2008. Available online: http://www.nps.gov/muwo/upload/unigrid_muwo.pdf (accessed on 22 October 2014).
- Ellen, H. Final Report: Golden Gate LiDAR Project; San Francisco State University: San Francisco, CA, USA, 2011. [Google Scholar]
- Stephen, R. GGLP SFSU Hyperspectral Processing Report; University of Victoria- Hyperspectral—LiDAR Research Laboratory: Victoria, BC, Canada, 2013. [Google Scholar]
- QCoherent. LP360, Version 2013. Available online: http://www.qcoherent.com/ (accessed on 30 April 2013).
- GRASS Development Team. Geographic Resources Analysis Support System (GRASS) Software, Version 6.4.4. Available online: http://grass.osgeo.org (accessed on 3 May 2015).
- Trimble. eCognition Developer, Version 9.1. Available online: http://www.ecognition.com (accessed on 12 May 2015).
- Trimble. eCognition: User Guide 9.1; Trimble: Munich, Germany, 2015. [Google Scholar]
- McCoy, R.M. Field Methods in Remote Sensing; Guilford Press: New York City, NY, USA, 2005. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: http://www.R-project.org/ (accessed on 10 June 2015).
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Foody, G. Thematic map comparison: Evaluating the statistical significance differences in classification accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Everitt, B.S. The Analysis of Contingency Tables; Chapman and Hall: London, UK, 1977. [Google Scholar]
- Dietterich, T. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Object-based vegetation mapping in the Kissimmee River watershed using HyMap data and machine learning techniques. Wetlands 2013, 33, 233–244. [Google Scholar] [CrossRef]


| Data | Sensor | Date of Acquisition | Spatial Resolution | Spectral Range | Bands |
|---|---|---|---|---|---|
| Hyperspectral | AISA Eagle | 5–7 May 2010 | 2 m | 397.78–997.96 nm | 128 |
| LiDAR | Leica ALS60 | 5–7 May 2010 | 4–8 points/m2 | 1064 nm | 1 |
| MNF | Eigenvalue | Percent | MNF | Eigenvalue | Percent |
|---|---|---|---|---|---|
| 1 | 1769.69 | 55.56% | 15 | 12.60 | 72.15% |
| 2 | 148.59 | 60.23% | 16 | 12.05 | 72.53% |
| 3 | 79.96 | 62.74% | 17 | 11.37 | 72.89% |
| 4 | 56.29 | 64.51% | 18 | 10.97 | 73.23% |
| 5 | 51.37 | 66.12% | 19 | 10.02 | 73.55% |
| 6 | 31.97 | 67.12% | 20 | 9.48 | 73.84% |
| 7 | 27.03 | 67.97% | 21 | 9.07 | 74.13% |
| 8 | 21.76 | 68.65% | 22 | 8.90 | 8.9096 |
| 9 | 21.35 | 69.33% | 23 | 8.87 | 74.69% |
| 10 | 19.37 | 69.93% | 24 | 8.79 | 74.96% |
| 11 | 16.71 | 70.46% | 25 | 8.73 | 75.24% |
| 12 | 14.09 | 70.90% | 26 | 8.66 | 75.51% |
| 13 | 13.95 | 71.34% | 27 | 8.59 | 75.78% |
| 14 | 13.28 | 71.76% |
| Class | Percent Coverage 1 | Object-Based Small Training Sample Size | Pixel-Based Training Sample Size | Accuracy Assessment Samples |
|---|---|---|---|---|
| Arroyo Willow (Salix lasiolepis) | 1.0% | 10 | 139 | 19 |
| California Bay Laurel (Umbellularia californica) | 26.2% | 27 | 371 | 152 |
| California Buckeye (Aesculus californica) | 0.1% | 12 | 180 | 15 |
| Coast Live Oak (Quercus agrifolia) | 5.1% | 16 | 192 | 30 |
| Coast Redwood (Sequoia sempervirens) | 40.0% | 24 | 254 | 276 |
| Douglas Fir (Pseudotsuga menziesii) | 26.0% | 25 | 236 | 135 |
| Eucalyptus (Eucalyptus globulus) | 0.5% | 23 | 134 | 10 |
| Red Alder (Alnus rubra) | 1.10% | 16 | 201 | 26 |
| Total | 100% | 143 | 1707 | 663 |
| Classification Set | Training Sample Type | Segmentation Object Size |
|---|---|---|
| Classification Set 1: SVM and RF | Object-based reflectance | Small object |
| Classification Set 2: SVM and RF | Object-based reflectance | Large object |
| Classification Set 3: SVM and RF | Pixel-based reflectance | Small object |
| Classification Set 4: SVM and RF | Pixel-based reflectance | Large object |
| Classification Set | Classifier | Overall Accuracy | p-Value | Statistical Significance |
|---|---|---|---|---|
| Classification Set 1 | SVM | 92.61% | 0.3408 | Not significant |
| RF | 91.55% | |||
| Classification Set 2 | SVM | 92.76% | 0.4404 | Not Significant |
| RF | 92.31% | |||
| Classification Set 3 | SVM | 94.72% | 0.0119 | Significant |
| RF | 92.46% | |||
| Classification Set 4 | SVM | 95.02% | 0.0164 | Significant |
| RF | 92.91% |
| Classifier: SVM | DF | RW | Bay | CLO | BU | RA | E | W | Total | User’s Accuracy |
| DF | 126 | 4 | 1 | 2 | 1 | 1 | 0 | 3 | 138 | 91.30 |
| RW | 0 | 271 | 1 | 0 | 0 | 0 | 0 | 0 | 272 | 99.63 |
| Bay | 1 | 0 | 147 | 0 | 0 | 0 | 0 | 0 | 148 | 99.32 |
| CLO | 6 | 1 | 3 | 28 | 0 | 0 | 1 | 3 | 42 | 66.67 |
| BU | 0 | 0 | 0 | 0 | 14 | 0 | 0 | 1 | 15 | 93.33 |
| RA | 1 | 0 | 0 | 0 | 0 | 24 | 0 | 1 | 26 | 92.31 |
| E | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 9 | 100.00 |
| W | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 11 | 13 | 84.62 |
| Total | 135 | 276 | 152 | 30 | 15 | 26 | 10 | 19 | 663 | |
| Producer’s Accuracy | 93.33 | 98.19 | 96.71 | 93.33 | 93.33 | 92.31 | 90.00 | 57.89 | ||
| Overall Accuracy | 95.02 | |||||||||
| Classifier: RF | DF | RW | Bay | CLO | BU | RA | E | W | Total | User’s Accuracy |
| DF | 117 | 3 | 1 | 3 | 0 | 0 | 0 | 2 | 126 | 92.86 |
| RW | 3 | 272 | 2 | 1 | 0 | 0 | 1 | 0 | 279 | 97.49 |
| Bay | 4 | 1 | 146 | 1 | 0 | 0 | 1 | 0 | 153 | 95.42 |
| CLO | 6 | 0 | 3 | 25 | 1 | 1 | 0 | 4 | 40 | 62.50 |
| BU | 0 | 0 | 0 | 0 | 14 | 0 | 0 | 1 | 15 | 93.33 |
| RA | 3 | 0 | 0 | 0 | 0 | 23 | 0 | 1 | 27 | 85.19 |
| E | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 8 | 100.00 |
| W | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 11 | 15 | 73.33 |
| Total | 135 | 276 | 152 | 30 | 15 | 26 | 10 | 19 | 663 | |
| Producer’s Accuracy | 86.67 | 98.55 | 96.05 | 83.33 | 93.33 | 88.46 | 80.00 | 57.89 | ||
| Overall Accuracy | 92.91 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sens. 2016, 8, 445. https://doi.org/10.3390/rs8060445
Ballanti L, Blesius L, Hines E, Kruse B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sensing. 2016; 8(6):445. https://doi.org/10.3390/rs8060445
Chicago/Turabian StyleBallanti, Laurel, Leonhard Blesius, Ellen Hines, and Bill Kruse. 2016. "Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers" Remote Sensing 8, no. 6: 445. https://doi.org/10.3390/rs8060445
APA StyleBallanti, L., Blesius, L., Hines, E., & Kruse, B. (2016). Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sensing, 8(6), 445. https://doi.org/10.3390/rs8060445







