Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa
Abstract
:1. Introduction
2. The SEVIRI Sensor
3. LSA SAF LST&E Products for MSG/SEVIRI
3.1. Generalized Split Window Algorithm
3.2. Vegetation Cover Method for LSE Retrieval
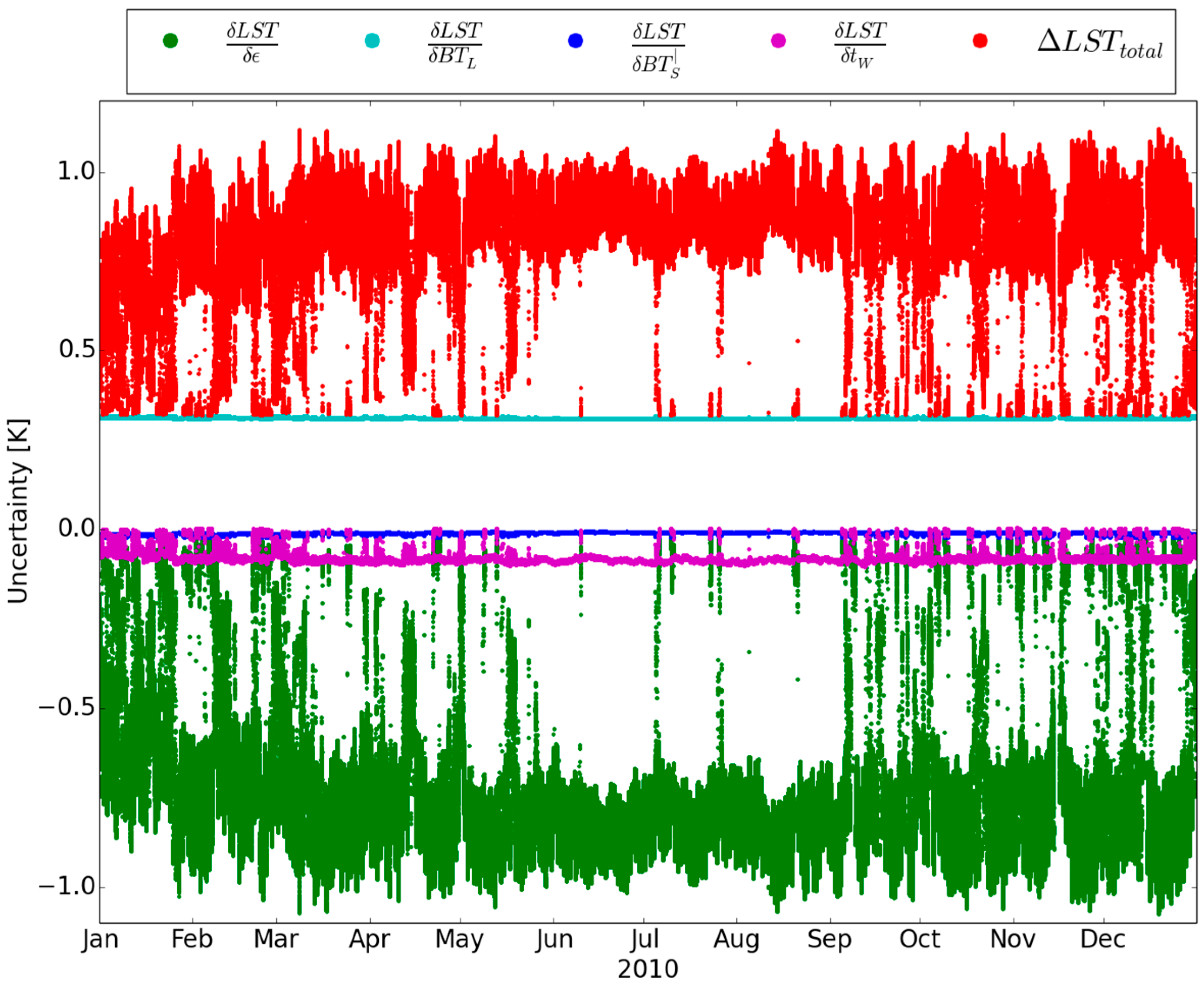
3.3. Uncertainty Associated with LST&E Estimation
4. In-Situ Measurements and LST Determination
4.1. LST Derivation from in-Situ Measurements
4.2. Land Surface Emissivity Determination
4.3. Uncertainty of in-Situ LST
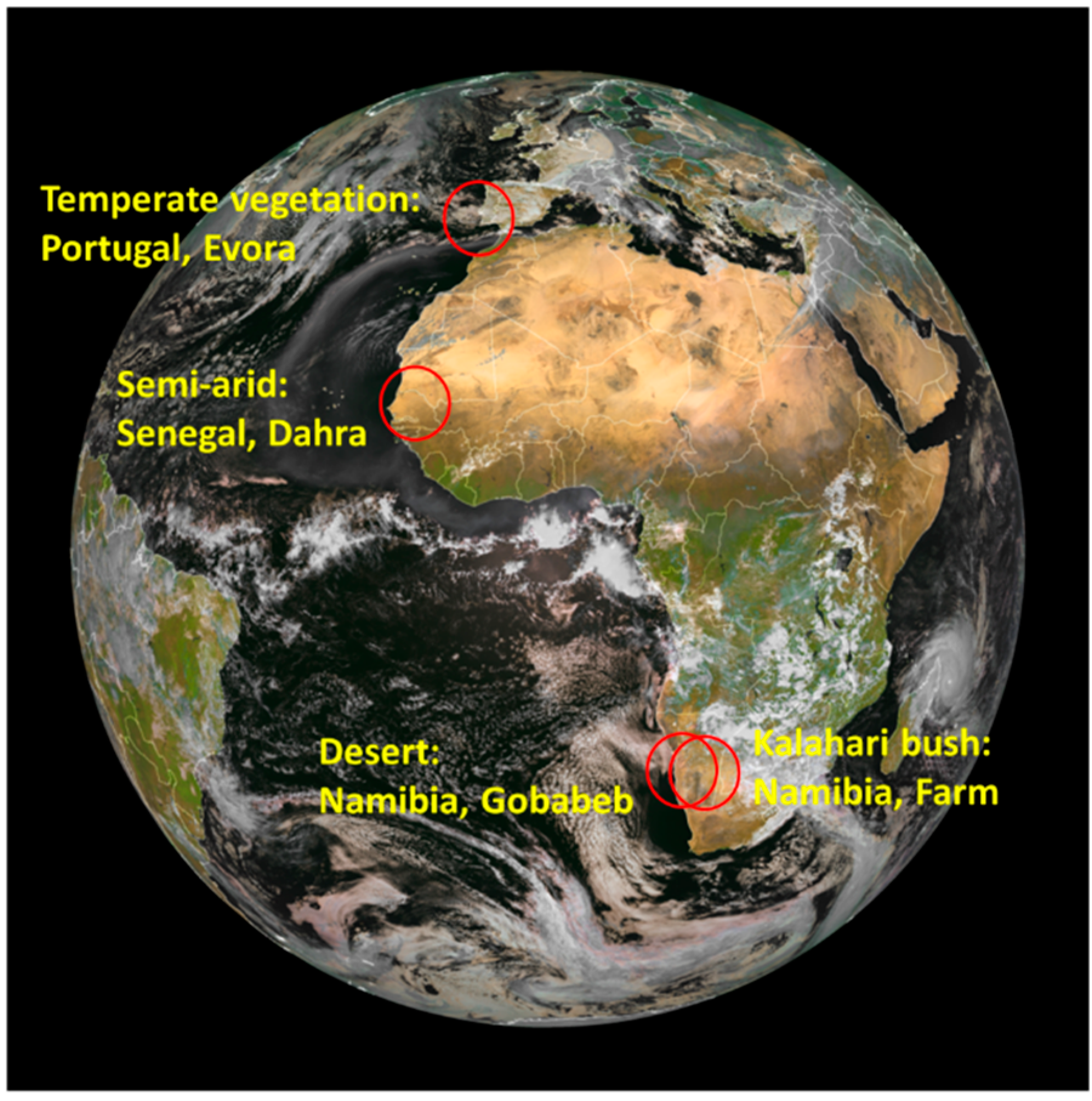
5. LST Validation Stations
5.1. Dahra, Senegal
5.1.1. Estimation of Land Surface Cover and Representative in-Situ LSTs
5.1.2. Land Surface Emissivity at Dahra
5.2. Gobabeb, Namibia
Land Surface Emissivity at Gobabeb
5.3. Farm Heimat, Namibia
5.3.1. Estimation of Land Surface Cover and Representative in-Situ LSTs
5.3.2. Land Surface Emissivity at Farm Heimat
6. Results and Discussion
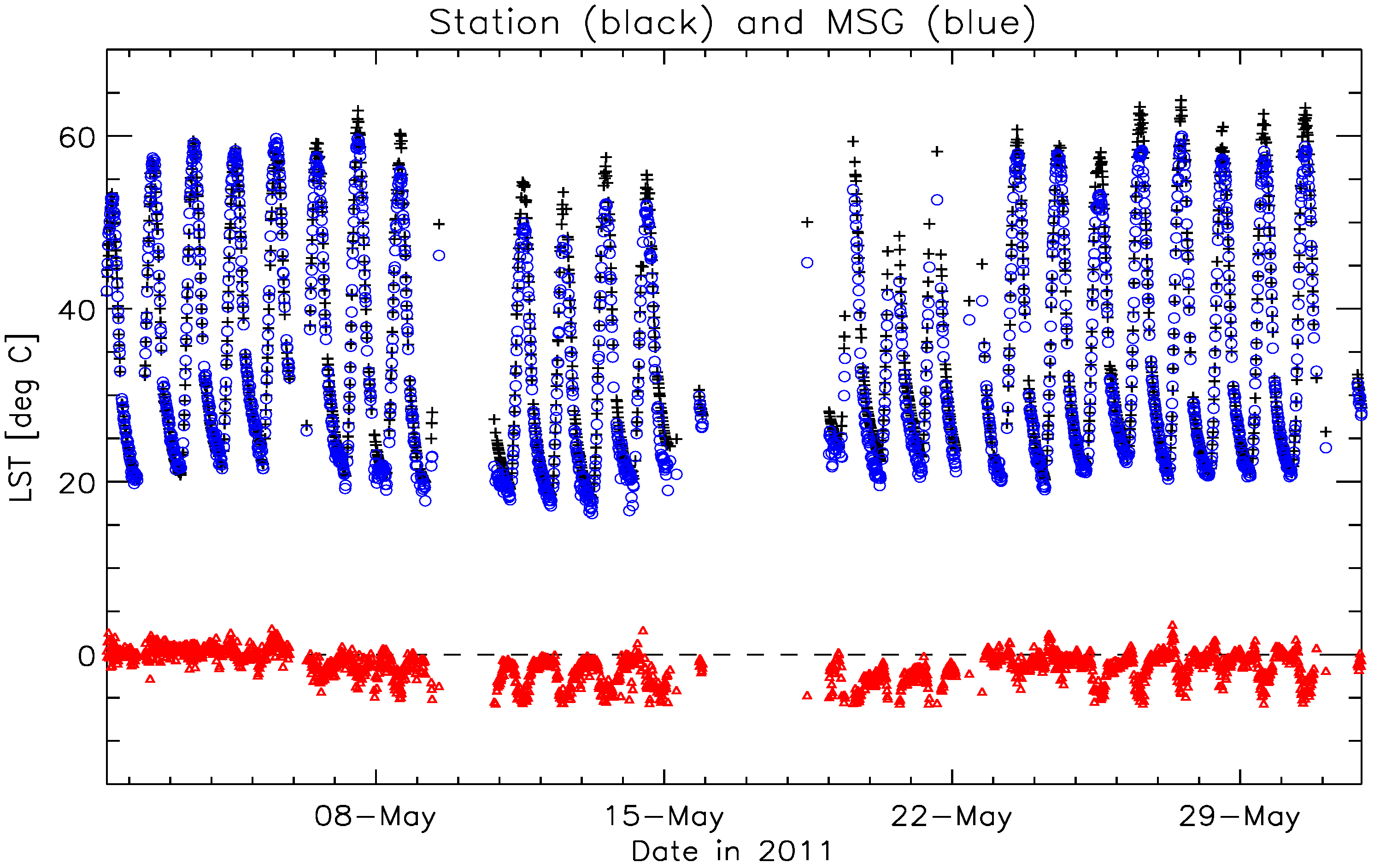
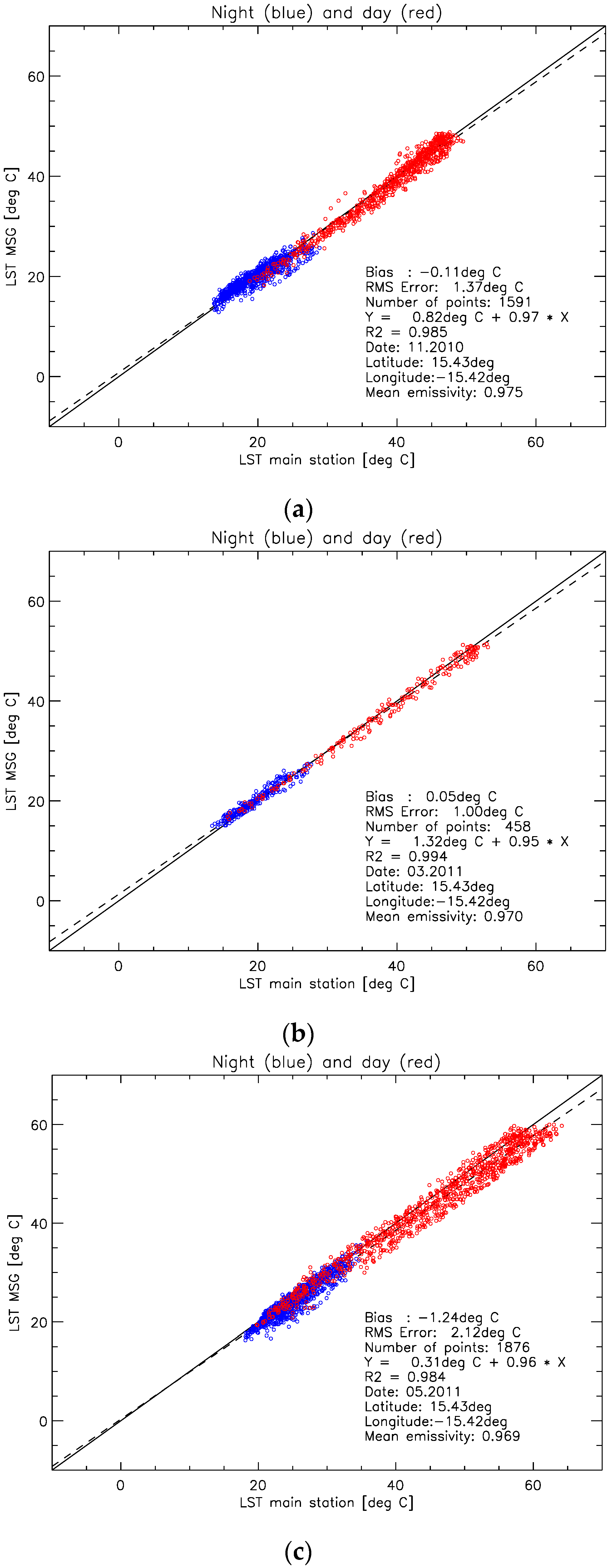
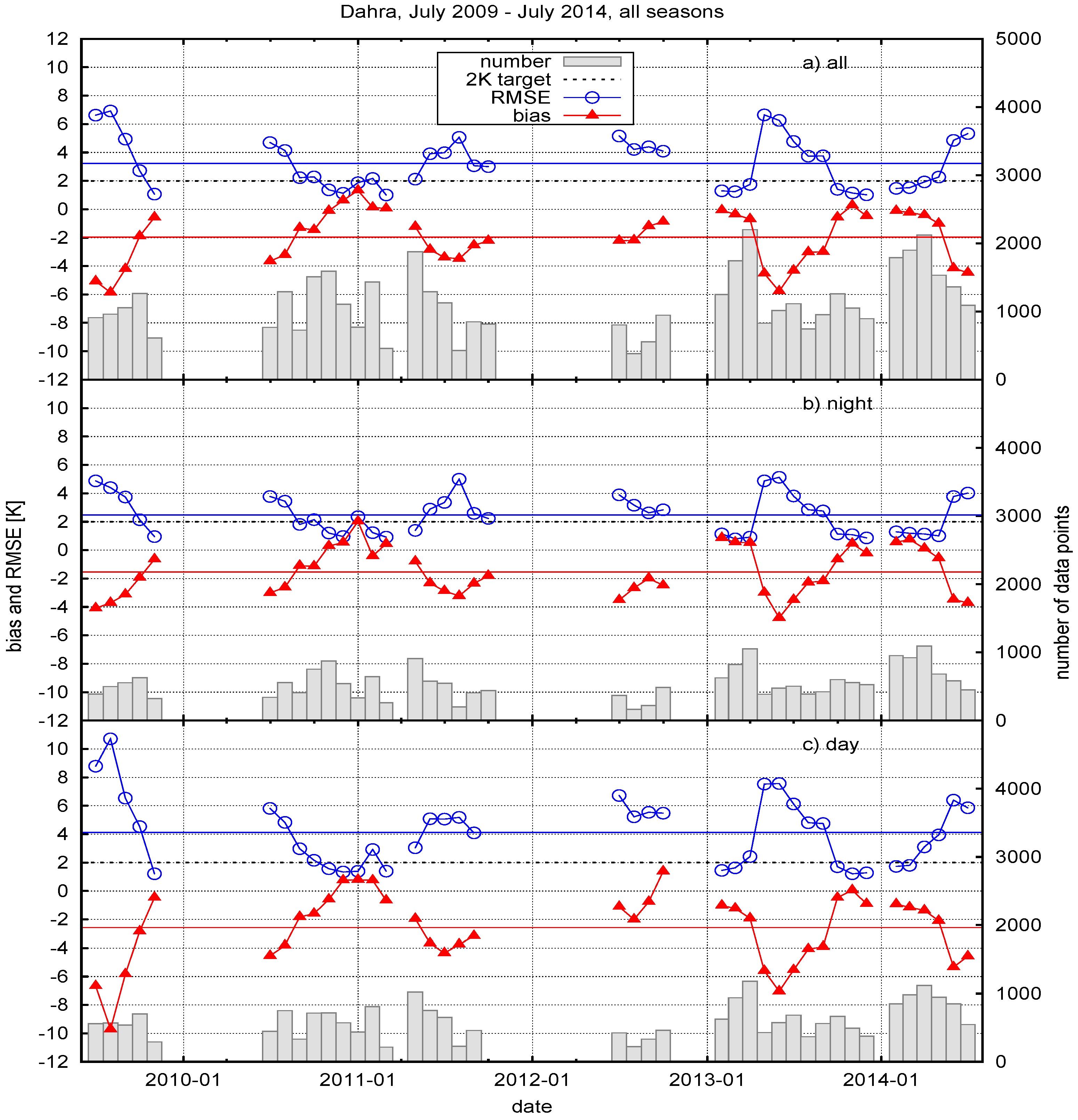
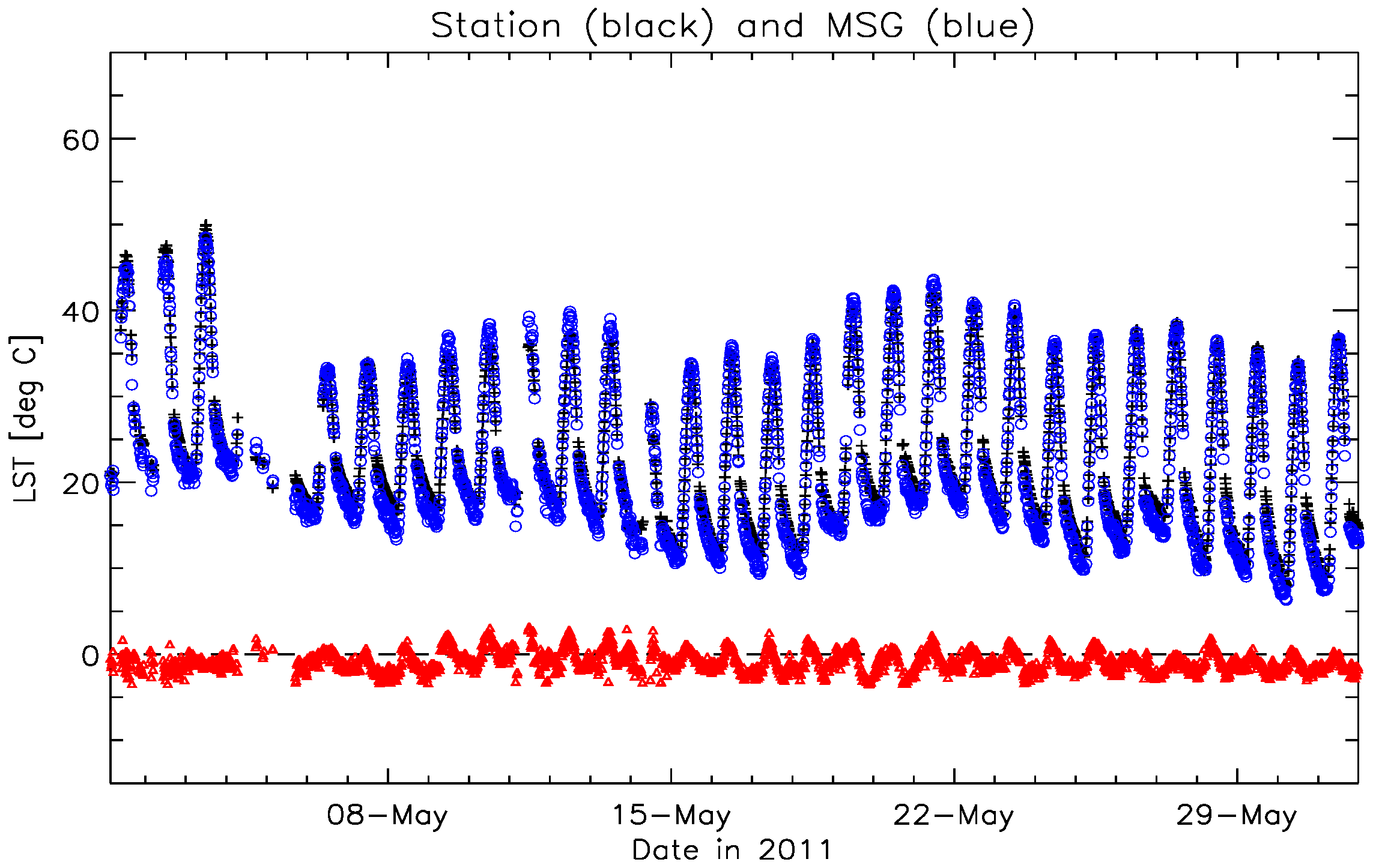
6.1. Results for Dahra
6.2. Discussion for Dahra
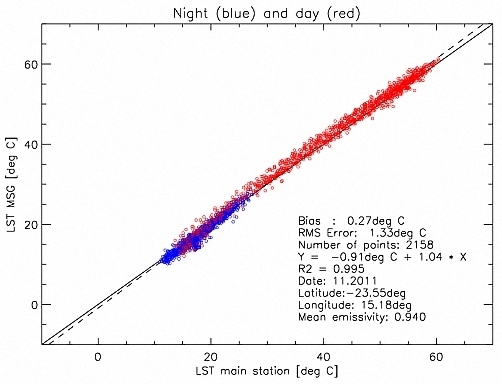
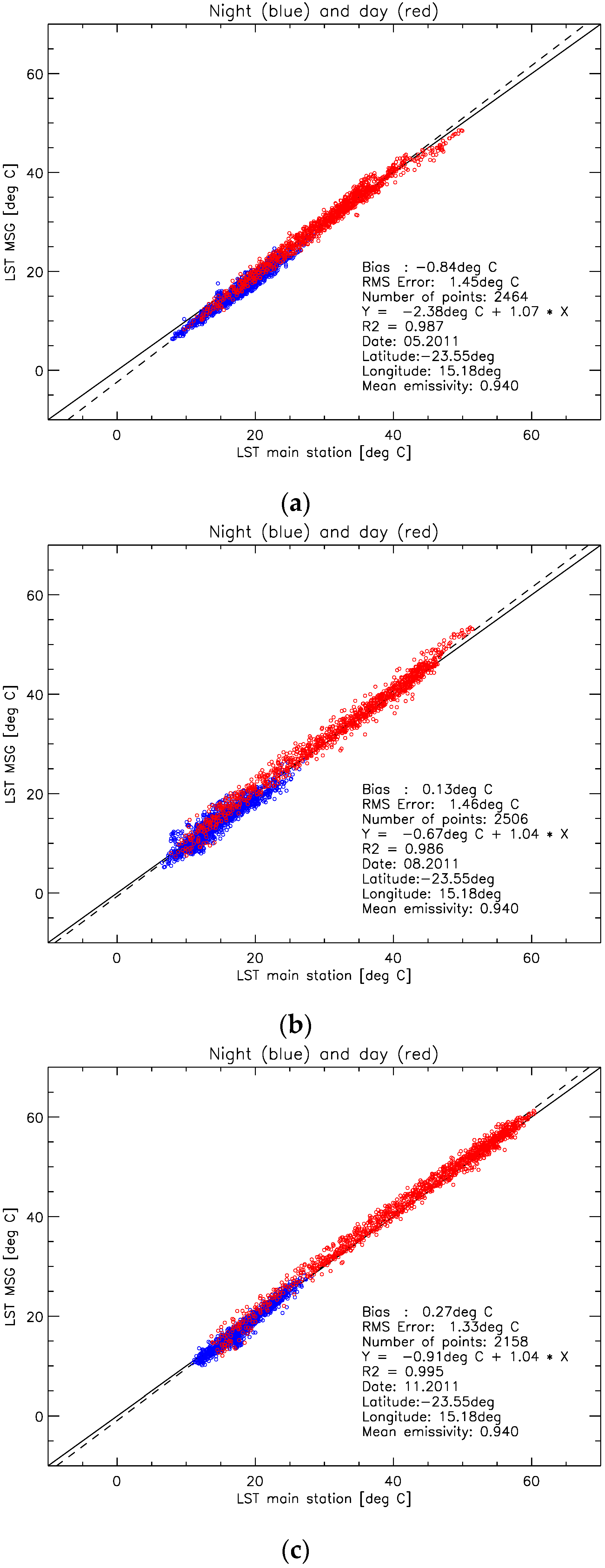
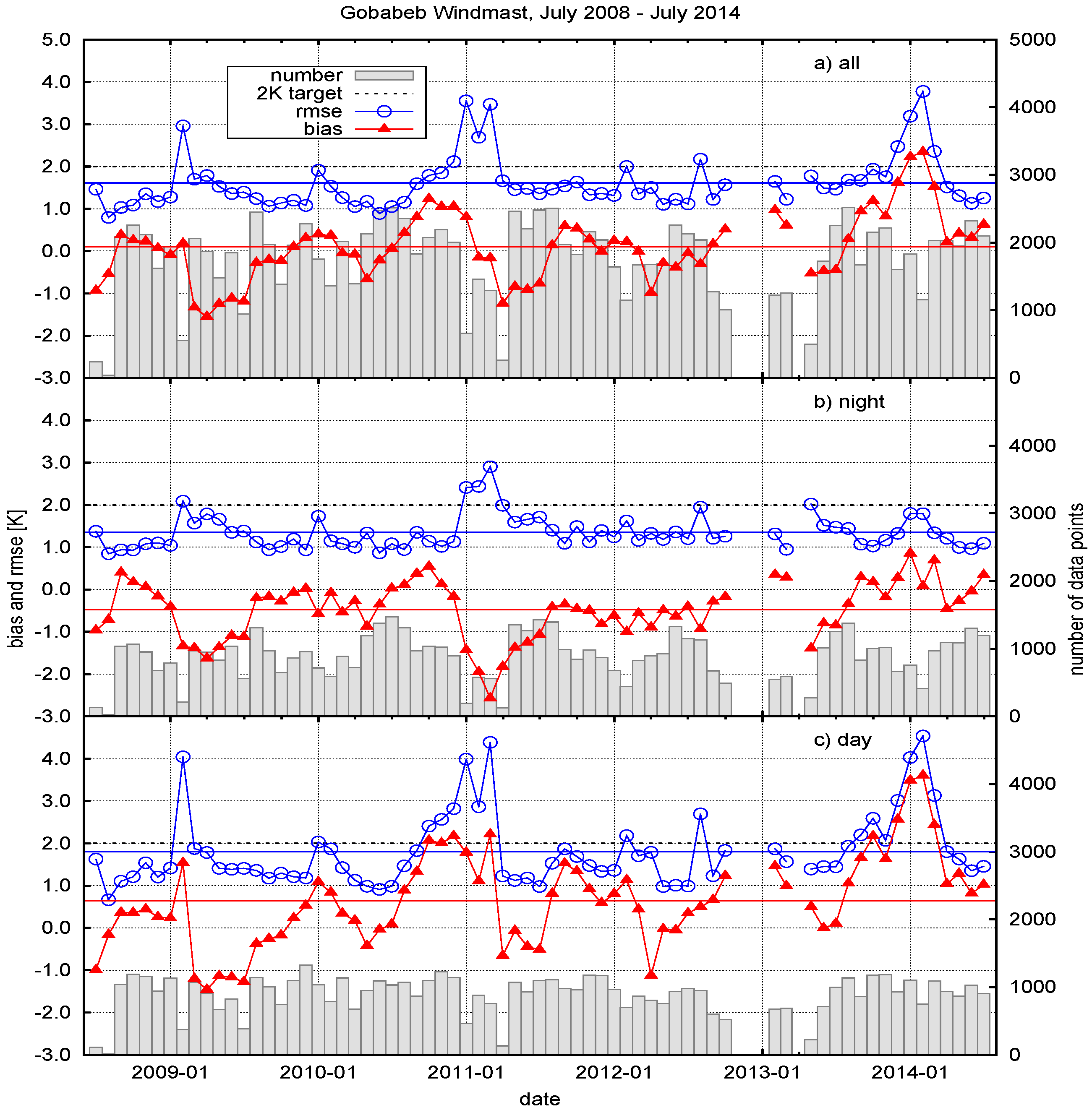
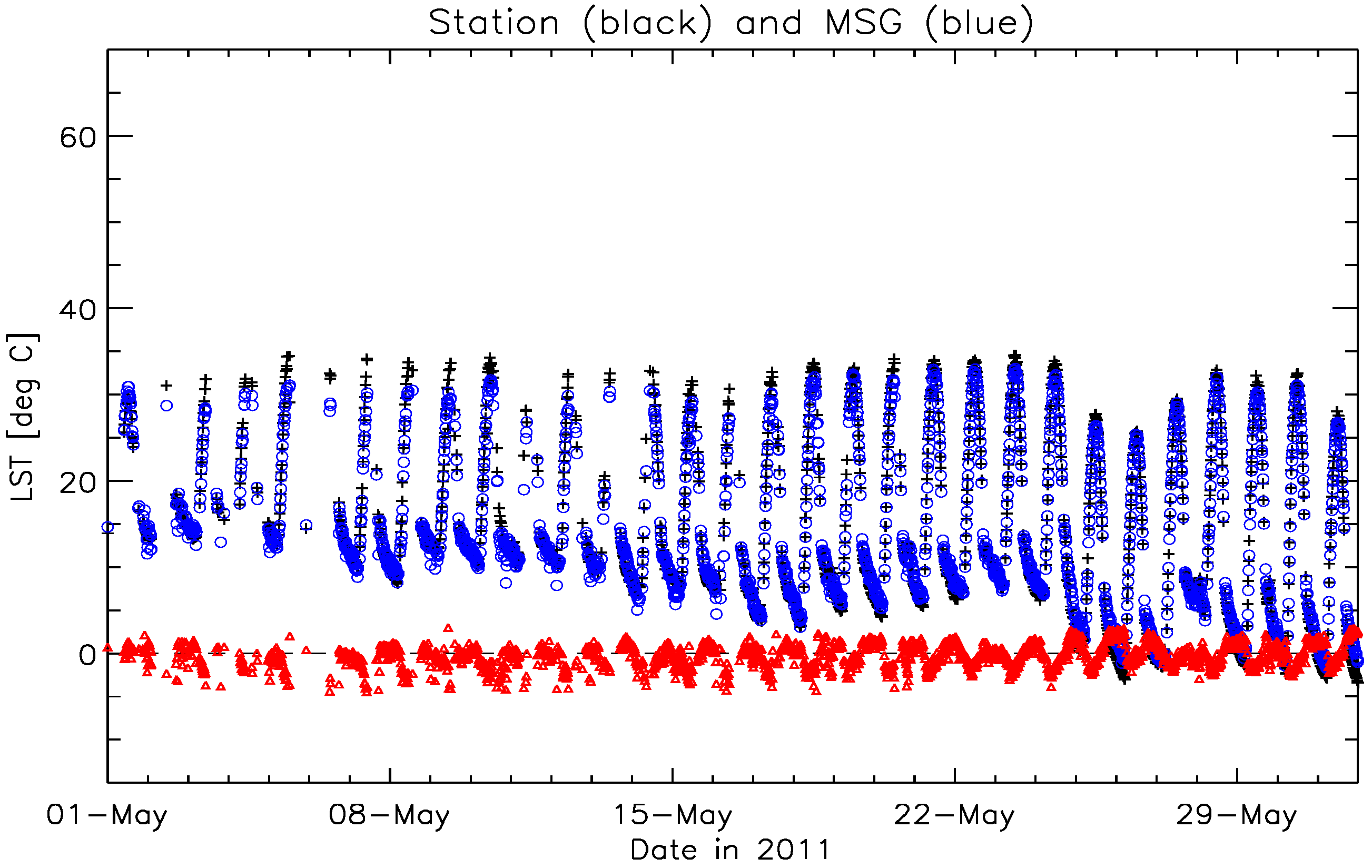
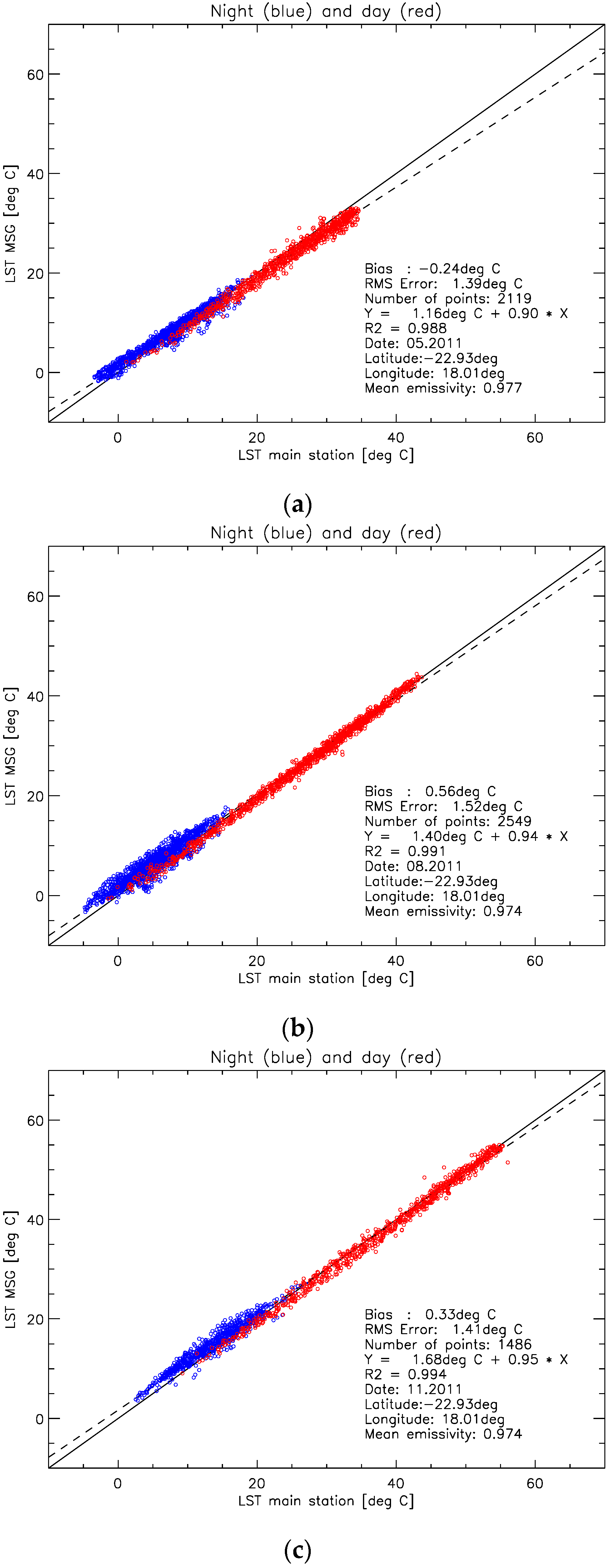
6.3. Results for Gobabeb
6.4. Discussion for Gobabeb
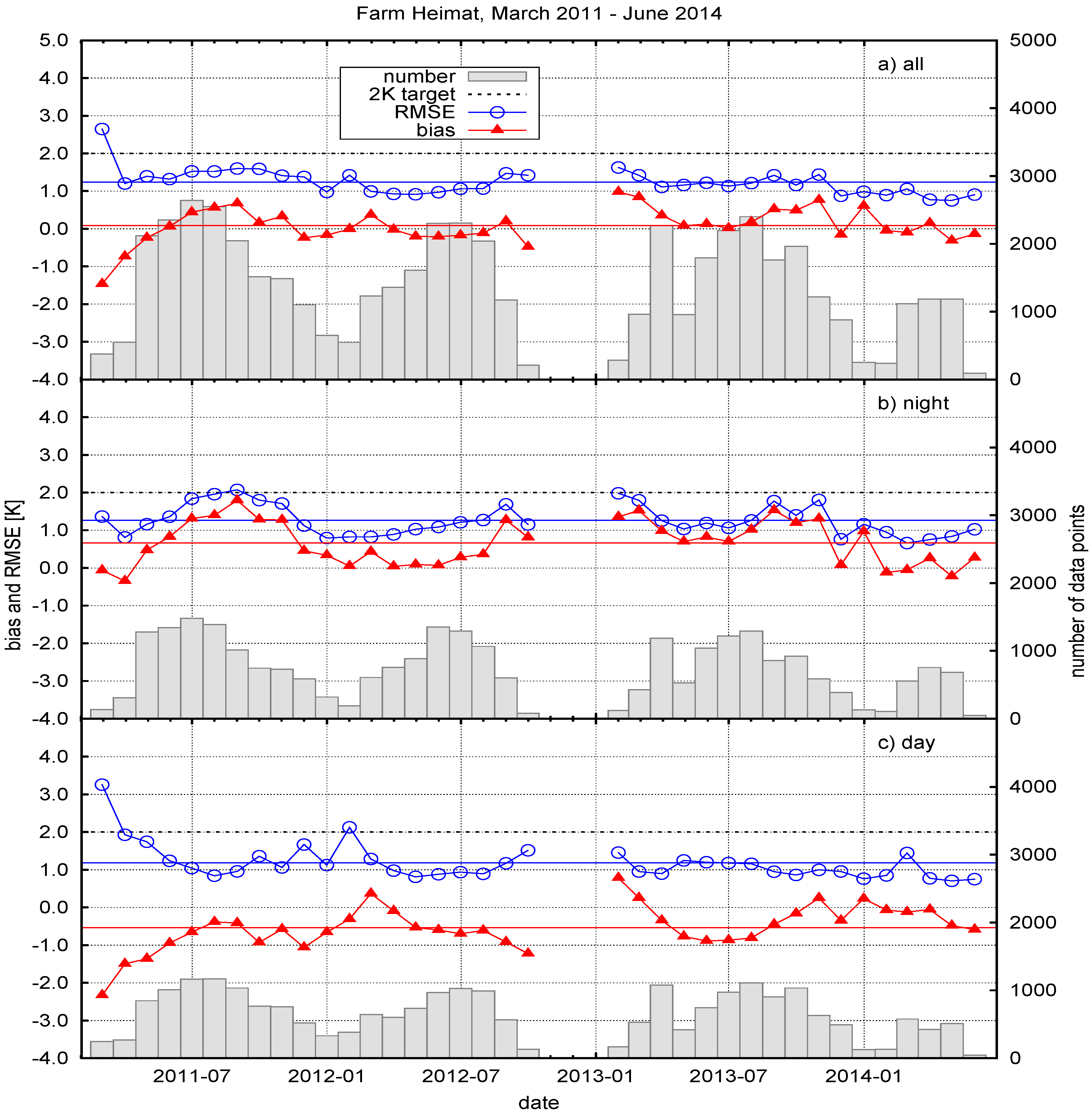
6.5. Results for Farm Heimat
6.6. Discussion for Farm Heimat
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FVC | Fraction of Vegetation Cover |
| GSW | Generalized split-window |
| LSA SAF | Land Surface Analysis Satellite Application Facility |
| LSE | Land Surface Emissivity |
| LST | Land Surface Temperature |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MSG | Meteosat Second Generation |
| SEVIRI | Spinning Enhanced Visible and Infrared Imager |
| TES | Temperature-Emissivity Separation |
Appendix A
References
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-de Coca, F.; Carrer, D.; Freitas, S.C.; Garcia-Haro, J.; et al. The satellite application facility for land surface analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Freitas, S.; Trigo, I.; Bioucas-Dias, J.; Gottsche, F.M. Quantifying the Uncertainty of Land Surface Temperature Retrievals from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Peres, L.; DaCamara, C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1834–1844. [Google Scholar] [CrossRef]
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Macedo, J.; Barroso, C.; Silva, R.; Perdigão, R. Land surface temperature from multiple geostationary satellites. Int. J. Remote Sens. 2013, 34, 3051–3068. [Google Scholar] [CrossRef]
- Schneider, P.; Ghent, D.; Corlett, G.; Prata, F.; Remedios, J. AATSR Validation: LST Validation Protocol; ESA Report Contract No. 9054/05/NL/FF; European Space Agency (ESA): Paris, France, 2012. [Google Scholar]
- Wan, Z.; Li, Z.L. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Niclos, R.; Galve, J.M.; Valiente, J.A.; Estrela, M.J.; Coll, C. Accuracy assessment of land surface temperature retrievals from MSG2-SEVIRI data. Remote Sens. Environ. 2011, 115, 2126–2140. [Google Scholar] [CrossRef]
- Salisbury, J.; D’Aria, D.M. Emissitivity of Terrestrial Materials in the 8–14 micrometer Atmospheric Window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. The North American ASTER Land Surface Emissivity Database (NAALSED) Version 2.0. Remote Sens. Environ. 2009, 113, 1967–1975. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Manning, E.; Lee, S.Y.; Fetzer, E. Validation of the Atmospheric Infrared Sounder (AIRS) version 5 land surface emissivity product over the Namib and Kalahari deserts. J. Geophys. Res. 2009, 114, 1–11. [Google Scholar] [CrossRef]
- Göttsche, F.M.; Hulley, G.C. Validation of six satellite-retrieved land surface emissivity products over two land cover types in a hyper-arid region. Remote Sens. Environ. 2012, 124, 149–158. [Google Scholar] [CrossRef]
- Göttsche, F.M.; Olesen, F.S.; Bork-Unkelbach, A. Validation of land surface temperature derived from MSG/SEVIRI with in situ measurements at Gobabeb, Namibia. Int. J. Remote Sens. 2013, 34, 3069–3083. [Google Scholar] [CrossRef]
- Bork-Unkelbach, A. Extrapolation von in-situ Landoberflächentemperaturen auf Satellitenpixel. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2012. [Google Scholar]
- Kabsch, E.; Olesen, F.S.; Prata, F. Initial results of the land surface temperature (LST) validation with the Evora, Portugal ground-truth station measurements. Int. J. Remote Sens. 2008, 29, 5329–5345. [Google Scholar] [CrossRef]
- Rasmussen, M.O.; Gottsche, F.M.; Olesen, F.S.; Sandholt, I. Directional effects on land surface temperature estimation from Meteosat second generation for savanna landscapes. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4458–4468. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Bork-Unkelbach, A.; Gottsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.P.; Olesen, F.S.; Privette, J.L. Directional viewing effects on satellite land surface temperature products over sparse vegetation canopies—A multisensor analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Xu, H.; Yu, Y.; Tarpley, D.; Gottsche, F.; Olesen, F.S. Evaluation of GOES-R land surface temperature algorithm using SEVIRI satellite retrievals with in situ measurements. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3812–3822. [Google Scholar] [CrossRef]
- Duguay-Tetzlaff, A.; Bento, V.A.; Göttsche, F.M.; Stöckli, R.; Martins, J.P.; Trigo, I.; Olesen, F.; Bojanowski, J.S.; da Camara, C.; Kunz, H. Meteosat land surface temperature climate data record: Achievable accuracy and potential uncertainties. Remote Sens. 2015, 7, 13139–13156. [Google Scholar] [CrossRef]
- Köppen, W. Handbuch der Klimatologie. Das Geographische System der Klimate; Gebrüder Borntraeger: Berlin, Germany, 1936. [Google Scholar]
- Hook, S.J.; Prata, F.J.; Alley, R.E.; Abtahi, A.; Richards, R.C.; Schladow, S.G.; Pálmarsson, S.Ó. Retrieval of lake bulk skin and temperatures using Along-Track Scanning Radiometer (ATSR-2) data: A case study using lake Tahoe and California. J. Atmos. Ocean. Technol. 2003, 20, 534–548. [Google Scholar] [CrossRef]
- Coll, C.; Hook, S.J.; Galve, J.M. Land surface temperature from the advanced along-track scanning radiometer: Validation over inland waters and vegetated surfaces. IEEE Trans. Geosci. Remote Sens. 2009, 47, 350–360. [Google Scholar] [CrossRef]
- Rubio, E.; Caselles, V.; Badenas, C. Emissivity measurements of several soils and vegetation types in the 8–14 micrometer wave band: Analysis of two field methods. Remote Sens. Environ. 1997, 59, 490–521. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat Second Generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 992–992. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. Radiometric performance of SEVIRI. Bull. Am. Meteorol. Soc. 2002, 83, ES50–ES51. [Google Scholar] [CrossRef]
- Derrien, M.; Gléau, H.L. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Caselles, V.; Valor, E.; Coll, C.; Rubio, E. Thermal band selection for the PRISM instrument: 1. Analysis of emissivity-temperature separation algorithms. J. Geophys. Res. 1997, 102, 11145–11164. [Google Scholar] [CrossRef]
- Garcia-Haro, F.J.; Sommer, S.; Kemper, T. A new tool for variable multiple endmember spectral mixture analysis (VMESMA). Int. J. Remote Sens. 2005, 26, 2135–2162. [Google Scholar] [CrossRef]
- Belward, A. The IGBP-DIS Global 1 km Land Cover Data Set (DISCover)—Proposal and Implementation Plans; Technical Report 13; IGBP-DIS: Toulouse, France, 1996. [Google Scholar]
- Siljamo, N.; Hyvärinen, O. New geostationary satellite-based snow-cover algorithm. J. Appl. Meteorol. Climatol. 2011, 50, 1275–1290. [Google Scholar] [CrossRef]
- Schädlich, S.; Göttsche, F.; Olesen, F.S. Influence of Land Surface Parameters and Atmosphere on METEOSAT Brightness Temperatures and Generation of Land Surface Temperature Maps by Temporally and Spatially Interpolating Atmospheric Correction. Remote Sens. Environ. 2001, 75, 39–46. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J. Generating consistent land surface temperature and emissivity products between ASTER and MODIS data for earth science research. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1304–1315. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Mattar, C.; Hulley, G.; Gottsche, F.M. Temperature and emissivity separation from MSG/SEVIRI data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5937–5951. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; De Feis, I.; Amoroso, M.; Venafra, S.; Trigo, I.F.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from geostationary infrared radiances. Atmos. Meas. Tech. 2013, 6, 3613–3634. [Google Scholar] [CrossRef]
- Masiello, G.; Serio, C.; Venafra, S.; Liuzzi, G.; Göttsche, F.; Trigo, I.; Watts, P. Kalman filter physical retrieval of surface emissivity and temperature from SEVIRI infrared channels: A validation and intercomparison study. Atmos. Meas. Tech. 2015, 8, 2981–2997. [Google Scholar] [CrossRef]
- Theocharous, E.; Usadi, E.; Fox, N. CEOS Comparison of IR Brightness Temperature Measurements in Support of Satellite Validation. Part I: Laboratory and Ocean Surface Temperature Comparison of Radiation Thermometers; NPL Report OP 3; National Physical Laboratory: Teddington, UK, 2010. [Google Scholar]
- Becker, F. The impact of spectral emissivity on the measurement of land surface temperature from a satellite. Int. J. Remote Sens. 1987, 8, 1509–1522. [Google Scholar] [CrossRef]
- Kondratyev, K.Y. Radiation in the Atmosphere; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Dash, P.; Goettsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Olioso, A.; Soria, G.; Sobrino, J.; Duchemin, B. Evidence of low land surface thermal infrared emissivity in the presence of dry vegetation. IEEE Geosci. Remote Sens. Lett. 2007, 4, 112–116. [Google Scholar] [CrossRef]
- French, A.; Schmugge, T.; Kustas, W. Discrimination of Senescent Vegetation Using Thermal Emissivity Contrast. Remote Sens. Environ. 2000, 74, 249–254. [Google Scholar] [CrossRef]
- Combs, A.; Weickmann, H.; Mader, C.; Tebo, A. Application of infrared radiometers to meteorology. J. Appl. Meteorol. 1965, 4, 253–262. [Google Scholar] [CrossRef]
- Rubio, E.; Caselles, V.; Coll, C.; Valour, E.; Sospedra, F. Thermal-infrared emissivities of natural surfaces: improvement on the experimental set-up and new measurements. Int. J. Remote Sens. 2003, 24, 5379–5390. [Google Scholar] [CrossRef]
- Dash, P.; Goettsche, F.M.; Olesen, F.S. Potential of MSG for surface temperature and emissivity estimation: considerations for real-time applications. Int. J. Remote Sens. 2002, 23, 4511–4518. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I. Evaluation of MODIS and NOAA AVHRR vegetation indices with in situ measurements in a semi-arid environment. Int. J. Remote Sens. 2005, 26, 2561–2594. [Google Scholar] [CrossRef]
- Tagesson, T.; Fensholt, R.; Guiro, I.; Rasmussen, M.O.; Huber, S.; Mbow, C.; Garcia, M.; Horion, S.; Sandholt, I.; Holm-Rasmussen, B.; et al. Ecosystem properties of semiarid savanna grassland in West Africa and its relationship with environmental variability. Glob. Chang. Biol. 2014, 21, 250–264. [Google Scholar] [CrossRef] [PubMed]
- Batjes, N. Options for increasing carbon sequestration in West African soils: An exploratory study with special focus on Senegal. Land Degrad. Dev. 2001, 12, 131–142. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Rasmussen, M.O.; Göttsche, F.M.; Diop, D.; Mbow, C.; Olesen, F.S.; Fensholt, R.; Sandholt, I. Tree survey and allometric models for tiger bush in northern Senegal and comparison with tree parameters derived from high resolution satellite data. Int. J. Appl. Earth Obs. Geoinformation 2011, 13, 517–527. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Gillespie, A.; Sabol, D.; Gustafson, W.T. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006, 103, 474–487. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Baldridge, A.M. Validation of the North American ASTER Land Surface Emissivity Database (NAALSED) version 2.0 using pseudo-invariant sand dune sites. Remote Sens. Environ. 2009, 113, 2224–2233. [Google Scholar] [CrossRef]
- Lancaster, J.; Lancaster, N.; Seely, M. Climate of the central Namib Desert. Madoqua 1984, 14, 5–61. [Google Scholar]
- Eckardt, F.; Soderberg, K.; Coop, L.; Muller, A.; Vickery, K.; Grandin, R.; Jack, C.; Kapalanga, T.; Henschel, J. The nature of moisture at Gobabeb, in the central Namib Desert. J. Arid Environ. 2013, 93, 7–19. [Google Scholar] [CrossRef]
- Mason, S.J.; Jury, M.R. Climate variability and change over southern Africa: A reflection on underlying processes. Prog. Phys. Geogr. 1997, 21, 25–50. [Google Scholar] [CrossRef]
- Seely, M.K. Standing crop as an index of precipitation in the central Namib grassland. Madoqua 1978, 9, 5–13. [Google Scholar]
- Pearson, R.K. Outliers in Process Modeling and Identification. IEEE Trans. Control Syst. Technol. 2002, 10, 55–63. [Google Scholar] [CrossRef]

| Dahra | Gobabeb | Farm Heimat | |
|---|---|---|---|
| Location | Senegal; Lat: 15.402, Lon: −15.443 | Namibia; Lat: −23.551, Lon: 15.051 | Namibia; Lat: −22.933, Lon: 17.992 |
| Elevation | 45 m | 450 m | 1380 m |
| Climate Zone | Sub-tropical, hot semi-arid | Desert | Semi-Desert |
| Land Cover | Grassland; 96% sand/grass, 4% tree | Baren; 75% sand/gravel, 25% dry grass | Savanna; 63% soil/grass, 37% tree/bush |
| Variable | Uncertainty Type | Magnitude |
|---|---|---|
| ε | random | ±0.015 |
| BTL | random | ±0.3 °C |
| BT’S | random | ±0.3 °C |
| tW | systematic | −0.045 |
| Station | Bias (°C) | RMSE (°C) | ||||
|---|---|---|---|---|---|---|
| All Data | Night | Day | All Data | Night | Day | |
| Dahra | −2.0 (0.0) | −1.5 (0.4) | −2.6 (−0.6) | 3.2 (1.4) | 2.5 (1.1) | 4.1 (1.7) |
| Gobabeb | 0.1 | −0.5 | 0.6 | 1.6 | 1.4 | 1.8 |
| Heimat | 0.1 | 0.7 | −0.5 | 1.2 | 1.3 | 1.2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Göttsche, F.-M.; Olesen, F.-S.; Trigo, I.F.; Bork-Unkelbach, A.; Martin, M.A. Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sens. 2016, 8, 410. https://doi.org/10.3390/rs8050410
Göttsche F-M, Olesen F-S, Trigo IF, Bork-Unkelbach A, Martin MA. Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sensing. 2016; 8(5):410. https://doi.org/10.3390/rs8050410
Chicago/Turabian StyleGöttsche, Frank-M., Folke-S. Olesen, Isabel F. Trigo, Annika Bork-Unkelbach, and Maria A. Martin. 2016. "Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa" Remote Sensing 8, no. 5: 410. https://doi.org/10.3390/rs8050410
APA StyleGöttsche, F.-M., Olesen, F.-S., Trigo, I. F., Bork-Unkelbach, A., & Martin, M. A. (2016). Long Term Validation of Land Surface Temperature Retrieved from MSG/SEVIRI with Continuous in-Situ Measurements in Africa. Remote Sensing, 8(5), 410. https://doi.org/10.3390/rs8050410