Abstract
GPS has become a very effective tool to remotely sense precipitable water vapor (PWV) information, which is important for weather forecasting and nowcasting. The number of geodetic GNSS stations set up in China has substantially increased over the last few decades. However, GPS PWV derivation requires surface pressure to calculate the precise zenith hydrostatic delay and weighted mean temperature to map the zenith wet delay to precipitable water vapor. GPS stations without collocated meteorological sensors can retrieve water vapor using standard atmosphere parameters, which lead to a decrease in accuracy. In this paper, a method of interpolating NWP reanalysis data to site locations for generating corresponding meteorological elements is explored over China. The NCEP FNL dataset provided by the NCEP (National Centers for Environmental Prediction) and over 600 observed stations from different sources was selected to assess the quality of the results. A one-year experiment was performed in our study. The types of stations selected include meteorological sites, GPS stations, radio sounding stations, and a sun photometer station. Compared with real surface measurements, the accuracy of the interpolated surface pressure and air temperature both meet the requirements of GPS PWV derivation in most areas; however, the interpolated surface air temperature exhibits lower precision than the interpolated surface pressure. At more than 96% of selected stations, PWV differences caused by the differences between the interpolation results and real measurements were less than 1.0 mm. Our study also indicates that relief amplitude exerts great influence on the accuracy of the interpolation approach. Unsatisfactory interpolation results always occurred in areas of strong relief. GPS PWV data generated from interpolated meteorological parameters are consistent with other PWV products (radio soundings, the NWP reanalysis dataset, and sun photometer PWV data). The differences between them were approximately 1~3 mm at most at our selected stations, and GPS data processing is the main factor influencing the agreement of the GPS PWV results with those of other methods.
1. Introduction
Water vapor plays a key role in many weather and climate processes (e.g., see [1,2]). Many instruments can be employed to retrieve the atmospheric water vapor content, such as radiosondes, microwave radiometers, sun photometers, and ground-based GPS devices [3]. GPS meteorology, which was first proposed in 1992 by Bevis [4], has proven to be a very effective method to estimate precipitable water vapor (PWV) (e.g., see [5,6]). Information about atmospheric water vapor provided by ground-based GPS meteorology can be significant in many areas, such as numerical weather forecasting (NWP) (e.g., see [7,8]), global or regional atmospheric research (e.g., see [9,10]), and others (e.g., see [11]). In addition to numerous efforts to improve the accuracy of ground-based GPS meteorology (e.g., see [12,13]), the density of GPS sites has also increased in many countries, leading to a considerable increase in the PWV observation density (e.g., see [14,15]). These developments strongly promote the application of ground-based GPS PWV detection in the meteorological field.
A GPS signal is delayed when it propagates through the neutral atmosphere, and part of this delay is caused by atmospheric water vapor, which is mostly concentrated in the troposphere. To derive GPS PWV, tropospheric zenith total delay (ZTD) is estimated by first processing GPS data; then the zenith hydrostatic delay (ZHD) should be subtracted from ZTD to obtain the zenith wet delay (ZWD); finally, ZWD can be converted to PWV by a ratio value , which is related to the weighted mean temperature Tm. The Saastamoinen model [16] has been widely used to estimate ZHD because of its high accuracy of approximately 1–2 mm, and the surface barometric pressure Ps is one of the essential parameters in this model. Tm is often calculated from its linear relationship with the near-surface air temperature Ts. Therefore, to derive GPS PWV with high accuracy, site-specific surface pressure Ps and Tm are also essential, which are, respectively, used to calculate ZHD and in combination with the GPS data. However, collecting such meteorological parameters requires collocated meteorological sensors, which are often not present at many geodetic GPS stations. To employ those sites without collocated meteorological sensors in GPS meteorology, different methods were studied in various areas. For example, Jade [17] firstly interpolated the 2.5° × 2.5° National Centers for Environmental Prediction (NCEP)/National Center for Atmospheric Research (NCAR) reanalysis data to obtain site-specific meteorological parameters for estimating GPS PWV. An interpolation of the NCEP pressure level data and NCEP surface data was explored. The experiments, conducted over a four-year period in India, indicated that the GPS PWV data derived using the interpolated surface pressure and weighted mean temperature from NCEP data were in strong agreement with those from real meteorological observations. However, bias between GPS PWV and horizontally interpolated NCEP PWV results apparently increased with highly undulated terrain. Vey [18] derived GPS PWV data that were obtained by using 141 global GPS stations over a 10-year period from 1994 to 2004, in which Tm data were obtained from the European Center for Medium-Range Weather Forecasts (ECMWF) and Ps data were interpolated from neighboring World Meteorological Organization (WMO) stations. In Karabatic’s study [19], Ps and Ts data of the nearest meteorological station were extrapolated to GPS stations in Austria, and they found that a PWV accuracy better than ±1 mm could be achieved when the distance between the two sites was within 20 km. In Poland, Bosy obtained specific GPS site Ps and Ts data by interpolating nearby meteorological data to the GPS site locations [20]. However, some systematic bias in the interpolation results appeared at some stations, which was attributed to unknown deficiencies in their interpolation procedure. The North American Regional Reanalysis (NARR) dataset for the year 2009 was used to estimate GPS PWV in California and Nevada by Means and Cayan [21]. The surface pressure and temperature were determined by the elevation of a specific station and the geopotential heights of the standard pressure levels of neighboring grids, and simple two-dimensional interpolation of the reanalysis gridpoint surface temperatures was performed. Means [22] also employed the same technique to obtain GPS PWV of over 500 sites from 2003 to 2009. Then, using these GPS PWV data, he studied the temporal and spatial extent of the North American monsoon in California and Nevada. Luo [12] presented a height-dependent linear ZHD correction model using freely accessible meteorological measurement data near GPS sites, and the mean ZHD bias was approximately 5 mm.
The number of GPS receivers deployed in China has greatly increased in recent years [23]. However, many stations are deployed for geodetic applications, leading to few collocated surface meteorological measurements, except at stations within the GPS meteorology network. In this paper, we employ a three-dimensional interpolation methodology and NCEP Final (NCEP FNL) Analysis data to generate surface pressure and temperature data for GPS stations over China. The goal of our study is to demonstrate that either the present available GPS networks or the historical data from previous GPS geodetic observations have great potential to reconstruct the precipitable water field with higher spatial and temporal resolution, which can be used to study the characteristics of water vapor (e.g., see [24]) or analyze the water vapor movement during severe weather (e.g., see [25]) in more detail.
In the following section, we describe the multi-source data and their processing strategy, including the three-dimensional interpolation algorithm applied in our research. Error analyses for the interpolated surface meteorological elements are presented in Section 3. Section 4 provides the results of the interpolation products, and the accuracy of GPS PWV from interpolation products is analyzed by comparison with the PWV results from other approaches. Conclusions are given in Section 5.
2. Methodology
2.1. GPS PWV Estimation
Basically, two solution approaches can be selected for GPS data processing: double-difference (DD) solution mode and precise point positioning (PPP) mode. For PPP, ZTDs are directly estimated together with other unknown parameters, such as the station coordinates or receiver clock-offsets. However, it requires a high-precision satellite clock and ephemeris product [26]. For the DD model, common errors between different receivers and satellites, e.g., the clock-offsets, can be eliminated or greatly reduced. However, to reduce the correlation of observations, it is necessary to introduce three or more distant stations into the network to form long baselines for estimating the absolute ZTD [27]. In fact, each ZTD can be regarded as an average of projection values in the zenith direction of the neutral atmospheric delays along the available slant signal paths from GPS satellites to the receiver during a short time period, which is dependent on the time interval for ZTD estimation. As previously mentioned, we applied the Saastamonien model to separate ZHD from ZTD. This model is expressed as a function of latitude in radians and height above the geoid H in km:
where P0 represents surface pressure in hPa and
After the ZHD is calculated, ZWD can be generated by following equation:
Then, the ratio value Π can convert ZWD to PWV:
The relational expression between Π and Tm (see [28]) is:
where is the density of liquid water, Rv is the specific gas constant for water vapor, = (17 ± 10) K·mbar−1, and = (3.776 ± 0.014) × 105 K2·mbar−1. Tm is defined as:
where e and T represent vapor pressure and absolute temperature along the zenith path, respectively, and the integral intervals are from the earth surface to the atmospheric top. Simply, Tm can be estimated using the surface temperature measurement Ts:
The frequently used values for coefficients a and b are, respectively, 0.72 and 70.2, proposed by Bevis [4]. However, their values can vary in different areas [29].
Numerous studies regarding ground-based GPS PWV estimations in different regions or under different weather conditions have indicated that the accuracy of the above derivation method reached 1~2 mm compared to other high-precision measuring techniques (e.g., see [30,31,32]). In this study, we used GPS data from the Crustal Movement Observation Network of China (CMONOC) and GAMIT/GLOBK software for GPS data processing. The CMONOC network was built to monitor crustal deformation, water vapor distribution, ionospheric variability, and other geophysical parameters. It consists of GNSS, VLBI, SLR, gravity, and level measurement sites. High spatial-temporal resolution observations are provided by 260 GNSS continuously operating stations, and the distribution of these reference stations is shown in Figure 1. Each station is equipped with a high-precision Trimble NetR8/R9 GNSS receiver, a meteorological sensor, and other auxiliary instruments. With this equipment, GPS data and surface meteorological parameters are continuously collected. GAMIT/GLOBK software was employed as a comprehensive suite of programs developed by MIT to process GPS data. The double-difference model is used in GAMIT software, so at least three long baselines should be included during the GPS data processing procedure. However, no external GPS data are required because of the large areas that CMONOC covers in our study.
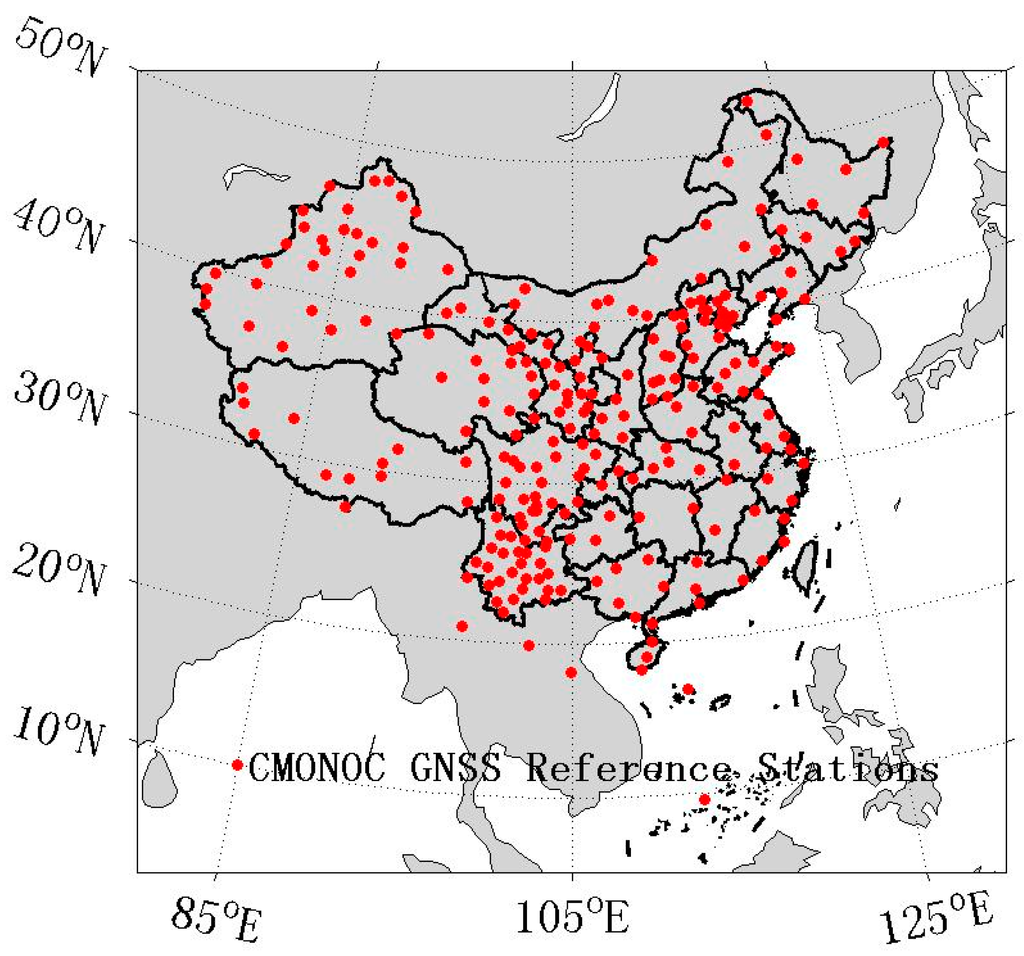
Figure 1.
Distribution of CMONOC GNSS reference stations.
2.2. Interpolation of NCEP FNL Global Analysis Data
Interpolating surface meteorological parameters Ps and Ts from the NWP data can be an effective complement for ground-based GPS meteorology as a solution for the absence of collocated meteorological sensors. In this study, we used the NCEP FNL Operational Global Analysis historical data to perform these interpolations. The NCEP FNL Operational Global Analysis data are produced from the same data assimilation and forecast system as the NCEP Global Forecast System (GFS) data. The difference between these two datasets is that approximately 10% more observations are assimilated into the initial condition for FNL than that for GFS. However, because it takes some time to wait for more observational data to be collected, the FNL analysis data are delayed by approximately 60–90 min compared with those from GFS analysis. These data can be downloaded freely from the website http://rda.ucar.edu/datasets/ds083.2/.
The NCEP FNL Analysis data are published every six hours and consist of 1° × 1° horizontal grids. The analyses provide various parameters on the surface, at 26 mandatory levels from 1000 millibars to 10 millibars, as well as at a few other levels. However, only several parameters are used in the interpolation. First, the four neighboring grid nodes are selected according to the latitude and longitude of specific stations. Assuming that the grid node number is i, we extracted pressure values and geopotential heights of the two mandatory levels nearest to the specific station’s height. Then, the scale height between these two levels is calculated as:
where hlower and hupper represent the upper and lower level geopotential height and plower and pupper are the air pressure of the lower and upper level, respectively. Pressure at a GPS site’s height z is estimated by the following equation:
where pi is the pressure of height hi and hi is the height of one of the chosen mandatory levels or that of the surface, depending on which is the nearest level to the GPS station’s elevation.
After the vertical interpolations at the neighboring grid nodes, we horizontally interpolated the four pressure values to each GPS site’s position. The interpolation formula is expressed as:
where ps is the station’s surface pressure and wi represents the interpolation coefficients of the vertical interpolated pressure at point i. wi is determined by the following formula (see [17]):
where R = 6378.17 km is the mean radius of the earth, C is the scale factor, which equals one in this study, and is the angular distance between the grid node i and the GPS receiver’s position (φ,θ):
In the above equation, φ and θ represent latitude and longitude, respectively. Because the reanalysis grids are definite, the interpolation coefficients in Equation (10) for the stationary GPS site are also fixed and can be stored as constants to avoid duplicate calculation.
Surface temperature generation also starts with vertical interpolation at neighboring points. The adiabatic lapse rate between two levels can be calculated simply from their temperatures and geopotential heights. We first estimated the mean adiabatic lapse rate between the 1000 hPa and 500 hPa pressure levels, and then, temperature at the height of the GPS station was given by:
where is the computed adiabatic lapse rate, is the temperature at 2 m above the surface, and is the corresponding height. Finally, horizontal interpolation was employed to generate the temperature of the GPS station’s point. Equations (10)–(12) are used, while the pressure parameters in Equation (10) are replaced by temperature.
It is worth mentioning that the difference between the altitude height and geopotential height is neglected in our study (see [33]) because the top height we interpolated was below 30 km. However, only the geodetic height can be estimated from GPS data processing. Therefore, we used the EGM2008 model, which was developed by the U.S. National Geospatial-Intelligence Agency (NGA) to convert one GPS station’s geodetic height to the altitude height. Details of the EGM2008 model can be found at http://earth-info.nga.mil/GandG/wgs84/gravitymod/egm2008/egm08_wgs84.html. The accuracy of the EGM2008 model with 1° × 1° resolution can reach up to the sub-meter level over China [34]. The change of air pressure produced by several sub-meters of height difference can be ignored; we believe this sub-meter-level accuracy is acceptable for our purposes.
3. Interpolation Results
To assess the quality of interpolated surface pressure and temperature for GPS PWV derivation, we introduced two observation datasets for comparison: CMONOC meteorological measurements and the Integrated Surface Database (ISD), which are provided freely by the U.S. National Climatic Data Center (NCDC).
Specific altitude height is a key parameter during our interpolation procedure. From GAMIT/GLOBK processing, the geodetic height of each CMONOC GNSS station can be estimated. Then, conversion from the geodetic height to the altitude height has to be performed, and NCEP FNL data are interpolated to one site’s altitude height instead of at the geodetic height. As previously mentioned, geoid undulations of CMONOC GNSS sites estimated from the EGM2008 model were used to approximately adjust the geodetic heights to altitude heights. Their values are illustrated in Figure 2. It can be seen that they vary from approximately 20 m in eastern China to approximately −60 m in northwest China, which indicates that an apparent bias in the interpolation of air pressure would exist if no conversion between different height systems was performed.
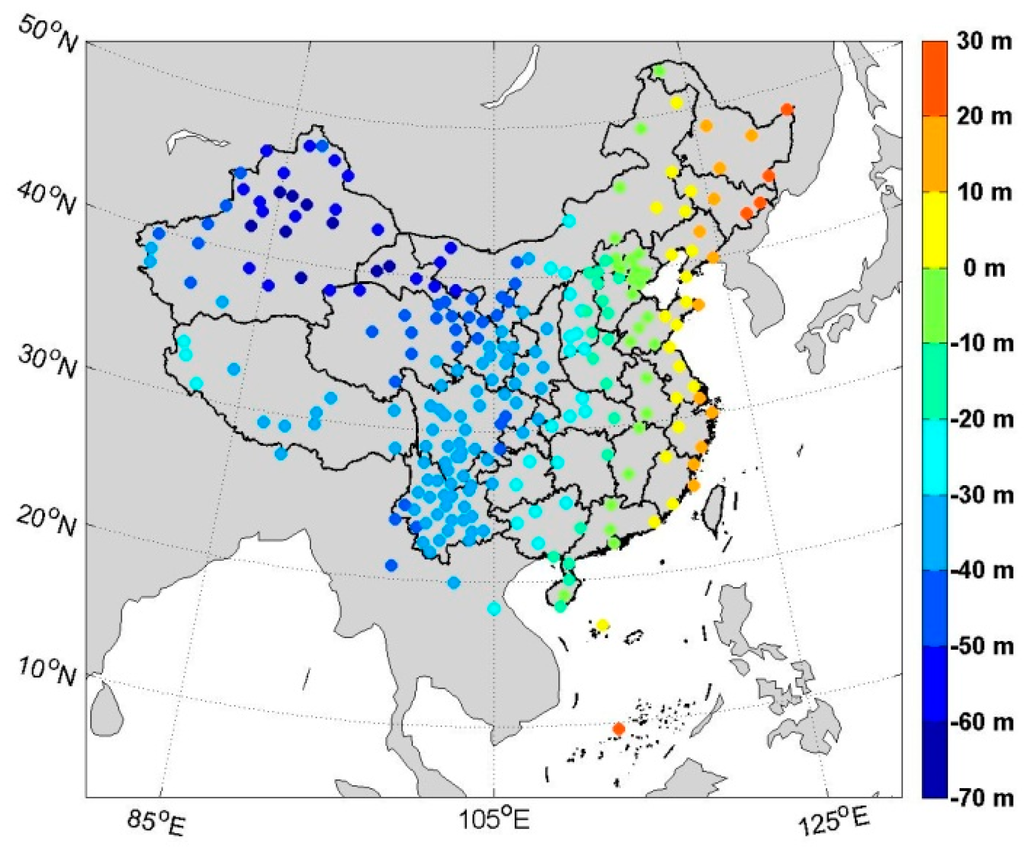
Figure 2.
EGM2008 model’s geoid undulations of CMONOC GNSS sites.
ISD provides global hourly and synoptic observations of various parameters, such as temperature, dew point, sea level pressure, station pressure, and other observed elements (see [35]). Although ISD data originate from numerous sources, a single common ASCII format and common data model are still developed by ISD to facilitate the use of data. The input data sources compiled by ISD have to be previously processed through quality control. Currently, high spatial coverage is obtained by ISD stations in most parts of China, except some areas in western China. The number of active stations in China included in the ISD database is over 350, and their distribution in 2012 is shown in Figure 3. For some ISD sites, surface pressures have to be generated from sea level pressure.
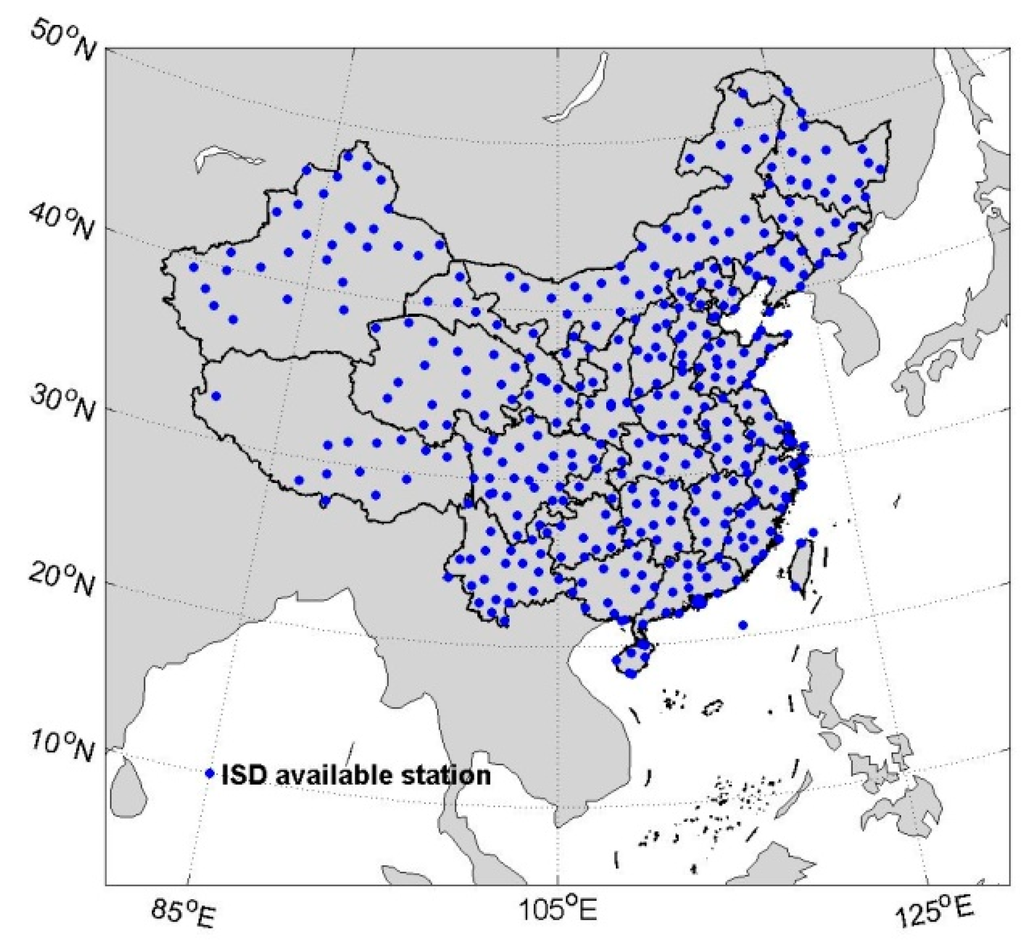
Figure 3.
Distribution of ISD active stations over China in 2012.
3.1. Comparison between Interpolated and Observed Ps
Taking the first derivative of Equation (1) with respect to the surface pressure P0, we can obtain the following formula:
For a stable reference site, and H are constants, so the relationship between the errors of ZHD and P0 is linear. From Equation (14), it can be inferred that the surface pressure error of 2.8 hPa produces an approximately 6.7 mm error in ZHD, and the equivalent error will be transferred to ZWD through the computation of Equation (3). This equates to a 1-mm error in PWV. The comparison between interpolated and measured surface pressure is based on the above analysis.
Considering that the CMONOC data and ISD data are derived from different sources and that most of the ISD observed data were likely previously assimilated into the NCEP FNL data, we compared the interpolated Ps with their corresponding measured values from two datasets. In our study, we make these comparisons using the full-year data of 2012 from both datasets. BIAS and RMSE are selected as the statistics, and their mathematical expressions are as follows:
where INT is the interpolated value and OBS represents the observed value for the same element.
We calculated BIAS and RMSE between the interpolated and observed Ps at all of the selected CMONOC and ISD sites. Table 1 gives the number of ISD and CMONOC sites at which absolute BIAS or RMSE were within the given value domain. This clearly indicates that both statistical values were below 1 hPa, that is, there was less than 0.5-mm error in the GPS PWV derivation, at most sites. Only at a few sites was the absolute BIAS or RMSE more than 2.8 hPa, which equates to more than a 1 mm GPS PWV error, as previously derived. Furthermore, it can be seen from Figure 4, which illustrates the BIAS and RMSE of all of the selected stations together with their locations on the map, that stations with a larger BIAS or RMSE are mainly distributed in southwest China or the northern part of Xinjiang Province. These sites had a common property in that they are all located in regions of higher relief. Taking the JIULONG station in Sichuan Province (ISD number: 564620) as an example, we found that it had a great difference in height with the four neighboring grids of the NCEP FNL model. The height of this station was 2994 m, whereas the lowest neighboring node’s height was 3703 m, so the altitude height differences were higher than 651 m, reflecting undulating terrain. Its interpolated and measured Ps time series is illustrated in Figure 5. There is an obvious system bias between the two series. The reason for such a system deviation may be that the four pressure values used for horizontal interpolation were all one-side vertical extrapolated instead of interpolated because the JIULONG station was lower than all of the neighboring nodes, and the accuracy would decrease substantially if the vertical extrapolation distances were too long. The other stations that exhibit large interpolation errors also faced the same problem, including the XJWQ and QHME stations in CMONOC. However, more than 97.5% of stations with GPS PWV derivation errors of interpolated Ps were below 1 mm. This demonstrates the effectiveness of our interpolation method in areas without significant relief.

Table 1.
Number of sites at which absolute BIAS or RMSE of interpolated surface pressure were within a given special value domain.
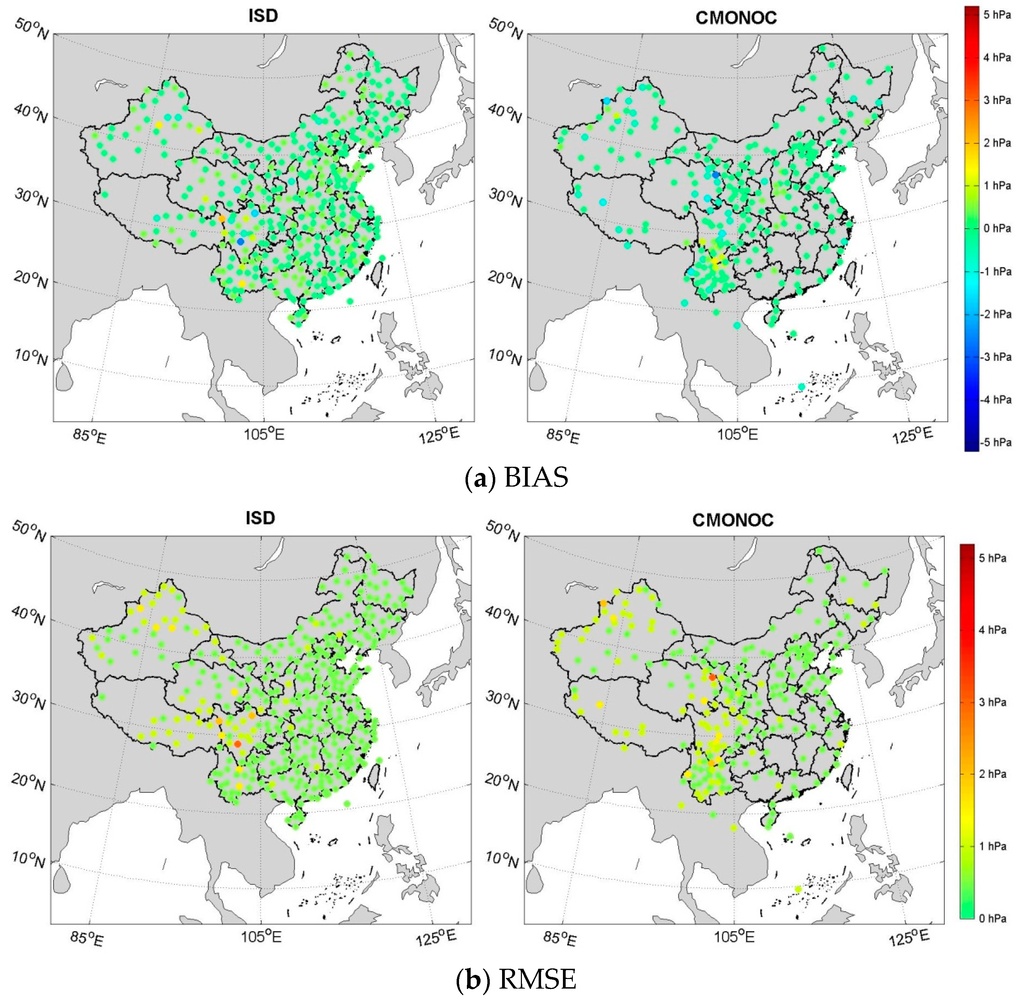
Figure 4.
(a) BIAS and (b) RMSE between interpolated and measured surface pressure of stations from ISD and CMONOC.
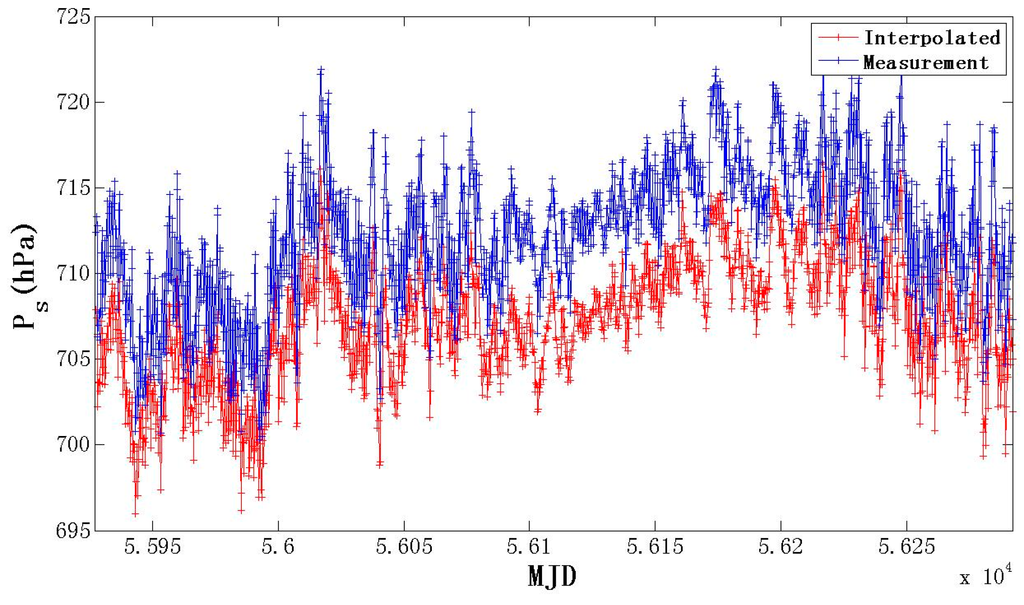
Figure 5.
Interpolated and measured surface pressure time series at ISD station 564620.
Even under extreme weather conditions, the accuracy of the interpolated Ps did not decrease dramatically according to our experiment. Taking the Haikui typhoon, which landed in Ningbo City, Zhejiang Province on 8 August 2012, as an example, we compared the measured and interpolated Ps of the ZJZS station, which is the nearest CMONOC station to the typhoon landing position. As Figure 6 shows, the differences between the two Ps time series remain very small during the typhoon period from 5 to 11 August 2012. Their mean difference was −0.89 hPa, with a standard derivation of 0.37 hPa, and the largest difference was only −1.75 hPa. We also use the Ps series generated from the GPT model (see [36]) for comparison purposes; its difference from real observations could be as high as 20.51 hPa, which obviously cannot be accepted in GPS PWV retrieval.
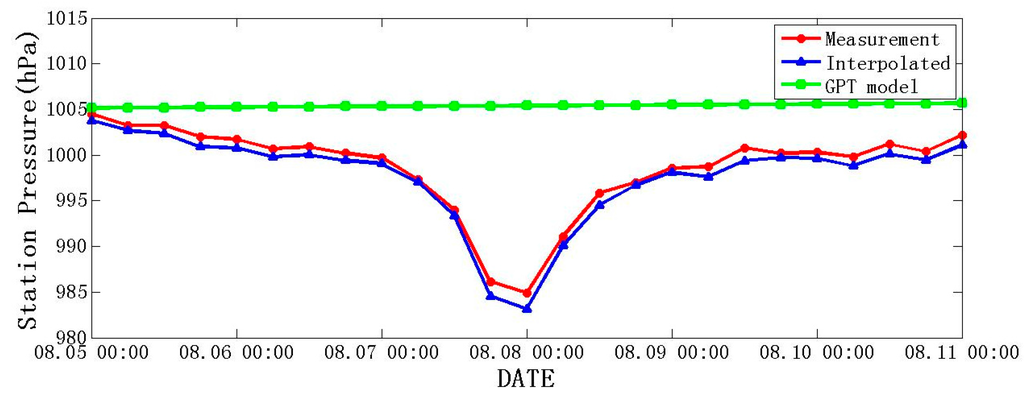
Figure 6.
ZJZS station’s surface pressure time series respectively from observation, interpolation, and the GPT model. The period is 5 to 11 August 2012, during which the Haikui typhoon landed in Ningbo City, Zhejiang Province, China.
3.2. Comparison between Interpolated and Observed Ts
The same statistics were employed to assess the quality of interpolated surface temperature Ts. We also take the first derivative of Equation (5) with respect to the weighted mean temperature Tm:
Figure 7 visualizes the relationship between Π and Tm. Π increases from 0.1363 to 0.1699 with the increase of Tm from 240 K to 300 K, while the first derivative of Π with respect to Tm only decreases from 5.6198 × 10−4 K−1 to 5.5907 × 10−4 K−1. The growth rate of Π is 20%, while the decline rate of Π’s derivative is merely 0.52%, which suggests that the derivative of Π with respect to Tm is not sensitive to changes in Tm and remains at a low value. When Tm equals 290 K and Π is 0.1643, even if Tm changed more than 5 K, the value of Π varied by only approximately 2.8 × 10−3, which represents a nearly 1.8% relative difference. The largest mean PWV value of approximately 50~60 mm occurs in Southern China in July, so such a relative difference is acceptable. This demonstrates that the impact of Tm error on GPS PWV derivation is substantially lower than that of surface pressure error because Π is less sensitive to Tm error.
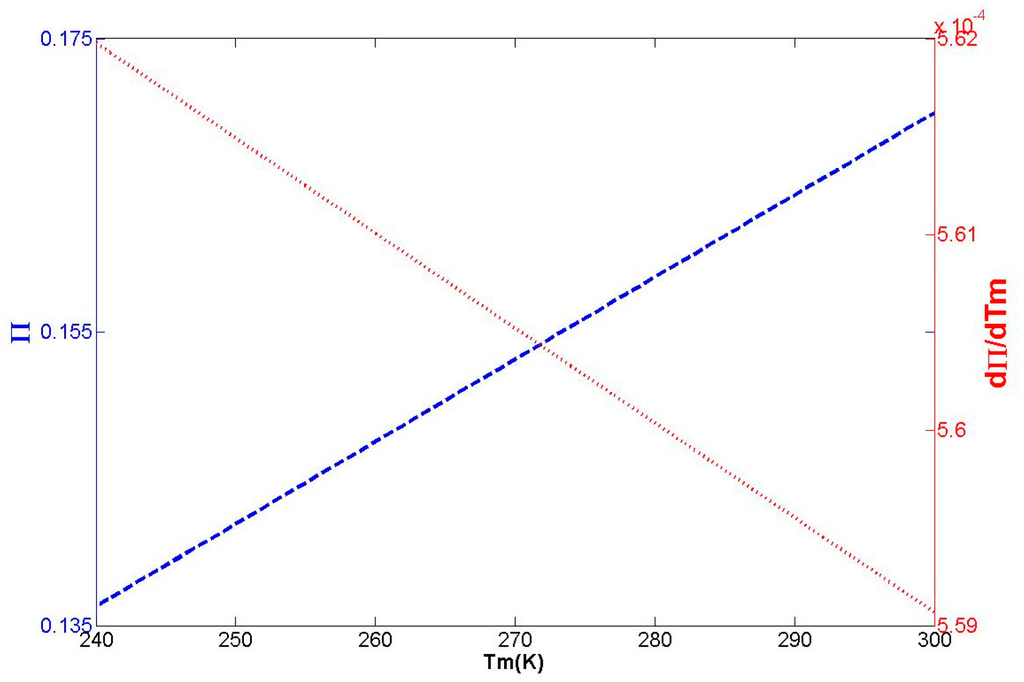
Figure 7.
Change of Π and its first derivative with respect to Tm.
To assess the quality of the interpolated Ts, we chose 5.0 K as the threshold value of absolute BIAS and RMSE between the interpolated and measured values based on the above analysis. During these comparisons, a few gross differences between the interpolated and observed temperatures were found. These errors were attributed to the obvious measurement errors. Using the CMONOC station QHBM as an example, abnormal measured temperature values of −167 °C or 145 °C occurred for unknown reasons. Therefore, it is necessary to perform a quality check before performing statistical work. We marked differences with absolute values larger than 20 °C as false and excluded them from the final statistical analysis; 0.003% of the data from ISD and 0.035% of the data from CMONOC were deleted. The corrected statistical results are given in Table 2 and illustrated in Figure 8. Although the accuracy of the GPS-PWV derivation is not directly determined by Ts, as it is also affected by the precision of the Tm–Ts conversion formula, the quality of the interpolated Ts can also be a useful index to indicate the effectiveness of our interpolation scheme. The interpolation results for surface temperature at most stations showed the satisfactory accuracy of near-ground air temperatures for GPS-PWV derivation. However, sites with larger interpolation errors, which were mainly distributed in Southwestern and Northwestern China, also showed large surface temperature interpolation errors. The landforms of these regions included steep undulations, which likely led to poor outcomes. Overall, the accuracy of the interpolated Ts is slightly lower than that of the interpolated Ps, but their influences on the accuracy of the GPS-PWV derivation are of the same order because GPS-PWV is not as sensitive to Ts as to Ps.

Table 2.
Number of sites at which absolute BIAS or RMSE of interpolated surface air temperature were within a given special value domain.
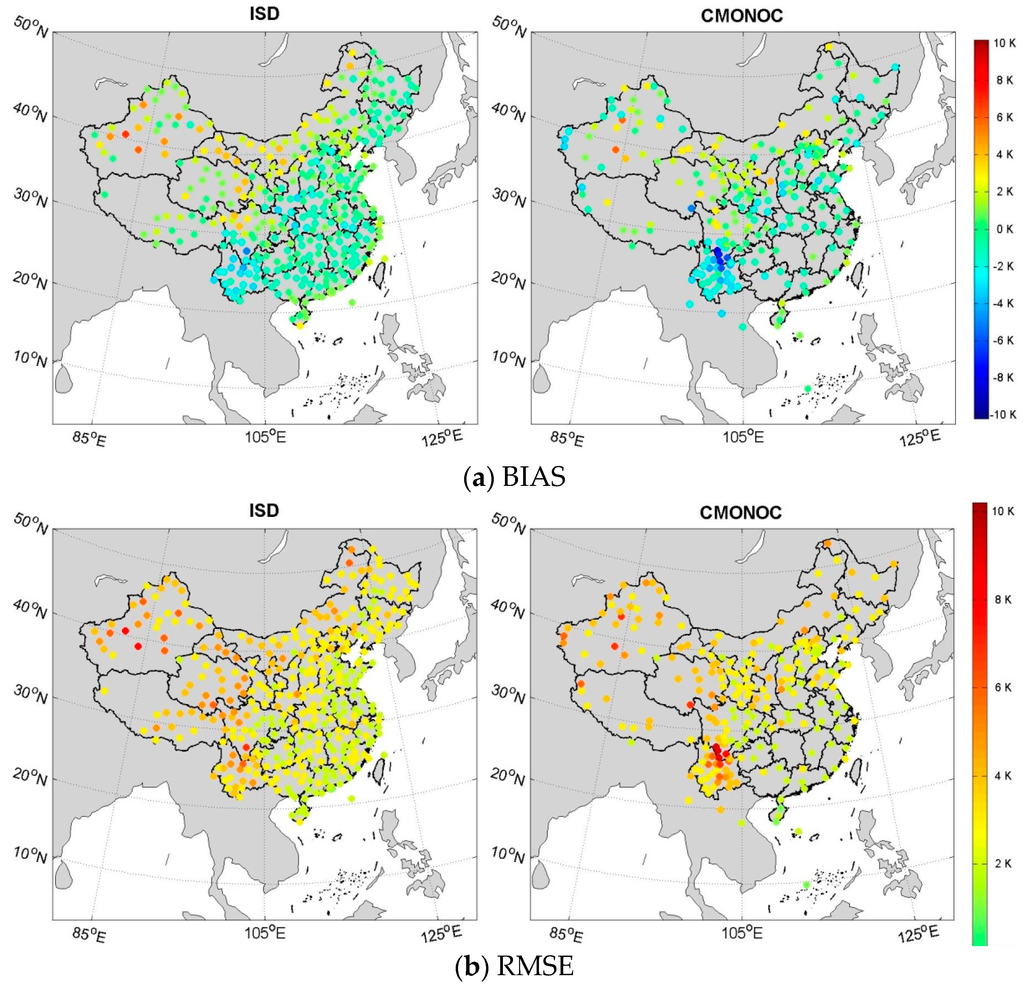
Figure 8.
(a) BIAS and (b) RMSE between interpolated and measured near-ground air temperature of stations from ISD and CMONOC.
4. Comparison of PWV Results
It is a difficult task to evaluate the precision of GPS PWV at every CMONOC station because there is a lack of alternative independent methods to measure PWV more precisely than the GPS measurements, which have a close temporal-spatial resolution. We attempted to use radiosonde data, which can be downloaded freely, to compare with the GPS PWV results. We selected 22 radiosonde stations from IGRA because there were CMONOC GNSS sites very close to them. The geodetic coordinates of the selected radiosonde stations and their nearest GNSS stations are given in Table 3. Their locations are shown in Figure 9. These stations are evenly distributed in China, and their altitudes ranged from several meters to higher than 4500 m. Therefore, they represent our derived GPS-PWV values under different conditions.

Table 3.
Geodetic coordinates of RS sites and their nearby CMONOC GNSS sites.
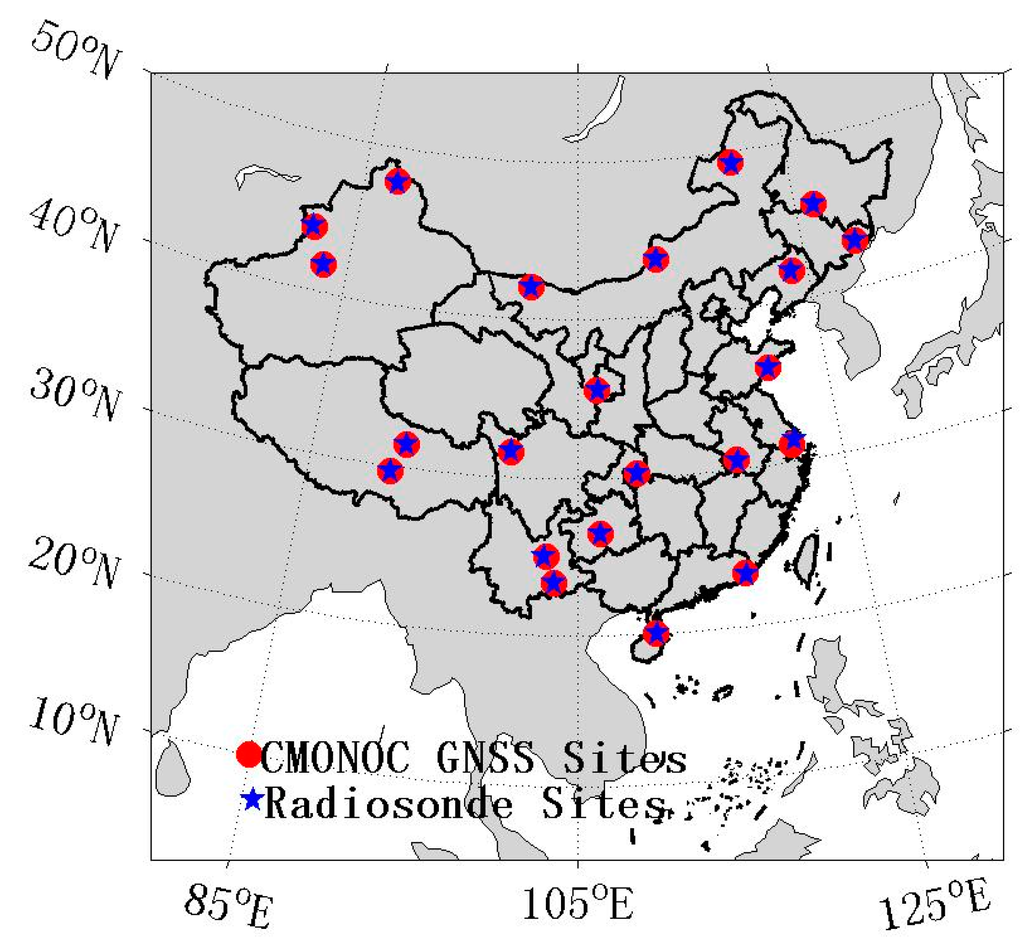
Figure 9.
Distribution of radiosonde and GNSS stations that were selected to compare their PWV results.
4.1. Results of Different Tm
We obtained the important parameter, the weighted mean temperature Tm, using three different approaches:
- (1)
- At all of the RS stations, we directly integrated the radiosonde data assuming that the balloon ascended along a vertical path. The following approximate formula is used:where water vapor pressure e is calculated by e = es ×RH, RH represents the relative humidity, and saturation vapor pressure is generated using ITS-90 equations proposed by [37]. We denoted Tm by this method as Tm_RS.
- (2)
- At selected CMONOC stations in Table 3, Tm was estimated from Ts using the Tm–Ts linear equation of Equation (7). From Wang’s research [38], coefficients a and b are determined by the climatic region of every site. Ts was measured by the meteorological sensors collocated to the CMONOC GNSS sites. Then, Tm_OW could be obtained.
- (3)
- The same method as in Equation (2) was employed, except that Ts was obtained from the interpolation schemes described in Section 2. To differentiate their results, we denoted the results from this method as Tm_IW.
The former two methods are both based on real observations, whereas the NCEP FNL dataset was employed in the third scheme. The RMSE between the different Tm results are shown in Table 4. In the comparisons, radio sounding was considered to be the most precise measuring method, so the results of the other two approaches were both compared with Tm_RS. At each site, the RMSE of both Tm_OWs and Tm_IW to Tm_RS were always below 5 K, and their values were very close at the same site. This indicates that the accuracies of Tm_OW and Tm_IW are equally acceptable.

Table 4.
RMSE between the Tm results from three different approaches.
In areas without any radiosonde or surface meteorological stations, the accuracy of the NWP data decreased due to the lack of assimilation data. However, there are several CMONOC GNSS sites located in such regions that can provide high-precision surface meteorological observations. Because the accuracy of Tm_OW will not change under the above conditions, we can use Tm_OW to evaluate Tm_IW. We selected 10 CMONOC GNSS stations that met such conditions for further comparisons. The RMSE between the Tm_IW and Tm_OW of these stations are given in Table 5. The values of the RMSE were still lower than 5 K at most of the selected sites, except SCPZ. This is attributed to, as is previously mentioned, the fact that the SCPZ site had a large height difference to its neighboring NWP grid nodes. Taking this factor out of consideration, we are confident that this dataset exhibits accuracy in terms of the Tm_IW that is acceptable, even if there was no precise meteorological data assimilated into the NCEP FNL dataset.

Table 5.
RMSE between Tm_IW and Tm_OW at CMONOC GNSS stations without nearby meteorological station.
4.2. Results of Different PWV
At the stations given in Table 3 and Figure 9, different PWV results were generated in our study using different derivation methods:
- (1)
- At the 22 CMONOC GNSS stations, we first employed GAMIT software to process GPS data under ITRF2008. The cut-off elevation angle was 10°, and ZTD was estimated with the GMF mapping function at each station. Because of the long distances between our selected stations, absolute ZTD and atmospheric delay horizontal gradient values, at intervals of one hour and two hours respectively, could be estimated directly without introducing any other GPS sites into this network. Then, we calculated GPS PWV, as described in Section 2.1. Real surface pressure measurements of Ps and Tm were computed from real near-ground air temperature observations Ts. We denoted the PWV results as GPS_PWVobs.
- (2)
- This scheme is similar to method (1), expect that Ps and Ts were generated from the interpolation of the NCEP FNL dataset, as proposed in Section 2.2. These GPS PWV results are referred to as GPS_PWVNCEP.
- (3)
- PWV can be integrated from the vertical profile of several meteorological parameters using the following formula:
The essential meteorological parameters can be obtained from the radio soundings. At the radiosonde stations listed in Table 3, the PWV integrated from the radiosonde data is denoted as RS_PWV.
- (4)
- PWV can also be integrated from NCEP FNL data using the same integral formula as Equation (19) and is referred to as NCEP_PWV.
First, we compared the GPS_PWVobs and GPS_PWVNCEP results. The only difference between them is the data source of Ps and Ts; therefore, such a comparison can directly indicate the feasibility of remedying the lack of Ps and Ts measurements in the NCEP FNL data interpolation. There were no meteorological data available at the XZNQ station, so it was excluded from the comparison. Figure 10 illustrates a scatter plot and several statistical and number density plots of differences between GPS_PWVobs and GPS_PWVNCEP. Simple linear regression shows that the two results are highly correlated, with a correlation coefficient of 0.9998 and a regression equation of y = 0.9983x − 0.1755, which is very close to y = x. All of the stations have BIAS within ±0.4 mm, and almost all of their absolute values are smaller than 0.2 mm; all of the RMSE values are smaller than 0.63 mm, with most below 0.4 mm. Deviations have a very low value in all of the PWV value fields. These comparisons clearly demonstrate that GPS_PWVobs and GPS_PWVNCEP are very similar. Therefore, the accuracy of deriving GPS PWV using Ps and Ts interpolated from NCEP reanalysis data is reliable compared with GPS PWV derived from real surface meteorological data.
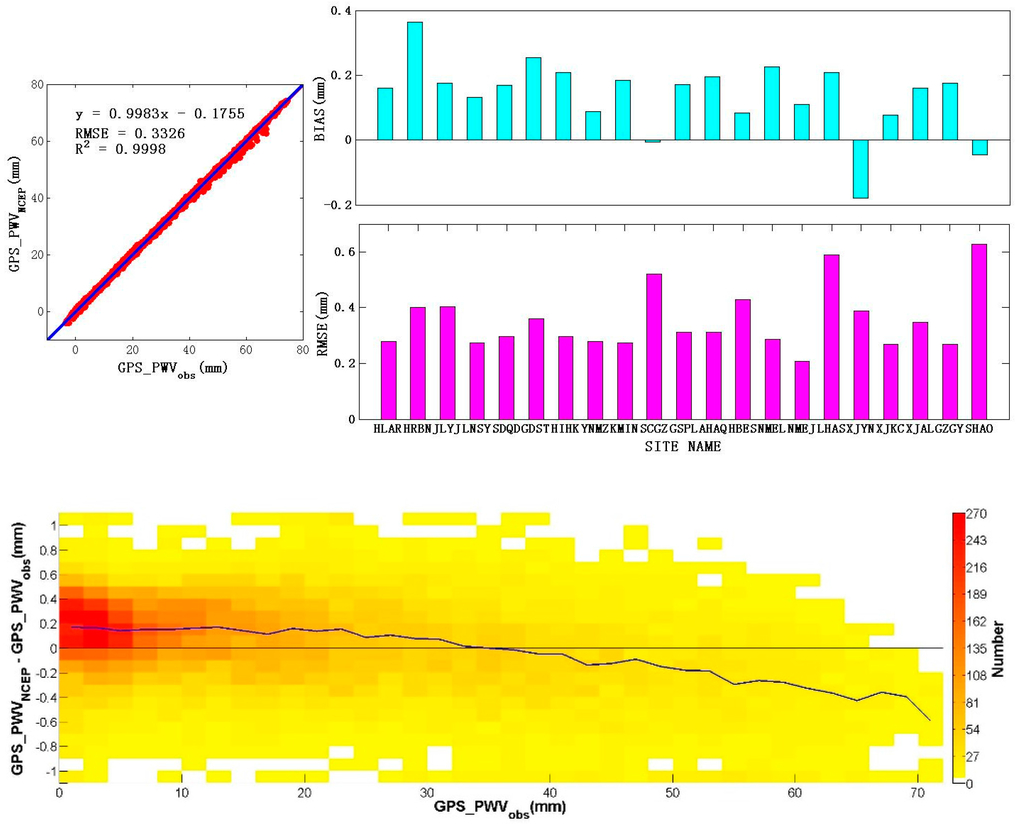
Figure 10.
Scatter plot (top left), BIAS, and RMSE at each GPS station (top right); and number density plot of differences (bottom) between GPS_PWVobs and GPS_PWVNCEP.
We also compared GPS_PWVNCEP with integrated PWV, including RS_PWV and NCEP_PWV. GPS_PWVobs was not included in this comparison because its results are very close to those of GPS_PWVNCEP. Figure 11 shows statistical and number density plots of differences between the three PWV result sets. High correlations exist between GPS_PWVNCEP and integrated PWV, as demonstrated by the unary linear regressions, with correlation coefficients higher than 0.97. Overall, NCEP_PWV is more strongly correlated to GPS_PWV than RS_PWV. It is common that GPS_PWVNCEP is more consistent with NCEP_PWV than with RS_PWV in our study. At most stations, the BIAS values between GPS_PWV and NCEP_PWV are within ±2 mm and the RMSEs are approximately 2~3 mm, whereas the BIAS values between GPS_PWV and RS_PWV are within ±3 mm and the RMSEs are approximately 2~4 mm. The number density plot of the differences between the three PWV results indicates that the PWVs were concentrated below 5 mm in our study, and the negative deviation between GPS_PWV and the other two PWVs was also mainly distributed within this PWV range. As the blue line indicates, GPS_PWV shows a dry bias compared with RS. However, this is probably because of the position offsets between the GPS and RS stations. The differences of their horizontal positions or height can also produce some PWV differences.
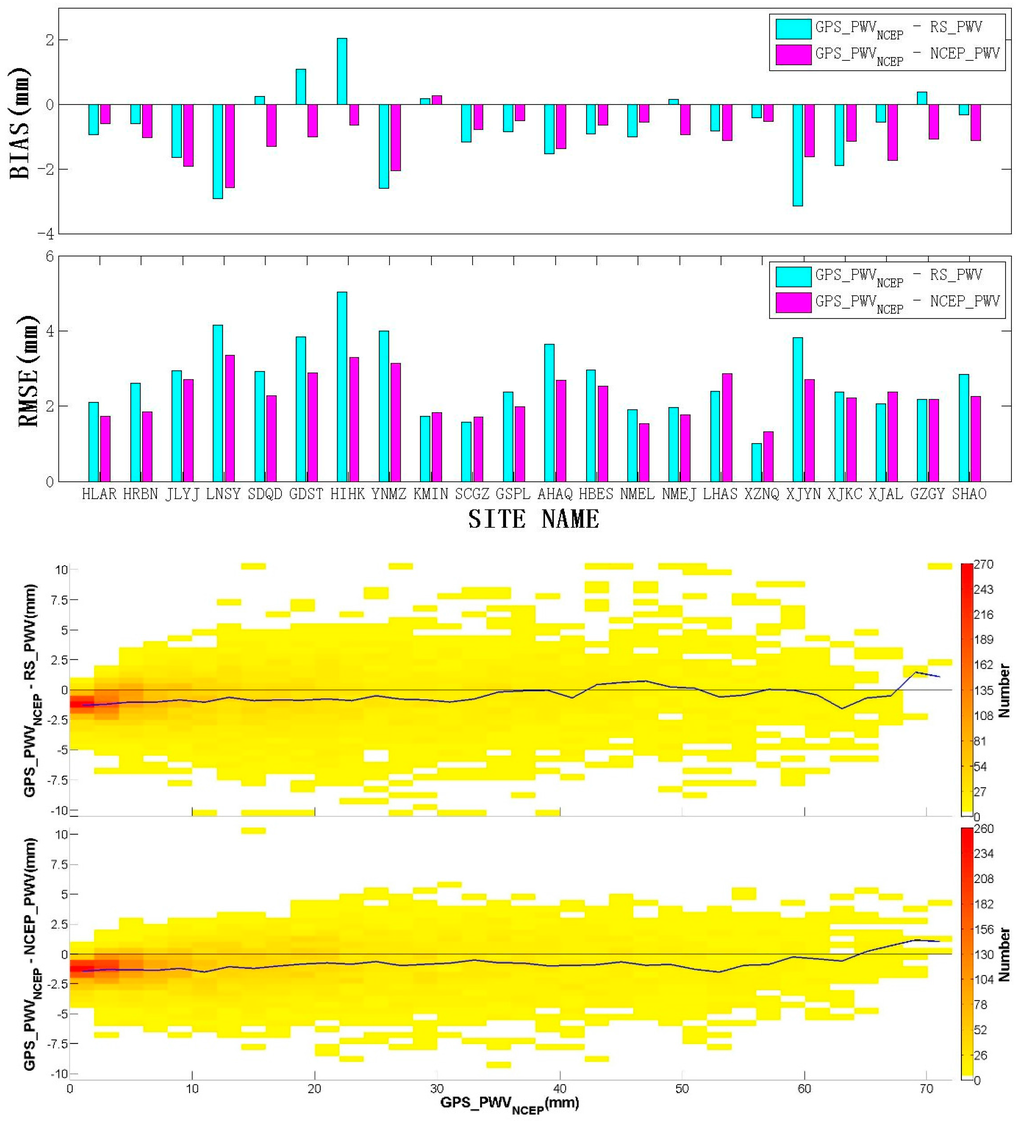
Figure 11.
BIAS and RMSE at each GPS station (top); and number density plot of differences (bottom) between GPS_PWVNCEP and RS_PWV or NCEP_PWV.
The higher RMSE at HIHK is attributed to the serious data loss and the very active ionosphere over this low latitude area. As Figure 12 shows, the ratio between L1 and L2 observations increased with increasing L2 data loss, which caused the difference between GPS_PWVNCEP and NCEP_PWV to increase dramatically. Therefore, it is essential to perform quality control for GPS PWV retrieval in future work [39].
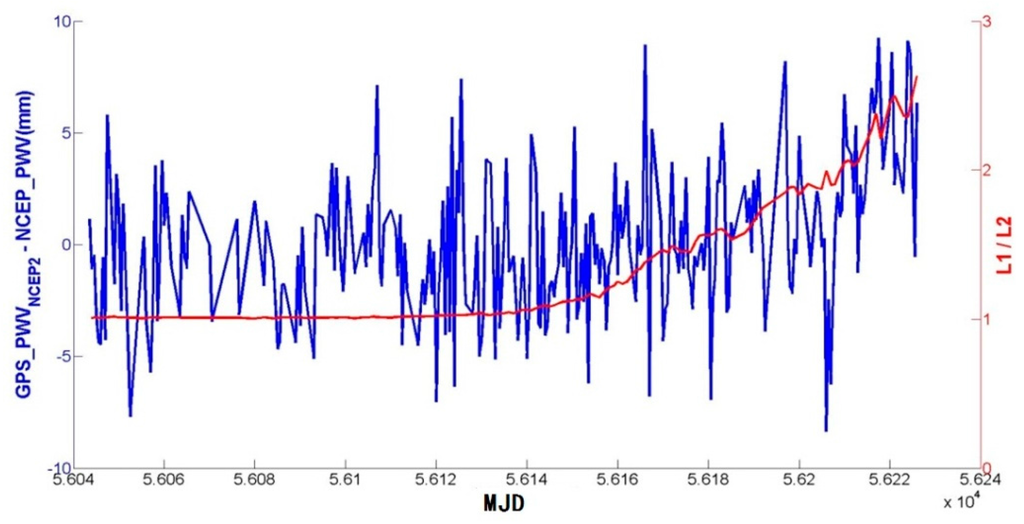
Figure 12.
Time series of difference between GPS_PWVNCEP and NCEP_PWV (blue line) and ratio between observation numbers of L1 and L2 (red line).
As previously mentioned, the accuracy of the NWP data will decline in regions without sufficient high-precision meteorological observations. Our NCWP_PWV is an indirect and integrated product of the NCEP FNL data; thus, its precision will also decrease. However, the derivation of GPS_PWVNCEP only requires the interpolation of two levels of NCEP data, so changes in the reanalysis data exert less influence on it. For stations located in regions without intensive radio sounding observations, such as the LHAS and XZNQ stations, the differences between GPS_PWVNCEP and RS_PWV are smaller than those between GPS_PWVNCEP and NCEP_PWV.
PWV can also be retrieved by sun photometers [40], and in this paper, we denote this type of PWV product as SP_PWV. Fortunately, there was an active AERONET (Aerosol Robotic Network) site in 2012 located at Taihu, which is in close proximity to the SHAO GNSS station in Table 3. The distance between these stations was approximately 100 km. More details about AERONET and its products are presented on its website. To further assess our PWV products, we compared the GPS_PWVNCEP of the SHAO site, RS_PWV of the 58362 radiosonde site and SP_PWV of the Taihu AERONET site. Figure 13 is a scatter plot of the three PWV datasets. Common observation times between GPS_PWV and SP_PWV occurred more frequently than between RS_PWV and SP_PWV. Statistics are given in Table 6. Clearly, GPS_PWVNCEP is highly consistent with SP_PWV, with a bias of only 0.3464 mm and RMSE of 3.3439 mm, and the correlation coefficient was higher than 0.98. Their agreement was even better than that of RS_PWV and SP_PWV.
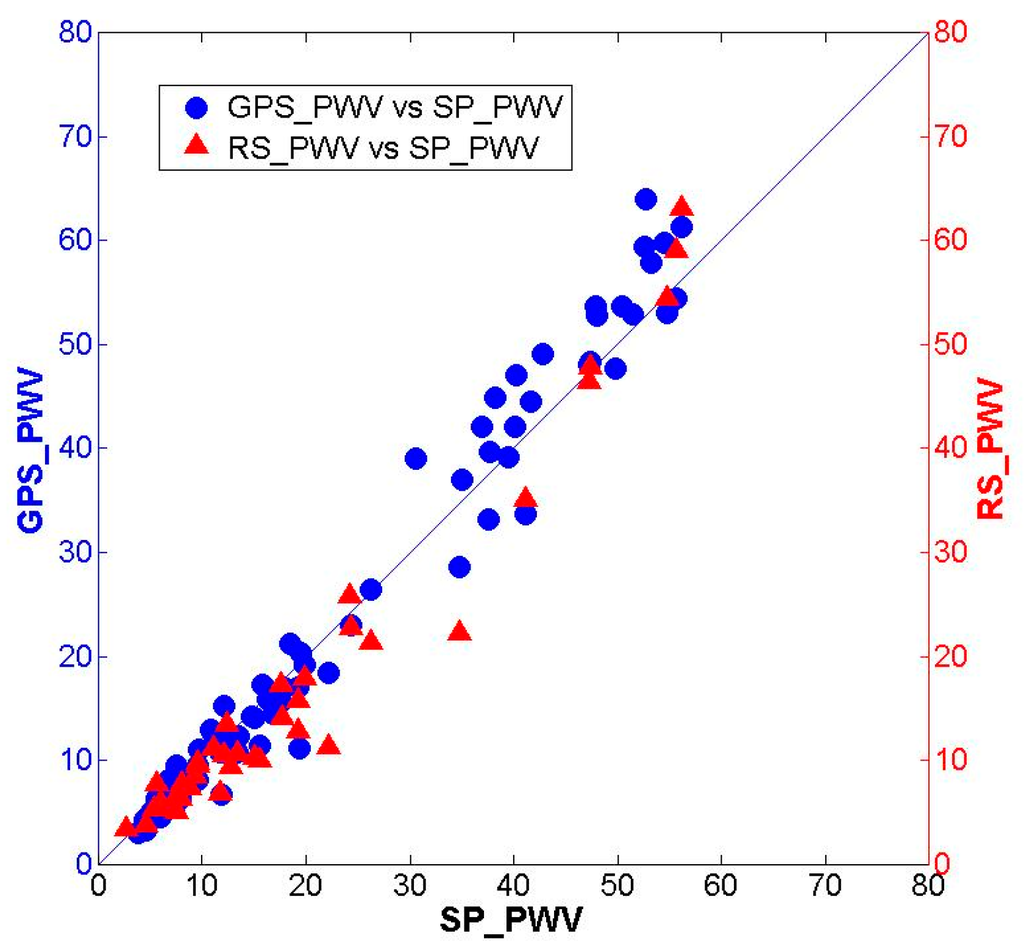
Figure 13.
Scatter plot between SP_PWV, GPS_PWVNCEP, and RS_PWV.

Table 6.
Statistics of differences between SP_PWV, GPS_PWVNCEP, and RS_PWV.
The accuracy of PWV retrieved using our scheme under extreme weather conditions also required verification. Figure 14 illustrates the time series of RS_PWV and GPS_PWVNCEP at the SHAO station from UTC time 00:00 28 July to 24:00 9 August in 2012. The time interval of GPS_PWVNCEP was 6 h, whereas that of RS_PWV was 12 h. The SHAO site is located in Shanghai city. During this period, Shanghai suffered from two severe typhoons, Damrey and Haikui, in rapid succession. However, the two PWV time series still agreed very well, with a bias of −1.05 mm and RMSE of 2.83 mm. It can be seen that the PWV value fluctuated very dramatically in a short time period. Two rapid continuous PWV increase processes, that is, from 33 mm to 72 mm between 01.08.2012 06:00 and 02.08.2012 06:00 and from 47 mm to 73 mm between 06.08.2012 18:00 and 08.08.2012 12:00, were both reflected in the GPS_PWVNCEP and RS_PWV time series.
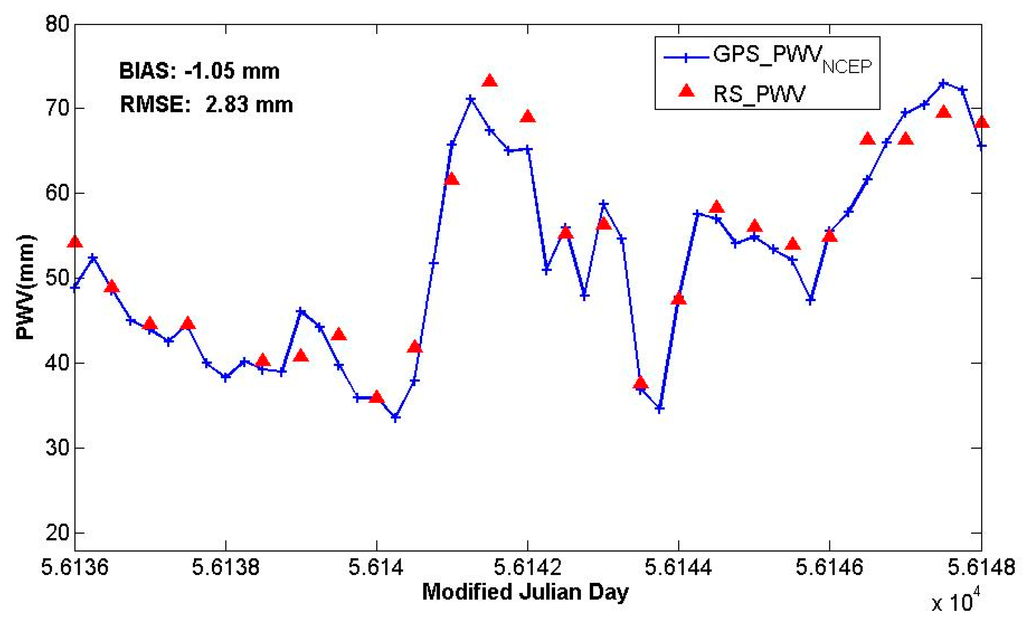
Figure 14.
Time series of GPS_PWVNCEP from 00:00 on 28 July to 24:00 on 8 August 2012 at SHAO station.
5. Conclusions and Outlook
Employing as many GPS sites as possible to obtain GPS PWV can provide higher spatial and temporal resolution PWV data than other traditional methods, such as radio soundings or GPS precipitable water vapor products from limited GPS stations that equipped meteorological sensors. High spatiotemporal resolution water vapor information is beneficial for studying the details of vapor properties at a specific site location, or during a particular weather event. However, there are many geodetic GPS stations that do not have collocated meteorological sensors. Using the NWP dataset can be an alternative to obtaining the required meteorological parameters necessary for the traditional GPS PWV derivation. In this paper, we studied the scheme of interpolating NCEP FNL reanalysis data to generate surface pressure or temperature over China. Comparisons with real meteorological measurements show the accuracies of the interpolated surface pressure or surface temperature are acceptable for the GPS PWV derivation over most Chinese regions, except for some strong relief areas, even under particular synoptic cases, such as typhoons. Compared with radio sounding data, the weighted mean temperature can also be calculated using the surface temperature interpolated from the NCEP FNL dataset. Our study indicates that GPS PWV products that use interpolated surface meteorological elements were very close to those based on real meteorological observations, with differences within ±0.4 mm and a RMSE mainly below 0.6 mm. These GPS PWV results also strongly agreed with radio sounding observations, as demonstrated by their high correlations and low differences. The main factor influencing the accuracy of GPS PWV is GPS data processing. In our study, serious loss of GPS L2 data reduced the accuracy of the estimated GPS ZTD dramatically, and led to a further decrease of GPS PWV accuracy. However, the feasibility of applying such GPS PWV solutions to research long-term trends of water vapor over certain region requires further investigation. For example, experiments should be carried out over decades to confirm the long-term accuracy of our interpolation method. Another key issue is that numerous historical GPS data should be re-processed, which may involve many problems such as the difference between relative calibration and absolute calibration of antenna phase center variations [41].
Because interpolation of NWP data can be used to generate surface meteorological parameters, we demonstrate that it can serve as a very promising complement to the present ground-based GPS meteorological observation networks under appropriate conditions, such as in relatively flat regions. The time duration and spatial range of GPS PWV should be extended through future research endeavors. Details of some interesting climatic phenomena or extreme weather conditions can consequently be studied better. Another relevant research topic is to calculate essential meteorological elements for GPS PWV using forecast data instead of reanalysis data. This can help forecasters develop real-time, high-resolution, and high-precision precipitable water vapor maps. Such products are reconstructed much faster than data assimilation of the NWP system. If the accuracies are found to be suitable, these products would be helpful for rainstorm warnings and forecasting of flood hazards.
Acknowledgments
This study was supported by the Doctoral Research Start-up Funds Projects of Anhui University (No. J01001966), National Natural Science Foundation of China (No. 41074008, 41271443), the National 973 Program of China (No. 2012CB957701), the Research Fund for the Doctoral Program of Higher Education of China (No. 20120141110025), and the Anhui Provincial Natural Science Foundation (No. 1308085MD52). The authors thank the Department of Earth Atmospheric and Planetary Sciences, MIT for providing GAMIT/GLOBK software. We also thank the National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce for contributing the NCEP FNL dataset. We appreciate the National Centers for Environmental Information for providing the ISD and IGRA datasets.
Author Contributions
Shirong Ye and Peng Jiang conceived and designed the experiments; Peng Jiang, Dezhong Chen, and Pengfei Xia performed the experiments; Dezhong Chen and Yanyan Liu analyzed the data. All authors contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kudo, T.; Kawamura, R.; Hirata, H.; Ichiyanagi, K.; Tanoue, M.; Yoshimura, K. Large-scale vapor transport of remotely evaporated seawater by a rossby wave response to typhoon forcing during the Baiu/Meiyu season as revealed by the JRA-55 reanalysis. J. Geophys. Res. Atmos. 2014, 119, 8825–8838. [Google Scholar] [CrossRef]
- Lee, J.; Park, J.-U.; Cho, J.; Baek, J.; Kim, H.W. A characteristic analysis of fog using GPS-derived integrated water vapour. Meteorol. Appl. 2010, 17, 463–473. [Google Scholar] [CrossRef]
- Cadeddu, M.P.; Liljegren, J.C.; Turner, D.D. The atmospheric radiation measurement (ARM) program network of microwave radiometers: Instrumentation, data, and retrievals. Atmos. Meas. Tech. 2013, 6, 2359–2372. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Haase, J.; Ge, M.; Vedel, H.; Calais, E. Accuracy and variability of GPS tropospheric delay measurements of water vapor in the western mediterranean. J. Appl. Meteorol. 2003, 42, 1547–1568. [Google Scholar] [CrossRef]
- Pacione, R.; Vespe, F. Comparative studies for the assessment of the quality of near-real-time GPS-derived atmospheric parameters. J. Atmos. Ocean. Technol. 2008, 25, 701–714. [Google Scholar] [CrossRef]
- Khodayar, S.; Kalthoff, N.; Wickert, J.; Kottmeier, C.; Dorninger, M. High-resolution representation of the mechanisms responsible for the initiation of isolated thunderstorms over flat and complex terrains: Analysis of csip and cops cases. Meteorol. Atmos. Phys. 2013, 119, 109–124. [Google Scholar] [CrossRef]
- Smith, T.L.; Benjamin, S.G.; Gutman, S.I.; Sahm, S. Short-range forecast impact from assimilation of GPS-IPW observations into the rapid update cycle. Mon. Weather Rev. 2007, 135, 2914–2930. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G. Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Ruelke, A.; Fritsche, M.; Steigenberger, P.; Rothacher, M. Validation of precipitable water vapor within the NCEP/DOE reanalysis using global GPS observations from one decade. J. Clim. 2010, 23, 1675–1695. [Google Scholar] [CrossRef]
- Sun, B.; Wang, H. Water vapor transport paths and accumulation during widespread snowfall events in northeastern China. J. Clim. 2013, 26, 4550–4566. [Google Scholar] [CrossRef]
- Luo, X.; Heck, B.; Awange, J.L. Improving the estimation of zenith dry tropospheric delays using regional surface meteorological data. Adv. Space Res. 2013, 52, 2204–2214. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Zhang, B.; Xu, C.; Yan, F. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based GPS meteorology. J. Geod. 2014, 88, 273–282. [Google Scholar] [CrossRef]
- Adams, D.K.; Fernandes, R.M.S.; Kursinski, E.R.; Maia, J.M.; Sapucci, L.F.; Machado, L.A.T.; Vitorello, I.; Monico, J.F.G.; Holub, K.L.; Gutman, S.I.; et al. A dense GNSS meteorological network for observing deep convection in the amazon. Atmos. Sci. Lett. 2011, 12, 207–212. [Google Scholar] [CrossRef]
- Shoji, Y. A study of near real-time water vapor analysis using a nationwide dense GPS network of Japan. J. Meteorol. Soc. Jpn. 2009, 87, 1–18. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. Use Artif. Satell. Geod. 1972, 15, 274–251. [Google Scholar]
- Jade, S.; Vijayan, M.S.M. GPS-based atmospheric precipitable water vapor estimation using meteorological parameters interpolated from NCEP global reanalysis data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Fritsche, M.; Ruelke, A.; Steigenberger, P.; Rothacher, M. On the homogeneity and interpretation of precipitable water time series derived from global GPS observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Karabatic, A.; Weber, R.; Haiden, T. Near real-time estimation of tropospheric water vapour content from ground based GNSS data and its potential contribution to weather now-casting in Austria. Adv. Space Res. 2011, 47, 1691–1703. [Google Scholar] [CrossRef]
- Bosy, J.; Kaplon, J.; Rohm, W.; Sierny, J.; Hadas, T. Near real-time estimation of water vapour in the troposphere using ground GNSS and the meteorological data. Ann. Geophys. 2012, 30, 1379–1391. [Google Scholar] [CrossRef]
- Means, J.D.; Cayan, D. Precipitable water from GPS zenith delays using North American regional reanalysis meteorology. J. Atmos. Ocean. Technol. 2013, 30, 485–495. [Google Scholar] [CrossRef]
- Means, J.D. GPS precipitable water as a diagnostic of the North American monsoon in California and Nevada. J. Clim. 2013, 26, 1432–1444. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, P. On the national projects for surveying and mapping datum in the twelfth five year plan of China. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 1135–1138. [Google Scholar]
- Wang, H.; Wei, M.; Li, G.; Zhou, S.; Zeng, Q. Analysis of precipitable water vapor from GPS measurements in Chengdu region: Distribution and evolution characteristics in autumn. Adv. Space Res. 2013, 52, 656–667. [Google Scholar]
- Xie, Y.; Wei, F.; Chen, G.; Zhang, T.; Hu, L. Analysis of the 2008 heavy snowfall over south China using GPS PWV measurements from the Tibetan plateau. Ann. Geophys. 2010, 28, 1369–1376. [Google Scholar] [CrossRef]
- Dousa, J. The impact of errors in predicted GPS orbits on zenith troposphere delay estimation. GPS Solut. 2010, 14, 229–239. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; van Hove, T.; Ware, R.; et al. GPS meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhang, L.Y.; Dai, A. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Bonafoni, S.; Mazzoni, A.; Cimini, D.; Montopoli, M.; Pierdicca, N.; Basili, P.; Ciotti, P.; Carlesimo, G. Assessment of water vapor retrievals from a GPS receiver network. GPS Solut. 2013, 17, 475–484. [Google Scholar] [CrossRef]
- Deng, Z.; Bender, M.; Zus, F.; Ge, M.; Dick, G.; Ramatschi, M.; Wickert, J.; Lhnert, U.; Schon, S. Validation of tropospheric slant path delays derived from single and dual frequency GPS receivers. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Van Hove, T.; Van Baelen, J. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Sheng, P.; Mao, J.; Li, J.; Ge, Z.; Zhang, A.; Sang, J.; Pan, N.; Zhang, H. Atmospheric Physics; Peking University Press: Beijing, China, 2003. [Google Scholar]
- Zhang, C.; Guo, C.; Chen, J.; Zhang, L.; Wang, B. EGM 2008 and its application analysis in Chinese mainland. Acta Geod. Cartograph. Sin. 2009, 38, 283–289. [Google Scholar]
- Smith, A.; Lott, N.; Vose, R. The integrated surface database recent developments and partnerships. Bull. Am. Meteorol. Soc. 2011, 92, 704–708. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Hardy, B. Its-90 formulations for vapor pressure, frostpoint temperature, dewpoint temperature, and enhancement factors in the range −100 to +100 c. In Proceedings of the Third International Symposium on the Humidity & Moisture, London, UK, 6–8 April 1998.
- Wang, X.; Dai, Z.; Cao, Y.; Song, L. Weighted mean temperature tm statistical analysis in ground-based GPS in China. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 412–416. [Google Scholar]
- Liang, H.; Cao, Y.; Wan, X.; Xu, Z.; Wang, H.; Hu, H. Meteorological applications of precipitable water vapor measurements retrieved by the national GNSS network of China. Geod. Geodyn. 2015, 6, 135–142. [Google Scholar] [CrossRef]
- Perez-Ramirez, D.; Whiteman, D.N.; Smirnov, A.; Lyamani, H.; Holben, B.N.; Pinker, R.; Andrade, M.; Alados-Arboledas, L. Evaluation of Aeronet precipitable water vapor versus microwave radiometry, GPS, and radiosondes at ARM sites. J. Geophys. Res. Atmos. 2014, 119, 9596–9613. [Google Scholar] [CrossRef]
- De Galisteo, J.P.O.; Toledano, C.; Cachorro, V.; Torres, B. Improvement in PWV estimation from GPS due to the absolute calibration of antenna phase center variations. GPS Solut. 2010, 14, 389–395. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).