Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements
Abstract
:1. Introduction
2. MODIS LAI/FPAR Products
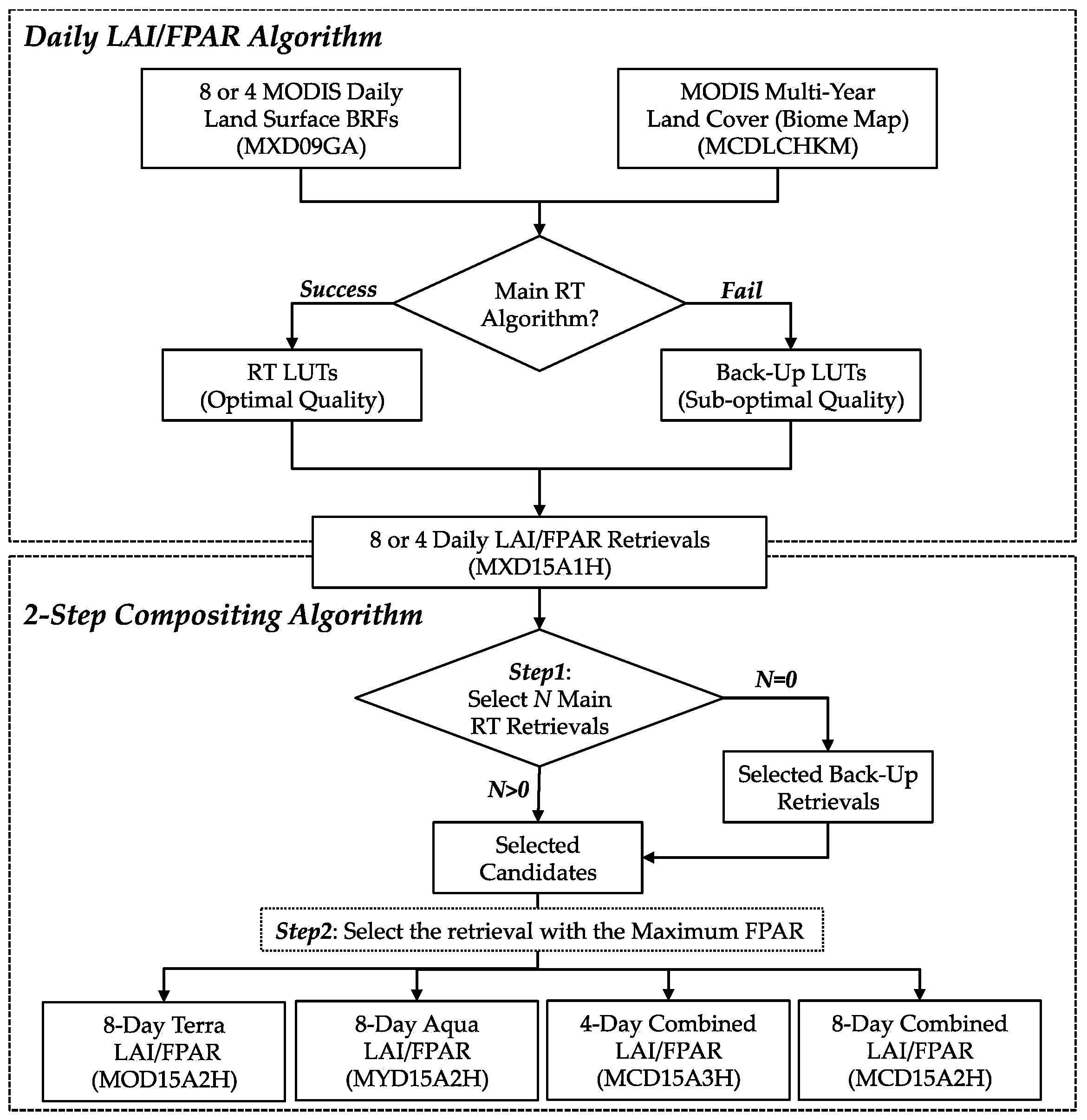
2.1. Algorithm Theoretical Description
2.2. Algorithm Inputs
2.3. Temporal Compositing and Quality Control
2.4. Improvements of Collection 6
3. Consistency between C5 and C6 LAI/FPAR Products
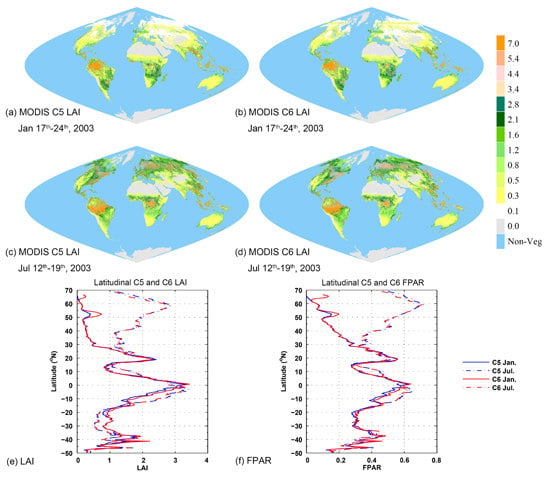
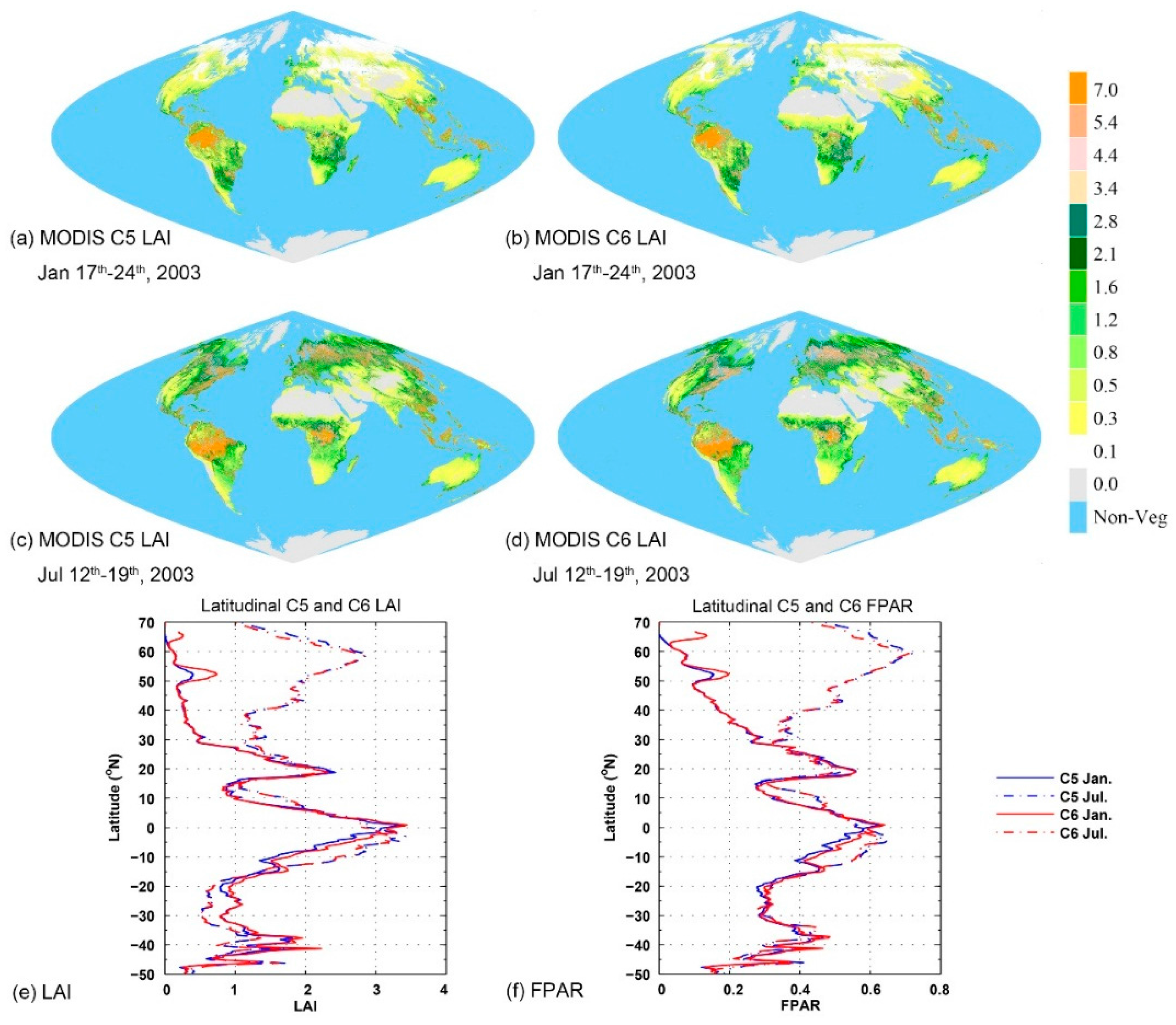
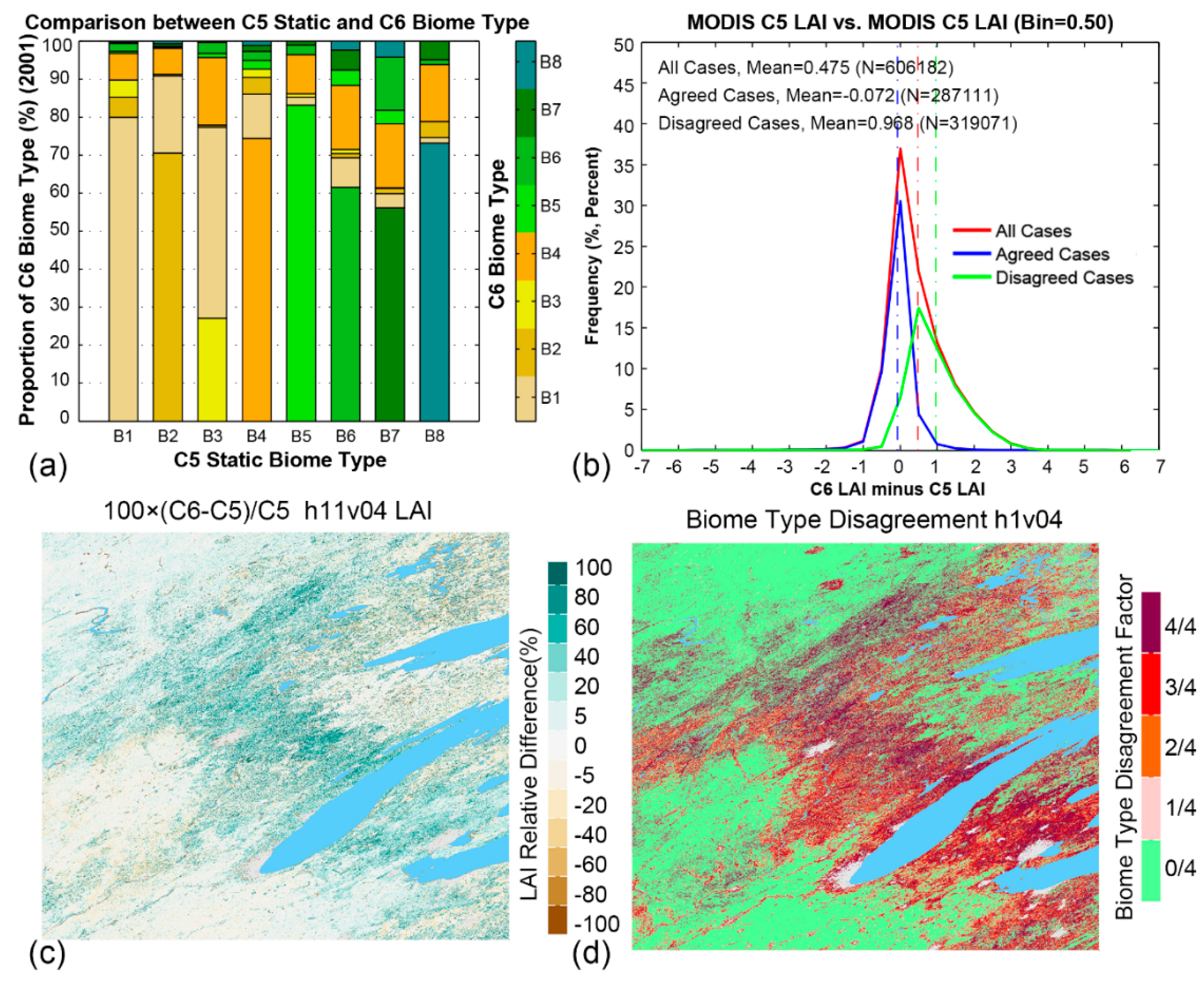
3.1. Global Distribution
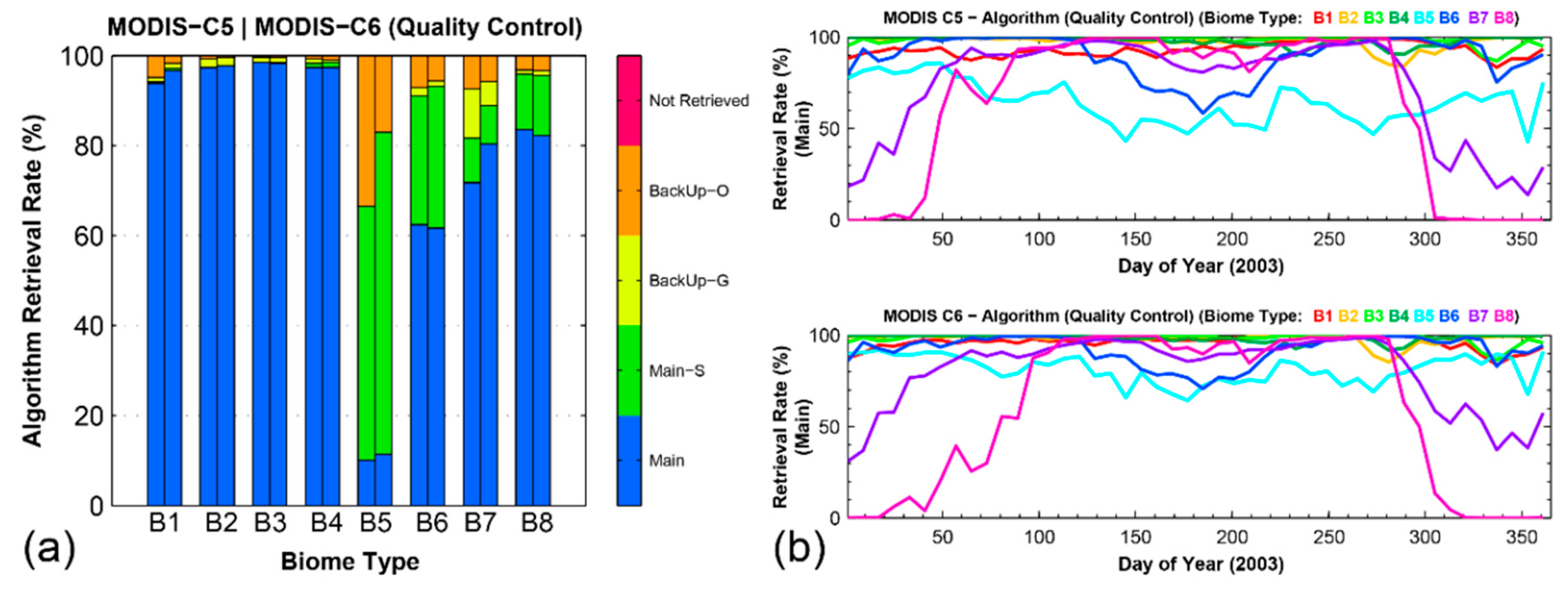
3.2. Spatial Coverage of Main Algorithm
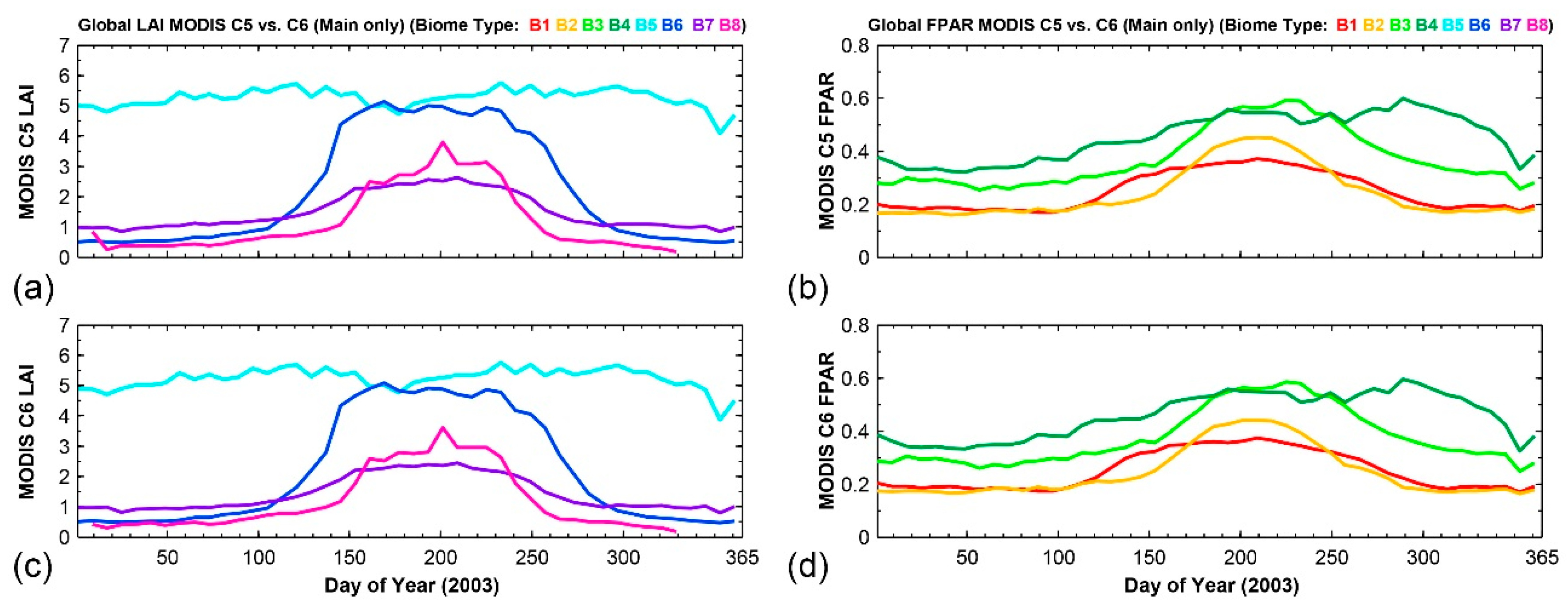
3.3. Seasonal LAI/FPAR Variations
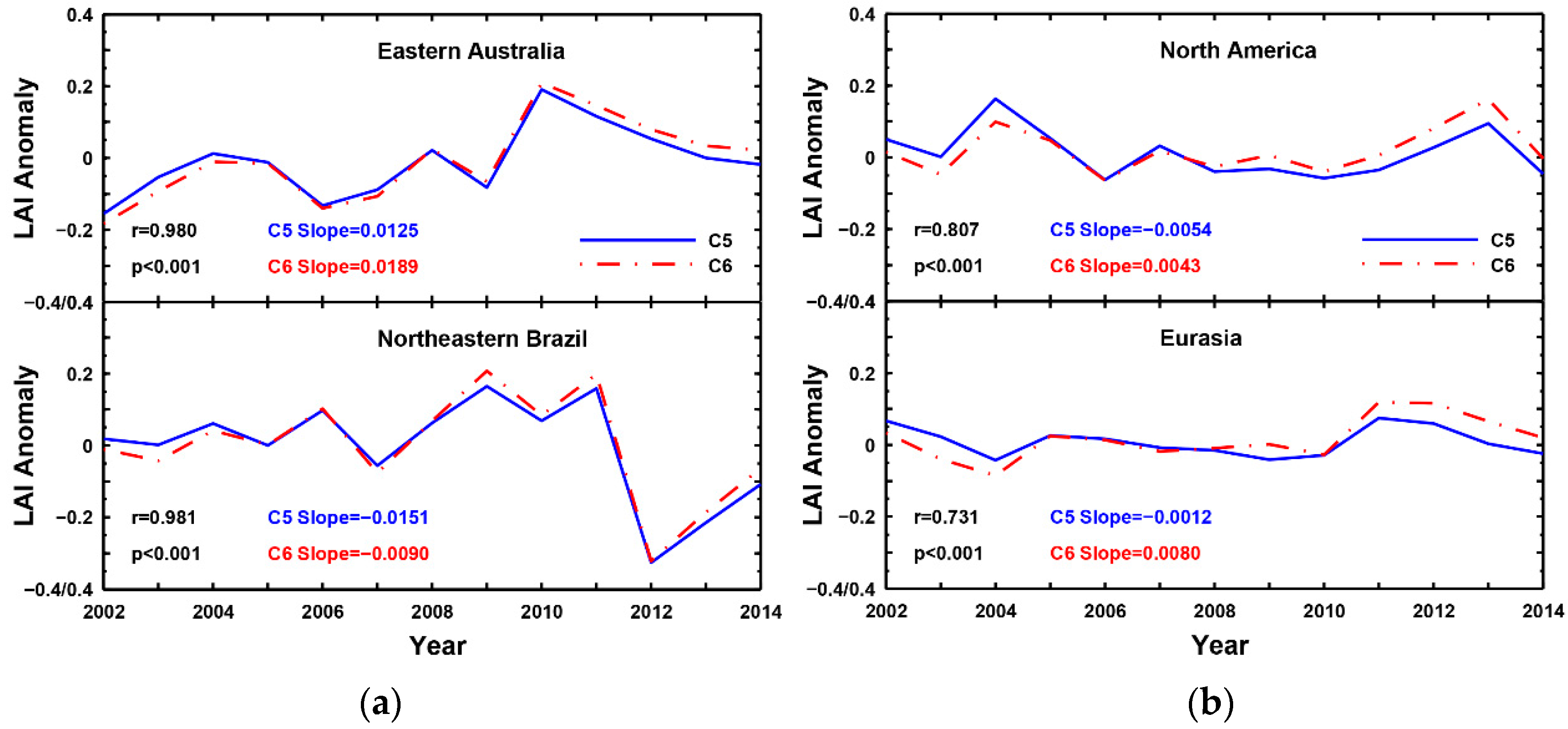
3.4. Inter-Annual LAI Anomalies
4. Benefits from Improved Input Data
4.1. Benefits from Biome Map Improvement
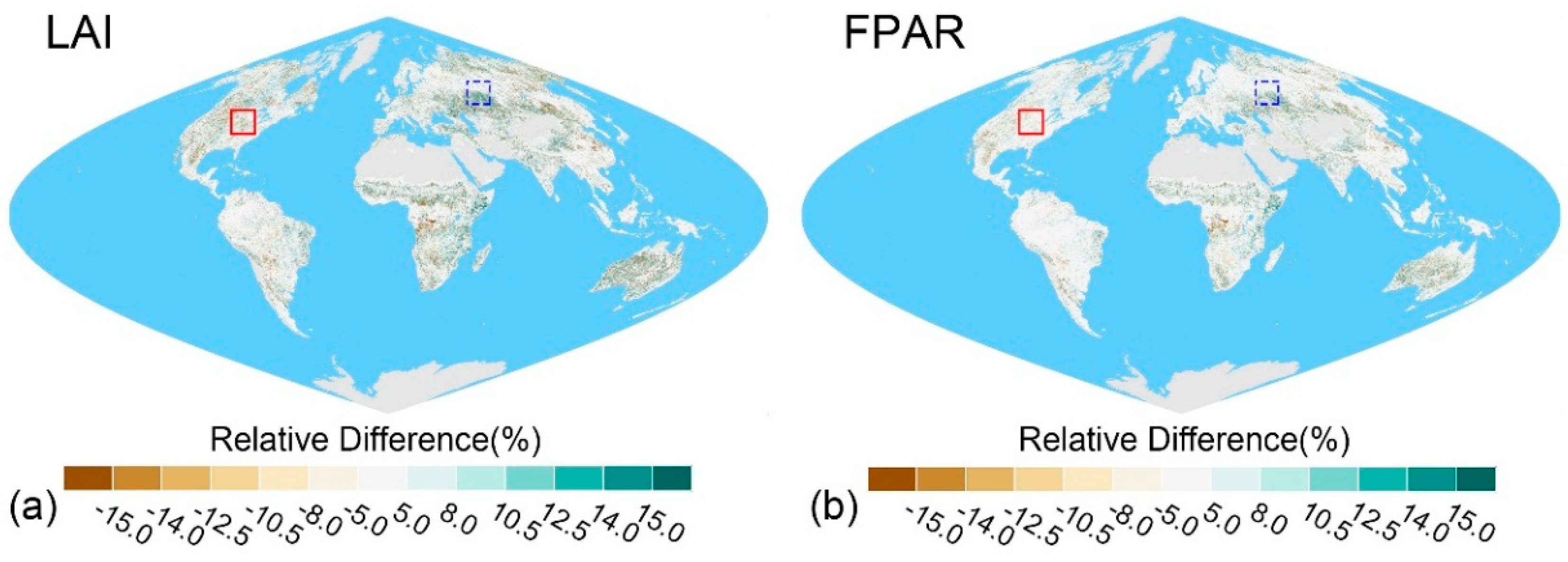
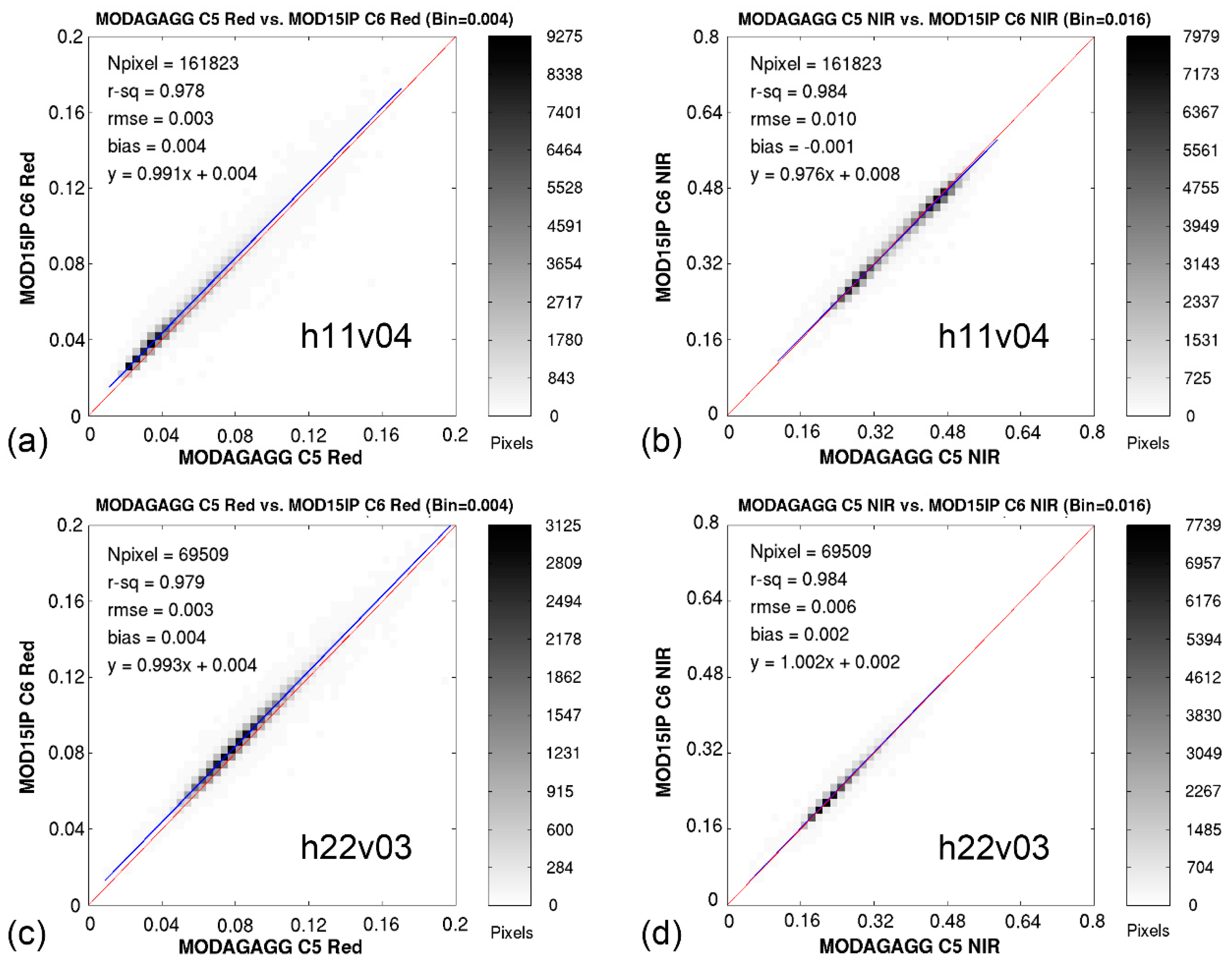
4.2. Benefits from Surface Reflectance Improvement
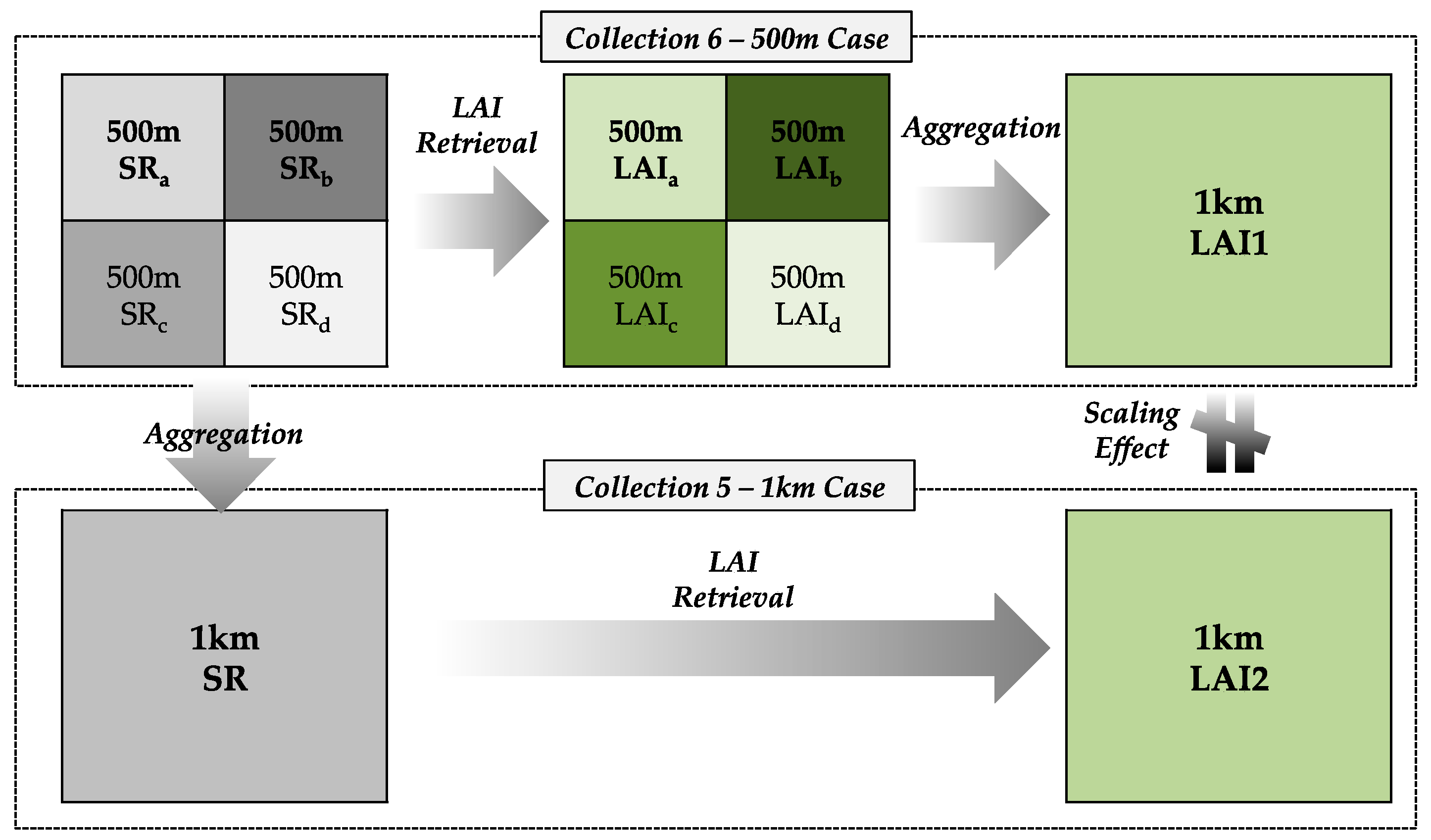
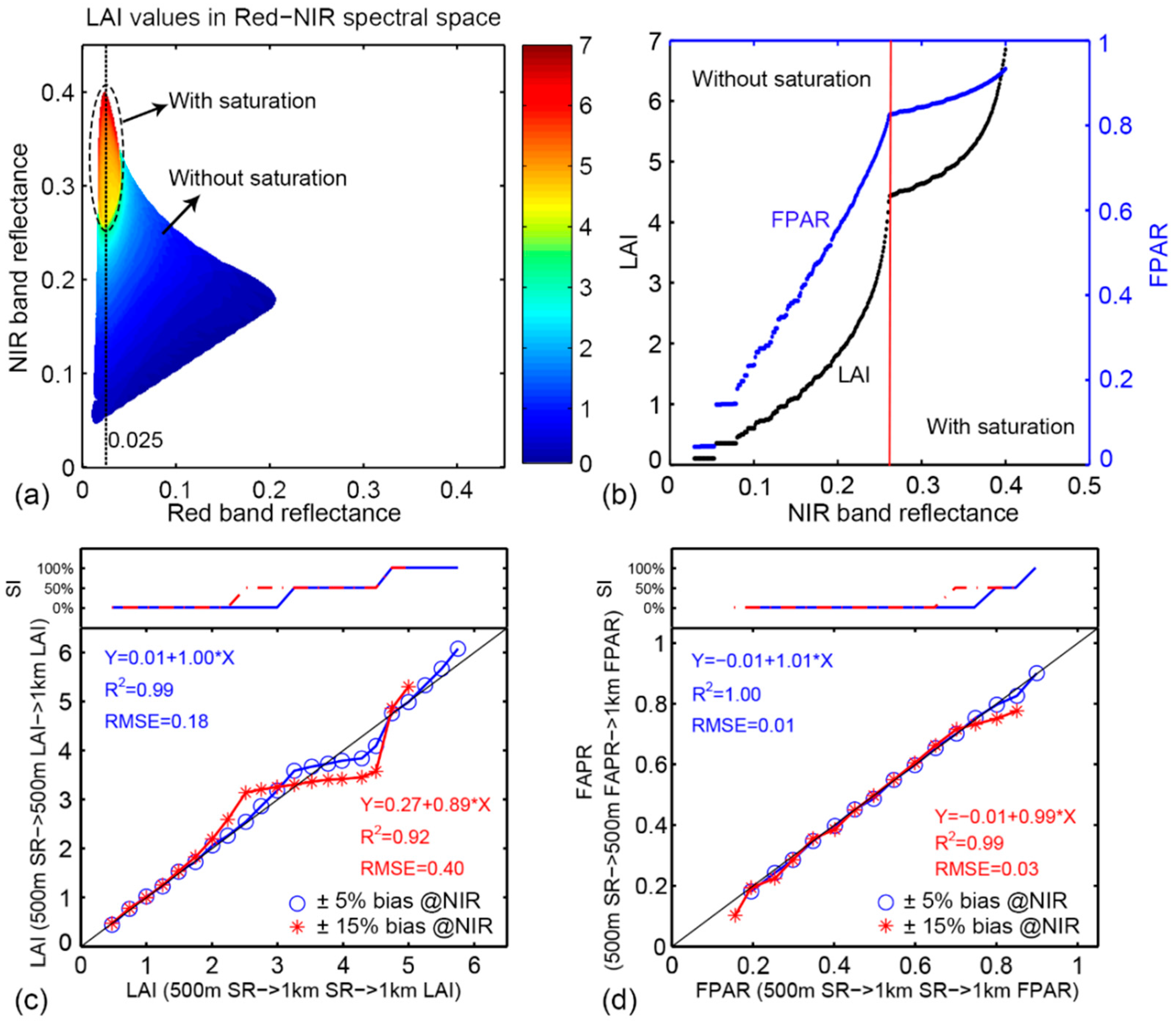
4.3. Impact of Scale Effect
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| LAI | Leaf Area Index |
| FPAR | Fraction of Photosynthetically Active Radiation |
| C3 | Collection 3 |
| C4 | Collection 4 |
| C5 | Collection 5 |
| C6 | Collection 6 |
| RT | Radiative Transfer |
| LUT | Look-Up-Table |
| BRF | Bi-directional Reflectance Factors |
| NDVI | Normalized Difference Vegetation Index |
| QC | Quality Control |
| BTDF | Biome Type Disagreement Factor |
| RI | Retrieval Index |
| SI | Saturation Index |
References
- Myneni, R.B.; Smith, G.R.; Lotsch, A.; Friedl, M.; Morisette, J.T.; Votava, P.; Running, S.W.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global data sets of vegetation leaf area index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.T.; Votava, P.; Myneni, R.B. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15) Algorithm Theoretical Basis Document; Theoretical Basis Document; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1999; pp. 1–170. [Google Scholar]
- Yang, W.; Tan, B.; Huang, D.; Rautiainen, M.; Shabanov, N.V.; Wang, Y.; Privette, J.L.; Huemmrich, K.F.; Fensholt, R.; Sandholt, I.; et al. MODIS leaf area index products: From validation to algorithm improvement. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1885–1898. [Google Scholar] [CrossRef]
- Yang, W.; Huang, D.; Tan, B.; Stroeve, J.C.; Shabanov, N.V.; Knyazikhin, Y.; Nemani, R.R.; Myneni, R.B. Analysis of leaf area index and fraction of PAR absorbed by vegetation products from the terra MODIS sensor: 2000–2005. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1829–1842. [Google Scholar] [CrossRef]
- Yang, W.; Shabanov, N.V.; Huang, D.; Wang, W.; Dickinson, R.E.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Analysis of leaf area index products from combination of MODIS Terra and Aqua data. Remote Sens. Environ. 2006, 104, 297–312. [Google Scholar] [CrossRef]
- Shabanov, N.V.; Knyazikhin, Y.; Baret, F.; Myneni, R.B. Stochastic Modeling of Radiation Regime in Discontinuous Vegetation Canopies. Remote Sens. Environ. 2000, 74, 125–144. [Google Scholar] [CrossRef]
- Buermann, W. Analysis of a multiyear global vegetation leaf area index data set. J. Geophys. Res. 2002, 107, D22. [Google Scholar] [CrossRef]
- Ganguly, S.; Samanta, A.; Schull, M.A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index Earth system data record from multiple sensors. Part 2: Implementation, analysis and validation. Remote Sens. Environ. 2008, 112, 4318–4332. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. Biogeosci. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- Majasalmi, T.; Rautiainen, M.; Stenberg, P.; Manninen, T. Validation of MODIS and GEOV1 fPAR Products in a Boreal Forest Site in Finland. Remote Sens. 2015, 7, 1359–1379. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.; Plummer, S.; Shabanov, N.V.; Myneni, R.B.; et al. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and Architecture of Plants Stands; Springer Science & Business Media: Medford, MA, USA, 1981. [Google Scholar]
- Myneni, R.B.; Ross, J. Photon-Vegetation Interactions: Applications in Optical Remote Sensing and Plant Ecology; Springer Science & Business Media: Medford, MA, USA, 1991. [Google Scholar]
- Huang, D.; Knyazikhin, Y.; Dickinson, R.E.; Rautiainen, M.; Stenberg, P.; Disney, M.; Lewis, P.; Cescatti, A.; Tian, Y.; Verhoef, W.; et al. Canopy spectral invariants for remote sensing and model applications. Remote Sens. Environ. 2007, 106, 106–122. [Google Scholar] [CrossRef]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Y.; Zhang, Y.; El-Saleous, N.; Knyazikhin, Y.; Vermote, E.; Myneni, R.B. Investigation of product accuracy as a function of input and model uncertainties: Case study with SeaWiFS and MODIS LAI/FPAR algorithm. Remote Sens. Environ. 2001, 78, 299–313. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.; Myneni, R.B. The impact of potential land cover misclassification on MODIS leaf area index (LAI) estimation: A statistical perspective. Remote Sens. 2013, 5, 830–844. [Google Scholar] [CrossRef]
- Garrigues, S.; Shabanov, N.V.; Swanson, K.; Morisette, J.T.; Baret, F.; Myneni, R.B. Intercomparison and sensitivity analysis of Leaf Area Index retrievals from LAI-2000, AccuPAR, and digital hemispherical photography over croplands. Agric. Forest Meteorol. 2008, 148, 1193–1209. [Google Scholar] [CrossRef]
- Vermote, E.F.; Vermeulen, A. Atmospheric Correction Algorithm: Spectral Reflectances (MOD09). Algorithm Theoretical Background Document. Available online: http://dratmos.geog.umd.edu/files/pdf/atbd_mod09.pdf (accessed on 7 March 2016).
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Wolfe, R.E.; Devadiga, S.; Masuoka, E.J.; Running, S.W.; Vermote, E.; Giglio, L.; Wan, Z.; Riggs, G.A.; Schaaf, C.; Myneni, R.B.; et al. Improvements to the MODIS Land Products in Collection Version 6. Available online: http://adsabs.harvard.edu/abs/2013AGUFM.B41D0430W (accessed on 7 March 2016).
- Masson, V.; Champeaux, J.; Chauvin, F.; Meriguet, C.; Lacaze, R. A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Climat. 2003, 16, 1261–1282. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A.; Camargo, H.; Riveros, M.P.; Pabló, A.D. Two contrasting severe seasonal extremes in tropical South America in 2012: Flood in Amazonia and drought in northeast Brazil. J. Climat. 2013, 26, 9137–9154. [Google Scholar] [CrossRef]
- Wang, D.; Morton, D.; Masek, J.; Wu, A.; Nagol, J.; Xiong, X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of sensor degradation on the MODIS NDVI time series. Remote Sens. Environ. 2012, 119, 55–61. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768–1793. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Wang, Y.; Zhang, Y.; Knyazikhin, Y.; Bogaert, J.; Myneni, R.B. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sens. Environ. 2003, 84, 143–159. [Google Scholar] [CrossRef]
- Ganguly, S.; Schull, M.A.; Samanta, A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index earth system data record from multiple sensors. Part 1: Theory. Remote Sens. Environ. 2008, 112, 4333–4343. [Google Scholar] [CrossRef]
| Biome Type | BTDF = 0/4 | BTDF = 1/4 | BTDF = 2/4 | BTDF = 3/4 | BTDF = 4/4 |
|---|---|---|---|---|---|
| Grasses/Cereal crops (B1) | 0.00 ± 0.24 (0.24) | −0.01 ± 0.30 (0.30) | 0.01 ± 0.33 (0.33) | 0.02 ± 0.39 (0.39) | 0.08 ± 0.43 (0.44) |
| Shrubs (B2) | −0.01 ± 0.15 (0.15) | 0.02 ± 0.21 (0.21) | 0.04 ± 0.24 (0.24) | 0.06 ± 0.25 (0.25) | 0.05 ± 0.23 (0.24) |
| Broadleaf crops (B3) | −0.02 ± 0.22 (0.22) | 0.11 ± 0.23 (0.25) | 0.21 ± 0.28 (0.35) | 0.31 ± 0.35 (0.46) | 0.42 ± 0.40 (0.57) |
| Savanna (B4) | 0.00 ± 0.26 (0.26) | −0.04 ± 0.30 (0.30) | −0.07 ± 0.36 (0.37) | −0.11 ± 0.42 (0.43) | −0.16 ± 0.40 (0.43) |
| 1 EBF (B5) | −0.08 ± 0.62 (0.63) | −0.45 ± 0.65 (0.79) | −0.88 ± 0.71 (1.12) | −1.32 ± 0.82 (1.55) | −1.71 ± 1.00 (1.98) |
| 2 DBF (B6) | −0.09 ± 0.48 (0.49) | −0.01 ± 0.48 (0.48) | 0.05 ± 0.52 (0.52) | 0.10 ± 0.58 (0.58) | 0.03 ± 0.52 (0.52) |
| 3 ENF (B7) | −0.17 ± 0.51 (0.54) | −0.23 ± 0.50 (0.55) | −0.31 ± 0.54 (0.62) | −0.40 ± 0.60 (0.72) | −0.45 ± 0.73 (0.85) |
| 4 DNF (B8) | −0.19 ± 0.57 (0.60) | −0.26 ± 0.56 (0.62) | −0.38 ± 0.61 (0.72) | −0.49 ± 0.68 (0.84) | −0.58 ± 0.82 (1.00) |
| Mean | −0.02 ± 0.29 (0.29) | −0.03 ± 0.33 (0.33) | −0.02 ± 0.40 (0.40) | −0.02 ± 0.50 (0.50) | 0.02 ± 0.60 (0.60) |
| Overall | −0.01 ± 0.39 (0.39) | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. https://doi.org/10.3390/rs8050359
Yan K, Park T, Yan G, Chen C, Yang B, Liu Z, Nemani RR, Knyazikhin Y, Myneni RB. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sensing. 2016; 8(5):359. https://doi.org/10.3390/rs8050359
Chicago/Turabian StyleYan, Kai, Taejin Park, Guangjian Yan, Chi Chen, Bin Yang, Zhao Liu, Ramakrishna R. Nemani, Yuri Knyazikhin, and Ranga B. Myneni. 2016. "Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements" Remote Sensing 8, no. 5: 359. https://doi.org/10.3390/rs8050359
APA StyleYan, K., Park, T., Yan, G., Chen, C., Yang, B., Liu, Z., Nemani, R. R., Knyazikhin, Y., & Myneni, R. B. (2016). Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sensing, 8(5), 359. https://doi.org/10.3390/rs8050359