A Memory-Based Learning Approach as Compared to Other Data Mining Algorithms for the Prediction of Soil Texture Using Diffuse Reflectance Spectra
Abstract
:1. Introduction
2. Materials and Methods
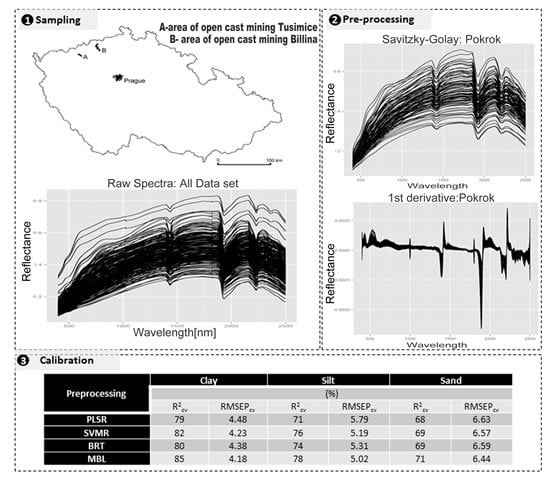
2.1. Study Area
2.2. Soil Sampling and Analysis
2.3. Spectral Data Measurements
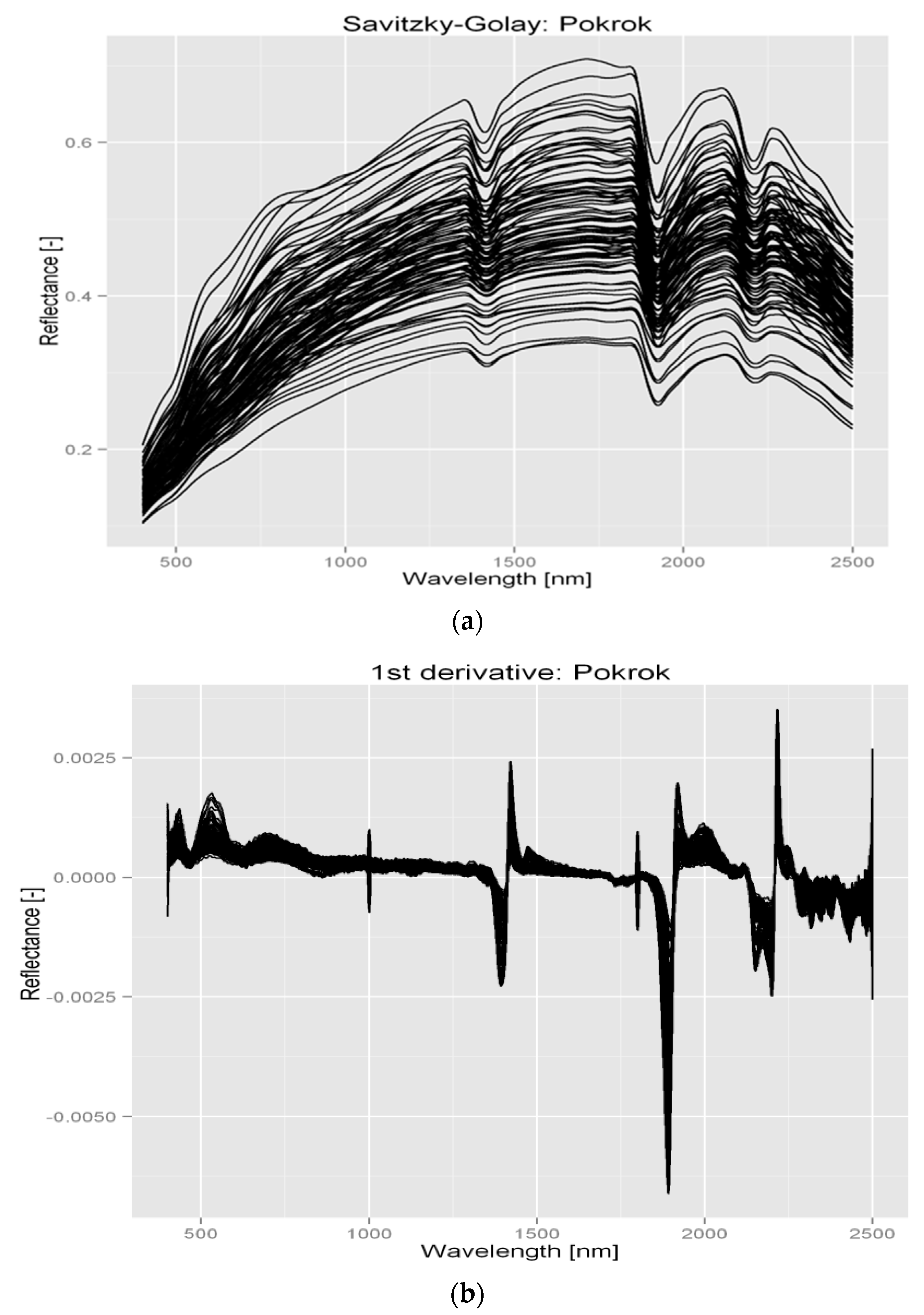
2.4. Spectra Preprocessing
2.5. Comparison of Algorithms
2.5.1. Partial Least Square Regression
- X, soil reflectance
- Y, measured soil property
- T, factor scores
- p’ and q, factor loadings
- E and F, residuals
2.5.2. Support Vector Machine Regression
- b, scalar threshold
- K (x, xk), kernel function
- α, Lagrange multiplier
- N, number of data
- xk, input data
- y, output
- , width of the radial basis function
- T, transpose
2.5.3. Boosted Regression Trees
- h (x; a), simple classification function or base learner with parameters a and input variables x
- m, model step
- βm, weighting coefficient
2.5.4. Memory-Based Learning
- , root mean square of the spectral residuals of the unknown sample when a total of j-th PLS components is used
- , root mean square of the regression coefficient corresponding to the j-th PLS components
2.6. Assessment of VNIR/SWIR Predictions Performances
- y´i, predicted value
- yi, observed value
- , mean of y value
- N, number of samples
3. Results and Discussion
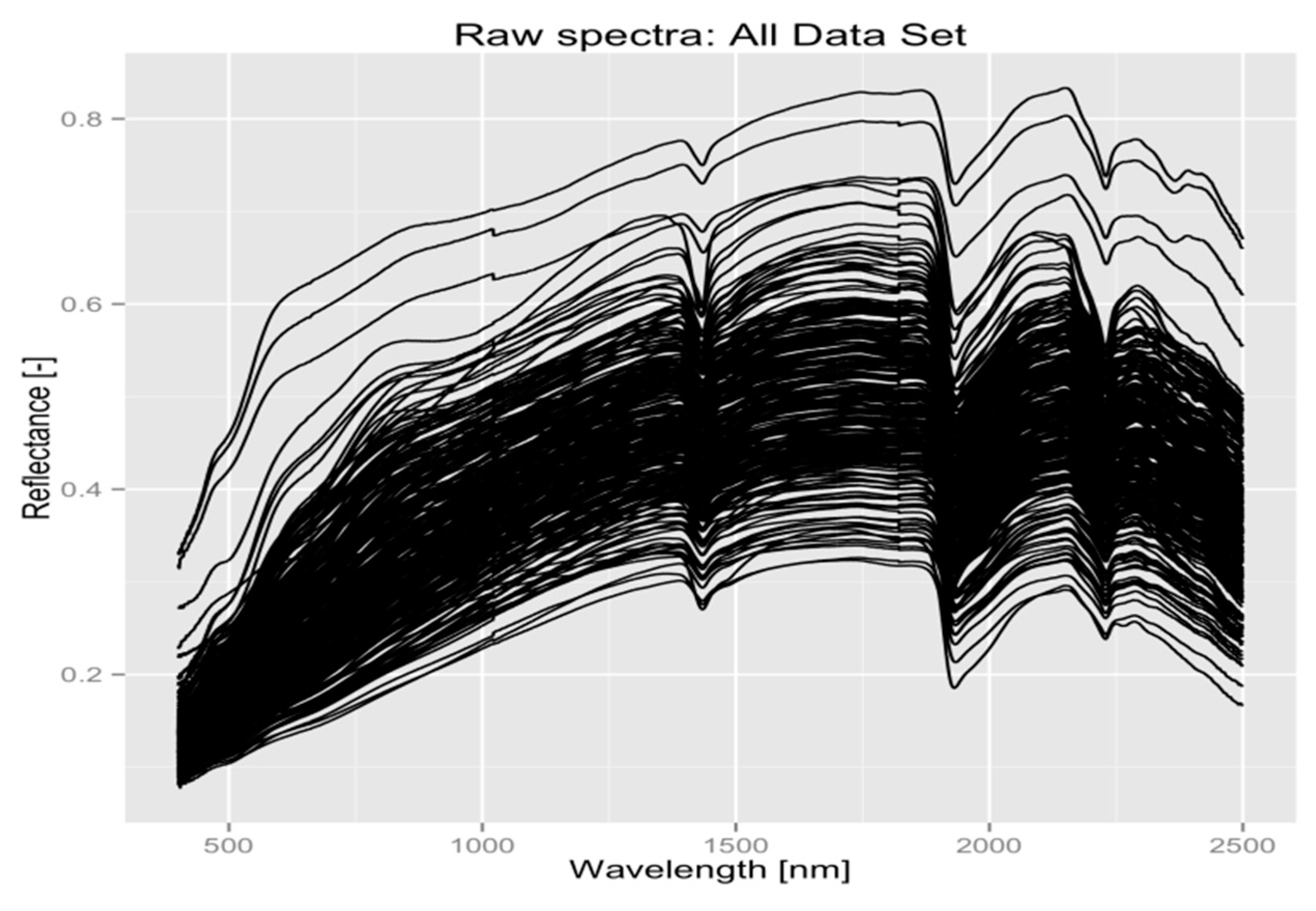
3.1. Soil Textural Properties
3.2. Soil Spectral Properties
3.3. Spectra Preprocessing and Model Calibration
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Viscarra Rossel, R.A.; McBratney, A.B. Soil chemical analytical accuracy and costs: Implications from precision agriculture. Aust. J. Exp. Agric. 1998, 38, 765–775. [Google Scholar] [CrossRef]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Improved estimates of organic carbon using proximally sensed vis–NIR spectra corrected by piecewise direct standardization. Eur. J Soil Sci. 2015, 66, 670–678. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near-infrared, mid-infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Cécillon, L.; Barthes, B.G.; Gomez, C.; Ertlen, D.; Genot, V.; Hedde, M.; Stevens, A.; Brun, J.J. Assessment and monitoring of soil quality using near-infrared reflectance spectroscopy (NIRS). Eur. J. Soil Sci. 2009, 60, 770–784. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. Trends Analyt. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Amin, M.S.M.; Borůvka, L.; Saberioon, M.M. Models for estimating the physical properties of paddy soil using visible and near infrared reflectance spectroscopy. J. Appl. Spectrosc. 2014, 81, 534–540. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and near infrared spectroscopy in soil science. Adv. Agron. 2010, 107, 163–215. [Google Scholar]
- Araújo, S.R.; Wetterlind, J.; Demattê, J.A.M.; Stenberg, B. Improving the prediction performance of a large tropical vis-NIR spectroscopic soil library from Brazil by clustering into smaller subsets or use of data mining calibration techniques. Eur. J. Soil Sci. 2014, 65, 718–729. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.M.; Vašát, R. Visible, near-infrared, and mid-infrared spectroscopy applications for soil assessment with emphasis on soil organic matter content and quality: State-of-the-art and key issues. Appl. Spectrosc. 2013, 67, 1349–1362. [Google Scholar] [CrossRef] [PubMed]
- Mouazen, A.M.; Maleki, M.R.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a VIS-NIR sensor. Soil Till. Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Waiser, T.H.; Morgan, C.L.S.; Brown, D.J.; Hallmark, C.T. In situ characterization of soil clay content with visible near-infrared diffuse reflectance spectroscopy. Soil Sci. Soc. Am. J. 2007, 71, 389–396. [Google Scholar] [CrossRef]
- Maleki, M.R.; Mouazen, A.M.; De Keterlaere, B.; Ramon, H.; De Baerdemaeker, J. On-the-go variable-rate phosphorus fertilisation based on a visible and near infrared soil sensor. Biosys. Eng. 2008, 99, 35–46. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Wold, S.; Martens, H.; Wold, H. The multivariate calibration method in chemistry solved by the PLS method. In Matrix Pencils, Lecture Notes in Mathematics; Ruhe, A., Kagstrom, B., Eds.; Springer-Verlag: Heidelberg, Germany, 1983; Volume 973, pp. 286–293. [Google Scholar]
- Moros, J.; De Vallejuelo, S.F.O.; Gredilla, A.; De Diego, A.; Madariaga, J.M.; Garrigues, S.; De La Guardia, M. Use of reflectance infrared spectroscopy for monitoring the metal content of the estuarine sediments of the Nerbioi-Ibaizabal River (Metropolitan Bilbao, Bay of Biscay, Basque Country). Environ. Sci. Technol. 2009, 43, 9314–9320. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Li, F.; Yang, Z.; Ayoko, G.A.; Frost, R.L.; Ji, J. Diffuse reflectance spectroscopy for monitoring potentially toxic elements in the agricultural soils of Changjiang River Delta, China. Appl. Clay Sci. 2012, 64, 75–83. [Google Scholar] [CrossRef]
- Saiano, F.; Oddo, G.; Scalenghe, R.; La Mantia, T.; Ajmone-Marsan, F. DRIFTS sensor: Soil carbon validation at large scale (Pantelleria, Italy). Sensors 2013, 13, 5603–5613. [Google Scholar] [CrossRef] [PubMed]
- Dalal, R.C.; Henry, R.J. Simultaneous determination of moisture, organic carbon, and total nitrogen by near infrared reflectance spectrophotometry. Soil Sci. Soc. Am. J. 1986, 50, 120–123. [Google Scholar] [CrossRef]
- Pirie, A.; Singh, B.; Islam, K. Ultra-violet, visible, near-infrared, and mid infrared diffuse reflectance spectroscopic techniques to predict several soil properties. Aus. J. Soil Res. 2005, 43, 713–721. [Google Scholar] [CrossRef]
- Daniel, K.W.; Tripathi, N.K.; Honda, K. Artificial neural network analysis of laboratory and in situ spectra for the estimation of macronutrients in soils of Lop Buri (Thailand). Aus. J. Soil Res. 2003, 41, 47–59. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Walsh, M.G. Development of reflectance spectral libraries for characterization of soil properties. Soil Sci. Soc. Am. J. 2002, 66, 988–998. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A. Robust modelling of soil diffuse reflectance spectra by bagging-partial least squares regression. J. Near Infrared Spec. 2007, 15, 39–47. [Google Scholar] [CrossRef]
- Stevens, A.; Van Wesemael, B.; Bartholomeus, H.; Rosillon, D.; Tychon, B.; Ben-Dor, E. Laboratory, field and airborne spectroscopy for monitoring organic carbon content in agricultural soils. Geoderma 2008, 144, 395–404. [Google Scholar] [CrossRef]
- Brown, D.J. Using a global VNIR soil-spectral library for local soil characterization and landscape modeling in a 2nd-order Uganda watershed. Geoderma 2007, 140, 444–453. [Google Scholar] [CrossRef]
- Kovačević, M.; Bajat, B.; Trivic, B.; Pavlovic, R. Geological units classification of multispectral images by using support vector machines. In International Conference on Intelligent Networking and Collaborative Systems; Badr, Y.K., Caballe, S., Xhafa, F., Abraham, A., Gros, B., Eds.; IEEE: New York, NY, USA, 2009; pp. 267–272. [Google Scholar]
- Gholizadeh, A.; Borůvka, L.; Vašát, R.; Saberioon, M.M.; Klement, A.; Kratina, J.; Tejnecký, V.; Drábek, O. Estimation of potentially toxic elements contamination in anthropogenic soils on a brown coal mining dumpsite by reflectance spectroscopy: A case study. PLoS ONE 2015, 10, e0117457. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Stevens, A.; Demattê, J.A.M.; Scholten, T. The spectrum-based learner: A new local approach for modeling soil vis-NIR spectra of complex datasets. Geoderma 2013, 195–196, 268–279. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Kang, P.; Cho, S. Locally linear reconstruction for instance-based learning. Pattern Recognit. 2008, 41, 3507–3518. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation, 3rd ed.; Blackwell: Malden, MA, USA, 2005. [Google Scholar]
- Kosmas, C.; Kirby, M.; Geeson, N. The Medalus Project Mediterranean Desertification and Land Use. Manual on Key Indicators of Desertification and Mapping Environmentally Sensitive Areas to Desertification; EUR 18882; European Commission, Energy, Environment and Sustainable Development: Brussels, Belgium, 1999. [Google Scholar]
- Hewson, R.D.; Cudahy, T.J.; Jones, M.; Thomas, M. Investigations into soil composition and texture using infrared spectroscopy (2–14 μm). Appl. Environ. Soil Sci. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Cozzolino, D.; Morón, A. The potential of near-infrared reflectance spectroscopy to analyse soil chemical and physical characteristics. J. Agric. Sci. 2003, 140, 65–71. [Google Scholar] [CrossRef]
- Sørensen, L.K.; Dalsgaard, S. Determination of clay and other soil properties by near infrared spectroscopy. Soil Sci. Soc. Am. J. 2005, 69, 159–167. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Karoui, R.; De Baerdemaeker, J.; Ramon, H. Characterization of soil water content using measured visible and near infrared spectra. Soil Sci. Soc. Am. J. 2006, 70, 1295–1302. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Banin, A. Near-infrared analysis as a rapid method to simultaneously evaluate several soil properties. Soil Sci. Soc. Am. J. 1995, 59, 364–372. [Google Scholar] [CrossRef]
- Brown, D.J.; Shepherd, K.D.; Walsh, M.G.; Mays, M.D.; Reinsch, T.G. Global soil characterization with VNIR diffuse reflectance spectroscopy. Geoderma 2006, 132, 273–290. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B. Near-infrared spectroscopy for within-field soil characterization: Small local calibrations compared with national libraries spiked with local samples. Eur. J. Soil Sci. 2010, 61, 823–843. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Vašát, R.; Saberioon, M.M. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106. FAO: Rome, Italy. Available online: http://www.fao.org/3/a-i3794e.pdf (accessed on 1 October 2015).
- Xie, X.; Pan, X.Z.; Sun, B. Visible and near-infrared diffuse reflectance spectroscopy for prediction of soil properties near a Copper smelter. Pedosphere 2012, 22, 351–366. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. In Methods of Soil Analysis, Part 1; Klute, A., Ed.; ASA and SSSA: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Mouazen, A.M.; De Baerdemaeker, J.; Ramon, H. Towards development of on-line soil moisture content sensor using a fibre-type NIR spectrophotometer. Soil Tillage Res. 2005, 80, 171–183. [Google Scholar] [CrossRef]
- Workman, J.J., Jr. Review of process and non-invasive near-infrared and infrared spectroscopy: 1993–1999. Appl. Spectrosc. Rev. 1999, 34, 1–89. [Google Scholar] [CrossRef]
- Murray, I. Aspects of interpretation of NIR spectra. In Analytical Application of Spectroscopy; Creaser, C.S., Davies, A.M.C., Eds.; Royal Society of Chemistry: London, UK, 1988; pp. 9–21. [Google Scholar]
- Mark, H.L.; Tunnell, D. Qualitative near-infrared reflectance analysis using Mahalanobis distances. Anal. Chem. 1985, 57, 1449–1456. [Google Scholar] [CrossRef]
- Shenk, J.S.; Westerhaus, M.O. Population definition, sample selection, and calibration procedure for near infrared reflectance spectroscopy. Crop Sci. 1991, 31, 469–474. [Google Scholar] [CrossRef]
- Cozzolino, D.; Morón, A. Potential of near-infrared reflectance spectroscopy and chemometrics to predict soil organic carbon fractions. Soil Till. Res. 2006, 85, 78–85. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Regional predictions of eight common soil properties and their spatial structures from hyperspectral Vis–NIR data. Geoderma 2012, 189–190, 176–185. [Google Scholar] [CrossRef]
- Duckworth, J. Mathematical data preprocessing. In Near-Infrared Spectroscopy in Agriculture; Roberts, C.A., Workman, J., Jr., Reeves, J.B., III, Eds.; ASA-CSSA-SSSA: Madison, WI, USA, 2004; pp. 115–132. [Google Scholar]
- Ren, H.Y.; Zhuang, D.F.; Singh, A.N.; Pan, J.J.; Qid, D.S.; Shi, R.H. Estimation of As and Cu contamination in agricultural soils around a mining area by reflectance spectroscopy: A case study. Pedosphere 2009, 19, 719–726. [Google Scholar] [CrossRef]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Fruend, H.C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Martens, H.; Næs, T. Multivariate Calibration; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Bilgili, A.V.; Van Es, H.M.; Akbas, F.; Durak, A.; Hively, W.D. Visible-near infrared reflectance spectroscopy for assessment of soil properties in a semi-arid area of Turkey. J. Arid Environ. 2010, 74, 229–238. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Hornik, K. Kernlab: Kernel-Based Machine Learning Lab. Available online: http://cran.r-project.org/web/packages/kernlab/index.html (accessed on 30 September 2015).
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In 5th Annual ACM Workshop on COLT; Haussler, D., Ed.; ACM Press: Pittsburgh, PA, USA, 1992; pp. 144–152. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and regression trees. In The Wadsworth Statistics/Probability Series; Wadsworth International Group: Belmont, CA, USA, 1984; p. 358. [Google Scholar]
- Steinberg, D.; Colla, P. CART: Tree-Structured Non-Parametric Data Analysis; Salford Systems: San Diego, CA, USA, 1997; p. 342. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–374. [Google Scholar] [CrossRef]
- An, A. Classification methods. In Encyclopedia of Data Warehousing and Mining; Wang, J., Ed.; Idea Group Inc.: New York, NY, USA, 2005; pp. 144–149. [Google Scholar]
- Daelemans, W.; van den Bosch, A. Memory-Based Language Processing; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Prentice Hall, Pearson Education Inc.: Upper Saddle River, NJ, USA, 2003; p. 733. [Google Scholar]
- Williams, P. Near-Infrared Technology-Getting the Best out of Light; PDK Projects: Nanaimo, BC, Canada, 2003. [Google Scholar]
- Sherman, D.M.; Waite, T.D. Electronic spectra of Fe3+ oxides and oxyhydroxides in the near infrared to ultraviolet. Am. Mineral. 1985, 70, 1262–1269. [Google Scholar]
- Ji, J.F.; Balsam, W.; Chen, J.; Liu, L.W. Rapid and quantitative measurement of hematite and goethite in the Chinese loess-paleosol sequence by diffuse reflectance spectroscopy. Clay Clay Min. 2002, 50, 208–216. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Wu, X.; Tian, Q.; Ji, J.; Qin, Z. Possibilities of reflectance spectroscopy for the assessment of contaminant elements in suburban soils. Appl. Geochem. 2005, 20, 1051–1059. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV–vis–NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Kooistra, L.; Wanders, J.; Epema, G.F.; Leuven, R.; Wehrens, R.; Buydens, L.M.C. The potential of field spectroscopy for the assessment of sediment properties in river floodplains. Anal. Chim. Acta 2003, 484, 189–200. [Google Scholar] [CrossRef]
- Bishop, J.L.; Lane, M.D.; Dyar, M.D.; Brown, A.J. Reflectance and emission spectroscopy study of four groups of phyllosilicates: Smectites, kaolinite-serpentines, chlorites and micas. Clay Clay Min. 1994, 43, 35–54. [Google Scholar] [CrossRef]
- Post, J.L.; Noble, P.N. The near-infrared combination band frequencies of dioctahedral smectites, micas, and illites. Clay Clay Min. 1993, 41, 639–644. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Hunt, G.R.; Salisbury, J.W. Visible and near-infrared spectra of minerals and rocks. I. Silicate Minerals. Mod. Geol. 1970, 4, 283–300. [Google Scholar]
- Awiti, A.O.; Walsh, M.G.; Shepherd, K.D.; Kinyamario, J. Soil condition classification using infrared spectroscopy: A proposition for assessment of soil condition along a tropical forest-cropland chronosequence. Geoderma 2008, 143, 73–84. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Influence of the number of samples on prediction error of visible and near infrared spectroscopy of selected soil properties at the farm scale. Eur. J. Soil Sci. 2012, 63, 421–429. [Google Scholar] [CrossRef]
- Eshel, G.; Levy, G.J.; Mingelgrin, U.; Singer, M.J. Critical evaluation of the use of laser diffraction for particle-size distribution analysis. Soil Sci. Soc. Am. J. 2004, 68, 736–743. [Google Scholar] [CrossRef]
- Chang, C.W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R., Jr. Near infrared reflectance spectroscopy-principal components regression analysis of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Regression rules as a tool for predicting soil properties from infrared reflectance spectroscopy. Chemometrics Intell. Lab. Syst. 2008, 94, 72–79. [Google Scholar] [CrossRef]
- Jalabert, S.S.M.; Martin, M.P.; Renaud, J.P.; Boulonne, L.; Jolivet, C.; Montanarella, L. Estimating forest soil bulk density using boosted regression modeling. Soil Use Manag. 2010, 26, 516–528. [Google Scholar] [CrossRef]
| Item | Clay | Silt | Sand |
|---|---|---|---|
| (%) | |||
| Pokrok (n = 103) | |||
| Min | 7.5 | 23.8 | 11.3 |
| Max | 53.3 | 44.9 | 63.6 |
| Mean | 36.7 | 33.9 | 29.3 |
| SD | 8.7 | 4.4 | 9.2 |
| CV (%) | 23.6 | 13.0 | 31.3 |
| Radovesice (n = 40) | |||
| Min | 18.1 | 28.2 | 11.1 |
| Max | 52.9 | 48.0 | 53.5 |
| Mean | 41.9 | 38.2 | 19.8 |
| SD | 7.8 | 5.7 | 10.3 |
| CV (%) | 18.5 | 14.9 | 51.9 |
| Březno (n = 25) | |||
| Min | 28.9 | 26.0 | 9.1 |
| Max | 61.4 | 44.6 | 34.8 |
| Mean | 39.9 | 32.9 | 22.1 |
| SD | 5.9 | 4.7 | 6.1 |
| CV (%) | 14.9 | 14.3 | 27.6 |
| Merkur (n = 38) | |||
| Min | 17.7 | 24.3 | 14.7 |
| Max | 59.9 | 37.6 | 54.9 |
| Mean | 47.5 | 30.2 | 22.4 |
| SD | 6.5 | 3.8 | 5.3 |
| CV (%) | 13.8 | 12.7 | 23.6 |
| Prunéřov (n = 48) | |||
| Min | 6.1 | 12.6 | 14.3 |
| Max | 60. 7 | 48.9 | 74.3 |
| Mean | 40.5 | 31.2 | 28.3 |
| SD | 12.6 | 7.6 | 12.7 |
| CV (%) | 31.1 | 24.4 | 45.0 |
| Tumerity (n = 10) | |||
| Min | 31.6 | 22.9 | 2.7 |
| Max | 68.4 | 30.6 | 37.8 |
| Mean | 50.7 | 22.9 | 21.3 |
| SD | 11.5 | 2.6 | 11.0 |
| CV (%) | 22.7 | 11.3 | 51.7 |
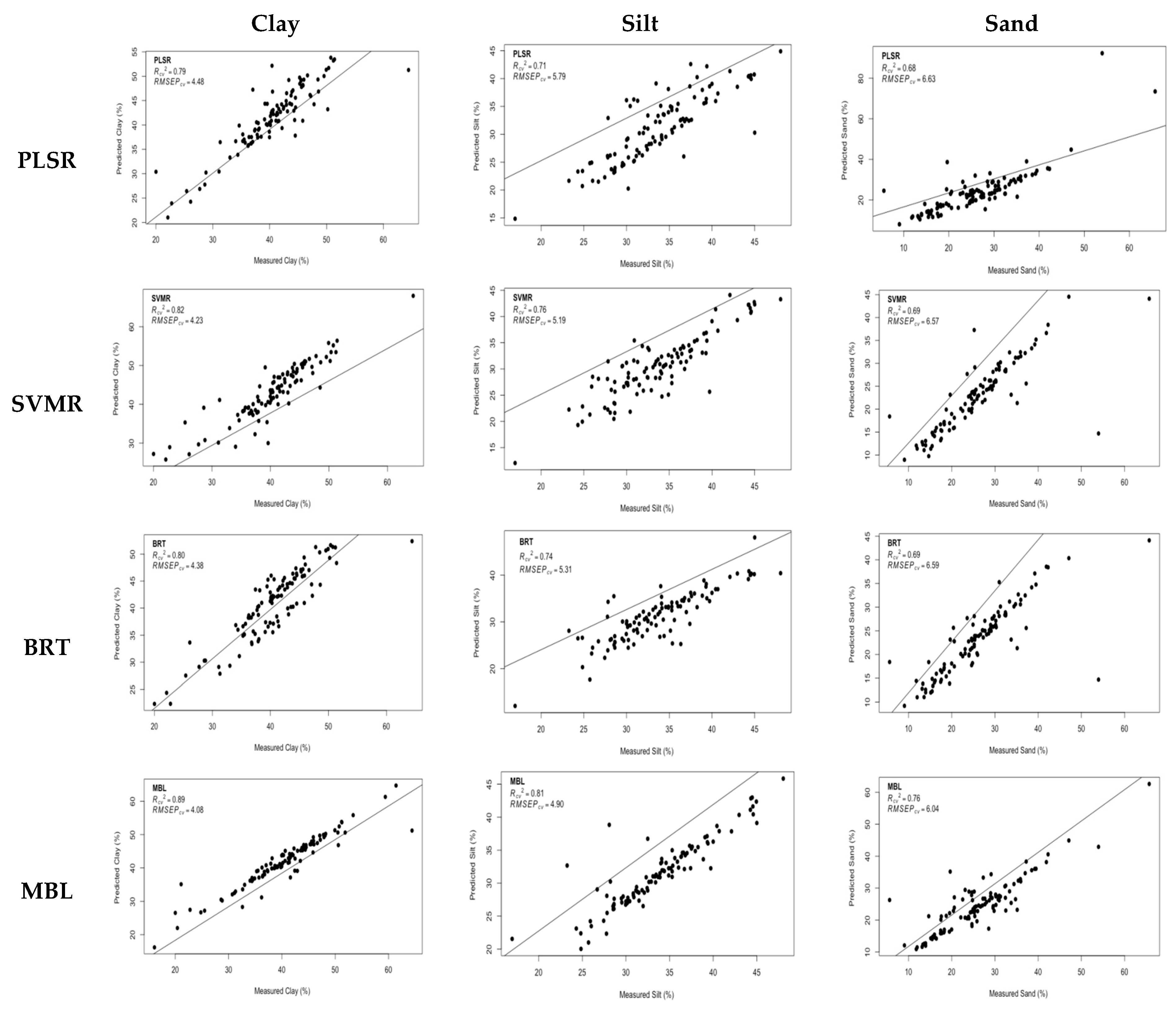
| Data Mining Algorithms | Clay | Silt | Sand | |||
|---|---|---|---|---|---|---|
| (%) | ||||||
| R2cv | RMSEPcv | R2cv | RMSEPcv | R2cv | RMSEPcv | |
| PLSR | 79 | 4.48 | 71 | 5.79 | 68 | 6.63 |
| SVMR | 82 | 4.23 | 76 | 5.19 | 69 | 6.57 |
| BRT | 80 | 4.38 | 74 | 5.31 | 69 | 6.59 |
| MBL | 89 | 4.08 | 81 | 4.90 | 76 | 6.04 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholizadeh, A.; Borůvka, L.; Saberioon, M.; Vašát, R. A Memory-Based Learning Approach as Compared to Other Data Mining Algorithms for the Prediction of Soil Texture Using Diffuse Reflectance Spectra. Remote Sens. 2016, 8, 341. https://doi.org/10.3390/rs8040341
Gholizadeh A, Borůvka L, Saberioon M, Vašát R. A Memory-Based Learning Approach as Compared to Other Data Mining Algorithms for the Prediction of Soil Texture Using Diffuse Reflectance Spectra. Remote Sensing. 2016; 8(4):341. https://doi.org/10.3390/rs8040341
Chicago/Turabian StyleGholizadeh, Asa, Luboš Borůvka, Mohammadmehdi Saberioon, and Radim Vašát. 2016. "A Memory-Based Learning Approach as Compared to Other Data Mining Algorithms for the Prediction of Soil Texture Using Diffuse Reflectance Spectra" Remote Sensing 8, no. 4: 341. https://doi.org/10.3390/rs8040341
APA StyleGholizadeh, A., Borůvka, L., Saberioon, M., & Vašát, R. (2016). A Memory-Based Learning Approach as Compared to Other Data Mining Algorithms for the Prediction of Soil Texture Using Diffuse Reflectance Spectra. Remote Sensing, 8(4), 341. https://doi.org/10.3390/rs8040341