Abstract
The availability of high-resolution remote sensing (HRRS) data has opened up the possibility for new interesting applications, such as per-pixel classification of individual objects in greater detail. This paper shows how a convolutional neural network (CNN) can be applied to multispectral orthoimagery and a digital surface model (DSM) of a small city for a full, fast and accurate per-pixel classification. The predicted low-level pixel classes are then used to improve the high-level segmentation. Various design choices of the CNN architecture are evaluated and analyzed. The investigated land area is fully manually labeled into five categories (vegetation, ground, roads, buildings and water), and the classification accuracy is compared to other per-pixel classification works on other land areas that have a similar choice of categories. The results of the full classification and segmentation on selected segments of the map show that CNNs are a viable tool for solving both the segmentation and object recognition task for remote sensing data.
1. Introduction
Aerial and satellite imagery collection is important for various application domains, including land inventory and vegetation monitoring [1,2]. Much research has been done on imagery collection techniques, rectification and georegistration of aerial imagery [3,4]. Rapid progress in data collection has been seen in recent years due to lower costs of data collection and improved technology [5]. However, imagery has little meaning unless it is processed and meaningful information is retrieved.
Recently, several techniques have emerged to automate the process of information retrieval from satellite imagery, and several application domains have been targeted [6,7,8]. Existing methods for solving the object recognition task usually rely on segmentation and feature extraction [9,10,11,12,13,14,15]. One of the major challenges that many developed algorithms face is their inapplicability to other domains. Many solutions for image segmentation and classification work perfectly for one particular problem and often for one particular region with well-known seasonal changes in imagery. It must be mentioned that due to the aforementioned progress in acquisition technology and excessive resolution, image segmentation is often not of interest, and image data can be cropped into regions with fixed dimensions.
For image classification, one possible way to address the problem of algorithm generalization is to utilize deep learning algorithms, for instance a convolutional neural network (CNN) [16]. The key feature of CNN-based algorithms is that they do not require prior feature extraction, thus resulting in higher generalization capabilities. Recently, CNNs have been shown to be successful in object recognition [17,18], object detection [19], scene parsing [20,21] and scene classification [22,23,24]. In this work, we investigate the use of a CNN for per-pixel classification of very high resolution (VHR) satellite imagery.
Many works on using CNNs for satellite imagery emerged in the recent four years. Nguyen et al. [25] presented an algorithm for satellite image classification using a five-layered network and achieved high classification accuracy between 75% and 91% using six classes: airport (78%), bridge (83%), forest (75%), harbor (81%), land (77%) and urban (91%). Hudjakov and Tamre [26] used a network with three inner layers (two convolutional and one linear classifier) to per-pixel classify terrain based on traversability (road, grass, houses, bushes) for long-term path planning for a UGV. A similar problem has been addressed by Wang et al. [27]. In their work, the authors combine CNN with a finite state machine (FSM) to extract a road network from satellite imagery. Chen et al. [28] applied CNN to find individual vehicles on the satellite data. CNNs have previously also been used for scene classification in high resolution remote sensing (HRRS) data [22,23,24] with impressive results on the UC Merced Land Use dataset [9]. These works use transfer learning by using a previously-trained CNN on object recognition and then fine-tuning it for a remote sensing application. Ishii et al. [29] compared CNN with support vector machine (SVM) for surface object recognition from Landsat 8 imagery and found CNN to outperform FSM. Zhang and Zhang [30] presented a boosting random convolutional network (GBRCN) framework for scene classification. The authors claim better performance of their algorithm on UC Merced and Sydney datasets (with 1.0-m spatial resolution) over known state-of-the-art algorithms, but the details of their implementation are not known yet (as of 27 November 2015).
While CNNs are commonly considered as a well-performing and promising solution for object classification, the problem of segmentation can have multiple solutions and thus defines the exact architecture of the CNN. For instance, previous per-pixel approaches that classify each pixel in remote sensing data have used the spectral information in a single pixel from hyperspectral imagery that consists of hundreds of channels with narrow frequency bands. This pixel-based classification method alone is known to produce salt-and-pepper effects of misclassified pixels [31] and has had difficulty with dealing with the rich information from very high-resolution data [32,33]. Works that include more spatial information in the neighborhood of the pixel to be classified have been done [34,35,36,37,38,39,40]. Contextual information has also been utilized to learn to differentiate roads from other classes using neural networks [41,42]. Many of these works limit the neighboring pixels to smaller areas around pixels, whereas in this work, we evaluate the use of a CNN on multispectral data with a bigger contextual area of up to 45 pixels. To overcome this problem, image segmentation can be done prior to classification (using various segmentation techniques).
We introduce a novel approach for per-pixel classification of satellite data using CNNs. In this paper, we first pre-train a CNN with an unsupervised clustering algorithm and then fine-tune it for the tasks of per-pixel classification, object recognition and segmentation. An interesting property of CNN is that it uses unsupervised feature learning to automatically learn feature representations. This has previously been done in other domains, such as computer vision [43], speech recognition [44,45] and time series data [46].
The main contributions of this paper can be summarized as follows:
- We used true ortho multispectral satellite imagery with a spatial resolution of 0.5 m along with a digital surface model (DSM) of the area.
- We provide an insightful and in-depth analysis of the application of CNNs to satellite imagery in terms of various design choices.
- We developed a novel approach for satellite imagery per-pixel classification of five classes (vegetation, ground, road, building and water) using CNNs that outperform the existing state-of-the-art, achieving a classification accuracy of 94.49%.
- We show how the proposed method can improve the segmentation and reduce the limitations of using per-pixel approaches, that is removing salt-and-pepper effects.
The remainder of the paper is organized as follows. The method is presented in Section 2. The experimental results and analysis are shown in Section 3. Finally, a conclusion and future work are given in Section 4.
Important terms and abbreviations are given in Table 1.

Table 1.
List of abbreviations and terms.
2. Method
The data and pre-processing are described in Section 2.1, and the process of manual labeling of the data is described in Section 2.2. An introduction to CNNs is given in Section 2.3, and the process of classifying a pixel using a single and multiple CNNs is given in Section 2.4 and Section 2.5, respectively.
2.1. Data and Pre-Processing
The data that are used in this work are a full city map whose location is in northern Sweden and consist of several north-oriented multispectral true orthography bands, several synthetic image bands, two near-infrared bands and a digital surface model (DSM) that was generated from the satellite imagery using stereo vision. True ortho is a composition of many images to an accurate, seamless 2D image mosaic that represents a true nadir rendering. Moreover, the true ortho imagery is exactly matched to the used DSM. The data have been kindly provided by Vricon [47]. Table 2 shows the bands and their respective bandwidths. The size of the orthographic images is pixels with a spatial resolution of 0.5 meters per pixel.

Table 2.
Spectral bands used in the multispectral orthography image.
The use of a DSM increases classification accuracy by providing height information that can help distinguish between similar looking categories, for example vegetation and dark-colored ground. Furthermore, a DSM is invariant to lighting and color variations and can give a better geometry estimation and background separation [48]. However, the measurements in a DSM need to be normalized because they are measured from a global reference point and not from the local surrounding ground level. Therefore, we use a local subtraction method that subtracts each non-overlapping region of the DSM with an estimate of the local ground level set as the minimum DSM value of that region. That is, , where is a local non-overlapping patch of the DSM band of size . In this work, we set pixels. Each band and the locally-normalized DSM band is then normalized with the standard score.
2.2. Manual Labeling
In remote sensing, the definition and acquisition of reference data are often critical problems [49]. Most datasets that use classification on a pixel-level only use a few hundred reference points [31,48,50,51,52]. In order to validate the classifier using a much larger pool of validation points and for supervised learning and fine-tuning, each pixel in the full map is manually labeled. Figure 1a shows the GUI that is used to manually classify the map, and Figure 1b shows the finished labeled map. The GUI contains options for toggling the RGB channels, height map, labeled map and segments on or off. The map is divided into regions of 1000-by-1000 pixels and initially segmented into 2000 segments using simple linear iterative clustering (SLIC) [53]. The number of segments can be dynamically increased or decreased depending on the level of detail that is necessary. A button for averaging the current labeled pixels into a new segmentation is available. The categories used in this work (and their prevalence) in the finished labeled map are vegetation (10.0%), ground (31.4%), road (19.0%), building (6.7%) and water (33.0%). The labeling process included the categories railroad and parking, but due to their low prevalence, these two categories were merged with road.
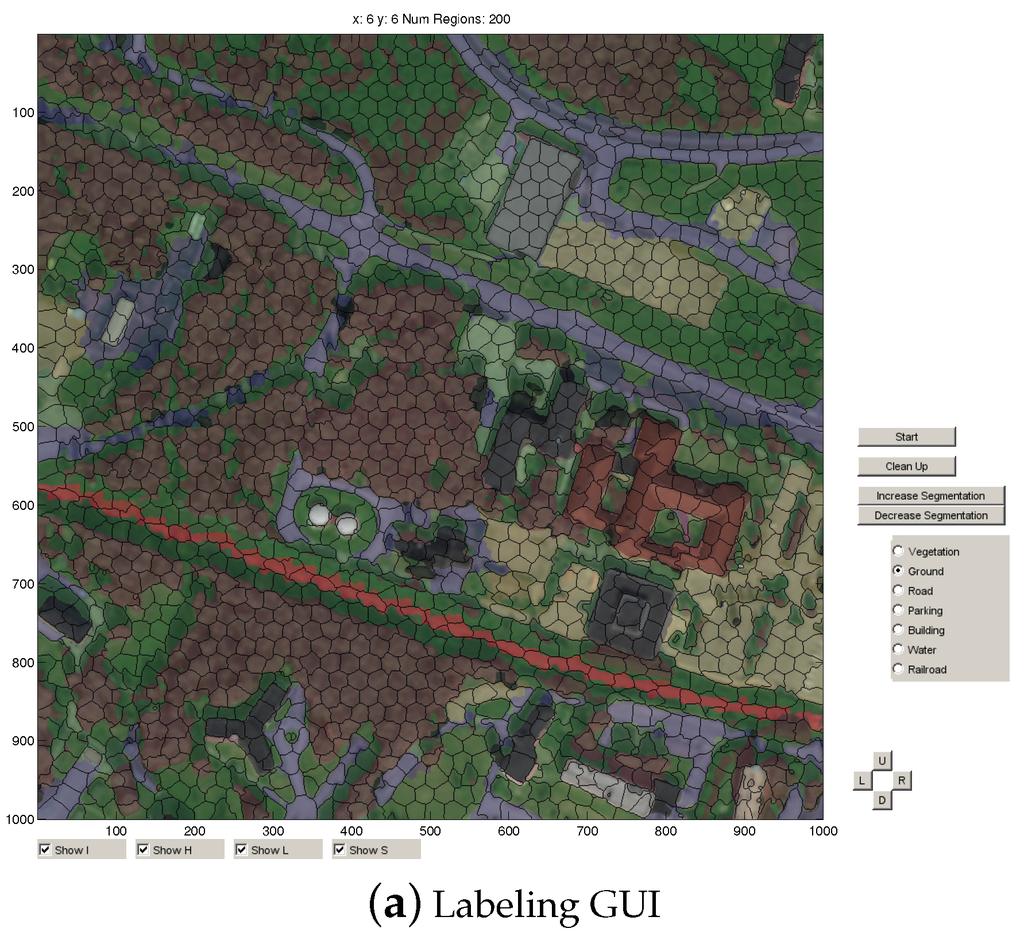
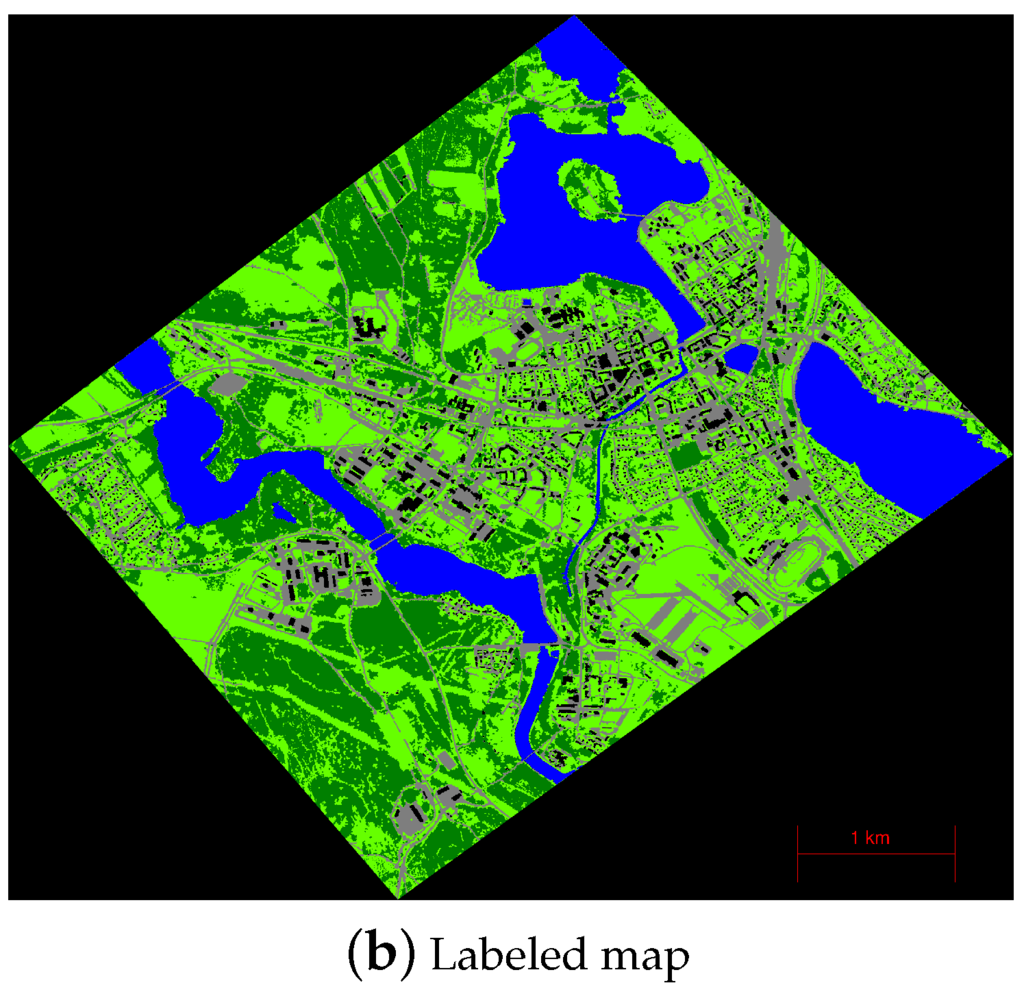
Figure 1.
(a) GUI used for labeling the map. The category is selected on the right, and segments are color-filled by clicking on them. (b) Finished labeled map of the land area used in this work.
2.3. Convolutional Neural Networks
Convolutional neural networks (CNNs or ConvNets) [16] are designed to process natural signals that come in the form of multiple arrays [54]. They have been successful in tasks with 2D structured multiple arrays, such as object recognition in images [17] and speech recognition from audio spectrograms [55], as well as 3D structured multiple arrays, such as videos [56]. CNNs take advantage of the properties of natural signals by using local connections and tied weights, which makes them easier to train, since they have fewer parameters compared to a fully-connected network. Another benefit of CNNs is the use of pooling, which results in the CNN learning slightly translational- and rotational-invariant features, which is a desirable property for natural signals. A deep CNN can be created by stacking multiple CNNs, where the low-level features (edges, corners) are combined to construct mid-level features with a higher level of abstraction (objects). One or several fully-connected layers (FC-layers) are typically attached to the last CNN layer. Finally, a classifier can be attached to the final FC-layer for the final classification.
More specifically, a single CNN layer (see Figure 2) performs the steps of convolution, non-linear activation and pooling. The convolutional layer consists of k feature maps, f. Each feature map is calculated by taking the dot product between the k-th filter of size , , and a local region x of size with c number of channels, . The feature map for the k-th filter is calculated as:
where σ is the non-linear activation function. A typical choice of activation function for CNNs are hyperbolic tangent [57] or rectified linear units (ReLU) [58]. The filters w can be pre-trained using an unsupervised feature learning algorithm (k-means, auto-encoder) or trained from random initialization with supervised fine-tuning of the whole network.
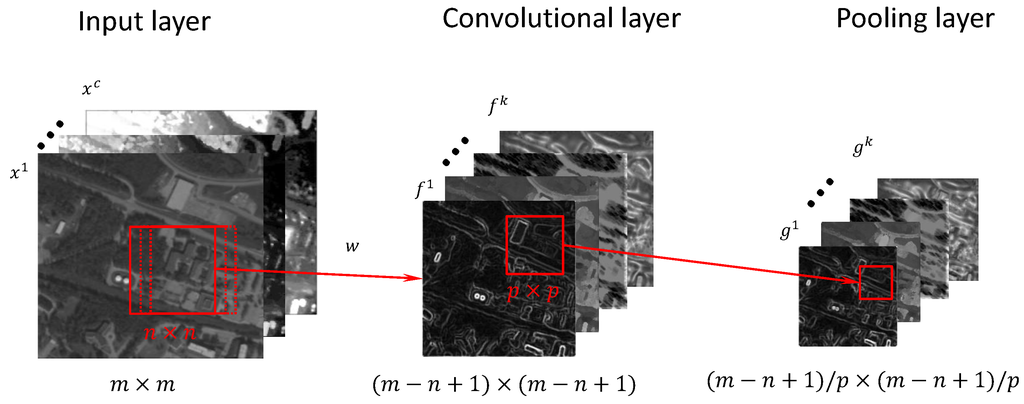
Figure 2.
The three layers that make up one CNN layer: input layer, convolutional layer and pooling layer. The input layer has c color channels, and the convolutional and pooling layer has k feature maps, where k is the number of filters. The size of the input image is and is further decreased in the convolutional and pooling layer with the filter size n and pooling dimension p.
The pooling step downsamples the convolutional layer by computing the maximum (or the mean) over a local non-overlapping spatial region in the feature maps. The pooling layer for the k-th filter, , is calculated as:
where p is the size of the local spatial region and .
2.4. Per-Pixel Classification Using a Single CNN
The process of classifying a single pixel in a satellite image using a CNN can be seen in Figure 3. The input to the first CNN layer consists of c number of spectral bands of contextual size , where the pixel to be classified is located at the center. The full architecture consists of L number of stacked standard CNN layers described in Section 2.3, followed by a fully-connected (FC) layer and, finally, a softmax classifier. The convolutional and pooling layer for the first CNN consists of number of feature and pooling maps, one for each filter. Rectified linear units (ReLU) are used as the non-linear activation function after the convolutional step, . A normalization step with local contrast normalization (LCN) [57] is performed after the non-linear activation function step in order to normalize the non-saturated output caused by the ReLU activation function. The process of selecting the contextual area surrounding the pixel to be classified m, the number of CNN layers L, the number of filters k, filter size n and pooling dimension p in each CNN layer is discussed in Section 3.2.3. A fully-connected layer is attached that uses the pooling layer of the last stacked CNN as input. The fully-connected layer is a denoising auto-encoder [59] with 1000 hidden units, using dropout [60], the L2-weight decay penalty, ReLU activation and the L1-penalty on the hidden unit activations [61]. The hidden layer of the fully-connected layer is then used as input to the softmax classifier for the final classification.
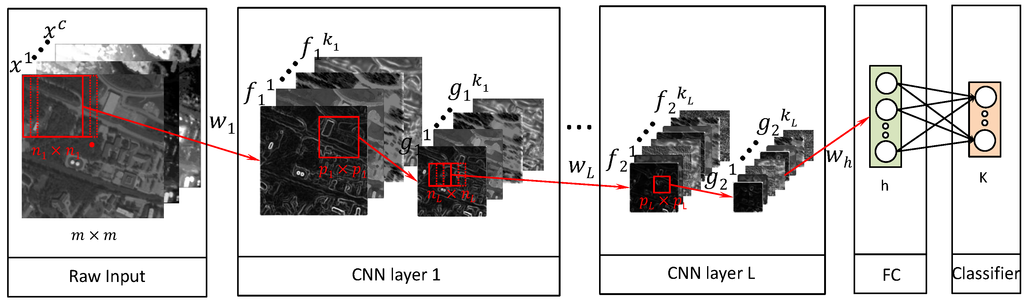
Figure 3.
Overview of the method used for per-pixel classification. The filters of size from the first CNN layer are convolved over the pixel to be classified and its contextual area of size with c color channels to create feature maps. The feature maps are pooled over an area of to create the pooling layer. The process is repeated for L number of CNN layers. The pooling layer of the last CNN is the input to a fully-connected auto-encoder. The hidden layer of the auto-encoder is the input to the softmax classifier.
Training of the filters, the fully-connected layer and the softmax classifier is done in two steps. First, the filters are learned with k-means by extracting 100,000 randomly-extracted patches of size and using them as input to the k-means algorithm. This allows the filters to be learned directly from the data without using any labels, and this approach has previously been used in works that use CNN for scene classification [62] and object recognition [63]. The parameters of the fully-connected layer and the softmax classifier are trained from random initialization and then trained with backpropagation using stochastic gradient descent (SGD).
Feed-forwarding the surrounding area for each pixel through a CNN can be time consuming, especially if each pixel is randomly drawn. Fortunately, this process can be quickened by placing smaller image patches side-by-side in a 100-by-100 large image on which the convolution is performed. The extra overlapping convolutions are deleted before the convolved patches are retrieved from the large image. This procedure has been reported to be faster than performing convolution one at a time on each training patch [64].
For the case of feed-forwarding the convolutions of all filters within a region, the filters are applied to the whole region, and the local feature map is then assigned to each individual pixel and its contextual area. This removes the extra unnecessary calculations of computing the same convolution for pixels that share the same contextual area.
2.5. Per-Pixel Classification Using Multiple CNNs
Recently, multiscale feature learning has been shown to be successful in tasks, such as scene parsing using CNNs [65] and recurrent neural networks [64]. The concept of multiscale feature learning is to run several CNN models with varying contextual input size in parallel and later to combine the output from each model to the fully-connected layer. The general structure can be seen in Figure 4 and shows N number of CNNs in parallel with depth L and with varying contextual size . The output from each CNN is then concatenated as input for the fully-connected layer. Finally, the hidden layer of the fully-connected layer is used as input to a softmax classifier. The filters of each CNN are learned similarly as described in Section 2.4 with k-means and the weights of the FC-layer, and the softmax classifier is learned with backpropagation. Another possibility of achieving multiscale feature learning is to use the same context size for all CNNs, but instead scale the input data. We chose to change the context size in this work instead in order to preserve the high-resolution information.
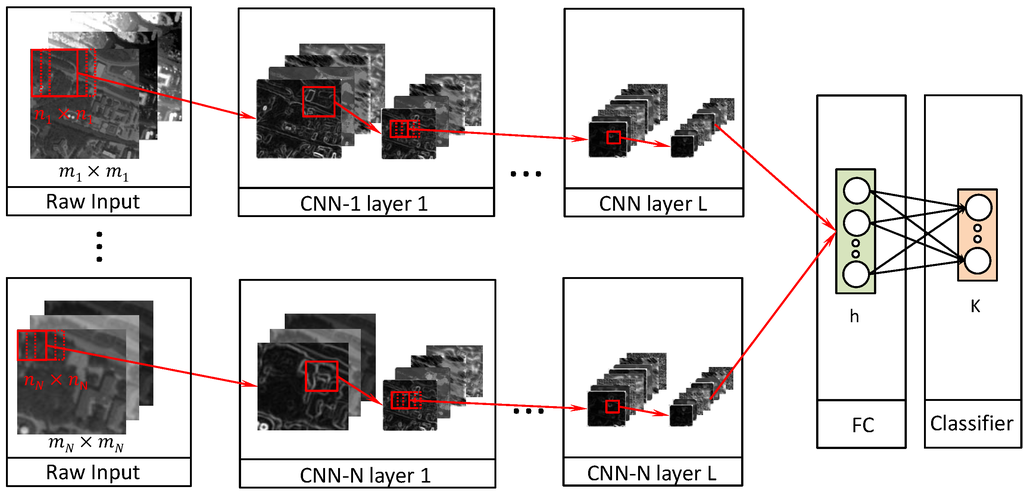
Figure 4.
Overview of the CNN architecture used for multiscale feature learning. The architecture consists of N CNNs with L layers that use a different size of contextual area . The concatenation of all of the pooling layers of the last layer in each CNN is used as input to a fully-connected auto-encoder. The hidden layer of the auto-encoder is used as input to a softmax classifier.
2.6. Post-Processing
A post-processing step is used to reduce the classification noise within each segment and also to merge segments to better represent real-world objects. An overview of the method used can be seen in Figure 5. The classified pixels are smoothed by averaging the classifications over all pixels within each segment from a segmentation method on the RGB channels. In this work, we used the simple linear iterative clustering (SLIC) [53] algorithm. The segments are then merged using the information from the classifier. Developing segmentation methods is an active research field [66], and some methods for merging regions include density-based spatial clustering of applications with noise (DBSCAN) [67] and mean brightness values [31]. These merging methods are based on only the input data, while our proposed merging method is based on the input data and the classified pixels. The intuition behind this is that if nearby segments are classified as the same class with high classification certainty, then those segments probably belong to the same real-world object and they should be merged.
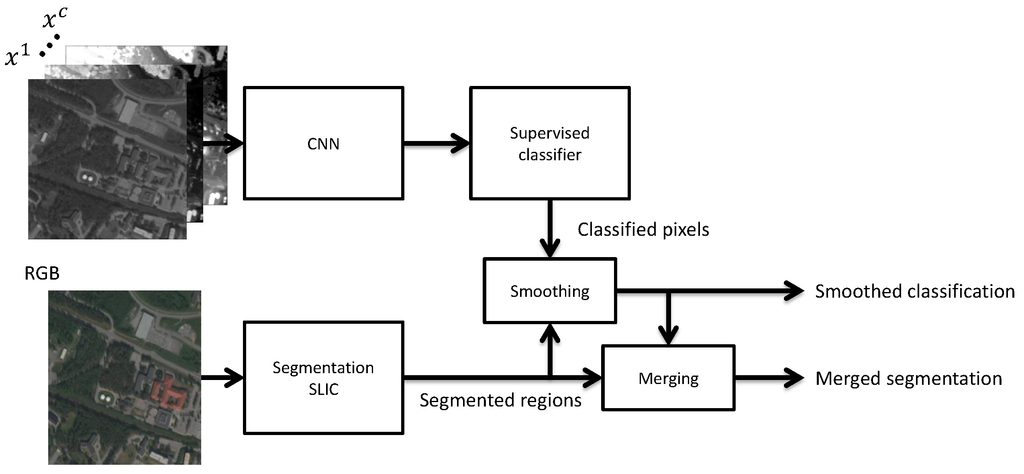
Figure 5.
Overview of the method used for classification and segment merging. Each pixel is first classified using a CNN and a softmax classifier. The segments from a SLIC segmentation are then merged using the prediction certainty of the classified pixels.
3. Experimental Results and Analysis
This section evaluates the use of the different CNN architectures for per-pixel classification on multispectral orthoimagery. First we describe the experimental setup with the data and the model used in Section 3.1. Then, we analyze the selection of spectral bands, the learned filters and the choice of architecture parameters for the CNN in Section 3.2. We present the classification results in Section 3.3 and the results of post-processing and merging of segments in Section 3.4.
3.1. Experimental Setup
The data consist of 14 multispectral orthographic images and a digital surface model with a spatial resolution of 0.5 meters per pixel of a small city in northern Sweden. The data are manually labeled into five categories (vegetation, ground, road, building, water) as described in Section 2.2. Normalization of the DSM is done with local subtraction and then normalized the same as the other bands with a standard score. A wrapper feature selection method is first used to select a subset of the bands.
One approach to selecting training and testing data is to manually divide up the map. However, this is non-trivial in our case because of the asymmetry of our map (big lakes to the north and north-east, small city center, clusters of sub-urban areas around the city), and it involves human decision making, which can influence the performance and makes cross-validation difficult. Instead, the training set, validation set and testing set are randomly drawn with an equal class distribution from the full map. The sets are created by randomly selecting 20,000 pixels from each of the five categories and then assigning of them as the training set, as the validation set and as the testing set. This means that the testing set contains a total of 20,000 validation points. The validation set is only used for channel selection, hyperparameter tuning and for early-stopping during training.
Since the training set is class-balanced, this could result in a model that is not representative of the population of the current map. However, due to the low amount of buildings (6.7%) in our map compared to other classes (vegetation (10.0%), ground (31.4%), road (19.0%) and water (33.0%)) and the fact that buildings is one of the classes that we are most interested in classifying correctly, in this map and future maps with more buildings, we did not want to risk getting more misclassified buildings for the sake of getting a higher overall accuracy on this map.
The CNN architectures that are used are described in Section 2.4 and Section 2.5. The fully-connected layer that is connected to the last CNN layer(s) has 1000 hidden units with a dropout rate and the L1-penalty on the activations. A softmax layer is attached to the fully-connected layer for the final classification. The filters of each CNN layer are pre-trained using k-means. Training of the fully-connected layer and softmax layer is done with supervised backpropagation using mini batch stochastic gradient descent (SGD) with 200 training examples per mini batch, momentum, decaying learning rate and early-stopping to prevent overfitting.
3.2. Analysis of Design Choices
This section gives insight into some of the design choices that have an influence on the performance and simulation time of the proposed approach. In particular, we investigate the process of selecting the spectral band in Section 3.2.1, give an analysis of the learned filters in Section 3.2.2 and the process and influence of different CNN hyperparameters in Section 3.2.3 and CNN architectures, such as the number of CNN layers, L, in Section 3.2.4 and the number of CNNs in parallel, N, in Section 3.2.5.
3.2.1. Spectral Band Selection
Feature selection plays a significant role in improving classification accuracy and reducing the dimensionality [68]. There are a number of works that use feature selection methods to select bands from hyperspectral images [69,70,71]. In this work, we use two wrapper feature selection methods [72], namely sequential forward selection (SFS) and sequential backward selection (SBS), to select a subset from the 15 spectral bands listed in Table 2. Figure 6 shows the classification accuracy on the validation set for the two feature selection methods using a one-layered CNN. It can be seen that the classification accuracy is increased when the channels pan sharpened, coastal, NIR2, DSM and NIR1 are added during SFS. Similarly, the accuracy is decreased when the same five channels and land cover are removed during SBS. Based on these observations, we select the following six channels to use in our experiments: pan sharpened, coastal, NIR2, DSM, NIR1 and land cover.
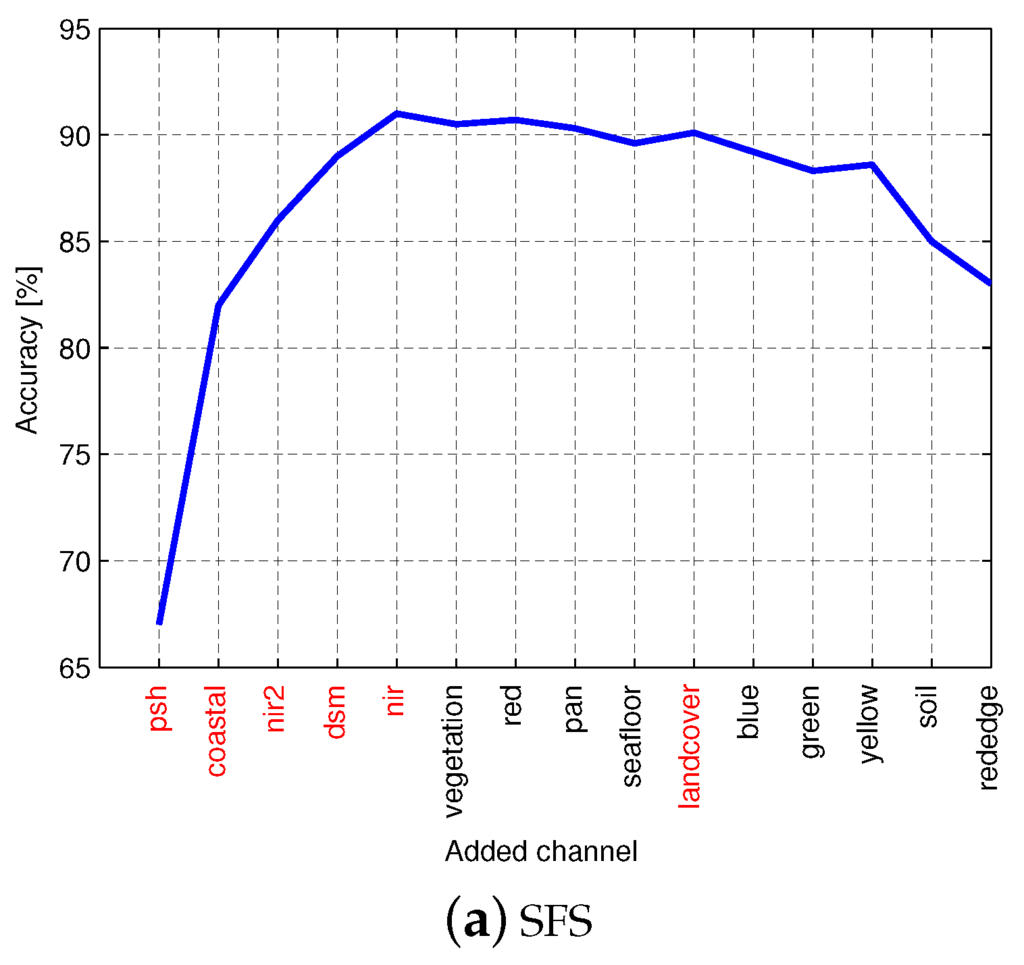
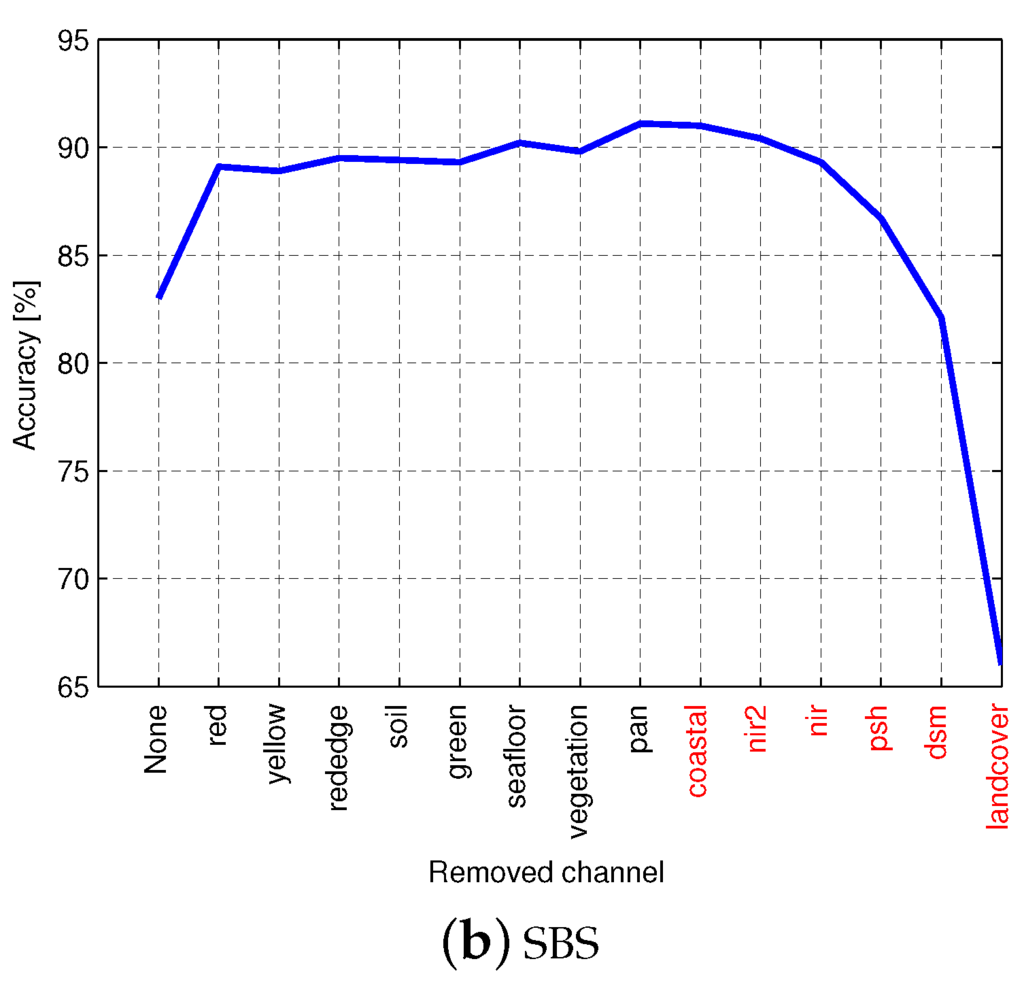
Figure 6.
Classification accuracy on a small randomly-drawn subset using (a) sequential forward selection (SFS) and (b) sequential backward selection (SBS). Selected channels are shown in red.
An analysis of the selected channels can be done by visualizing the bandwidth of the selected and removed channels; see Figure 7. It can be seen that the combination of the selected channels completely covers the spectrum between 400 and 1040 nm. Note that all of the channels from the visible spectrum, except coastal (blue, green, yellow and red), were removed, and the panchromatic channel was selected instead, which is a combination of visible light. Another interesting channel is the land cover, which could be removed to cover the full spectrum, but in the sequential backwards selection, the land cover channel was the last to be removed, probably due to its large spread along the spectrum.
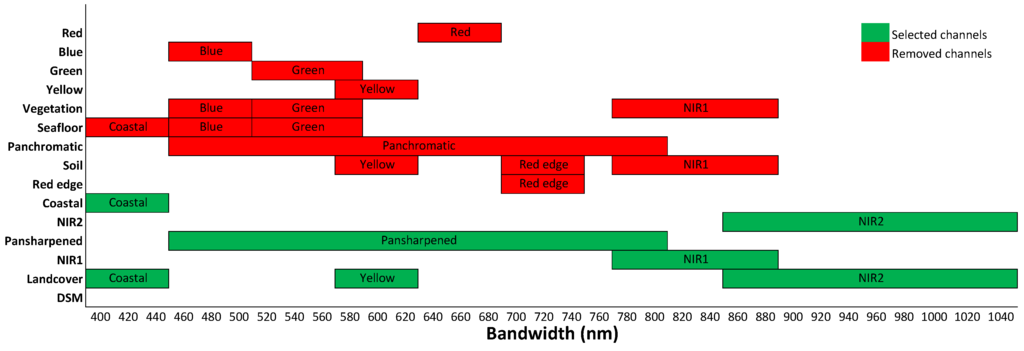
Figure 7.
A visualization of the bandwidth of all of the selected channels and the removed channels. The selected channels contain the full bandwidth between 400 and 1040 nm.
3.2.2. Pre-Training Filters
There are several strategies for learning the filters that are used for convolution in a CNN. In this work, the filters in each CNN layer are pre-trained by running the k-means algorithm for 200 iterations on 100,000 randomly-extracted patches from the previous layer. The size of the patches are , where n is the filter size and c is the number of channels in the input data. Figure 8 shows 50 learned filters with filter size . The number of channels of the input data c is set to the six channels that were selected from Section 3.2.1. It can be seen that each filter focuses on different channels, e.g., Filter 1 focuses on high values in the coastal channel, medium values in the pan-sharpened channel and low values in the other channels, while Filter 2 is similar to Filter 1, except it focuses on higher values in the DSM channel. It can also be seen that some filters focuses on a gradient going from low values in one corner to high values in another corner, e.g., Filters 3, 21 and 31.

Figure 8.
The learned 50 filters with filter size for the first CNN layer using k-means on the normalized six-channel data. Each column shows the filter for each patch for each of the six channels.
3.2.3. Influence of CNN Architecture Parameters
In this section, we evaluate the choice of the architecture model parameters for a one-layered CNN. The four parameters to be evaluated are context size m, filter size n, pooling dimension p and number of filters k. These four parameters are connected in a way that determines the number of output units according to . The context size m is the surrounding area around the pixel to be classified and is chosen among ; the pooling dimension is chosen among ; the number of filters is chosen among ; and the filter size n is chosen, as all of the allowed values are in the range 1–25, so that .
First, we evaluate the influence of the context size m and number of filters k on the classification accuracy. Figure 9a shows the highest accuracy of all parameter combinations for each context size and for three choices of numbers of filters. It can be seen that the accuracy is increased for all context sizes when the number of filters is increased. More filters and larger context sizes were not tested due to the longer simulation times and limited computer memory. It is worth noting that the classification accuracy is not greatly improved after increasing the context size beyond .
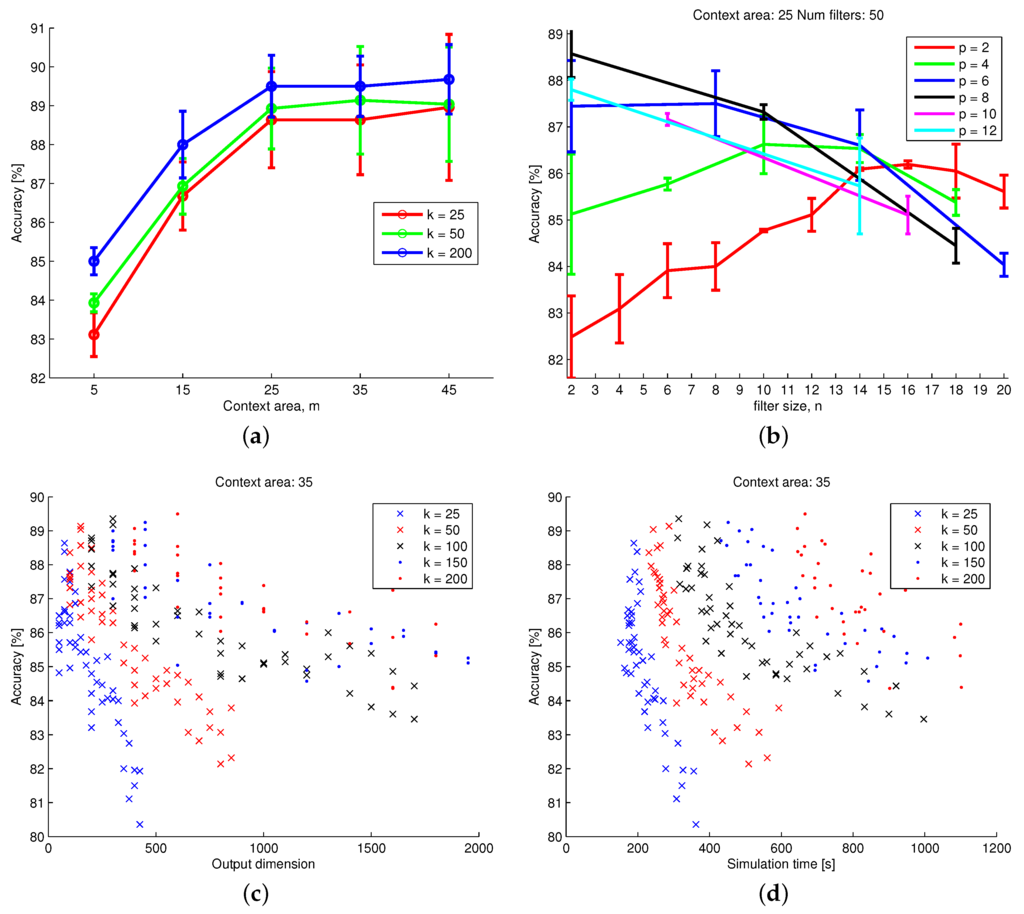
Figure 9.
Classification accuracy as a function of various CNN architecture model parameters. See the text for details. (a) Accuracy as a function of context size, m, for different numbers of filters, k; (b) accuracy with different filter size, n and pooling dimension, p; (c) accuracy and output dimension for different number of filters, k; (d) accuracy and simulation time for different number of filters, k.
The optimal choice of filter size and pooling dimension is different for each choice of context size. This is further analyzed in Figure 9b, which shows the classification accuracy for different filter sizes and pooling dimensions with context size and number of filters . It can be seen that a high pooling dimension generally requires a low filter size, while a low pooling dimension requires a medium-sized filter to achieve the highest accuracy. Based on this observation, it is theorized that a high accuracy can be achieved no matter which one of the parameter is set to, as long as the other parameter balances the number of output units.
This theory is further investigated in Figure 9c, which shows the accuracy as a function of the output dimension for different numbers of filters. A high accuracy is possible to achieve with all choices of the number of filters as long as the number of output units is below approximately 600 units. The choices that produce a higher number of output units achieve lower accuracy. It can be concluded that there exists a combination of filter size and pooling dimension that is capable of achieving high accuracy as long as the context size is large enough.
With the possibility of achieving high classification results with the right choice of architecture parameters, the optimal choice comes down to simulation time. Figure 9d shows the accuracy as a function of simulation time for different numbers of filters. It can be seen that the simulation time increases for a higher number of filters, but all choices are capable of achieving similar accuracy. For future experiments, we chose parameters that achieve a high accuracy while maintaining a low simulation time.
3.2.4. Influence of the Number of CNN Layers
Deep CNNs consist of multiple convolution and pooling layers and have been shown to increase performance on a number of tasks [43,54]. They have previously been used for large-scale image recognition [17] and scene classification of HRRS data [22,23,24]. To evaluate the influence of using L number of stacked CNN layers for our task of per-pixel classification, we use four different CNNs with varying context sizes and calculate the accuracy using numbers of CNN layers. The number of filters, filter size and pooling dimension are chosen in each layer, so that the size of the pooling layer in the last CNN layer is . Due to the small context area, the pooling dimension is set to one in all layers, except for the last layer. As an example, the filter sizes for the CNN with context area are set to in each layer and the pooling dimension . The accuracy as a function of the number of layers can be seen in Figure 10a. In our study, adding more layers did not increase the accuracy. In fact, the accuracy was decreased the more layers were used. Figure 10b shows the simulation time as a function of the number of layers, and it can be seen that adding more layers significantly increase the simulation time, especially for the CNNs with larger context areas.
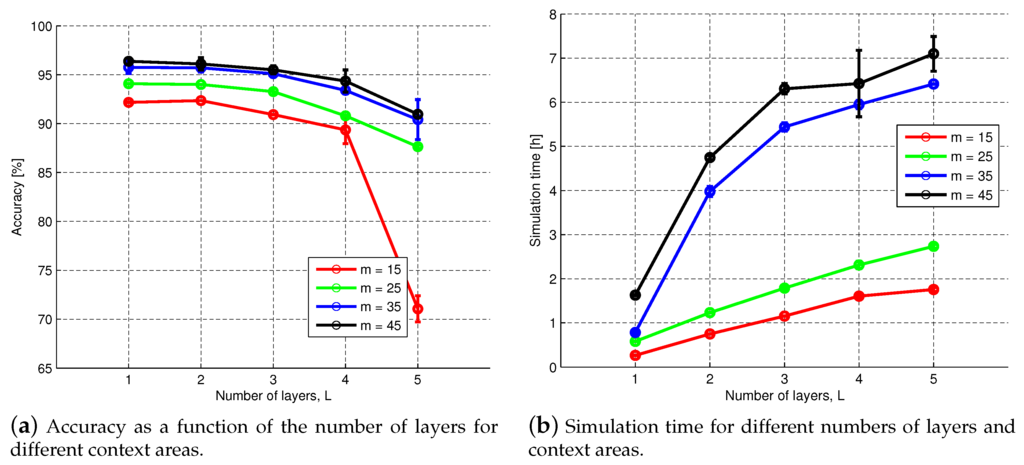
Figure 10.
The (a) classification accuracy and (b) simulation time as a function of the number of CNN layers, L, for various context areas, m.
Deep CNN structures are typically used for larger images of at least pixels, and from the experiments from Section 3.2.3, we know that using a context size larger than only gives a slight improvement in the performance at a cost of a much longer simulation time. A possible explanation for the poor results of using deep CNNs is the large amount of parameter choices for each layer. Furthermore, the size of the training set is the same, but the number of model parameters is increased, which could cause the model to underfit and could be solved by increasing the number of training data by using data from multiple maps or by data augmentation. Another possible solution could be to use backpropagation on the full network to learn the filters in each layer from random initialization instead of using k-means.
3.2.5. Influence of the Number of CNNs in Parallel
In Section 2.5, we described how N number of CNNs with different contextual areas could be run in parallel and their outputs concatenated as input to the FC layer. In this section, we evaluate the choice of N. We chose among four CNNs with varying context areas . The filter size and pooling dimension are set as the optimal for each choice of context area according to Section 3.2.3. The input to the fully-connected layer is the concatenation of the pooling layer of each CNN. Figure 11 shows the classification accuracy for all possible combinations of using 1,2,3 or all 4 of the CNNs in parallel. The highest accuracy when only one CNN is used is achieved when the CNN with the largest context area, 45, is used. However, a more stable model with lower variance on the accuracy is achieved when medium-sized context areas of 25 or 35 are used. The larger context areas are particularly useful for correctly classifying large buildings or wide roads, and the fact that our map has few of these objects might explain the large variance when using a very large context area. Adding multiple CNNs increases the performance, and the best performance is achieved when all four CNNs are used. This shows that the classifier works best if it looks at both the larger context, as well as a close-up on the details. A second conclusion is that using multiple CNNs in parallel is more important for achieving a higher classification accuracy than using deep CNNs. The downside of using multiple CNNs in parallel is, of course, the increased simulation time. The time for training each of the four CNNs with context area takes approximately 1 h, 1.5 h, 3 h and 4 h, respectively.
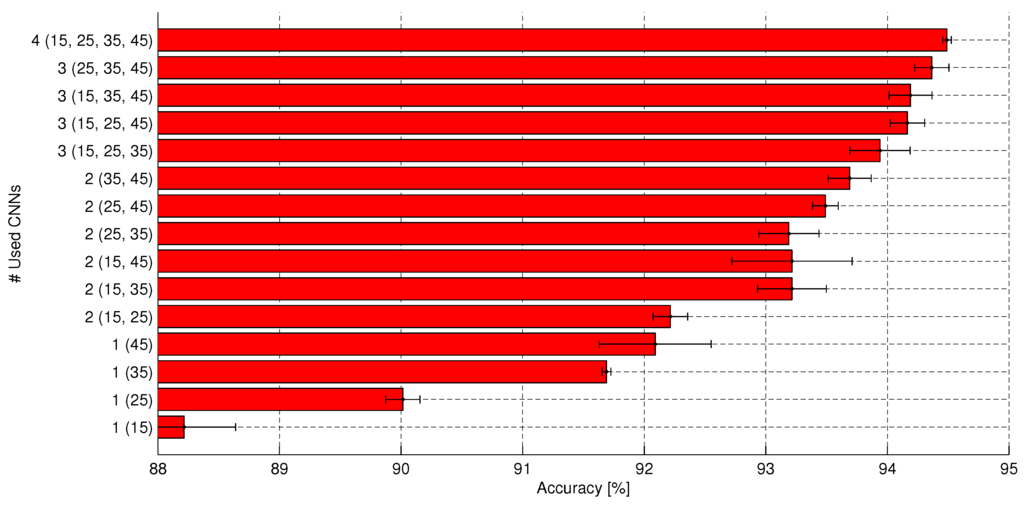
Figure 11.
Influence of using multiple CNNs with varying context sizes. The context areas that are used are shown in parenthesis. Using larger context areas and multiple CNNs in parallel increases the performance.
3.3. Classification Results
In this section, we present the classification results on the testing set using a single CNN and a combination of multiple CNNs. The design choices for single CNN are made so that a fast, but yet accurate, model is achieved, while the design choices for the multiple CNN are made so that the highest classification accuracy is achieved. The model parameters for the single CNN is set to , , and , and the model parameters for the combination of four CNNs is set to context size , number of filters and their respective optimal choice of n and p. The classification result with the single CNN is , and the accuracy with the multiple CNN architecture is . The simulation time (training and inference) of the single and multiple CNNs was approximately h and h, respectively. Table 3 shows a comparison with similar works that have done per-pixel classification estimation with similar choices of categories, but that cover other land areas. A direct comparison of different studies is not possible, because of different study areas, data acquisition methods and resolutions, reference datasets and class definitions [48]. However, it can be concluded that the use of CNNs for per-pixel classification is capable of achieving comparable results to the typically-regarded state-of-the-art object-based image analysis (OBIA) methods. It should also be noted that many of these works do not use a fully-labeled map, but instead use only a couple hundred validation points that where manually labeled and therefore potentially manually selected, while in this work, we used 20,000 randomly-extracted validation points.

Table 3.
Comparison of classification accuracy (%) with previous methods. OBIA, object-based image analysis.
Table 4 shows the confusion matrix for the classification of the held-out test set for the multiple CNN architecture. It can be seen that the largest confusion is between ground that was classified as roads and vice versa. We believe this is caused by the large amount of shadows that exist on many of the roads from the surrounding forest and buildings, which is known to complicate the interpretation of areas nearby such objects [48]. There is also a small confusion between buildings and forest. We believe this occurs when buildings are located close to dense forest areas.

Table 4.
Confusion matrix for a randomly-drawn test set. Each category contains around 4000 validation points each.
The problematic classes can be further investigated by visualizing the classification results on a whole region. Figure 12 shows the classification results on randomly-selected regions of the map. It can be seen that the misclassifications of the road usually occur when the road is covered by shadows. There is also a misclassification of the bridge over water that is classified as a building. It can also be seen that dark buildings that are surrounded by forests are sometimes misclassified as vegetation.

Figure 12.
Classification results on six small segments. The first and third rows are input regions. The second and fourth rows are the classification of each pixel after segmentation smoothing. The classes are marked as vegetation (dark green), ground (light green), roads and parking (gray), buildings (black) and water (blue).
3.4. Post-Processing Results
In this section, we show how the post-processing techniques described in Section 2.6 are used to smooth out the classification result and how the pre-defined segments are merged. We illustrate the effects of the post-processing techniques on a small pixel segment of the map.
3.4.1. Effects of Classification Averaging
The effects of classification averaging can be seen in Figure 13. The left figure shows the selected region, which contains all five classes. The middle figure shows the classification of all pixels without any averaging. It can be seen that there are some salt-and-pepper misclassifications, e.g., small islands in the river, small puddles of water on the ground, trees being classified as buildings and patches of ground in the middle of the road. Furthermore, the shadows from the buildings cause the road to be misclassified as ground. The right figure shows the result after averaging, and it can be seen that the salt-and-pepper effects have been removed.
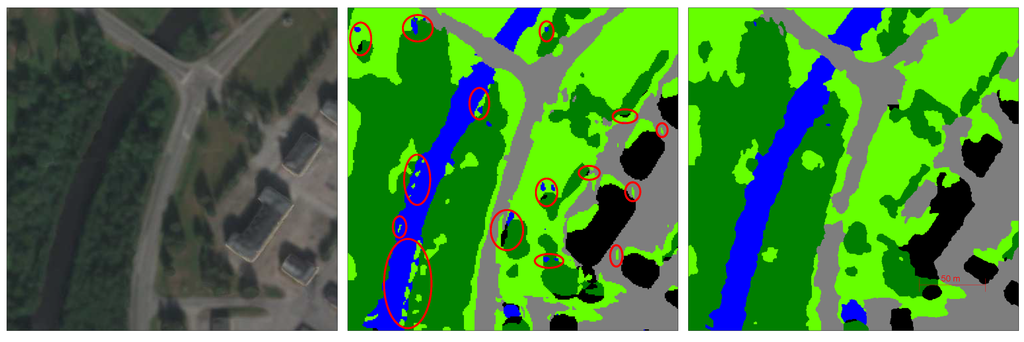
Figure 13.
This figure illustrates the effects of classification averaging on a selected region. Left: Selected region shown in RGB. Middle: Classification result without averaging. Red circles indicate salt-and-pepper effects. Right: Classification result after averaging, where it can be seen that the salt-and-pepper effects have been removed.
Table 5 shows the accuracy before and after using classification averaging on the whole map. For the multiple CNNs model, the average accuracy increased from –, which confirms that a post-processing step of classification averaging is still necessary to achieve a good performance when using a pixel-based classification approach.

Table 5.
Performance comparison between using and not using pixel classification averaging.
3.4.2. Effects of Region Merging
The region merging process is done by first segmenting each 250 by 250 pixel area into approximately 500 segments using the SLIC algorithm and then merging the segments based on the averaged classifications. The effects of region merging can be seen in Figure 14. The left figure shows the selected region. The middle figure shows the initial segmentation using SLIC. It can be seen that individual objects, such as buildings, are poorly segmented, contain multiple segments and sometimes are merged together from the shadow on the ground. The right figure shows the segmentation after the merging of segments. The merging is based on the predicted class of each segment, as well as the prediction certainty. Each pixel that is classified with the softmax classifier returns the class and the classification certainty. The merging of two neighboring segments is done if the two segments are classified as the same class with certainty over a certain threshold. We empirically set this threshold at , meaning that two adjacent segments were merged if the average classification accuracy of all pixels within each segment were over this threshold. It can be seen that the number of segments is fewer, that they are of varying sizes after the merging and that they better represent real-world objects. This shows that the process of segmentation does not necessarily only have to depend on the input data, but can also depend on the predictions from a per-pixel classifier.

Figure 14.
This figure illustrates the effects of region merging. Left: Selected region in RGB. Middle: Initial segmentation using the SLIC algorithm where each region is of equal size. Right: Segmentation after nearby segments that have the same predicted class with over classification certainty have been merged. The segments after the merging have varying sizes and more accurately represent real-world objects.
4. Conclusions
We have shown how a CNN can be used for per-pixel classification and later used for improving the segmentation. A large area of a town was fully labeled on the pixel-level into five classes: vegetation, ground, road/parking/railroad, building and water. The choices for the architecture parameters of a single-layered CNN were evaluated and used for classification. It was discovered that a context size of around 25 pixels, a filter size and a pooling dimension that resulted in under 600 output units and a low number of filters, namely 50, were able to achieve a stable and high classification accuracy, while still keeping a low training and testing simulation time. Using higher contextual areas of 35 and 45 resulted in slightly higher classification accuracies, but the result was more unstable and had a longer simulation time. Building on this discovery, multiple CNNs in parallel with varying context areas were used to achieve a stable and accurate classification result. A combination of four CNNs with varying contextual size that ran in parallel achieved the best classification accuracy of . Deep single CNNs were also tested, but did not increase the classification accuracy. The filters in the CNN were pre-trained with a fast unsupervised clustering algorithm, and the fully-connected layer and softmax classifier were fine-tuned with backpropagation. The classifications were smoothed out with averaging over each pre-generated segment from an image segmentation method. The segments were then merged using the information from the classifier in order to get a segmentation that better represents real-world objects.
Future work includes investigating the use of a CNN for pixel classification in an unsupervised fashion using unlabeled data. Another direction for future work is to develop a method that better deals with shadows. Shadows are artifacts that are inherent in orthographic images and difficult for a CNN to reason about. A top-down reasoning approach could be used to infer estimated locations for shadows and use this relationship information in order to change the classifications of segments with low prediction certainty.
The MATLAB code that was used for this work can be downloaded at [74].
Acknowledgments
This work has been supported by the Swedish Knowledge Foundation under the research profile on Semantic Robots, contract number 20140033.
Author Contributions
All authors conceived and designed the experiments; M.L. and A.K. and M.A. performed the experiments; M.L. analyzed the data; M.L. and A.K. and M.A. contributed reagents/materials/analysis tools; M.L. and A.K. and M.A. wrote the paper. All authors read and approved the submitted manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reed, B.; Brown, J.; Vanderzee, D.; Loveland, T.; Merchant, J.; Ohlen, D. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Running, S.; Nemani, R.; Heinsch, F.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Glenn, N.; Mundt, J.; Weber, K.; Prather, T.; Lass, L.; Pettingill, J. Hyperspectral data processing for repeat detection of small infestations of leafy spurge. Remote Sens. Environ. 2005, 95, 399–412. [Google Scholar] [CrossRef]
- Netanyahu, N.; Le Moigne, J.; Masek, J. Georegistration of Landsat data via robust matching of multiresolution features. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1586–1600. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Chanussot, J.; Moon, W.M. Advances in very-high-resolution remote sensing. IEEE Proc. 2013, 101, 566–569. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Delineation of landslide hazard areas on Penang Island, Malaysia, by using frequency ratio, logistic regression, and artificial neural network models. Environ. Earth Sci. 2010, 60, 1037–1054. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the ACM International Symposium on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279.
- Lai, K.; Bo, L.; Ren, X.; Fox, D. A large-scale hierarchical multi-view RGB-D object dataset. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1817–1824.
- Xia, G.S.; Yang, W.; Delon, J.; Gousseau, Y.; Sun, H.; Maître, H. Structural high-resolution satellite image indexing. In Proceedings of the ISPRS TC VII Symposium-100 Years ISPRS, Vienna, Austria, 5–7 July 2010; Volume 38, pp. 298–303.
- Vaduva, C.; Gavat, I.; Datcu, M. Latent Dirichlet Allocation for spatial analysis of satellite images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2770–2786. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Comparing SIFT descriptors and gabor texture features for classification of remote sensed imagery. In Proceedings of the International Conference on Image Processing (ICIP), Cairo, Egypt, 7–11 November 2008; pp. 1852–1855.
- Dos Santos, J.; Penatti, O.; Da Torres, R. Evaluating the potential of texture and color descriptors for remote sensing image retrieval and classification. In Proceedings of the International Conference on Computer Vision Theory and Applications, Angers, France, 17–21 May 2010; pp. 203–208.
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. IEEE Proc. 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Curran Associates: North Miami Beach, FL, USA, 2012; pp. 1097–1105. [Google Scholar]
- Socher, R.; Huval, B.; Bath, B.; Manning, C.D.; Ng, A.Y. Convolutional-recursive deep learning for 3D object classification. In Advances in Neural Information Processing Systems; Curran Associates: North Miami Beach, FL, USA, 2012; pp. 665–673. [Google Scholar]
- Quigley, M.; Batra, S.; Gould, S.; Klingbeil, E.; Le, Q.V.; Wellman, A.; Ng, A.Y. High-accuracy 3D sensing for mobile manipulation: improving object detection and door opening. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 2816–2822.
- Couprie, C.; Farabet, C.; LeCun, Y.; Najman, L. Indoor Semantic Segmentation using depth information. In Proceedings of the International Conference on Learning Representation, Scottsdale, Arizona, 2–4 May 2013.
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning hierarchical features for scene labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks; Available online: http://arxiv.org/abs/1508.00092 (accessed on 12 April 2016).
- Penatti, O.A.; Nogueira, K.; dos Santos, J.A. Do deep features generalize from everyday objects to remote sensing and aerial scenes domains? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015.
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Nguyen, T.; Han, J.; Park, D.C. Satellite image classification using convolutional learning. In Proceedings of the AIP Conference, Albuquerque, NM, USA, 7–10 October 2013; pp. 2237–2240.
- Hudjakov, R.; Tamre, M. Ortophoto analysis for UGV long-range autonomous navigation. Estonian J. Eng. 2011, 17, 17–27. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Chen, M.; Yang, Z. Road network extraction: A neural-dynamic framework based on deep learning and a finite state machine. Int. J. Remote Sens. 2015, 36, 3144–3169. [Google Scholar] [CrossRef]
- Chen, X.; Xiang, S.; Liu, C.L.; Pan, C.H. Vehicle detection in satellite images by hybrid deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1797–1801. [Google Scholar] [CrossRef]
- Ishii, T.; Nakamura, R.; Nakada, H.; Mochizuki, Y.; Ishikawa, H. Surface object recognition with CNN and SVM in Landsat 8 images. In Proceedings of the IEEE 2015 14th IAPR International Conference on Machine Vision Applications (MVA), Tokyo, Japan, 18–22 May 2015; pp. 341–344.
- Zhang, F.; Du, B.; Zhang, L. Scene classification via a gradient boosting random convolutional network framework. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1793–1802. [Google Scholar] [CrossRef]
- Li, X.; Shao, G. Object-based land-cover mapping with high resolution aerial photography at a county scale in midwestern USA. Remote Sens. 2014, 6, 11372–11390. [Google Scholar] [CrossRef]
- Lucieer, V. Object-oriented classification of sidescan sonar data for mapping benthic marine habitats. Int. J. Remote Sens. 2008, 29, 905–921. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Rogan, J.; Kellndorfer, J. Assessment of spectral, polarimetric, temporal, and spatial dimensions for urban and peri-urban land cover classification using Landsat and SAR data. Remote Sens. Environ. 2012, 117, 72–82. [Google Scholar] [CrossRef]
- Plaza, A.; Plaza, J.; Martin, G. Incorporation of spatial constraints into spectral mixture analysis of remotely sensed hyperspectral data. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, Grenoble, France, 1–4 September 2009; pp. 1–6.
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 499–515. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Midhun, M.; Nair, S.R.; Prabhakar, V.; Kumar, S.S. Deep model for classification of hyperspectral image using restricted boltzmann machine. In Proceedings of the 2014 International Conference on Interdisciplinary Advances in Applied Computing (ACM), Amritapuri, India, 10–11 October 2014; pp. 35:1–35:7.
- Chen, Y.; Zhao, X.; Jia, X. Spectral—Spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Zhang, Y. Classification of hyperspectral image based on deep belief networks. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5132–5136.
- Mnih, V.; Hinton, G.E. Learning to detect roads in high-resolution aerial images. In Computer Vision–ECCV 2010; Springer: Medford, MA, USA, 2010; pp. 210–223. [Google Scholar]
- Boggess, J.E. Identification of Roads in Satellite Imagery Using Artificial Neural Networks: A Contextual Approach; Mississippi State University: Starkville, MS, USA, 1993. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Dahl, G.; Yu, D.; Deng, L.; Acero, A. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 30–42. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 38th International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–30 May 2013.
- Längkvist, M.; Karlsson, L.; Loutfi, A. A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit. Lett. 2014, 42, 11–24. [Google Scholar] [CrossRef]
- Vricon, Homepage. Available online: http://www.vricon.com (accessed on 3 January 2016).
- Matikainen, L.; Karila, K. Segment-based land cover mapping of a suburban area—Comparison of high-resolution remotely sensed datasets using classification trees and test field points. Remote Sens. 2011, 3, 1777–1804. [Google Scholar] [CrossRef]
- Chi, M.; Feng, R.; Bruzzone, L. Classification of hyperspectral remote-sensing data with primal SVM for small-sized training dataset problem. Adv. Space Res. 2008, 41, 1793–1799. [Google Scholar] [CrossRef]
- Huang, M.J.; Shyue, S.W.; Lee, L.H.; Kao, C.C. A knowledge-based approach to urban feature classification using aerial imagery with Lidar data. Photogramm. Eng. Remote Sens. 2008, 74, 1473–1485. [Google Scholar] [CrossRef]
- Sanchez, C.; Gladstone, C.; Holland, D. Classification of urban features from Intergraph’s Z/I Imaging DMC high resolution images for integration into a change detection flowline within Ordnance Survey. In Proceedings of the 2007 Urban Remote Sensing Joint Event, Paris, France, 11–13 April 2007; pp. 1–8.
- Thomas, N.; Hendrix, C.; Congalton, R.G. A comparison of urban mapping methods using high-resolution digital imagery. Photogramm. Eng. Remote Sens. 2003, 69, 963–972. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Largman, Y.; Pham, P.; Ng, A.Y. Unsupervised feature learning for audio classification using convolutional deep belief networks. In Advances in Neural Information Processing Systems 22; Curran Associates: Vancouver, BC, Canada, 2009; pp. 1096–1104. [Google Scholar]
- Taylor, G.; Fergus, R.; LeCun, Y.; Bregler, C. Convolutional learning of spatio-temporal features. In Proceedings of the European Conference on Computer Vision (ECCV’10), Crete, Greece, 5–11 September 2010.
- Jarrett, K.; Kavukcuoglu, K.; Ranzato, M.; LeCun, Y. What is the best multi-stage architecture for object recognition? In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2146–2153.
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–25 June 2010; pp. 807–814.
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103.
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323.
- Hu, F.; Xia, G.S.; Wang, Z.; Zhang, L.; Sun, H. Unsupervised feature coding on local patch manifold for satellite image scene classification. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1273–1276.
- Coates, A.; Lee, H.; Ng, A.Y. An analysis of single-layer networks in unsupervised feature learning. Engineering 2011, 15, 215–223. [Google Scholar]
- Pinheiro, P.; Collobert, R. Recurrent convolutional neural networks for scene labeling. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 82–90.
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Scene parsing with multiscale feature learning, purity trees, and optimal covers. In Proceedings of the 29th International Conference on Machine Learning (ICML), Edinburgh, UK, 26 June–1 July 2012; Volume 1, pp. 575–582.
- Mylonas, S.K.; Stavrakoudis, D.G.; Theocharis, J.B.; Mastorocostas, P.A. A region-based genesis segmentation algorithm for the classification of remotely sensed images. Remote Sens. 2015, 7, 2474–2508. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases With Noise; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Chang, C.I.; Du, Q.; Sun, T.L.; Althouse, M.L. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Serpico, S.B.; Bruzzone, L. A new search algorithm for feature selection in hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1360–1367. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Hasani, H.; Schenk, T. Simultaneous feature selection and SVM parameter determination in classification of hyperspectral imagery using Ant Colony Optimization. Can. J. Remote Sens. 2012, 38, 139–156. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Gamba, P.; Houshmand, B. Joint analysis of SAR, LiDAR and aerial imagery for simultaneous extraction of land cover, DTM and 3D shape of buildings. Int. J. Remote Sens. 2002, 23, 4439–4450. [Google Scholar] [CrossRef]
- Martin Längkvist. Academic Website. Available online: http://aass.oru.se/mlt/cnncode.zip (accessed on 12 April 2016).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).