Registration of Long-Strip Terrestrial Laser Scanning Point Clouds Using RANSAC and Closed Constraint Adjustment
Abstract
:1. Introduction
2. Literature Review
3. Methodology
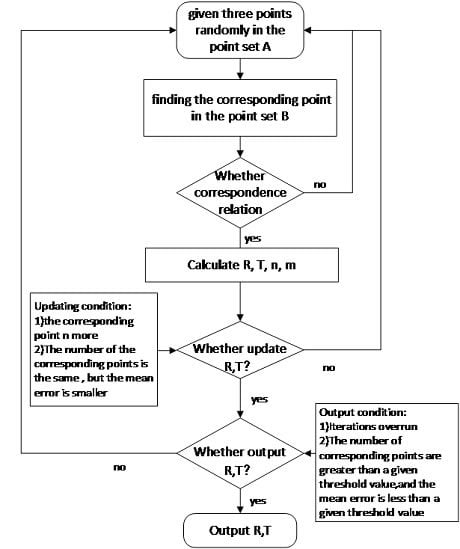
3.1. RANSAC Algorithm
3.2. RANSAC-Based Registration of TLS Data
- (1)
- Given two point sets and , randomly select three points and similarly select three points in the point set B. First, calculate the mode of the vector and the vector , with the constraints of .
- (2)
- Find the correspondence relations from the point set vector in the same way. If the correspondence in the three groups is exactly three points in the point set , the relationship of the point set and point set is:.where R and T the corresponding rotation matrix and translation vector.
- (3)
- Calculate R, T, n, and m according to Equations (1) and (2). The initial value of the rotation and translation between the two scanning positions is obtained through these equations, and the resulting the residual vector of the points is calculated using through Equation (3). In Equation (3), and are the conjugate coordinates in the scanning positions and , respectively. In addition, the mean error of the registration for the two scanning positions is obtained from Equation (4).
- (4)
- Iterations follow in order to refine the solution as needed. The above steps are repeated, and the matrices R and T are updated if one of the following two conditions is met in the iteration:
- (i)
- The number of corresponding points in the point set : or
- (ii)
- The number of the corresponding points in the point set :, and residuals .
- (5)
- A convergence is achieved and R and T are estimated in a typical adjustment fashion when the number of the conjugate points is > the threshold and the mean error of registration is < the threshold.
3.3. Closed Constraint Adjustment (CCA) Based Registration for Point Cloud Data
3.3.1. Sources of Error Analysis
- (1)
- Range accuracy of a three-dimensional scanner is limited;
- (2)
- Scanning in different angles generates errors due to different incident angles;
- (3)
- Extraction accuracy for the center of the target is affected, as the target has strong reflection and will be "floated" from the background objects; and
- (4)
- External environmental factors, including atmospheric conditions and scattered light, might affect the working status of the scanner and the reflection of the target.
3.3.2. Propagation of Registration Error
3.3.3. The CCA by Redundant Observation Conditions
4. Experimental Results and Discussion
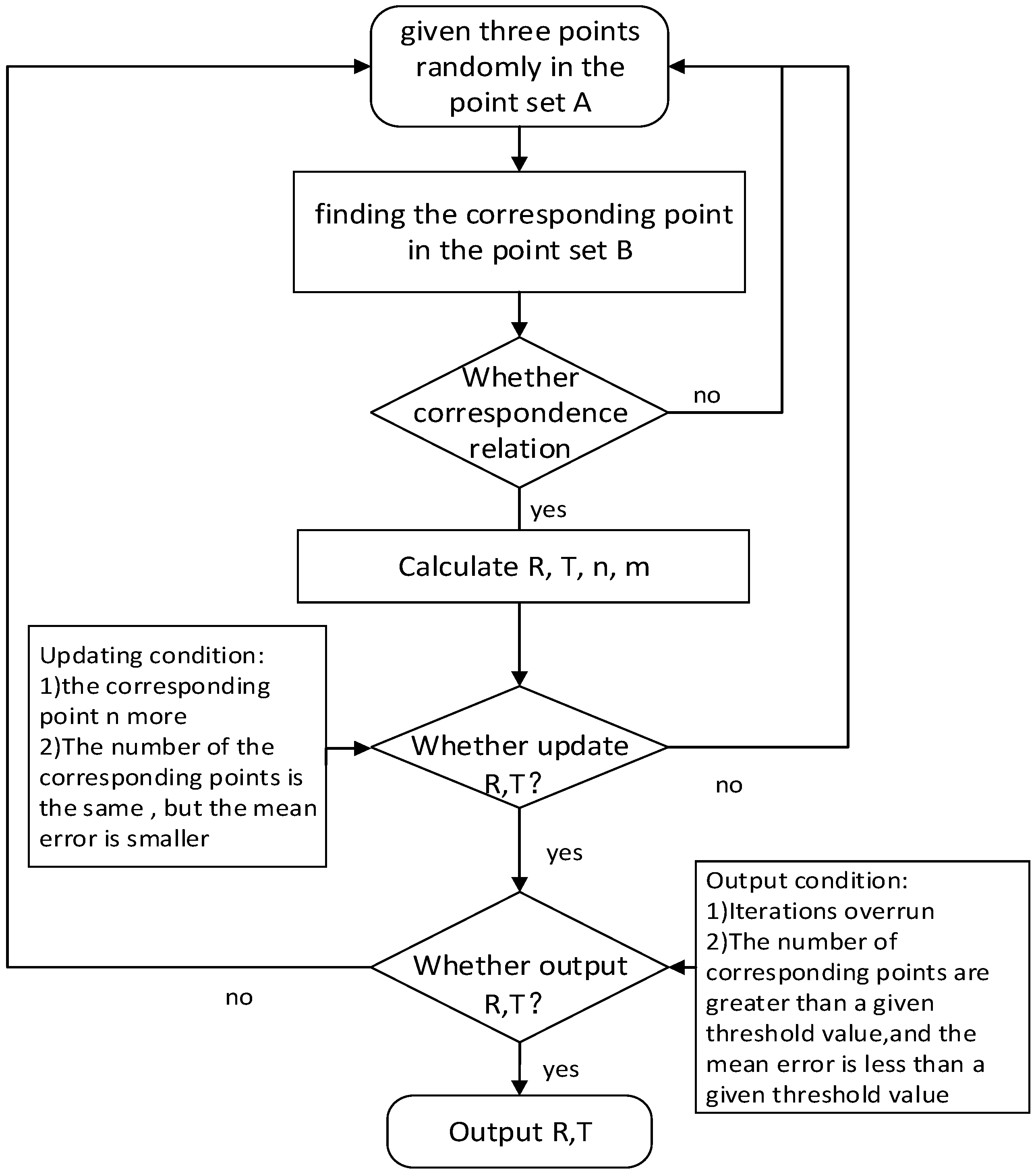
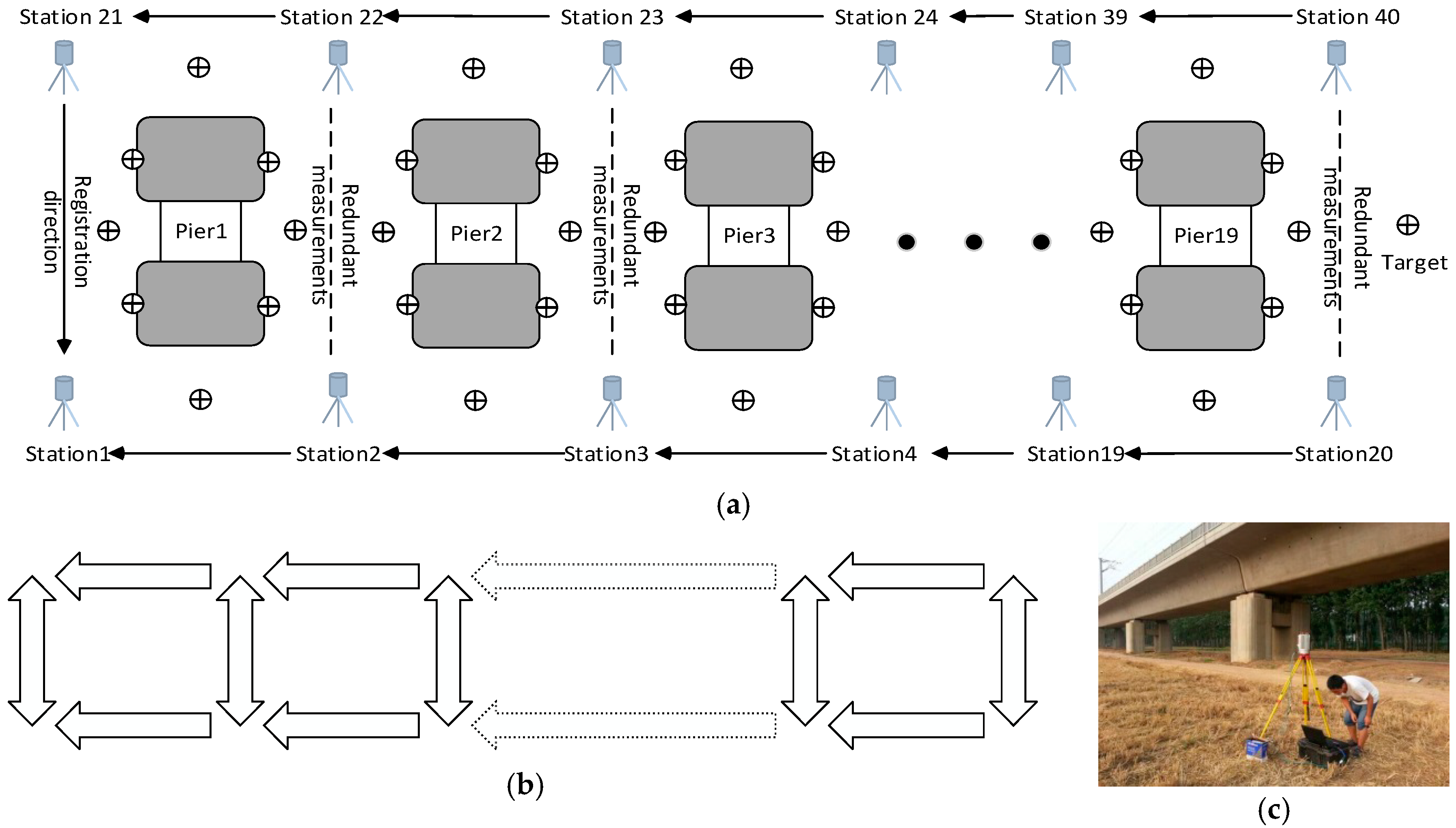
4.1. Experimental Scene and Device Description
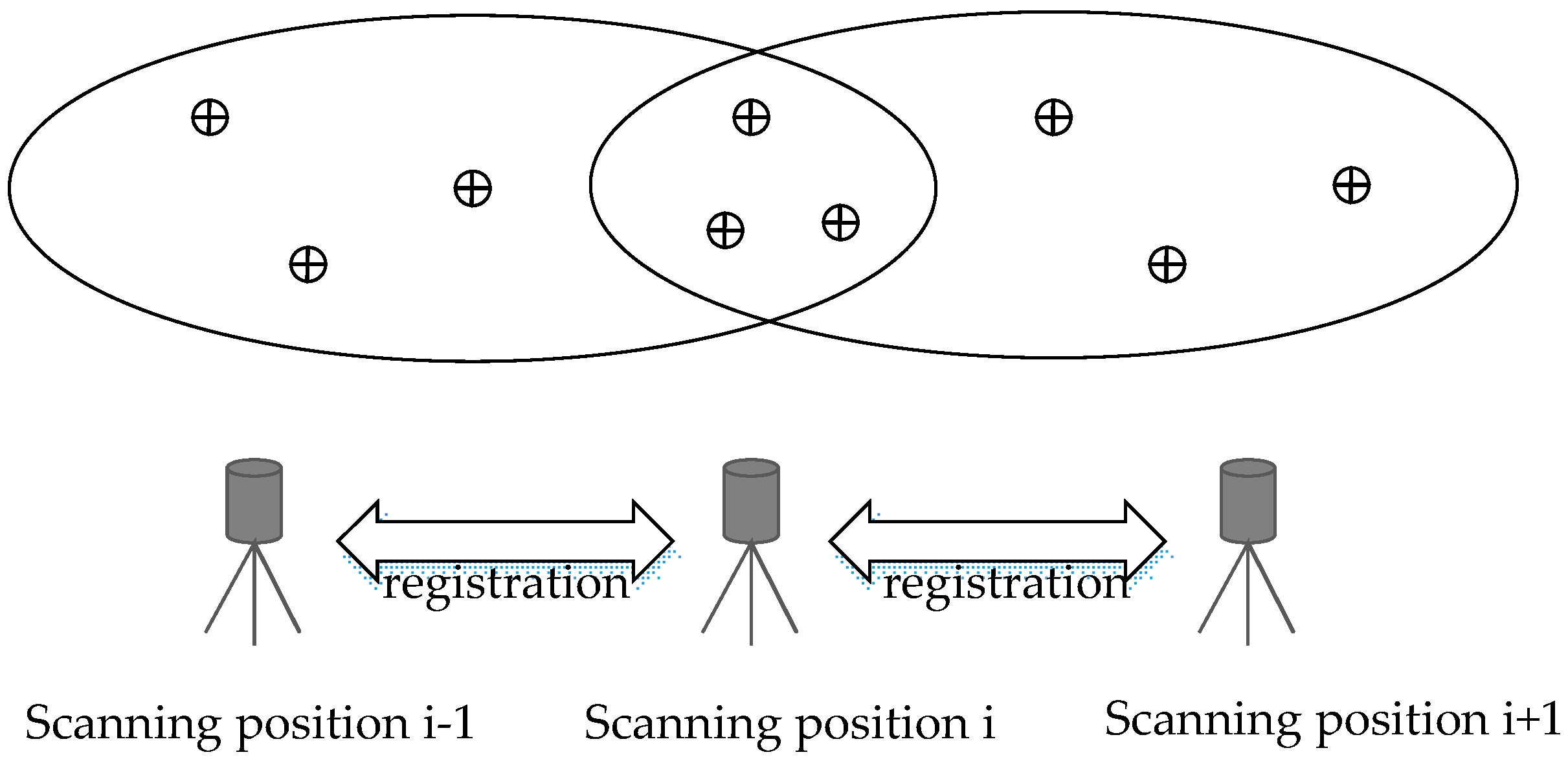
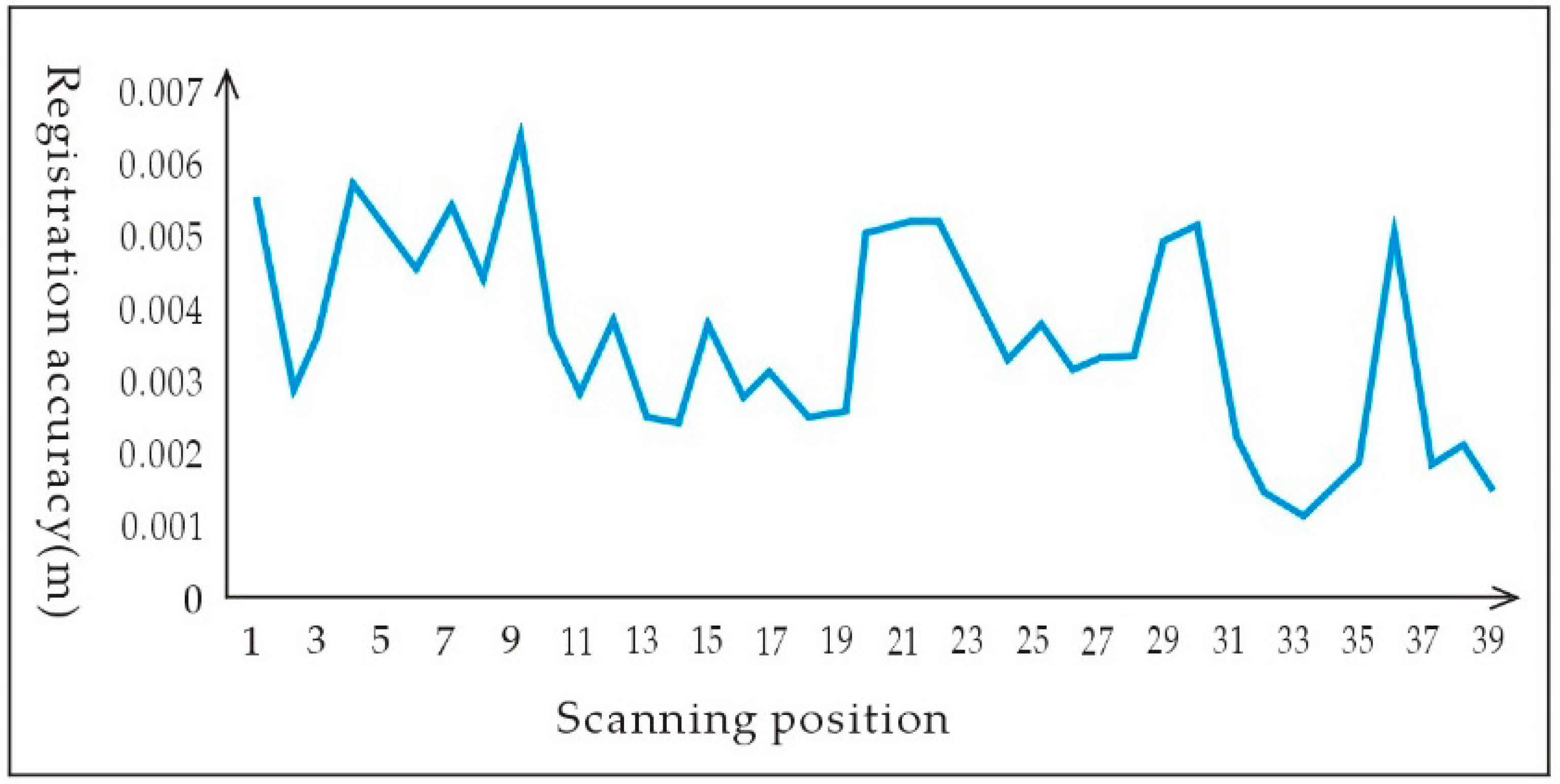
4.2. Registration Test between the Adjacent Scanning Positions
4.3. Registration Experiment for all Scanning Positions
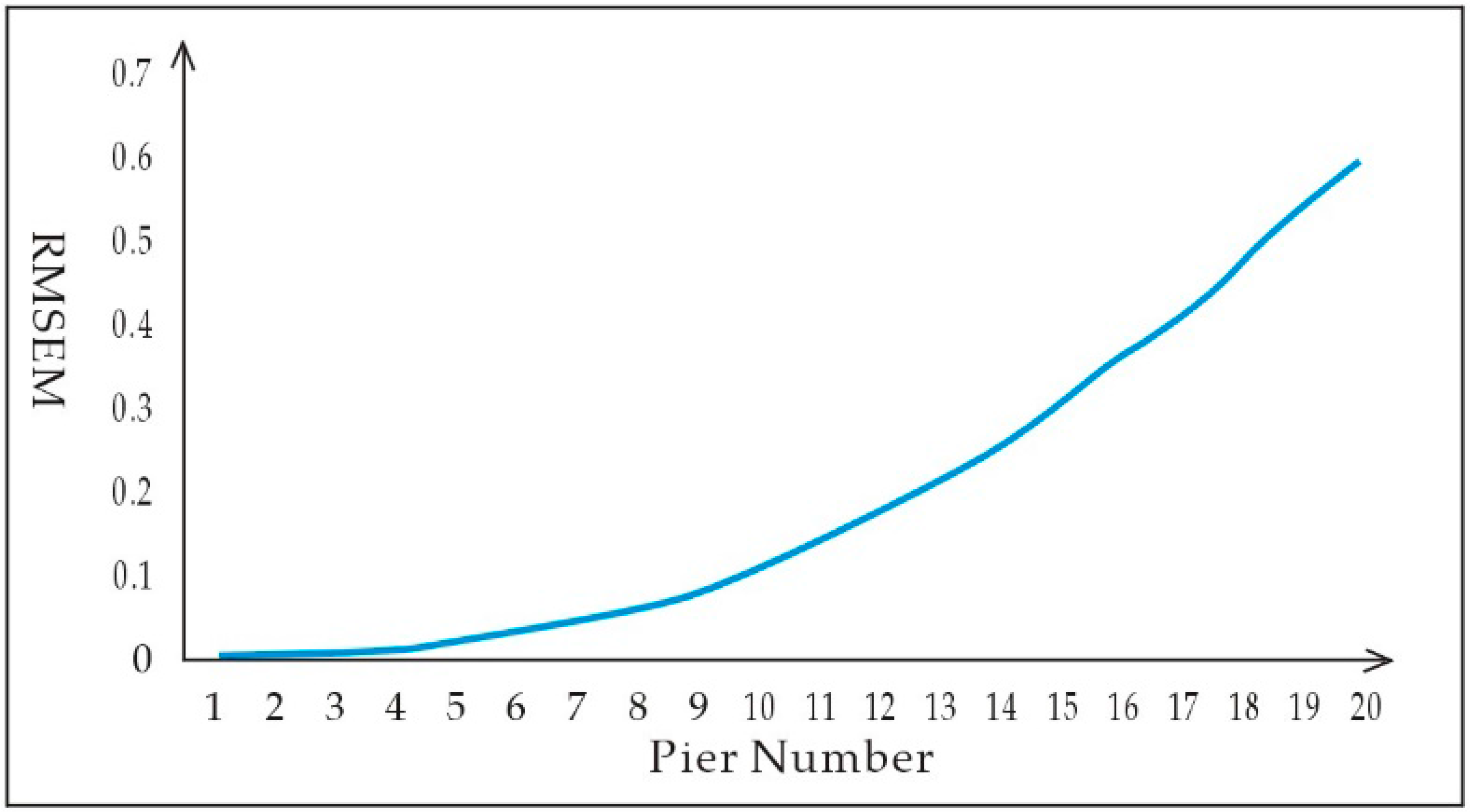
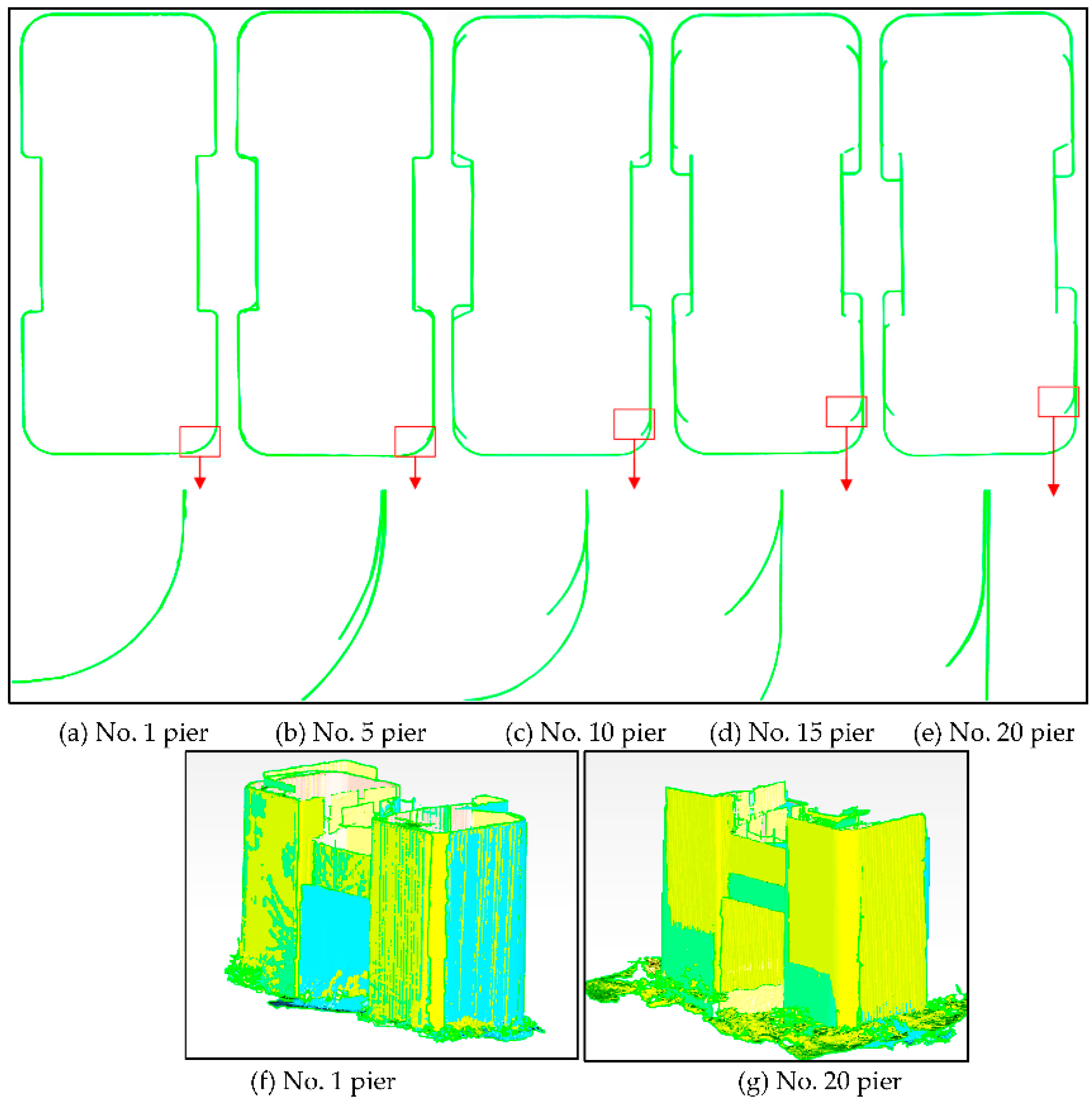
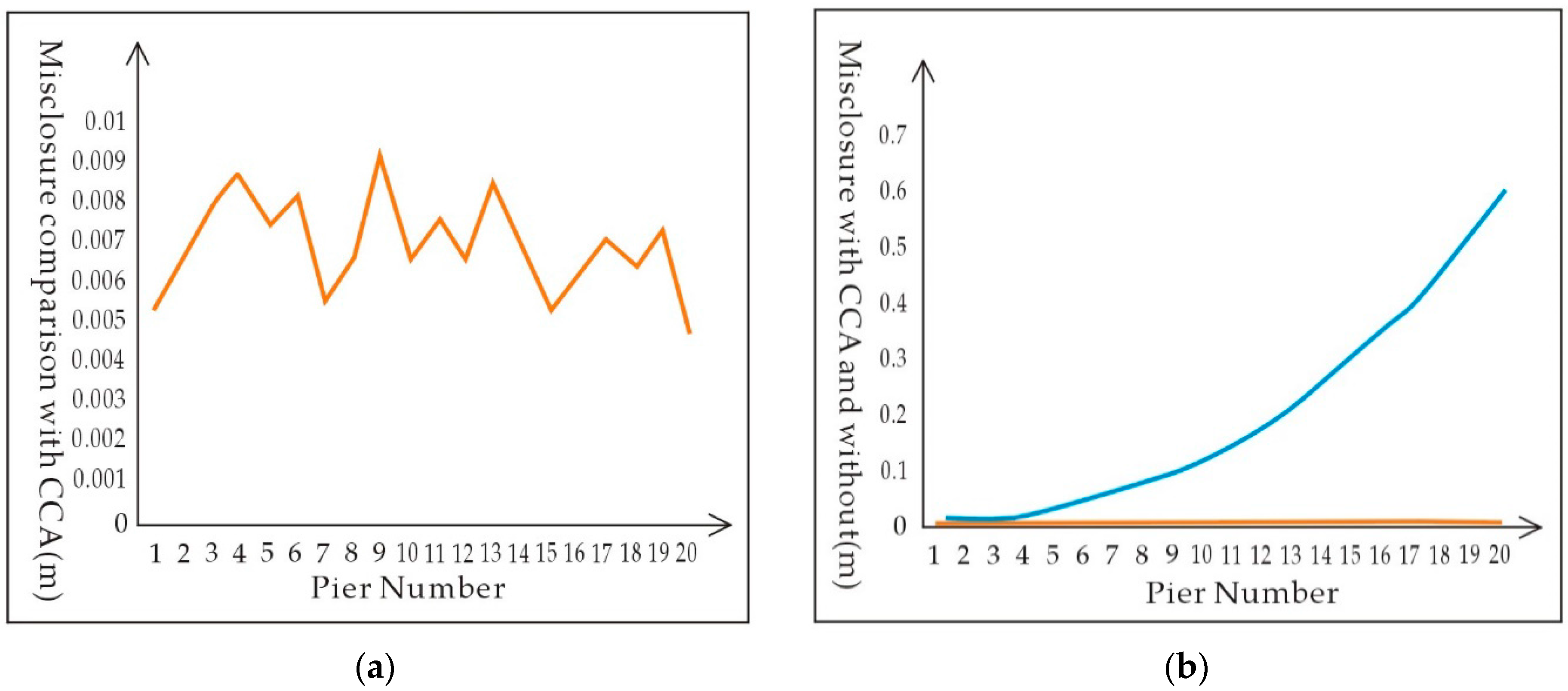
4.3.1. Registration Experiment Using Adjustment Processing
4.3.2. The CCA Experiment
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krzyzanowski, M.; Apte, J.S.; Bonjour, S.P.; Brauer, M.; Cohen, A.J.; Prüss-Ustun, A.M. Air pollution in the mega-cities. Curr. Environ. Health Rep. 2014, 1, 185–191. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, M. Status and development of terrestrial laser scanner. Bull. Surv. Mapp. 2007, 1, 47–50. [Google Scholar]
- Gikas, V. 3D Terrestrial laser scanning for geometry documentation and construction management of highway tunnels during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, N.; Wu, H.; Meng, X. Detection of high-speed railway subsidence and geometry irregularity using terrestrial laser scanning. J. Surv. Eng. 2014, 140, 3. [Google Scholar] [CrossRef]
- Vezocnik, R.; Ambrozic, T.; Sterle, O.; Bilban, G.; Pfeifer, N.; Stopar, B. Use of Terrestrial laser scanning technology for long term high precision deformation monitoring. Sensors 2009, 9, 9873–9895. [Google Scholar]
- Wang, C.; Stefanidis, A.; Croitoru, A.; Agouris, P. Map registration of image sequences using linear features. Photogramm. Eng. Remot Sens. 2008, 74, 25–38. [Google Scholar] [CrossRef]
- Huising, E.J.; Pereira, L.M.G. Errors and accuracy estimates of laser data acquired by various laser scanning systems for topographic applications. ISPRS J. Photogramm. Remote Sens. 1998, 53, 245–261. [Google Scholar] [CrossRef]
- Zheng, D.; Shen, Y.; Liu, C. 3D laser scanner and its effect factor analysis of surveying error. Eng. Surv. Mapp. 2005, 14, 32–34. [Google Scholar]
- Fisher, M.; Bolles, R. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Besl, P.J.; Makay, N.D. A method for registration of 3-d shapes. IEEE TPAMI 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Habib, A.; Ghanma, M.; Morgan, M. Photogrammetric and LiDAR data registration using linear features. Photogramm. Eng. Remote Sens. 2005, 71, 699–707. [Google Scholar]
- Al-Durgham, M.; Detcheve, I.; Habib, A. Analysis of two triangle-based multi-surface registration algorithms of irregular point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 61–66. [Google Scholar] [CrossRef]
- Sequeira, V.; Ng, K.; Wolfart, E.; Goncalves, J.G.M.; Hogg, D. Automated reconstruction of 3D models from real environments. ISPRS J. Photogramm. Remote Sens. 2012, 54, 1–22. [Google Scholar] [CrossRef]
- Bae, K.; Lichti, D.D. A method for automated registration of unorganised point clouds. ISPRS J. Photogramm. Remote Sens. 2008, 63, 36–54. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. Image Vis. Comput. 1992, 14, 145–155. [Google Scholar]
- Habib, A.F.; Detchev, I.; Bang, K.I. Comparative analysis of two approaches for multiple-surface registration of irregular point clouds. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 61–66. [Google Scholar]
- Zheng, D.; Yue, D. Geometric feature constraint based algorithm for building scanning point cloud registration. J. Surv. Mapp. 2008, 37, 464–468. [Google Scholar]
- Ma, H.; Yao, C. Registration of LiDAR point clouds and high resolution images based on linear features. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 136–139. [Google Scholar]
- Rabbani, T.; Dijkman, S.; Heuvel, F.; Vosselman, G. An integrated approach for modelling and global registration of point clouds. ISPRS J. Photogramm. Remote Sens. 2007, 61, 355–370. [Google Scholar] [CrossRef]
- Eo, Y.D.; Pyeon, M.W.; Kim, S.W.; Kim, J.R.; Han, D.Y. Coregistration of terrestrial LiDAR points by adaptive scale-invariant feature transformation with constrained geometry. Autom. Constr. 2012, 25, 49–58. [Google Scholar] [CrossRef]
- Sibel, C. Planar and Linear Feature-Based Registration of Terrestrial Laser Scans with Minimum Overlap using Photogrammetric Data. Master’s Thesis, Department of Geomatics Engineering, Calgary University, Alberta, China, 2012. [Google Scholar]
- Brenner, C.; Dold, C.; Ripperda, N. Coarse orientation of terrestrial laser scans in urban environments. ISPRS J. Photogramm. Remote Sens. 2008, 63, 4–18. [Google Scholar] [CrossRef]
- Jaw, J.J.; Chuang, T.Y. Registration of ground‐based LiDAR point clouds by means of 3D line features. J. Chin. Instit. Eng. 2008, 31, 1031–1045. [Google Scholar]
- Huang, T.; Zhang, D.; Li, G.; Jiang, M. Registration method for terrestrial LiDAR point clouds using geometric features. Opt. Eng. 2012, 51, 21111–21114. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, G. Research on point cloud registration error propagation. J. Tongji Univ. 2009, 37, 1668–1672. [Google Scholar]
- Xu, Y.; Gao, J. Research on point cloud registration error of terrestrial laser scanning. J. Geod. Geodyn. 2011, 32, 129–132. [Google Scholar]
- Zheng, M.; Zhang, Y.; Zhu, J.; Xiong, X. Self-Calibration adjustment of CBERS-02B long-strip imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3847–3854. [Google Scholar] [CrossRef]
- Ji, Z.; Song, M.; Guan, H.; Yu, Y. Accurate and robust registration of high-speed railway viaduct point clouds using closing conditions and external geometric constraints. ISPRS J. Photogramm. Remote Sens. 2015, 106, 55–67. [Google Scholar] [CrossRef]
- Anders, H.; Johan, N. Optimal RANSAC—Towards a repeatable algorithm for finding the optimal set. J. Wscg 2013, 21, 21–30. [Google Scholar]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- Isack, H.; Boykov, Y. Energy-Based geometric multi-model fitting. Int. J. Comput. Vis. 2012, 97, 123–147. [Google Scholar] [CrossRef]
- Tao, B.; Qiu, W.; Yao, Y. The Base of Errors Theory and Surveying Adjustment; Wuhan University Press: Wuhan, China, 2009; pp. 106–111. [Google Scholar]
- RIEGL VZ-400 Data Sheet. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/10_DataSheet_VZ-400_2014-09-19.pdf (accessed on 19 September 2014).

| Initial Value | Need External Control | Using Point Cloud | Using Target Point | Precision &Stability Depend on | |
|---|---|---|---|---|---|
| ICP | Yes | No | Yes | No | Feature |
| Geometric Primitive | Yes | No | Yes | No | Feature |
| RANSAC & CCA | No | No | No | Yes | Target point |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Yu, M.; Song, M.; Stefanidis, A.; Ji, Z.; Yang, C. Registration of Long-Strip Terrestrial Laser Scanning Point Clouds Using RANSAC and Closed Constraint Adjustment. Remote Sens. 2016, 8, 278. https://doi.org/10.3390/rs8040278
Zheng L, Yu M, Song M, Stefanidis A, Ji Z, Yang C. Registration of Long-Strip Terrestrial Laser Scanning Point Clouds Using RANSAC and Closed Constraint Adjustment. Remote Sensing. 2016; 8(4):278. https://doi.org/10.3390/rs8040278
Chicago/Turabian StyleZheng, Li, Manzhu Yu, Mengxiao Song, Anthony Stefanidis, Zheng Ji, and Chaowei Yang. 2016. "Registration of Long-Strip Terrestrial Laser Scanning Point Clouds Using RANSAC and Closed Constraint Adjustment" Remote Sensing 8, no. 4: 278. https://doi.org/10.3390/rs8040278
APA StyleZheng, L., Yu, M., Song, M., Stefanidis, A., Ji, Z., & Yang, C. (2016). Registration of Long-Strip Terrestrial Laser Scanning Point Clouds Using RANSAC and Closed Constraint Adjustment. Remote Sensing, 8(4), 278. https://doi.org/10.3390/rs8040278