Stereoscopic Estimation of Volcanic Ash Cloud-Top Height from Two Geostationary Satellites
Abstract
:1. Introduction
2. Datasets
2.1. MVIRI
2.2. SEVIRI
3. The Parallax Method
3.1. Projection of MVIRI Data onto the SEVIRI Grid
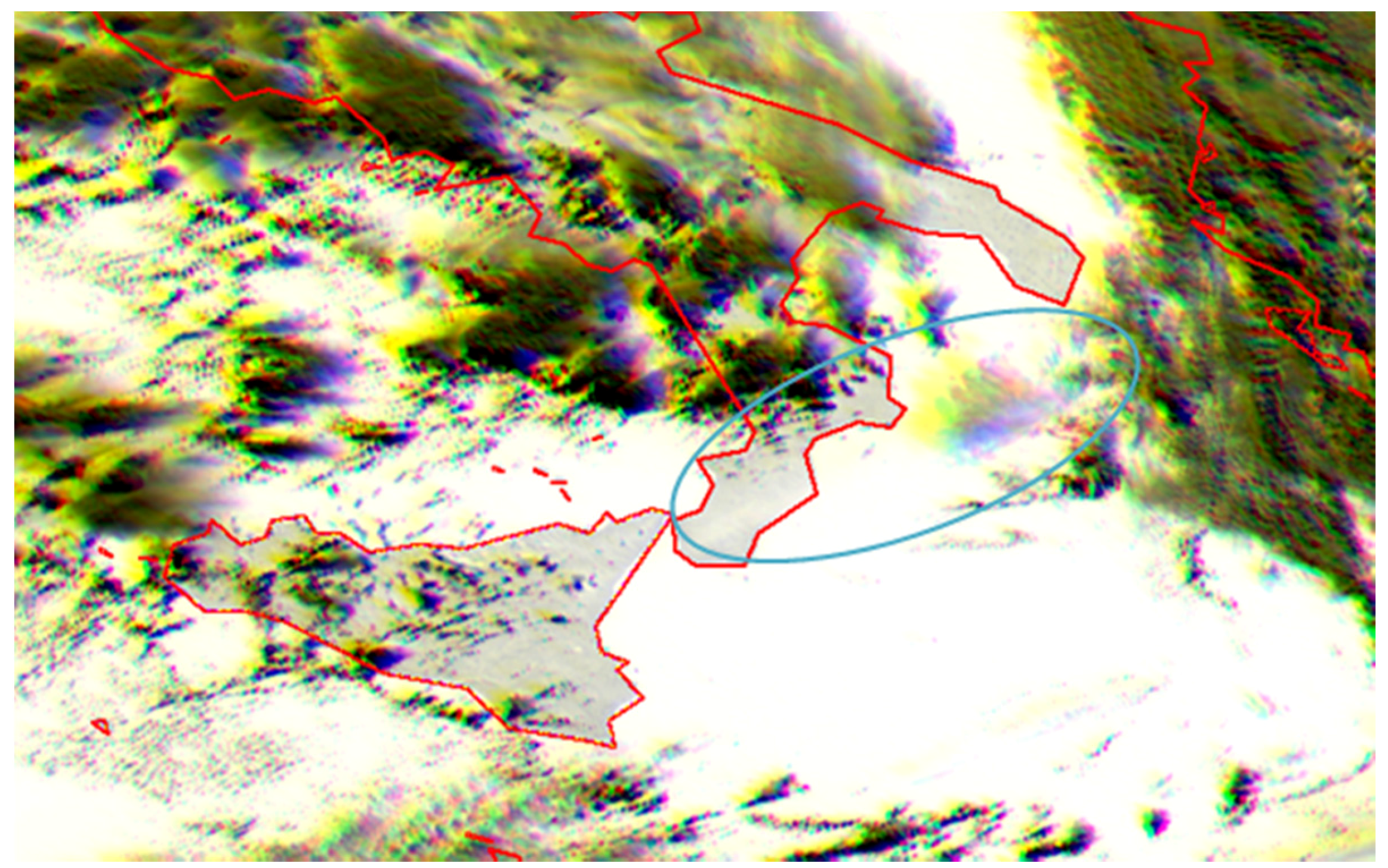
3.2. Automatic Image Matching
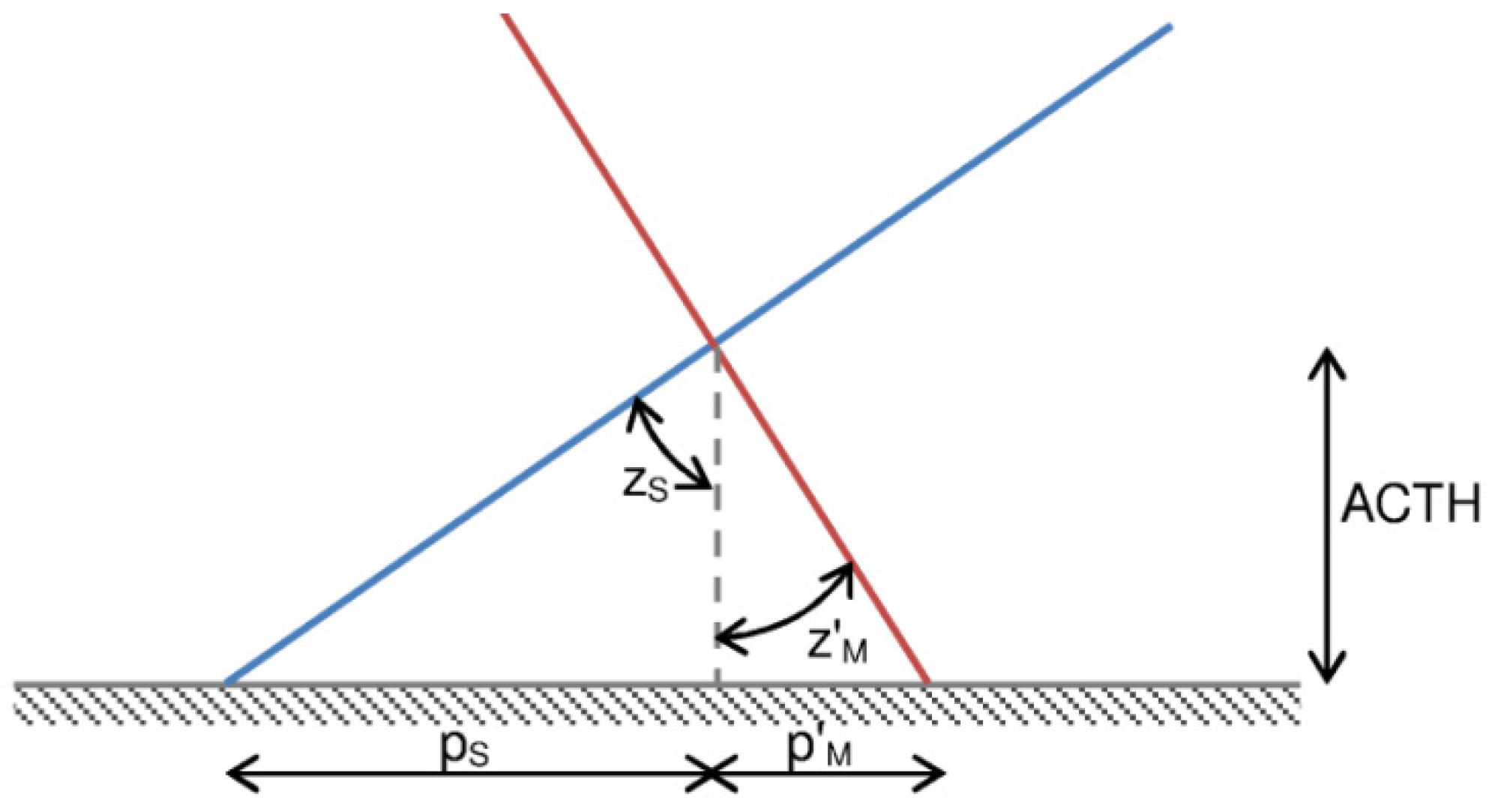
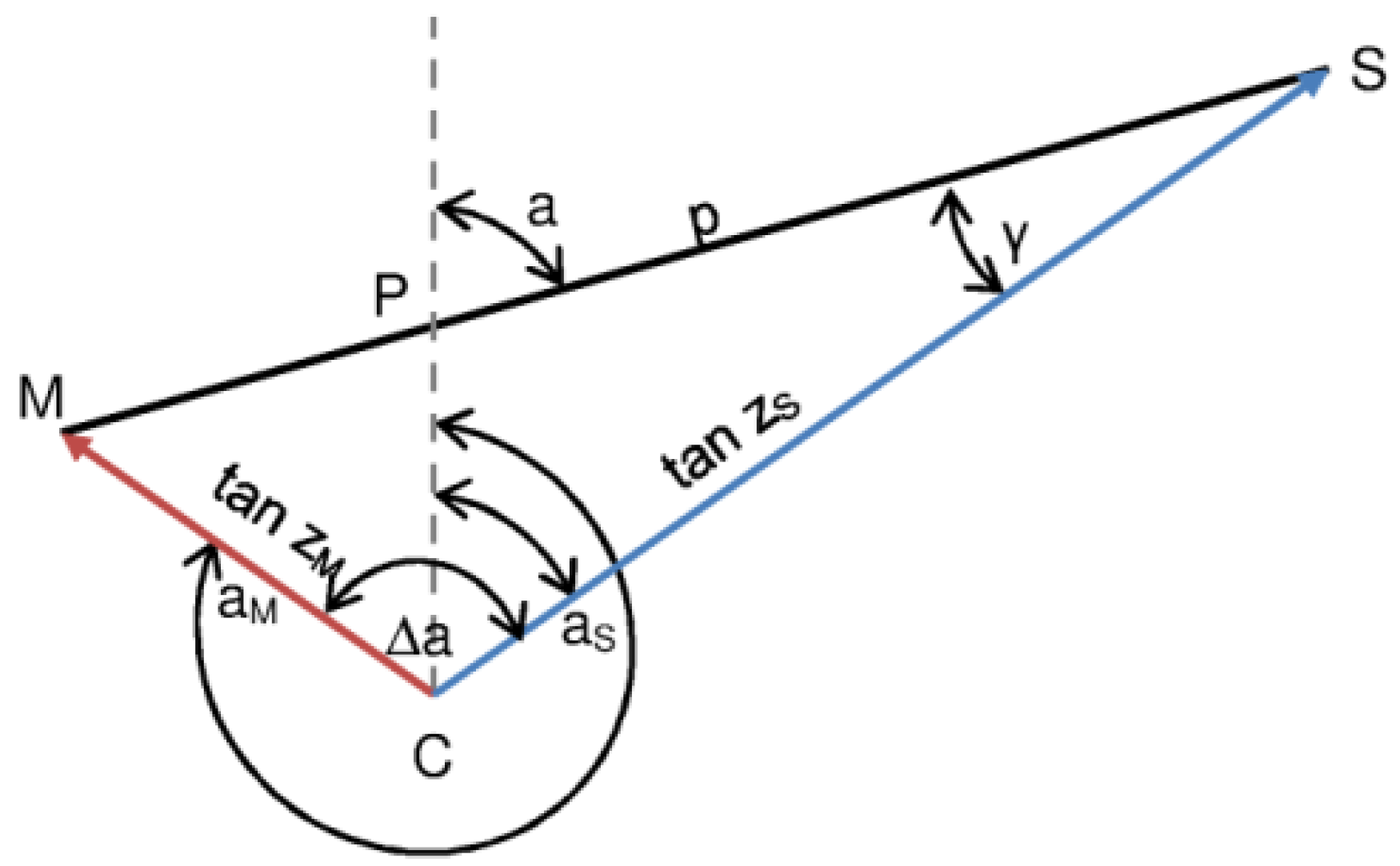
3.3. ACTH Estimation from the Intersection of Lines of Sight
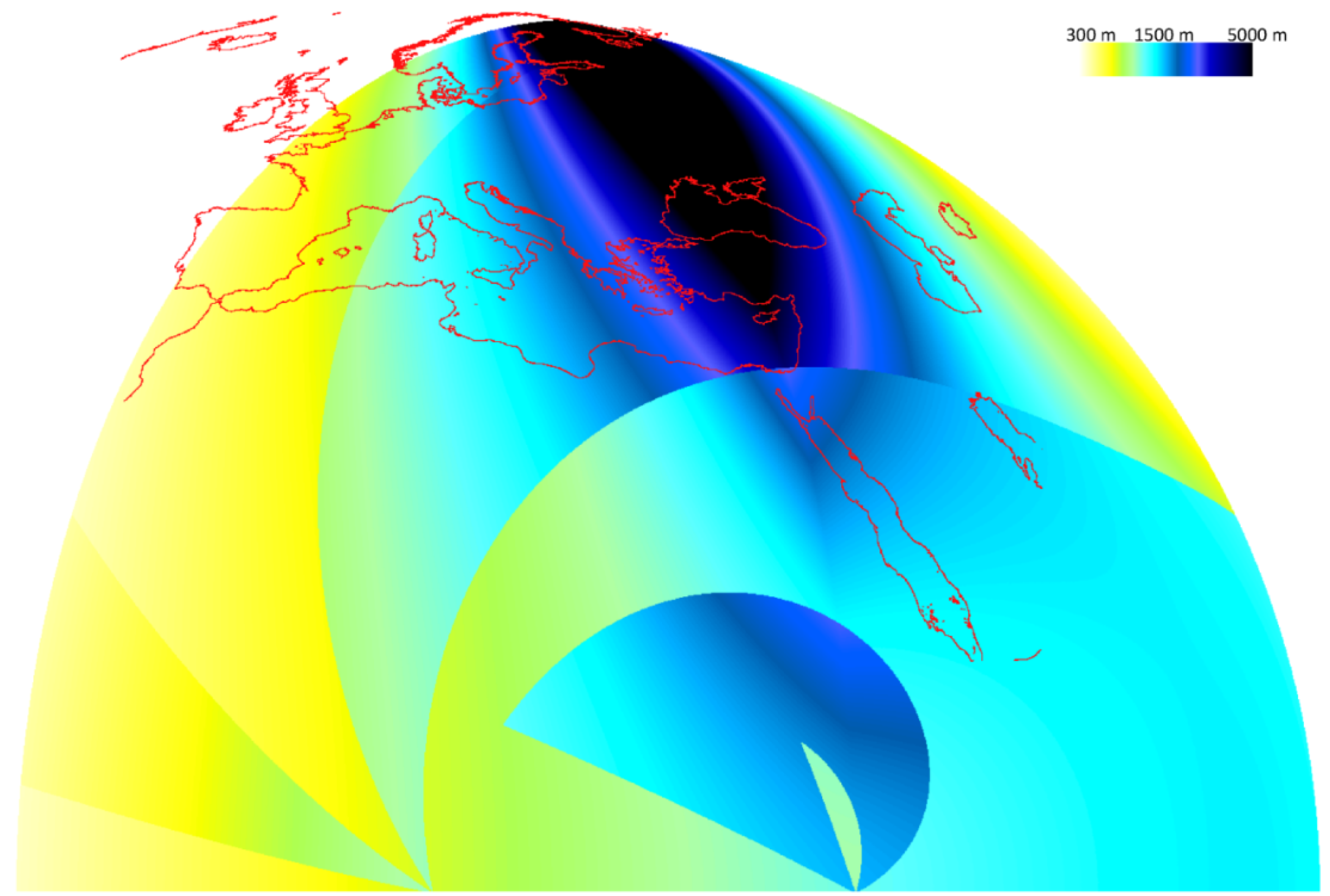
3.4. ACTH Estimation Error
4. Results
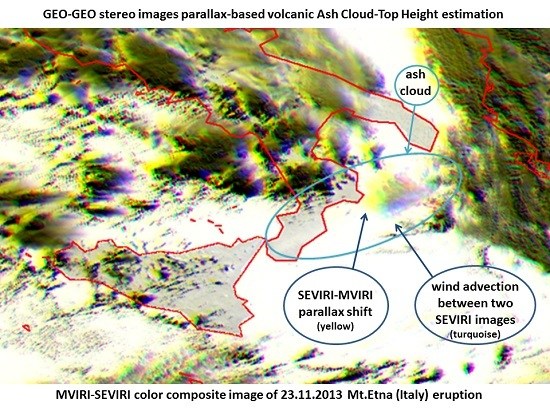
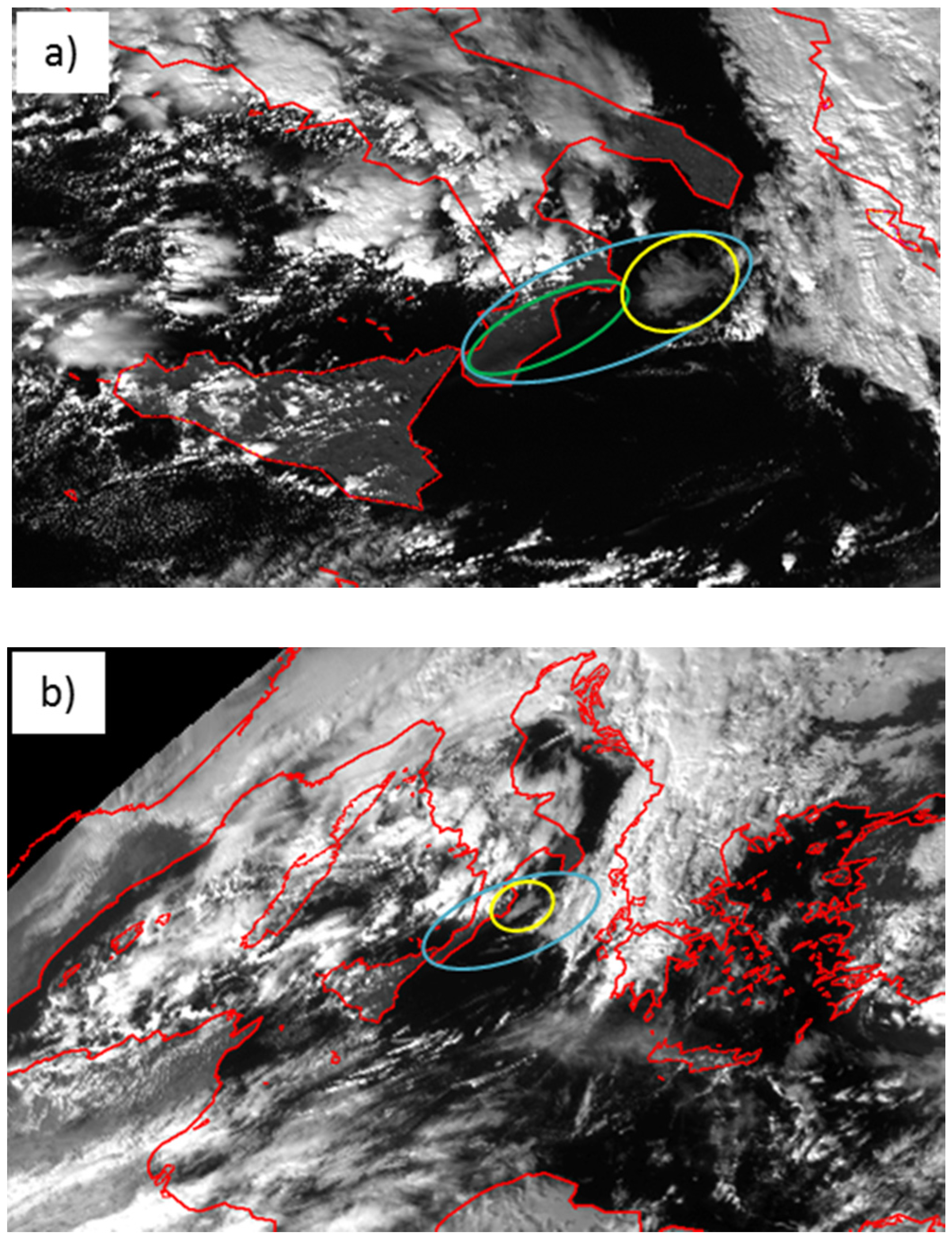
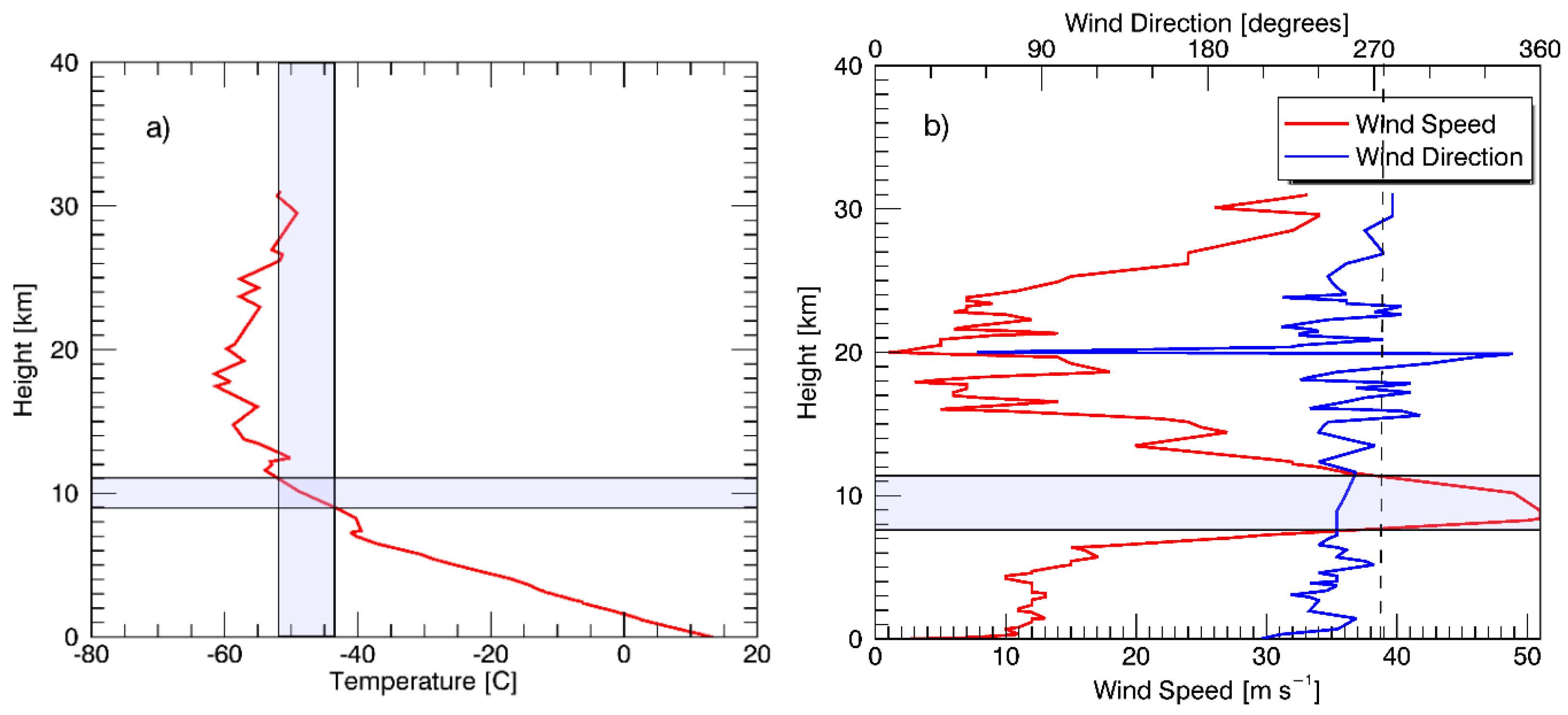
4.1. Etna 23.11.2013 Case Study
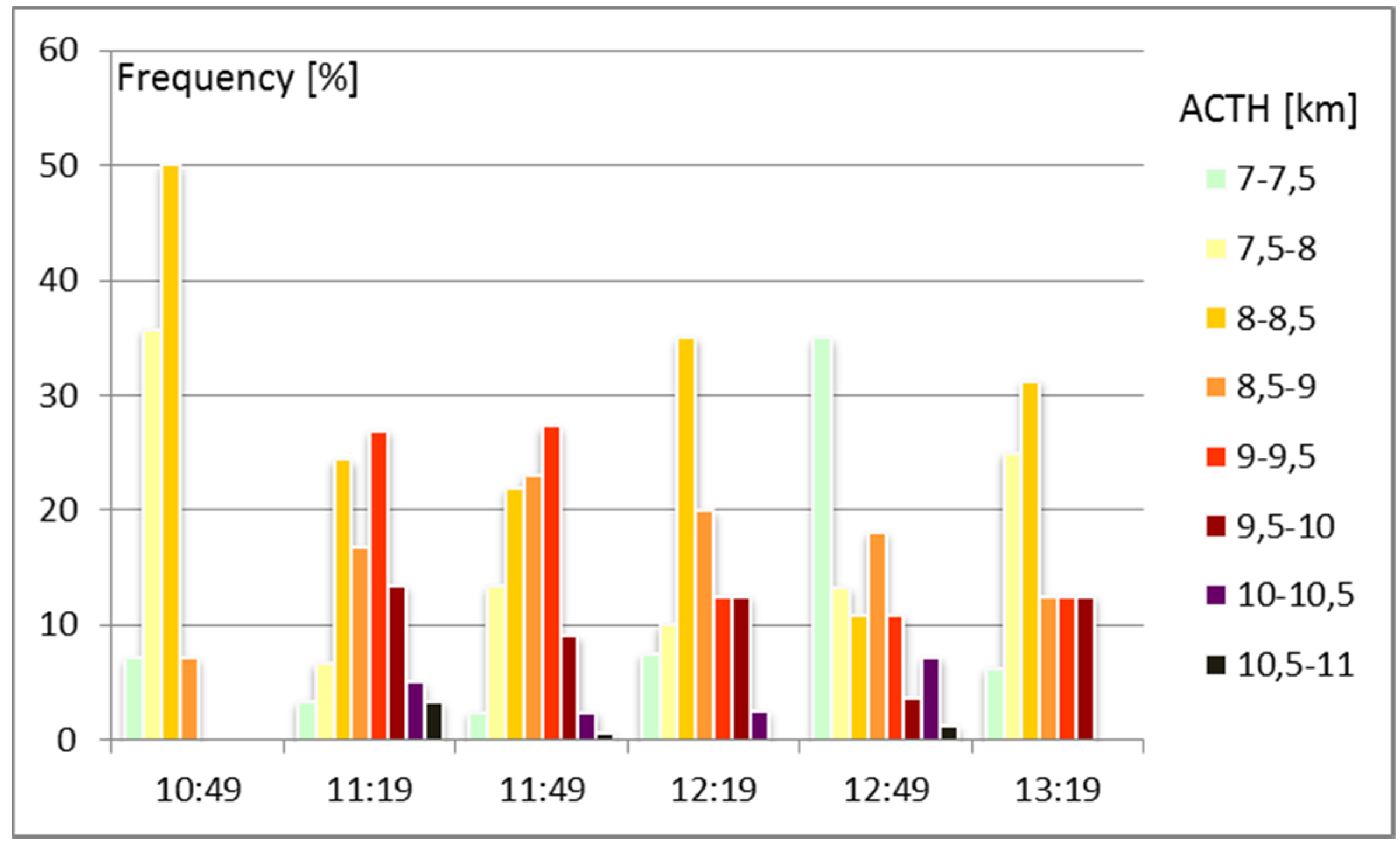
4.2. ACTH Results
4.3. Validation
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heinold, B.; Tegen, I.; Wolke, R.; Ansmann, A.; Mattis, I.; Minikin, A.; Schumann, U.; Weinzierl, B. Simulations of the 2010 Eyjafjallajökull volcanic ash dispersal over Europe using COSMO–MUSCAT. Atmos. Environ. 2012, 48, 195–204. [Google Scholar] [CrossRef]
- Wen, S.; Rose, W.I. Retrieval of sizes and total masses of particles in volcanic clouds using AVHRR bands 4 and 5. J. Geophys. Res. Atmos. 1994, 99, 5421–5431. [Google Scholar] [CrossRef]
- Prata, A.J.; Grant, I.F. Retrieval of microphysical and morphological properties of volcanic ash plumes from satellite data: Application to Mt Ruapehu, New Zealand. Q. J. Royal Meteorol. Soc. 2001, 127, 2153–2179. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Prata, A.J. Retrieval of SO2 from thermal infrared satellite measurements: Correction procedures for the effects of volcanic ash. Atmos. Meas. Tech. 2009, 2, 177–191. [Google Scholar] [CrossRef]
- Mastin, L.G.; Guffanti, M.; Servranckx, R.; Webley, P.; Barsotti, S.; Dean, K.; Durant, A.; Ewert, J.W.; Neri, A.; Rose, W.I.; et al. A multidisciplinary effort to assign realistic source parameters to models of volcanic ash-cloud transport and dispersion during eruptions. J. Volcanol. Geotherm. Res. 2009, 186, 10–21. [Google Scholar] [CrossRef]
- Stohl, A.; Prata, A.J.; Eckhardt, S.; Clarisse, L.; Durant, A.; Henne, S.; Kristiansen, N.I.; Minikin, A.; Schumann, U.; Seibert, P.; et al. Determination of time- and height-resolved volcanic ash emissions and their use for quantitative ash dispersion modeling: The 2010 Eyjafjallajökull eruption. Atmos. Chem. Phys. 2011, 11, 4333–4351. [Google Scholar] [CrossRef]
- Rose, W.I.; Kostinski, A.B.; Kelley, L. Real-time C-band radar observations of 1992 eruption clouds from Crater Peak, Mount Spurr volcano, Alaska. US Geol. Surv. Bull. 1995, 2139, 19–26. [Google Scholar]
- Lacasse, C.; Karlsdóttir, S.; Larsen, G.; Soosalu, H.; Rose, W.I.; Ernst, G.G.J. Weather radar observations of the Hekla 2000 eruption cloud, Iceland. Bull. Volcanol. 2003, 66, 457–473. [Google Scholar] [CrossRef]
- Marzano, F.S.; Lamantea, M.; Montopoli, M.; Di Fabio, S.; Picciotti, E. The Eyjafjöll explosive volcanic eruption from a microwave weather radar perspective. Atmos. Chem. Phys. 2011, 11, 9503–9518. [Google Scholar] [CrossRef]
- Scollo, S.; Prestifilippo, M.; Pecora, E.; Corradini, S.; Merucci, L.; Spata, G.; Coltelli, M. Eruption column height estimation of the 2011–2013 Etna lava fountains. Ann. Geophys. 2014, 57, S0214. [Google Scholar]
- Scollo, S.; Boselli, A.; Coltelli, M.; Leto, G.; Pisani, G.; Spinelli, N.; Wang, X. Monitoring Etna volcanic plumes using a scanning LiDAR. Bull. Volcanol. 2012, 74, 2383–2395. [Google Scholar] [CrossRef]
- Wang, X.; Boselli, A.; D’Avino, L.; Pisani, G.; Spinelli, N.; Amodeo, A.; Chaikovsky, A.; Wiegner, M.; Nickovic, S.; Papayannis, A.; et al. Volcanic dust characterization by EARLINET during Etna’s eruptions in 2001–2002. Atmos. Environ. 2008, 42, 893–905. [Google Scholar] [CrossRef]
- Emeis, S.; Forkel, R.; Junkermann, W.; Schäfer, K.; Flentje, H.; Gilge, S.; Fricke, W.; Wiegner, M.; Freudenthaler, V.; Groβ, S.; et al. Measurement and simulation of the 16/17 April 2010 Eyjafjallajökull volcanic ash layer dispersion in the northern Alpine region. Atmos. Chem. Phys. 2011, 11, 2689–2701. [Google Scholar] [CrossRef]
- Gasteiger, J.; Groß, S.; Freudenthaler, V.; Wiegner, M. Volcanic ash from Iceland over Munich: Mass concentration retrieved from ground-based remote sensing measurements. Atmos. Chem. Phys. 2011, 11, 2209–2223. [Google Scholar] [CrossRef]
- Hervo, M.; Quennehen, B.; Kristiansen, N.I.; Boulon, J.; Stohl, A.; Fréville, P.; Pichon, J.-M.; Picard, D.; Labazuy, P.; Gouhier, M.; et al. Physical and optical properties of 2010 Eyjafjallajökull volcanic eruption aerosol: Ground-based, Lidar and airborne measurements in France. Atmos. Chem. Phys. 2012, 12, 1721–1736. [Google Scholar] [CrossRef]
- Merucci, L.; Burton, M.; Corradini, S.; Salerno, G.G. Reconstruction of SO2 flux emission chronology from space-based measurements. J. Volcanol. Geotherm. Res. 2011, 206, 80–87. [Google Scholar] [CrossRef]
- Genkova, I.; Seiz, G.; Zuidema, P.; Zhao, G.; Di Girolamo, L. Cloud top height comparisons from ASTER, MISR, and MODIS for trade wind cumuli. Remote Sens. Environ. 2007, 107, 211–222. [Google Scholar] [CrossRef]
- Winker, D.M.; Liu, Z.; Omar, A.; Tackett, J.; Fairlie, D. CALIOP observations of the transport of ash from the Eyjafjallajökull volcano in April 2010. J. Geophys. Res. 2012, 117, D00U15. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.; Coakley, J.A.J.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The CALIPSO Mission: A Global 3D View of Aerosols and Clouds. Bull. Am. Meteorol. Soc. 2010, 91, 1211. [Google Scholar] [CrossRef]
- Wiegner, M.; Madonna, F.; Binietoglou, I.; Forkel, R.; Gasteiger, J.; Geiß, A.; Pappalardo, G.; Schäfer, K.; Thomas, W. What is the benefit of ceilometers for aerosol remote sensing? An answer from EARLINET. Atmos. Meas. Tech. 2014, 7, 1979–1997. [Google Scholar] [CrossRef]
- Frey, R.A.; Baum, B.A.; Menzel, W.P.; Ackerman, S.A.; Moeller, C.C.; Spinhirne, J.D. A comparison of cloud top heights computed from airborne lidar and MAS radiance data using CO2 slicing. J. Geophys. Res. 1999, 104, 24547–24555. [Google Scholar] [CrossRef]
- Holz, R.E.; Ackerman, S.A.; Nagle, F.W.; Frey, R.; Dutcher, S.; Kuehn, R.E.; Vaughan, M.A.; Baum, B. Global Moderate Resolution Imaging Spectroradiometer (MODIS) cloud detection and height evaluation using CALIOP. J. Geophys. Res. 2008, 113, D00A19. [Google Scholar] [CrossRef]
- Zakšek, K.; Hort, M.; Zaletelj, J.; Langmann, B. Monitoring volcanic ash cloud top height through simultaneous retrieval of optical data from polar orbiting and geostationary satellites. Atmos. Chem. Phys. 2013, 13, 2589–2606. [Google Scholar] [CrossRef]
- Carn, S.A.; Pallister, J.S.; Lara, L.; Ewert, J.W.; Watt, S.; Prata, A.J.; Thomas, R.J.; Villarosa, G. The Unexpected Awakening of Chaitén Volcano, Chile. Eos. Trans. AGU 2009, 90, 205–206. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekanandan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors, and other particulates. J. Geophys. Res. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Oppenheimer, C. Review article: Volcanological applications of meteorological satellites. Int. J. Remote Sens. 1998, 19, 2829–2864. [Google Scholar] [CrossRef]
- Eckhardt, S.; Prata, A.J.; Seibert, P.; Stebel, K.; Stohl, A. Estimation of the vertical profile of sulfur dioxide injection into the atmosphere by a volcanic eruption using satellite column measurements and inverse transport modeling. Atmos. Chem. Phys. 2008, 8, 3881–3897. [Google Scholar] [CrossRef]
- Dubuisson, P.; Frouin, R.; Dessailly, D.; Duforêt, L.; Léon, J.-F.; Voss, K.; Antoine, D. Estimating the altitude of aerosol plumes over the ocean from reflectance ratio measurements in the O2 A-band. Remote Sens. Environ. 2009, 113, 1899–1911. [Google Scholar] [CrossRef]
- Richards, M.S. Volcanic Ash Cloud Heights Using the MODIS CO2-Slicing Algorithm. M.Sc. Thesis, University of Wisconsin, Madison, WI, USA, 6 January 2006. [Google Scholar]
- Chang, F.-L.; Minnis, P.; Lin, B.; Khaiyer, M.M.; Palikonda, R.; Spangenberg, D.A. A modified method for inferring upper troposphere cloud top height using the GOES 12 imager 10.7 and 13.3 μm data. J. Geophys. Res. 2010, 115, D06208. [Google Scholar]
- Glaze, L.S.; Francis, P.W.; Self, S.; Rothery, D.A. The 16 September 1986 eruption of Lascar volcano, North Chile: Satellite investigations. Bull. Volcanol. 1989, 51, 149–160. [Google Scholar] [CrossRef]
- Hasler, A.F. Stereographic observations from geosynchronous satellites: An important new tool for the atmospheric sciences. Bull. Amer. Meteor. Soc. 1981, 62, 194–212. [Google Scholar] [CrossRef]
- Prata, A.J.; Turner, P.J. Cloud-top height determination using ATSR data. Remote Sens. Environ. 1997, 59, 1–13. [Google Scholar] [CrossRef]
- Scollo, S.; Kahn, R.A.; Nelson, D.L.; Coltelli, M.; Diner, D.J.; Garay, M.J.; Realmuto, V.J. MISR observations of Etna volcanic plumes. J. Geophys. Res. 2012, 117, D06210. [Google Scholar] [CrossRef]
- Virtanen, T.H.; Kolmonen, P.; Rodríguez, E.; Sogacheva, L.; Sundström, A.-M.; de Leeuw, G. Ash plume top height estimation using AATSR. Atmos. Meas. Tech. 2014, 7, 2437–2456. [Google Scholar] [CrossRef]
- Carboni, E.; Grainger, R.G.; Thomas, G.E.; Poulsen, C.A.; Siddans, R.; Smith, A.; Sayer, A.; Peters, D. Volcanic Plume Characterization Using Satellite Measurements in the Visible and Thermal Infrared; USEReST Workshop: Neaples, Italy, 2008. [Google Scholar]
- Francis, P.N.; Cooke, M.C.; Saunders, R.W. Retrieval of physical properties of volcanic ash using Meteosat: A case study from the 2010 Eyjafjallajökull eruption. J. Geophys. Res. 2012, 117, D00U09. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Heidinger, A.K.; Sieglaff, J. Automated retrievals of volcanic ash and dust cloud properties from upwelling infrared measurements. J. Geophys. Res. Atmos. 2013, 118, 1436–1458. [Google Scholar] [CrossRef]
- Poulsen, C.A.; Siddans, R.; Thomas, G.E.; Sayer, A.M.; Grainger, R.G.; Campmany, E.; Dean, S.M.; Arnold, C.; Watts, P.D. Cloud retrievals from satellite data using optimal estimation: Evaluation and application to ATSR. Atmos. Meas. Tech. 2012, 5, 1889–1910. [Google Scholar] [CrossRef]
- Stoter, A. Observations of the Karthala Eruption, Mph Report; University of Oxford: Oxford, UK, 2009. [Google Scholar]
- Scambos, T.A.; Dutkiewicz, M.J.; Wilson, J.C.; Bindschadler, R.A. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Adelson, E.H.; Anderson, C.H.; Bergen, J.R.; Burt, P.J.; Ogden, J.M. Pyramid methods in image processing. RCA Eng. 1984, 29, 33–41. [Google Scholar]
- Valentine, G.A.; Gregg, T.K.P. Continental basaltic volcanoes—Processes and problems. J. Volcanol. Geotherm. Res. 2008, 177, 857–873. [Google Scholar] [CrossRef]
- Vergniolle, S.; Ripepe, M. From Strombolian explosions to fire fountains at Etna Volcano (Italy): What do we learn from acoustic measurements? Geol. Soc. Lond. Spec. Publ. 2008, 307, 103–124. [Google Scholar] [CrossRef]
- UFVG Rapporto UFVG del 28 Novembre 2013: L’attività Parossistica del 23 Novembre 2013 al Nuovo Cratere di SE: Dispersione del Deposito di Caduta e Caratteristiche dei Prodotti Eruttati. Available online: http://www.ct.ingv.it/it/rapporti/vulcanologia.html?view=docman (accessed on 25 February 2016).
- Bollettino settimanale sul monitoraggio vulcanico, geochimico e sismico del vulcano Etna 26/11/2013. Available online: http://www.ct.ingv.it/it/rapporti/multidisciplinari.html?view=docman&start=210 (accessed on 25 February 2016).
- Prata, A.J. Observations of volcanic ash clouds in the 10–12 μm window using AVHRR/2 data. Int. J. Remote Sens. 1989, 10, 751–761. [Google Scholar] [CrossRef]
- Prata, F.; Bluth, G.; Rose, B.; Schneider, D.; Tupper, A. Comments on “Failures in detecting volcanic ash from a satellite-based technique”. Remote Sens. Environ. 2001, 78, 341–346. [Google Scholar] [CrossRef]
- Corradini, S.; Montopoli, M.; Guerrieri, L.; Ricci, M.; Scollo, S.; Merucci, L.; Marzano, F.S.; Pugnaghi, S.; Prestifilippo, M.; Ventress, L.J.; et al. A Multi-Sensor Approach for Volcanic Ash Cloud Retrieval and Eruption Characterization: The 23 November 2013 Etna Lava Fountain. Remote Sens. 2016, 8, 58. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Prata, A.J.; Piscini, A. Volcanic ash and SO2 in the 2008 Kasatochi eruption: Retrievals comparison from different IR satellite sensors. J. Geophys. Res. 2010, 115, D00L21. [Google Scholar]
- WMO, OSCAR. Available online: http://www.wmo-sat.info/oscar/ (accessed on 25 February 2016).
- WMO, OSCAR. Available online: http://www.wmo-sat.info/oscar/observingmissions/view/2 (accessed on 25 February 2016).

| Methodology | Pros/Cons |
|---|---|
| LiDAR and radar [6,19,24] | + very high vertical resolution and accuracy – excessive revisit time (16 days) and only nadir observations from currently-operational instruments (LiDAR CALIOP, radar CPR) |
| Radio occultation [25,26] | + high resolution in lower troposphere – globally available only about 2000 times per day |
| Backward trajectory modeling [27,28] | + estimate possible even for clouds drifted away from the source – requires wind field data for a large area and a reliable trajectory model (e.g., turbulence not easy to handle); homogenous wind field results with high uncertainty of the source height |
| Brightness temperature [3,17,27] | + easy to apply, possible with instruments with a short revisit time – requires atmospheric profile and emissivity of the cloud; assumption of thermal equilibrium; problems around tropopause |
| O2 A-band absorption [29] | + high accuracy – requires high spectral resolution data (not available on many satellites, long revisit time); good performance only over dark surfaces; requires radiative transfer modeling; daytime only |
| CO2 absorption [21,30,31] | + good performance also with semi-transparent clouds – accurate only in the high levels of the troposphere; problems around tropopause |
| Shadow length [3,32] | + easy to apply; requires no additional data – possible only during daytime; retrieves the height of the cloud horizontal edge and not its top |
| Stereoscopy [17,23,33,34,35,36,37] | + high accuracy; requires no additional data; based on geometry→no problems in the case of ash reaching the stratosphere – requires simultaneous data from two different viewpoints |
| Optimal estimation [38,39,40] | + includes error estimate − requires atmospheric profiles, ash optical properties, and radiative transfer |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merucci, L.; Zakšek, K.; Carboni, E.; Corradini, S. Stereoscopic Estimation of Volcanic Ash Cloud-Top Height from Two Geostationary Satellites. Remote Sens. 2016, 8, 206. https://doi.org/10.3390/rs8030206
Merucci L, Zakšek K, Carboni E, Corradini S. Stereoscopic Estimation of Volcanic Ash Cloud-Top Height from Two Geostationary Satellites. Remote Sensing. 2016; 8(3):206. https://doi.org/10.3390/rs8030206
Chicago/Turabian StyleMerucci, Luca, Klemen Zakšek, Elisa Carboni, and Stefano Corradini. 2016. "Stereoscopic Estimation of Volcanic Ash Cloud-Top Height from Two Geostationary Satellites" Remote Sensing 8, no. 3: 206. https://doi.org/10.3390/rs8030206
APA StyleMerucci, L., Zakšek, K., Carboni, E., & Corradini, S. (2016). Stereoscopic Estimation of Volcanic Ash Cloud-Top Height from Two Geostationary Satellites. Remote Sensing, 8(3), 206. https://doi.org/10.3390/rs8030206