Methods to Quantify Regional Differences in Land Cover Change

Abstract

This paper describes and illustrates methods for quantifying regional differences in land use/land cover changes. A series of approaches are used to analyse differences in land cover change from data held in change matrices. These are contingency tables and are commonly used in remote sensing to describe the spatial coincidence of land cover recorded over two time periods. Comparative analyses of regional change are developed using odds ratios to analyse data in two regions. These approaches are extended using generalised linear models to analyse data for three or more regions. A generalised Poisson regression model is used to generate a comparative index of change based on differences in change likelihoods. Mosaic plots are used to provide a visual representation of statistically surprising land use losses and gains. The methods are explored using a hypothetical but tractable dataset and then applied to a national case study of coastal land use changes over 50 years conducted for the National Trust. The suitability of the different approaches to different types of problem and the potential for their application to land cover accuracy measures are briefly discussed.

1. Introduction

The correspondence matrix has become the de facto method for reporting on post classification land cover change [1,2,3]. There are many examples of its use to describe land cover and land use change (e.g., [4,5,6,7]). It is a form of contingency table, summarising the coincident areas or spatial intersection of land classified over two time periods and is referred to as the change, correspondence or transition matrix. A number of summary measures are commonly derived from the change matrix including the overall change/no change proportions and class probabilities of change from the margin totals (columns and rows), described in terms of per class Losses from Time 1 and Gains at Time 2. Various Kappa statistics are frequently used to describe global changes and per class rates of landscape and land cover changes (e.g., [8]) although these measures are not without their critics [1,9,10].

The purpose of this paper is not to contribute to the debate about the salience of Kappa and similar statistics for describing change or accuracy. Rather, it is to explore how methods for analysing contingency tables may be applied to correspondence matrices arising from analyses of land cover and land use data in order to generate comparative measures of land use/land cover change. Specifically, the aim is to describe how land changes observed in one area relate to those observed in another. Methods for quantifying regional differences are lacking in the land use/land cover and remote sensing literature and yet the object of much geographical analysis is to determine how processes vary spatially. Variation may be a result of different underlying environmental processes (e.g., geological, climatic, etc.), different socio-economic activities, spatial planning policies or different ownership and management regimes. Possible objectives include determining how much more probable land cover change is in Region A compared to Region B or C, or the relative likelihood of a specific change (e.g., from forest to agriculture) in Zone Z compared to Zone Y.

It is within this context that this paper suggests some statistical approaches that can be readily applied to land cover change data, as summarised in a correspondence matrix. These are used to generate comparative statistical measures of per class land cover changes, of regional differences in change and of the likelihood of specific class to class transitions, arising perhaps as a result of different land management strategies.

2. Background

There is a longstanding body of literature describing approaches for measuring land cover change detection. A recent review of land cover change using optical remote sensing identified post-classification comparison as the most widely used change analysis along with the correspondence matrix [3,11]. Methods for quantifying regional differences in land cover changes are, however, surprisingly lacking in the remote sensing literature. For example, Lambin et al. [12] describe the different causes of variation in land cover change operating at regional scales and Lunetta et al. [13] identified variations in the rates of land cover change in different ecological zones using MODIS data but these present only high level explanations for observed regional differences. Some reports of regional analyses can be found. For example, Balzter et al. [14] compared SAR-derived forest maps of Siberia for different forest enterprise districts, and Pijanowski and Robinson [15] compared transition percentages in different metropolitan regions at different spatial scales in the USA using the concept of land cover persistence with ratios of loss and gain. Kumar et al. [16] examined the underlying social and physical reasons for historical cropland cover change associated with different eco-regions using nonlinear bi-analytical statistics to model discrete trajectories for different regions. Balej et al. [17] compared the regional relationships between change and external variables associated with land cover changes, but sought to identify the regionally varying drivers of change rather than to compare regional changes per se. In summary, very few regional comparisons of land cover change have been undertaken and where they have, only simple areal comparisons have been made, with no statistical tests of difference.

In many inter-regional land cover change analyses, the independent probabilities arising from separate correspondence matrices are compared. For example, Duveiller et al. [18] compared the proportions of deforestation and reforestation in different regions in Central Africa under a range of different sampling regimes. Interestingly, Colditz et al. [19] compared land cover in different bio-geographic regions in Mexico but made no statistical comparison. Indeed, these authors comment that such regions cannot be compared because of the uneven spatial distribution of land cover classes across them (“there are known issues in the spatial distribution of classes for specific regions, which can hardly be quantified with statistical measures” p. 551). Concerns over the use of summary statistics, commonly in the form of proportions and percentages of loss or gain for different classes, from matrix row or column totals for regional comparisons may be well-founded: while they provide unconditional probability measures, these are specific to each matrix and to each regional analysis. As a result, they may not provide information about how the changes observed in one zone relate statistically to those in another. In other areas of information sciences and statistics, a number of different approaches have been developed for analysing and comparing frequencies in contingency tables such as correspondence matrices, and for performing simple tests to identify statistically surprising results. These are applied in the next section, as well as odds ratios and relative likelihoods from generalized linear models, to allow direct statistical comparisons across different regions.

3. Methods

3.1. Hypothetical Data

A simulated or hypothetical dataset was generated to illustrate the methods and to provide clarity and transparency. These are presented in a series of change matrices and are shown in

Table 1. Land cover changes for (a) overall; (b) Region 1; (c) Region 2 and (d) Region 3.

Overall		Time 2
		Farmland	Grass	Urban	Woodland	Loss
Time 1	Farmland	67	2	30	15	47
	Grass	7	49	4	2	13
	Urban	0	5	66	1	6
	Woodland	1	0	4	47	5
	Gain	8	7	38	18
(a)
Region 1		Time 2
		Farmland	Grass	Urban	Woodland	Loss
Time 1	Farmland	35	0	6	1	7
	Grass	0	19	1	1	2
	Urban	0	2	11	0	2
	Woodland	0	0	2	22	2
	Gain	0	2	9	2
(b)
Region 2		Time 2
		Farmland	Grass	Urban	Woodland	Loss
Time 1	Farmland	20	2	6	7	15
	Grass	7	19	0	1	8
	Urban	0	1	22	1	2
	Woodland	1	0	0	13	1
	Gain	8	3	6	9
(c)
Region 3		Time 2
		Farmland	Grass	Urban	Woodland	Loss
Time 1	Farmland	12	0	18	7	25
	Grass	0	11	3	0	3
	Urban	0	2	33	0	2
	Woodland	0	0	2	12	2
	Gain	0	2	23	7
(d)

. These describe the intersecting areas, in pixel counts, of different land classes over two time periods for three hypothetical regions.

3.2. Visualising Change Matrices

A number of tools are available to analyse contingency tables such as correspondence matrices and to depict the results of simple statistical tests. These include agreement plots [20] and mosaic plots [21,22]. Their implementation within the vcd package in R is described in code snippets accompanying the package and worked examples are given in Meyer et al. [23], Zeileis et al. [24] and Friendly [25]. All of the statistical analyses, tables and figures in this paper were implemented in R version 3.2.1, the open source statistical software, using the vcd and gplot packages. The data and code used in this analysis will be freely provided to interested researchers on request.

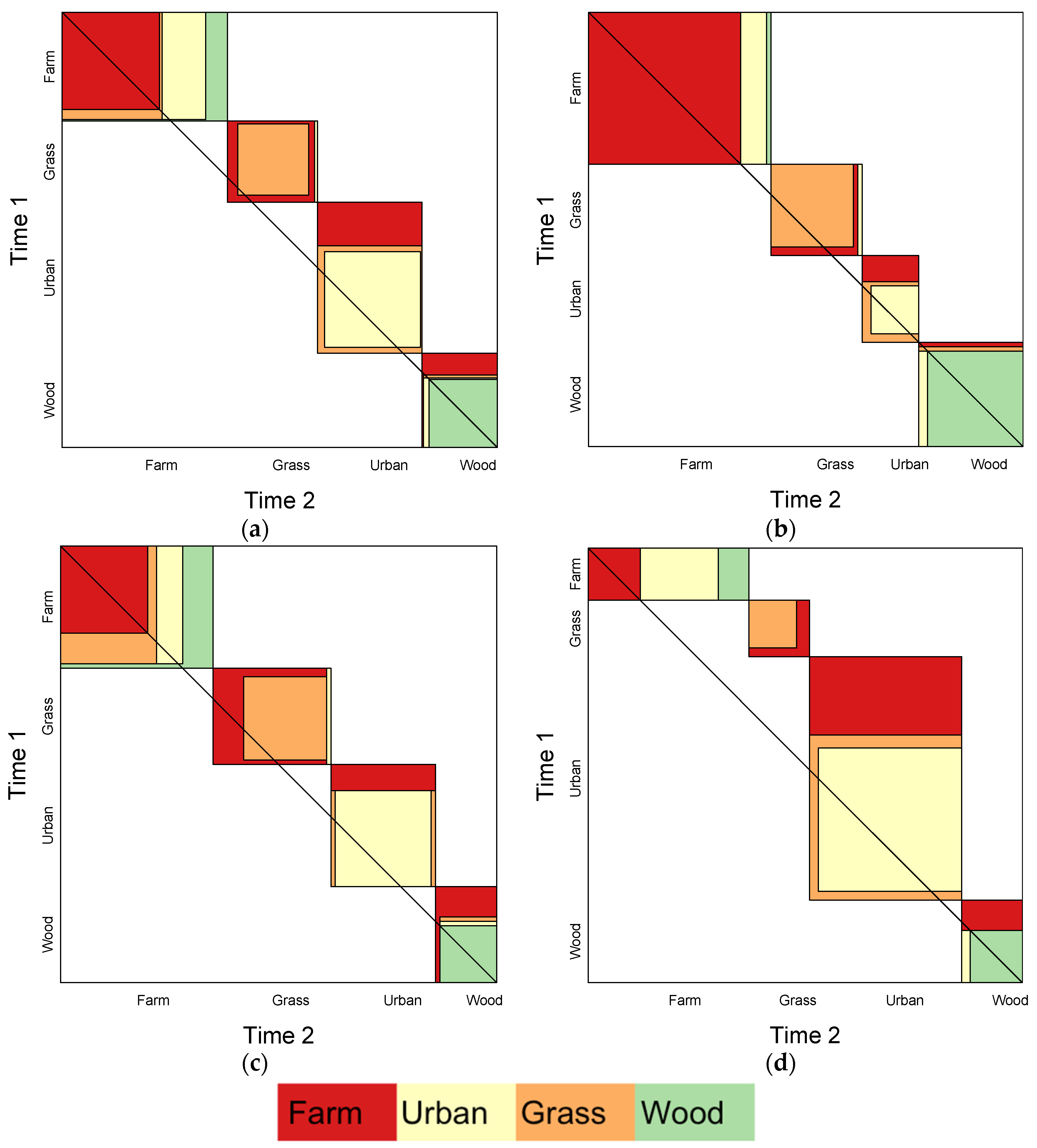
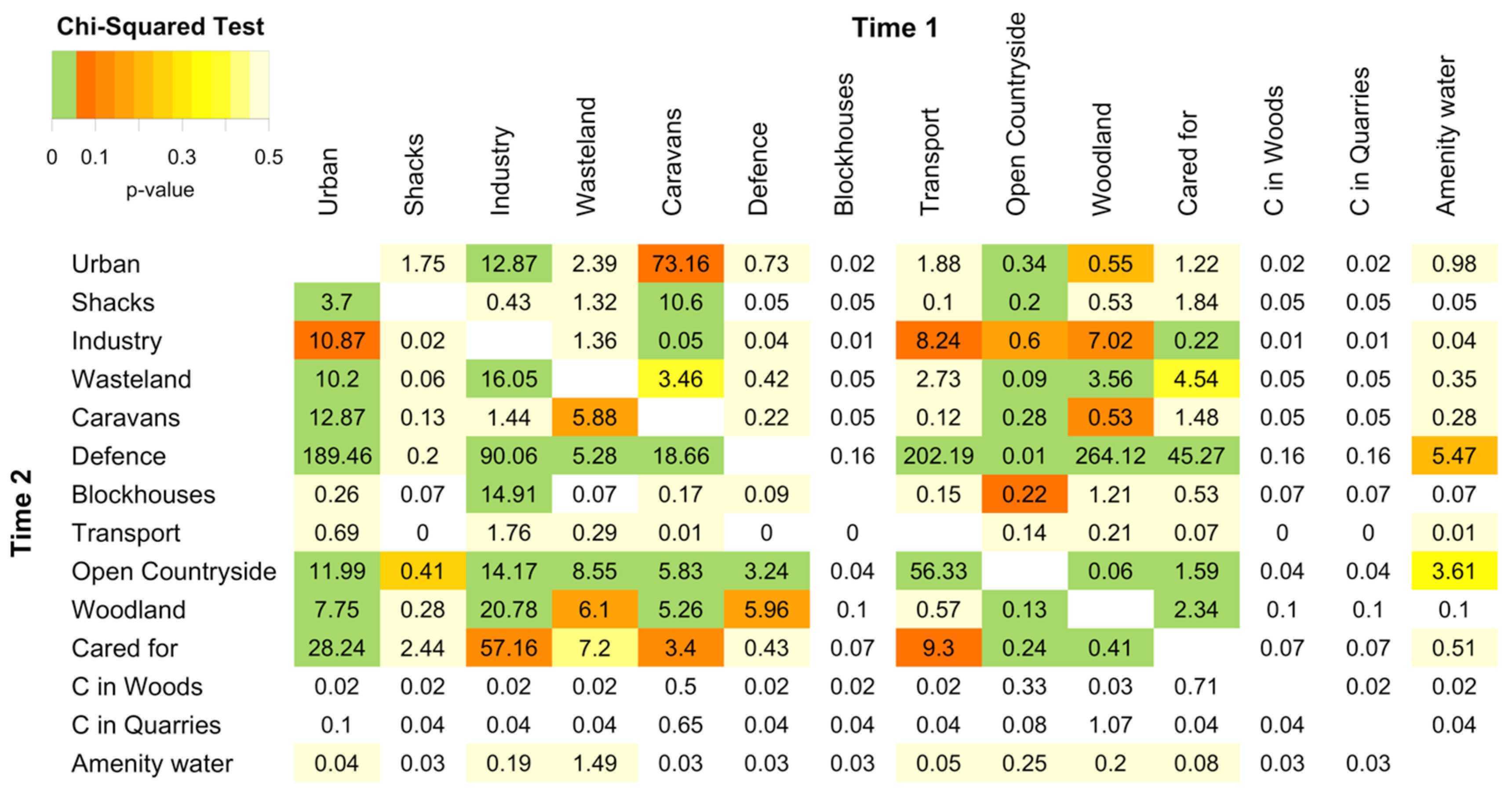
Agreement plots [20] provide a graphical representation of the diagonal and off-diagonal elements in a correspondence matrix. The agreement plots arising from the correspondence matrices in Table 1 are shown in Figure 1. Large off-diagonal values in the matrix are indicated by the areas around the diagonal and their size, orientation and shading indicates the direction of change. A number of statements about the correspondence matrices can be very quickly deduced from Figure 1. For example, the agreement plot shows:

• high overall losses from Farmland to Urban and Woodland (Figure 1a);
• high overall gains to Urban from Farmland (Figure 1a);
• relatively high levels of change in Region 3 compared to the other regions;
• high gains in Woodland from Farmland in Region 2 (Figure 1c);
• large areas of Urban in Region 3 and its gains from Farmland (Figure 1d).

3.3. Comparing Changes in Two Regions Using Odds Ratios

It is possible to make a number of statements from the regional change matrices in Table 1 about the probability of change for any given class in any given region. Losses and gains are derived from the row and column marginal totals and diagonals. For example, the probability of Farmland losses are as follows:

Overall: 47/(67 + 2 + 30 + 15) = 0.41

Region 1: 7/(35 + 0 + 6 + 1) = 0.17

Region 2: 15/(20 + 2 + 6 + 7) = 0.43

Region 3: 25/(12 + 0 + 18 + 7) = 0.68

The objective in some land cover change studies is to compare changes in different regions, perhaps relating to management, policy or ownership. Probabilities provide useful descriptive statistics of the change but they are not directly comparable in this form as they are specific to each region. Odds ratios provide a widely used technique in land use modelling and assessment, principally to examine the underlying drivers and factors associated with land use but as yet they have not been used to compare regional differences.

Odds ratios can be used to compare any two individual regions or class-to-class changes. They indicate the relative likelihood of change between different treatments. Thus, they provide a comparative measure of change and can be used to describe regional differences, differences between land cover classes and differences in specific class to class changes observed in two regions. The odds ratio, θ, of the relative likelihood of change is defined as follows:

$$\mathsf{\theta }=\frac{Odds(change|Regio{n}_A)}{Odds(change|Regio{n}_B)}$$

(1)

An odds ratio of 1 indicates change is equally likely to occur in both regions. If it is greater than 1, then this suggests that change is more likely to occur in Region A. If the odds ratio is less than 1, then this indicates that change is less likely in Region A than in Region B and, in this case, the ratio is inverted to describe likelihood of change in Region B relative to Region A.

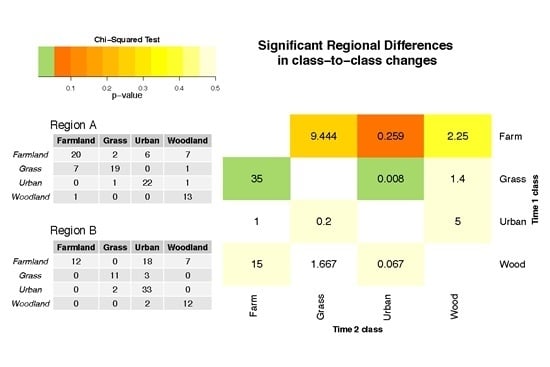
To determine odds ratios, the diagonal and off-diagonal elements of the change matrices are collapsed into 2 by 2 matrices, which can then be used to calculate the relative odds of changes in one region compared to another. The overall changes in Regions 1 and 2 indicate change in 13 out of 100 pixels in Region 1 and in 26 out of 100 pixels in Region 2. This results in no change totals of 87 and 74 pixels respectively. The relative likelihood of land cover change in Region 1 compared to Region 2 is:

$$\mathsf{\theta }=\frac{13/87}{26/74}=\frac{0.13}{0.26}=0.425$$

That is, relative odds of change in Region 2 are 0.425⁻¹ or 2.35 times higher than in Region 1. The significance of the interactions between regions and land cover change can be tested using a χ²-test and in this case it indicates a significant difference at the 95% level between Regions 1 and 2 (p-value = 0.032).

It is also possible calculate to the relative odds and associated significance for changes to different classes.

Table 2. The odds ratios of land cover losses and gains in Region 1 compared to Region 2.

	Class	Odds Ratio	Log Odds Ratio	Std. Error	z Value	Pr (>|z|)
Loss	Farmland	0.267	−1.322	0.537	−2.463	0.014
	Grass	0.250	−1.386	0.855	−1.622	0.105
	Urban	2.000	0.693	1.066	0.650	0.516
	Woodland	1.182	0.167	1.274	0.131	0.896
Gain	Farmland	0.034	−3.382	1.481	−2.283	0.022
	Grass	0.714	−0.336	0.888	−0.379	0.705
	Urban	2.860	1.051	0.625	1.681	0.093
	Woodland	0.158	−1.846	0.790	−2.337	0.019

shows the relative odds of land cover losses and gains comparing Region 1 with Region 2.

A number of significant differences in land cover change are suggested by Table 2:

• the relative odds of loss from Farmland is 3.7 (0.267⁻¹) times greater in Region 2 than in Region 1;
• the relative odds of gains in Farmland and Woodland area are 29.4 (0.034⁻¹) and 6.3 (0.158⁻¹) times greater in Region 2 than in Region 1.

Other losses and gains are not significant.

The gross changes may hide more subtle changes in each class. As a result, the odds ratios may present an example of Simpson’s paradox [26], where different rates (and directions) of per class changes may be masked by the aggregate gross changes. It is possible to quantify differences in the likelihood of specific class-to-class transitions, rather than just losses and gains, and how they vary in different regions. As an example of a specific direction of change, consider the transitions from Farmland to Urban class in Regions 2 and 3 (Table 1). The diagonal and off-diagonal elements of the correspondence matrices are collapsed into a 2 by 2 contingency matrix, which is used to generate the relative odds of a specific land cover transition in one region compared to another, as in

Table 3. The 2 by 2 contingency table describing the areas of change from Farmland to Urban in Regions 2 and 3 and the associated odds ratios. The table values summarise the losses from Farmland to Urban and to other classes (Urban).

Region	Urban	Urban
Region 2	6	29
Region 3	18	19

. The odds ratios suggest that the relative odds of Farmland changing to Urban are (0.218⁻¹) 4.59 times more likely in Region 3 than in Region 2.

$${\mathsf{\theta }}_1=\frac{6/29}{18/19}=0.218$$

Of course, it is important to consider the data that are used to populate the contingency table: by including the areas that did not change as well as those that did, the correct interpretation of this odds ratio above is, change from Farmland to Urban is 4.6 (0.218⁻¹) times more likely in Region 3 than in Region 3, when all possible states of change and no change are considered, and the χ²-test showed this to be significant at the 95% confidence level (p-value = 0.0098). This analysis can be further refined to consider only land use changes (i.e., without considering areas Farmland that did not change). The data are shown in

Table 4. The 2 by 2 contingency table showing the areas of change from Farmland to Urban and from Farmland to other land covers in Regions 1 and 2 and the associated odds ratios.

Region	Farmland to Urban	Farmland to Other
Region 1	6	9
Region 2	18	7

and the odds ratio now describes a different problem: that change from Farmland to Urban is 3.8 times more likely in Region 1 than in Region 2, when only observed changes from Farmland are considered, although in this case the differences were not found to be significant (χ² p-value = 0.0956) when only changes were considered.

$${\mathsf{\theta }}_2=\frac{6/9}{18/7}=18.591$$

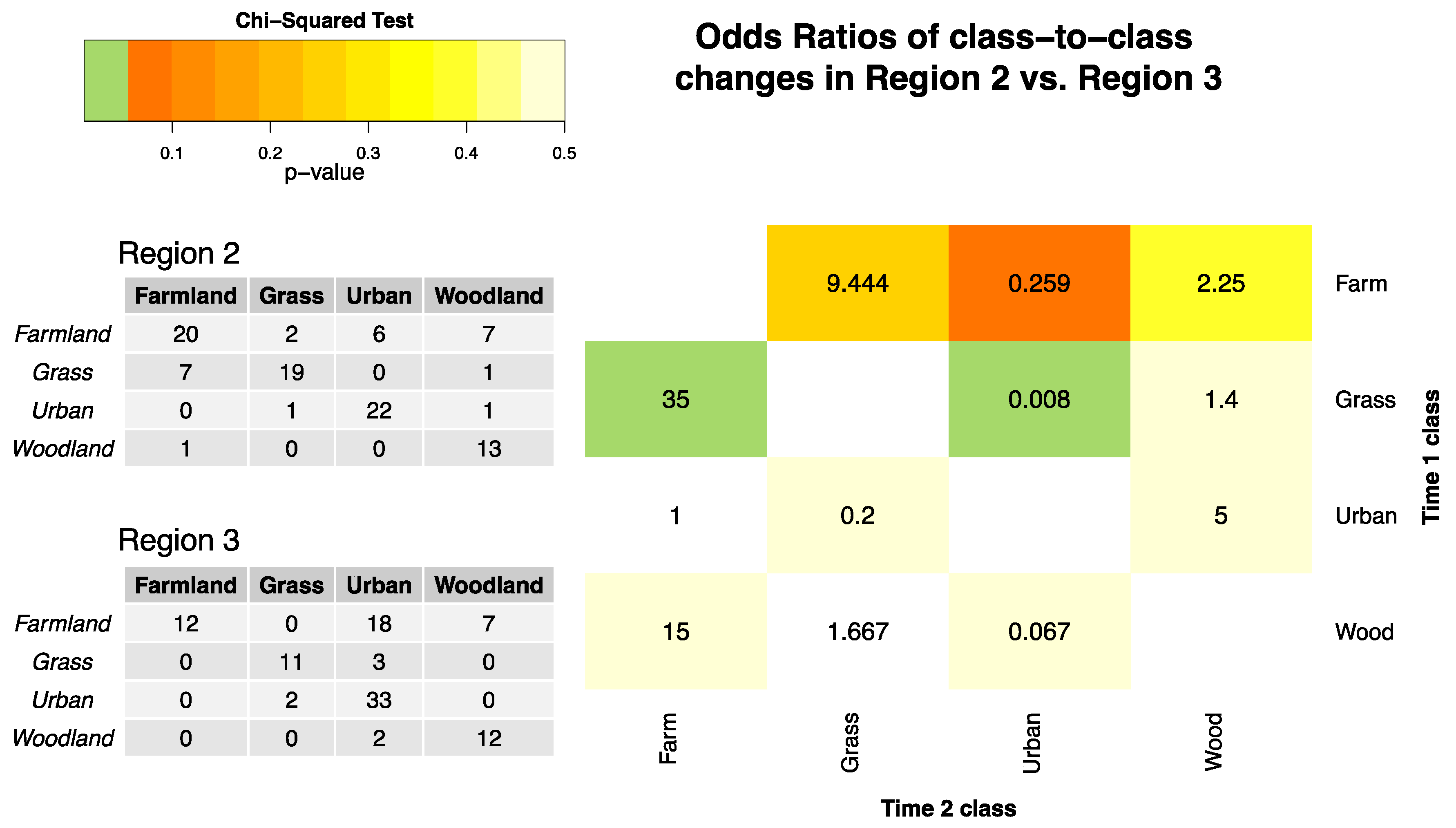
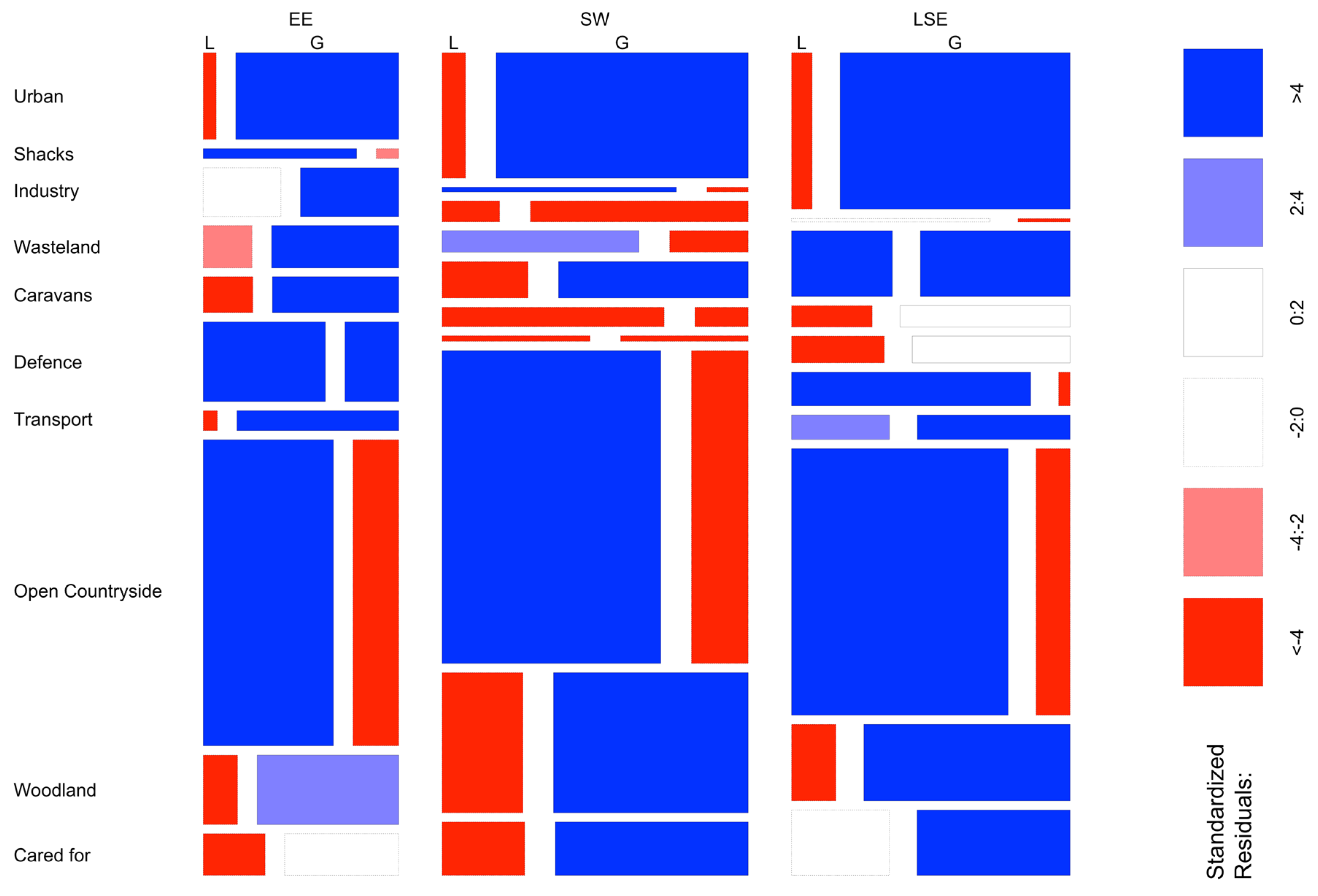
Finally, the analysis can be extended to determine the relative odds of change to and from all possible classes. Figure 2 shows the odds ratios for each class to class pair, comparing changes in Region 2 with those in Region 3. The table elements are shaded by the significance arising from the χ²-test. Figure 2 describes the relative odds of class-to-class changes in Region 2 compared to Region 3, when only changes from the original class are considered. It is easy to identify significant regional differences (shaded in green) and to make the following statements:

• changes from Grass to Farmland changes are 35 times more likely in Region 2 than Region 3;
• changes from Farmland to Urban change are 125 times more likely (0.008⁻¹) in Region 3 than in Region 2.

3.4. Comparing Changes in More than Two Regions

The preceding analyses compared only two regions, with data collapsed into 2 by 2 contingency tables. However, in many studies, the objective is to compare more than two treatments and to evaluate differences across multiple factors. Consider, for example, the regional losses and gains in

Table 5. The losses and gains in three different regions.

Status	Region	Farmland	Grass	Urban	Woodland
Loss	Region 1	7	2	2	2
	Region 2	15	8	2	1
	Region 3	25	3	2	2
Gain	Region 1	0	2	9	2
	Region 2	8	3	6	9
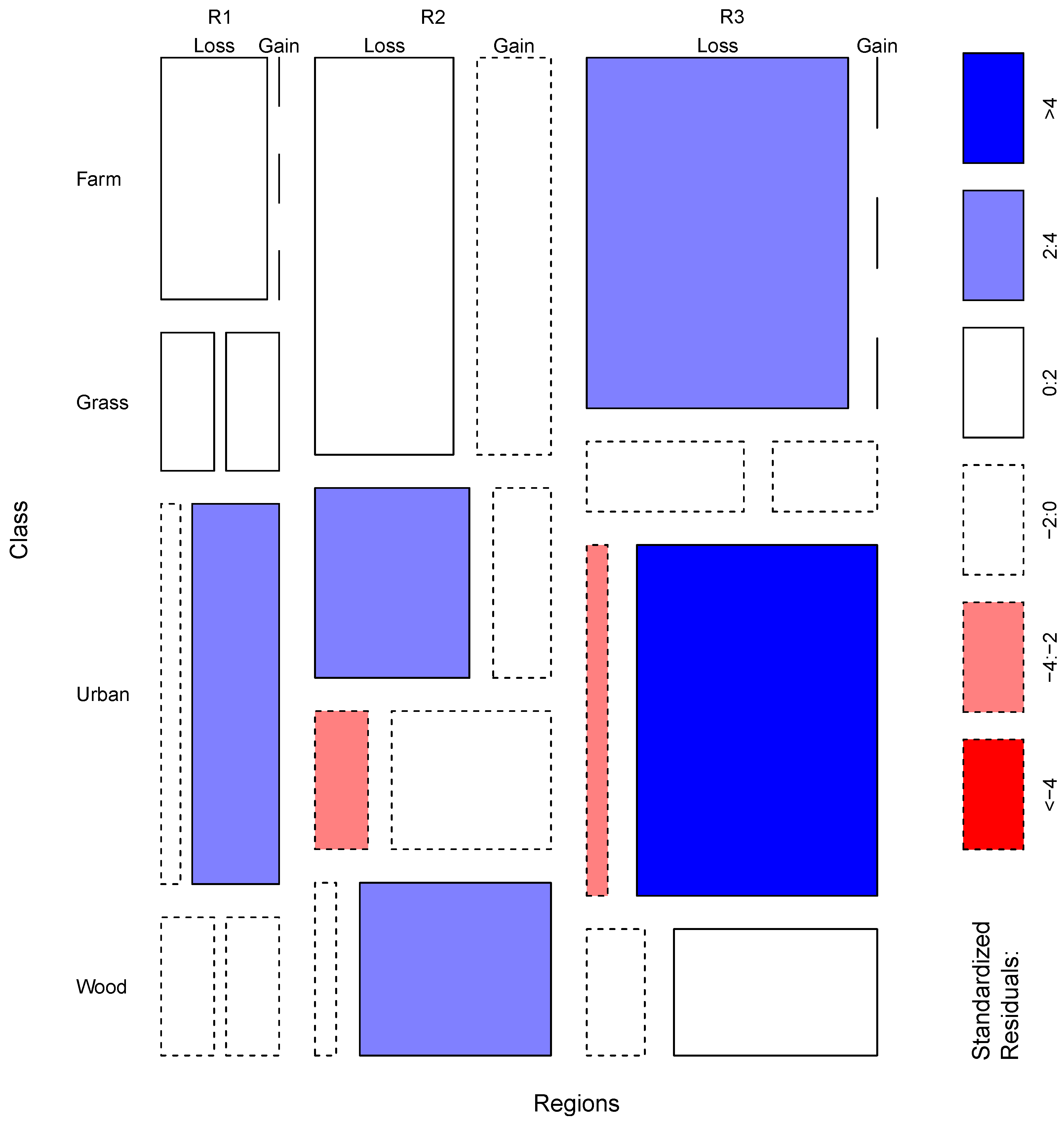
	Region 3	0	2	23	7

. These can be analysed using mosaic plots which provide a method to evaluate and visualise statistical differences in contingency tables (symmetrical and non-symmetrical).

Mosaic plots were proposed by Hartigan and Kleiner [21] and extended by Friendly [22]. In these, the significance of the interactions between column and row factors are indicated by the shading, in which the standardised residuals of a log-linear model are indicated by the colour and outline of the mosaic tiles. The mosaic plot in Figure 3 has axes for the different regions being compared and the land cover change types. The size of the plot tiles is proportionate to the land cover areas (counts in the contingency tables). Their shading indicates whether the combinations of groups, regions, classes etc. are less or greater than expected under a model of proportionality. In the examples below, tiles shaded deep blue show interactions that are significantly higher than would be expected (i.e., corresponding to combinations of change and region whose standardized residuals are greater than +4), when compared to a model of proportionally equal levels of change. Tiles shaded deep red correspond to residuals less than −4 indicating significantly lower frequencies than would be expected when compared to the model. The standardized Pearson residuals measure the deviation of each tile from independence. From Figure 3, statements can be extracted under the assumption of proportionally equal levels of change (loss and gain) for each land cover class and region. In this case, the mosaic plot indicates that the gains to Urban in Region 3 are much greater than expected.

It is possible to apply a different type of analysis to the correspondence matrix in order to compare regional land use changes against a model that expects proportionally equal levels of change in each region. Generalised linear models can be used to estimate the likelihood of change as a function of the regions. The counts of change (loss) and no change are summed for each region in a table of counts. In this, the rows indicate whether change had occurred or not and the columns indicate the region—a transpose of Table 5. To test for an association, A, between the row and column effects, the Poisson regression model is applied:

$$A\left(c_{ij}\right)=\text{log}\left(r+C_i+R_j\right)$$

(2)

where the count in column i and row j is denoted by c_ij and has a Poisson distribution, r is an intercept term, C_i is a column effect and R_j is a row effect, which is compared against the model:

$$A\left(c_{ij}\right)=\text{log}\left(r+C_i+R_j+I_{ij}\right)$$

(3)

where the extra term I_ij is an interaction effect between rows and columns. If this is significantly different from zero, then it suggests that there is some degree of association between the row and column effects. Values of I_ij were estimated by fitting Equation (3) to the regional data and the resulting coefficients were related to a comparative index of loss for each of the row categories, using the formula:

$$CHANGE=100\left(\exp \left(I_{ij}\right)-1\right)$$

(4)

In summary, Equations (2)–(4) apply a generalized linear model to a cross-tabulation of how different factors interact (regions and classes) in order to predict the frequency of occurrence of the count under a Poisson distribution. Note that in the analyses below the CHANGE term in Equation (4) is used to evaluate land cover losses from Time 1 and gains at Time 2. Due to the way the interaction terms are calibrated, this compares each column category j (regions) against a “reference” category which is usually the region with largest area. However, in this case all of the regions have the same number of pixels and so the reference is Region 1. A value of 0 suggests the likelihood of loss for category j is the same as for the reference category. A value of +50 for category j suggests loss is one-and-a-half times as likely as the reference category, a value of −50 that it is half as likely, and so on. The analysis of loss from a transpose of Table 5 was calculated and the results are shown in

Table 6. The likelihood of land use changes for different regions in the study area, relative to Region 1.

Region	Change Likelihood	Pr (>|z|)
Region 2	135.1	0.0225
Region 3	214.9	0.0018

.

The results in Table 6 suggest that the likelihood of change in Region 2 is 135% greater than in Region 1 and that the likelihood of change in Region 3 is 215% greater than in Region 1.

The application of the generalised linear models can be further extended to consider how specific class-to-class transitions vary in different regions. Consider the summary data in

Table 7. The regional changes from Farmland at Time 1 to Urban and other classes (non-Urban) at Time 2.

Change from Farmland	Region 3	Region 2
To Urban	18	6
To non-Urban	7	9

. This describes the changes from Farmland to Urban and to non-Urban classes (i.e., Grass and Woodland) in the three regions, ordered left to right by the largest column totals. It is possible to determine the likelihood of change to Urban in different regions relative to the region with the largest area of change, in this case Region 3. The results are shown in

Table 8. The likelihood of regional land cover changes from Farmland to Urban relative to Region 3.

	Change Likelihood	Pr (>|z|)
Region 2	285.7	0.0504
Region 1	−57.1	0.4683

and indicate that likelihood of land cover change from Farmland to Urban is 286% greater in Region 2 than in Region 3 and 57% less in Region 1 compared to Region 3, although this difference was not found to be significant.

Finally, it is sometimes useful to be able to compare different land cover transitions. Consider the data in

Table 9. The changes from Farmland at Time 1 to Urban and to Woodland at Time 2.

Change from Farmland	Region 3	Region 2	Region 1
To Urban	18	6	6
To Woodland	7	7	1

. They summarise the changes from Farmland to Urban and to Woodland in the three regions, again ordered left to right by the greatest volume of change. The results are shown in

Table 10. The likelihood of land cover changes from Farmland to Urban rather than Farmland to Woodland in Region 2 and Region 1 relative to Region 3.

	Change Likelihood	Pr (>|z|)
Region 2	200.0	0.1232
Region 1	−57.1	0.4683

and indicate that likelihood of change from Farmland to Urban rather than from Farmland to Woodland is 200% greater in Region 2 compared to Region 3 and 57% less in Region 1 compared to Region 3, although in this case neither of these differences are significant.

3.5. Summary

The methods presented in this section describe analyses to compare two treatments using odds ratios (Section 3.3) which are extended to approaches for comparing more than two treatments using generalized linear models. These approaches are not new, for example, Comber et al. [27] applied the methods presented in Section 3.4, but they have not been applied in the context of land cover analysis and data which are commonly summarised in contingency tables.

4. Case Study

4.1. Introduction

The methods presented in Section 3 were developed using a simple, hypothetical case study. In this section, these are applied to the results of a national coastal land use change study that compared data from 1965 and 2014. The research was commissioned by the National Trust as part of the Neptune initiative [28]. The full results are in [29] as well as some press reports [30], and the 1965 and 2015 data are provided online [31]. In brief, coastal land use was recorded in 1965 in a survey conducted by students from the University of Reading. The survey was updated manually in 2014 using freely available, open source aerial photography and mapping software, with the remote sensing imagery providing critical evidence for the update mapping. The project adopted a set of change mapping protocols that were specifically developed to ensure robust measures of land use change by minimising spurious or methodological inconsistency between the surveys, details of which are in [29]. Figure 4 shows examples of the hand drawn and annotated basemaps and data from the two time periods, as well as the National Trust administrative regions.

The National Trust was critically interested in two specific aspects of land use change. First, the Trust manages around 775 km of the coastline in England, Wales and Northern Ireland (Scotland has a separate organisation). Consequently, it wanted to understand what the impacts were of their land management policies on land use change, in part to demonstrate the conservation value of its activities. Second, it wanted to understand how changes in coastal land uses varied regionally, specifically across and between its administrative regions.

4.2. Non-National Trust vs. National Trust Change

It is important to recall that land use changes are composed of losses and gains and these may occur to and from the same class at different locations, reflecting local land use churn—for example, where a campsite is relocated to a larger field by a farmer, this is both a loss to the Campsite land use (e.g., to Open countryside) and a larger gain.

Table 11. The losses from and gains to different land use classes in hectares on land managed by the National Trust and other land.

Class	Non-National Trust Land			National Trust Land
	Same	Loss	Gain	Same	Loss	Gain
Urban	40,075	1772	19,277	193	35	86
Shacks	61	762	94	2	34	4
Industry	5404	3985	7662	2	39	13
Wasteland	523	2287	2988	7	109	22
Caravans, campsites	3060	1722	3923	8	81	34
Defence	11,622	4757	1302	209	767	13
Blockhouses *	0	197	0	0	12	0
Transport	2324	1489	3644	3	1	0
Open Countryside	283,558	36,654	21,655	32,207	1565	1765
Woodland	15,306	3088	10,556	2200	305	1221
Cared for but non-productive	11,034	2880	6302	515	198	137
Caravans in Woods *	0	31	0	0	0	0
Caravans in Quarries *	0	11	0	0	0	0

* Not mapped in 2014.

shows the overall losses and gains in coastal land use recorded on non-National Trust and National Trust land. These are derived from the marginal totals of the full change matrices included in the Appendices. The data reflect recent, general land use trends: urbanisation, increases in woodland at the arable fringe, decreases of defence land uses and increases in leisure activities (camping, caravans, recreational land such as golf-courses and sports fields which are labelled as Cared for but non-productive).

The data in Table 11 can be used to compare losses and gains in areas managed by the National Trust with those in other areas using odds ratios (Equation (1)). These generate regional comparative measures of the relative odds of change and a χ²-test indicates the significance (statistical likelihood) of the differences. The results of comparing the losses and gains for each land use class in this way are shown in

Table 12. The Odds Ratios of losses and gains for changes on non-National Trust vs. National Trust land. Bold values show significant likelihoods of greater change on National Trust land.

Class	Loss				Gain
	OR	2.5%	97.5%	p-Value	OR	2.5%	97.5%	p-Value
Urban	4.05	2.81	5.83	0.000	0.92	0.71	1.19	0.575
Shacks	1.18	0.30	4.57	1.000	1.24	0.25	6.29	1.000
Industry	26.19	6.32	108.55	0.000	4.67	1.06	20.68	0.048
Wasteland	3.63	1.67	7.89	0.001	0.55	0.23	1.30	0.263
Caravans, campsites	18.36	8.82	38.25	0.000	3.34	1.54	7.27	0.002
Defence	8.95	7.65	10.46	0.000	0.54	0.30	0.95	0.039
Transport	0.29	0.01	5.95	0.779	0.10	0.01	1.97	0.154
Open Countryside	0.38	0.36	0.40	0.000	0.72	0.68	0.75	0.000
Woodland	0.69	0.61	0.78	0.000	0.80	0.75	0.87	0.000
Cared for but non-productive	1.47	1.24	1.74	0.000	0.47	0.39	0.57	0.000

and indicate the relative odds of change on non-National Trust land compared to National Trust land. The 95% confidence intervals of the odds for losses and gains are also included.

A number of statements about significant land use losses can be made from Table 12. The relative odds of land use losses on non-National Trust land compared to National Trust land are:

• 4.05 times greater for Urban land uses
• 26.19 times greater for Industrial land uses
• 2.63 times greater for Wasteland
• 8.95 times greater for Defence land uses
• 18.36 times greater for Caravans and campsites
• 1.47 times greater for Cared for but non-productive land

The relative odds of land use losses on National Trust land verses non-National Trust land are:

• 3.44 times greater (0.29⁻¹) for Transport land uses
• 2.66 times greater (0.38⁻¹) for Open Countryside
• 1.46 times greater (0.69⁻¹) for Woodland

A number of statements about significant land use gains can be made from Table 12. The relative odds of land use gains on non-National Trust land compared to National Trust land are:

• 4.67 times greater for Industrial land uses
• 3.34 times greater for Caravans and campsites

The relative odds of land use gains on National Trust land versus non-National Trust land are:

• 1.82 times greater (0.55⁻¹) for Wasteland
• 1.87 times greater (0.54⁻¹) for Defence land uses
• 1.39 times greater (0.72⁻¹) for Open Countryside
• 1.24 times greater (0.80⁻¹) for Woodland
• 2.14 times greater (0.47⁻¹) for Cared for but non-productive land

It also possible to compare the class to class changes on National Trust land with those recorded on non-National Trust land and to identify any significant differences. The relative odds of class-to-class changes on non-National Trust land compared to National Trust land, when only changes from the original class are considered are shown in Figure 5. So, for example, changes from Open Countryside at Time 1 to Urban at Time 2 (i.e., Urban gains from Open Countryside) were 11.99 times more likely on non-National Trust land.

4.3. Regional Comparison

One of the main reasons for the original survey in 1965 was concern over what was seen as unfettered development. In the update, there was particular interest in quantifying how rates of development varied in different parts of England, Wales and Northern Ireland. To consider this, the changes (gains) to the land use classes of Urban, Industry, Transport and Caravan and campsites (

Table 13. The areal changes in hectares to land use associated with development (Urban, Industry, Transport and Caravan and campsites).

Region	No Change	Change
East of England	57,861	2909
Yorkshire & North East	36,401	3007
North West	35,229	2564
Wales	87,868	5589
South West	87,922	4768
London & South East	60,143	5866
Midlands	12,675	495
Northern Ireland	29,822	2122

) were evaluated using the generalized linear models described in Equations (2) to (4). The data used for this analysis are the gains to these classes and the amount of land that did not change (Table 13). The results indicate the relative likelihoods of these changes across the National Trust regions (

Table 14. The likelihood of developmental changes in different regions relative to Wales, the region with the largest area.

Region	Change Likelihood	Pr (>|z|)
South West	−14.74	0.0000
London & South East	53.33	0.0000
East of England	−20.95	0.0000
Yorkshire & North East	29.85	0.0000
North West	14.42	0.0000
Northern Ireland	11.85	0.0000
Midlands	−38.64	0.0000

) and show that development, for example, is 53% greater in London and the South East region than in Wales, whereas it is ~15% less likely in the South West region. All of the differences were found to be significant.

The mosaic plot in Figure 6 provides a statistical summary of losses and gains for three regions: East of England, South West and London & South East. The classes are on the Y-axis and the X-axis columns indicate the regional losses and gains. The table should be read horizontally to interpret regional differences in class losses and gains. It provides a convenient statistical summary of the per class losses and gains, summarising the areas of loss and gain by the size of the tiles which can have the consequence that the classes may be at different “heights”. It also provides a statistical measure of the unexpectedness of the observed changes in each region (under a model that assumes equal areas of change). Tiles that are shaded deep blue show interactions that are significantly higher than would be expected and those shaded deep red indicate significantly lower frequencies than would be expected. This provides a detailed comparison of specific losses and gains for individual classes in different regions. Figure 6 indicates that, for example, Urban gains are greater than would be expected in all regions, that losses to Cared for but non-productive were less than expected in the East of England and the South West regions (but not in London and South East) and that gains to Caravan and campsites were greater than expected in the East of England and the South West regions (but not in London and South East).

5. Discussion

This paper describes a series of approaches for statistically comparing land cover change in different regions (or treatments) based on analyses of data held in correspondence matrices. The methods provide a suite of approaches from which appropriate techniques can be selected depending on the task in hand. They are not intended to be used together as they relate to different questions about change: Section 3.3 describes methods for comparing two treatments or regions and Section 3.4 for comparing more than two treatments. The methods are based odds ratios and generalised linear models, are commonly applied to data held in correspondence matrices in other disciplines but have not been previously applied to quantify differences in land cover change or error matrices.

Each of the approaches uses slightly different formulations of the correspondence matrix, the most commonly used framework for describing and analysing land use/land cover changes (and also for accuracy assessments in remote sensing). Odds ratios were used to compare changes in two regions. They describe the relative likelihood of a change occurring in one region compared to another. Generalised linear models (Poisson regression models) were used to quantify the relative differences between changes in three or more regions. An index of change was proposed to compare the likelihood of changes in multiple regions. This measures the relative change likelihood of regions, when compared to one “reference” region. In that sense, they perform a series of binary comparisons of each region to the reference region. This is the nature of comparative statistics—they are by definition relative. However, each region could be specified as the referent in turn to compare all regions against each other.

The approaches described above are relatively easy to compute from the either the raw, classified data or from correspondence matrices. These methods are commonly used to analyse data in contingency tables in many areas of information science and statistics but have not been applied within land cover research, despite the correspondence matrix being the method of reporting change and error in land cover and land use analyses. This paper has sought to illustrate that such statistics are also widely applicable, especially in analyses of land cover change, and have the capacity to generate more informative reporting of change and error than simple consideration of different correspondence matrices.

The correspondence matrix is also the de facto approach for assessing error and accuracy in land cover and land use. In this context, it is frequently referred to in the literature as the error, validation or accuracy matrix. In the error matrix, predicted or modelled data, for example from a classification of remotely sensed imagery, are cross tabulated with observed or ground truth data, commonly derived from a field survey or data that are deemed to be of higher quality. A number of statistics are commonly generated describing from the correspondence matrix including overall accuracy and per class Type I and Type II errors (errors of omission and commission, user and producer accuracies). The generalised linear models suggested by Equation (4) could be modified such that Accuracy is predicted by the regression rather than Change (loss or gain) and an Index of error constructed to allow the likelihood of errors in multiple regions to be compared. Future work will explore these approaches in accuracy reporting.

6. Conclusions

In much of land mapping work, there is a need to report how “different” changes observed in one region are from those observed in another. This research was motivated by the need within a project to generate statistics comparing land ownership regions, but the regions may relate to spatial feature: management practices, ecological zones, underlying geological process, etc. Methods for doing this are lacking in the remote sensing and land cover literature and within the sub-disciplines concerned with quantifying land cover change and accuracy. The analyses described in this paper use odds ratios and generalised linear models to compare change in different regions. These approaches are commonly applied in other information sciences. They are simple and intuitive and can be used to compare overall changes, specific class to class changes and per class loss and gains arising in different locations or as a result of different treatments.