Abstract
There is an increasing need to consistently combine observations from different sensors to monitor the state of the land surface. In order to achieve this, robust methods based on the inversion of radiative transfer (RT) models can be used to interpret the satellite observations. This typically results in an inverse problem, but a major drawback of these methods is the computational complexity. We introduce the concept of Gaussian Process (GP) emulators: surrogate functions that accurately approximate RT models using a small set of input (e.g., leaf area index, leaf chlorophyll, etc.) and output (e.g., top-of-canopy reflectances or at sensor radiances) pairs. The emulators quantify the uncertainty of their approximation, and provide a fast and easy route to estimating the Jacobian of the original model, enabling the use of e.g., efficient gradient descent methods. We demonstrate the emulation of widely used RT models (PROSAIL and SEMIDISCRETE) and the coupling of vegetation and atmospheric (6S) RT models targetting particular sensor bands. A comparison with the full original model outputs shows that the emulators are a viable option to replace the original model, with negligible bias and discrepancies which are much smaller than the typical uncertainty in the observations. We also extend the theory of GP to cope with models with multivariate outputs (e.g., over the full solar reflective domain), and apply this to the emulation of PROSAIL, coupled 6S and PROSAIL and to the emulation of individual spectral components of 6S. In all cases, emulators successfully predict the full model output as well as accurately predict the gradient of the model calculated by finite differences, and produce speed ups between 10,000 and 50,000 times that of the original model. Finally, we use emulators to invert leaf area index (), leaf chlorophyll content () and equivalent leaf water thickness () from a time series of observations from Sentinel-2/MSI, Sentinel-3/SLSTR and Proba-V observations. We use sophisticated Hamiltonian Markov Chain Monte Carlo (MCMC) methods that exploit the speed of the emulators as well as the gradient estimation, a variational data assimilation (DA) method that extends the problem with temporal regularisation, and a particle filter using a regularisation model. The variational and particle filter approach appear more successful (meaning parameters closer to the truth, and smaller uncertainties) than the MCMC approach as a result of using the temporal regularisation mode. These work therefore suggests that GP emulators are a practical way to implement sophisticated parameter retrieval schemes in an era of increasing data volumes.
1. Introduction
As more spaceborne Earth Observation EOsensors start capturing data over the land surface, there is an increased need to develop methods to optimally combine these observations, making an optimal use of data from as many sensors as possible, a concept sometimes termed “virtual constellation“ [1]. This requires the use of physical models that describe both the imaged scene as well as the acquisition parameters (bandpass characteristics, view/illumination configuration, etc.). In the solar reflective domain, these models mainly describe scattering and absorption of radiation by the atmosphere, vegetation canopies and soils, effectively providing a mapping from parameters that describe the state of soil, leaf, canopy and atmosphere to the reflectance or radiance that would be observed by a sensor. In practice, we are more often concerned about the so-called “inverse problem”, where the model is used to map from the observations of reflectance or radiance, back to the land surface parameters of interest [2,3]. Due to the complex non-linear nature of the models and the presence of uncertainties in the data gathering processes, the solution to this problem is often non unique, and the problem is said to be “ill posed” [4]. Methods based on minimising the misfit between model and observations (e.g., least squares) can thus appear to be noisy and unstable, a situation that is usually dealt with using post-inversion filtering (e.g., [5]. Recasting the problem in a Bayesian framework opens the possibility of adding extra constraints in the form of a priori parameter distributions, as well as producing probability density functions (pdfs) of the parameters, which are effectively a statement of the uncertainty on the retrieved parameters [6,7]. The use of non-linear radiative transfer models in conjunction with Bayesian methods is however computationally very expensive, requiring either Monte Carlo based approaches, or iterative cost function minimisations if some assumptions allow a variational approach. In some cases, the Jacobian of the physical models is required to use quasi-Newton methods. Obtaining the Jacobian is far from trivial, requiring the use of automatic differentiation (AD) techniques [8], or its computationally costly numerical evaluation using finite differences (e.g., [9]). This situations is complicated further by the complexity of the physical models.
Over time, a number of different approaches have appeared to deal with the limitations outlined above. Perhaps one of the earliest has been look-up tables (LUTs), where the model to invert is run over parameter space, producing a dense sampling of this space, and both input parameters and outputs are stored. Observations are then compared with the results of the forward model, and the solution that is (in some sense, like least squares) closer is chosen. These methods are practical, and have had a wide use (for example, the widely used MODIS LAI/fAPAR product [10] is produced with a LUT approach), but have problems in adequately diagnosing uncertainty, are inflexible in their application to combinations of sensors, and it is hard to define the denseness of parameter space sampling. Additionally, it is quite hard to add a priori knowledge to this formulation. Other efforts have focused on using regression and “learning” approaches, such as the use of artificial neural networks (ANNs) [11,12] or other regression approaches (see e.g., [13]). These approaches have in common the aim of producing a mapping from observations to parameter space. The mapping is said to be “learned” from known pairings of parameters and forward model runs (or sometimes, ground measurements). This methods can be made to work well, but their generalisation to any kind of inverse problem is complicated, if not impossible, as a general solution would require training/learning against all possible observational configurations. Additionally, adding prior constraints and merging different datasets is also problematic, since training typically results in a mapping from observations from a sensor with particular characteristics to a set of biophysical parameters, so extending these methods to other sensors requires extra training, and effectively, solving a new problem. Since the physical RT models encompass a number of strong physical constraints (energy conservation, reciprocity, ...), it begs the question of whether we should be “learning” these concepts, or enforcing them directly in the inverse problem, in a similar way with some a priori information. This is hard to do with practical machine learning algorithms, as the priors are typically on the distribution of the state parameters, effectively the output of the mapping, and only limited prior information can be added through the training phase. Finally, a number of methods make direct use of the physical models directly within a fully Bayesian scenario [6,7], with a robust estimation of uncertainties and a flexible mechanism for exploiting prior information. A more complete recent survey of other methods for biophysical parameter retrieval is given in [14], but in general there is a clear trade-off between flexibility and robustness in the inversion (such as the ability to easily include data from different sensors, extra a priori constraints, realistic evaluation of uncertainties, generalisation of the approach to different regions) and the ability to apply the different algorithms in practice. The most flexible approaches require a statement of the problem where the physical model is explicitly required, and are thus limited in their application to large datasets by the need to repeatedly evaluate a complex physical model. This is particularly the case for data assimilation (DA) schemes, where the Bayesian paradigm is extended to estimate not just parameters directly exposed by the RT model, but also unobservable parameters coupled to the observations by a set of mechanistic models, the mechanistic model providing in this case an expectation of the land surface parameters [15,16,17].
In this contribution, after having identified that one of the main bottlenecks in using advanced DA techniques with EO data is the computational cost of the RT models, we introduce the concept of emulators to the inverse RT problem. An emulator is a surrogate function that given an input parameter vector, produces an approximation to what a full RT model would produce, and this approximation is qualified by an uncertainty in the emulation. A critical property of the emulator is that its execution is much faster than running the full model, and for this reason they have been widely used in statistics [18,19,20,21]. We focus our attention in Gaussian process (GP) emulators, which have been widely used in a number of fields (e.g., the climate and vegetation modelling communities have used emulators for some time [22,23,24,25]). In Earth Observation, GPs have been used as fast surrogates to computationally expensive models in [26] for sensitivity analysis. However, most of the recent use (e.g., [13,27,28]) has used the GP as a traditional regression method, where for example, the emulator is trained to provide a mapping between a set of input bands and an output parameter such as LAI or fractional cover. More recently, the case of using machine learning techniques as emulators has also started to be explored [14,29].
In an early work, O’Hagan [18] introduced the concept of emulators as a form of inference over functions, and used to demonstrate analysis of the “emulated” functions. This concept is also introduced by [19], and from there, exploited in a large number of scenarios (e.g., [20,21]). Although most of these references refer to Gaussian Processes, other kinds of functions, from simple polynomials to other more complex regression methods can be used. A good pair of review papers in the practical use of emulation for engineering problems are given in [30,31].
2. Gaussian Process Emulator
is a function that maps from a set of input parameters (here combined in a vector ) to an output scalar t. We can picture emulation as an inference problem: an emulator is a prediction of the value of , when only a limited set of N input vectors , and the corresponding function realisations (or outputs) are available. The goal here is to infer the underlying function from this reduced training set. In order to do this, it is useful to propose a Bayesian model, where the likelihood is assumed to be Gaussian with variance (in other words, the mismatch between the emulator and the true model is Gaussian, or ), and a prior probability distribution function (pdf). A general prior over a space of functions should encompass our understanding of the nature of the function, but in general, we expect the function to be smooth and continuous, so that a useful prior to use is the GP, a generalisation of the concept of a multivariate Gaussian distribution to functions. A GP states that the value of a function at some location can be modelled using a mean function and a covariance function. Assuming that the mean function is 0 (this is a bias term that can be readily added if needed), we are left with choosing a covariance function to fully determine the GP prior. The posterior of this combination of GP prior and Gaussian likelihood results in a GP posterior, effectively predicting a mean and variance of the output of the original as a function of the input vector. The process only requires the selection of a covariance function, which has the role of estimating the smoothness of the emulated function, and fitting its hyperparameters to the training data. In this work, we will focus on one of the simplest covariance functions available, the squared exponential, which encodes a prior belief of a stationary covariance structure:
In Equation (1), describes the variance, whereas the elements of the diagonal matrix encode the so-called roughness along each direction in input parameter space, where roughness refers to the level of smoothness of the function. Once the likelihood and prior have been selected, the inference reduces to inferring values for the hyperparameters (ν, and ) with a training set of input/output pairs. While methods based on sampling can be used to infer the hyperparameters (e.g., [21]), simple expressions for the Maximum Likelihood Estimate for these parameters are readily available, based on minimising a log-likelihood function using gradient descent (see, for example [32] for details). Once this step is carried out, the emulator is ready to be used. The expressions for the posterior mean and variance due to an input can be calculated as [20,21,32,33]
Here, denotes the covariance between the training samples set and the sample , whose prediction we are interested in. K is the covariance between the pairs of training samples, and is given by . Equation (2) shows that the predictive mean is just a linear combination of the model outputs used for training, weighted by their distance to , which is controlled by the choice of covariance function. This is identical to kriging in geostatistics, and we can indeed picture the emulation process as one of interpolation of the function output given some observations and an indication of how the function output varies with input parameters through the covariance function. The predictive variance is independent of the training set , and only given by the covariance function, and the distance of the test vector from the training input set. We can see that as the distance grows between and the samples in , the uncertainty will also grow, assuming a squared exponential covariance function as in Equation (1). From the point of view of computational effort, once the hyperparameters that control the covariance function have been defined (and maybe stored for later retrieval), predictions only require the calculation of a few Euclidean distances and some vector-matrix products. Provided the training set is small, these are fast operations (but note that if the N is very large, the Euclidean distance calculation required for estimating will dominate evaluating Equations (2) and (3)). The simplicity encoded in Equations (2) and (3) is what makes emulation fast: if the size of the training set is small (less than e.g., 500 samples), then the emulator will be very fast. The fact that we are inferring an approximate function of the computationally complex model that is e.g., smooth and continuous allows for this approach to accommodate complex non-linear models, as we shall demonstrate. A further important point is to note that once we have predicted the mean value of the function and its variance, it is simple to calculate the partial derivatives from the definition in Equation (2):
In Equation (4) we have a remarkable result: a generic way to calculate the partial derivatives of an arbitrary function given only a set of paired input/output model runs [20], a result that removes the need of using automatic differentiation tools to calculate gradients. In addition to being simple, note also by comparison to Equation (2) that evaluating the partial derivatives using Equation (4) will also be very fast. In contrast, automatic differentiation adjoint evaluation computational costs are of the same order of the original model (e.g., [7,8]). Having access to a good approximation to the gradient of an arbitrary function is a also major step in using GPs in many DA algorithms, where these are used for cost function minimisation, but also to produce linear approximations to non-linear models. Note that higher order derivatives are calculated directly from the repeated application of Equation (4), and allow the evaluation of e.g., Hessian matrices.
Given the reliance of the emulator in the training set, it is important to consider how to choose the input parameters to run the original model and subsequently collect the outputs. A common assumption is that the input parameters are uniformly distributed between a lower and upper boundary, so that a simple way to maximise the sampling of the resulting multidimensional space is to use a Latin hypercube sampling (LHS) scheme [19]. If the sensitivity of the model is expected to be higher in some regions, the LHS can be rephrased to use a different probability density function (pdf) than the uniform one introduced here to account for denser sampling in regions of very high sensitivity. This is a straightforward modification of the standard LHS algorithm.
Extension to Full Spectrum Emulation
So far, we have only considered the mapping of an input vector to a single scalar output. However, in many applications, the emulation of a vector output, such as a reflectance spectrum in the solar reflective domain is required. We demonstrate a way of doing this for functions that (typically, but not only) return a smooth output. The approach can be simply described as a decomposition of the model outputs produced during the GP training into a number of basis functions using e.g., principal component analysis (PCA). The spectral model outputs ( can then be written as a sum of weighted basis functions, , with weights given by . Typically, only a few basis functions are required to explain a vast percentage of the variation. A model output spectra can thus be written.
The basis functions (at lest in the space spanned by the training set) are orthogonal, suggesting that one could train a set of GP emulators to the weights in Equation (5), thus providing a set of mappings between the input vector to the model, and the weights . The reconstruction of the output spectrum is simply done by the linear expansion shown in Equation (5), which makes it straightforward to extend this formalism to calculate spectral gradients, uncertainty in the prediction, etc. We note that in the models that we have used below, the values of oscillate between 10 and 20. A larger number of basis functions will probably be needed for very detailed high spectral resolution models, and although this requires evaluating potentially many GPs, resulting in a slower emulator, in comparison with the original model, the run time of these emulators will still be orders of magnitude less than that of the original model. Note that in these cases, if looking for particular spectral features (e.g., absorption lines), it is important to ensure that the chosen subset of basis functions actually encode that very localised effect, which might require deploying a hierarchical structure of emulators, with a generic spectral emulator being used as a background emulator for particular regions where very accurate evaluation of the model is required. This is a topic that we will not cover in this paper.
In the following Section, we demonstrate the use of GP emulators to the emulation of state of the art vegetation canopy RT models, combinations of atmospheric and canopy RT models. We also show how parts of a model can be emulated, thus allowing the direct coupling of models using emulators.
3. GP Emulation Examples
The aim of this Section is to demonstrate the effectiveness of emulators in approximating common RT models used in remote sensing applications. In particular, we show emulators that emulators can be used as a “drop-in” replacement for common leaf and canopy RT models. We also show the use of the emulator approach in an atmospheric RT model across the solar reflective spectrum. By showing that it is entirely feasible to replace both leaf/canopy and atmospheric RT schemes with GP emulators, we highlight the possibilities for parameter retrieval in each case, which will be demonstrated in Section 4.
3.1. Emulating Soil-Leaf-Canopy RT Models
In this Section, we show the effectiveness of using emulators to emulate two typical canopy RT models: SAIL [34] and SEMIDISCRETE [35]. In both cases, leaf optical properties are provided by the PROSPECT model [36,37]. For these examples, we assume further that a particular viewing/illumination geometry is used, and we will emulate the directional surface reflectance in the seven MODIS bands located in the visible near- and shortwave-infrared, assuming a flat bandpass function for each band. The emulators are “trained” by running the original model combination with a set of input parameters given by a Latin hypercube sampling scheme between the minimum and maximum parameter boundaries (see Table 1). Both for PROSAIL and SEMIDISCRETE, we have used 300 samples for the training. The emulators will be trained by maximising the log-likelihood as indicated in [32] using a gradient descent algorithm, and assuming the covariance function introduced in Equation (1). To avoid local minima in the minimisation stage, we start the minimisation from five different random positions in hyperparameter space (we found that for these examples, five different realisations are often enough, but for other examples with poorer conditioning, more “restarts” might be needed). Once the hyperparameters have been thus elucidated, the emulators are ready to use.

Table 1.
Parameters for PROSAIL and SEMIDISCRETE, their symbols, units, quasi-linearising transformations and boundaries (both in real and in transformed space). ( Only PROSAIL, Only Semidiscrete.)
| Parameter | Symbol | Units | Minimum | Maximum | Transformation | Transformed Min | Transformed Max |
|---|---|---|---|---|---|---|---|
| Leaf layers | xleafn | – | 0.8 | 2.5 | – | – | – |
| Leaf chlorophyll
concentration | Cab | μ g·cm | 0.2 | 77 | 0.46 | 1 | |
| Leaf carotenoid concentration | Car | μ g·cm | 0 | 15 | 0.95 | 1 | |
| Senescent fraction | Csen | – | 0 | 1 | – | – | – |
| Equivalent water thickness | Cw | cm | 0.0043 | 0.0753 | 0.028 | 0.81 | |
| Leaf dry matter | Cm | g·cm | 0.0017 | 0.0331 | 0.037 | 0.84 | |
| Leaf area index | LAI | m ·m | 0 | 8 | 0.05 | 1 | |
| Average Leaf Angle | ALA | 0 | 90 | 0.44 | 0.56 | ||
| Soil brightness scalar | Bs | – | 0 | 2 | – | – | – |
| Soil moisture endmember | Ps | – | 0 | 1 | – | – | – |
| Weight of the first Price function | P1 | – | −0.5 | 1 | – | – | – |
| Weight of the second Price function | P2 | – | −0.5 | 1 | – | – | – |
An independent set of 1000 parameters drawn from a uniform distribution extending to the minimum and maximum boundaries of each parameter will be used to assess the quality of the emulation. To this end, a number of different metrics will be reported, such as root mean squared error (RMSE) as well as simple linear correlation. A good emulator is one that is faithful to the original model, exhibiting a strong linear correlation coefficient (e.g., upwards of 0.9), a small RMSE error. In addition to this, the slope and intercept of the linear model between emulator and simulator should be close to one and 0, respectively. Finally, the maximum absolute error (MAE) should be of the same order as the RMSE. A small RMSE value is defined in relation to the typical observational error in surface reflectance (around 0.01 in units of reflectance, or around 10%–15% of the value of reflectance [38] (note that due to the likely correlation induced by the atmospheric correction retrieval, this value is probably optimistic). The rationale behind this is based on the fact that if the error in the emulation is assumed to be independent of the observational error, and much smaller, then it can be neglected.
The first example shows the results of emulating the SAIL and SEMIDISCRETE canopy models, with leaf transmittance and reflectance provided by the PROSPECT model. The models were run to estimate surface directional reflectance at a particular acquisition geometry, for the MODIS bands (assuming a flat bandpass function over each band), as these bands are representative of a large number of sensors. In both cases, the input training sets was of 300 samples. The results in Figure 1 (summarised in Table 2) show that the emulation performance is excellent: the correlation coefficient is in excess of 0.99 for all bands, and the RMSE is two orders of magnitude less than the typical observational error in surface reflectance. Additionally, the emulators provide an approximation to the Jacobian and Hessian of the RT model. Although in Figure 1 we only show the results for a single geometry, very similar results (i.e., RMSE errors of the same order, and correlation coefficients in excess of 0.99) are obtained using other geometries.

Table 2.
Results of the validation for the SEMIDISCRETE emulator using an independent set of 1000 model realisations over the MODIS bands. The emulator was created by using 300 forward simulator model runs, selected with a Latin hypercube sampling design between the boundaries indicated in Table 1.
| MODIS Band | Slope | Intercept | R | RMSE | MAE |
|---|---|---|---|---|---|
| 1 | 1.002 | 1.222e-05 | 0.9995 | 9.774e-04 | 5.175e-03 |
| 2 | 0.999 | 1.562e-04 | 0.9998 | 5.602e-04 | 1.063e-02 |
| 3 | 1.004 | −3.362e-05 | 0.9996 | 9.181e-04 | 2.371e-03 |
| 4 | 1.000 | 2.784e-05 | 0.9999 | 5.255e-04 | 2.048e-03 |
| 5 | 0.993 | 1.591e-03 | 0.9990 | 1.437e-03 | 3.588e-02 |
| 6 | 0.998 | 4.182e-04 | 0.9995 | 9.490e-04 | 1.587e-02 |
| 7 | 1.000 | 1.183e-04 | 0.9997 | 8.194e-04 | 1.135e-02 |
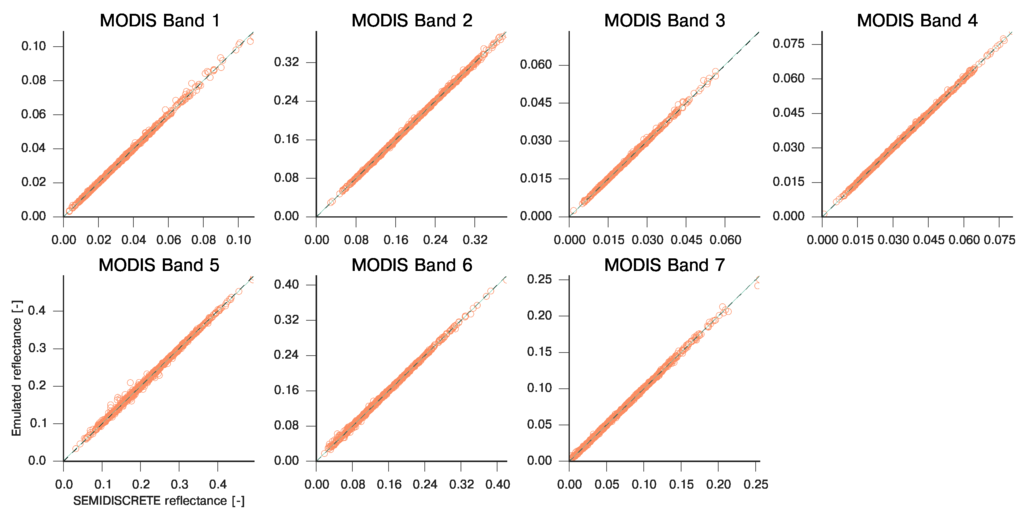
Figure 1.
Emulation performance for SEMIDISCRETE over the seven MODIS bands. The emulator was trained with 300 forward model runs, and validated with an independently produced set of 1000 parameters. Acquisition geometry was set to nadir illumination and viewing zenith.
Figure 1.
Emulation performance for SEMIDISCRETE over the seven MODIS bands. The emulator was trained with 300 forward model runs, and validated with an independently produced set of 1000 parameters. Acquisition geometry was set to nadir illumination and viewing zenith.
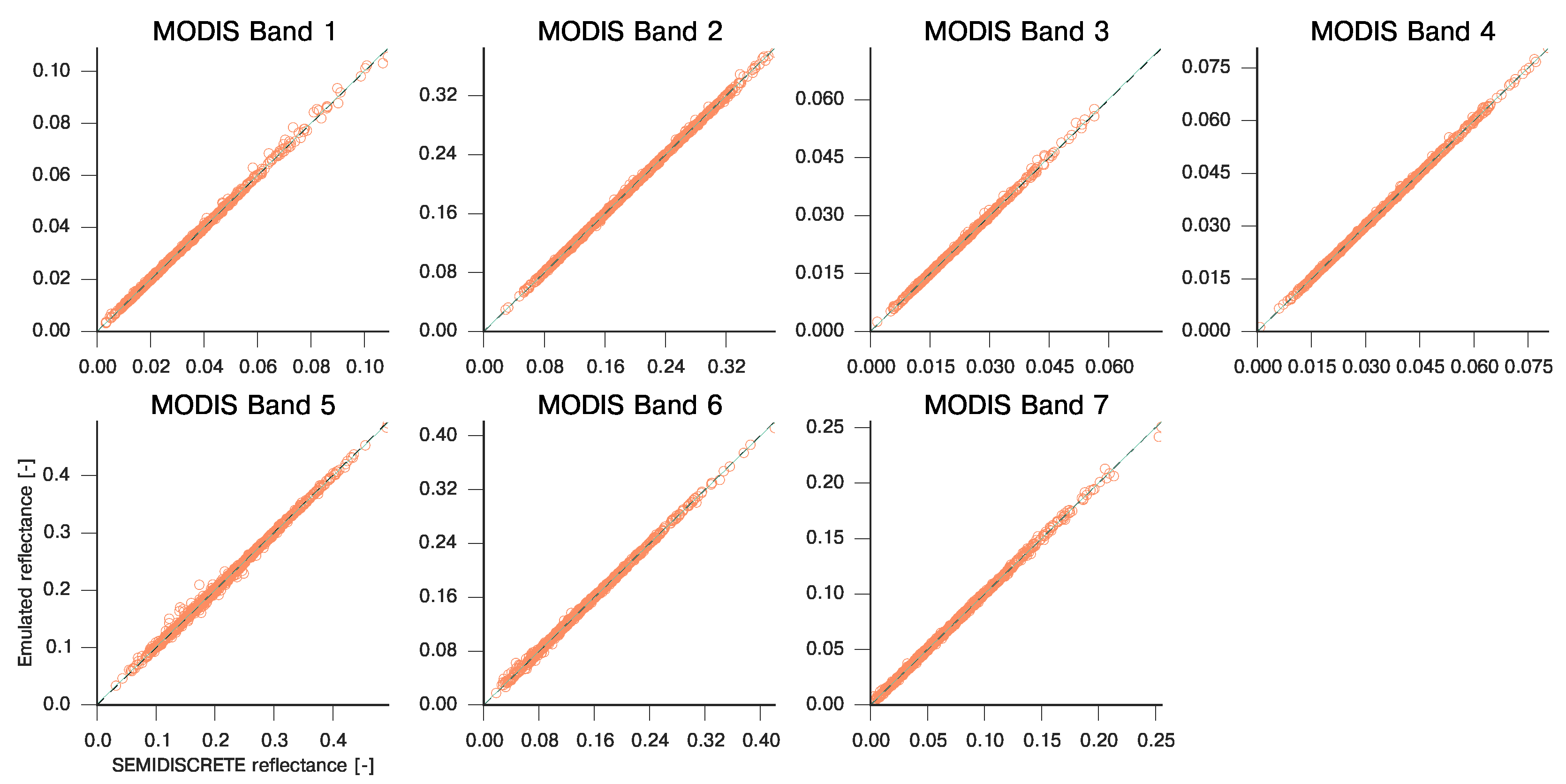
Figure 2 shows the same results for the PROSAIL leaf and canopy model (results are summarised in Table 3). For the tested scenarios, emulation results in a near perfect reconstruction of the original model, with just some small but still acceptable error for larger reflectances in the blue and green bands for MODIS due to poorly sampled parameter space. This demonstrates the suitability of the emulators for this task. In terms of timing on a standard Intel Core5 quadcore CPU, running at 2.2 GHz, a spectral run of PROSAIL took 10 s, whereas the spectral SEMIDISCRETE run took around 40 s. The emulator for each band takes of around 1 ms, so the speed-up in the emulation between 10,000 and 40,000 times the original model (note that this figures are only indicative). The speed of the emulator is only a factor of the size of training sample, so faster emulators can be obtained with fewer training samples, paying a price in terms of emulation accuracy. We have found that for these models, using between 200 and 300 samples to train the emulator is often enough, but this will be application dependent.
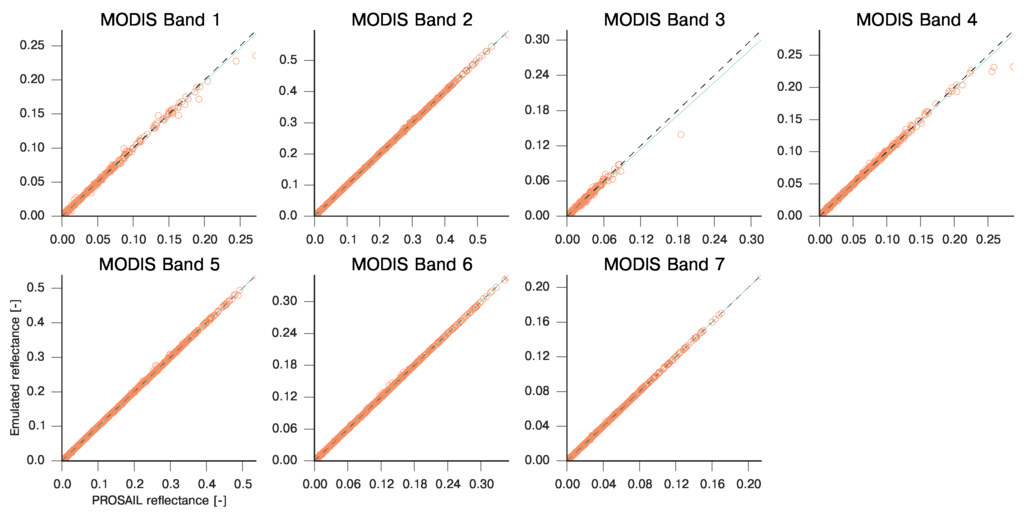
Figure 2.
Emulation performance for PROSAIL over the seven MODIS bands. The emulator was trained with 300 forward model runs, and validated with an independently produced set of 1000 parameters. Acquisition geometry was set to nadir illumination and viewing zenith.
Figure 2.
Emulation performance for PROSAIL over the seven MODIS bands. The emulator was trained with 300 forward model runs, and validated with an independently produced set of 1000 parameters. Acquisition geometry was set to nadir illumination and viewing zenith.
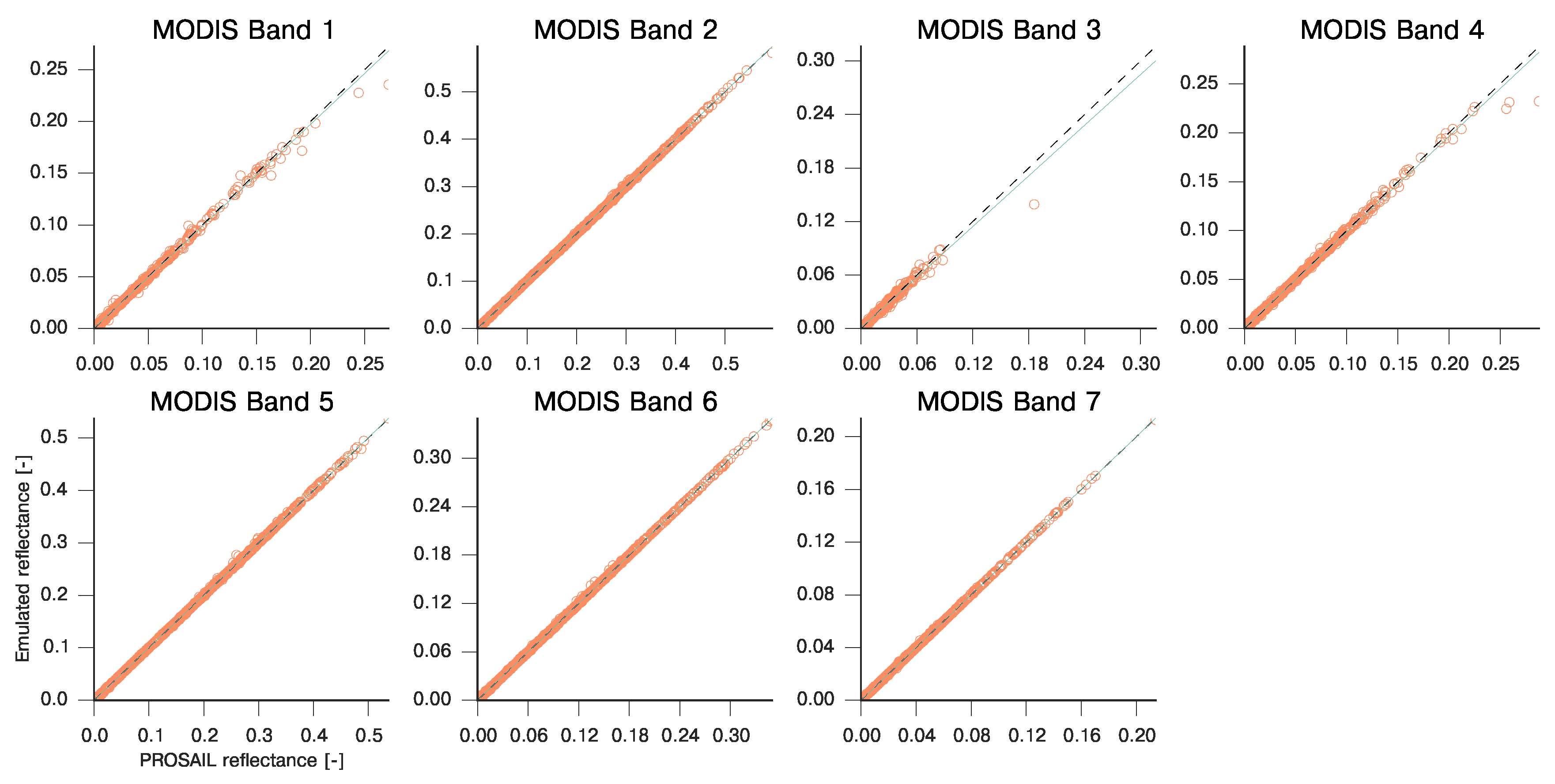

Table 3.
Results of the validation for the PROSAIL emulator using an independent set of 1000 model realisations over the MODIS bands. The emulator was created by using 300 forward simulator model runs, selected with a Latin hypercube sampling design between the boundaries indicated in Table 1.
| MODIS Band | Slope | Intercept | R | RMSE | MAE |
|---|---|---|---|---|---|
| 1 | 0.984 | 0.000 | 0.999 | 1.669e-03 | 3.679e-02 |
| 2 | 1.000 | −0.000 | 1.000 | 2.681e-04 | 1.307e-02 |
| 3 | 0.947 | 0.001 | 0.990 | 4.349e-03 | 4.678e-02 |
| 4 | 0.977 | 0.001 | 0.998 | 1.987e-03 | 5.585e-02 |
| 5 | 1.001 | −0.000 | 1.000 | 3.523e-04 | 1.722e-02 |
| 6 | 1.000 | 0.000 | 1.000 | 3.210e-04 | 7.791e-03 |
| 7 | 1.000 | 0.000 | 1.000 | 2.416e-04 | 2.392e-03 |
3.2. Emulation of a Coupled Soil-Leaf-Canopy-Atmosphere RT Model Combination: PROSAIL and 6S
A further important example is the emulation of top-of-atmosphere (TOA) reflectance as a function of the surface state, but also of atmospheric composition. This is done by coupling the PROSPECT and SAIL models with the 6S atmospheric RT model of [39]. We assume a Lambertian surface for the surface-atmosphere coupling, flat bandpass function for each band, and a constant illumination/acquisition geometry (in this case, the solar zenith angle was set to and the view zenith angle was set to . The relative azimuth angle was also set to ). The Lambertian assumption results in the following expression for TOA reflectance [39,40,41]:
where is the intrinsic reflectance of the atmosphere, is the gaseous transmittance, and are respectively the downward and upward transmission factors, S is the spherical albedo of the atmosphere and ρ is the surface reflectance. E is the extraterrestrial radiation and is the cosine of the solar zenith angle. Assuming a continental aerosol distribution, the atmospheric effect is governed by three parameters: (i) the aerosol optical thickness at 550 nm (AOT); (ii) the total water vapour content (WVC); and (iii) the ozone concentration. Therefore, we extend the state vector to include these three terms (in addition to the leaf and canopy parameters), and as before, train an emulator per MODIS band mapping from canopy and atmospheric parameters to TOA reflectance, using 400 samples chosen using a Latin hypercube sampling design.
The results from validation using an independent 1000 samples (drawn using the same procedure as for the previous Section) set are shown in Figure 3 and summarised in Table 4, showing again the excellent predictive ability of the emulators (e.g., slope of the validation regression close to unity, correlation in excess of 0.99 and RMSE small compared with typical TOA reflectance uncertainty). The emulation error, results in this case in a signal to noise ratio (SNR) of around 40 dB. In terms of SNR, the emulation error is larger than the noted observation uncertainty for MODIS (with a design goal for the MODIS sensor of SNR better than 70 dB [42]. Remember that as well as emulating the original model, the emulators are also providing an approximation to the Jacobian of the model. The latter has been compared with numerical estimates obtained by finite differences using the full model, and found to be accurate: correlation is in excess of 0.99 and bias is better than 0.01 (results not shown).
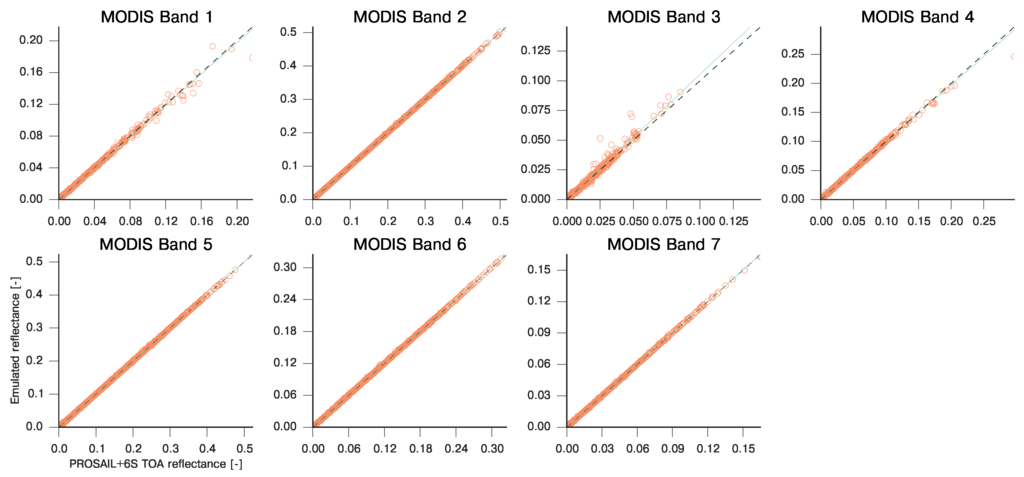
Figure 3.
Validation result of the single band coupled PROSAIL and 6S models of top-of-atmosphere reflectance over the MODIS bands. The coupling is done under the assumption that the land surface is Lambertian, and using a continental aerosol model. The emulator uses the PROSAIL parameters as inputs, extended by aerosol optical thickness (AOT), atmospheric water vapour content (WVC) and ozone concentration (). The validation has been carried out on a set of 1000 parameter values drawn from uniform independent distribution over the parameter ranges.
Figure 3.
Validation result of the single band coupled PROSAIL and 6S models of top-of-atmosphere reflectance over the MODIS bands. The coupling is done under the assumption that the land surface is Lambertian, and using a continental aerosol model. The emulator uses the PROSAIL parameters as inputs, extended by aerosol optical thickness (AOT), atmospheric water vapour content (WVC) and ozone concentration (). The validation has been carried out on a set of 1000 parameter values drawn from uniform independent distribution over the parameter ranges.
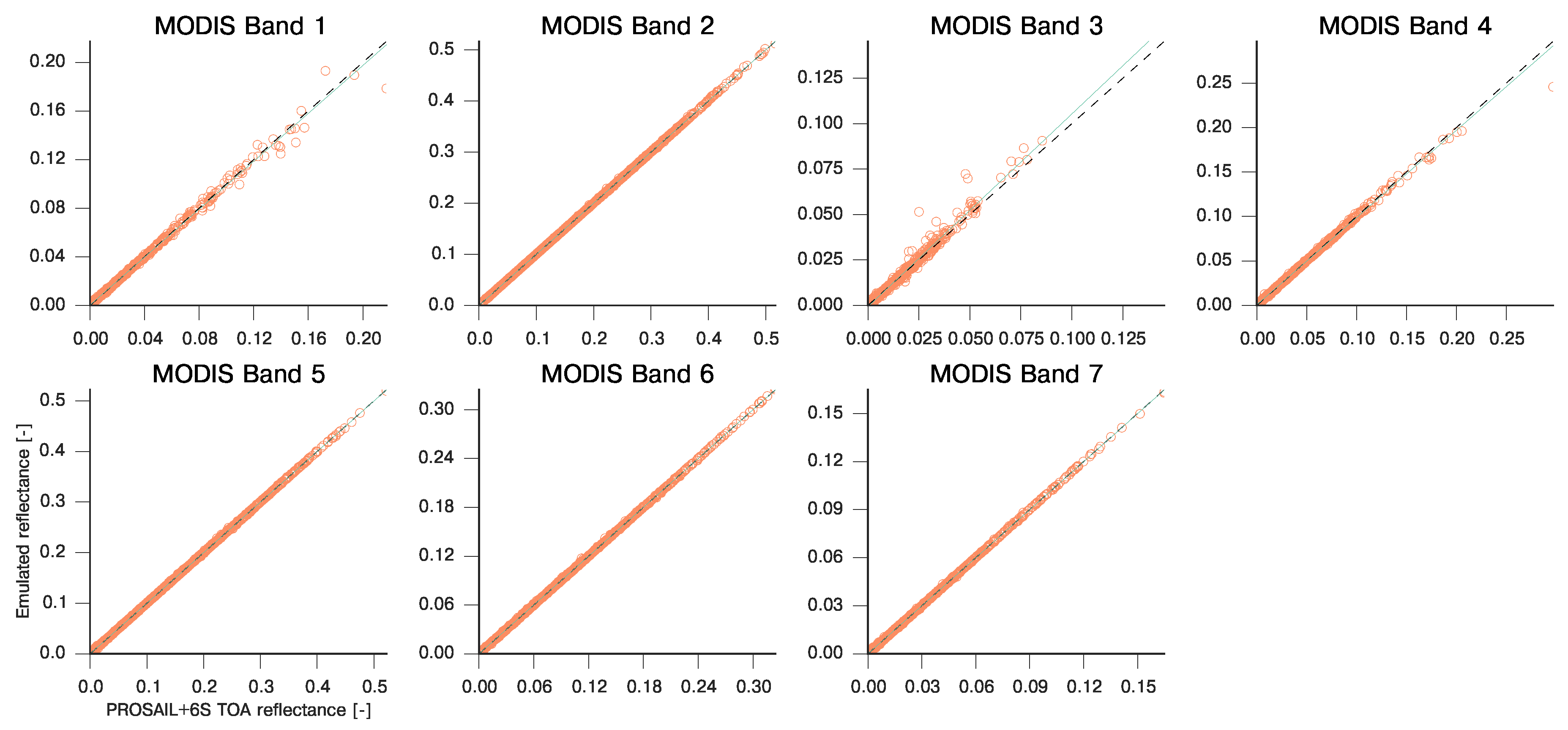

Table 4.
Results of the validation for the coupled PROSAIL + 6S emulator using an independent set of 1000 model realisations over the MODIS bands. The emulators were trained running the PROSAIL + 6S model combination 400 times over a sampling pattern determined by Latin hypercube design. The coupling between the surface and atmosphere is assumed Lambertian.
| MODIS Band | Slope | Intercept | R | RMSE | MAE |
|---|---|---|---|---|---|
| 1 | 0.985 | 0.000 | 0.998 | 2.087e-03 | 3.889e-02 |
| 2 | 1.001 | −0.000 | 1.000 | 1.888e-04 | 5.694e-03 |
| 3 | 1.061 | −0.001 | 0.989 | 4.996e-03 | 2.635e-02 |
| 4 | 0.981 | 0.001 | 0.998 | 1.730e-03 | 5.136e-02 |
| 5 | 0.999 | 0.000 | 1.000 | 2.282e-04 | 5.256e-03 |
| 6 | 1.000 | 0.000 | 1.000 | 2.342e-04 | 4.954e-03 |
| 7 | 0.999 | 0.000 | 1.000 | 2.885e-04 | 1.857e-03 |
The emulation of the reflectance and its partial derivatives is done in a small fraction of the time it would take to run the coupled model. In the previous three examples, the run time of the emulation is the same: each emulation (and gradient estimation) takes around 1.5 ms in a contemporary computer, and the cost scales with number of training sample (in the previous example, we have used 400 for all the three experiments). Running the coupled atmospheric and canopy model takes on the same computer around 45 s per model, which results in a speed-up factor of 30,000. It is important to remark that this is done using a simple approach that only requires a few linear algebra operations, and where the biggest cost is the training of the emulators (typically, this takes less than a minute per band), a one-off cost as the hyperparameters and training set can be stored for re-use. Also, generating the training set is a task that is trivial to parallelise in a computer cluster, even if the model cost is more expensive than the ones envisaged here. Note that if the gradient estimation was required, each full model run would require 15 model runs to calculate the finite differences, effectively making the equivalent simulator take more than 11 min, whereas the cost of the emulation already includes the estimation of the gradient.
These results indicate that even a naive approach to emulation is able to replicate fairly sophisticated RT models of vegetation over individual bands. Moreover, the fact that a coupled surface-atmosphere system works opens the door to direct parameter retrievals that include atmospheric composition parameters, with the desirable property that the effect of the uncertainty that results from the atmospheric RT model in the surface parameters is directly accounted for. If surface reflectance is used, full uncertainty on the surface reflectance data is required. This is usually not reported with products, and assumptions of band independence and constant uncertainties are typically assumed [15,43].
3.3. Spectral Emulation of a Coupled Soil-Leaf-Canopy RT Model Combination
The previous examples show the feasibility of emulating complex models over relatively narrow spectral bands. While these cases are important in practice, it is sometimes desirable to emulate over the entire optical reflective region of the spectrum, e.g., from 400 to 2500 nm. This might be because hyperspectral data might be available, or because different bandpass functions need to be simulated. In some cases, bands that are very close to each other might exhibit strong correlations that might in some cases not be resolved by the individual band emulators described above. To demonstrate the multivariate output of the emulators, we demonstrate the same soil-leaf-canopy setup presented above, focussing on the PROSPECT+PROSAIL combination. The method has already been introduced in Section 2, and as said there, relies on the ability to apply a principal component transformation to the spectral data, and emulating a subset of the loadings. For this experiment, we have taken 250 spectra, the result of running the PROSAIL model with 250 input vectors determined by Latin hypercube sampling over the ranges in Table 1. We have chosen to keep the first 11 principal components, which in this case resulted in 99% of the total variance retained, and fitted emulators to each of the loadings. As above, we have produced a random set of 1000 input vectors (again chosen within the boundaries in Table 1) as an independent validation.
In the top panel of Figure 4 we show the results of the validation. We can see that the mean emulation error is very close to zero, as well as being spectrally flat. The spread over the validation set is very small, with maximum deviations of around in units of reflectance, and it appears larger around the visible-red edge region. Note that the emulation error is about one order of magnitude less than the observational error in typical instruments (as earlier, assuming an observational uncertainty variance of around 0.1 in units of reflectance as per [38] although these figures are given for atmospherically corrected multispectral sensors). This good performance is shown in the bottom panel of Figure 4, where some of the validation spectra and their emulations are plotted together, in many cases being hard to differentiate from each other. Although the results shown here are for a particular angular configuration, similar results (with residuals not larger than 0.006 in units of reflectance) have been obtained for other geometries. Additionally, we show a validation of the emulated gradient against an estimate of the model gradient using finite differences in Figure 5. We show the case of the gradient of PROSAIL with respect to leaf chlorophyll concentration at 650 nm and with respect to at 850 nm. The emulated gradient is very close to the finite differences estimate, with the emulator showing a small discrepancy for lower gradient values of at 850 nm, which could well be an issue with the finite differences estimate, itself an approximation to the gradient.
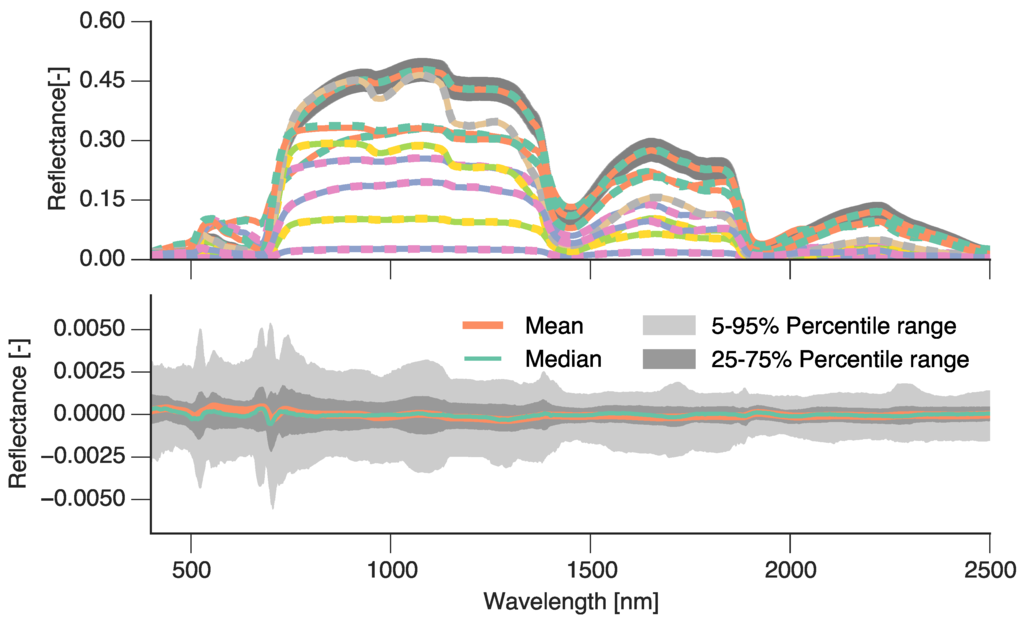
Figure 4.
(Top panel) A set of ten simulated PROSAIL spectra (full lines) and their emulated spectra using 250 forward model runs as a training set (dashed lines). The topmost emulated spectrum has a grey area around it showing the emulation error. (Bottom panel) Distribution of the residuals (full model minus emulator) of the 1000 model realisations validation dataset. We show the mean (orange line), median (green line), and the 5%–95% (light grey) and 25%–75% (dark grey) percentile ranges.
Figure 4.
(Top panel) A set of ten simulated PROSAIL spectra (full lines) and their emulated spectra using 250 forward model runs as a training set (dashed lines). The topmost emulated spectrum has a grey area around it showing the emulation error. (Bottom panel) Distribution of the residuals (full model minus emulator) of the 1000 model realisations validation dataset. We show the mean (orange line), median (green line), and the 5%–95% (light grey) and 25%–75% (dark grey) percentile ranges.
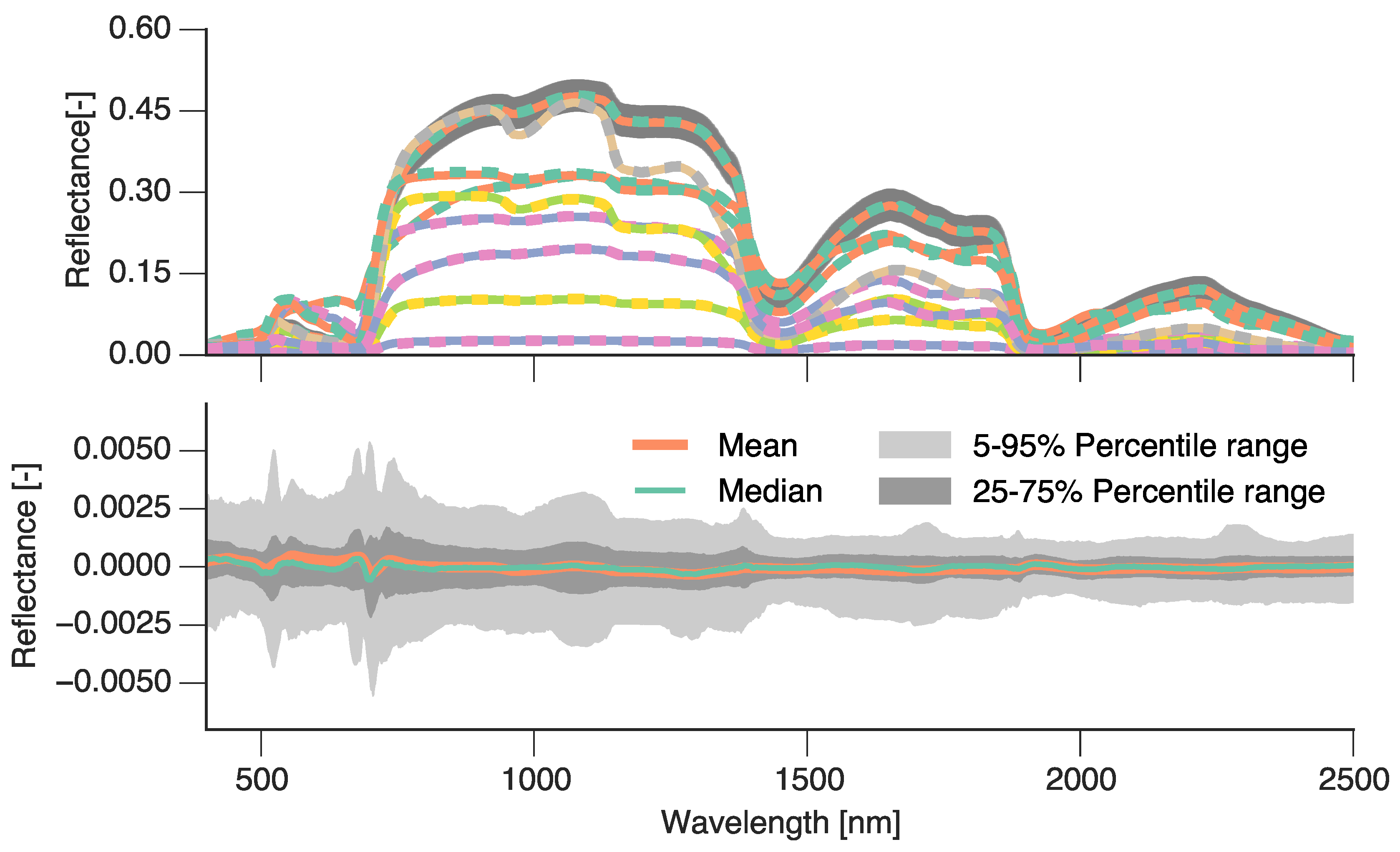
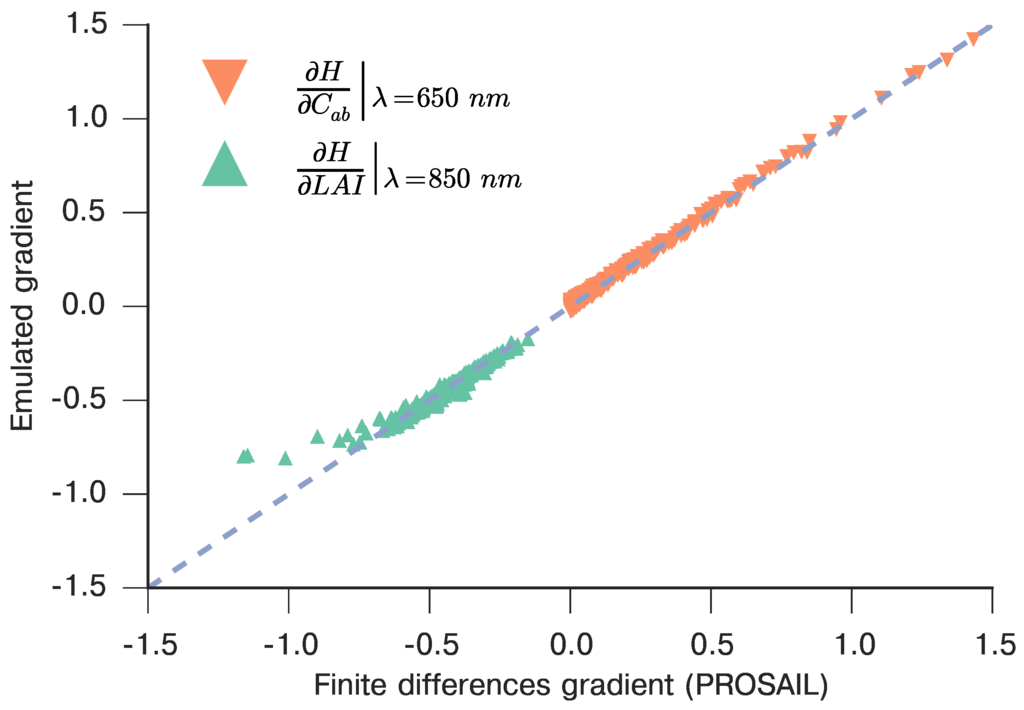
Figure 5.
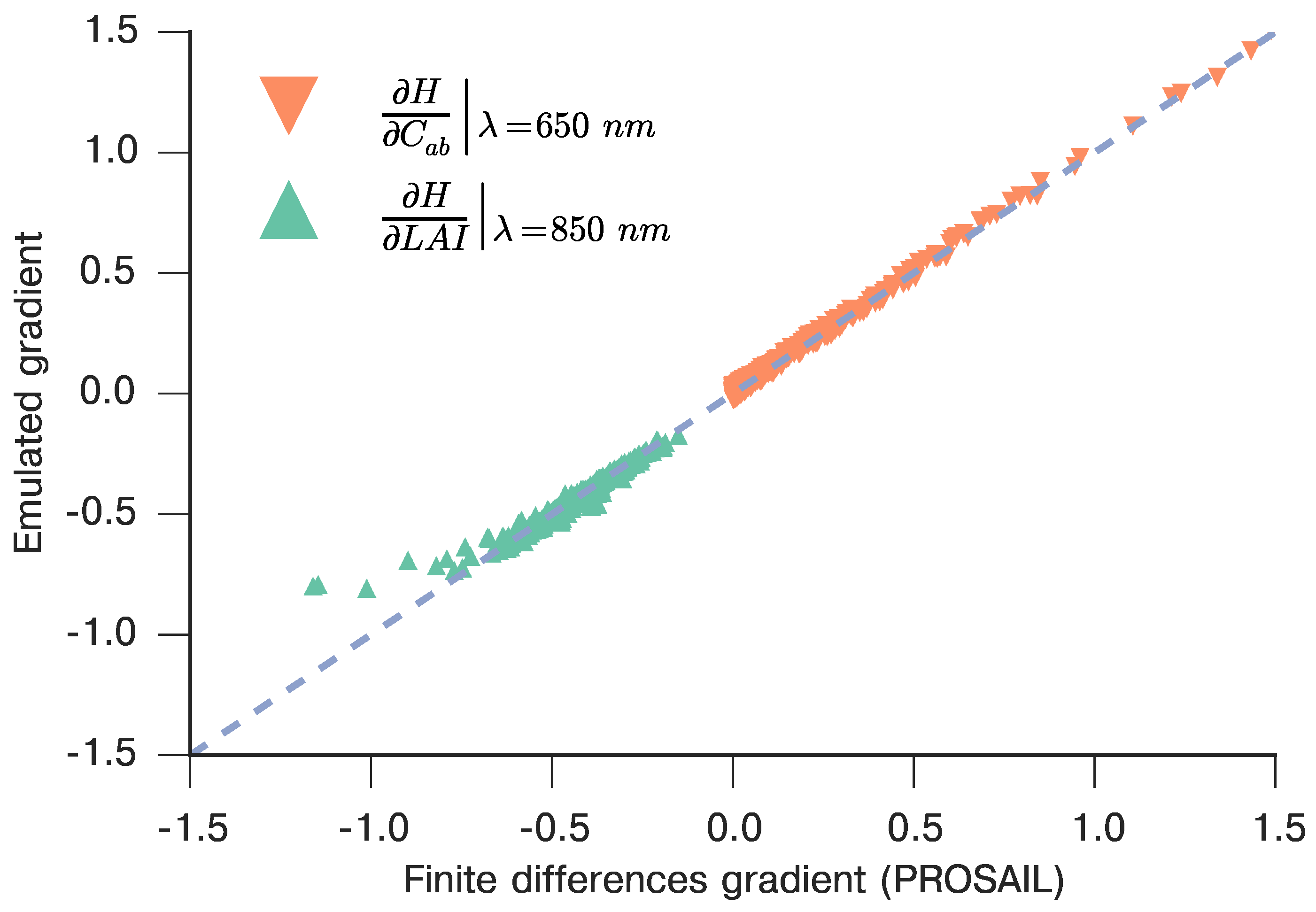
The emulated gradient of the PROSAIL RT model (estimated using a finite difference approximation with a step size of which was set to of the transformed parameter range). We show the gradient with respect to leaf chlorophyll concentration at 650 nm (orange triangles) and with respect to at 850 nm (green triangles). The gradient is calculated around the 1000 independent samples used to validate the model in Figure 4.
Figure 5.
The emulated gradient of the PROSAIL RT model (estimated using a finite difference approximation with a step size of which was set to of the transformed parameter range). We show the gradient with respect to leaf chlorophyll concentration at 650 nm (orange triangles) and with respect to at 850 nm (green triangles). The gradient is calculated around the 1000 independent samples used to validate the model in Figure 4.
3.4. Spectral Emulation of Atmospheric Effects
The examples introduced in the previous Section demonstrate the ability of emulators to accurately model single waveband, single acquisition scenarios. Using the approach introduced in Section 2, we can demonstrate the emulation of full spectra. A particularly useful application is the emulation of the different components of Equation (6): rather than emulate the coupled model, it might instead be desirable to emulate the atmospheric effects over the solar reflective spectrum. This opens the possibility of using other surface reflectance models (e.g., linear kernel models [44]), and applying the approach to generic sensors, not only to a particular sensor as in the previous examples where we only considered an idealised instrument with “MODIS-like” spectral properties. To demonstrate this approach, we rewrite Equation (6) as
where we have written the top-of-atmosphere reflectance, as a function of the path radiance (scattered incoming radiation inside the atmosphere), , a (bi-directional) transmittance term, , the spherical albedo of the atmosphere, and the top-of-canopy reflectance, ρ. , and can be calculated with e.g., 6S, and are functions of gas concentrations, aerosol species and abundance, illumination/acquisition geometry, incoming solar radiation and the amount of atmosphere the incoming radiation has to cross. In Figure 6 we show two examples of , and between 400 and 2500 nm. In order to test the emulation of the 6S model, we run the complete model for 200 sets of parameters, for a particular acquisition geometry. The parameters were specified using a Latin hypercube sampling scheme. Secondly, a set of 500 forward model runs where also run, but in this case, the input parameters were chosen using a uniform random scheme. The outputs of these 700 model runs were spectra of , and . The first batch of 200 simulations was used for training, whereas the second batch of 500 was used for validation. Additionally, strong absorption regions (1100–1140 nm, 1325–1475 and 1800–2000 nm)were removed from the spectra. For the first batch (the training set), the three output spectra of , and were decomposed using PCA. For , we chose the first four principal components (which account for more than 97% of the variance). For and , we chose two and one principal components, which respectively accounted for more than 99% of the variance. This is unsurprising, given the relatively simple shapes of of and in comparison with , which suggest that only one or two basis functions will be required. The emulators were then used to predict the validation dataset. Three individual examples of the validation set are shown in Figure 7, with the full statistics of the spectral mismatch of the emulation versus the true model shown in Figure 8, where we see that the results of the emulation are excellent, with the mismatch between full and emulated model output being mostly flat and very close to zero over the entire spectral range for the three output parameters, and showing very small deviations from the zero line. Note that the vertical scales in Figure 6 and Figure 8 are different). Although these experimental results are shown here only for a single acquisition/illumination geometry and time of the year, the results are similar for other geometric configurations and other periods. Given the small emulation error, it would appear that emulating the different atmospheric components is a feasible way to derive powerful methods for atmospheric correction which are still based on the physics embedded in the original atmospheric RT model.
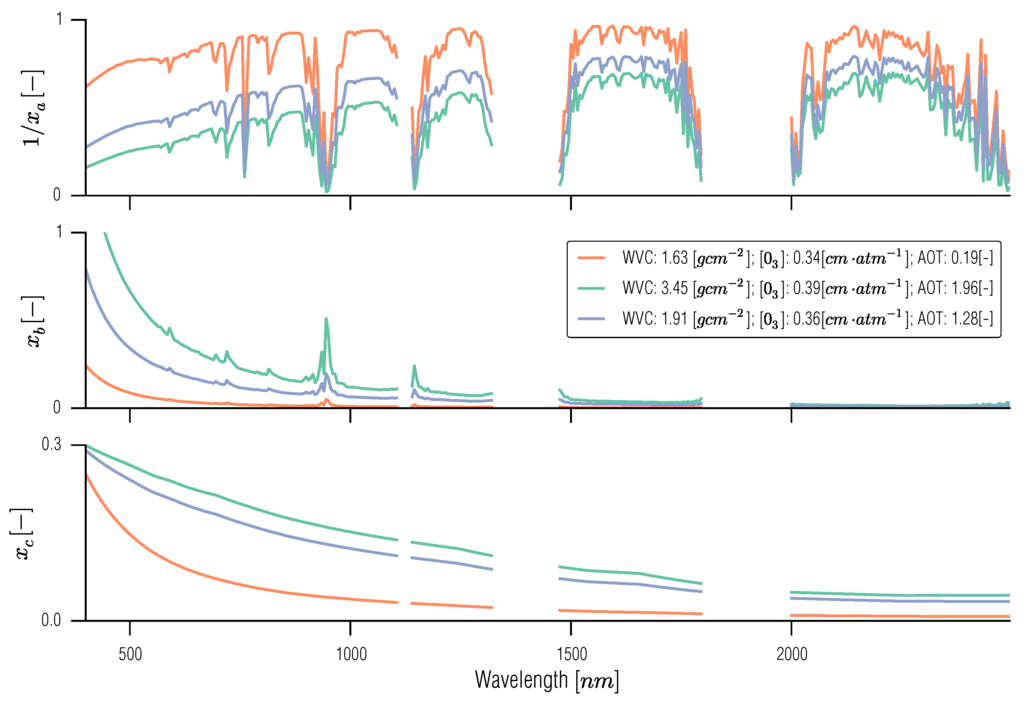
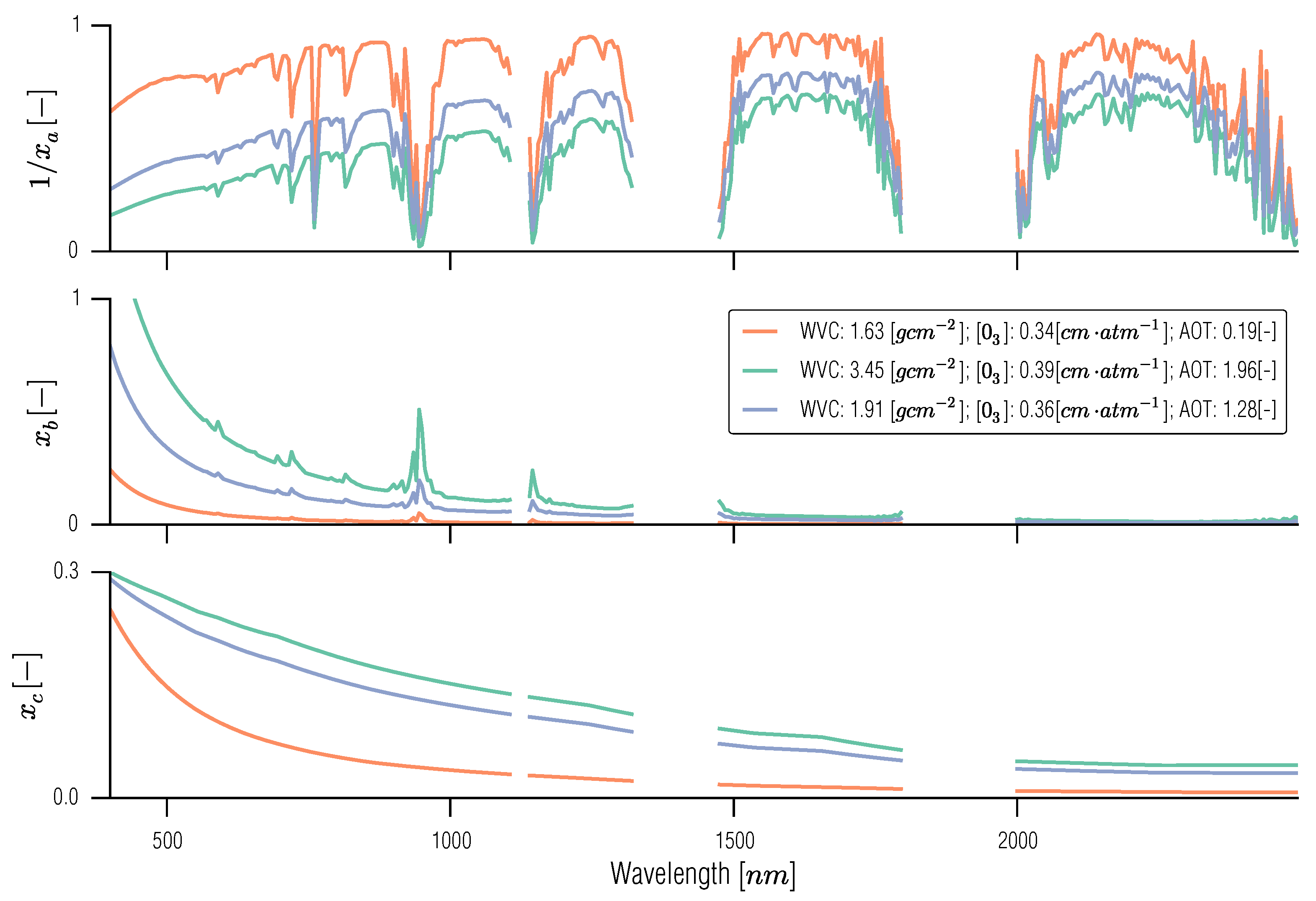
Figure 6.
Sample spectra for , and simulated with 6S, assuming “Continental” aerosol type, nadir looking illumination geometry and view zenith of . The simulation was done for day of year 138 (mid-may), and shows two spectra for two different atmospheric compositions, having different water vapour, ozone and aerosol optical depths.
Figure 6.
Sample spectra for , and simulated with 6S, assuming “Continental” aerosol type, nadir looking illumination geometry and view zenith of . The simulation was done for day of year 138 (mid-may), and shows two spectra for two different atmospheric compositions, having different water vapour, ozone and aerosol optical depths.
3.5. Full BRDF Coupling of a Soil-Leaf-Canopy Model and Atmospheric Spectral RT Model
In the previous sections, we have seen how to spectrally emulate vegetation RT models and atmospheric models. In this section, we demonstrate the emulation of the coupled vegetation and atmospheric models, providing a mapping from both atmospheric and vegetation parameters to TOA reflectance. In this case, we will relax the Lambertian assumption introduced in Equation (7) and will instead implement a full BRDF coupling of the land surface and atmosphere. The set of input parameters for this experiment now comprises the aerosol optical thickness (AOT), atmospheric water vapour content, leaf chlorophyll concentration, leaf brown matter pigment fraction, leaf dry matter, canopy LAI, and soil brightness parameter. We additionally set the illumination/acquisition to a solar zenith angle of , a view zenith angle of and a relative azimuth angle of . The spectral resolution was set to 5 nm over the 400–2500 nm range. A set of 200 parameters was used to train the emulators (as above, chosen using a Latin hypercube sampling design), and an independent set of 1000 parameters, with their elements uniformly distributed were used for validation. In this case, the water absorption bands were taken into account for the emulation training (as opposed to the previous section, where they were masked out). This resulted in the PCA requiring a total of 59 principal components to capture 99% of the variance (although this number drops significantly if the strong absorption bands are removed). An example of typical spectra and their emulation pairs is shown in Figure 9, where it is clear that the emulator is able to reproduce the general trend of the full model simulation, as well as being able to reproduce the small scale features. The validation results with the 1000 independent parameter set are shown in Figure 10. It is immediately clear that the mean difference between emulator and full model is very close to zero over the entire spectrum. The RMSE distribution has is bounded to for 5%–95% quantile range, although a few outliers remain. Most of the disagreement occurs in a few distinct spectral bands, and a slight decrease in this disagreement can be seen moving from lower to higher wavelengths. Overall, the emulation is extremely successful at replicating the full model, and although 59 basis functions were required, the emulator prediction time is negligible in comparison to the coupled model run time (which on a contemporary Intel Corei5 2.2 GHz CPU took 12 min versus 0.3 s that the emulator takes).
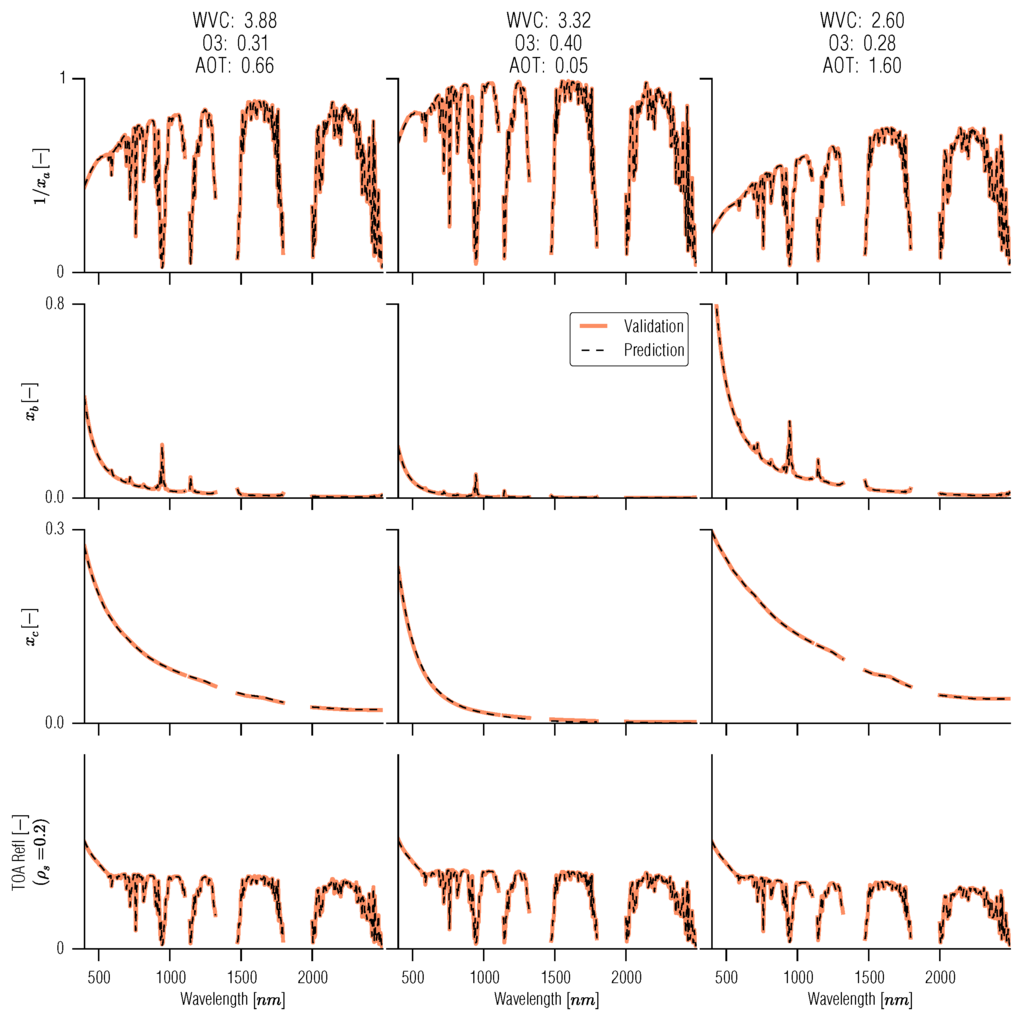
Figure 7.
Three examples of emulation of the 6S RT model. The three columns show three different input parameter sets (indicated at the top). The set-up was for day 138 (mid-may), with nadir illumination geometry and view zenith or , aerosol properties are selected as “Continental”, and we show the output spectra from the model and the emulation (note that these particular model configurations were not part of the data used to train the emulators).
Figure 7.
Three examples of emulation of the 6S RT model. The three columns show three different input parameter sets (indicated at the top). The set-up was for day 138 (mid-may), with nadir illumination geometry and view zenith or , aerosol properties are selected as “Continental”, and we show the output spectra from the model and the emulation (note that these particular model configurations were not part of the data used to train the emulators).
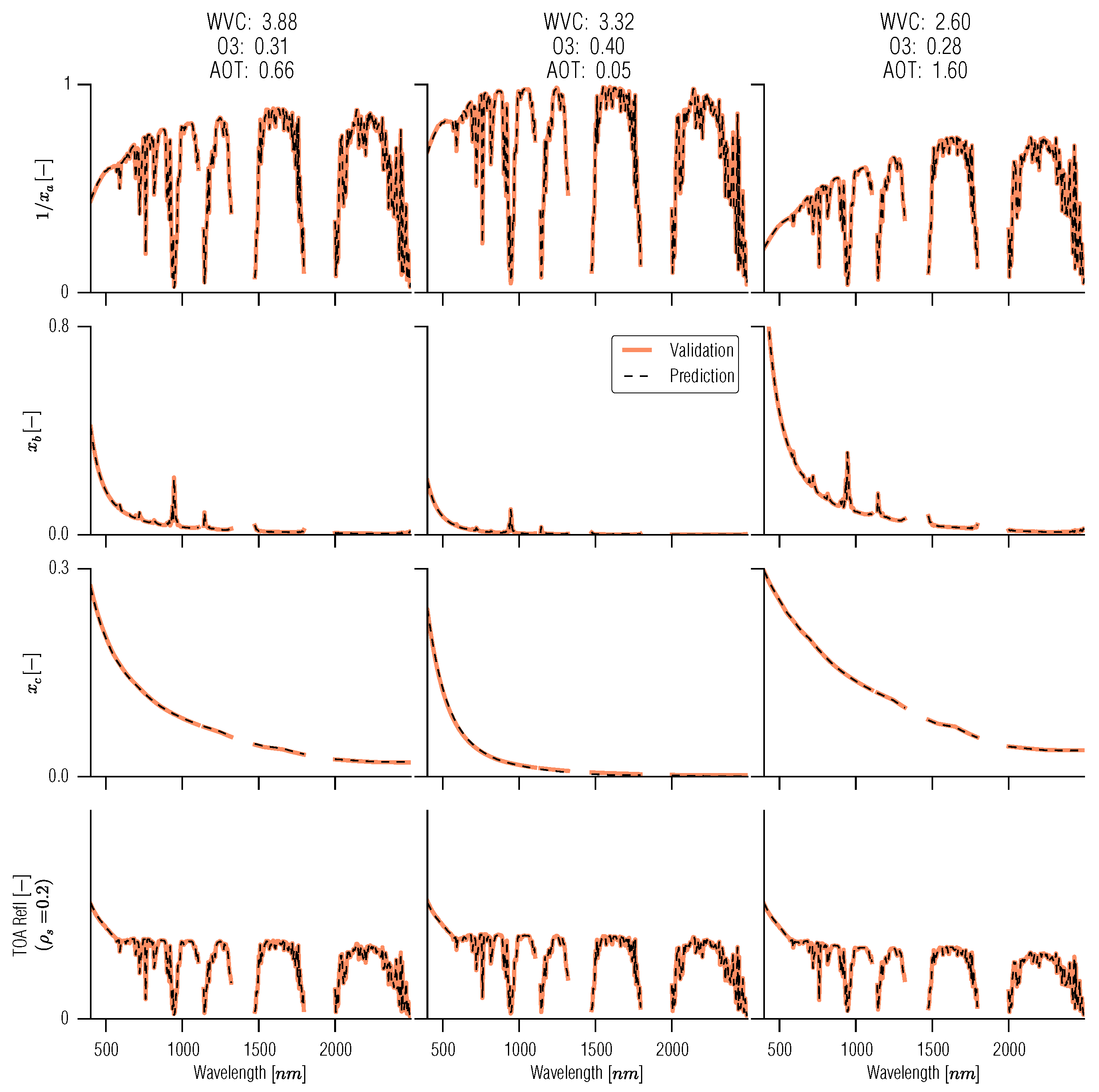
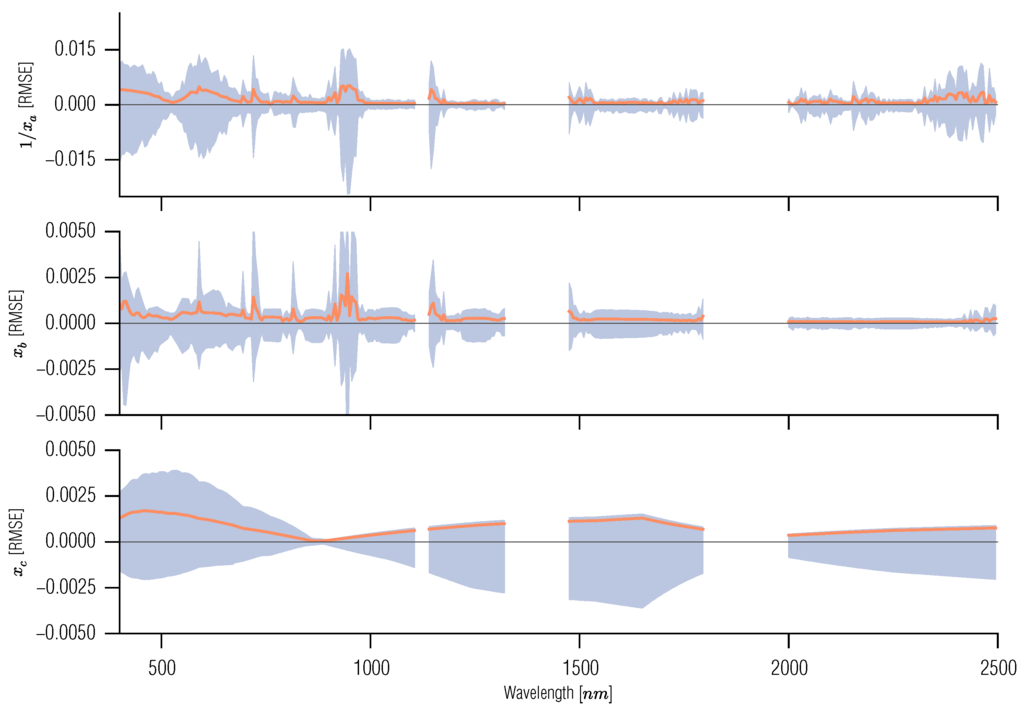
Figure 8.
Validation of the 6S spectral emulation. The black line shows the mean difference over the 500 sample validation set, whereas the grey areas show the RMSE.
Figure 8.
Validation of the 6S spectral emulation. The black line shows the mean difference over the 500 sample validation set, whereas the grey areas show the RMSE.
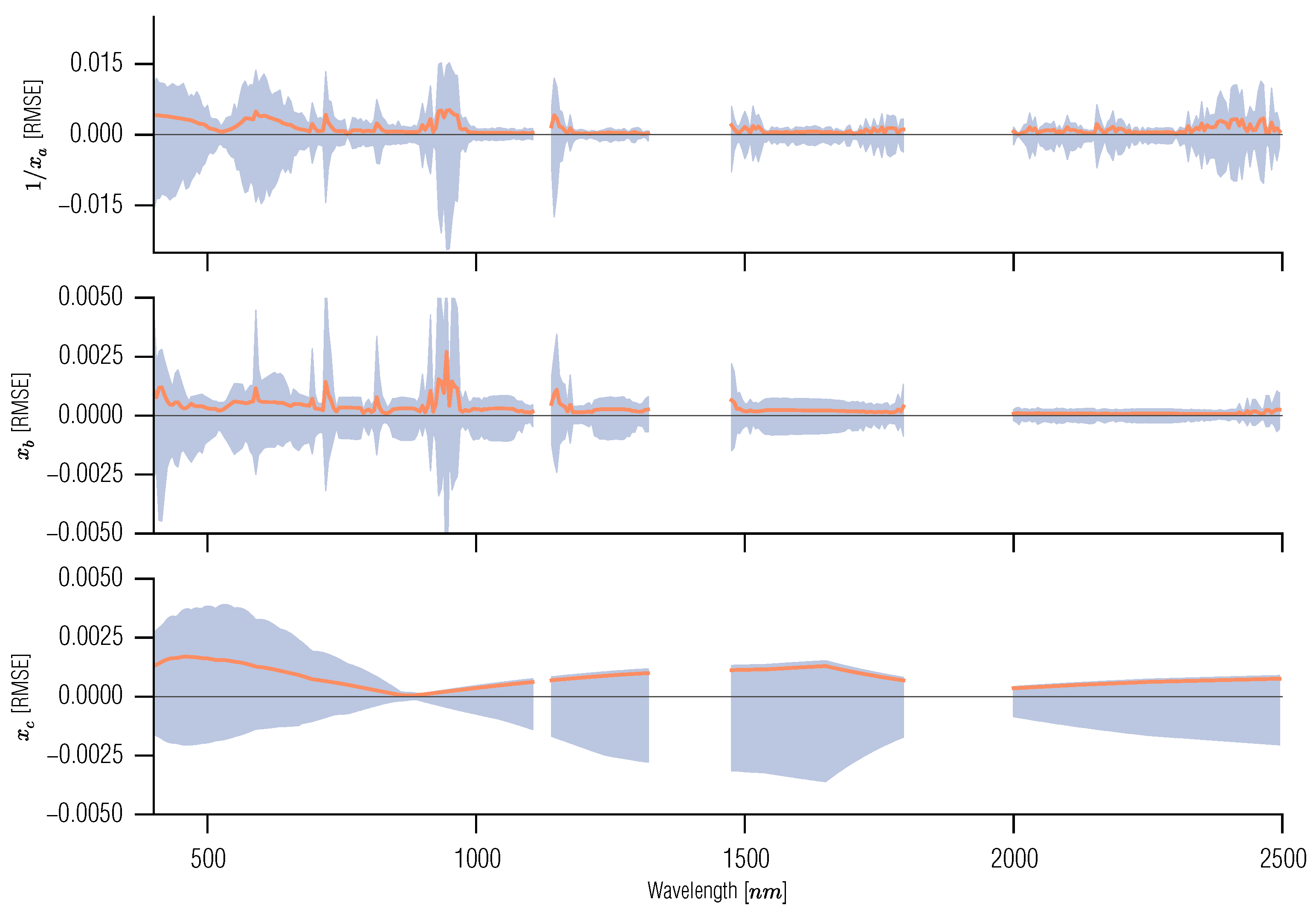
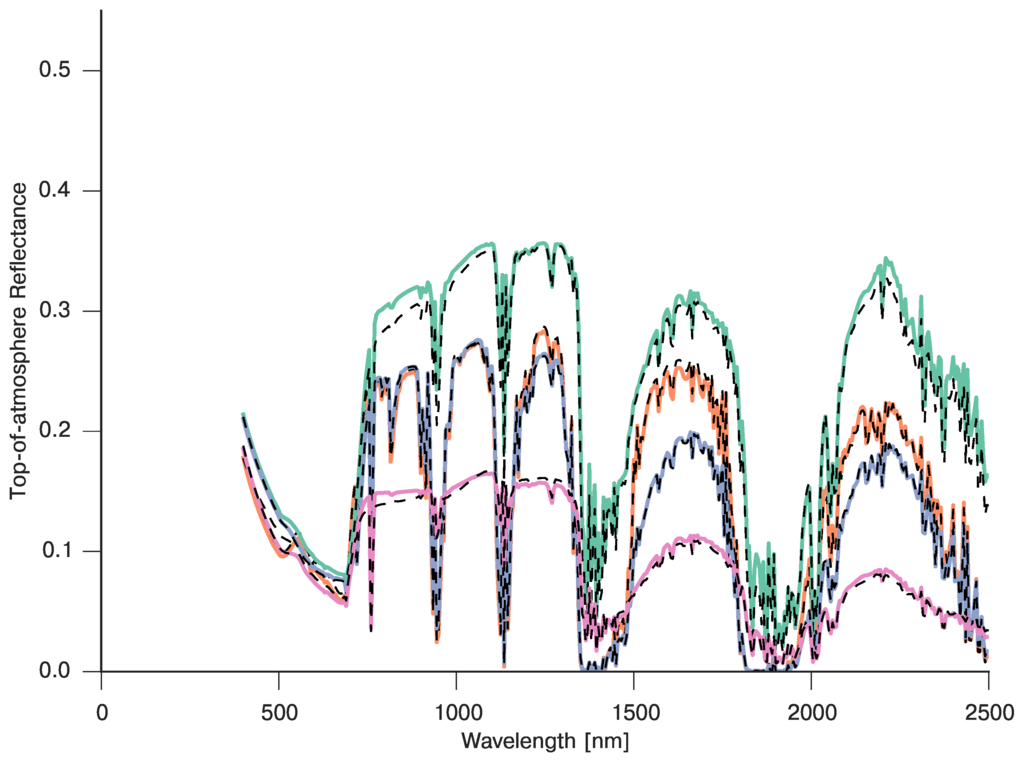
Figure 9.
Three examples of emulation of the coupled PROSAIL and 6S RT models. The three traces show the full model (full line) for a particular set of input parameters, and the emulator prediction for the same input parameters (dashed lines). The set-up was for day 138 (mid-may), with nadir illumination geometry and view zenith or , aerosol properties are selected as “Continental”.
Figure 9.
Three examples of emulation of the coupled PROSAIL and 6S RT models. The three traces show the full model (full line) for a particular set of input parameters, and the emulator prediction for the same input parameters (dashed lines). The set-up was for day 138 (mid-may), with nadir illumination geometry and view zenith or , aerosol properties are selected as “Continental”.
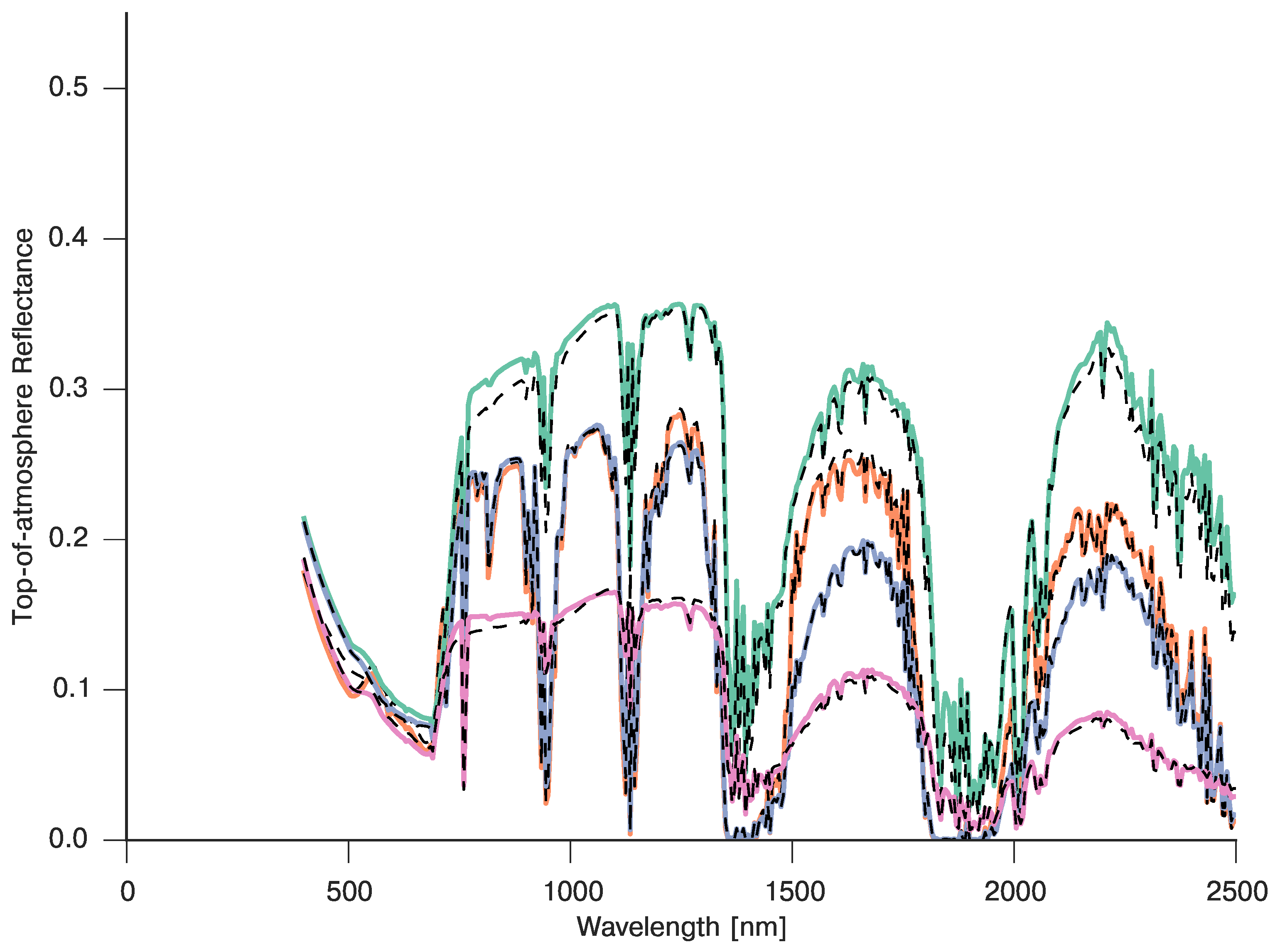
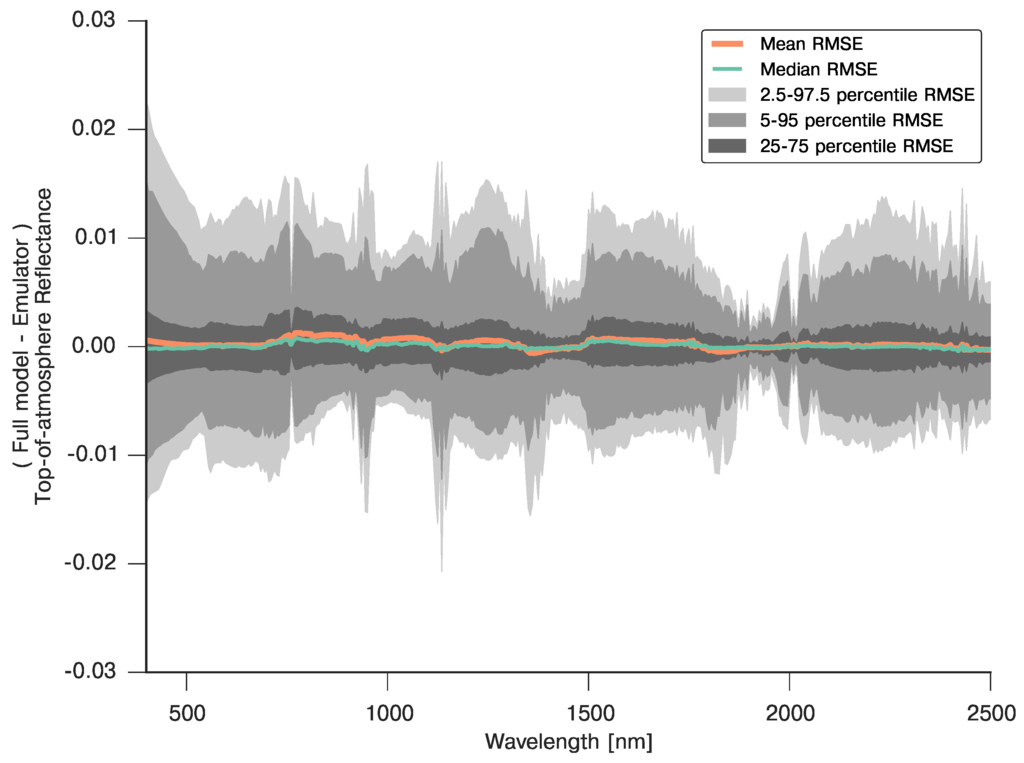
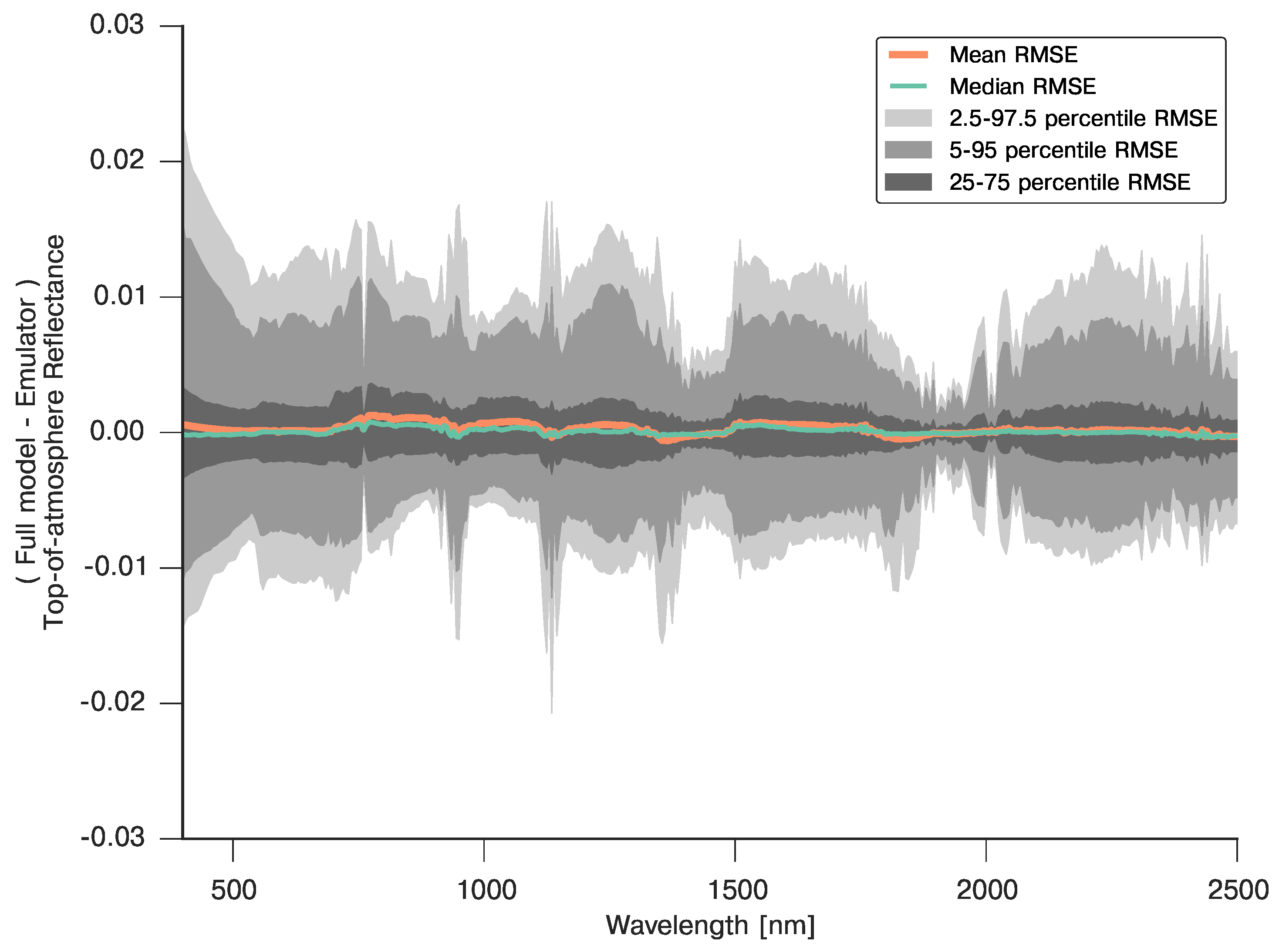
Figure 10.
Validation of the coupled PROSAIL+6S spectral emulation. The mean RMSE (blue line) shows the mean RMSE, whereas the grey shaded areas show different quantiles (95, 90 and 50%).
Figure 10.
Validation of the coupled PROSAIL+6S spectral emulation. The mean RMSE (blue line) shows the mean RMSE, whereas the grey shaded areas show different quantiles (95, 90 and 50%).
4. Examples of the Use of GPs in Inverse Problems in Remote Sensing
The previous section has demonstrated the feasibility of emulating complex RT models and model combinations, both on a “per band” and spectral basis. We turn now to the practical use of these emulators in a number of inverse problems in remote sensing. To do this, we will demonstrate the retrieval of land surface parameters from a set of realistic synthetic observations modelling different sensors acquiring data over the same site over the course of a year. The simulated site will have temporal dynamics of , leaf chlorophyll () and leaf equivalent water (), and we will use the PROSAIL model to both simulate the observations and to retrieve the parameters. The latter will be demonstrated using PROSAIL through suitable emulators. The aim of these experiments is to show different approaches to the task of retrieving LAI, chlorophyll and leaf water from possible satellite observation configurations, and to demonstrate that emulators play an important role in making these methods applicable to practical problems.
4.1. The Synthetic “Satellite” Observations
We will simulate acquisitions for a site at a latitude of 42 N. The dynamics of LAI, leaf chlorophyll concentration and leaf equivalent water are governed by a double logistic function. This form was chosen because it has been widely used in other studies (e.g., [45,46]), as it shows distinct high/low periods which can have different transition dynamics. The form of the logistic function is given as
(see Table 5 for the different parameters used in Equation (8)).
We will simulate observations from the upcoming Sentinel2/MSI [47], Sentinel3/SLSTR [48] and Proba-V [49] sensors. Table 6 shows the different properties of the sensors. These include the revisit period in days, the percentage of observations that are cloud free, the average correlation length of the cloudiness field, the overpass time, as well as the sensor uncertainty that scales the generic uncertainty (where the standard deviation for a particular band is calculated as ). We ignore any correlations between noise in the different bands, although there will likely be induced by the atmospheric correction. Also note that we assume cloudiness to be independent of the sensor, although it is likely that cloudiness will be strongly correlated for the sensors, given their overpass times. Note that these decisions are approximate, and differ from the actual characteristics of the three sensors. In Figure 11, the temporal trajectories of reflectance for the different sensors are shown.

Table 5.
Default parameters and temporal parameter trajectories for the synthetic experiments.
| Parameter | Value | ||||||
|---|---|---|---|---|---|---|---|
| N | 2.1 | – | – | – | – | – | – |
| 60 | 5 | 55 | -0.3 | 122 | 0.1 | 240 | |
| 7 | – | – | – | – | – | – | |
| 0.5 | – | – | – | – | – | – | |
| 0.0176 | 0.004 | 0.043 | −0.31 | 121 | 0.07 | 235 | |
| 0.002 | – | – | – | – | – | – | |
| 2 | 0.1 | 5 | −0.29 | 120 | 0.1 | 240 | |
| 70 | – | – | – | – | – | – | |
| 1.0 | – | – | – | – | – | – | |
| 0.3 | – | – | – | – | – | – |
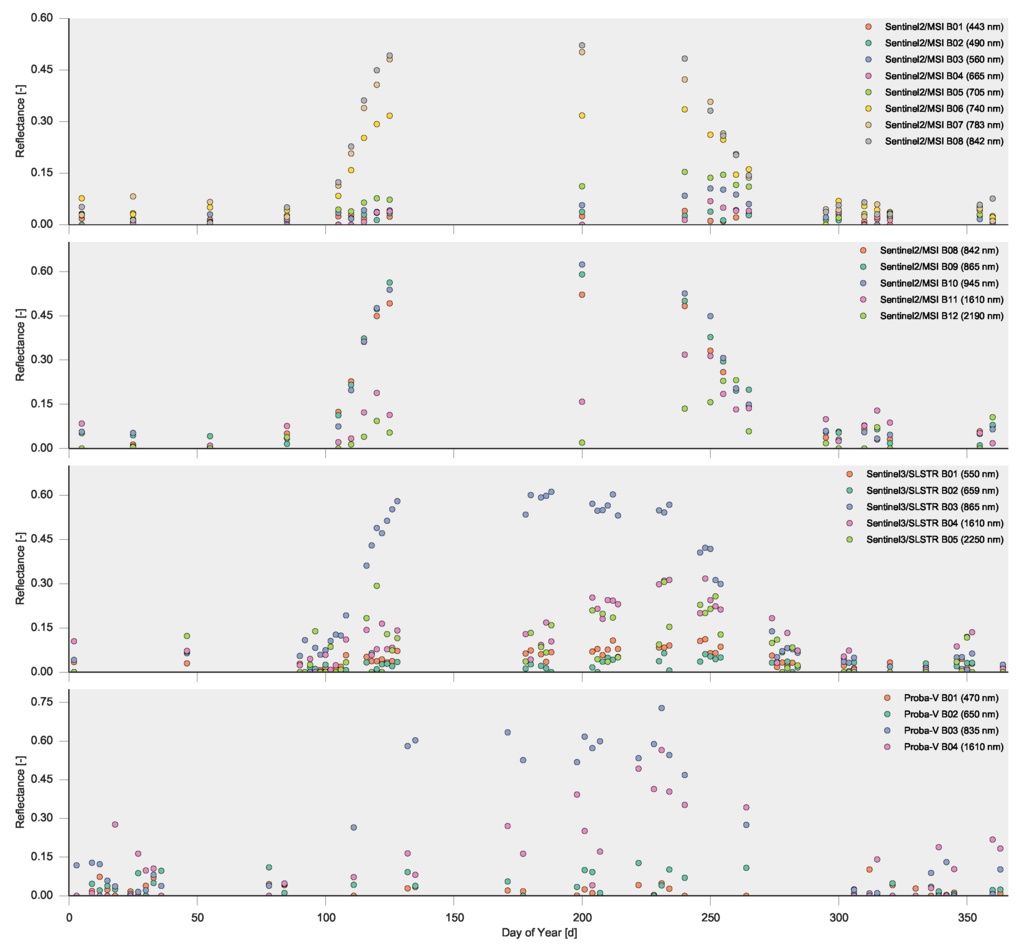
Figure 11.
Temporal evolution of the forward modelled reflectances for the three sensors considered in this work over a year.
Figure 11.
Temporal evolution of the forward modelled reflectances for the three sensors considered in this work over a year.
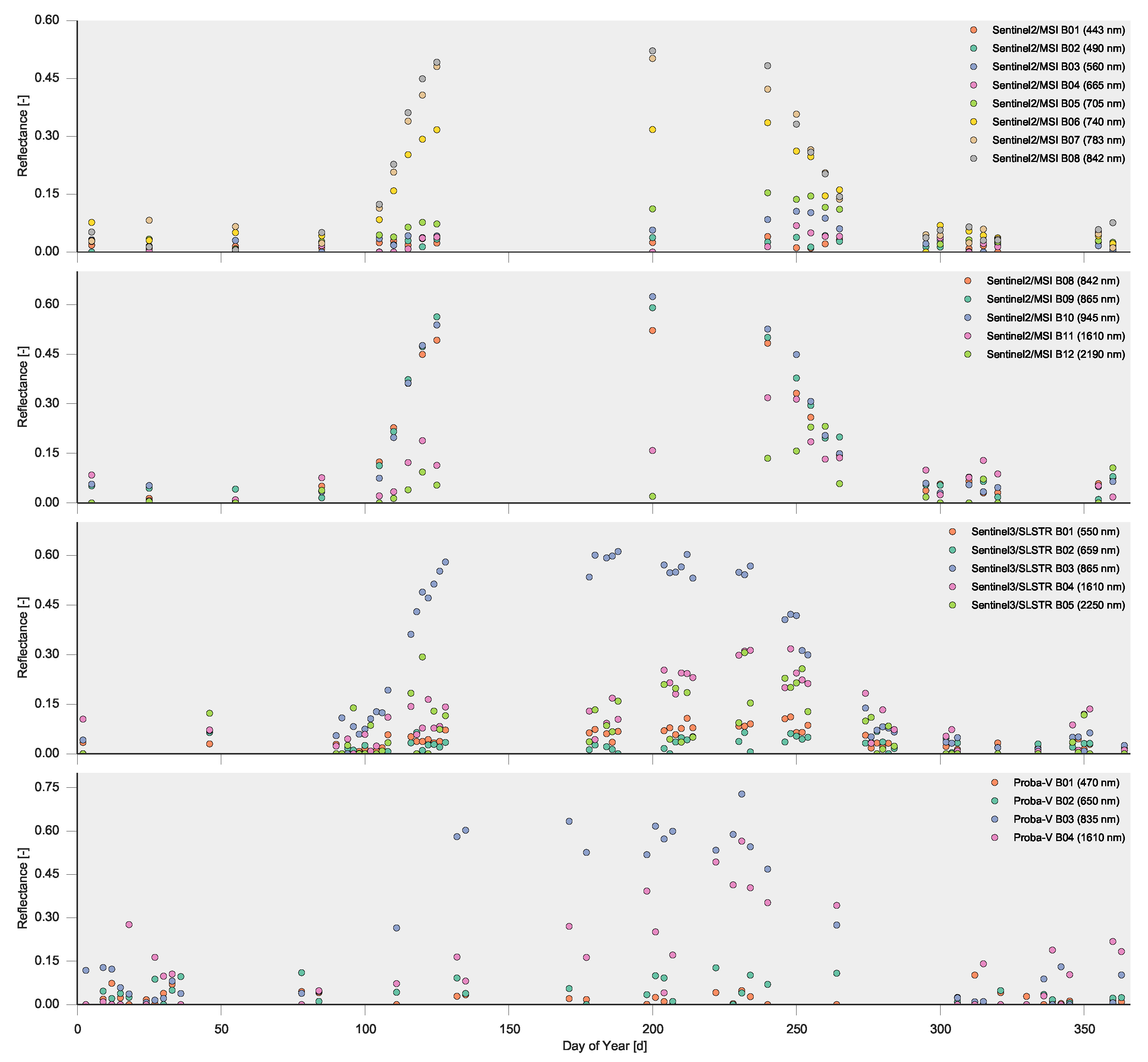

Table 6.
Description of the different parameters used for simulating the different sensors in the synthetic experiments. Noise model parameters are in units of reflectance.
| Parameter | Sentinel2/MSI | Sentinel3/SLSTR | Proba-V |
|---|---|---|---|
| Number of bands | 12 | 5 | 4 |
| Revisit frequency | 5 days | 2 days | 2 days |
| Overpass time | 10:30 AM | 10:00 AM | 11:00 AM |
| Variation in viewing zenith angle (VZA) | |||
| Percentage valid observations | 30% | 30% | 30% |
| Average temporal window | 12 days | 10 days | 11 days |
| Noise model slope m | 0.0042 | 0.0075 | 0.108 |
| Noise model intercept c | 0.0028 | 0.005 | 0.007 |
4.2. Generic Strategy for the Inverse Problem
The observations presented above need to be “inverted” against an RT model or observation operator in order to obtain land surface parameters. We will now develop a generic strategy to obtain the posterior distribution, which we shall solve using different sets of computational tools that will add extra constraints on the inversion. The first part of this is the specification of the likelihood function. Under the assumptions that the model error is negligible (a given in this case that the same model is used for creating the observations and inverting them), and that the observational uncertainty is additive Gaussian with a zero mean and a covariance structure , then the log-likelihood is given by
where is the RT model (PROSAIL) for a particular state and acquisition geometry Ω. In the examples below, rather than use directly, we shall use an emulator of the RT model. Moreover, the actual acquisition geometry will be slightly different, as the library of single geometry emulators we are using only sample discrete illumination/acquisition geometries. These two decisions would induce some model error, that would be added to the inevitable emulation error (this term is estimated directly using Equation (3)). However, we shall assume for simplicity that these two are negligible: we have seen that the emulator uncertainty using a similar emulator to the ones used in this problem (see Figure 4) is very small compared to the observational uncertainty. Angular sampling is also fine enough to minimise the introduction of large errors. In case of considering them, and assuming their are independent of the observational uncertainty, we would just have to change in Equation (9) to . The log-likelihood is thus the term that relates the state to the observations. In our set-up we have assumed that the observational uncertainty is independent for each band and sensor, implying that is diagonal. The value of that minimises Equation (9) is the maximum likelihood estimate of the state, or the best fit of the model parameters to the observations, modulated by the uncertainty.
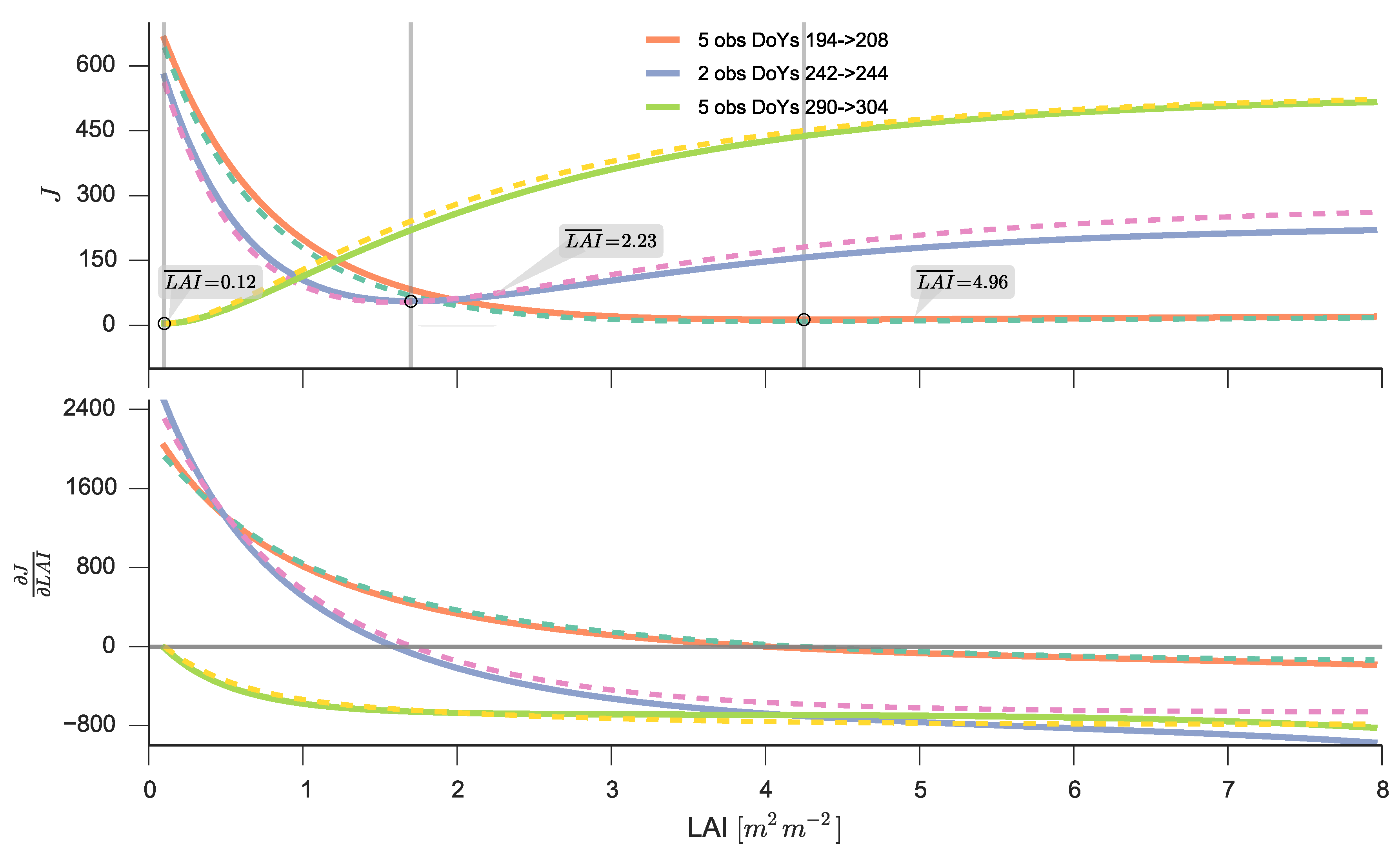
It is interesting to visualise a simplified version of Equation (9) and try to understand the inversion task from it. Assume that other surface parameters except are known, and we select three different periods to plot as a function of . This is shown in Figure 12, where both the cost function and its derivative are plotted. The plots show the effect of replacing the full RT model with its emulators. It is clear that the differences are very small, both in the value of the cost function and its gradient (the comparison here is between the gradient of the full model calculated by finite differences and that estimated using the emulator). We see that the minimum of the full model and emulated cost function occur in the same region, and coincide with the derivative being zero. Note that the minimum does not necessarily correspond with the true value, particularly for the examples where . The strong asymmetry of the cost function indicates that we do not have a linear problem (which would be given by a quadratic shape), and shows the effect of saturation of the signal with high . The large flat area around the minimum for the high cases is also suggestive of a large uncertainty in the estimate, a demonstration of the ill-posed nature of the problem, and suggests that any method just based on the observations without any additional constraints will struggle to retrieve a useful value of the land surface state. Additionally, the shape of the cost function implies that information on the uncertainty is critical to fully understand the problem.
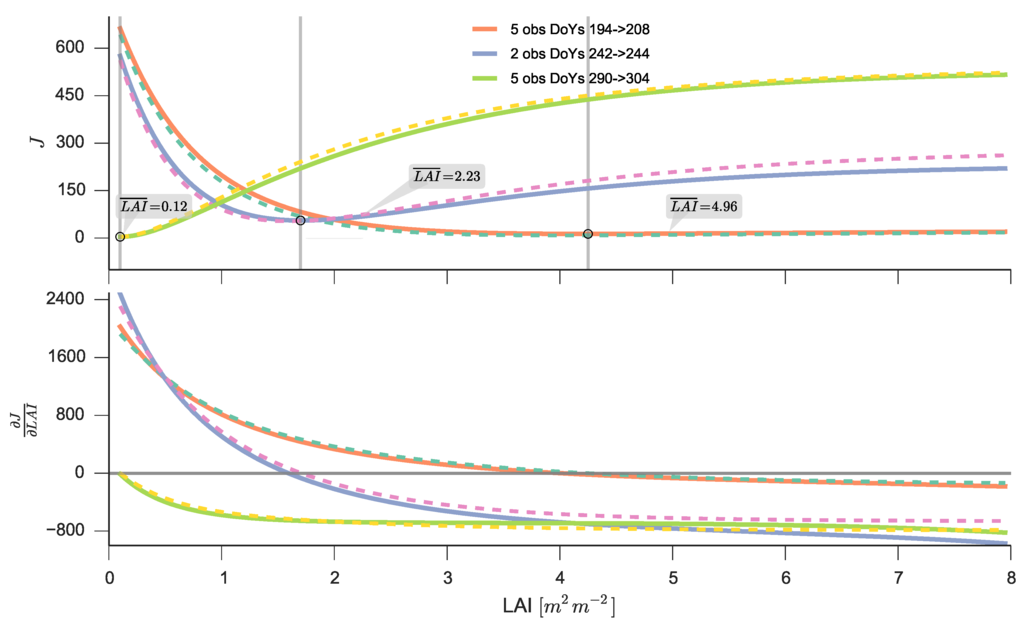
Figure 12.
(Top) Shows the difference between the cost function for three different acquisition periods using the Sentinel3/SLSTR synthetic data. The full lines show the cost function value as a function of using the full PROSAIL model, whereas the dashed lines show the value of the cost function using the emulators (and using the emulator with acquisition geometry closest to the observations). The circle represents the minimum of the cost function, and the grey call out is the mean value of for each period. (Bottom) The difference between the gradient of the cost function calculated with the full PROSAIL model (approximated by finite differences, full line), and the gradient approximated by using the emulators (dashed line) for the same cost functions shown in the top panel.
Figure 12.
(Top) Shows the difference between the cost function for three different acquisition periods using the Sentinel3/SLSTR synthetic data. The full lines show the cost function value as a function of using the full PROSAIL model, whereas the dashed lines show the value of the cost function using the emulators (and using the emulator with acquisition geometry closest to the observations). The circle represents the minimum of the cost function, and the grey call out is the mean value of for each period. (Bottom) The difference between the gradient of the cost function calculated with the full PROSAIL model (approximated by finite differences, full line), and the gradient approximated by using the emulators (dashed line) for the same cost functions shown in the top panel.
A way to improve on the limited information content provided by the observations is to add more constraints in the form of prior information. A first step is to provide a prior distribution for the parameters to be inverted. We will assume a fairly uninformative prior distribution, with the parameter values being independent, and distributed as a Gaussian with a particular mean value of 0.41, 0.78 and 0.37 (respectively, in transformed units using the transformations in Table 3, which correspond to real parameter values of 1.8, 25 and 0.02, roughly the average value of , and over the simulated time series), and a standard deviation or 3 (in transformed units),
Solving for the Posterior
Most methods will explore , with a different set of assumptions that can be made of shape of . The limited information content that is encoded in the observations, as well as little additional information available in the prior we have decided to use will in all likelihood result in large uncertainties in our estimation of the state. Advanced DA methods allow us to cleanly incorporate more information into the inference problem, extending the form of with, for example, dynamic models of the temporal evolution of parts of the state vector. While these methods tend to be computationally costly (typically requiring many evaluations of , and of in particular), they also provide not just an estimate of the state but also the associated uncertainty. We believe this is a crucial part of the inversion problem. We will showcase three different methods of inversion. The problems which we will solve are slightly different, deploying different assumptions on the shape of the posterior distribution, and different prior assumptions. Each method uses the same observations and likelihood, but the amount (and nature) of the prior information are different.
The first method (Section 4.3) follows quite directly from typical LAI inversion schemes, such as the MODIS LAI algorithm [10], where all observations within a temporal window are inverted together, with the assumption that the state is constant within the inversion period. Typically, look-up table (LUT) methods have been applied to this problem. However, in the multisensor case, these methods become more complex, due to the need to accommodate the different uncertainties and acquisition times in consistent fashion. We choose to use a classical approach in Bayesian statistics, Markov Chain Monte Carlo (MCMC). MCMC exploit the fact that samples from the posterior distribution can be produced by drawing samples from a Markov chain with an appropriate stationary (or equilibrium) distribution. Typical methods such as the Metropolis-Hastings approach are computationally very expensive, typically requiring tens or hundreds of thousands of evaluations of the posterior to reach convergence. Provided convergence is reached, the samples will be drawn from the posterior pdf, so MCMC is a very general method. In this work, we use recent advances in MCMC that exploit the gradient of to reach convergence faster (i.e., requiring far fewer iterations). A common strategy in MCMC problems is to start sampling from close the maximum a posteriori (MAP). We do this by starting the MCMC inversion from the point indicated by the minimum of obtained by using a gradient descent method. This last method can also serve as a benchmark of typical cost-function minimisation approaches.
The MCMC inversion approach, while being in many ways close to the state of the art shows some limitations. The first one is that where no observations are available, the land surface estimation system results in gaps or a fairly uninformative prior distribution. A second problem is the large uncertainty in the estimates. Finally, although MCMC methods that employ gradient information are more efficient than traditional MCMC approaches, the use of such methods is impractical, even with very fast emulators. In [7], the idea of variational DA system in a scenario similar to the one we have here was proposed. In that paper, the authors used the SEMIDISCRETE model, and used AD tools to calculate its adjoint and thus have access to the gradient. Another innovation shown in that paper is the use of regularisation, essentially a model of parameter evolution that is enforced as a “weak constraint” [7,50,51]; in other words, this simple model is assumed to have an error. The dynamic model states that state of the land surface does not change between two consecutive time steps. This extra information results in a transfer of information in time that exploits the temporal correlation in the land surface, resulting in an important reduction of uncertainty in the estimates of model parameters, as well as an ability to optimally interpolate over regions where no observations are available. We implement this method in Section 4.4. Note that a number of assumptions are made on the shape of the posterior using this method. These include the requirement of the statistics to be Gaussian, and an assumption that the models are linear.
The third example is the particle filter (PF) (Section 4.5). In some applications, we require near real time monitoring capabilities. This means that only data up to a particular time t is available, in contrast to the variational system in Section 4.4, where the entire time series is available, and we wish to infer the state at times . We will still want to use models as a weak constraint (such as before) to better condition the inference, but clearly the quality of the results should be inferior, as the estimate of the state will only be constrained by past observations and not future ones. The tools to perform this kind of analysis are called “filters“, perhaps the best well known filter is the Kalman filter, a simple method but constrained by a number of strong assumptions (linearity of the observation operator that translates the state to observation space, linearity of the dynamic model, and Gaussian statistics). Extensions to the original Kalman filter [52], such as the Ensemble Kalman filter (EnKF) [53], Extended Kalman filter (EKF, [54]) try to circumvent these limitations. Another family of filters are particle filters (PFs) [55], which work on the assumption that a finite set of particles can be seen as samples from the state. In a PF, a set of particles (vectors describing a realisation of the state) are propagated with a dynamic model, with an additional uncertainty inflation due to the model error, which is conceptually the same as the weak constraint in the variational scheme presented in Section 4.4. When an observation is present, it is assimilated, meaning that the particles are updated to reflect the information content of the assimilated data. A number of different PF schemes have been devised [17,56,57], but we will focus on the sequential Monte Carlo particle filter introduced by [58,59]. In this filter, a set of particles are propagated individually by the model and its uncertainty. When an observation is assimilated, a particle is chosen randomly and the value of the posterior for the state represented by the particle is evaluated. Next, another particle is chosen and the value of the posterior is evaluated. This new state is accepted or rejected using a Metropolis test with respect to the first particle, and the process is repeated for all other particles in the ensemble, resulting in the new set of particles sampling the state conditioned on the observations up to the current time step. We will apply this filter to obtain daily estimates of , and from the set of observations introduced in Section 4.1.
4.3. Inversion Using Markov Chain Monte Carlo (MCMC)
In this section, we will gather all the available observations in an eight day period, broadly the temporal reporting period for the MODIS (Collection 5) or CYCLOPES LAI products, see [12,60], and infer , and , conditioning the problem with some uninformative prior distributions. If no observations are available in a particular period, no inference will be made (in these cases, the system would just return the prior distribution). The observations will give rise to the negative log-likelihood function, , which will be added to the prior distribution to obtain the log posterior. To sample the posterior distribution, we will use the NUTS (No U-Turn Sampler) MCMC sampler introduced by [61]. The novelty of this sampler is that rather than sample from the posterior using a random walk behaviour like the traditional Metropolis-Hastings sampler, it uses information on the gradient of the posterior to optimise the exploration of the posterior parameter space. The benefit of a more efficient exploration of posterior parameter space has the added burden of the need to calculate the gradient of the posterior, a task that in our case, is easily done with the emulators. We will run the NUTS sampler with 500 iterations per observation period, and will run ten independent chains to check for convergence.
We will use the MAP value as the starting point for the MCMC chains, to ensure faster convergence. The MAP approach is an interesting comparison, as it is a very fast method with the emulators, although the lack of meaningful prior information will probably make the effort unreliable due to the existence of local minima, or as seen in Figure 12, due to the very broad shape of .
The results are shown in Figure 13. For , and if , retrievals are accurate, with a small uncertainty. As increases, the uncertainty grows notably, and we note how the medians on the posterior distribution, as well as the shape of the distribution itself show notable changes from one 8-day period to the next. In some cases, the MCMC sampler is able to correct the initial starting MAP point, but the general trend is one of underestimation of , probably a consequence of the saturation of reflectance with . For , in the low period, the MAP starting points show either very high or very low values. This is consistent with the lack of influence of leaf pigments when is very low. We note how the distributions are very broad throughout the entire inversion period, and in some cases, the NUTS sampler brings the result closer to the synthetic truth. The period between DoYs 100 and 150 is poorly predicted. This is a consequence of the paucity of observations (see Figure 11) (this effect is also noticeable for , although not as marked). shows a pattern of high uncertainty in the starting period, but the result is often closer to the true value than is the case for . The plateau is often underestimated, but with significant uncertainties (around 0.02 for the 5%–95% posterior interval). For the three parameters, inference of the state is much more robust on the trailing edge than on the leading edge of the plateau, an effect of the lack of Sentinel-2 observations throughout the period between DoYs 110–220. The limited SLSTR and ProbaV observations have higher noise contributions, and are not as informative (in particular for , where the red edge bands in Sentinel-2 prove decisive). This results in an uncertain estimate of , and during the plateau period. This situation can be fairly typical, and shows the limitations of data availability.
4.4. Variational DA Solution: EO-LDAS Framework
In this section, we will use a new version of the same code library introduced in [7] (available online [62]) to solve the problem introduced in Section 4.2. We will extend the cost function that was being explored in Section 4.3 with a new term with the dynamic model constraint, resulting in the following cost function to minimise with a gradient descent method:
In Equation (11), the main assumption is that the three terms are differences of the state vector (or transformations of the state vector) and other constraints: the first one is the mismatch of the state (transformed into reflectance using the RT model) with the observations (modulated by their uncertainty, given by ), the second is the mismatch of the state from the prior distribution (given by the mean vector and covariance matrix ), and the final term is the mismatch of the state from what the dynamic model predicts (modulated by the uncertainty in the dynamic model, (in this case, . For the model, we shall use a first order difference model, applied to each parameter individually (see [7] for more details). The regularisation parameter Γ in this example has been chosen for , and by inspection of the results, but in a practical setting, this would need to be done by using some form of crossvalidation.
The cost function in Equation (11) is simply minimised using a gradient descent algorithm. Uncertainty is calculated by evaluating the Hessian at the MAP point, and inverting it to obtain the posterior covariance matrix (note that this approach is only strictly true if the model is linear). The results are shown in Figure 14, and show a marked improvement with respect to those shown in Figure 13. We can see how the regularisation has resulted in a complete time series with no gaps, reporting the value of the three inferred parameters for each day in the year. and retrieval fairly good, with in the plateau being slightly underestimated. has more problems, showing a poor performance in the earlier “green up” edge, but in a pattern similar to that shown for in Figure 13. Using the selected regularisation results in very smooth time series, but also reduces the uncertainty considerably, resulting in the undesired effect of the predictions and the uncertainty bounds not covering a substantial period of the e.g., high period.
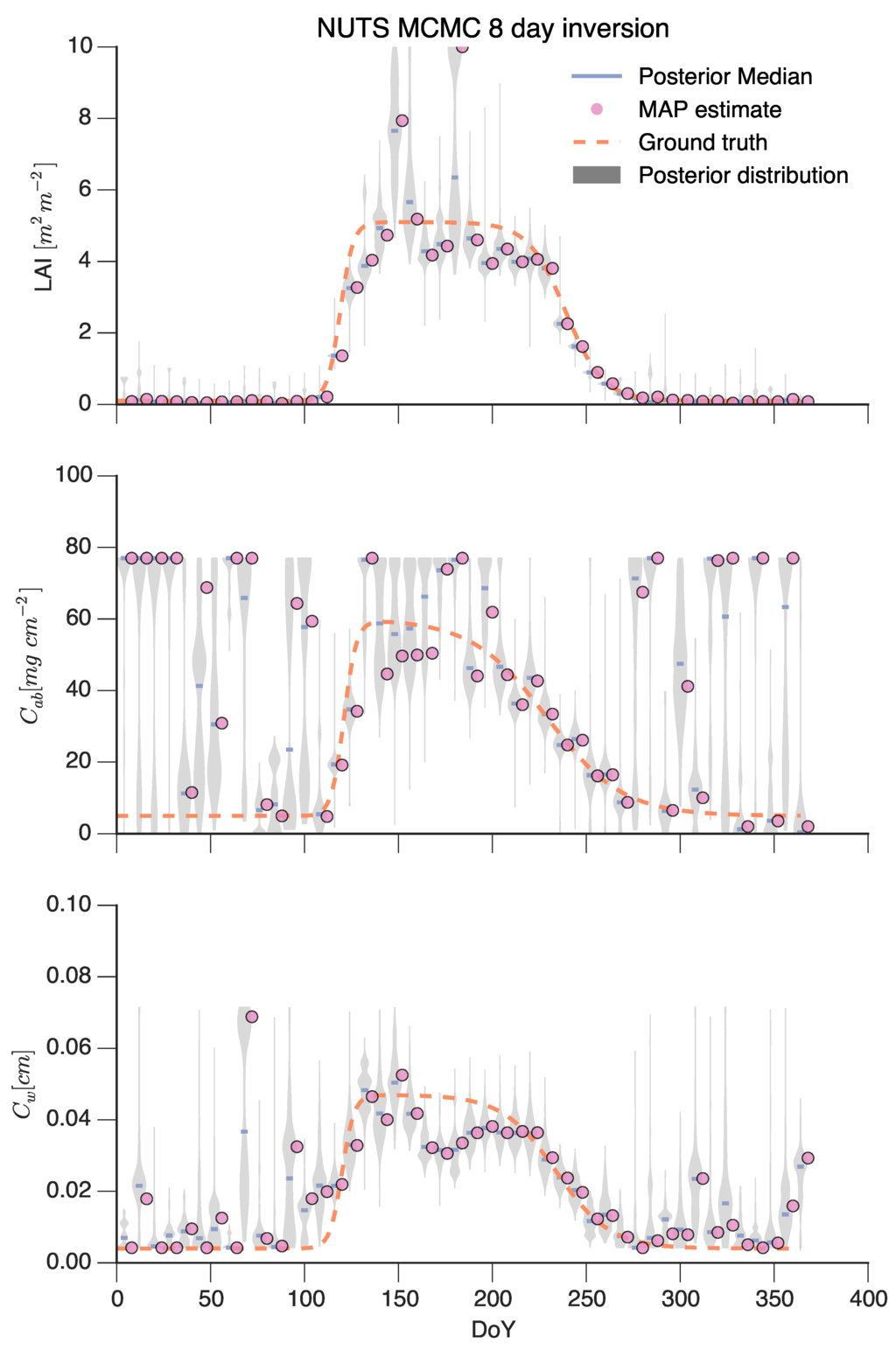
Figure 13.
Results of inferred posterior parameter distributions for the inversion with simple gradient descent algorithm and NUTS MCMC sampler, in both cases using GP emulators in lieu of the full RT model. The observations of every eight day period have been inverted assuming that the parameters are constant within the inversion window. A Gaussian uninformative prior is used to constrain the observations. The dashed line shows the ground truth, the dots show the value of the minimisation, and the grey areas represent the posterior parameter distribution. The dash indicates the median of the posterior parameter distribution.
Figure 13.
Results of inferred posterior parameter distributions for the inversion with simple gradient descent algorithm and NUTS MCMC sampler, in both cases using GP emulators in lieu of the full RT model. The observations of every eight day period have been inverted assuming that the parameters are constant within the inversion window. A Gaussian uninformative prior is used to constrain the observations. The dashed line shows the ground truth, the dots show the value of the minimisation, and the grey areas represent the posterior parameter distribution. The dash indicates the median of the posterior parameter distribution.
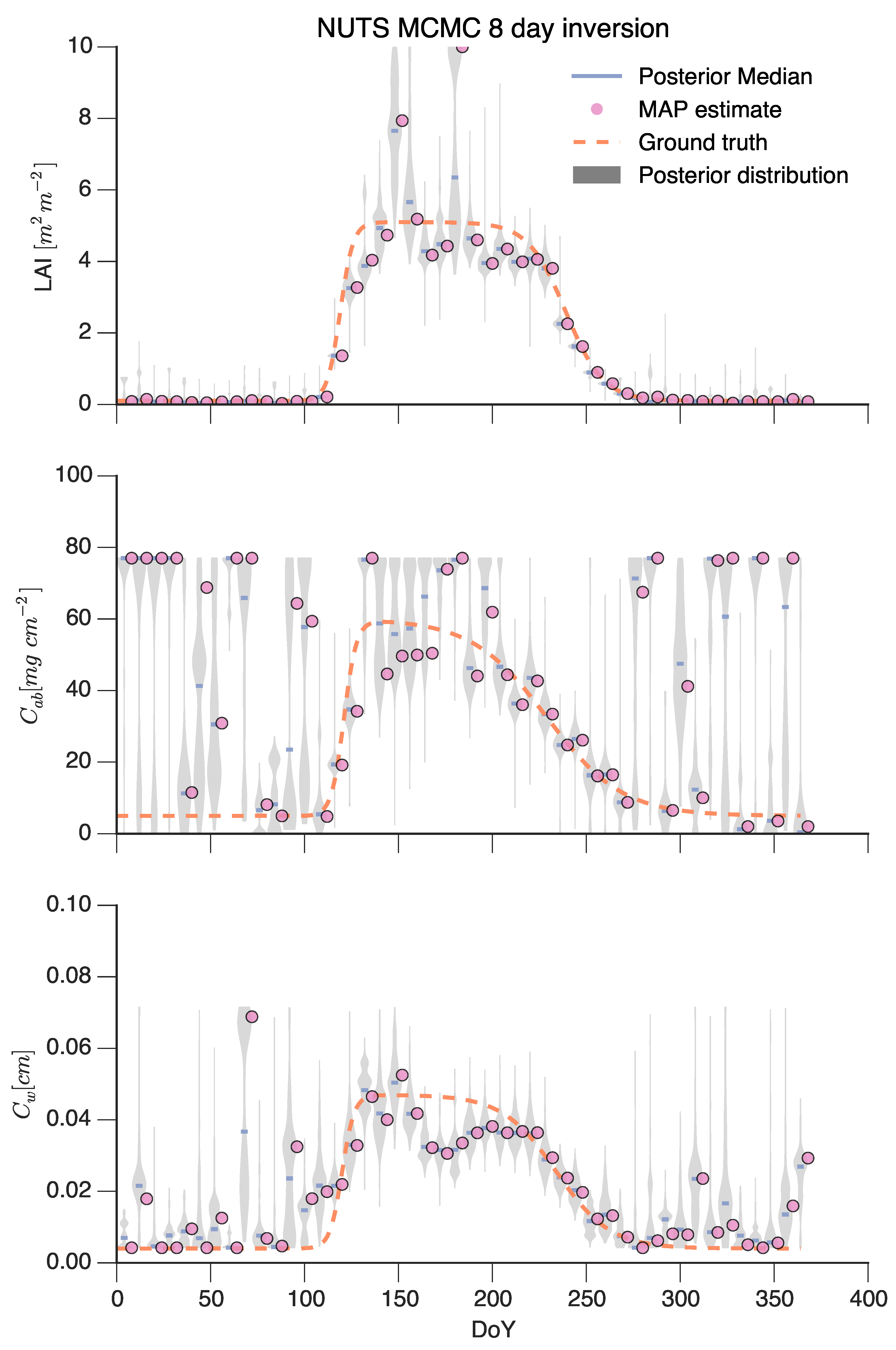
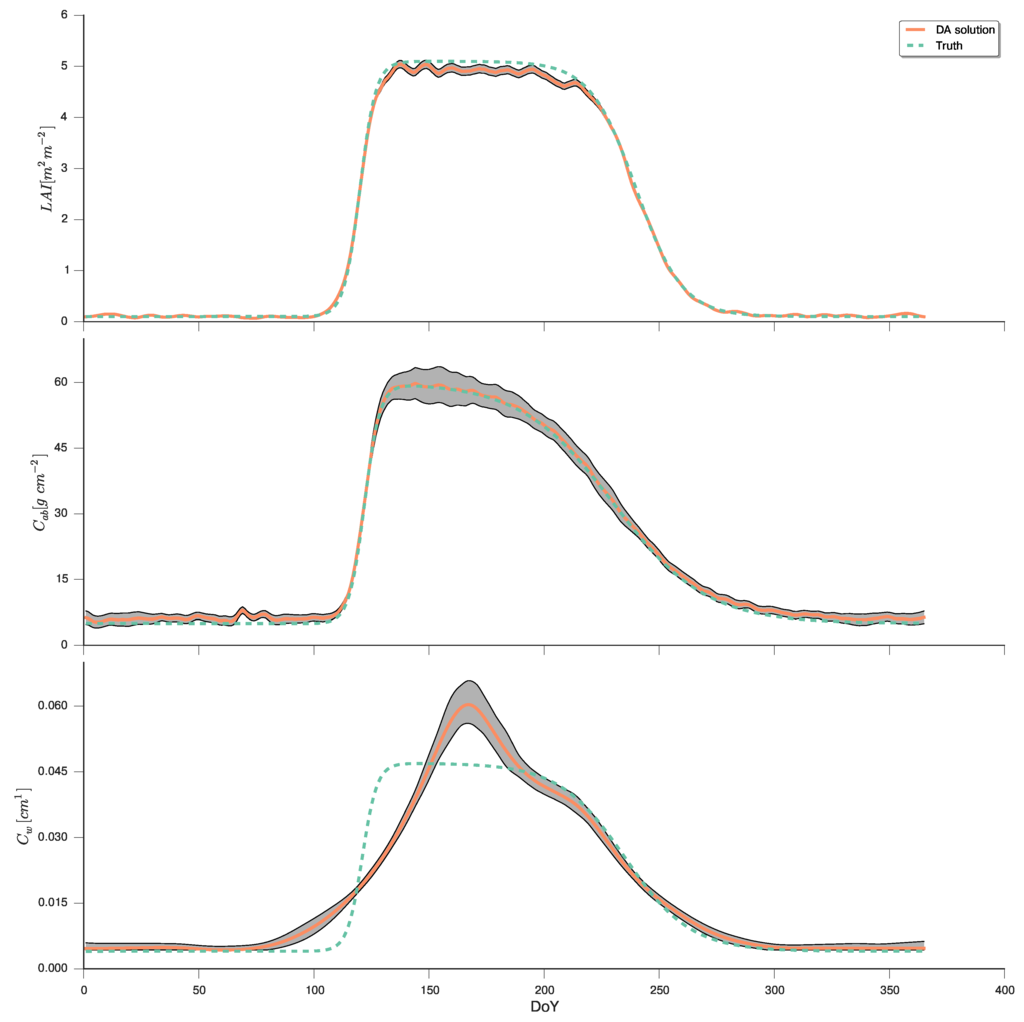
Figure 14.
Results of inferred posterior parameter distributions using the eoldas_ng package, supplementing the fit to the observations by a prior distribution and a first order regularisation model. The orange line shows the value of the maximum a posteriori (MAP) estimate, with the grey area representing the 5%–95% posterior interval. The green dashed line shows the truth.
Figure 14.
Results of inferred posterior parameter distributions using the eoldas_ng package, supplementing the fit to the observations by a prior distribution and a first order regularisation model. The orange line shows the value of the maximum a posteriori (MAP) estimate, with the grey area representing the 5%–95% posterior interval. The green dashed line shows the truth.
4.5. Simple Particle Filter
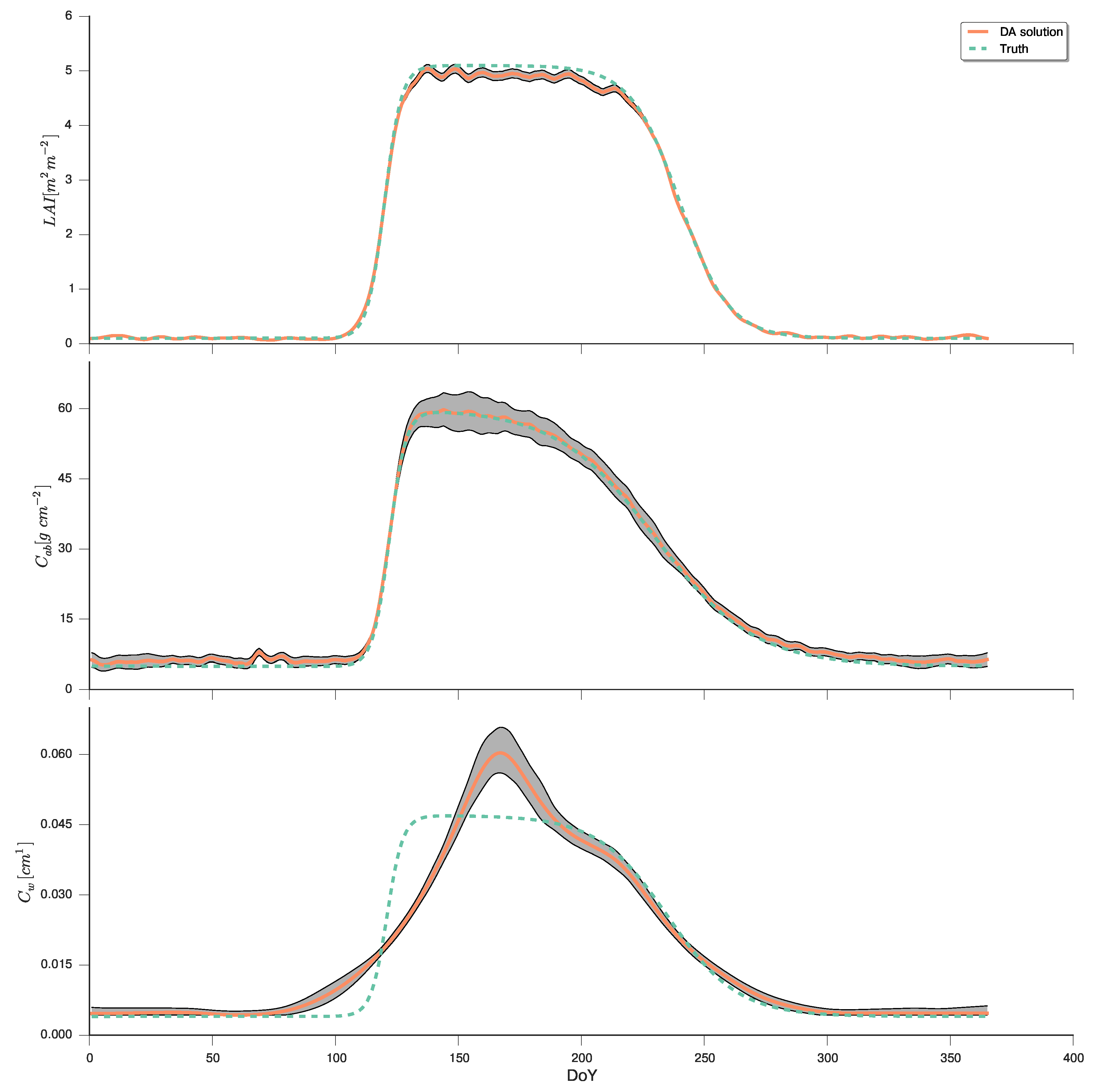
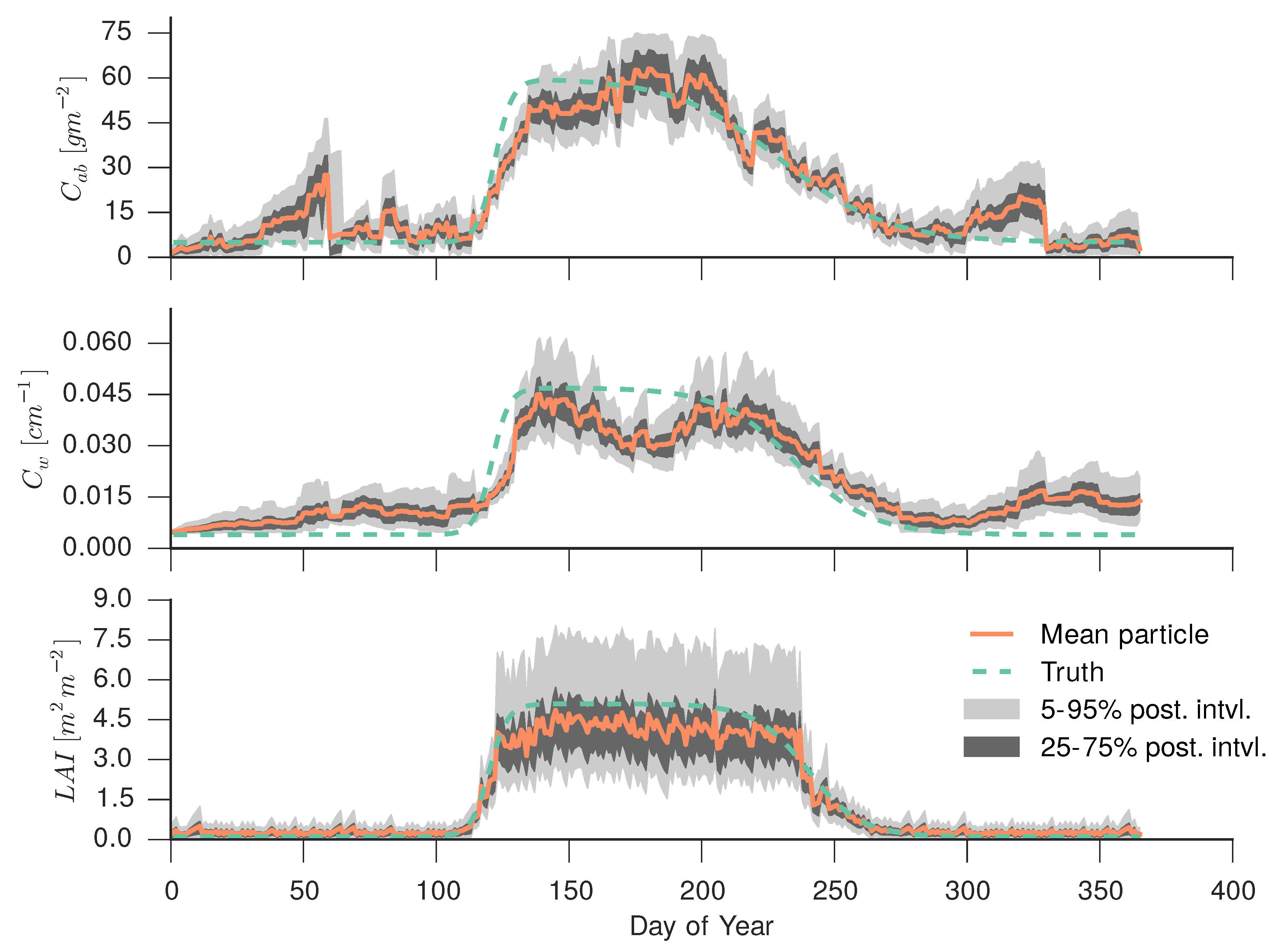
In the PF example, we shall be using as the regularisation model introduced in Section 4.4, so that , where is a diagonal matrix with entries encoding a model error (standard deviation) of 0.025, 0.032 and 0.032 for , and , respectively. As before, note that this uncertainty refers to transformed units (Table 3). We have used 1000 particles for this experiment, although the results were very similar (in terms of posterior parameter distributions) using only 500 particles. The results are shown in Figure 15. Tracking of is good, with the true value being inside the 25%–75% percentile range most of the time, except towards DoY 250, where the modest number of observations results in the model taking precedence over the data, and thus delaying the decay of . We also note the large asymmetry of the uncertainty in the plateau period, a symptom of the saturation effect. Estimation of is poorer than . As before, the period without Sentinel-2 data around DoY 125 results in the model taking precedence and not tracking the ground truth. Similar explanations explain the funnel shape of the uncertainty envelope around DoY 50 and after DoY 310. The evolution of is similar to that shown in the Figure 13 and Figure 14. We can see how the uncertainty is larger in the PF example, due to the filter only using information up to the current time step.
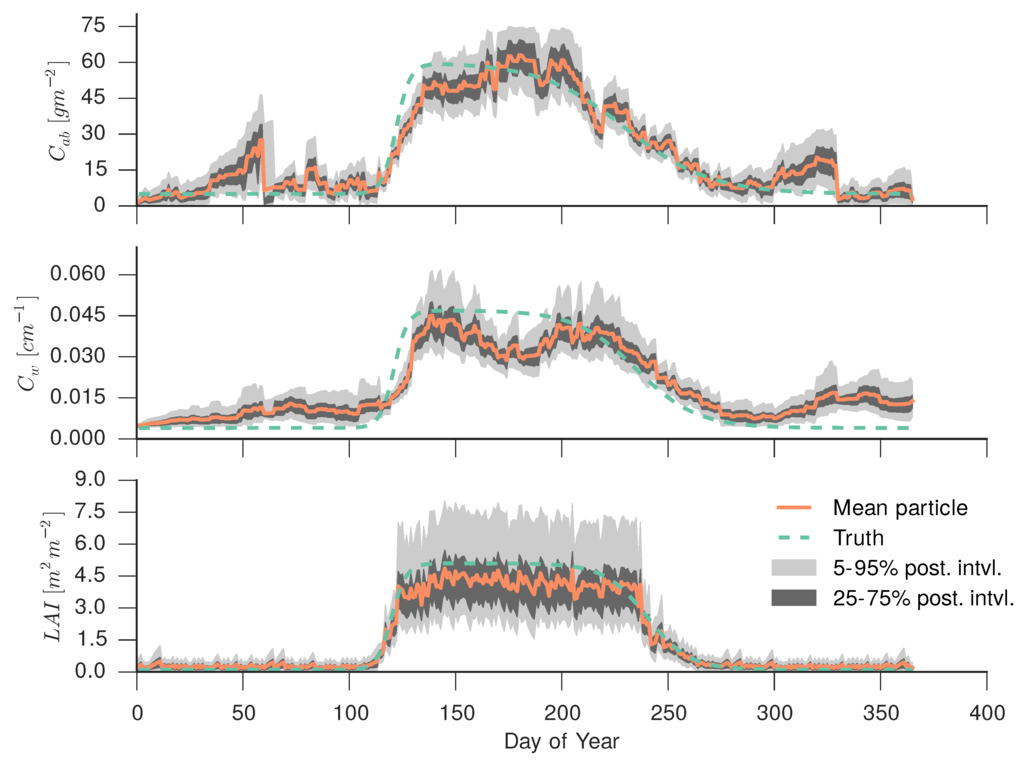
Figure 15.
Evolution of the land surface parameters (from top to bottom: leaf chlorophyll concentration, leaf equivalent water thickness and leaf area index) derived from the synthetic observations introduced in Section 4.1. The parameters were inferred using a particle filter. The dynamic model used is a first order regularisation model, and we have used 10,000 particles. The plots show the mean particle, the 5%–95% and 25%–75 % posterior intervals, as well as the ground truth.
Figure 15.
Evolution of the land surface parameters (from top to bottom: leaf chlorophyll concentration, leaf equivalent water thickness and leaf area index) derived from the synthetic observations introduced in Section 4.1. The parameters were inferred using a particle filter. The dynamic model used is a first order regularisation model, and we have used 10,000 particles. The plots show the mean particle, the 5%–95% and 25%–75 % posterior intervals, as well as the ground truth.
5. Discussion and Outlook
In this paper, we have demonstrated the use of Gaussian Processes as emulators for computationally demanding radiative transfer codes typically used in land vegetation and atmospheric remote sensing. The emulators work well as fast surrogates of the models tested here, providing not only an accurate prediction of the model output, qualified by a predictive uncertainty, but also an approximation to the partial derivatives of the emulated model. The standard GP fitting method has been extended to deal with multivariate output (e.g., spectra) in Section 2, which is attained simply by a principal component transformation of the spectra, and then using univariate emulators on the principal component weights. The univariate emulators (Section 3.1 and Section 3.2), where the emulator produces a mapping between input land surface parameters and the reflectance or radiance over a particular band. The results of these experiments show that it is possible to produce extremely accurate predictions (in the sense that the residual of the emulated model with respect to the full model is always much smaller than the typical observational error) of the RT models that we have used here, which are typical of a typical complexity. The spectral emulators have also been successfully demonstrated for a vegetation RT model (Section 3.3, and for a coupled vegetation and atmospheric RT model (Section 3.5). In either of these two examples, the results of the emulation were excellent (i.e., over an independent validation dataset, the difference between emulator and model is very small compared with typical observational uncertainties) and as the complexity of the emulated model increases (e.g., in terms of processes modelled), so does the relative speed up of the emulation. The previous examples show a fairly inflexible approach to emulation: a model (or a set of models) are emulated together. In some cases, more flexibility is required, and in Section 3.4 we have demonstrated how this can be achieved by emulating individual parts of the model with the 6S atmospheric RT model. The emulators are able to replicate the spectral functions from atmospheric path length, two-way transmittance and spherical albedo with a very small error in terms of reflectance. If this ability can be generalised to other models or parts of models, we envisage the development of models made up of generic coupling terms that link different emulators, linking for example different vegetation layers, the atmosphere, ..., and realising a very versatile RT model in which individual parts can be exchanged by just using a different emulator.
A particular problem with approximating any function from a few samples is how to ascertain that the approximation is robust when predicting new outputs. We have used a limited validation set in this work, assuming that the statistics resulting from a comparison of the emulator output with this validation dataset are sufficient to use the emulators reliably, an approach not dissimilar to that in [63]. However, work on more formal methods to validate the emulators, including the predictive uncertainty, are clearly required.
The results shown in this paper have been achieved with perhaps the simplest covariance function available, the “squared exponential” introduced in Equation (1). A limiting problem that has hitherto been ignored in this work is the emulation of angular effects, as for all the models we have used, we have assumed a fixed illumination/acquisition geometry. In practice, we have got over this limitation by creating a library of emulators sampling over a range of illumination/acquisition values. However, emulation of the entire BRDF is of importance, as one can then use emulators to calculate the angular integrals that result in e.g., albedo, paving the way for a consistent treatment of biophysical parameters, as recently shown by [64]. The main difficulty in emulating full BRDF is due to the output space being non-stationary, due to sharp localised angular effects such as the hotspot effect. These could potentially be dealt with using a different covariance function that deals with non-stationarity as shown in e.g., [65,66]. Another approach could be to detrend the data using a simpler model, so that the resulting residual meets the stationarity condition better. We have not yet investigated these avenues, and they remain an important area to explore in the future.
The results shown in Section 4 are indicative of what is possible when fast RT models (and their gradients) are available through emulation. In the illustrative experiments introduced in the previous section, we demonstrate novel biophysical parameter inversion approaches using data assimilation techniques that were up to now impractical. These include using advanced MCMC techniques that rely on the use of the gradient of the log posterior to sample parameter space more efficiently (although just having faster RT models would be an enormous advance for the use of MCMC techniques). The importance of this approach is that it allows one to test the assumptions embedded in retrieval algorithms. For example, in [7] the posterior covariance matrix is calculated as the inverse of the Hessian, something that will only hold if the uncertainties are Gaussian and the model is linear (to some extent, the use of linearising transformations partly resolves this problem), but this assumption can be tested now by using MCMC methods, which directly provide samples of the true posterior distribution of parameters.
A number of authors use gradient descent methods to minimise a cost function within a retrieval scheme [7,9,67,68,69]. In some cases, approximations to the RT model gradient are produced using automatic differentiation tools, whereas in other cases, a numerical approximation to the gradient using finite differences is used. Both methods are in practice limited by the size of the state space, which requires many evaluations of the cost function and its gradient. Finite differences can also in some cases result in unstable results. These problems are circumvented by the use of emulators, providing a very fast alternative way to evaluate the RT model and its gradient (as well as higher order terms, such as the Hessian). Efficiency is also important in these methods, as in order to avoid local minima, a large number of starting points are typically used in the optimisation procedure. If the optimisation is lengthy, the number of starts might result in many optimizations not moving from the local minimum.
Finally, we have also shown the use advance DA concepts in the inversion. While DA methods allow a direct way to incorporate prior knowledge, including from complex dynamic models of the land surface, their implementation is typically complex, requiring either access to gradients (variational methods, Section 4.4) or to Monte Carlo approaches (Section 4.5). In either case, the exploration of the problem is time consuming, requiring many iterations in a cost function optimisation, or requiring many evaluations of the model to create e.g., an ensemble of particles. These are all situations where emulators shine, as they greatly reduce the computational cost associated with running a potentially costly observation operator. In the examples we have shown, it is clear that the use of more sophisticated inversion approaches results in better estimates of land surface parameters. While we have not done so in this work, the inclusion of parameter trajectories predicted by dynamic vegetation models [15] or crop models [70] might also be of interest. Given the complexity of these models, particular care should be paid to their emulation [71,72]. Complexities of dynamic models arise from the fact that the output is an update of the input (e.g., in a vegetation or crop model, the at one time step is used as an input to the model, and is modified internally to provide an update on the value of for the next time step). A simpler way forward might also be to use the same RT models in the retrieval schemes as within vegetation models, as this would ensure consistency of the vegetation model and observational parameters [73].
The spectral decomposition method introduced in Section 2 appears to be robust in the kind of problems that we are considering, but the PCA decomposition might blur particular narrowband features. To this end, a multiscale approach, where a first emulator over the entire range is provided, with narrowband detailed emulators are used to add detail in the regions of interest [74].
In general, emulators provide a generic way to incorporate different models in inversion schemes. This facilitates the inclusion of different physical models, as all that is needed to incorporate a new model is the relevant definition of the emulator (e.g., the training input/output pairs and the hyperparameters). The gain in speed also suggests that a generic function like a GP might be a better target for optimisation and the use of massive parallel architectures: rather than adapt the physical RT model to meet the requirements of the parallel architecture (as done in e.g., [75]), it is easier to provide a parallel implementation of the emulator code, that is then generic for many models. It should also be noted that emulators allow model developers to be more ambitious with the numerical complexity of their models: it is possible to start considering more realistic or accurate models, as provided a fast emulator is available, running the original model will not result in a processing bottleneck.
While in this work we have developed and tested emulators for some widely used RT models, we have not tested the limits of emulation. For example, some RT models might have e.g., more detailed descriptions of the canopy, and thus require a larger set of input parameters. The sensitivity of these input parameters might result in non stationary outputs, something with which the current version of the emulators struggle. In some cases, training sets might require to provide a more targetted approach than the current Latin hypercube sampling design. In some cases, initial coarse emulators might be used to infer local sensitivity indices, and these used to inform the Latin hypercube design (by using an underlying pdf that is more informative than a uniform distribution between two values).
The increasing range of higher spatial and temporal resolution observations available from current and planned EO missions presents a challenge in turning these observations into uncertainty-quantified estimates of the state of the land surface. Robust and consistent methods that are able to use data from all sensors are computationally costly, and require the use of RT models, which render approaches based on sophisticated DA concepts impractical. Emulation using Gaussian Processes, as demonstrated in this contribution, should be considered as a way to continue exploring the use of DA concepts in parameter retrieval, and in blending models of the land surface with observations.
6. Conclusions
In this paper, we have introduced the concept of emulation to radiative transfer (RT) models using Gaussian processes (GPs). An emulator is an approximation of a complex function, and thus acts as a very fast drop-in replacement for the original RT code in e.g., a biophysical parameter retrieval scheme. An important additional benefit oemulators is that they provide a very good and fast approximation to the full model output, as well as providing an estimate of the uncertainty of this approximation and very fast access to an approximation of the gradient of the original RT model. We have shown that emulators can be produced for typical RT codes that are widely used by the land surface and atmospheric remote sensing community, both targeting particular spectral bands, or used over the solar reflective domain (wavelenghts between 400 and 2500 nm). Typical speed ups were in the range of 10,000 to 50,000 times, with very modest emulator training requirements. Python code for the emulators introduced in this work is available from the authors [76].
We have used emulators of the PROSAIL RT model in novel parameter retrieval approaches, including Markov Chain Monte Carlo methods that exploit the gradient information, variational DA methods and a sophisticated particle filter. These experiments were run with a synthetic multi-sensor data acquisition scheme. In all three cases, emulators were shown to be suitable for parameter retrieval purposes. The experiments highlighted how emulators can be used with sophisticated inversion methods practical, and also how these sophisticated methods (in particular, the addition of simple models of the temporal evolution of the land surface parameters) lead to complete and gap-filled time series of the parameters, as well as a better estimation of the parameters with reduced uncertainties.
Emulators provide a pragmatic approach to speed up complex RT codes, opening the door to more computationally ambitious retrieval schemes. The rapid access to model gradients also opens the door to more efficient and sophisticated approaches parameter inversion methods. Additionally, emulators might be used to bypass individual processes within a larger model. An example of this would be the nesting of a complex canopy radiative transfer (RT) model in a dynamic vegetation model. The canopy RT model could be emulated for numerical efficiency. The concept can be taken further towards nesting models within models, in a similar fashion to what is shown in Section 3.4.
The rich data acquisition environment that is envisaged for the Sentinel era requires a combination of sound physical RT models and inference schemes to optimally combine all available observations to produce our best estimate of the state of the land surface, fully qualified by a credible uncertainty estimate. We have shown that emulators can play a critical role in advancing biophysical parameter schemes.
Acknowledgments
José Gómez-Dans has been supported by NERC National Centre for Earth Observation (NCEO). We are grateful to the European Space Agency, who has funded parts of this work under projects OPTImisation environment for joint retrieval of multi-sensor RADiances (OPTIRAD, ESA contract 00010977313I/13/I-AM) and “SEOM SY-4Sci Synergy: S2-S3 Land Products”. We thank Nicola Pounder, Jochem Verrelst, Gustau Camps, José Moreno, Thomas Kaminski, Alex Löw, Wout Verhoef and Joris Timmermans for valuable discussions on emulation. We are grateful to Robin Wilson for making his Python bindings to 6S [77] available.
Author Contributions
J.G.D. and P.L. designed and carried out the experiments, and wrote the manuscript. M.D. suggested experiments, and contributed to the drafting of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wulder, M.A.; Hilker, T.; White, J.C.; Coops, N.C.; Masek, J.G.; Pflugmacher, D.; Crevier, Y. Virtual constellations for global terrestrial monitoring. Remote Sens. Environ. 2015, 170, 62–76. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Rodgers, C.D. Others. In Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; Volume 2. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnere, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS Leaf Area Index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Pinty, B.; Andredakis, I.; Clerici, M.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Plummer, S.; Widlowski, J.L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC-TIP): 1. Effective leaf area index, vegetation, and soil properties. J. Geophys. Res. 2011, 116, D09105. [Google Scholar] [CrossRef]
- Lewis, P.; Gómez-Dans, J.; Kaminski, T.; Settle, J.; Quaife, T.; Gobron, N.; Styles, J.; Berger, M. An earth observation land data assimilation system (EO-LDAS). Remote Sens. Environ. 2012, 120, 219–235. [Google Scholar] [CrossRef]
- Giering, R.; Kaminski, T. Recipes for adjoint code construction. ACM Trans. Math. Softw. 1998, 24, 437–474. [Google Scholar] [CrossRef]
- Laurent, V.C.E.; Verhoef, W.; Clevers, J.G.P.W.; Schaepman, M.E. Estimating forest variables from top-of-atmosphere radiance satellite measurements using coupled radiative transfer models. Remote Sens. Environ. 2011, 115, 1043–1052. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Kimes, D.S.; Nelson, R.F.; Manry, M.T.; Fung, A.K. Review article: Attributes of neural networks for extracting continuous vegetation variables from optical and radar measurements. Int. J. Remote Sens. 1998, 19, 2639–2663. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Quaife, T.; Lewis, P.; De Kauwe, M.; Williams, M.; Law, B.E.; Disney, M.; Bowyer, P. Assimilating canopy reflectance data into an ecosystem model with an Ensemble Kalman Filter. Remote Sens. Environ. 2008, 112, 1347–1364. [Google Scholar] [CrossRef]
- Peng, C.; Guiot, J.; Wu, H.; Jiang, H.; Luo, Y. Integrating models with data in ecology and palaeoecology: advances towards a model–data fusion approach. Ecol. Lett. 2011, 14, 522–536. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Ogle, K.; Tucker, C.; Fei, S.; Gao, C.; LaDeau, S.; Clark, J.S.; Schimel, D.S. Ecological forecasting and data assimilation in a data-rich era. Ecol. Appl. 2011, 21, 1429–1442. [Google Scholar] [CrossRef] [PubMed]
- O’Hagan, A.; Kingman, J.F.C. Curve Fitting and Optimal Design for Prediction. J. R. Stat. Soc. Series B Stat. Methodol. 1978, 40, 1–42. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- O’Hagan, A. Some Bayesian numerical analysis. Bayesian Stat. 1992, 4, 345–363. [Google Scholar]
- Kennedy, M.C.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- Challenor, P.G.; Hankin, R.K.S.; Marsh, R. Towards the probability of rapid climate change. In Avoiding Dangerous Climate Change; Cambridge University Press: Cambridge, UK, 2006; pp. 55–63. [Google Scholar]
- Rougier, J.; Sexton, D.M.H.; Murphy, J.M.; Stainforth, D. Analyzing the Climate Sensitivity of the HadSM3 Climate Model Using Ensembles from Different but Related Experiments. J. Climate 2009, 22, 3540–3557. [Google Scholar] [CrossRef]
- Picard, G.; Woodward, F.I.; Lomas, M.R.; Pellenq, J.; Quegan, S.; Kennedy, M. Constraining the Sheffield dynamic global vegetation model using stream-flow measurements in the United Kingdom. Glob. Chang. Biol. 2005, 11, 2196–2210. [Google Scholar] [CrossRef]
- Kennedy, M.; Anderson, C.; O’Hagan, A.; Lomas, M.; Woodward, I.; Gosling, J.P.; Heinemeyer, A. Quantifying uncertainty in the biospheric carbon flux for England and Wales. J. R. Stat. Soc. Ser. A 2008, 171, 109–135. [Google Scholar] [CrossRef]
- Morris, R.D.; Kottas, A.; Taddy, M.; Furfaro, R.; Ganapol, B.D. A statistical framework for the sensitivity analysis of radiative transfer models. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4062–4074. [Google Scholar] [CrossRef]
- Pasolli, L.; Melgani, F.; Blanzieri, E. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 464–468. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Rivera Caicedo, J.P.; Verrelst, J.; Munoz-Mari, J.; Moreno, J.; Camps-Valls, G. Toward a semiautomatic machine learning retrieval of biophysical parameters. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of metamodeling techniques in support of engineering design optimization. J. Mech. Des. 2007, 129, 370–380. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- MacKay, D.J.C. Gaussian Processes—A Replacement for Supervised Neural Networks? 1997. Available online: http://www.inference.eng.cam.ac.uk/mackay/gp.pdf (accessed on 28 January 2016).
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Govaerts, Y. A semidiscrete model for the scattering of light by vegetation. J. Geophys. Res. 1997, 102, 9431–9446. [Google Scholar] [CrossRef]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejadae, P.J.; Asnerf, G.P.; Françoisg, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 13, 56–66. [Google Scholar] [CrossRef]
- Ju, J.; Roy, D.P.; Vermote, E.; Masek, J.; Kovalskyy, V. Continental-scale validation of MODIS-based and LEDAPS Landsat ETM+ atmospheric correction methods. Remote Sens. Environ. 2012, 122, 175–184. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Tanre, D.; Herman, M.; Deschamps, P.; Leffe, A.D. Atmospheric modeling for space measurements of ground reflectances, including bidirectional properties. Appl. Opt. 1979, 18, 3587–3594. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1424. [Google Scholar] [CrossRef]
- MODIS Moderate resolution image spectroradiometer. Available online: http://modis.gsfc.nasa.gov/about/specifications.php (accessed on 28 January 2016).
- Roy, D.P.; Jin, Y.; Lewis, P.E.; Justice, C.O. Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data. Remote Sens. Environ. 2005, 97, 137–162. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Koetz, B.; Baret, F.; Poilvé, H.; Hill, J. Use of coupled canopy structure dynamic and radiative transfer models to estimate biophysical canopy characteristics. Remote Sens. Environ. 2005, 95, 115–124. [Google Scholar] [CrossRef]
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandeza, V.; Gasconb, F.; Hoerschb, B.; Isolaa, C.; Laberintia, P.; Martimorta, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The global monitoring for environment and security (GMES) sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Dierckx, W.; Sterckx, S.; Benhadj, I.; Livens, S.; Duhoux, G.; Achteren, T.V.; Francois, M.; Mellab, K.; Saint, G. PROBA-V mission for global vegetation monitoring: Standard products and image quality. Int. J. Remote Sens. 2014, 35, 2589–2614. [Google Scholar] [CrossRef]
- Zupanski, D. A general weak constraint applicable to operational 4DVAR data assimilation systems. Mon. Weather Rev. 1997, 125, 2274–2292. [Google Scholar] [CrossRef]
- Quaife, T.; Lewis, P. Temporal constraints on linear BRDF model parameters. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2445–2450. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Corporation, T.A.S.; Gelb, A. Applied Optimal Estimation; The MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N.J. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Van Leeuwen, P.J. Particle filtering in geophysical systems. Mon. Weather Rev. 2009, 137, 4089–4114. [Google Scholar] [CrossRef]
- Kantas, N.; Doucet, A.; Singh, S.S.; Maciejowski, J.; Chopin, N. On particle methods for parameter estimation in State-Space models. Stat. Sci. 2015, 30, 328–351. [Google Scholar] [CrossRef]
- Dowd, M. A sequential Monte Carlo approach for marine ecological prediction. Environmetrics 2006, 17, 435–455. [Google Scholar] [CrossRef]
- Dowd, M. Bayesian statistical data assimilation for ecosystem models using Markov Chain Monte Carlo. J. Mar. Syst. 2007, 68, 439–456. [Google Scholar] [CrossRef]
- Yang, W.; Tan, B.; Huang, D.; Rautiainen, M.; Shabanov, N.V.; Wang, Y.; Privette, J.L.; Huemmrich, K.F.; Fensholt, R.; Sandholt, I.; et al. MODIS leaf area index products: From validation to algorithm improvement. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1885–1898. [Google Scholar] [CrossRef]
- Homan, M.D.; Gelman, A. The No-U-turn Sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- The eoldas_ng library. Available online: http://github.com/jgomezdans/eoldas_ng (accessed on 28 January 2016).
- Bastos, L.S.; O’Hagan, A. Diagnostics for Gaussian process emulators. Technometrics 2009, 51, 425–438. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xie, D.; Song, J.; Fensholt, R. A framework for consistent estimation of Leaf Area Index, fraction of absorbed photosynthetically active radiation, and surface albedo from MODIS Time-Series data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3178–3197. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Schmidt, A.M.; Banerjee, S.; Sirmans, C.F. Nonstationary multivariate process modeling through spatially varying coregionalization. Test 2004, 13, 263–312. [Google Scholar] [CrossRef]
- Paciorek, C.J.; Schervish, M.J. Nonstationary covariance functions for Gaussian process regression. In Advances in Neural Information Processing Systems 16; Thrun, S., Saul, L.K., Schölkopf, B., Eds.; MIT Press: Cambridge, MA, USA, 2004; pp. 273–280. [Google Scholar]
- Lauvernet, C.; Baret, F.; Hascoët, L.; Buis, S.; le Dimet, F.X. Multitemporal-patch ensemble inversion of coupled surface–atmosphere radiative transfer models for land surface characterization. Remote Sens. Environ. 2008, 112, 851–861. [Google Scholar] [CrossRef]
- Laurent, V.C.E.; Verhoef, W.; Clevers, J.G.P.W.; Schaepman, M.E. Inversion of a coupled canopy–atmosphere model using multi-angular top-of-atmosphere radiance data: A forest case study. Remote Sens. Environ. 2011, 115, 2603–2612. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Multi-temporal, multi-sensor retrieval of terrestrial vegetation properties from spectral–directional radiometric data. Remote Sens. Environ. 2015, 158, 311–330. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Conti, S.; Gosling, J.P.; Oakley, J.E.; O’Hagan, A. Gaussian process emulation of dynamic computer codes. Biometrika 2009. [Google Scholar] [CrossRef]
- Rougier, J. Efficient emulators for multivariate deterministic functions. J. Comput. Graph. Stat. 2008, 17, 827–843. [Google Scholar] [CrossRef]
- Loew, A.; van Bodegom, P.M.; Widlowski, J.L.; Otto, J.; Quaife, T.; Pinty, B.; Raddatz, T. Do we (need to) care about canopy radiation schemes in DGVMs? Caveats and potential impacts. Biogeosciences 2014, 11, 1873–1897. [Google Scholar] [CrossRef]
- Higdon, D.; Swall, J.; Kern, J. Non-stationary spatial modeling. Bayesian Stat. 1999, 6, 761–768. [Google Scholar]
- Efremenko, D.S.; Loyola, D.G.; Doicu, A.; Spurr, R.J. Multi-core-CPU and GPU-accelerated radiative transfer models based on the discrete ordinate method. Comput. Phys. Commun. 2014, 185, 3079–3089. [Google Scholar] [CrossRef]
- Gomez-Dans, J.L.; Lewis, P.E. Python code for Gaussian process emulation of radiative transfer models. Available online: http://jgomezdans.github.io/gp_emulator (accessed on 28 January 2016). [CrossRef]
- Wilson, R. Py6S: A Python interface to the 6S radiative transfer model. Comput. Geosci. 2013, 51, 166–171. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
