1. Introduction
Wheat is an important food source for the rapidly increasing population in China [
1]. The attention paid to national food security and sustainable agricultural development has increased over recent years, with increased concern for the improvement of field wheat management. Therefore, it is important to estimate wheat growth status and predict wheat yield in a timely and accurate way [
2]. The integration of crop models and remote sensing data has become a useful method for monitoring crop growth status and crop yield based on data assimilation over extensive regions [
3,
4].
In most cases, researches have developed remote sensing and crop models used in their respective study areas [
5]. Crop models simulate crop physiological growth status using mathematical formulas [
6]. They have been used to analyze the influences of climate, soil conditions, and management strategies on agronomic parameters (e.g., canopy aboveground biomass, LAI, and grain yield) [
7]. The Agricultural Model Intercomparison and Improvement Project (AgMIP) recently reviewed 27 wheat models from around the world [
8]. This review showed that poor performance may be obtained when a crop model is applied over a large region due to uncertainties in the spatial distribution of soil properties, initial model conditions, crop parameters, and field management practices, resulting in biased simulations [
9,
10]. Large amounts of high-quality data have been used to improve the calibration and parameterization of crop models, thereby increasing the simulation accuracy of crop models on a regional scale.
Rapid development of remote sensing technology has facilitated the acquisition of crop growth information with high temporal and spatial resolutions [
5,
11,
12,
13,
14,
15,
16]. Previous studies have indicated that combining crop models and remote sensing data can be used to improve the accuracy of crop yield estimates [
17,
18,
19,
20,
21,
22,
23,
24,
25]. Curnel et al. [
17] evaluated the feasibility of assimilating wheat leaf area index (LAI) derived from remote sensing data into the World Food Studies’ (WOFOST) crop growth model using a recalibration-based assimilation method; the results indicated that remote sensing data can be used to improve yield estimations. Dente et al. [
19] assimilated LAI from Environment Satellite (ENVISAT) Advanced Synthetic Aperture Radar (ASAR) and Medium Resolution Imaging Spectrometer (MERIS) data into the Crop Estimation through Resource and Environment Synthesis-Wheat (CERES-Wheat) model at a catchment scale using a variational assimilation algorithm; the results suggested that this approach minimizes the difference between simulated and remotely-sensed LAI and achieves high estimation accuracy. Soil moisture data from the Advanced Microwave Scanning Radiometer-EOS (AMSR-E) and LAI from the Moderate Resolution Imaging Spectroradiometer-LAI (MODIS-LAI) were assimilated into the Decision Support System for Agro-technology Transfer-Cropping System Model (DSSAT-CSM)-Maize using an Ensemble Kalman Filter algorithm, and simulated yield was more accurate when both LAI and soil moisture were used [
22]. The ensemble-based four-dimensional variational method was used to assimilate HJ-1A/B satellite data into the CERES-Wheat model, and estimates of winter wheat yield in field plots were reported (R
2 = 0.73; RMSE = 319 kg/ha) [
23]. Huang et al. [
25] assimilated time series of LAI data with a 30-m spatial resolution into the WOFOST model with a Kalman Filter (KF) algorithm and reported more accurate estimates of regional winter wheat yield compared with more traditional approaches.
The integration of crop models and remotely sensed data using optimization algorithms (data assimilation methods) is becoming an effective and potential method for monitoring crop growth status and estimating crop yields, as it overcomes certain defects and combines the advantages of individual methods [
5,
26,
27,
28,
29,
30]. The data assimilation method can be used to reduce uncertainty in crop models to ensure that the simulated state variables (e.g., LAI and biomass) are in agreement with the measured state variables from remote sensing data. Several assimilation schemes have been developed [
3,
12,
31,
32,
33]. Delecolle et al. [
34] divided schemes into three categories. The first is the forcing method, in which state variables in crop models are directly substituted by remote sensing variables. This method is easy to use, but it relies on the calibrated parameters of crop models and the accuracy of remote sensing data [
5,
12]. The second is the calibration method, in which the initial parameters of crop models are recalibrated, based on the relationship between the remote sensing state variables and the simulated state variables [
5,
10,
34]. In recent years, the calibration method has gained more attention, as it has greatly benefited from several intelligent optimization algorithms. The main shortcoming of the calibration method is that a great deal of computation time is required [
3,
5,
30]. The third is the updating method, in which the simulated state variables are continuously renewed whenever remote sensing state variables are available. It is more flexible than the forcing method, but the remote sensing data must be of a higher accuracy than those of the simulated state variables, and this method heavily relies on the selection of the remote sensing data [
4,
33,
35].
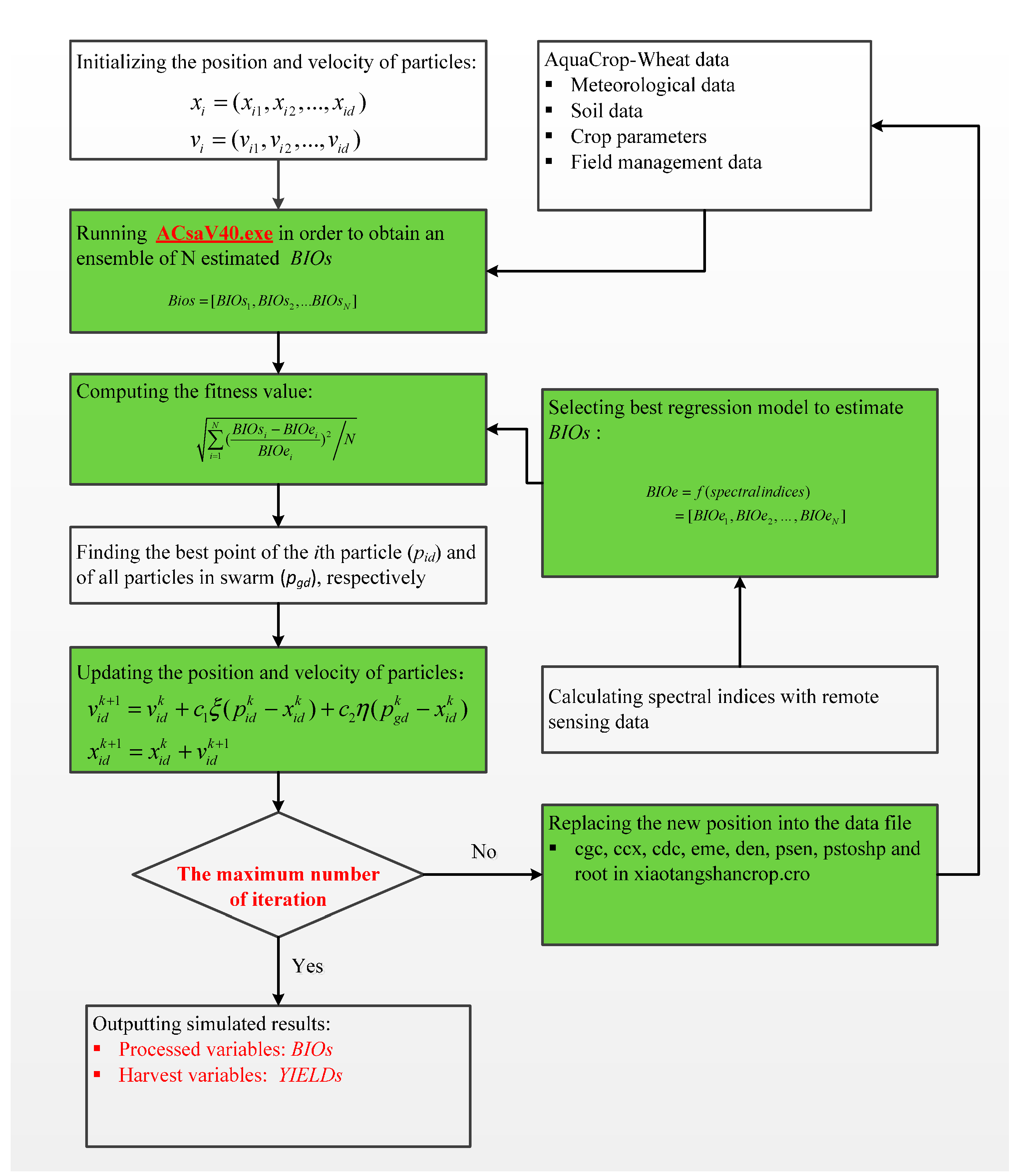
The combination of remote sensing data and light-driven or carbon-driven models has been widely studied, but few studies have focused on water-driven models for estimating the biomass and yield of crops. Therefore, in this study we focused on the AquaCrop model, a water-driven crop model, which was recently introduced to optimize crop water management strategies and improve crop yield in irrigation regions [
36]. Winter wheat is the main crop grown in the North China Plain (NCP), and thus an important food source in China. Increased industrial and domestic water use has resulted in reduced water availability for irrigation of winter wheat crops. Therefore, improving water resource management in this region is crucial for increasing winter wheat yield. The main goal of this study was to improve estimates of winter wheat biomass and yield by assimilating field spectroscopic data into the AquaCrop model with a Particle Swarm Optimization (PSO) algorithm. The biomass and yield of winter wheat were used to optimize field irrigation management strategies and then to increase water use efficiency under different planting dates and irrigation management strategies. The specific objectives of this study were: (1) to select the best spectral indices from hyperspectral data for estimating winter wheat biomass; (2) to calibrate the AquaCrop model with biomass estimates derived from these indices using the PSO algorithm for improving accuracy of biomass and yield estimates; and (3) to evaluate the performance of the data assimilation method in estimating wheat biomass and yield.
4. Discussion
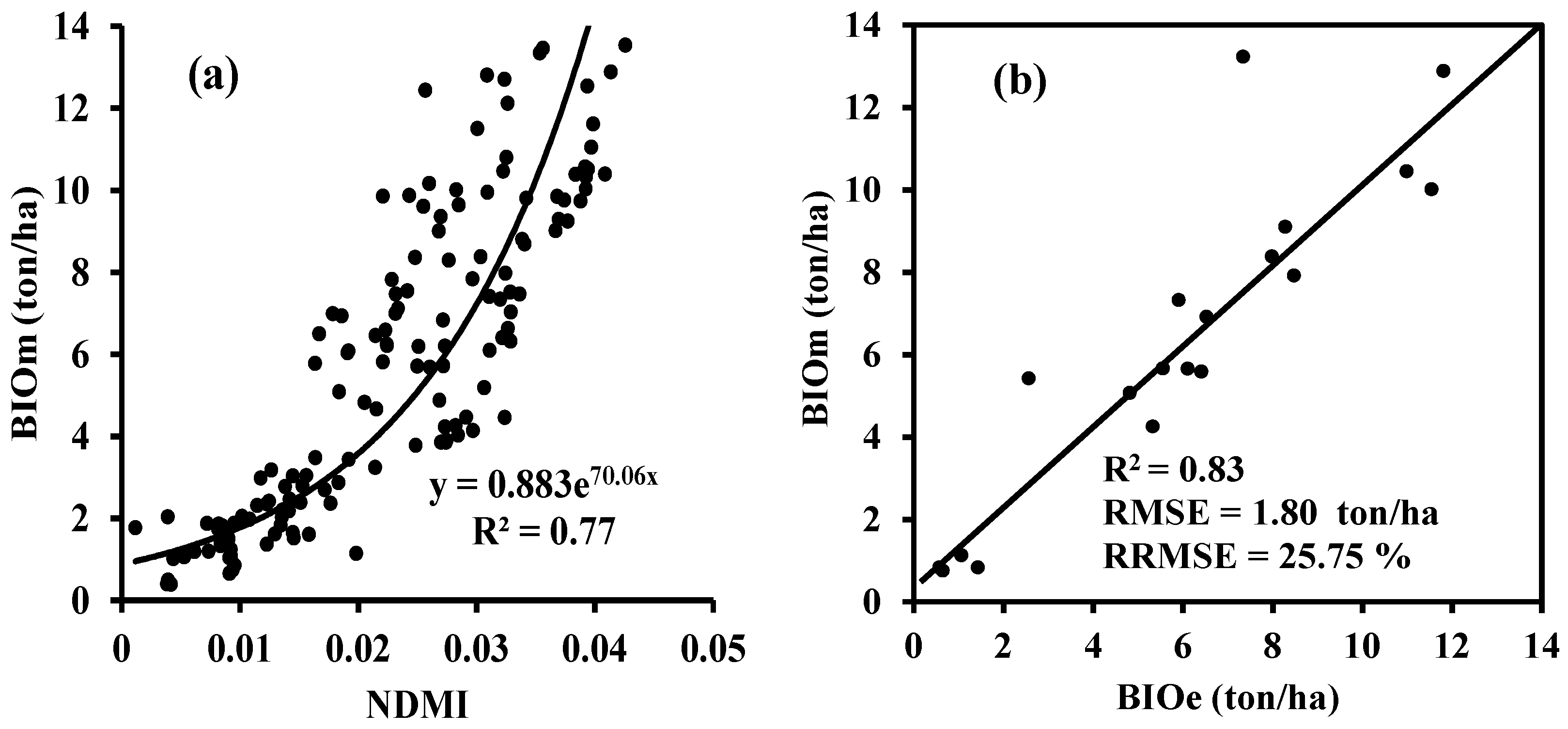
Spectral data and concurrent biomass and yield were acquired during four winter wheat growing seasons. Fifteen spectral indices were related to biomass (
Table 5); this is because red edge (670–780 nm) and near infrared (short NIR, 800-1100 nm) data contain useful information regarding vegetation biomass [
13,
39,
44,
50]. In particular, NDMI was found to be highly correlated with biomass, with R
2 and RMSE values of 0.77 and 1.80 ton/ha, respectively. NDMI does not contain red edge or short NIR data because absorption at these wavelengths is strongly influenced by chlorophyll content and canopy structure, which reduce the signal compared with that of dry matter. However, NDMI contains data at 1649 and 1722 nm, which are more sensitive to changes in dry matter [
42]. These data were combined to establish NDMI, which includes signals from dry matter. For this reason, NDMI was more highly related with biomass than the other spectral indices and achieved more accurate biomass estimations. In this study, the linear and nonlinear regression relationships between each spectral index and biomass were analyzed to select the best-fitting regression equations. The results show that some models were fitted using power regression, and others fitted using exponential regression (
Table 5). The difference between two regressions may have a close relationship with each spectral index and biomass dataset.
The model’s initial variables (
num and
eme) and crop parameters (
cgc,
ccx,
cdc,
eme,
psen, and
rootdep) were calibrated by combining biomass retrieved from spectral indices and the AquaCrop model via the PSO assimilation algorithm, thereby achieving optimal biomass estimations. The simulated biomass values were consistent with the measured values. These findings are consistent with those of Soddu et al. [
58]. Heng et al. [
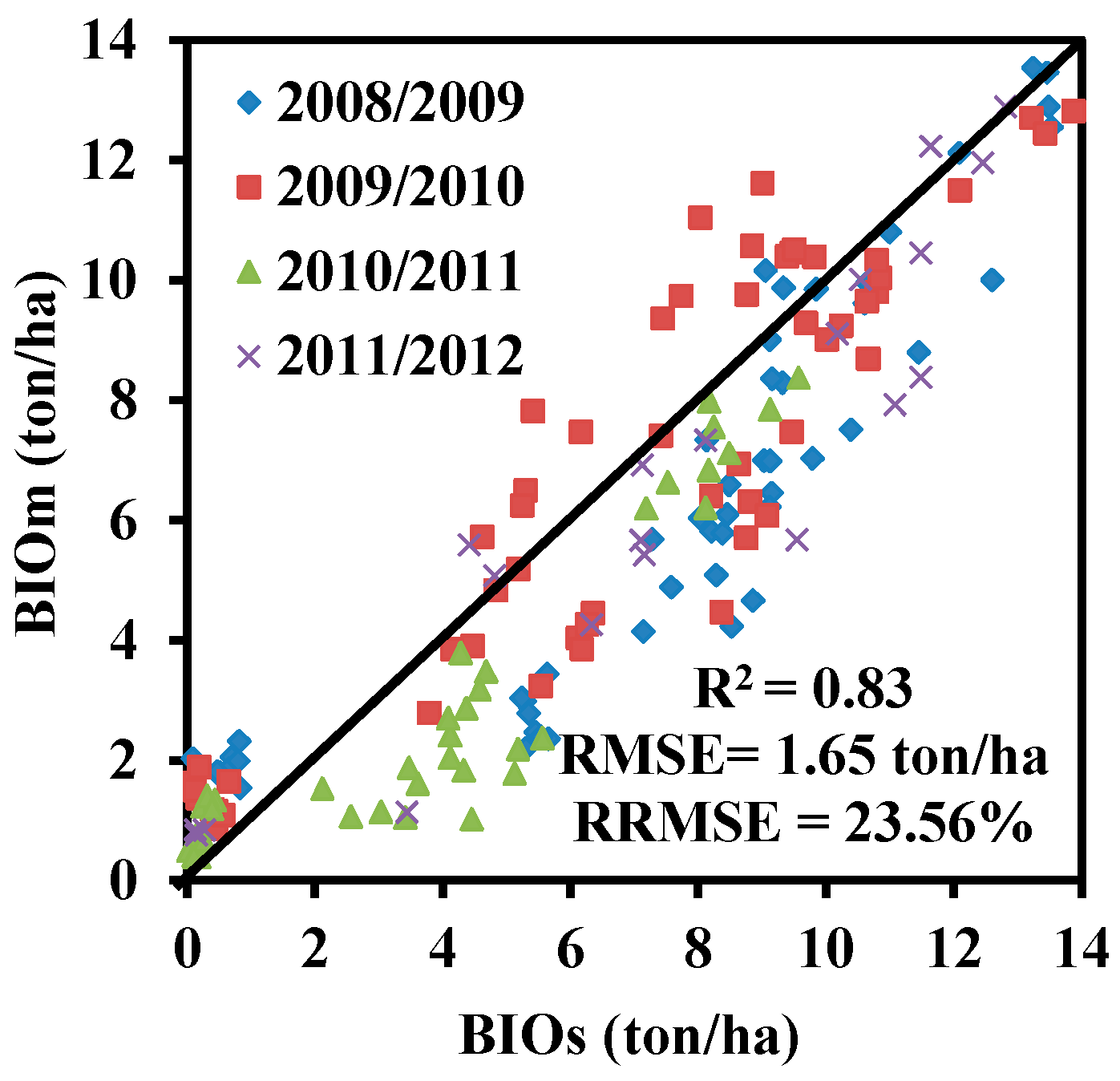
59] showed that the AquaCrop model is used to better simulate biomass when irrigation is adequate. Our results suggest that the AquaCrop model could be used to simulate winter wheat biomass. The data assimilation method, based on the PSO algorithm, achieved better biomass estimations than the spectral index method (
Table 5 and
Table 6). The main reasons are as follows: (i) The AquaCrop model can be used to simulate dry biomass accumulation on the basis of a plant’s physiological processes, and the effects of field management strategies and weather [
36,
37,
59,
60]; and (ii) the data assimilation method was used to minimize errors between the observed values from field spectroscopic data and the simulated values from the AquaCrop model, and the errors in the remote sensing data were reduced during data assimilation [
10]. Typically, biomass simulated with the data assimilation method was overestimated when the measured values exceeded 2 ton/ha, but was underestimated when the measured values were less than 2 ton/ha (
Figure 3). This explains why the regression equations between NDMI and biomass were similar. Therefore, the integration of spectral indices into the AquaCrop model, using the PSO assimilation algorithm, is a useful tool for winter wheat biomass estimation.
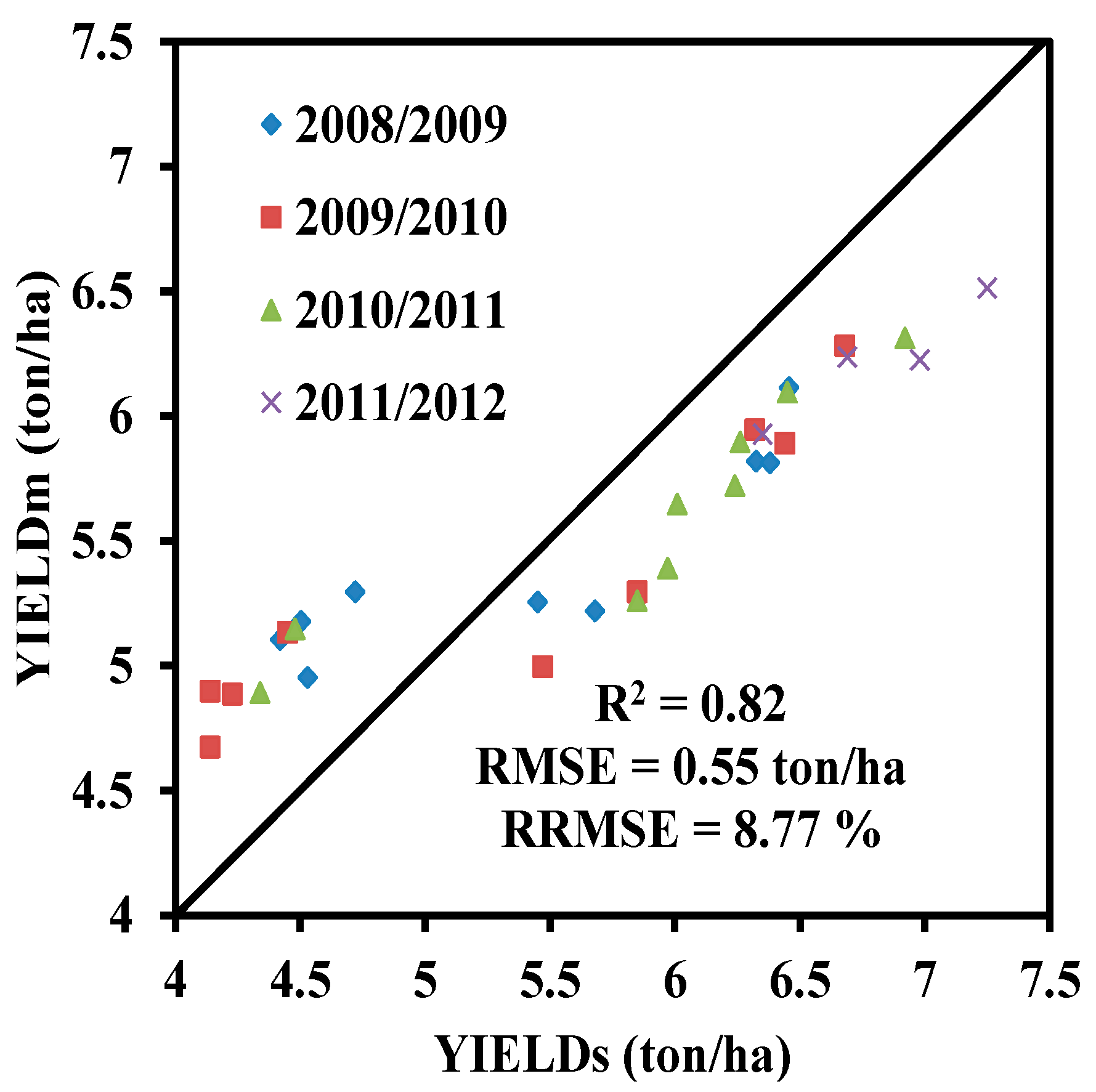
Winter wheat grain yield was simulated according to the optimized values of the initial variables and calibrated crop parameters using the PSO data assimilation algorithm. A good relationship between the measured and simulated yields was found across all four years (R
2 = 0.82 and RMSE = 0.55 ton/ha). However, the RRMSE for yield was lower than that for biomass (
Table 6 and
Table 7), mainly because the latest biomass measurements were taken at the grain filling stage (12 June) rather than at maturity and biomass simulated with the AquaCrop model becomes more accurate with the development of winter wheat [
37,
61]. Our results are in agreement with those of Wang et al. [
61] and Jin et al. [
37]. The AquaCrop model considers the effects of interannual variations in weather and field management strategies, as well as interactions between the two, on wheat growth status; therefore, it was used to analyze the nonlinear interannual variability in crop grain yield [
36]. The results suggest that the AquaCrop model is an effective tool for deriving crop management strategies, and can be used to simulate biomass and grain yield of winter wheat. First, biomass retrieved from spectral indices is used to calibrate crop biomass simulated with the AquaCrop model. If crop biomass is accurately simulated, it can be used to simulate yield. The simulated yield is finally obtained directly from the AquaCrop model after data assimilation. Simulated grain yield is a useful measurement for informed decision-making regarding national food security issues. However, it is more important to obtain crop growth status information and then to improve field crop management for improving grain yield to ensure national food security, In short, the dynamic simulated biomass of wheat is used to enhance wheat management and decision-making, and then to ensure wheat yield.
The data assimilation accuracy of biomass and grain yield was acceptable according to the R
2, RSME, and RRMSE values (
Table 6 and
Table 7). The results of Dente et al. [
19] and Jiang et al. [
23] indicated that assimilating remote sensing data (ENVISAT ASAR, MERIS, and HJ-1A/B satellites images) into the CERES-Wheat model with optimization algorithms (variational assimilation algorithm and Ensemble-Based Four-Dimensional Variational algorithm) can improve the estimation accuracy of wheat yield. Huang et al. [
25] recently suggested that combining the WOFOST model and remote sensing data (MODIS and Landsat TM images) with a KF algorithm also increases the estimation accuracy of wheat yield. Our results are in agreement with the results of these studies and demonstrate that the combination of the AquaCrop model and spectral indices with a PSO algorithm can be used to enhance the estimation accuracy of winter wheat yield. A good relationship between the simulated and measured yields was found (
Figure 4); however, the relationship between measured and simulated biomass was not reliable during each growth stage (
Figure 3). This can be attributed to the influence of a large difference in the biomass measurement date on biomass simulation [
37], which then introduced uncertainties into the process of data assimilation. However, the yield simulations were consistent during all crop growth stages. Therefore, the data assimilation method can improve crop yield estimations because the AquaCrop model considers the effects of management strategies and environmental factors on winter wheat growth status, based on a plant’s physiological processes. Our results suggest that integrating remote-sensing data into the AquaCrop model is a feasible method for estimating winter wheat biomass and yield.
In this study, the hyperspectral data that were obtained were ground-based data. To improve our model for estimating biomass and yield in winter wheat, and to make it more practical, it is important to estimate the accuracy and stability of the model using hyperspectral satellite data. The current Landsat and Sentinel-2 satellites provide high spatial resolution imagery data (10–60 m) with relatively short revisit periods. Based on this, Landsat and Sentinel-2 sensors have the potential for improved estimates of biomass and yield in winter wheat at regional scales. With the development of unmanned aerial vehicles (UAV), the combination of UAV and hyperspectral imaging data should allow for the timely estimation of the growth status of crops, with high spatial resolution image data at the field and farm scales, in the future. In this study, we only carried out experiments at a single-site, and obtained good results over four years. The method used in this study is transferrable to other sites. The main insights from this study are as follows: (i) The crop parameters of the AquaCrop model for different crops are parameterized to better-simulate different crop biomass and yields, during all growth stages under different environmental conditions and experimental sites; (ii) different crops should be accurately classified using high temporal and spatial resolution image data when this method is applied to regional scales; (iii) PSO will further enhance the advantages of a parallel algorithm to quickly obtain estimated results at regional scales; (iv) corresponding field crop management strategies (such as water and fertilizer management) can then be carried out, based on the estimated crop biomass, resulting in improved crop yields at regional scales; and (v) in addition, this method can be combined with higher temporal and spatial resolution image data and the AquaCrop model to improve field crop management, and then to enhance crop yield at the sub-field and sub-farm scales in the future. The positive results obtained here were based on single-site experiments over four years, however, further experiments should be carried out to adjust crop parameters of the AquaCrop model under water and fertilizer stress treatments to maintain the stability of the simulated results. The effect of the soil parameter variations on the simulated results in the AquaCrop model should be further investigated to better apply it at regional scales. Further studies are needed to verify these results for different crops, and in different ecological areas, as this study was limited to winter wheat in Beijing, China.