Deformation Monitoring and Analysis of the Geological Environment of Pudong International Airport with Persistent Scatterer SAR Interferometry
Abstract
:1. Introduction
2. Description of the Study Area and SAR Dataset
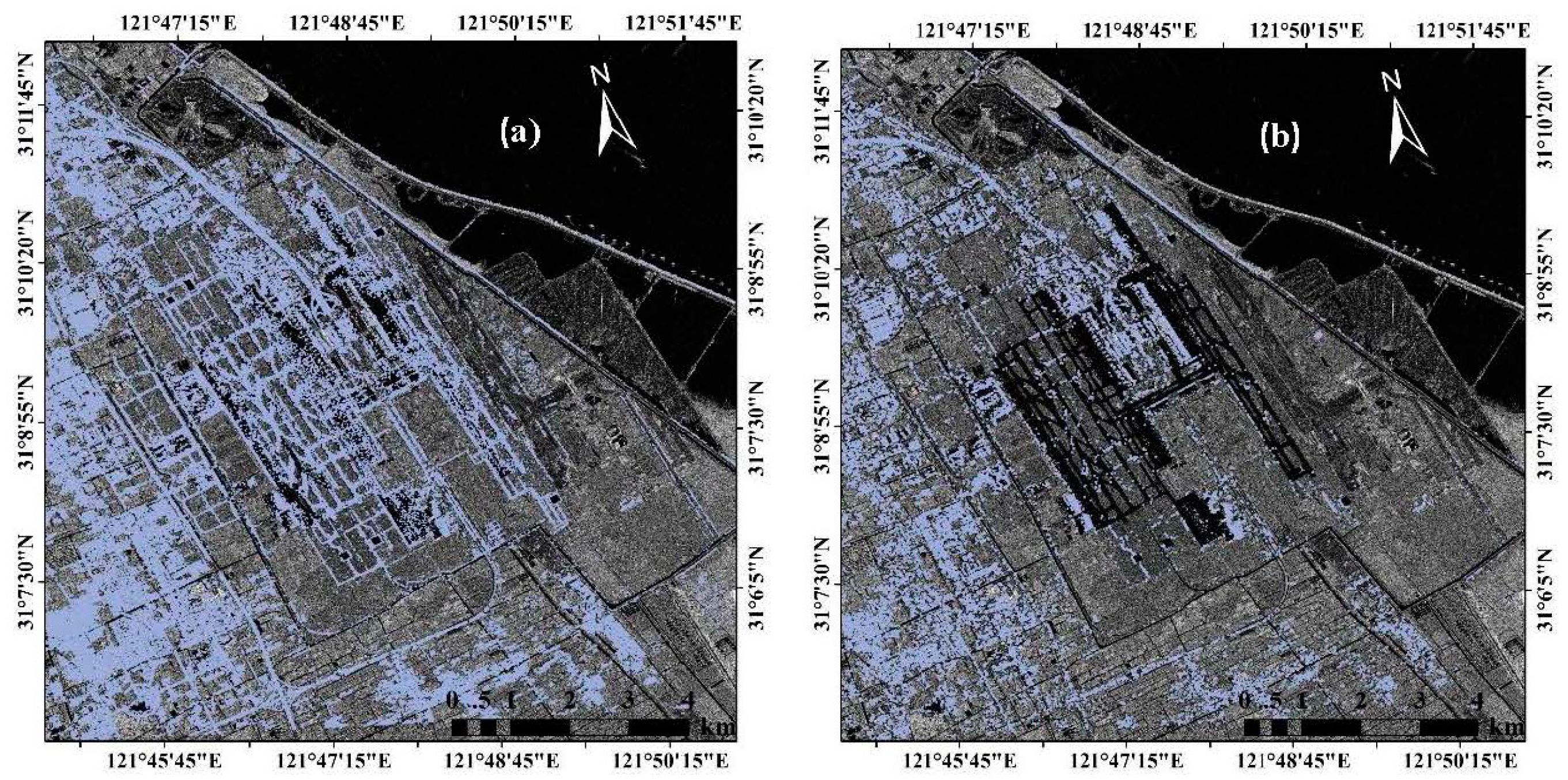
2.1. Study Area
2.2 Dataset and Data Pre-Processing
3. Methodology
3.1. The PSI Technology
3.2. Point Target Extraction in a Low-Coherence Area
- Initial pixel candidates are selected based on the amplitude stability of individual pixels, using a higher amplitude dispersion threshold value (0.4).
- Preliminary elimination of pixel candidates is then carried out based on the phase stability of the pixels. High coherence PS candidates are chosen by iteration using the coherence-like coefficient method [20].
- A standard deviation (STD) threshold for the phase is set for PS candidates to exclude pseudo PS points; in the case of Pudong International Airport, points with phase STDs larger than the indicated threshold value (>0.7) were considered as unstable points and rejected.
3.3. Phase Analysis and Deformation Calculation
4. Results and Reliability Analysis
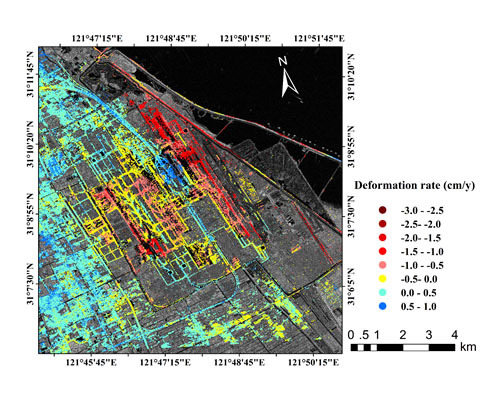
4.1. InSAR-Derived Results
- The first runway has a moderate deformation status with little change in deformation characteristics. The maximum deformation rates in the first runway area was approximately −1.5 cm/year;
- The second runway shows the most serious deformation among the three runways. Different degrees of uneven deformation rates can be seen in both the north-south profile and east-west profile.
- The third runway has the most complex difference in deformation rates among the three runways. It has a relatively large deformation gradient in the east-west direction. The displacement in the P7 area was approximately −0.5 cm/year, while the displacement in the P8 area was more than −2.5 cm/year, a 2.0 cm/year difference.
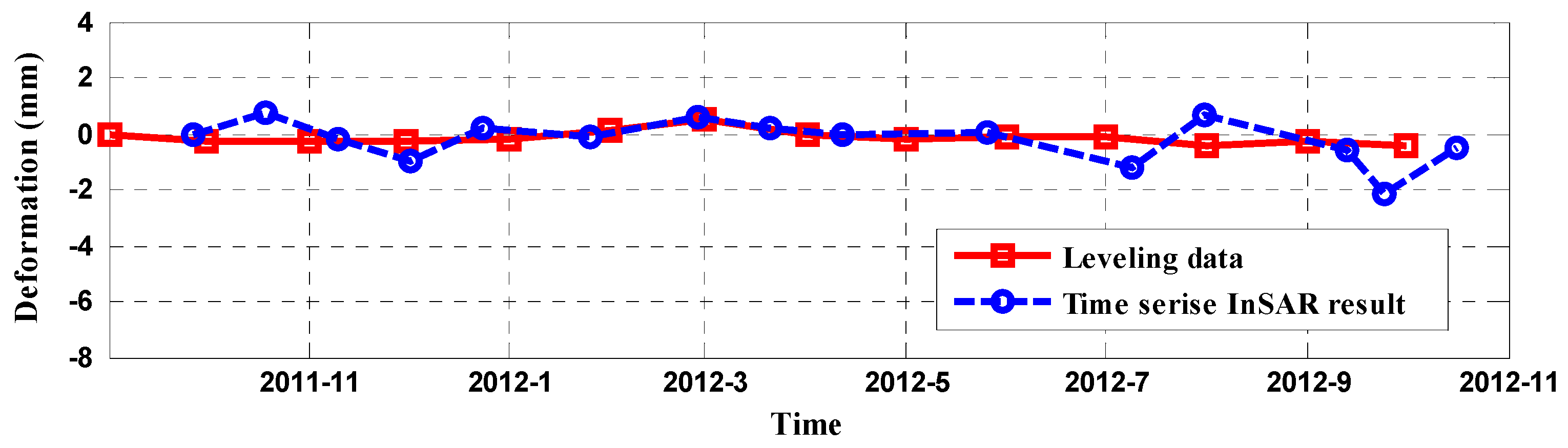
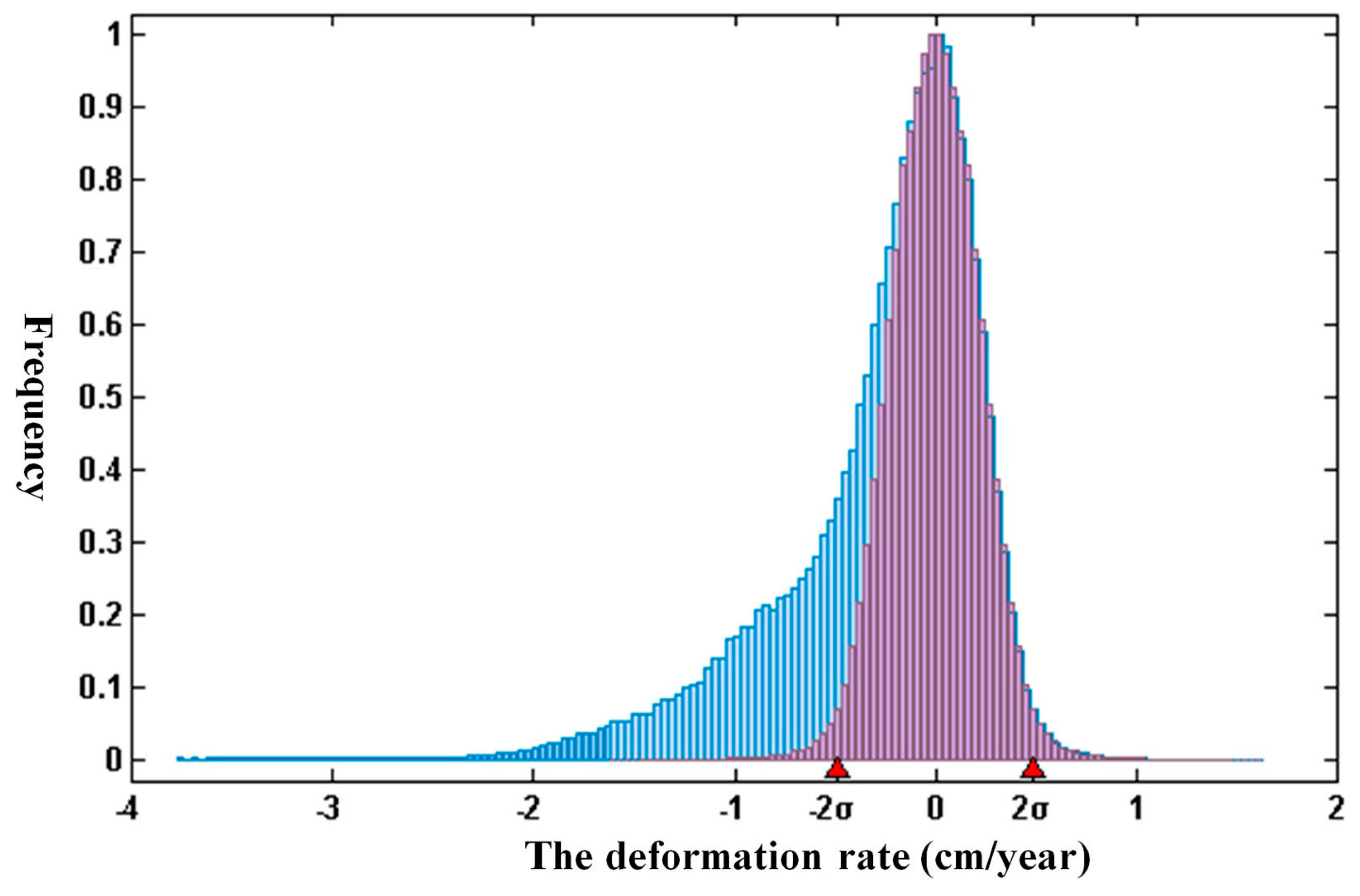
4.2. Reliability Analysis of the Derived Deformation
5. Discussion
5.1. Runways Subgrade
- The first runway was put into use in 1999; since then, the subgrade settlement of the runway remained large; subsequently the average cumulative deformation reached 59 cm by 2009. However, during this period, the deformation rate also displayed a slight slowing trend. After more than a decade of consolidation effects of the soft clay, we can infer that the foundation settlement rate should have continuous decreased during the study period [7]. As shown in the deformation result plotted in Figure 4, InSAR results of the ground settlement continued to slow from September 2011 to October 2012, to less than 1.5 cm/year.
- The second runway, in operation since 2005, lies in the eastern part of the reclaimed land of the airport. The time over which the land formed here was the shortest; the foundation of the second runway was not formed until a 2001 reclamation project [42]. Due to this kind of weak basic geology, the second runway exhibited the most serious deformation, with a maximum deformation rate greater than 2.5 cm/year.
- The third runway, lying to the west of the first runway, was completed in 2008, with a foundation relatively similar to the first runway. However, since it was completed nine years later than the first runway, the geological base itself still needs further consolidation. Consequently, the third runway underwent more pronounced settlement than the first runway, with a maximum deformation rate greater than 2 cm/year.
5.2. Geological Environment
5.2.1. Paleo-Rivers
5.2.2. Seawater Influence
5.2.3. Static Load
- The geological foundation.
- Construction time. Under similar geological conditions (e.g., the first and the third runway), the later the time of completion (the third runway), the more serious soil un-compaction and the larger the settlement will be.
- Paleo-rivers. The soil around the paleo-rivers is weaker than that in other places, thus the paleo-river is an important factor causing inhomogeneous deformation at the airport.
- Seawater influence. The side of the airport closer to the sea experiences seawater influence, such as salt-water intrusion and flushing corrosion, and thus is weaker than other sides of the airport.
- Static load. This is likely the primary factor contributing to the uniform deformation pattern found in the third runway area.
5.3. Potential and Notes of InSAR in Monitoring Coastal Subsidence
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Glaser, R.; Haberzettl, P.; Walsh, R. Land reclamation in Singapore, Hong Kong and Macau. GeoJ 1991, 24, 365–373. [Google Scholar] [CrossRef]
- Stuyfzand, P.J. The impact of land reclamation on groundwater quality and future drinking water supply in the Netherlands. Water Sci. Technol. 1995, 31, 47–57. [Google Scholar] [CrossRef]
- Kim, S.W.; Lee, C.W.; Song, K.Y.; Min, K.; Won, J.S. Application of L-band differential SAR interferometry to subsidence rate estimation in reclaimed coastal land. Int. J. Remote Sens. 2005, 26, 1363–1381. [Google Scholar] [CrossRef]
- Hoeksema, R.J. Three stages in the history of land reclamation in the Netherlands. Irrig. Drain. 2007, 56, S113–S126. [Google Scholar] [CrossRef]
- Pickles, A.; Tosen, R. Settlement of reclaimed land for the new Hong Kong international airport. ICE Proc. Geotech. Eng. 1998, 131, 191–209. [Google Scholar] [CrossRef]
- Douglas, I.; Lawson, N. Airport construction: Materials use and geomorphic change. J. Air Transp. Manag. 2003, 9, 177–185. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, H. Integrated analysis of SAR interferometric and geological data for investigating long-term reclamation settlement of Chek Lap Kok airport, Hong Kong. Eng. Geol. 2010, 110, 77–92. [Google Scholar] [CrossRef]
- Wang, T.; Perissin, D.; Rocca, F.; Liao, M.S. Three Gorges Dam stability monitoring with time-series InSAR image analysis. Sci. China Earth Sci. 2011, 54, 720–732. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001; Volume 2. [Google Scholar]
- Ding, X.; Liu, G.; Li, Z.W.; Li, Z.L.; Chen, Y.Q. Ground subsidence monitoring in Hong Kong with satellite SAR interferometry. Photogramm. Eng. Remote Sens. 2004, 70, 1151–1156. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, M.S.; Li, D.R.; Wei, Z.X.; Fang, Z. Subsidence velocity retrieval from long-term coherent targets in radar interferometric stacks. Chin. J. Geophs. Chin. Ed. 2007, 50, 598–604. [Google Scholar]
- Jiang, M.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Feng, G.C. Modeling minimum and maximum detectable deformation gradients of interferometric SAR measurements. Int. J. Appl. Earth Obs. 2011, 13, 766–777. [Google Scholar] [CrossRef]
- Tomás, R.; Romero, R.; Mulas, J.; Marturià, J.J.; Mallorquí, J.J.; López-Sánchez, J.M.; Herrera, G.; Gutiérrez, F.; González, P.J.; Fernández, J. Radar interferometry techniques for the study of ground subsidence phenomena: A review of practical issues through cases in Spain. Environ. Earth Sci. 2014, 71, 163–181. [Google Scholar] [CrossRef]
- Dong, S.; Samsonov, S.; Yin, H.; Yao, S.; Xu, C. Spatio-temporal analysis of ground subsidence due to underground coal mining in Huainan coalfield, China. Environ. Earth Sci. 2015, 73, 5523–5534. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. SAR monitoring of progressive and seasonal ground deformation using the Permanent Scatterers Technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Lyons, S.; Sandwell, D. Fault creep along the southern San Andreas from interferometric synthetic aperture radar, permanent scatterers, and stacking. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Hooper, A.J. Persistent scatter radar interferometry for crustal deformation studies and modeling of volcanic deformation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2006. [Google Scholar]
- Kampes, B.M. Radar Interferometry: Persistent Scatterer Technique; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Sousa, J.J.; Ruiz, A.M.; Hanssen, R.F.; Bastos, L.; Gil, A.J.; Galindo-Zaldívar, J.; de Galdeano, C.S. PS-InSAR processing methodologies in the detection of field surface deformation—Study of the Granada Basin (Central Betic Cordilleras, southern Spain). J. Geodyn. 2010, 49, 181–189. [Google Scholar] [CrossRef]
- Pei, Y.; Liao, M.; Wang, H. Monitoring subsidence in reclamation area with time series DInSAR images. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 1092–1095. [Google Scholar]
- Jendryke, M.; Balz, T.; Jiang, H.; Liao, M.; Stilla, U. Using open-source components to process interferometric TerraSAR-X spotlight data. Int. J. Antennas Propag. 2013, 2013, 275635. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Osmanoğlu, B.; Dixon, T.H.; Wdowinski, S.; Cabral-Cano, E.; Jiang, Y. Mexico city subsidence observed with persistent scatterer InSAR. Int. J. Appl. Earth Obs. 2011, 13, 1–12. [Google Scholar] [CrossRef]
- Abdikan, S.; Arıkan, M.; Sanli, F.B.; Cakir, Z. Monitoring of coal mining subsidence in peri-urban area of Zonguldak city (NW Turkey) with persistent scatterer interferometry using ALOS-PALSAR. Environ. Earth Sci. 2014, 71, 4081–4089. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, Z.; Lin, H. Shanghai subway tunnels and highways monitoring through Cosmo-SkyMed Persistent Scatterers. ISPRS J. Photogramm. 2012, 73, 58–67. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, L.; Chen, J.; Li, T. Monitoring ground subsidence in shanghai maglev area using two kinds of SAR data. J. Appl. Geod. 2012, 6, 209–213. [Google Scholar] [CrossRef]
- Dong, S.C.; Samsonov, S.; Yin, H.W.; Ye, S.J.; Cao, Y.R. Time-series analysis of subsidence associated with rapid urbanization in Shanghai, China measured with SBAS InSAR method. Environ. Earth Sci. 2014, 72, 677–691. [Google Scholar] [CrossRef]
- Zhao, Q.; Pepe, A.; Gao, W.; Lu, Z.; Bonano, M.; He, M.L.; Wang, J.; Tang, X. A DInSAR investigation of the ground settlement time evolution of ocean-reclaimed lands in Shanghai. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1673–1781. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, H.; Cheng, S. Monitoring and assessing reclamation settlement in coastal areas with advanced InSAR techniques: Macao city (China) case study. Int. J. Remote Sens. 2011, 32, 3565–3588. [Google Scholar] [CrossRef]
- Zhao, Q.; Lin, H.; Gao, W.; Zebker, H.A.; Chen, A.; Yeung, K. InSAR detection of residual settlement of an ocean reclamation engineering project: A case study of Hong Kong international airport. J. Oceanogr. 2011, 67, 415–426. [Google Scholar] [CrossRef]
- Baeteman, C. Vulnerability of coastal lowlands. A case study of land subsidence in Shanghai, P.R. China. In Greenhouse Effect, Sea Level and Drought; Paepe, R., Fairbridge, R.W., Jelgersma, S., Eds.; Springer: Dordrecht, The Netherlands, 1990; pp. 415–426. [Google Scholar]
- Gong, S. Effects of urban construction on the land subsidence in Shanghai. Chin. J. Geol. Hazard Control 1998, 9, 108–111. [Google Scholar]
- U.S. Geological Survey. USGS EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 9 December 2016).
- Zebker, H.; Chen, K. Accurate estimation of correlation in InSAR observations. IEEE Lett. Geosci. Remote Sens. 2005, 2, 124–127. [Google Scholar] [CrossRef]
- Hooper, A. A Statistical-Cost Approach To Unwrapping The Phase Of InSAR Time Series. In Proceedings of the International Workshop on ERS SAR Interferometry, Frascati, Italy, 30 November–4 December 2009.
- Samsonov, S.V.; d’Oreye, N.; González, P.J.; Tiampo, K.F.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the greater vancouver region from two decades of ERS-ENVISAT-RADARSET-2 DInSAR measurements. Remote Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef]
- Wang, X.H.; Yin, C.L.; Si, B.F.; Li, J.S.; Liu, S.; Su, E.H. Foundation bed treatment for high-grade taking-off and landing runway-study on construction proposal for the third runway of Shanghai Pudong international airport building construction. Build. Constr. 2007, 29, 275–277. [Google Scholar]
- Wang, G.D.; Han, L.M.; Chai, Z.L. Subgrade settlement rules of first runway of Pudong airport in Shanghai. J. Eng. Geol. 2012, 20, 131–137. [Google Scholar]
- Wang, Z. A Combined Reinforcement Method for Shallow Soft Soil Foundation; Shanghai Scientific and Technical Publishers: Shanghai, China, 2006. [Google Scholar]
- Slatton, K.C.; Crawford, M.M.; Gibeaut, J.C.; Gutierrez, R. Removal of residual errors from SAR -derived digital elevation models for improved topographic mapping of low-relief areas. In Proceedings of International Geoscience and Remote Sensing Symposium on Remote Sensing: A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; pp. 457–459.
- Crosetto, M.; Monserrat, O.; Cuevas-Gonzaìlez, M.; Devantheìry, N.; Crippa, B. Analysis of X-band very high resolution persistent scatterer interferometry data over urban area. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science, Hannover, Germany, 1–24 May 2013; pp. 21–24.



| No. | Acquisition Date | Orbit | Time Baseline (Days) | Perpendicular Baseline (m) |
|---|---|---|---|---|
| 1 | 27 September 2011 | 23,772 | −66 | −26 |
| 2 | 19 October 2011 | 24,106 | −44 | 22 |
| 3 | 10 November 2011 | 24,440 | −22 | −41 |
| 4 | 2 December 2011 | 24,774 | 0 | 0 |
| 5 | 24 December 2011 | 25,108 | 22 | 157 |
| 6 | 26 January 2012 | 25,609 | 55 | −60 |
| 7 | 28 February 2012 | 26,110 | 88 | −159 |
| 8 | 21 March 2012 | 26,444 | 110 | 117 |
| 9 | 12 April 2012 | 26,778 | 132 | 119 |
| 10 | 26 May 2012 | 27,446 | 176 | 102 |
| 11 | 9 July 2012 | 28,114 | 220 | −31 |
| 12 | 31 July 2012 | 28,448 | 242 | 50 |
| 13 | 13 September 2012 | 29,116 | 286 | −71 |
| 14 | 24 September 2012 | 29,283 | 297 | 38 |
| 15 | 16 October 2012 | 29,617 | 319 | 59 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Liao, M.; Wang, H.; Zhang, L.; Balz, T. Deformation Monitoring and Analysis of the Geological Environment of Pudong International Airport with Persistent Scatterer SAR Interferometry. Remote Sens. 2016, 8, 1021. https://doi.org/10.3390/rs8121021
Jiang Y, Liao M, Wang H, Zhang L, Balz T. Deformation Monitoring and Analysis of the Geological Environment of Pudong International Airport with Persistent Scatterer SAR Interferometry. Remote Sensing. 2016; 8(12):1021. https://doi.org/10.3390/rs8121021
Chicago/Turabian StyleJiang, Yanan, Mingsheng Liao, Hanmei Wang, Lu Zhang, and Timo Balz. 2016. "Deformation Monitoring and Analysis of the Geological Environment of Pudong International Airport with Persistent Scatterer SAR Interferometry" Remote Sensing 8, no. 12: 1021. https://doi.org/10.3390/rs8121021
APA StyleJiang, Y., Liao, M., Wang, H., Zhang, L., & Balz, T. (2016). Deformation Monitoring and Analysis of the Geological Environment of Pudong International Airport with Persistent Scatterer SAR Interferometry. Remote Sensing, 8(12), 1021. https://doi.org/10.3390/rs8121021