Abstract
Water body detection worldwide using spaceborne remote sensing is a challenging task. A global scale multi-temporal and multi-spectral image analysis method for water body detection was developed. The PROBA-V microsatellite has been fully operational since December 2013 and delivers daily near-global synthesis with a spatial resolution of 1 km and 333 m. The Red, Near-InfRared (NIR) and Short Wave InfRared (SWIR) bands of the atmospherically corrected 10-day synthesis images are first Hue, Saturation and Value (HSV) color transformed and subsequently used in a decision tree classification for water body detection. To minimize commission errors four additional data layers are used: the Normalized Difference Vegetation Index (NDVI), Water Body Potential Mask (WBPM), Permanent Glacier Mask (PGM) and Volcanic Soil Mask (VSM). Threshold values on the hue and value bands, expressed by a parabolic function, are used to detect the water bodies. Beside the water bodies layer, a quality layer, based on the water bodies occurrences, is available in the output product. The performance of the Water Bodies Detection Algorithm (WBDA) was assessed using Landsat 8 scenes over 15 regions selected worldwide. A mean Commission Error (CE) of 1.5% was obtained while a mean Omission Error (OE) of 15.4% was obtained for minimum Water Surface Ratio (WSR) = 0.5 and drops to 9.8% for minimum WSR = 0.6. Here, WSR is defined as the fraction of the PROBA-V pixel covered by water as derived from high spatial resolution images, e.g., Landsat 8. Both the CE = 1.5% and OE = 9.8% (WSR = 0.6) fall within the user requirements of 15%. The WBDA is fully operational in the Copernicus Global Land Service and products are freely available.
1. Introduction
Inland water surface mapping is important to budget freshwater supply for human and animals [1,2,3], and agriculture [4,5,6], but also to monitor ecological issues and to perform ecosystem management [7,8,9,10]. However, water body detection worldwide using spaceborne remote sensing is a challenging task because many objects on the Earth’s surface have similar spectral properties (within the spectral range of the applied sensor) as water bodies. Nevertheless, several spaceborne missions have been used to address this. The Moderate Resolution Imaging Spectrometer (MODIS) sensor was used to create the 250 m land-water mask (MOD44W) for the year 2000 [11]. Recently, MODIS data were used to assess global inland water body dynamics on a daily basis [12]. The SPOT VEGETATION (VGT) sensor was first used to create the dynamic Small Water Bodies (SWB) monitoring product for the African continent [13]. The same sensor is used to construct the global water bodies products for the whole archive, years 1999 to 2014, based on the work presented in this paper and becoming available by the end of 2016. The thematic Mapper (TM) and Enhanced Thematic Mapper Plus (ETM+) sensors (Landsat 5 and Landsat 7, respectively), which allow high-resolution mapping of small water bodies, were used for water quality assessment [14] and water bodies extraction [15]. The latter were also used for mapping inland surface water at global scale for the years 2000 and 2010 resulting in the Global Land 30-water 2000 and Global Land 30-water 2010 datasets, respectively [16]. The Global Land Survey (GLS) Landsat data collection was used to produce a global, 30-m-resolution inland surface water body dataset (GIW) for circa-2000 [17], as well as to produce the Global 3 arc-second Water Body Map (G3WBM) [18] and to study Earth’s surface water change over the past 30 years [19]. Progress was made with Landsat 8, containing the nine-band Operational Land Imager (OLI) sensor and the Thermal InfraRed Sensor (TIRS) featuring two spectral bands. The cirrus band (band 9) allows for a better cloud screening while the coastal band might improve water detection [20]. Recently, all Landsat 8 acquisitions between June 2013 and June 2014 were processed using the Google Earth Engine platform to map water surfaces at global scale [21]. Although these sensors have a high spatial resolution (30 m), their revisit time is long (16 days), which makes near real-time water body mapping at global scale impossible.
Medium resolution missions, like PROBA-V, with a near-daily revisit time are more suited for near real-time water body mapping at global scale. The PROBA-V microsatellite was launched in May 2013 as a successor for the SPOT-VEGETATION missions. The instrument has been fully operational since December 2013 and delivers daily near-global synthesis with a spatial resolution of 1 km and 333 m. The high revisit time and the four spectral bands (Blue, Red, NIR and SWIR) make this instrument ideal for climate impact assessments, agricultural monitoring, food security estimates and surface water resources management.
Several techniques are available for water surface extraction. Supervised classification methods make use of ground reference data [22], while unsupervised classification methods first search for suitable endmembers [22,23]. Linear spectral unmixing uses endmembers to unravel the image spectra and, in this case, decide on the fraction of water within each pixel spectrum [24]. Spectral indices are the most frequently used. Well known is the normalized difference water index (NDWI) using the reflectance of the green and NIR bands [25]. Bands thresholding makes use of thresholds that are applied directly on the reflectance bands, on derived spectral indices or on transformed bands [1,26,27]. An overview of global-scale water body products developed in recent years using different techniques is presented by Yamazaki [18].
The objective of the research presented was to develop a global, multi-temporal and multi-spectral image analysis method for near real-time dynamic water body detection using PROBA-V 10-day composite images and which is based on the approach developed by Pekel [28]. This algorithm, which applies bands thresholding, was previously developed for MODIS and, after extensive validation, proved to be very successful [28]. The final output product (i.e., “Area of Water Bodies detected worldwide”) identifies the pixels covered by water on a global scale. The areas of water bodies are understood here with respect to the instrument resolution, i.e., surfaces more or less covered by water with a size of one PROBA-V pixel, about 1 km² [29].
2. Materials and Methods
2.1. Overview
As shown by the general overview in Figure 1, the Water Body Detection Algorithm (WDBA) uses five different sets of input data, which are processed in four different steps. Firstly, the PROBA-V daily Top-Of-Canopy synthesis products (S1-TOC) are assembled into a 10-day mean composite (MC10). During the mean compositing process, the MC10 Status Map (MC10-SM) is constructed, which, in turn, is used as input for the water body detection algorithm. Secondly, the SWIR, NIR and Red bands are transformed to HUE, SATURATION and VALUE using a RGB to HSV color transformation, a technique often used in image processing. Thirdly, the application of specific threshold values on HUE and VALUE applied per pixel allows water body detection. To minimize commission errors, four additional data layers are taken into account, i.e., the MC10 Status Map, Water Body Potential Mask (WBPM), Permanent Glacier Mask (PGM) and the Volcanic Soils Mask (VSM). Finally, to obtain qualitative information about the detected water bodies, an occurrence is calculated which is provided in the output product as a quality layer. The input data and the different steps of the algorithm are described in more detail in the subsequent paragraphs.
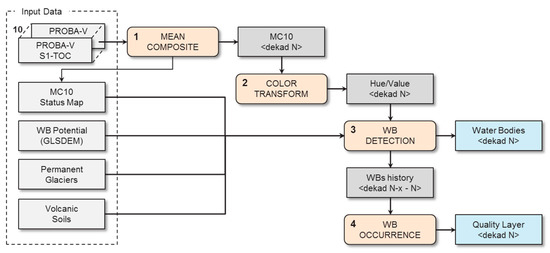
Figure 1.
General overview of the Water Bodies Detection Algorithm. Five sets of input data are processed in four main steps to finally obtain two output layers, i.e., the detected water bodies and the water bodies occurrence.
2.2. Input Data
2.2.1. Daily Top-Of-Canopy Synthesis Product (S1-TOC)
The PROBA-V instrument ensures a daily coverage between Lat. 35°N and 75°N, and 35°S and 56°S, and a full coverage every two days at the equator. The S1-TOC product is provided at 1 km spatial resolution. Surface reflectance is available for four spectral bands: Blue, 0.447–0.493 µm, Red, 0.610–0.690 µm; NIR, 0.770–0.893 µm; and SWIR, 1.570–1.650 µm. The atmospheric correction is performed using SMAC 4.0 [30]. Standard input data layers includes Normalized Difference Vegetation Index (NDVI), geometric viewing and illumination conditions, reference to date and time of observations, status map (containing identification of snow, ice, clouds, land/sea for every pixel) and four reflectance bands. More info can be found in the Products User Manual [31].
2.2.2. MC10 Status Map (MC10-SM)
At the final stage of the mean compositing step, a status map is created. The status map indicates which observation type was used in the mean compositing step, i.e., un-obscured, cloud or snow. It also has a flag that indicates if the observation was done above land or sea. Finally, it has for each reflectance band an additional quality flag that is set to 0 in case no compositing is done. This is caused when there was no valid observation to be used in the 10-day period. The water bodies detection process only takes un-obscured land pixels into account.
2.2.3. Water Body Potential Mask (WBPM)
Pixels located in mountainous areas often have lowered reflectance values due to shadow or dark vegetation and are as such confused with water bodies because their VALUE drops below the threshold level. Moreover, water bodies cannot exist or appear for pixels located in hilly terrain having steep slopes and a large height difference with their neighboring pixels. To minimize the commission errors in hilly terrain a Water Bodies Potential Mask (WBPM), derived from the Global Land Survey Digital Elevation Model (GLSDEM) [32] (data collected in the early 2000s), is used as an extra input in the water bodies detection process. The GLSDEM has a 90 m spatial and 1 m vertical resolution. Compared to the PROBA-V 1 km product the spatial resolution of the GLSDEM is much higher. To prepare the GLSDEM for use in water body detection, flat areas were considered and extracted as a WBPM. This mask was constructed in three steps.
- First the pixels having the lowest elevation in their local neighborhood are located, i.e., a pixel is indicated as a lowest point when its elevation is lower than or equal to its eight neighbors.
- Next, the detected lowest points are filtered and expanded depending on the topography in order to obtain a 90 m spatial resolution potential water body mask. For each detected lowest point, an imaginary water level is raised in steps of 1 m till the maximum rise of 5 m or the flooding condition is reached. Flooding in this context means detection of a neighboring pixel having an elevation that is lower than the rise level. As long as the edge of the potential water body is not flooded, its area is extended according to the raised level, i.e., all neighboring pixels having the additional elevation are added to the potential water body area. This is schematically shown in a two dimensional representation in Figure 2. The initial detected lowest point contains two pixels. Rising the water level 1 m will expand the potential water body with an additional 5 pixels. Because no flooding occurs the water level is increased again with 1 m. Now, an additional 3 pixels are added to the potential water body. Further rising the water level will start flooding the water body because the first pixel elevation right to the expanded water body is lower. If the size of the final expanded water body is less than nine pixels, it is removed from further processing and therefore not considered as a potential water body. Otherwise, the pixels initially detected as lowest point and surrounded by eight neighbors of equal height are marked as level-1. The other initially detected lowest points and the expanded pixels are marked as level-2. The two levels are used in the last step when resizing the potential water body map to the PROBA -V spatial resolution to obtain the final WBPM.
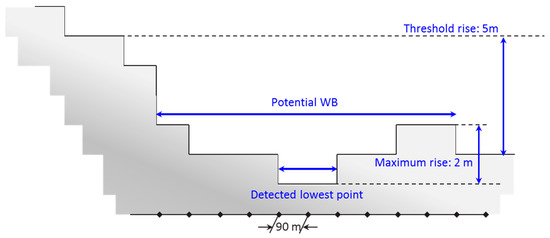 Figure 2. Expanding the initially detected lowest point by systematically rising an imaginary water level in steps of 1 m. The corresponding 90 m spatial resolution pixels are indicated by the dots at the bottom.
Figure 2. Expanding the initially detected lowest point by systematically rising an imaginary water level in steps of 1 m. The corresponding 90 m spatial resolution pixels are indicated by the dots at the bottom. - In the last step, the 90 m spatial resolution potential water body mask is resampled to the PROBA-V 1 km spatial resolution. For each pixel in the georeferenced PROBA-V image, the corresponding pixels in the georeferenced potential water body mask are located. The 1 km resized pixel is indicated as a potential water body when at least one of the corresponding 90 m pixels is labeled as level-1 or when at least nine of the corresponding 90 m pixels are labeled as level-2.
An example of the final obtained WBPM, for the Rift Valley test area in Ethiopia (Table A1 in Appendix A), is shown in Figure 3. A profile according to the red line on the images is shown in the elevation plot. Seven potential water bodies are located along the transect and are indicated by the blue shaded boxes. Two of those potential water bodies are real lakes, Lake Abijato and Lake Langano, and are indicated in Figure 3a.
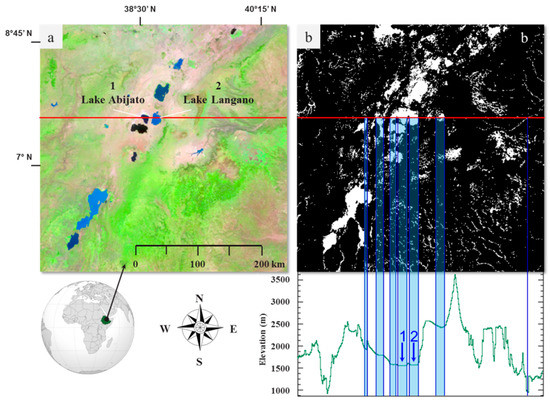
Figure 3.
(a) PROBA-V mean composite for the dekad 21 October 2013 taken over the Rift Valley in Ethiopia (SWIR, NIR and Red bands assigned to the Red, Green and Blue (RGB) channels, respectively). Some of the larger lakes can be easily recognized. (b) The Water Body Probability Mask for the same area. The white pixels indicate locations of potential water bodies. The plot shows the vertical profile according to the red line. Marked with the blue boxes are the seven larger potential water bodies. The arrows indicate the location of: Lake Abijato (1); and Lake Langano (2).
2.2.4. Permanent Glacier Mask (PGM)
To avoid commission errors due to confusion with permanent glaciers, which often have spectral properties similar to water bodies, a permanent glacier mask was constructed. The most recent permanent glacier data were downloaded from the National Snow and Ice Data Centre [33]. The data were provided as a shape file, which was subsequently rasterized to the PROBA-V pixel size to obtain the permanent glacier mask at global scale.
2.2.5. Volcanic Soil Mask (VSM)
Locations comprised of dark volcanic soils which are spread over wider flat areas are easily confused with water bodies because their pixel VALUE drops below the threshold level. To account for these commission errors, a volcanic soil mask was made. A list of volcanoes worldwide was obtained from the Smithsonian Institution, National Museum of Natural History, Global Volcanism Program. The Holocene Volcano List was used as a reference for the construction of a volcanic soil mask. Volcanic soils could be easily located on Google Earth using the information from the Holocene Volcano List. These areas were manually delineated on Google Earth and were subsequently exported and converted to shape files from which a volcanic soil mask was made by rasterizing the shape files to the PROBA-V pixel size at global scale.
2.3. Mean Compositing
In the first processing step, temporal mean compositing over a 10-day window is performed to obtain (to the degree possible) a cloud free image. The MC10 composites (SWIR, NIR, Red, and Blue) are obtained using the mean compositing method [34] applied on the PROBA-V S1 daily reflectance values over a 10-day window. The mean compositing algorithm improves the radiometric quality of the temporal synthesis by averaging the reflectances and therefore reduces the random component of the noise. The mean composite is calculated, pixel by pixel, across the four spectral band simultaneously. For each pixel location, the input data over a time period of 10 days are handled sequentially. Only valid reflectances of a given pixel for a given date in the 10-day period are considered in the computation. These valid reflectances are determined using the actual reflectance value. The PROBA-V S1 input images define a “No data” reflectance value for each spectral band. All four spectral bands must have a valid reflectance value otherwise the given day does not contribute to the mean composition for that pixel location. To achieve consistency with the SPOT-VGT sensor, and enable the creation of a large time-series, a spectral correction is applied on the different spectral bands before calculating the mean reflectance values. The mean compositing algorithm always tries to return the most optimal result. To achieve this, it only composites the most optimal daily observations. For each day in the 10-day period, a pixel’s observation class is first determined as depicted in Figure 4.
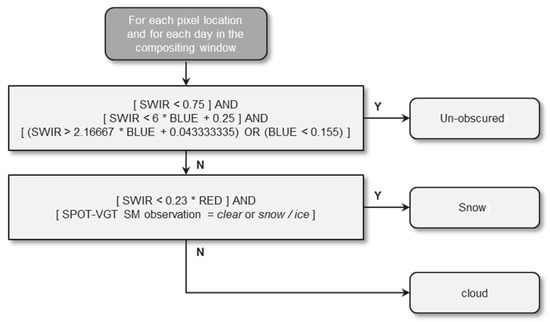
Figure 4.
The MC10 algorithm assigns an observation class to each pixel location each and every day that is computed.
Un-obscured land pixels are preferred before pixels that are classified as snow or cloudy, with cloudy pixels having the least priority. Input pixels not marked as land are not processed. To compute the mean value of all reflectance bands and the SZA, the algorithm keeps track of the reflectance bands and SZA sum of the corresponding pixel values and the number of pixels contributing to these sums, for a given observation class. If a more preferred observation class is detected for a pixel location, the sum and number of observation of the less preferred class are discarded and a new sum and number of observations is calculated, containing only pixel values of the new class. Once all days in the compositing window are computed, the reflectance band sum and SZA sum are divided by the number of observations to obtain the mean reflectance values and an averaged SZA.
2.4. Water Bodies Detection by Decision Tree Classification
An essential step before the actual water bodies detection takes place is the transformation of the Red, NIR and SWIR bands to the HSV (HUE, SATURATION and VALUE) color space as described by Pekel [28]. The detection of water bodies involves three main steps: (i) invalid data filtering; (ii) incompatibility masking; and (iii) water body detection. The decisions made in these three steps were implemented in a Decision Tree Classifier (DTC). Once water bodies are detected, the occurrence of the detection is estimated. An overview of the water body detection algorithm is shown in Figure 5.
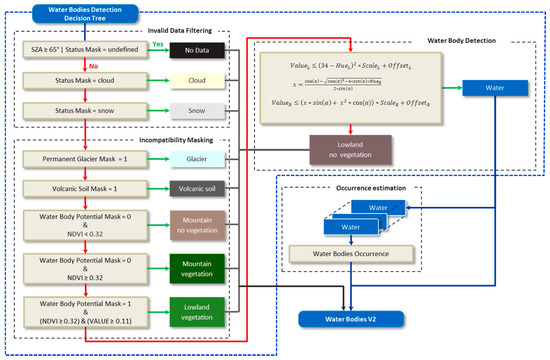
Figure 5.
The Water Body Detection Algorithm consists of three main steps: (i) invalid data filtering; (ii) incompatibility masking; and (iii) water body detection. Qualitative information about the detected water bodies is expressed by the occurrence estimation. Both layers, i.e., the detected water bodies and the occurrences, are available in the Water Bodies V2 product.
2.4.1. Invalid Data Filtering
A low sun elevation causes elongated shadows, which are observed in the remote sensing imagery as darkened Earth surfaces. These might be detected as water bodies when the VALUE drops below the threshold level. A check on the MC10’s averaged Solar Zenith Angle (SZA) prohibits the detection of invalid WBs, i.e., when a MC10 pixel has a SZA larger than 65° no WB detection is done and the pixel is classified as “No Data”.
The next step in the WBDA is filtering the invalid data comprising snow, cloud and cloud shadow, using the information from the MC10 Status Map. Each image pixel has a bit array assigned reflecting its status, pixels indicated as cloud or snow are not considered in the WB detection algorithm. Cloud shadow on the Earth’s surface often has similar spectral properties as WBs and is as such regularly classified as WB. Therefore, to avoid confusion due to cloud shadow in the immediate neighborhood of the initial defined cloud pixel, an additional dilate filtering is performed. In the case a pixel is indicated as cloud, its twelve neighboring pixels (the circular neighborhood with radius 2 pixels) are indicated as cloud as well and are therefore not taken into account for WB detection.
2.4.2. Incompatibility Masking
In addition to glaciers, dark soils and shadows, vegetated surfaces are also often a cause of confusion with WBs. Therefore, the NDVI value, computed as Equation (1) from the Red (ρRed) and NIR (ρNIR) reflectances of MC10, is used to identify the vegetated areas.
Pixels having an NDVI value higher or equal to 0.32 and having a WBPM pixel set (locating lowland areas where holding a WB is possible) are considered to be “Lowland Vegetation”. Some WBs have a high NDVI value (due to algae load or adjacency effect of the surrounding vegetation) and could as such wrongly be classified as “Lowland Vegetation”. To avoid these omission errors an additional check on VALUE is added, this threshold level is denoted as NV. If the VALUE of a pixel which is designated as “Lowland Vegetation”, is less or equal to 0.11 (a value empirically defined) it is classified as “Water”. These thresholds were empirically defined over the Rift Valley test area. The Rift Valley area is unique in the sense that it contains some larger lakes with a wide variety of reflectance values, some are bright blue, others are dark blue while others are almost black (see Figure 3). Besides, these lakes are surrounded with different shades of green vegetation (especially after the rain season). This situation easily allows observing how different thresholds levels influence the detection of WBs.
2.4.3. Water Body Detection
Threshold values on the HUE and VALUE bands are used for detecting WBs worldwide. The thresholds were iteratively and empirically defined by decision tree classifications using different settings for the thresholds levels. First, initial fixed thresholds were obtained by observing the HUE and VALUE for the lakes in the Ethiopian Rift Valley test region shown in Figure 3a. The initial fixed threshold for HUE and VALUE was set to 100 and 0.13, respectively. Subsequently, the threshold levels were iteratively adapted in different steps (VALUE = 0.13, 0.14; HUE = 100, 95; NDVI = 0.32, 0.42; and NV = 0.11, 0.13) while introducing an innovative refinement using quadratic functions, which were empirically defined. The performance of the various cases were evaluated and the thresholds were calibrated over 19 test regions worldwide (Table A2 of Appendix A) according to the Water Surface Ratio (WSR) and the metrics Commission Error (CE) and Omission Error (OE) as defined by Equations (C1)–(C3) in Appendix C. The choice of the final threshold levels is a balance between omission and commission errors: the best settings in terms of fixed thresholds are VALUE = 0.14, HUE = 100, NDVI = 0.32, and NV = 0.11 while the best quadratic functions (shown by the red lines in Figure 6) are defined as:
- The left part (for the HUE value = 0 till 34) can be written as:
- The right part (for the HUE value = 34 till 100) is a bit more complex because it is based on a parabola rotated over 0.2° for which the rotated coordinates can be written as:This equation can be solved using the standard form:
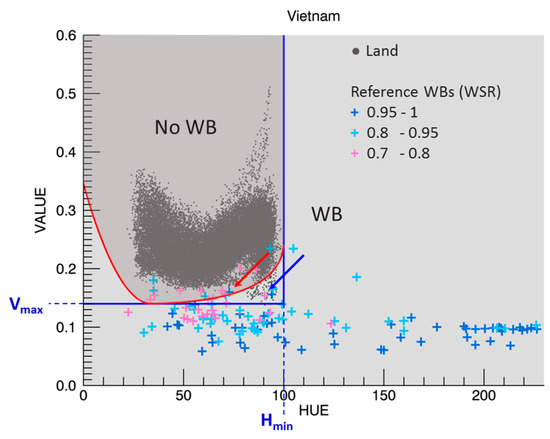
Figure 6.
2D scatter plots of the Vietnam test area showing the final threshold levels. Land pixels are indicated by the dark grey dots, reference WBs (obtained from Landsat 8) are indicated by the colored plus symbols for different ranges of water surface ratios. The fixed threshold levels are indicated by the blue lines (Vmax and Hmin). The refined threshold levels, indicated by the red parabolic lines, allow the detection of WBs outside the fixed threshold levels as indicated by the blue arrow. The red arrow locates the intermixed water and land pixels.
From which, only one solution is used to calculate the corresponding VALUE threshold:
with
The division by two in both Equation (2) and Equation (10) is done to lower the parabolic curve in order to reduce the commission errors. The value 28.5 in Equation (12) was empirically defined, and is used to broaden the parabolic curve (higher values will broaden the curve). The value 95,000 in the scale factor was empirically deined, and defines the height of the parabolic curve (higher values will lower the curve).
The 2D scatter plot in Figure 6 gives a visual representation of the threshold levels. The fixed threshold levels (Hmin = 100, Vmax = 0.14) are indicated by the blue lines and the refined threshold levels are indicated by the red parabolic lines. The plot shows the reference WBs for the Vietnam test area indicated by the colored plus symbols and this for three ranges of Water Surface Ratio (WSR), i.e., blue for WSR = 0.95 to 1, cyan for WSR = 0.8 to 0.95 and magenta for WSR = 0.7 to 0.8. The other WSR ranges are not indicated as they would overrule the plot. The non-WB pixels, which are denoted as land, are indicated by the dark grey dot symbols. The refined thresholds allow the detection of WBs outside the fixed threshold levels as indicated by the blue arrow. Although the refined thresholds are tuned to detect as much WBs as possible, not all WBs can be detected because they are intermixed with land pixels as indicated by the red arrow. The 2D scatter plots of the eight first test areas are shown in Appendix B.
2.5. Water Bodies Occurrence Estimation
To qualify the occurrence of the detected WBs, a Water Body Occurrence (WBO) is calculated for each detected WB pixel in each dekad. This measure gives an idea about the permanency or seasonality of the detected WBs. To obtain a WBO map for each dekad, per pixel statistics are calculated by temporal-sequential processing of the available dekads. To get an idea of the WB occurrence, the observation period over which the statistics are calculated has to be long enough. An observation period over two years requires 72 dekads. However, for computational reasons, only 64 dekads are observed; that is, information that can be stored in one “long word” (64 bits). If more than 64cloud free MC10 composite observations are available, only the last 63 cloud free observations and the actual observation are used for calculating the statistics. The per-pixel temporal-sequential statistics are calculated over the available observation dekads (max 64) and can be summarized as:
- Total number of temporal cloud free observations (ntObs);
- Total number of temporal WB detections (ntWBs); and
- Maximum number of continuous temporal WB detections (mctWBs).
From these statistics, the frequency of detected WBs can be calculated as:
As shown in Figure 7, the calculated WB frequency (WBf) and the maximum number of continuous temporal WB detections (mctWBs) can be visualized in a 2D scatter plot, which, in turn, was used for defining the occurrence threshold levels. The different occurrence levels are indicated by the different colored regions in the figure. The slope and position of the four threshold lines, marked L (Low), M (Medium), H (High) and VH (Very High), define the WBO threshold levels and were empirically defined by observations of WB time series as shown in Section 3. WBs that appear with a high frequency (WBf) or with long continuous observation periods (mctWBs) are most likely stable WBs that exist for a longer period and therefore have a higher occurrence than those with lower frequency (WBf) or shorter continuous observation periods (mctWBs). The defined occurrence threshold levels can be expressed as:
where αx is the slope of the threshold line x, for example,
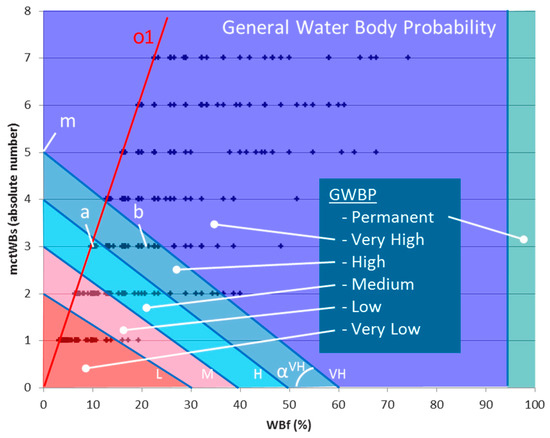
Figure 7.
Example of a 2D scatter plot of the WB frequency (WBf) and the number of continuous temporal WB observations (mctWBs). The plus symbols belong to pixels of detected WBs for the Rift Valley test area calculated for the 31 available dekads. The Water Body Occurrence threshold levels are indicated by the different colored areas.
The red line (o1) in Figure 7 shows the minimum WBf in relation to the mctWBs. The slope depends on the maximum number of observations (ntObs). The plot shows that a certain pixel is classified as a “Very High” WBO if it is identified as WB in at least five consecutive dekads (point “m” in the plot). Note that this number is independent of the ntObs. As an example, if a pixel was detected as a WB in three consecutive dekads (with nObs = 31), its WBf will be 9.7% and therefore will have a WBO “Medium” (point “a”). If this pixel would have subsequently four additional WB detections in separate single dekads, its WBf will rise to 22.6% and its WBO will increase to “High” (point “b”). Note also that if pixels have a WBf of at least 95% their WBO will be “Permanent”.
2.6. Minimum Size of Detectable Water Bodies
A WB has to have a minimum spatial size in order to be detected by the WB detection algorithm. To find the minimum sub-pixel size of a detectable WB, linear spectral mixture analysis was used. Therefore, five water spectra (Figure 8a) with an increasing reflectance level were spectrally mixed with a dark and bright vegetation and soil spectrum (Figure 8b). Only the Red, NIR and SWIR bands were used as these are transformed to HUE and VALUE after the mixture. The mixing was done by increasing the sub-pixel fraction of the WB from 0 to 1 in steps of 0.05.
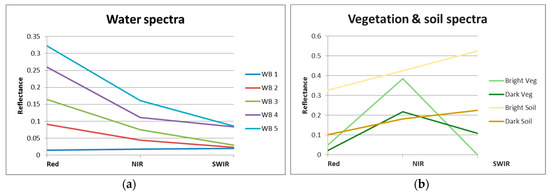
Figure 8.
Spectra used in the spectral mixture analysis to define the minimum WB size in relation to the PROBA-V pixel size: (a) five water spectra with an increasing intensity; and (b) two vegetation and two soil spectra having a low and high reflectance.
The WB detection threshold levels were set fixed to HUE = 100 and VALUE = 0.14. By analyzing the HUE and VALUE of the mixed spectra in relation to the detection threshold levels, the minimum fraction of the pixel to be covered by water could be derived. Figure 9 summarizes the results obtained after the mixed pixel analysis. In general, the dark WBs (WB 1, WB 2) needs larger sub-pixel water coverage than the bright WBs (WB 4, WB 5) in order to be detected. E.g., the dark WB 1 needs a water coverage of 45% when mixed with “Dark Veg” and this increases to a water coverage of 85% when mixed with the “Bright Soil”. The bright WB 5 needs a water coverage of 15% when mixed with “Dark Veg” and 40% when mixed with “Bright Soil”. As could be observed on different WB detection results worldwide, small (single pixel) WBs are mostly dark and therefore need a large sub-pixel coverage in order to be detected.
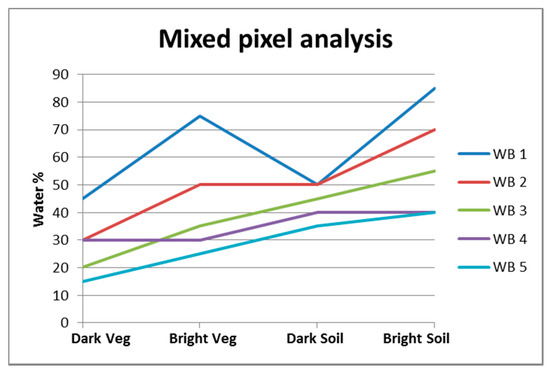
Figure 9.
The minimum fraction of the pixel to be covered by water in order to be detected as WB.
3. Results
Figure 10 shows an example of the Decision Tree Classification (DTC) result using the final threshold levels. The image shows the detection obtained for the 10-days composite of the first dekad of December 2013 (MC10_20131201) over the Rift Valley test area in Ethiopia for which the visual representation is given in Figure 3a. As shown in detail, some smaller lakes with size in the order of one PROBA-V pixel are detected. Figure 11 shows the Water Body Occurrences (WBO) for the same area. Because the larger lakes are detected in each cloud free dekad, they have a detection frequency of more than 95% and are therefore indicated with a “Permanent” occurrence. As shown in the detail window in Figure 11, the smaller lakes have a WBO ranging from “Very High” to “Very Low” due to temporal variability and are, as such, not detected in each dekad. This is indicated in the time series analysis shown in Figure 12.
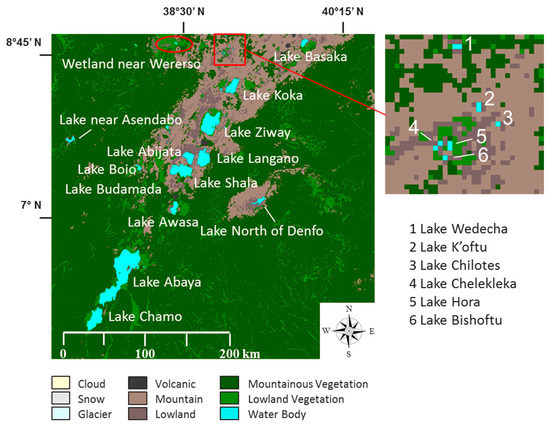
Figure 10.
Decision Tree Classification (DTC) result for the part of image MC10_20131201 taken over Rift Valley in Ethiopia (center: 7°11′31′′N, 38°51′10′′E) for which the visual representation is given in Figure 3a. Beside the larger lakes in the area, some smaller lakes are detected as shown by the detail window.
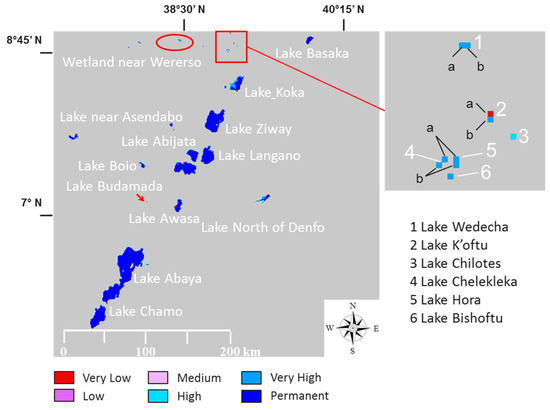
Figure 11.
The Water Body Occurrence (WBO) for part of image MC10_20131201 taken over Rift Valley in Ethiopia (center: 7°11′31′′N, 38°51′10′′E).
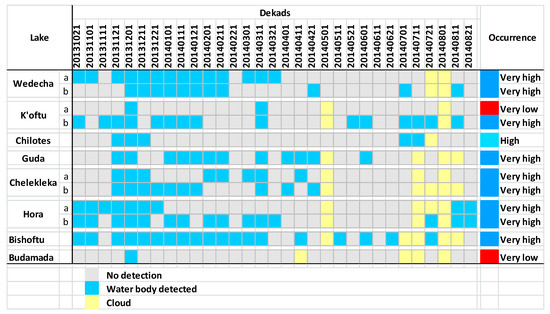
Figure 12.
Time series analysis for several small lakes showing the detections per dekad and the resulting WB occurrence. Each row shows the behavior of one pixel of the water body during the 31 dekads starting from 21 October 2013 to 21 August 2014. The blue marked dekads show the dekads where the pixel is detected as WB.
Figure 12 shows the time series analysis for several smaller lakes, some of them are indicated in detail in Figure 11. Lake Wedecha consists of 2 pixels that have a “Very High” occurrence because they were detected in more than five consecutive dekads. A “Very High” occurrence can also be found for several other lakes which have frequent WBs detected, i.e., K’oftu (pixel b), Chelekleka, Hora and Bishoftu. One pixel (a) of Lake K’oftu has a “Very Low” occurrence because it was detected in two non-consecutive dekads only. Lake Chilotes has a “High” occurrence because it was detected in three and two consecutive dekads. Lake Budamada, indicated by the red arrow in Figure 11, is a small lake of about 1 km diameter. It was detected in only one dekad and therefore has a “Very Low” occurrence. Nevertheless, this crater lake is permanent, i.e., it will not dry up during the drought period. Its irregular detection is due to its small size which is in the order of one PROBA-V pixel. The small size causes mixed pixels, i.e., the water body spectral response is mixed with the spectral response of the surroundings, and therefore it is not detected as WB. This phenomenon accounts for all WBs with size in the order of one PROBA-V km pixel.
The rain season over the Ethiopian Rift Valley peaks in the months July and August while the dry season appears in the period between mid-October and mid-March. This seasonal variation can be observed in the appearance of some WBs as shown in Figure 13. The wetland area near Wererso contains no WB pixels at the end of March, i.e., at the end of the dry season. In the next three dekads, the number of detected WB pixels increases. In the last dekad of July and the first dekad of August, an extremely large number of pixels indicate WBs for this wetland area and its neighborhood. The two other lakes, Lake Boio and the Lake Koka, show a similar behavior, i.e., their size grows over time, which is in accordance with the progression of the rain season.

Figure 13.
Water body evolution for three WBs in the Rift Valley, the wetland near Wererso (Centre: 8°52′46″N, 38°22′46″E), Lake Boio (Centre: 7°30′48″N, 38°2′24″E) and Lake Koka (Centre: 8°23′50″N, 39°4′33″E). The water bodies grow in size during the rainy season, which peaks in the months July and August.
Figure 14 shows the Water Body Occurrence (WBO) time series for the Rift Valley test area. The plot shows per dekad the cumulated number of pixels for the occurrences ranging from “Very Low” to “Very High”. The WBs with a “Permanent” occurrence are very large and would overrule the plot, therefore they are not indicated. Note that cloud cover may mask WBs with the result that those WBs are not accounted for in the plot and therefore the plot may show some irregularity. Nevertheless, the plot shows some correlation with the seasonal variation as described before. From the first observed dekad, end of October 2013, to mid-February 2014, there is a gradual decrease of detected WB pixels which is in accordance with the dry season. The amount of detected WB pixels with a “Very High” occurrence stays more or less stable. This period is followed by a more random increase of detected WBs as a result of the upcoming rain season. The pixels that have a “Low” and “Very Low” occurrences show the largest variability. In general the number of detected WBs clearly correlates with the seasonal variability, i.e., the rain season, which also correlates with the cloud cover.
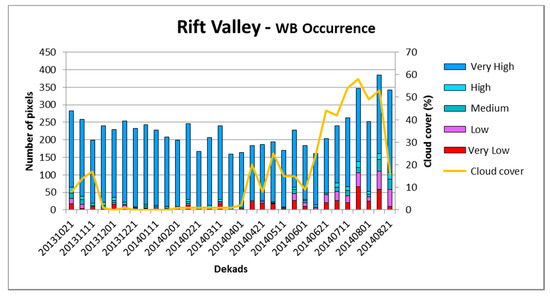
Figure 14.
The Water Body Occurrence (WBO) time series for the Rift Valley test area. The “Permanent” larger lakes are not shown in the graph because their large size would overrule the plot.
4. Assessment of Algorithm Performance
To demonstrate the maturity of the PROBA-V WBDA, reference water bodies were extracted from high spatial resolution Landsat 8 images over 15 regions selected worldwide (Table A3 of Appendix A). The workflow and algorithm to derive the reference WBs from Landsat 8 images is described in Appendix C.
The reference water bodies extracted from Landsat 8 imagery might also contain omission and commission errors and might influence the PROBA-V performance analysis. The reference commission errors occur at the Landsat 8 spatial resolution and it concerns groups of pixels ranging from one to several tens. The corresponding calculated WSR is therefore very small (a PROBA-V pixel for which the WSR is calculated comprises a few hundred Landsat 8 pixels). Typically, the WSR for the wrongly detected WB is much lower than the minimum WSR of 0.5 used in the analysis. Omission errors are much more difficult to quantify. Nevertheless, it can be said that these also concern small groups of pixels resulting in a very small reference error not influencing the analysis.
Table 1 shows the commission and omission errors on the PROBA-V images for six minimum WSR ranges and this for the 15 test areas.

Table 1.
Assessment results for the 15 test areas. The user requirements define a maximum omission and commission error of 15%. All commission errors fall within the requirements. The acceptable omission errors for the highest WSR are highlighted.
As seen in Table 1, the commission and omission errors vary for the different test areas. An average commission error of 1.5% was obtained with an average omission error of 9.8% for minimum WSR 0.6 and 15.4% for minimum WSR 0.5. Notice that the user requirements define a maximum omission and commission error of 15% [35]. The acceptable omission errors for the highest minimum WSR are highlighted in the table. Though the Argentina test area shows the best results for the omission errors it has the highest commission error of all test areas (10.7%). This high commission error is due to dark soil pixels, which were wrongly detected as water bodies. The commission error of 4.9% for the Zambia test area is also due to dark soil pixels while the commission error of 4.0% for the Canada test area is due to dark vegetation pixels, which were detected as water bodies. The Finland test area shows the worst performance for the omission error, i.e., an acceptable omission error of 13.6% for minimum WSR 0.95. These high omission errors are due to the presence of many small and narrow lakes, in the order of the size of a PROBA-V 1 km pixel, by which they were not detected. This effect accounts for all other regions as well, i.e., for the Russian test area: 12.2% for minimum WSR 0.8; and, for the USA test area: 14.9% for minimum WSR 0.7. The other test areas show the highest omission errors for minimum WSR 0.6 and 0.5.
5. Discussion
The user requirements define a maximum omission and commission error of 15% [36]. As shown in this work, a mean commission error of 9.8% is obtained for minimum WSR = 0.6 while the mean omission error is 1.5%. Though minimization of omission and commission errors is achieved by the use of additional data layers, WBPM, VSM, PGM and NDVI, they sometimes are inevitably. Small sized WBs in the order of one PROBA-V 1km pixel and WBs with spectral properties that fall outside the defined thresholds are the cause of omission errors. Commission errors are mostly caused by anthropogenic structures having spectral signatures equal to WBs, e.g., some agricultural fields, green houses, build-up areas, etc. In addition, natural surfaces like salt planes, dark soils, mining sites, etc. might cause commission errors. An important source of commission errors are dark surfaces, e.g., due to undetected cloud shadows, dark soils due to heavy industry, dark surfaces due to shadow of high structures, etc. Therefore, to minimize confusion the user should use the water body product with attention to the quality layer which reflects the history of the detected WBs.
Special attention has to be paid to the three layers used during incompatibility masking. The WBPM was made based on the GLSDEM for which data was collected in the early 2000s. Because of the high resolution of the GLSDEM dataset (90 m spatial and 1 m vertical), the derived WBPM (1 km spatial resolution) reveals the finest detail (as shown in Figure 3b). Although the Earth’s topography changes only notably over large geological time scales, natural events (e.g., earthquakes) or anthropogenic activities (e.g., dam building) can influence the topography on shorter time scales. Therefore, when such events take place, the WBPM needs to be updated. Just to give an idea; the PROBA-V 1 km world image contains 40,320 samples × 15,680 lines or 632.22 × 106 pixels. Of those, 29% (183.5 × 106 pixels) consist of landmass (i.e., not ocean), and 50.5% (92.7 × 106 pixels) of the landmass is indicated as potential water body.
Because the extent of glaciers worldwide are strongly influenced by climate (global warming), the PGM needs to be frequently updated. Frequent updates of the permanent glacier data are available at the National Snow and Ice Data Center (NSIDC). The geological situation in the volcanic areas of South America, i.e., Chili and Peru, is very complex and delineating the volcanic soils in these areas was not always easy. It is therefore very well possible that some smaller regions in this area are still missing in the VSM. On the other hand, future volcanic eruptions might produce new dark volcanic soils leading to false detected WBs. In both cases, an update of the VSM is needed.
6. Conclusions
This water bodies detection algorithm is implemented in the operational processing chain of the Copernicus Global Land Service (http://land.copernicus.eu/global/). It delivers 10-day global water bodies detection maps accompanied by a quality layer map.
Although some minor artifacts were introduced during the algorithm assessment using Landsat 8 reference WBs, the assessment gives a good idea about the algorithm performance. The analysis, performed over 15 test regions, shows that the product reaches a mean commission error of 1.5% while the mean omission error for minimum WSR = 0.6 is 9.8%.
The developed methodology can easily be applied to the 333 m and 100 m PROBA-V products and 300 m Sentinel-3 products, by which smaller water bodies will be detected. Applying the methodology on higher resolution sensors as Sentinel-2 is possible, but its dynamics will be hampered by the lower temporal frequency of such sensors. The water bodies detection algorithm is also tuned to detect water bodies on 1 km SPOT-VGT dataset. The whole SPOT-VGT archive is being processed and water body detection maps from 1999 to 2014 will become available by the end of 2016. An exhaustive validation exercise of the PROBA-V and SPOT/VGT 1 km WB products has been performed by independent entity and the report is available on the Copernicus Global Land Service website. The water bodies products can be downloaded from the Copernicus Global Land Service data portal: http://land.copernicus.vgt.vito.be. Additional information is available at: http://land.copernicus.eu/global/products/wb.
Acknowledgments
The product was generated by the land service of Copernicus, the Earth Observation programme of the European Commission. The research leading to the current version of the product has received funding from various European Commission Research and Technical Development programmes. The product is based on PROBA-V 1km data ((c) ESA and distributed by VITO).
Author Contributions
Luc Bertels designed the water bodies detection algorithm. Davy Wolfs implemented the algorithm in the operational processing chain. Bruno Smets managed the project and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1 lists the region for fixed thresholds definition, Table A2 lists the 19 test regions used for refining the threshold levels, and Table A3 lists the 10 test regions selected worldwide to assess the performance of the detection algorithm.

Table A1.
The Ethiopian Rift Valley test area used for fixed threshold definition, the upper left corner coordinate and number of samples (ns) and lines (nl) are given.
| Area | Dekad | Upper Left Coordinate | PROBA-V | ||
|---|---|---|---|---|---|
| Lat | Lon | ns | nl | ||
| Rift Valley | 20131201 | 8.96429722 | 37.08032222 | 400 | 400 |

Table A2.
Landsat 8 scenes of the 19 test regions selected worldwide were used to refine the threshold levels. As much as possible, cloud free scenes were selected. The corresponding PROBA-V dekad and the upper left corner coordinate are given with the corresponding number of samples (ns) and lines (nl).
| Area | Landsat 8 Scene | Dekad | Upper Left Coordinate | PROBA-V | ||
|---|---|---|---|---|---|---|
| Lat | Lon | ns | nl | |||
| Argentina 1 | LC82270862014111LGN00 | 20140421 | −36.40625000 | −63.94196429 | 299 | 239 |
| Argentina 2 | LC82310932014011LGN00 | 20140111 | −46.29910714 | −73.83482143 | 376 | 257 |
| Australia | LC81110782014131LGN00 | 20140511 | −24.94196429 | 118.49553571 | 267 | 236 |
| Bangladesh | LC81380442014112LGN00 | 20140421 | 24.17410714 | 87.74553571 | 244 | 240 |
| Bolivia | LC82330692013310LGN00 | 20131101 | −11.95089286 | −66.85267857 | 232 | 239 |
| Brazil | LC82220742014028LGN00 | 20140121 | −19.17410714 | −51.55803571 | 248 | 237 |
| Canada | LC80180272014151LGN00 | 20140521 | 48.53125000 | −80.06696429 | 332 | 246 |
| China | LC81210382014121LGN00 | 20140501 | 32.79910714 | 116.05803571 | 271 | 240 |
| Congo | LC81740662014140LGN00 | 20140521 | −7.62053571 | 25.22767857 | 235 | 238 |
| India | LC81460422014072LGN00 | 20140311 | 27.04910714 | 76.05803571 | 249 | 240 |
| Mali | LC81950502013332LGN00 | 20131121 | 15.51339286 | −2.25446429 | 234 | 239 |
| Mexico | LC80270422014118LGN00 | 20140421 | 27.04017857 | −100.12053571 | 260 | 238 |
| Poland | LC81870222014087LGN00 | 20140401 | 55.60267857 | 21.60267857 | 393 | 250 |
| Rusia | LC81770212014129LGN00 | 20140501 | 56.99553571 | 37.60267857 | 426 | 248 |
| South Africa | LC81690802014121LGN00 | 20140501 | −27.77232143 | 28.12946429 | 277 | 246 |
| Spain | LC82010332014121LGN00 | 20140501 | 39.95089286 | −5.66517857 | 306 | 239 |
| Turkey | LC81730332013306LGN00 | 20131101 | 39.95982143 | 37.65625000 | 299 | 240 |
| USA | LC80430342014134LGN00 | 20140511 | 38.54017857 | −121.87946429 | 281 | 242 |
| Vietnam | LC81240512014062LGN00 | 20140301 | 14.08482143 | 107.11160714 | 241 | 242 |

Table A3.
Landsat 8 scenes of the 15 test regions selected worldwide were used to assess the water bodies detection algorithm. As much as possible, cloud free scenes were selected. The corresponding PROBA-V dekad and the upper left corner coordinate are given with the corresponding number of samples (ns) and lines (nl).
| Area | Landsat 8 Scene | Dekad | Upper Left Coordinate | PROBA-V | ||
|---|---|---|---|---|---|---|
| Lat | Lon | ns | nl | |||
| Argentina | LC82310872014011LGN00 | 20140111 | −37.83418611 | −70.58413611 | 303 | 241 |
| Australia | LC80950832013304LGN00 | 20131021 | −32.12027778 | 141.27138333 | 288 | 238 |
| Bolivia | LC82330692014233LGN00 | 20140821 | −11.95757500 | −66.85950000 | 233 | 239 |
| Canada | LC80180262014295LGN00 | 20141021 | 49.94476111 | −79.54769167 | 340 | 247 |
| Chad | LC81830512014011LGN00 | 20140111 | 14.06290278 | 15.97345556 | 234 | 238 |
| China | LC81210392014121LGN00 | 20140501 | 31.35326944 | 115.68581667 | 270 | 239 |
| Finland | LC81920132014154LGN00 | 20140601 | 68.02264167 | 21.52997222 | 686 | 253 |
| India | LC81420442014028LGN00 | 20140121 | 24.16315278 | 81.55028611 | 247 | 239 |
| New Zealand | LC80750912014294LGN00 | 20141021 | −43.52644444 | 168.42483889 | 329 | 243 |
| Russia | LC81100132014252LGN00 | 20140901 | 68.03188333 | 148.26286944 | 676 | 255 |
| Swiss | LC81950272014079LGN00 | 20140311 | 48.49976111 | 6.28843889 | 360 | 241 |
| Thailand | LC81280482014090LGN00 | 20140321 | 18.38631389 | 101.85821667 | 247 | 237 |
| Turkmenistan | LC81570332014133LGN00 | 20140511 | 39.95980833 | 62.34785278 | 298 | 242 |
| USA | LC80260372014207LGN00 | 20140721 | 34.21517222 | −96.81486667 | 290 | 237 |
| Zambia | LC81730712014133LGN00 | 20140511 | −14.84697222 | 25.17750000 | 240 | 238 |
Appendix B
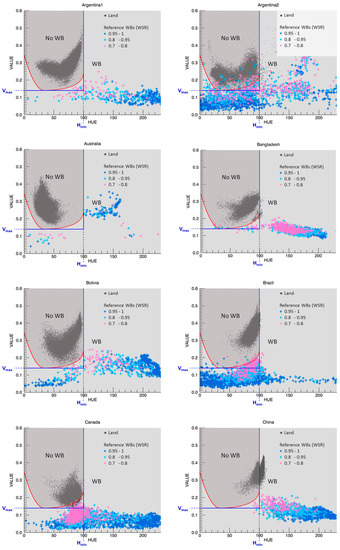
Figure B1.
2D scatter plots of the first eight test areas.
Appendix C
Figure C1 shows the workflow for extracting the reference WBs and for defining the Water Surface Ratio (WSR).
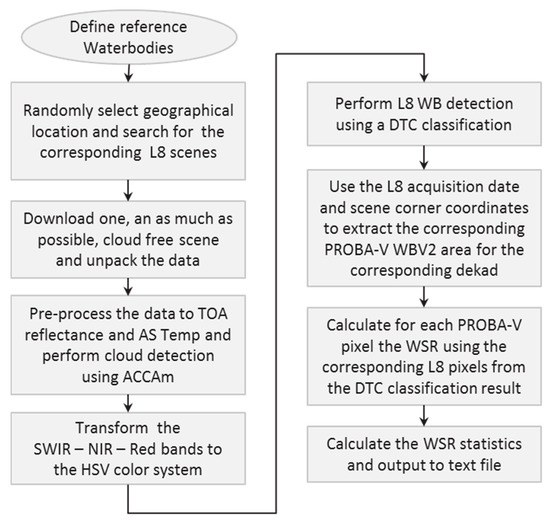
Figure C1.
Workflow for the extraction and definition of reference water bodies using Landsat 8 scenes. TOA: Top Of Atmosphere; AS Temp: At satellite Brightness Temperature; ACCAm: Automatic Cloud Cover Assessment-modified.
Appendix C.1. Building the Reference Dataset
The USGS “EarthExplorer” was used to search for Landsat 8 OLI/TIRS cloud free scenes over 19 selected test areas worldwide. These test areas were selected based on visual observations using Google Earth (water bodies must be present). Subsequently one cloud free scene, or one which is as much as possible cloud free, was downloaded and unpacked. The data was subsequently pre-processed to convert the eleven bands to TOA radiance, the 9 OLI bands to TOA reflectance and the 2 TIRS bands to at-satellite brightness temperature.
The “Automatic Cloud Cover Assessment–modified” (ACCAm) was used for cloud detection. ACCAm is a modified version of the ACCA [36] developed for Landsat 7. In this modified cloud detection algorithm only the spectral cloud identification is retained and an additional check on the cirrus band is added.
In the next step the “SWIR 1”, “NIR” and “Red” bands are color transformed to the HSV-color system. This allows for an easy water bodies detection using thresholds on the HUE and VALUE band. As shown by the Decision Tree Classifier (DTC) in Figure C2, the class “No Data” is based on a zero value in the TIR 1, SWIR 1, NIR or Red band. The “Cloud” class is set according the cloud mask generated by ACCAm (1 means cloud detected). In the final step, water is separated from land by a threshold value on HUE (≥160) and VALUE (<0.4).
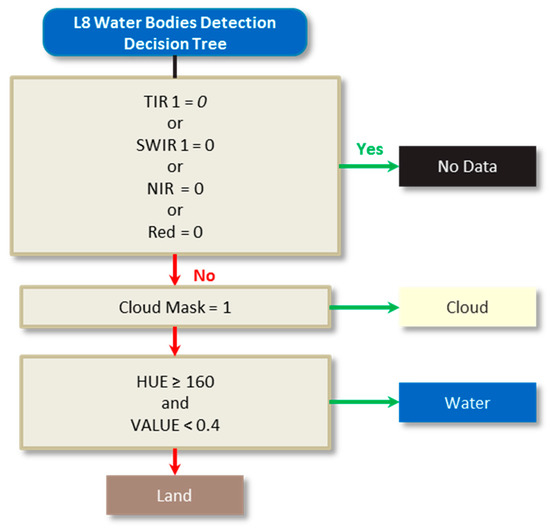
Figure C2.
Decision Tree Classifier for WB detection on Landsat 8 images. A check on different bands and on cloud cover removes incompatible pixels from the scene. A check on HUE and VALUE is used to detect water bodies.
Appendix C.2. Calculation of the Water Surface Ratio and Evaluation Metrics
For each pixel (xy) of the PROBA-V WB product, the Water Surface Ratio (WSRxy) is calculated as the ratio of the number of Landsat 8 water pixels (DTC results) by the total number of valid Landsat 8 pixels contained in the PROBA-V pixel (Equation (C1)).
The WSRxy has a value greater than zero and less than or equal to one when the PROBA-V pixel has “Water” classified pixels present in the corresponding Landsat 8 DTC pixels. The WSRxy is not calculated when the cloud cover of the corresponding Landsat 8 DTC pixels is more than 10% or if more than 10% of the pixels contain no data. Pixels in the final WSR image are indicated as “Cloud” (WSR = 3) or “No Data” (WSR = 0), respectively. When no “Water” classified pixels are present in the corresponding DTC pixels (WSRxy = 0), the final WSR pixel is set to “Land” (WSR = 2).
Figure C3a,c shows the Landsat 8 scene LC82270862014319LGN00, downloaded for test location Argentina1 (37°S, 63°W). Figure C3b,d shows the Decision Tree Classifier (DTC) result for the same scene. The details in Figure C3c,d shows four corresponding PROBA-V pixels, indicated by the blue squares. In this particular case, each PROBA-V pixel contains 858 pixels, however this number varies depending on the latitude.
Figure C4a shows the corresponding PROBA-V WB product extracted for the second dekad of November 2014. Figure C4b shows the calculated WSR. The detail in Figure C4c indicates the same four pixels as in Figure C3c,d. These pixels have a WSR of: 0.7 (a); 0.03 (b); 0.02 (c); and 0.09 (d).
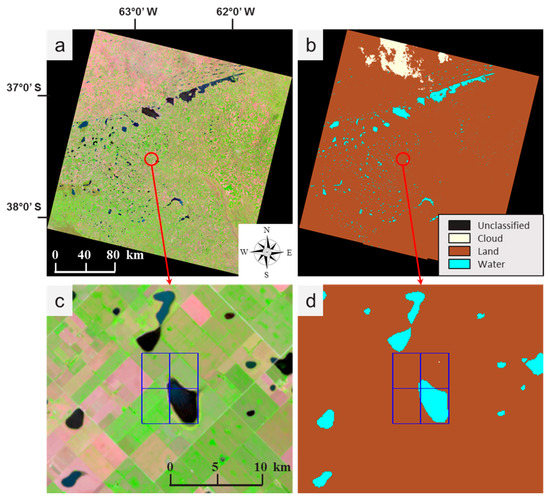
Figure C3.
(a) The Landsat 8 scene LC82270862014319LGN00, downloaded for location: 37°S, 63°W (Argentina), was acquired on 15 November 2014. (b) Decision Tree Classifier (DTC) result for the same Landsat 8 scene. (c,d) Details showing in blue the four PROBA-V pixels overlaid, which are also indicated in Figure C4.
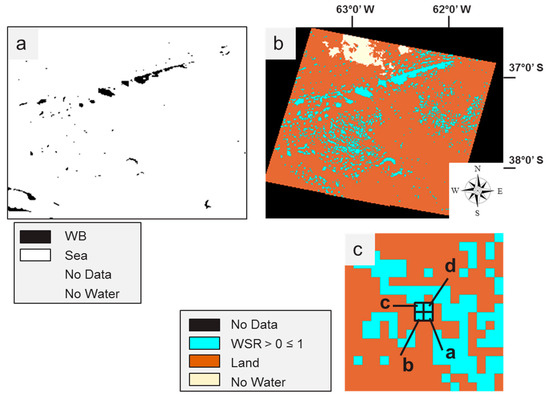
Figure C4.
(a) The PROBA-V WB area extracted from 2nd dekad of November 2014, which corresponds with the downloaded Landsat 8 area. (b) The Water Surface Ratio (WSR) (PROBA-V spatial resolution) which is calculated using the Landsat 8 DTC result. (c) The four indicated pixels have a different WSR: (a) 0.7; (b) 0.03; (c) 0.02; and (d) 0.09. These four pixels are also overlaid on the images in the previous figure.
In the final step, the omission errors (OE) and commission errors (CE) are derived from the confusion matrix [37,38]. The omission error is calculated per minimum WSR range, i.e., 0.95, 0.9, 0.8, 0.7, 0.6 and 0.5 (e.g., a minimum WSR of, e.g., 0.95 means only water body pixels with a WSR ≥ 0.95 are considered as reference water body) and per test area. The confusion matrix can be written as shown in Table C1.

Table C1.
Confusion matrix frim which the Commission and omission errors are calculated.
| Reference | |||
|---|---|---|---|
| WB | No WB | ||
| WBV2 | WB | p11 | p12 |
| No WB | p21 | p22 | |
where
- p11 = the number of pixels indicated as WB in both reference and WBV2 and having a WSR larger or equal to the minimum WSR;
- p12 = the number of pixels not indicated as WB in the reference but indicated as WB in WBV2 and having a WSR larger or equal to the minimum WSR;
- p21 = the number of pixels indicated as WB in the reference but not in WBV2 and having a WSR larger or equal to the minimum WSR;
- p22 = the number of pixels not indicated as WB in both reference and WBV2 and having a WSR larger or equal to the minimum WSR.
From which, the CE and OE are calculated:
References
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Alsdorf, D.E.; Lettenmaier, D.P. Tracking fresh water from space. Science 2003, 301, 1491–1494. [Google Scholar] [CrossRef] [PubMed]
- Lacaux, J.-P.; Tourre, Y.M.; Vignolles, C.; Ndione, J.-A.; Lafaye, M. Classification of ponds from high-spatial resolution remote sensing: Application to Rift Valley fever epidemics in Senegal. Remote Sens. Environ. 2007, 106, 66–74. [Google Scholar] [CrossRef]
- Breman, H.; Groot, J.J.R.; Van Keulen, H. Resource limitations in Sahelian agriculture. Glob. Environ. Change Hum. Policy Dimens. 2001, 11, 59–68. [Google Scholar] [CrossRef]
- Haas, E.M.; Bartholomé, E.; Combal, B. Time series analysis of optical remote sensing data for the mapping of temporary surface water bodies in sub-Saharan Western Africa. J. Hydrol. 2009, 370, 52–63. [Google Scholar] [CrossRef]
- Hein, L. The impacts of grazing and rainfall variability on the dynamics of a Sahelian rangeland. J. Arid Environ. 2006, 64, 488–504. [Google Scholar] [CrossRef]
- Shevyrnogov, A.P.; Kartushinsky, A.V.; Vysotskaya, G.S. Application of satellite data for investigation of dynamic processes in inland water bodies: Lake Shira (Khakasia, Siberia), a case study. Aquat. Ecol. 2002, 36, 153–164. [Google Scholar] [CrossRef]
- Carroll, M.L.; Townshend, J.R.G.; DiMiceli, C.M.; Loboda, T.; Sohlberg, R.A. Shrinking lakes of the Arctic: Spatial relationships and trajectory of change. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Cole, J.J.; Prairie, Y.T.; Caraco, N.F.; McDowell, W.H.; Tranvik, L.J.; Striegl, R.G.; Duarte, C.M.; Kortelainen, P.; Downing, J.A.; Middelburg, J.J.; et al. Plumbing the global carbon cycle: Integrating inland waters into the terrestrial carbon budget. Ecosystems 2007, 10, 172–185. [Google Scholar] [CrossRef]
- Craglia, M.; de Bie, K.; Jackson, D.; Pesaresi, M.; Remetey-Fülöpp, G.; Wang, C.; Annoni, A.; Bian, L.; Campbell, F.; Ehlers, M.; et al. Digital Earth 2020: Towards the vision for the next decade. Int. J. Digit. Earth 2012, 5, 4–21. [Google Scholar] [CrossRef]
- Carroll, M.L.; Townshend, J.R.; DiMiceli, C.M.; Noojipady, P.; Sohlberg, R.A. A new global raster water mask at 250 m resolution. Int. J. Digit. Earth 2009, 2, 291–308. [Google Scholar] [CrossRef]
- Klein, I.; Dietz, A.; Gessner, U.; Dech, S.; Kuenzer, C. Results of the Global WaterPack: A novel product to assess inland water body dynamics on a daily basis. Remote Sens. Lett. 2015, 6, 78–87. [Google Scholar] [CrossRef]
- Bartholomé, E. Monitoring the environment in Africa: The VGT4Africa and the AMESD projects. In Proceedings of the 2nd International Workshop on “Crop and Rangeland Monitoring in East Africa”, Nairobi, Kenya, 27–29 March 2007; pp. 303–317.
- Sudheer, K.; Chaubey, I.; Garg, V. Lake water quality assessment from Landsat thematic mapper data using neural network: An approach to optimal band combination selection 1. J. Am. Water Resour. Assoc. 2006, 42, 1683–1695. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, F.; Wei, Y.C. Water body extraction from Landsat ETM+ image using MNDWI and KT transformation. In Proceedings of the 21st International Conference on Geoinformatics, Kaifeng, China, 20–22 June 2013.
- Liao, A.; Chen, L.; Chen, J.; He, C.; Cao, X.; Chen, J.; Peng, S.; Sun, F.; Gong, P. High-resolution remote sensing mapping of global land water. Sci. China Earth Sci. 2014, 57, 2305–2316. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic-spectral classification algorithm. Int. J. Digit. Earth 2015, 9, 113–133. [Google Scholar] [CrossRef]
- Yamazaki, D.; Trigg, M.A.; Ikeshima, D. Development of a global ~90 m water body map using multi-temporal Landsat images. Remote Sens. Environ. 2015, 171, 337–351. [Google Scholar] [CrossRef]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Change 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Ko, B.C.; Kim, H.H.; Nam, J.Y. Classification of potential water bodies using Landsat 8 OLI and a combination of two boosted random forest classifiers. Sensors 2015, 15, 13763–13777. [Google Scholar] [CrossRef] [PubMed]
- Pekel, J.F.; Cottam, A.; Clerici, M.; Belward, A.; Dubois, G.; Bartholome, E.; Gorelick, N. A global scale 30 m water surface detection optimized and validated for Landsat 8. AGU Fall Meet. Abstr. 2014, 1, 01P. [Google Scholar]
- Nath, R.K.; Deb, S.K. Water-body area extraction from high resolution satellite images—An introduction, review, and comparison. Int. J. Image Process. 2010, 3, 353–372. [Google Scholar]
- Sivanpillai, R.; Miller, S.N. Improvements in mapping water bodies using ASTER data. Ecol. Inf. 2010, 5, 73–78. [Google Scholar] [CrossRef]
- Sethre, P.R.; Rundquist, B.C.; Todhunter, P.E. Remote detection of prairie pothole ponds in the Devils Lake Basin, North Dakota. GISci. Remote Sens. 2005, 42, 277–296. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Work, E.A., Jr.; Gilmer, D.S. Utilization of satellite data for inventorying prairie ponds and lakes. Photogramm. Eng. Remote Sens. 1976, 42, 685–694. [Google Scholar]
- Rundquist, D.C.; Lawson, M.P.; Queen, L.P.; Cerveny, R.S. The relationship between summer season rainfall events and lake-surface area. J. Am. Water Resour. Assoc. 1987, 23, 493–508. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Vancutsem, C.; Bastin, L.; Clerici, M.; Vanbogaert, E.; Bartholomé, E.; Defourny, P. A near real-time water surface detection method based on HSV transformation of MODIS multi-spectral time series data. Remote Sens. Environ. 2014, 140, 704–716. [Google Scholar] [CrossRef]
- Bartholomé, E.; Combal, B. VGT4Africa User Manual, 1st ed.; Office for Official Publication of the European Communities: Luxembourg, 2006. [Google Scholar]
- Rahman, H.; Dedieu, G. SMAC: A simplified method for the atmospheric correction of satellite measurements in the solar spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar] [CrossRef]
- Products User Manual. Available online: http://proba-v.vgt.vito.be/ (accessed on 25 May 2016).
- Global Land Cover Facility: 90m Scene GLSDEM_p123r024_utmz13; Global Land Cover Facility, University of Maryland: College Park, Maryland, 2008; Available online: http://glcf.umd.edu/data/glsdem/ (accessed on 17 July 2015).
- Global Land Ice Measurements from Space (GLIMS) Glacier Database; National Snow and Ice Data Center: Boulder CO, USA, 2014; Available online: http://glims.colorado.edu/glacierdata/ (accessed on 28 July 2015).
- Vancutsem, C.; Pekel, J.-F.; Bogaert, P.; Defourny, P. Mean compositing, an alternative strategy for producing temporal syntheses. Concepts and performance assessment for SPOT VEGETATION time series. Int. J. Remote Sens. 2007, 28, 5123–5141. [Google Scholar] [CrossRef]
- GCOS-154. Systematic Observation Requirements for Satellite-Based Products for Climate: Supplemental Details to the Satellite Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update)”; World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Irish, R.R.; Barker, J.L.; Goward, S.N.; Arvidson, T.J. Characterization of the Landsat-7 ETM+ automated cloud-cover assessment (ACCA) algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 1179–1188. [Google Scholar] [CrossRef]
- Padilla, M.; Stehman, S.V.; Litago, J.; Chuvieco, E. Assessing the temporal stability of the accuracy of a time series of burned area products. Remote Sens. 2014, 6, 2050–2068. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L. Southern Africa validation of the MODIS, L3JRC, and GlobCarbon burned-area products. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1032–1044. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).