Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins
Abstract
:1. Introduction
2. The Study Basins
3. Materials and Methods
4. Results
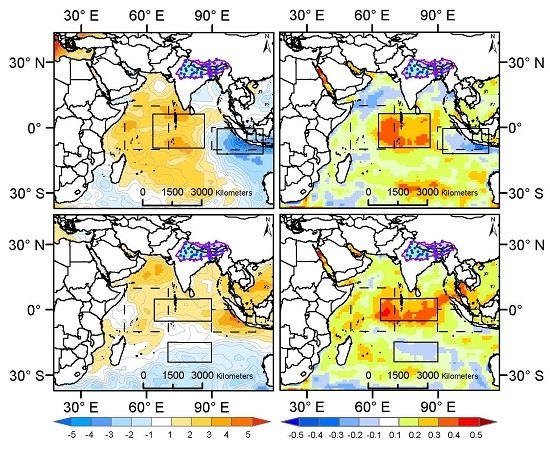
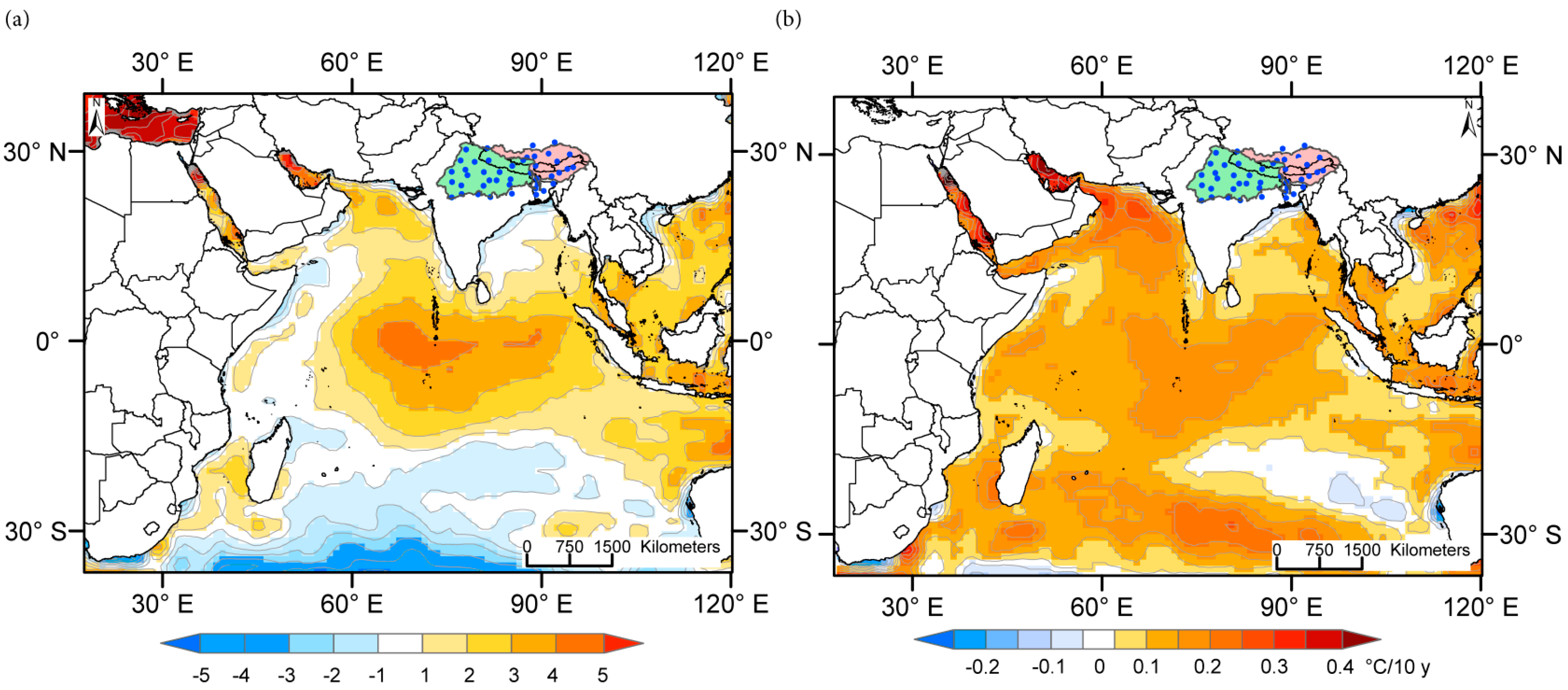
4.1. Patterns of IO SST Spatial Structure
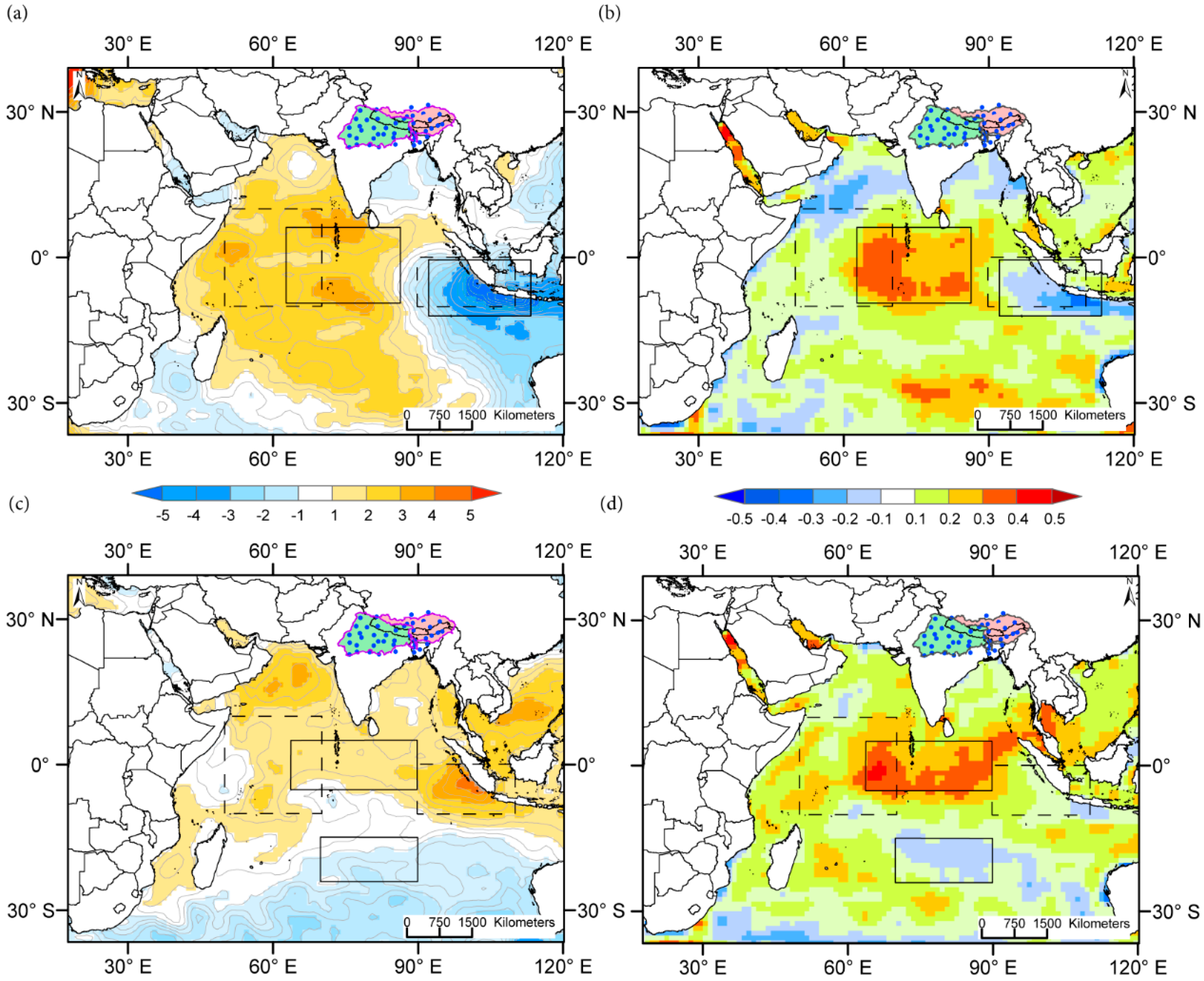
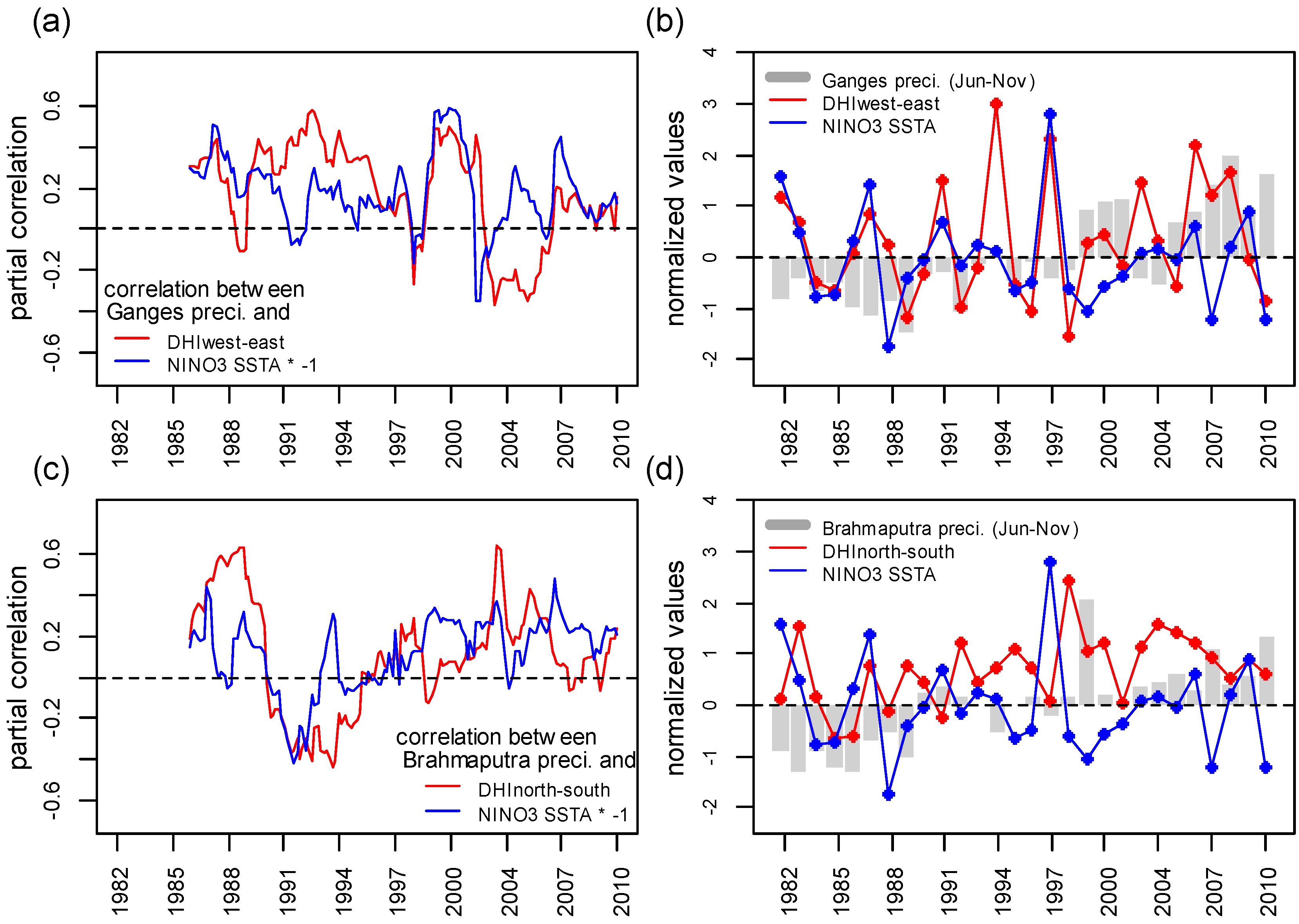
4.2. Interactive Influence of DHI and ENSO on Basin Precipitation
4.3. Wind, OLR, and Geopotential Height Anomalies during Interactive Climate Modes
5. Discussions
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lindzen, R.S.; Nigam, S. On the role of sea surface temperature gradients in forcing low-level winds and convergence in the tropics. J. Atmos. Sci. 1987, 44, 2418–2435. [Google Scholar] [CrossRef]
- Annamalai, H.; Liu, P.; Xie, S.P. Southwest Indian Ocean SST variability: Its local effect and remote influence on Asian monsoons. J. Clim. 2005, 18, 4150–4167. [Google Scholar] [CrossRef]
- Cherchi, A.; Gualdi, S.; Behera, S.; Luo, J.J.; Masson, S.; Yamagata, T.; Navarra, A. The influence of tropical Indian Ocean SST on the Indian summer monsoon. J. Clim. 2007, 20, 3083–3105. [Google Scholar] [CrossRef]
- Van Loon, H.; Meehl, G.A. The Indian summer monsoon during peaks in the 11 years sunspot cycle. Geophys. Res. Lett. 2012, 39, L13701. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Webster, P.J.; Moore, A.M.; Loschnigg, J.P.; Leben, R.R. Coupled ocean-atmosphere dynamics in the Indian Ocean during 1997–1998. Nature 1999, 401, 356–360. [Google Scholar] [CrossRef] [PubMed]
- Conway, D.; Hanson, C.E.; Doherty, R.; Persechino, A. GCM simulations of the Indian Ocean dipole influence on east african rainfall: Present and future. Geophys. Res. Lett. 2007, 34, L03705. [Google Scholar] [CrossRef]
- Reason, C.J.C. Subtropical Indian Ocean SST dipole events and southern african rainfall. Geophys. Res. Lett. 2001, 28, 2225–2227. [Google Scholar] [CrossRef]
- Abram, N.J.; Gagan, M.K.; McCulloch, M.T.; Chappell, J.; Hantoro, W.S. Coral reef death during the 1997 Indian Ocean dipole linked to indonesian wildfires. Science 2003, 301, 952–955. [Google Scholar] [CrossRef] [PubMed]
- Zubair, L.; Rao, S.A.; Yamagata, T. Modulation of Sri Lankan Maha rainfall by the Indian Ocean dipole. Geophys. Res. Lett. 2003, 30, 1063. [Google Scholar] [CrossRef]
- Ummenhofer, C.C.; Gupta, A.S.; Briggs, P.R.; England, M.H.; McIntosh, P.C.; Meyers, G.A.; Pook, M.J.; Raupach, M.R.; Risbey, J.S. Indian and Pacific Ocean influences on southeast Australian drought and soil moisture. J. Clim. 2011, 24, 1313–1336. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. Impact of the Indian Ocean dipole on the relationship between the Indian monsoon rainfall and ENSO. Geophys. Res. Lett. 2001, 28, 4499–4502. [Google Scholar] [CrossRef]
- Ashok, K.; Saji, N.H. On the impacts of ENSO and Indian Ocean dipole events on sub-regional Indian summer monsoon rainfall. Nat. Hazards 2007, 42, 273–285. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Spatial and seasonal responses of precipitation in the ganges and brahmaputra river basins to ENSO and Indian Ocean dipole modes: Implications for flooding and drought. Nat. Hazards Earth Syst. Sci. 2015, 15, 147–162. [Google Scholar] [CrossRef]
- Stocker, T.; Dahe, Q.; Plattner, G.; Alexander, L.; Allen, S.; Bindoff, N.; Breon, F.; Church, J.; Cubasch, U.; Emori, S.; et al. Climate Change 2013: The Physical Science Basis; Working Group I Contribution to the IPCC Fifth Assessment Report; Intergovernmental Panel on Climate Change: Stockholm, Sweden, 2013. [Google Scholar]
- Chowdhury, M.; Ward, N. Hydro-meteorological variability in the greater ganges–brahmaputra–meghna basins. Int. J. Climatol. 2004, 24, 1495–1508. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Projections of the ganges–brahmaputra precipitation—Downscaled from gcm predictors. J. Hydrol. 2014, 517, 120–134. [Google Scholar] [CrossRef]
- The World Bank South Asian Water Initiative. The Ganges Strategic Basin Assessment: A Discussion of Regional Opportunities and Risks; 67668-SAS; The World Bank: Washington, DC, USA, 2014. [Google Scholar]
- Rasul, G. Water for growth and development in the ganges, brahmaputra, and meghna basins: An economic perspective. Int. J. River Basin Manag. 2015, 13, 387–400. [Google Scholar] [CrossRef]
- Alexandratos, N.; Bruinsma, J. World Agriculture Towards 2030/2050: The 2012 Revision; ESA Working Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012. [Google Scholar]
- Thenkabail, P.S.; Schull, M.; Turral, H. Ganges and indus river basin land use/land cover (LULC) and irrigated area mapping using continuous streams of MODIS data. Remote Sens. Environ. 2005, 95, 317–341. [Google Scholar] [CrossRef]
- Ghosh, S.; Vittal, H.; Sharma, T.; Karmakar, S.; Kasiviswanathan, K.; Dhanesh, Y.; Sudheer, K.; Gunthe, S. Indian summer monsoon rainfall: Implications of contrasting trends in the spatial variability of means and extremes. PLoS ONE 2016, 11, e0158670. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W. Historical trends and future predictions of climate variability in the Brahmaputra basin. Int. J. Climatol. 2008, 28, 243–254. [Google Scholar] [CrossRef]
- Mirza, M.Q. Climate change, flooding in South Asia and implications. Reg. Environ. Chang. 2011, 11, 95–107. [Google Scholar] [CrossRef]
- Jian, J.; Webster, P.J.; Hoyos, C.D. Large-scale controls on ganges and brahmaputra river discharge on intraseasonal and seasonal time-scales. Q. J. R. Meteorol. Soc. 2009, 135, 353–370. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Liebmann, B.; Smith, C.A. Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1275–1277. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration, Oceanic and Atmospheric Research/Earth System Research Laboratory Physical Science Division, Climate Research and Reanalysis Datasets. Available online: http://www.esrl.noaa.gov/psd/ (accessed on 6 October 2012).
- National Climatic Data Center. Global Surface Summary of the Day—GSOD, Version 7. 2001. Available online: ftp://ftp.ncdc.noaa.gov/pub/data/gsod (accessed on 5 January 2012). [Google Scholar]
- Pervez, M.S.; Henebry, G.M. Assessing the impacts of climate and land use and land cover change on the freshwater availability in the Brahmaputra river basin. J. Hydrol. Reg Stud. 2015, 3, 285–311. [Google Scholar] [CrossRef]
- Qian, Y.; Gong, D.; Leung, R. Light rain events change over North America, Europe, and Asia for 1973–2009. Atmos. Sci. Lett. 2010, 11, 301–306. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Siddique-E-Akbor, A.H.M.; Hossain, F.; Sikder, S.; Shum, C.K.; Tseng, S.; Yi, Y.; Turk, F.J.; Limaye, A. Satellite precipitation data–driven hydrological modeling for water resources management in the Ganges, Brahmaputra, and Meghna basins. Earth Interact. 2014, 18, 1–25. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. Cmorph: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The trmm multi-satellite precipitation analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers, 5th ed.; Oliver and Boyd: London, UK, 1925. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods, 5th ed.; Griffin: London, UK, 1990. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Dommenget, D. An objective analysis of the observed spatial structure of the tropical Indian Ocean SST variability. Clim. Dyn. 2011, 36, 2129–2145. [Google Scholar] [CrossRef]
- Han, W.; Meehl, G.A.; Rajagopalan, B.; Fasullo, J.T.; Hu, A.; Lin, J.; Large, W.G.; Wang, J.W.; Quan, X.W.; Trenary, L.L.; et al. Patterns of Indian Ocean sea-level change in a warming climate. Nat. Geosci. 2010, 3, 546–550. [Google Scholar] [CrossRef]
- Abram, N.J.; Gagan, M.K.; Cole, J.E.; Hantoro, W.S.; Mudelsee, M. Recent intensification of tropical climate variability in the Indian Ocean. Nat. Geosci. 2008, 1, 849–853. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Caron, J.M. The southern oscillation revisited: Sea level pressures, surface temperatures, and precipitation. J. Clim. 2000, 13, 4358–4365. [Google Scholar] [CrossRef]
- National Center for Atmospheric Research Staff (Ed.) The Climate Data Guide: Outgoing Longwave Radiation (OLR): AVHRR. Available online: https://climatedataguide.ucar.edu/climate-data/outgoing-longwave-radiation-olr-avhrr (accessed on 6 October 2015).
- Ardanuy, P.E.; Kyle, H.L. El Niño and outgoing longwave radiation: Observations from Nimbus-7 ERB. Mon. Weather Rev. 1986, 114, 415–433. [Google Scholar] [CrossRef]
- Tymvios, F.; Savvidou, K.; Michaelides, S. Association of geopotential height patterns with heavy rainfall events in Cyprus. Adv. Geosci. 2010, 23, 73–78. [Google Scholar] [CrossRef]
- Xoplaki, E.; Luterbacher, J.; Burkard, R.; Patrikas, I.; Maheras, P. Connection between the large-scale 500 hPa geopotential height fields and precipitation over greece during wintertime. Clim. Res. 2000, 14, 129–146. [Google Scholar] [CrossRef]
- Kożuchowski, K.; Wibig, J.; Maheras, P. Connections between air temperature and precipitation and the geopotential height of the 500 hPa level in a meridional cross-section in Europe. Int. J. Climatol. 1992, 12, 343–352. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Saji, N.H.; Yamagata, T. Individual and combined influences of ENSO and the Indian Ocean dipole on the Indian summer monsoon. J. Clim. 2004, 17, 3141–3155. [Google Scholar] [CrossRef]
- Meyers, G.; McIntosh, P.; Pigot, L.; Pook, M. The years of el niño, la niña and interactions with the tropical Indian Ocean. J. Clim. 2007, 20, 2872–2880. [Google Scholar] [CrossRef]
- Wallace, J.M.; Rasmusson, E.M.; Mitchell, T.P.; Kousky, V.E.; Sarachik, E.S.; von Storch, H. On the structure and evolution of ENSO-related climate variability in the tropical Pacific: Lessons from TOGA. J. Geophys. Res. 1998, 103, 14241–14259. [Google Scholar] [CrossRef]
- Pervez, M.S.; Henebry, G.M. Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins. U.S. Geological Survey Data Release, 2016. Available online: https://dx.doi.org/10.5066/F77P8WH6 (accessed on 25 October 2016). [Google Scholar]

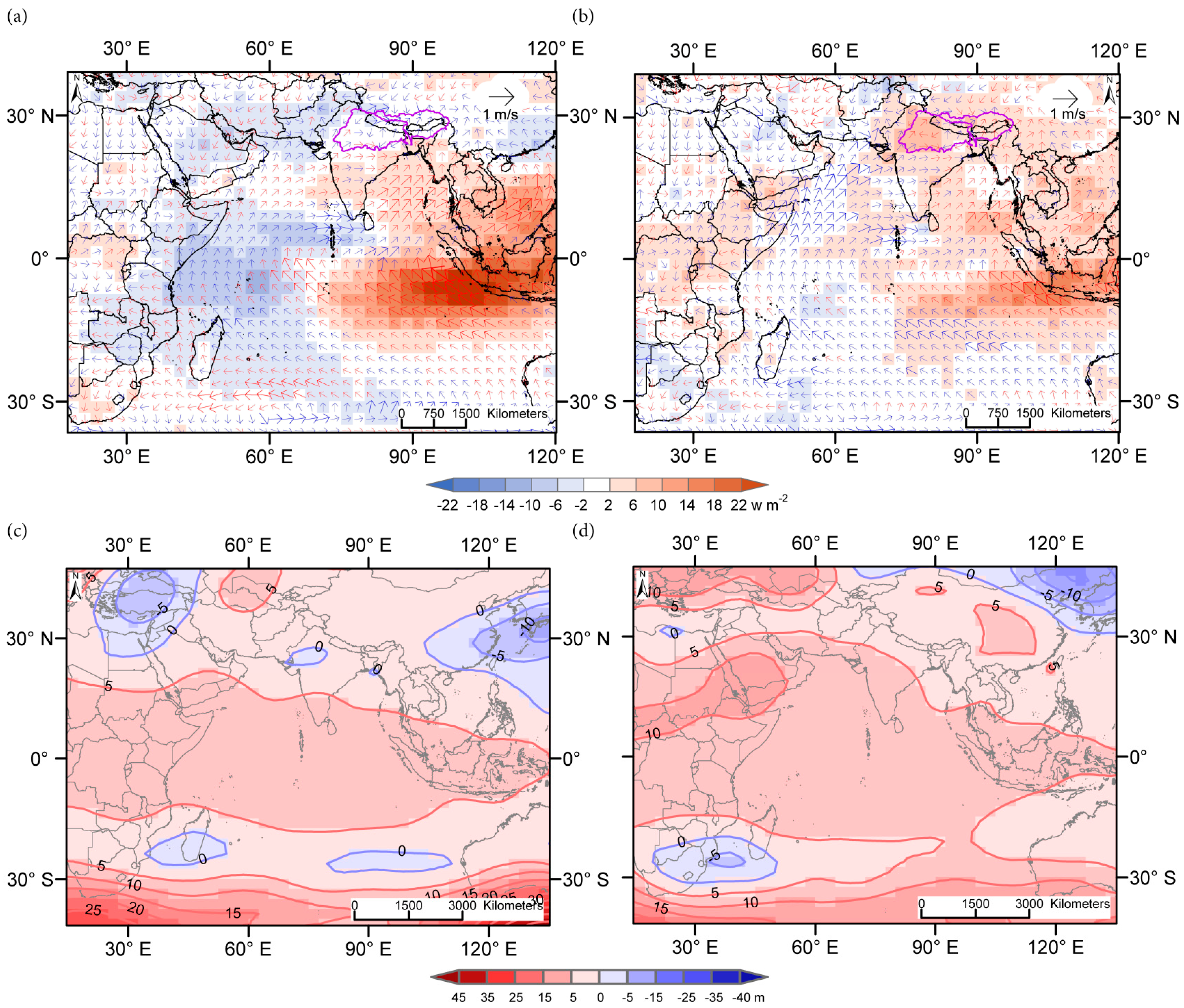
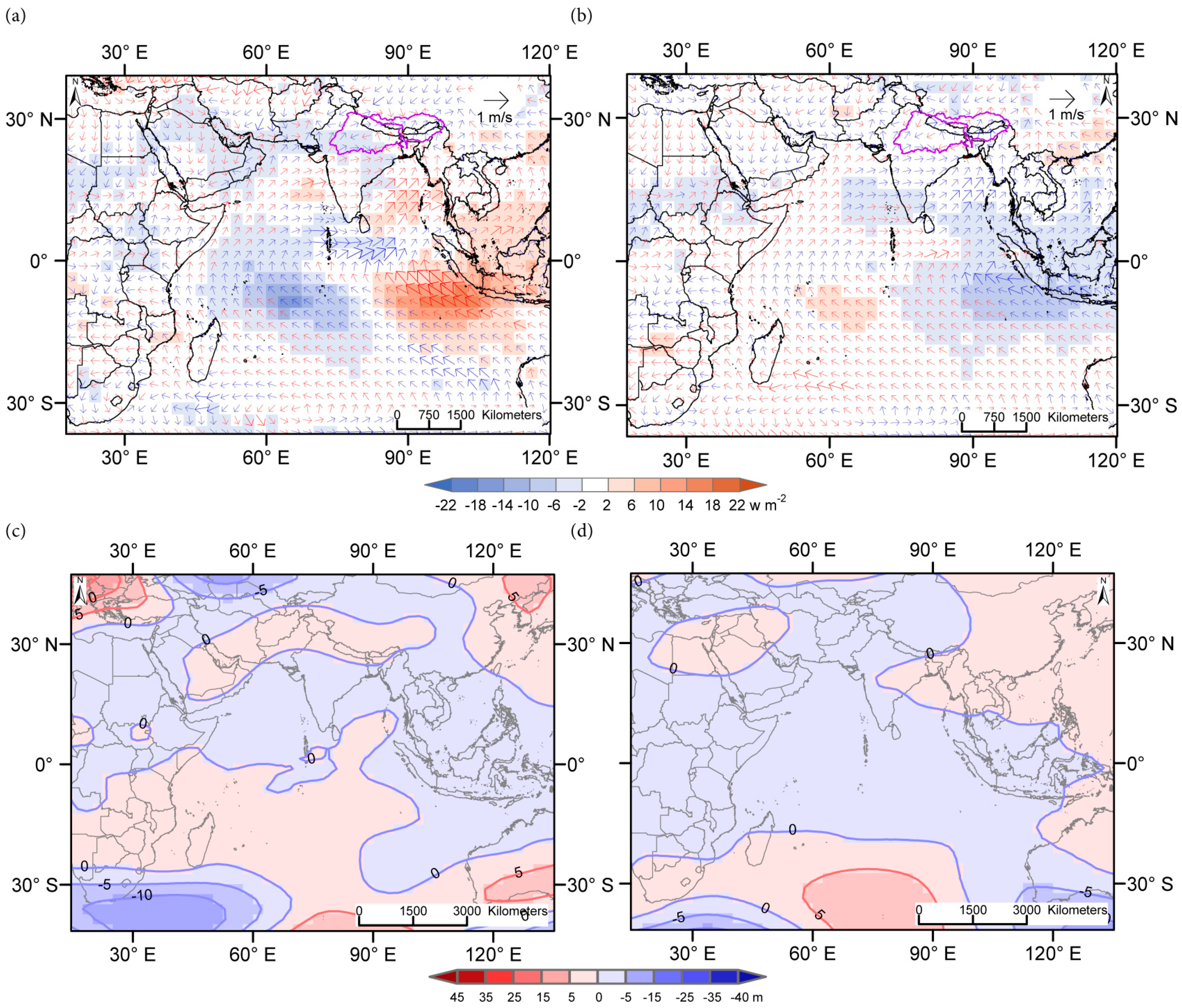
| El Niño & Negative DHIwest-east | El Niño& Neutral DHIwest-east | El Niño & Positive DHIwest-east |
|---|---|---|
| No years observed | 1987, 2009 | 1982, 1997, 2006 |
| Avg.: 651 mm, 71% of baseline | Avg.: 866 mm, 94% of baseline | |
| Neutral & Negative DHIwest-east | Neutral | Neutral & Positive DHIwest-east |
| 1989, 1992, 1996, 1998 | 1983, 1986, 1990, 1993, 1995, 2000, 2001, 2004, 2005 | 1991, 1994, 2003, 2008 |
| Avg.: 699 mm, 76% of baseline | Baseline = 921 mm | Avg.: 1022 mm, 111% of baseline |
| La Niña & Negative DHIwest-east | La Niña and Neutral DHIwest-east | La Niña & Positive DHIwest-east |
| 1984, 1985 | 1988, 2010 | 1999, 2007 |
| Avg.: 739 mm, 80% of baseline | Avg.: 1035 mm, 112% of baseline | Avg.: 1277 mm, 138% of baseline |
| El Niño & Negative DHInorth-south | El Niño & Neutral DHInorth-south | El Niño & Positive DHInorth-south |
|---|---|---|
| No years observed | 1982, 1997 | 1987, 2006, 2009 |
| Avg.: 609 mm, 87% of baseline | Avg.: 786 mm, 111% of baseline | |
| Neutral &Negative DHInorth-south | Neutral | Neutral & Positive DHInorth-south |
| No years observed | 1983, 1986, 1990, 1991, 1993, 1994, 1996, 2001, 2008 | 1989, 1992, 1995, 1998, 2000, 2003, 2004, 2005 |
| Baseline = 704 mm | Avg.: 799 mm, 113% of baseline | |
| La Niña & Negative DHInorth-south | La Niña & Neutral DHInorth-south | La Niña & Positive DHInorth-south |
| 1984, 1985 | 1988 | 1999, 2007, 2010 |
| Avg.: 606 mm, 86% of baseline | Avg.: 620 mm, 88% of baseline | Avg.: 1192 mm, 169% of baseline |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pervez, M.S.; Henebry, G.M. Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins. Remote Sens. 2016, 8, 901. https://doi.org/10.3390/rs8110901
Pervez MS, Henebry GM. Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins. Remote Sensing. 2016; 8(11):901. https://doi.org/10.3390/rs8110901
Chicago/Turabian StylePervez, Md Shahriar, and Geoffrey M. Henebry. 2016. "Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins" Remote Sensing 8, no. 11: 901. https://doi.org/10.3390/rs8110901
APA StylePervez, M. S., & Henebry, G. M. (2016). Differential Heating in the Indian Ocean Differentially Modulates Precipitation in the Ganges and Brahmaputra Basins. Remote Sensing, 8(11), 901. https://doi.org/10.3390/rs8110901