Scale-Aware Pansharpening Algorithm for Agricultural Fragmented Landscapes
Abstract
:1. Introduction
2. Background
2.1. Pansharpening Based on the Multi-Resolution Approach
2.2. Rolling Guidance Filter
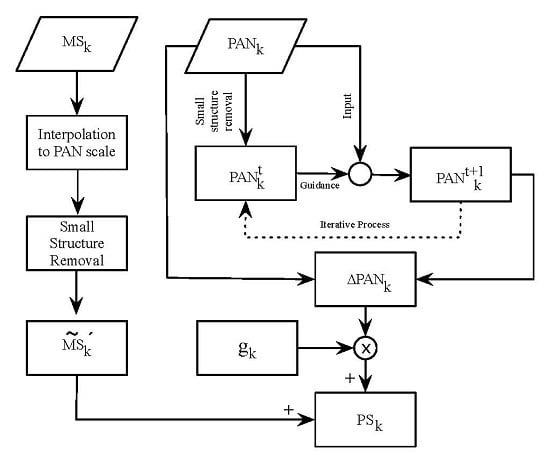
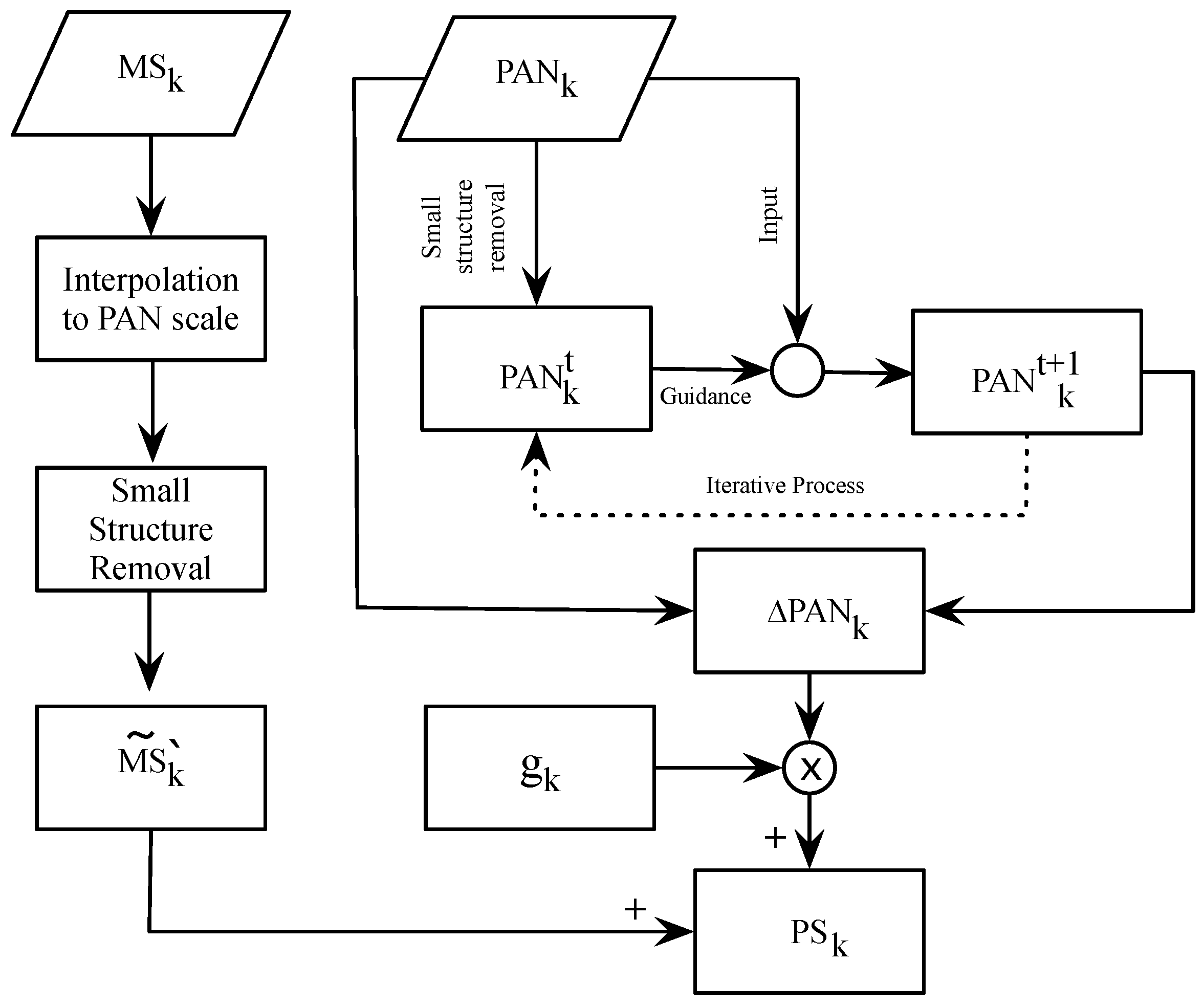
3. Proposed Pansharpening Method Based on the Rolling Guidance Filter
- (i)
- Pre-processing of the images: The MS and PAN (source images) were perfectly co-registered and the MS image resized to the PAN image size. In particular, in this work, the algorithm [36] was used, obtaining a , that corresponds to the MS image interpolated at the PAN scale. Moreover, a histogram-matched PAN image was produced using Equation (12):where μ and σ denote the mean and standard deviation of an image, respectively.
- (ii)
- Small structure removal: To completely remove structures with a scale of less than from the k-th band of the MS image, a weighted average Gaussian filter approach, formalized in Equation (13), was used.where is the low frequency content for the k-th band of the MS image and corresponds to the first iteration of the bilateral filter (), is the set of neighboring pixels of p and is a normalization of and defined in Equation (14):
- (iii)
- PAN edge recovery: Equation (15) was applied to recover the edges of the image, using the result of the RGF process at the t-th iteration:To obtain just the high frequency (edges) from the image, which will be injected into the MS image, the difference between the and image was calculated, using the Equation (16):
- (iv)
- Pansharpening image: The PS image was obtained using the MRA approach, formalized in Equation (17):
4. Results and Discussion
4.1. Testing Dataset
4.2. Quality Assessment
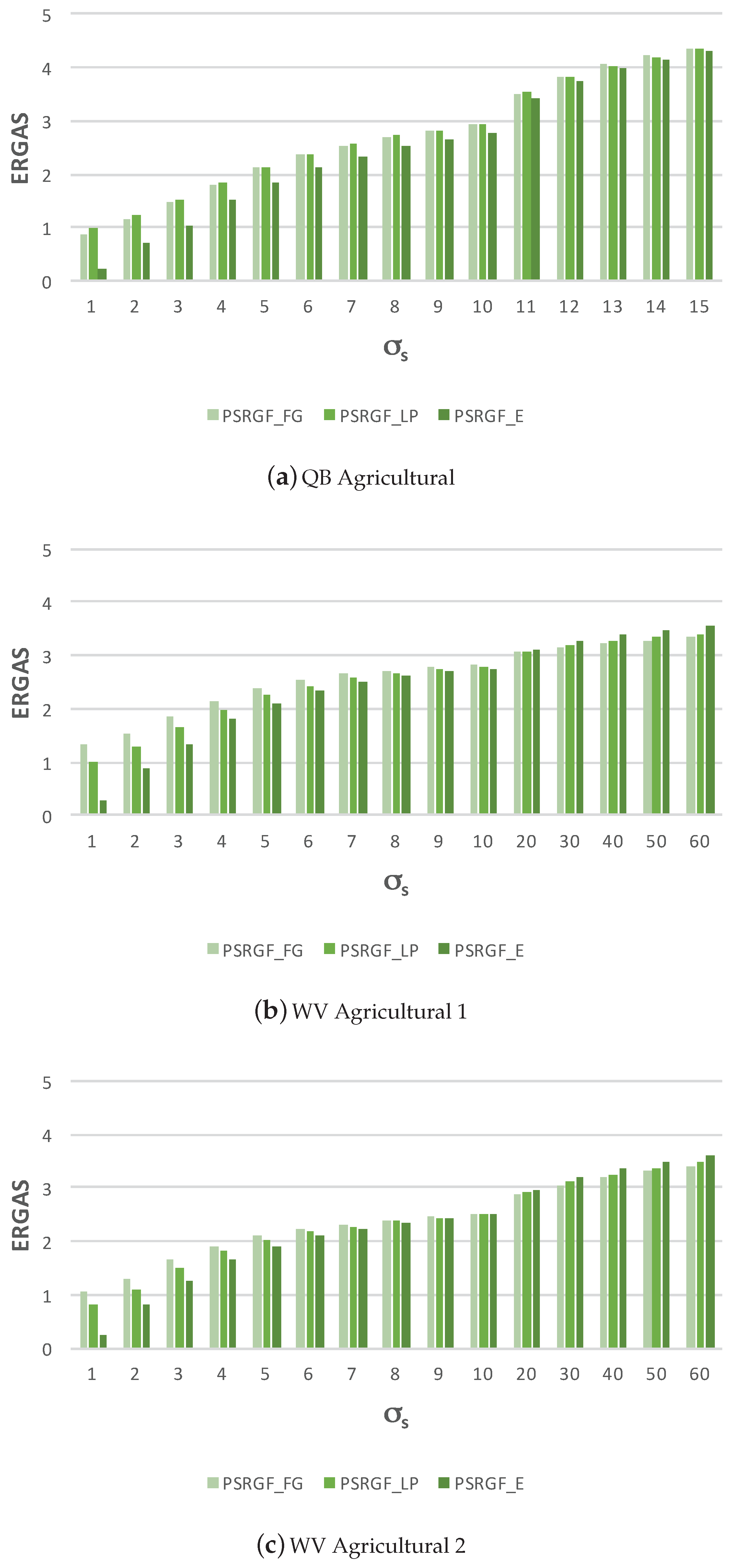
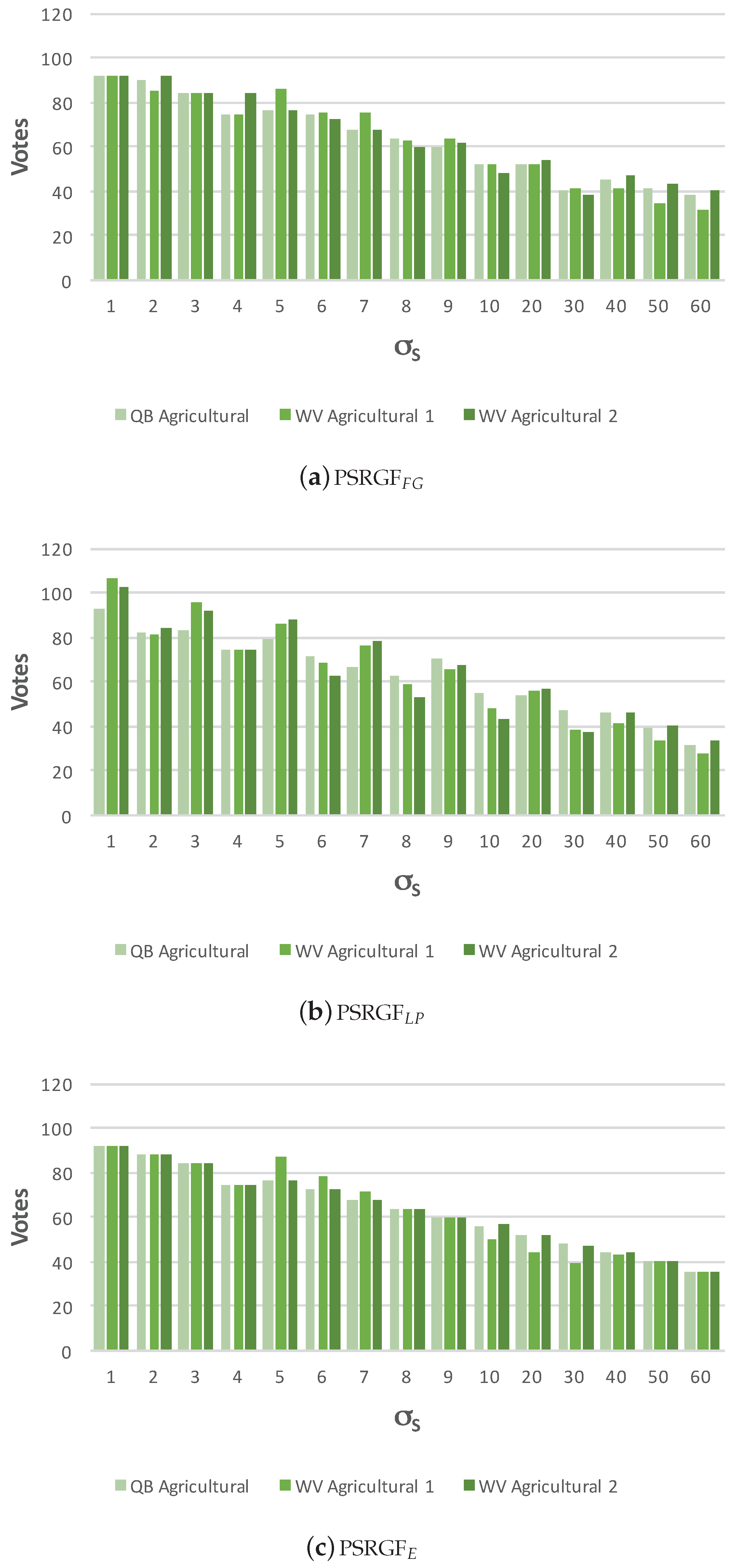
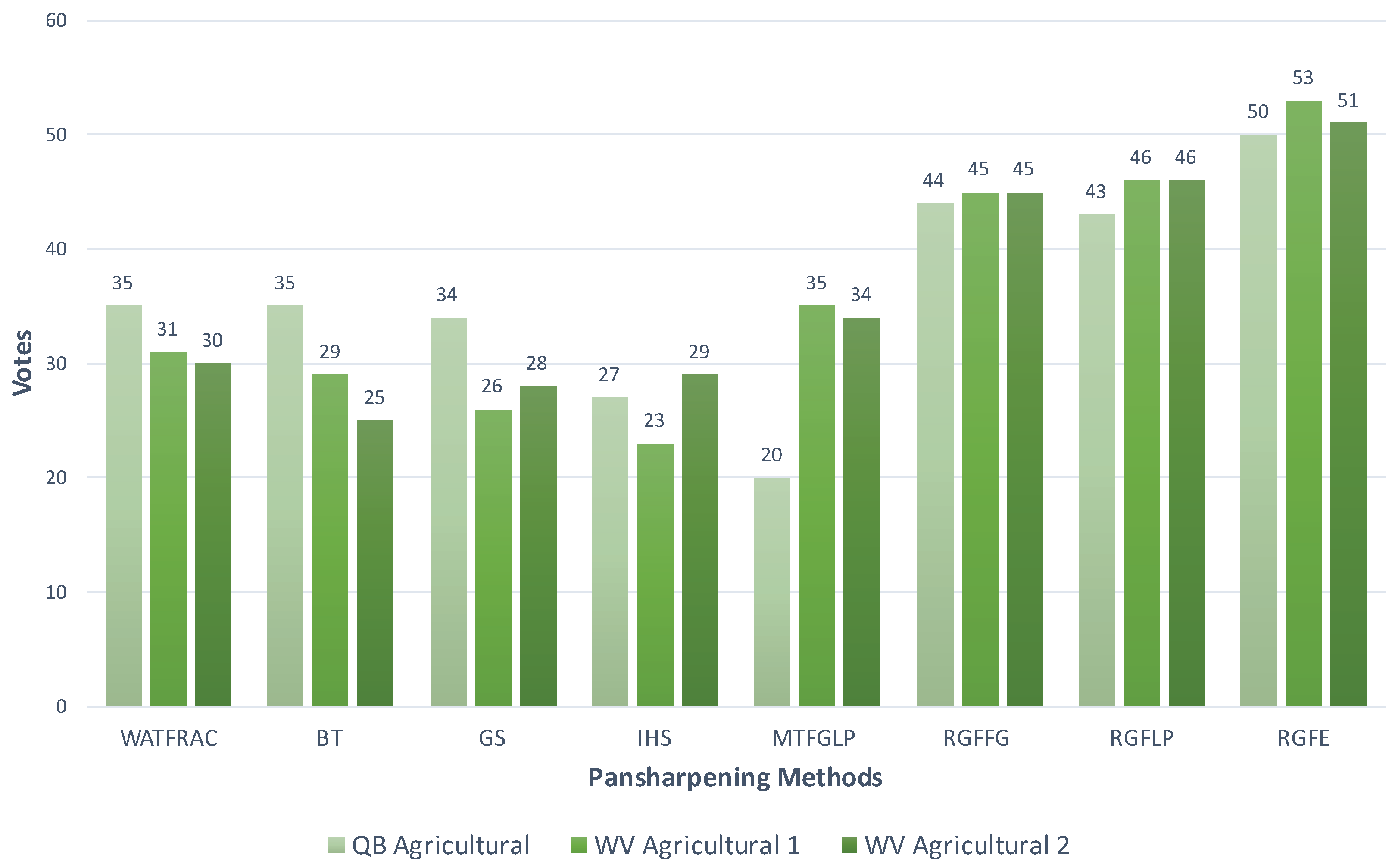
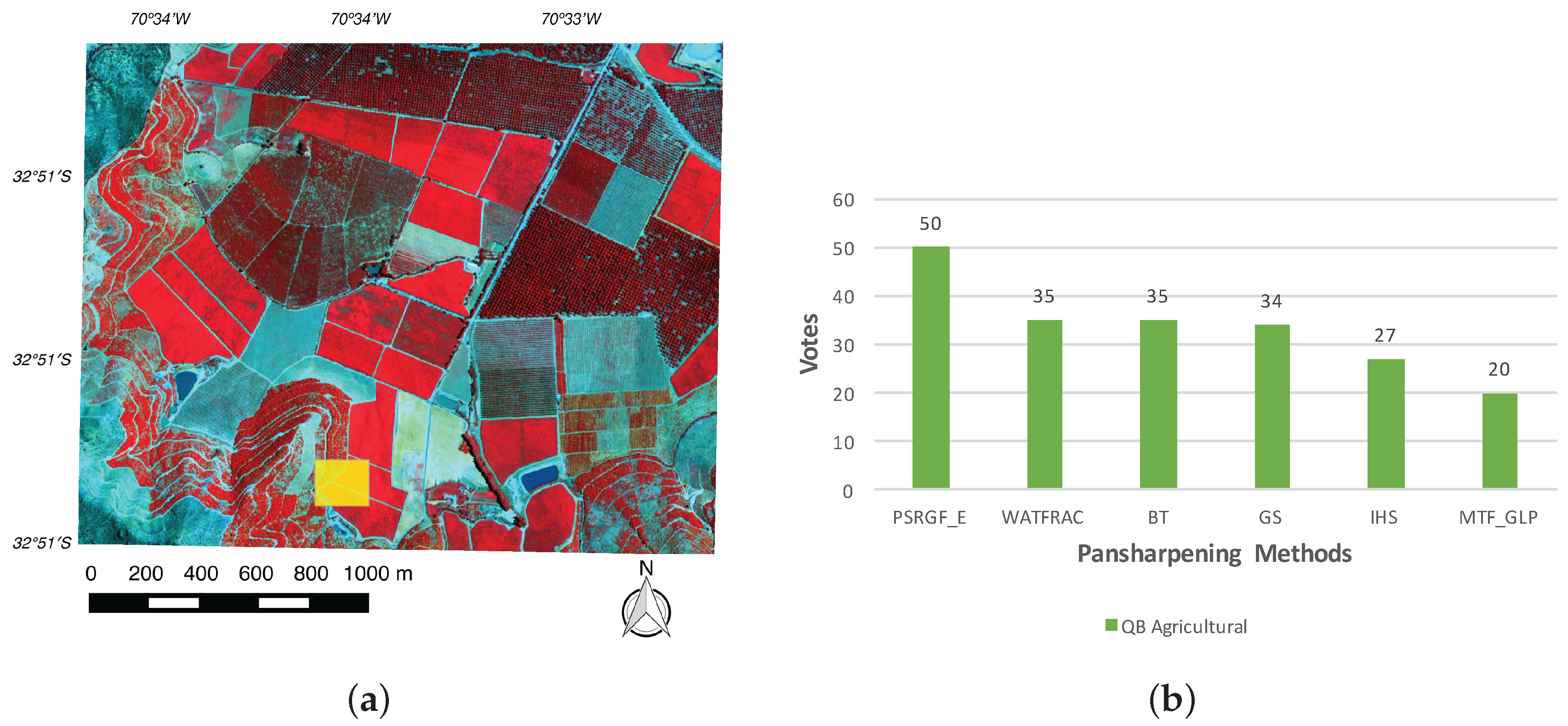
4.3. Visual Assessment of the Pansharpened Images
4.4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Löw, F.; Duveiller, G. Defining the spatial resolution requirements for crop identification using optical remote sensing. Remote Sens. 2014, 6, 9034–9063. [Google Scholar] [CrossRef]
- Imukova, K.; Ingwersen, J.; Streck, T. Determining the spatial and temporal dynamics of the green vegetation fraction of croplands using high-resolution RapidEye satellite images. Agric. For. Meteorol. 2015, 206, 113–123. [Google Scholar] [CrossRef]
- Lowder, S.K.; Skoet, J.; Raney, T. The number, size, and distribution of farms, smallholder farms, and family farms worldwide. World Dev. 2016, 87, 16–29. [Google Scholar] [CrossRef]
- Garcia-Pedrero, A.; Gonzalo-Martin, C.; Fonseca-Luengo, D.; Lillo-Saavedra, M. A GEOBIA methodology for fragmented agricultural landscapes. Remote Sens. 2015, 7, 767–787. [Google Scholar] [CrossRef]
- Lillo-Saavedra, M.; Gonzalo, C.; Lagos, O. Toward reduction of artifacts in fused images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 368–375. [Google Scholar] [CrossRef]
- Pohl, C.; van Genderen, J. Remote sensing image fusion: An update in the context of Digital Earth. Int. J. Digi. Earth 2014, 7, 158–172. [Google Scholar] [CrossRef]
- Vaibhav, R.; Pandit, R.; Bhiwani, J. Image fusion in remote sensing applications: A review. Int. J. Comput. Appl. 2015, 120, 22–32. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Selva, M. Twenty-five years of pansharpening. In Signal and Image Processing for Remote Sensing, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; pp. 533–548. [Google Scholar]
- Li, S.; Yang, B.; Hu, J. Performance comparison of different multi-resolution transforms for image fusion. Inf. Fusion 2011, 12, 74–84. [Google Scholar] [CrossRef]
- Lillo-Saavedra, M.; Gonzalo, C. Spectral or spatial quality for fused satellite imagery? A trade-off solution using the wavelet à trous algorithm. Int. J. Remote Sens. 2006, 27, 1453–1464. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Alparone, L.; Aiazzi, B.; Baronti, S. Pan-sharpening of multispectral images: A critical review and comparison. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium ( IGARSS ’04), Anchorage, AK, USA, 20–24 September 2004; pp. 81–84.
- Koutsias, N.; Karteris, M.; Chuvico, E. The use of intensity-hue-saturation transformation of Landsat-5 Thematic Mapper data for burned land mapping. Photogramm. Eng. Remote Sens. 2000, 66, 829–840. [Google Scholar]
- Chavez, P.S., Jr.; Kwarteng, A.Y. Extracting spectral contrast in Landsat Thematic Mapper image data using selective principal component analysis. Photogramm. Eng. Remote Sens. 1989, 55, 339–348. [Google Scholar]
- Laben, C.; Brower, B. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. II. Channel ratio and “chromaticity” transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Gonzalo, C.; Lillo-Saavedra, M. A directed search algorithm for setting the spectral–spatial quality trade-off of fused images by the wavelet à trous method. Can. J. Remote Sens. 2008, 34, 367–375. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening quality assessment using the modulation transfer functions of instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Massip, P.; Blanc, P.; Wald, L. A method to better account for modulation transfer functions in ARSIS-based pansharpening methods. IEEE Trans. Geosci. Remote Sens. 2012, 50, 800–808. [Google Scholar] [CrossRef]
- Ghassemian, H. A review of remote sensing image fusion methods. Inf. Fusion 2016, 32, 75–89. [Google Scholar] [CrossRef]
- Kaplan, N.; Erer, I. Bilateral filtering-based enhanced pansharpening of multispectral satellite images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1941–1945. [Google Scholar] [CrossRef]
- Paris, S.; Kornprobst, P.; Tumblin, J.; Durand, F. Bilateral filtering: Theory and applications. Found. Trends Comput. Graph. Vis. 2008, 4, 1–73. [Google Scholar] [CrossRef]
- Hu, J.; Li, S. The multiscale directional bilateral filter and its application to multisensor image fusion. Inf. Fusion 2012, 13, 196–206. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Liang, S. Pan-sharpening using a guided filter. Int. J. Remote Sens. 2016, 37, 1777–1800. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, X.; Xu, L.; Jia, J. Rolling guidance filter. In Computer Vision–ECCV 2014; Springer: Berlin, Germany, 2014; pp. 815–830. [Google Scholar]
- Liu, Y.; Li, M.; Mao, L.; Xu, F.; Huang, S. Review of remotely sensed imagery classification patterns based on object-oriented image analysis. Chin. Geogr. Sci. 2006, 16, 282–288. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Emerson, P. The original Borda count and partial voting. Soc. Choice Welf. 2013, 40, 353–358. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Pei, J.; Lin, X.; Lin, Q.; Li, A. Consensus-based ranking of multivalued objects: A generalized borda count approach. IEEE Trans. Knowl. Data Eng. 2014, 26, 83–96. [Google Scholar] [CrossRef]
- Amro, I.; Mateos, J.; Vega, M.; Molina, R.; Katsaggelos, A.K. A survey of classical methods and new trends in pansharpening of multispectral images. EURASIP J. Adv. Signal Process. 2011, 2011, 1–22. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Lotti, F.; Selva, M. A Comparison between global and context-adaptive pansharpening of multispectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 302–306. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, J.; Liu, S.; Cao, L.; Zhou, Q.; Huang, H. A GIHS-based spectral preservation fusion method for remote sensing images using edge restored spectral modulation. ISPRS J. Photogramm. Remote Sens. 2014, 88, 16–27. [Google Scholar] [CrossRef]
- Otazu, X.; Gonzalez-Audicana, M.; Fors, O.; Nunez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Bjørke, J.T. Framework for entropy-based map evaluation. Cartogr. Geogr. Inf. Syst. 1996, 23, 78–95. [Google Scholar] [CrossRef]
- Burger, W.; Burge, M.J. Principles of Digital Image Processing: Core Algorithms, 1st ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Kruse, F.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Wald, L. Quality of high resolution synthesised images: Is there a simple criterion. In Third Conference “Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images”; Ranchin, T., Wald, L., Eds.; SEE/URISCA: Sophia Antipolis, France, 2000; pp. 99–103. [Google Scholar]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi/hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]





| Satellite | Spatial Resolution (m) | |
|---|---|---|
| Panchromatic (PAN) | Multispectral (MS) | |
| Spot–6/7 | 1.50 | 6.00 |
| QuickBird–2 | 0.65 | 2.60 |
| Pleiades–1/2 | 0.50 | 2.00 |
| WorldView–1/2 | 0.46 | 1.84 |
| GeoEye–1 | 0.46 | 1.84 |
| GeoEye–2 | 0.34 | 1.36 |
| WorldView–3 | 0.31 | 1.24 |
| Index | Equation | Ideal Value | Reference |
|---|---|---|---|
| 1 | [37] | ||
| [38] | |||
| ERGAS | 0 | [39] | |
| SERGAS | 0 | [11] | |
| 1 | [39] | ||
| Q | 1 | [40] | |
| 1 | [41] |
| Injection Gain () | Equation | PS Method |
|---|---|---|
| Full Gain (FG) | 1 | |
| Luminance Proportional (LP) | ||
| Entropy (E) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lillo-Saavedra, M.; Gonzalo-Martín, C.; García-Pedrero, A.; Lagos, O. Scale-Aware Pansharpening Algorithm for Agricultural Fragmented Landscapes. Remote Sens. 2016, 8, 870. https://doi.org/10.3390/rs8100870
Lillo-Saavedra M, Gonzalo-Martín C, García-Pedrero A, Lagos O. Scale-Aware Pansharpening Algorithm for Agricultural Fragmented Landscapes. Remote Sensing. 2016; 8(10):870. https://doi.org/10.3390/rs8100870
Chicago/Turabian StyleLillo-Saavedra, Mario, Consuelo Gonzalo-Martín, Angel García-Pedrero, and Octavio Lagos. 2016. "Scale-Aware Pansharpening Algorithm for Agricultural Fragmented Landscapes" Remote Sensing 8, no. 10: 870. https://doi.org/10.3390/rs8100870
APA StyleLillo-Saavedra, M., Gonzalo-Martín, C., García-Pedrero, A., & Lagos, O. (2016). Scale-Aware Pansharpening Algorithm for Agricultural Fragmented Landscapes. Remote Sensing, 8(10), 870. https://doi.org/10.3390/rs8100870