1. Introduction
Various satellite and air techniques are currently used to detect and trace oil spills [
1,
2], including optical methods. When viewed using optical methods, oil on the sea surface manifests itself clearly through the modification of reflective features and transparency of the water–air interface, as well as the distribution of wave slopes [
3], whereas oil floating below the sea surface (e.g., after using dispersants) can manifest its presence to an observer (or receiver) located above the sea surface (aircraft, satellite) only in the visible range of the electromagnetic wave spectrum. In order for such a possibility to occur, oil must affect the solar photons penetrating the water column; furthermore, the impact of oil substances on light must differ from the similar impact of water together with its natural constituents (dissolved and suspended).
An above-water remote-sensing-reflectance (
Rrs) meter [
4,
5] would be a useful device to detect oil through the observation of changes in a light stream coming from the water column. Therefore, according to the definition of the
Rrs in Equation (1), the model for the detection of “clouds” of oil droplets suspended in the sea described in this paper refers to the vertical reflected radiance (
Lr) formed under the defined incident above water solar vector irradiance (
Ei).
where
Lr: reflected radiance (the vertical-to-sea-surface flux of radiant energy per unit of solid angle/unit of projected surface area)
Ei: the incident vector irradiance above the sea surface (expressed further in the denominator of Equation (2))
The model also takes into account the probability distribution of water impact and its components on photons migrating in the depths of the sea. These distributions reflect three phenomena: absorption and scattering in the water body, as well as reflection at the air–water interface. Moreover, scattering includes a probability distribution of scattering in a certain direction in space, whereas reflection involves the angular distribution of the surface wave slopes. The above-mentioned probability distributions are necessary as the input data for the simulation of the migration of a large number of virtual photons performed by the Monte Carlo method [
6].
2. Model
The remote sensing reflectance (Rrs), as a parameter characterizing light coming from the water column, depends on the interactions of photons with water molecules, water density fluctuations, and various suspended or diluted natural water constituents (or even man-made ones). These interactions find their quantitative expression in both absorption and scattering coefficients, as well as in the angular distribution of scattered light, together commonly known as inherent optical properties (IOPs). The probability distributions required in the Monte Carlo method are converted from the inherent optical properties of water and from Fresnel formulas for the air–water border, as well as from the surface wave slope distribution.
To a certain degree,
Rrs depends on the angular distribution of above-water downward (solar) radiance, which is a source of photons migrating in the water column (some of the photons are returned back into the atmosphere). From a remote-sensing point of view, a complete optical description of any area is a
bidirectional reflectance distribution function (BRDF). In this case,
Rrs for a specific wavelength is defined as follows:
where
: direction of the reflected light
: the upward (reflected) radiance under specified direction
): the solar and sky downward (incident) light radiance
: direction of the incident solar light (
Figure 1)
BRDF: Bidirectional Reflectance Distribution Function
If the sea surface is observed vertically (
θr), Equation (2) is simplified to the following form Equation(3):
BRDF is a physical quantity introduced in the 1970s [
7] to characterize ground optical features. BRDF cannot be measured directly in the water environment, but it can be modeled through Monte Carlo photon tracing (although this requires IOPs as the input data). On the other hand, it is possible to operationally measure
Rrs by a remote-sensing meter, i.e., an integrated device consisting of a downward plane irradiance (
Ei) meter and upward radiance (
Lr) meter. Prediction of
Rrs for a sea polluted with an oil-in-water emulsion is important because it can help in the interpretation of the
Rrs of a sea endangered by oil pollution. Essential elements of this interpretation include the detection of oil dispersed in the water column, possible identification of the kind of oil, and, most importantly, signaling that the remote sensing interpretive model (implemented for a specified area of the sea) is disturbed by the presence of oil.
There are several questions regarding the visibility of “underwater oil”; for example, the impact of the floating oil depth, the concentration of oil, the distribution of the size of oil droplets, the type of oil (its optical properties), and the thickness of the oiled water layer. Other questions include: the role of wavelength, solar radiance angular distribution, IOPs of seawater, and the degree of sea surface undulations.
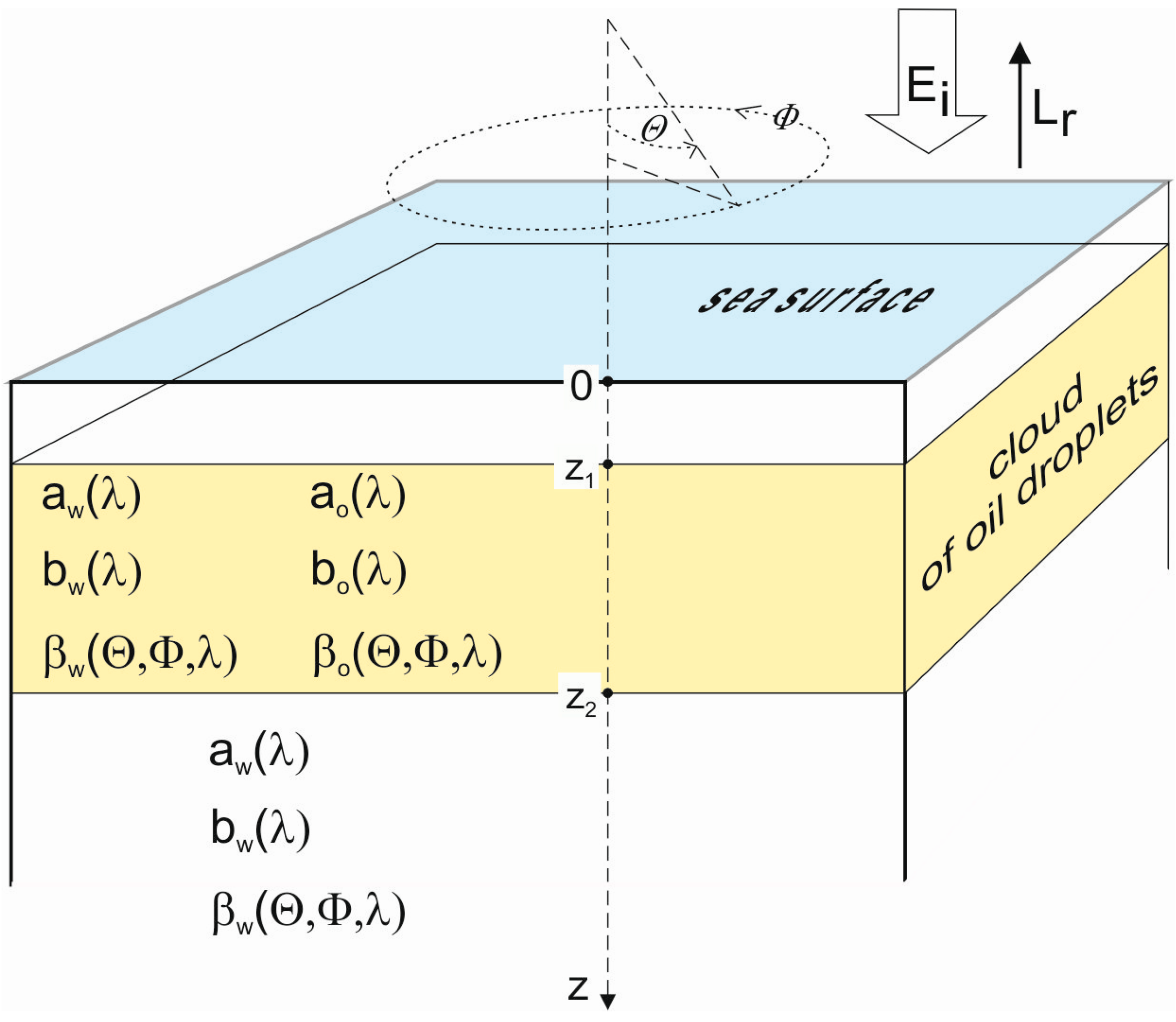
This paper presents a sample situation—the studied model includes selected parameters and functions for solar irradiation, IOPs of seawater, oil optical parameters, and oil droplet size distribution. It was assumed that the layer polluted by oil begins at a depth of z
1 = 1 m and ends at a depth of z
2 = 6 m (
Figure 1). A similar model was used by Otremba et al. [
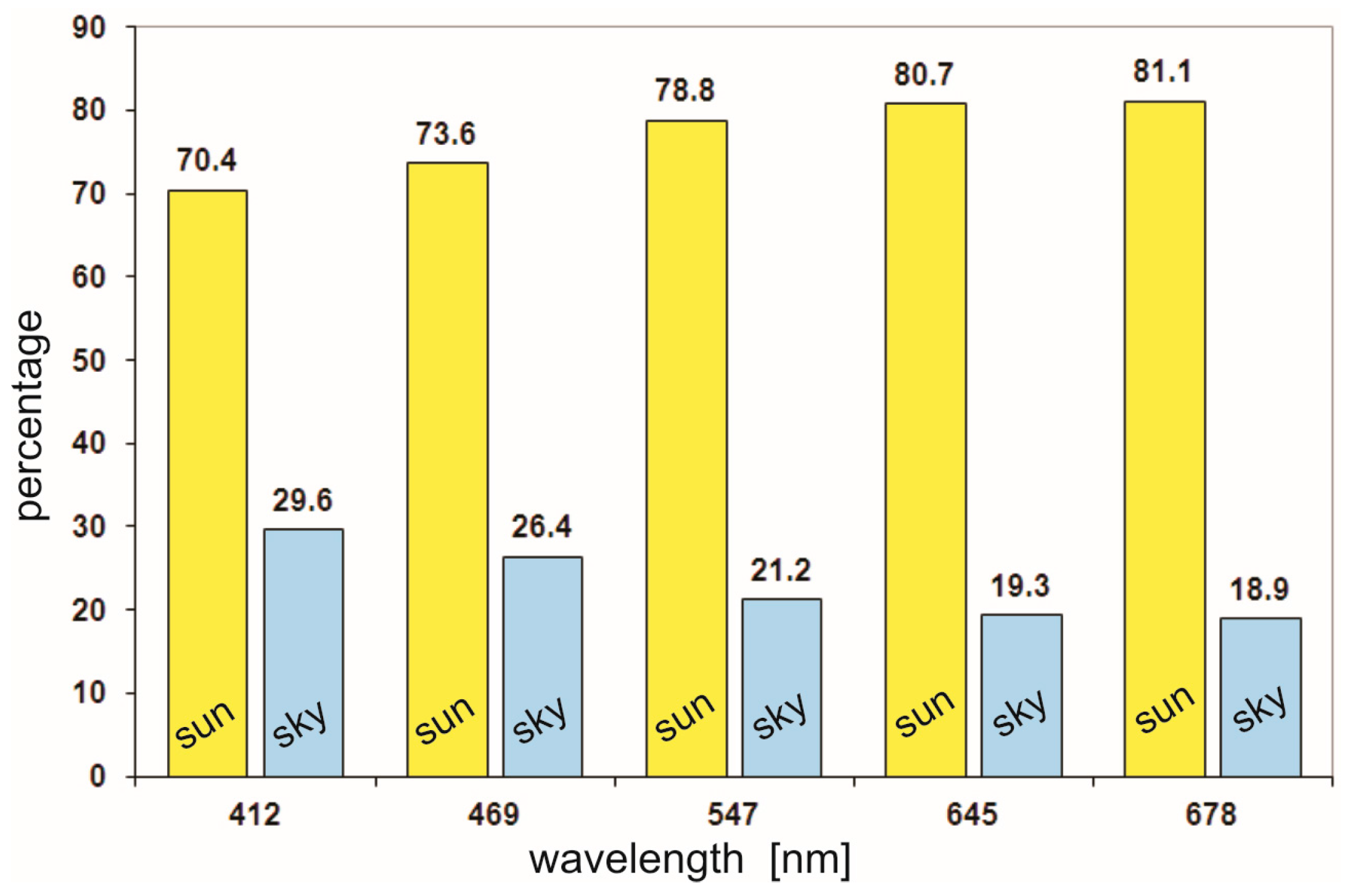
8], who adopted the lighting conditions shown in
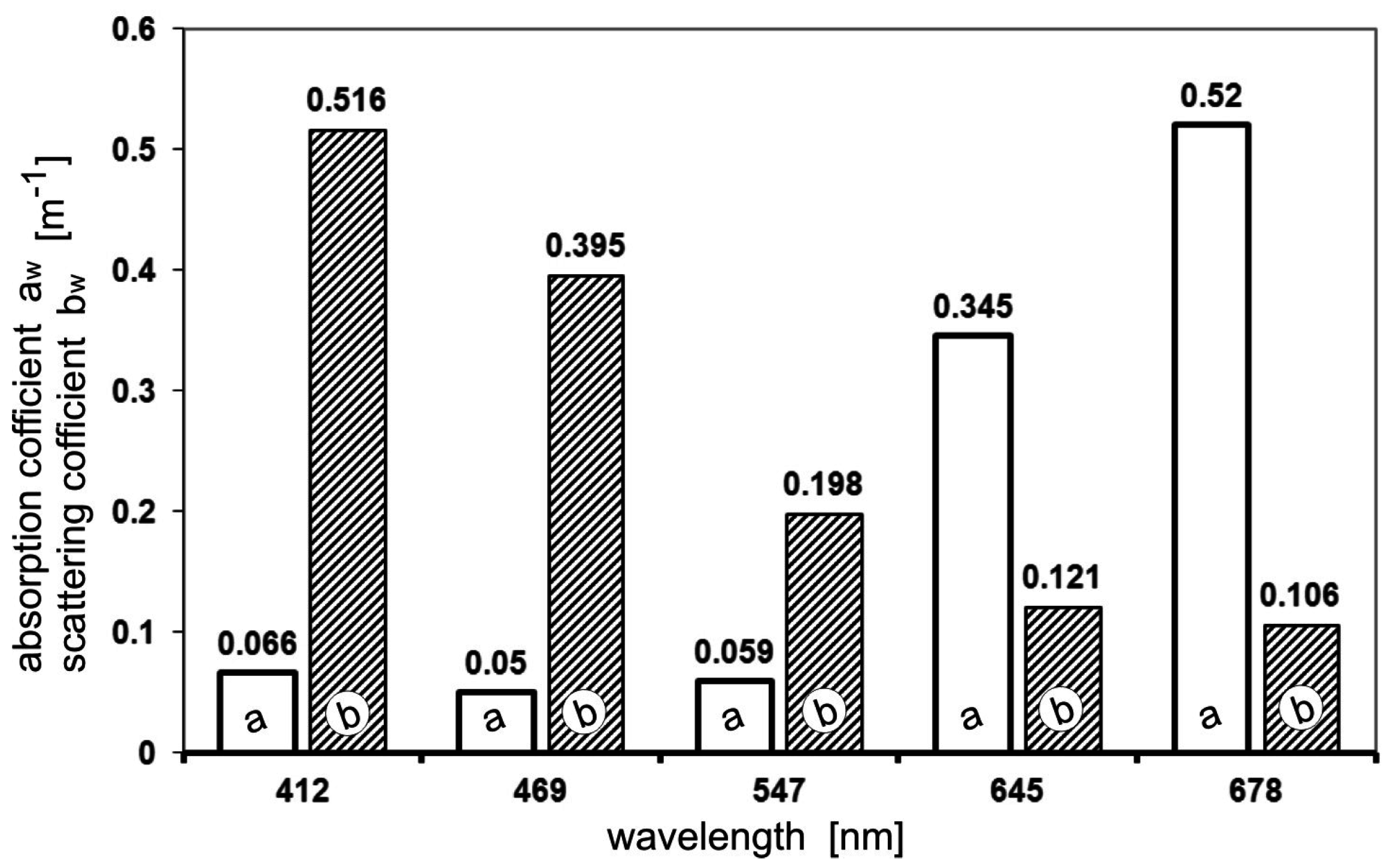
Figure 2, the IOPs of seawater in
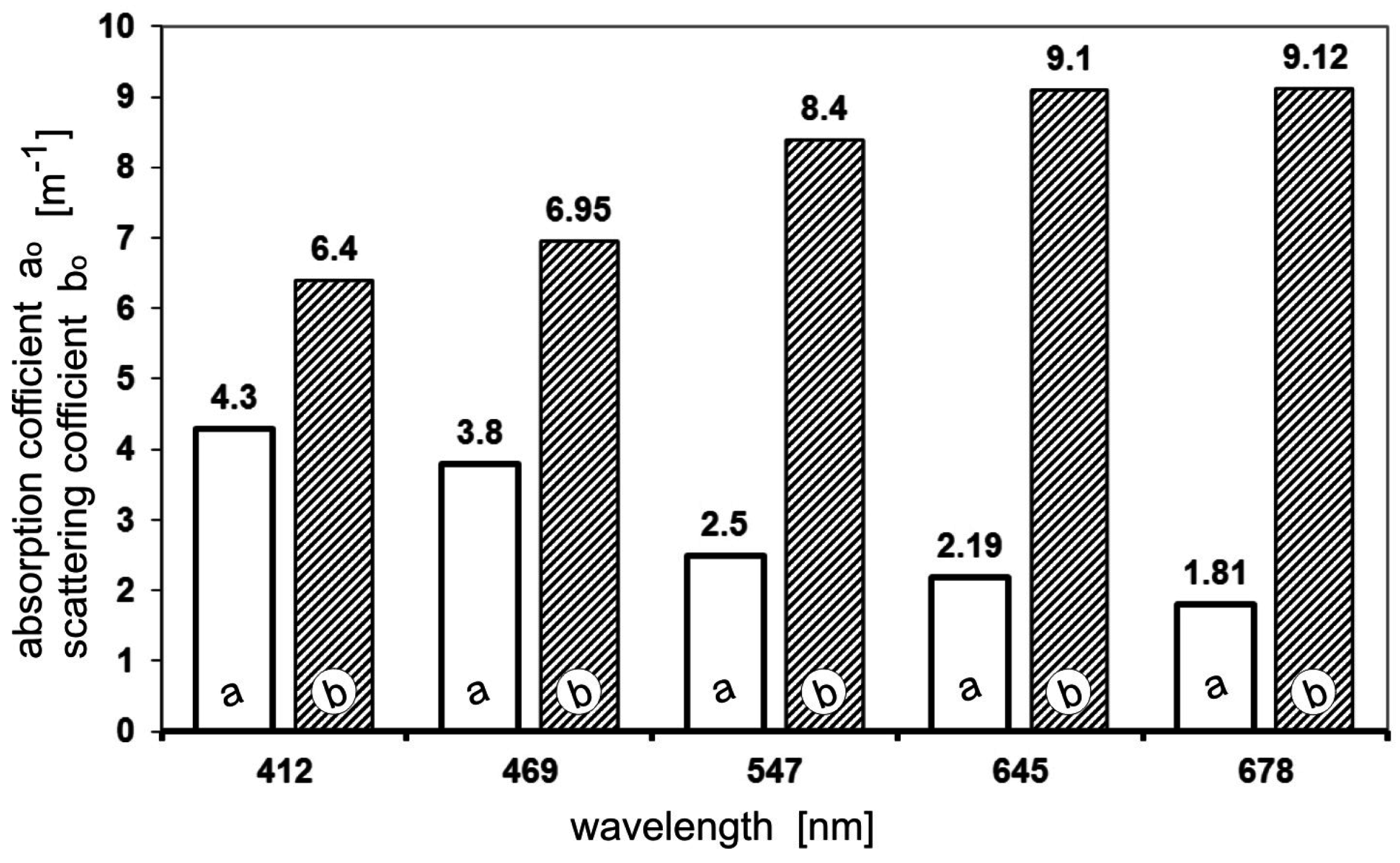
Figure 3, and the IOPs of an oil suspension in the “oil cloud” in
Figure 4. The model of solar light condition assumes some of the light coming directly from the sun (
Esun) is at a defined angle, and some is evenly from the whole sky (
Esky). The problem is similar to that described by Mobley et al. [
9], who analyzed the impact of the seabed on the above-water upward radiance. IOPs of water were estimated from MODIS remote sensing reflectance as a result of the SeaDAS processing software [
10], and IOPs of oil droplet suspensions were derived by Mie theory [
11,
12] using
Romashkino-type crude oil optical parameters [
13,
14,
15]. The fact that the model takes into account strictly defined characteristics constitutes its limitation to extend results to other weather and lighting conditions, as well as optical properties of oil and inherent optical properties of the seawater.
In the Monte Carlo simulation of the light transfer in an aquatic environment, the destinations of two billion virtual solar photons falling on the sea surface have been tracked. Photons returning vertically to the atmosphere were counted in the narrow conical sector (apex angle 8°—which means that the recorded radiance value was averaged in a solid angle of 0.0157 sr). Simulation of light propagation in the water environment using a traditional PC to achieve the accuracy of this study may take several weeks.
3. Results
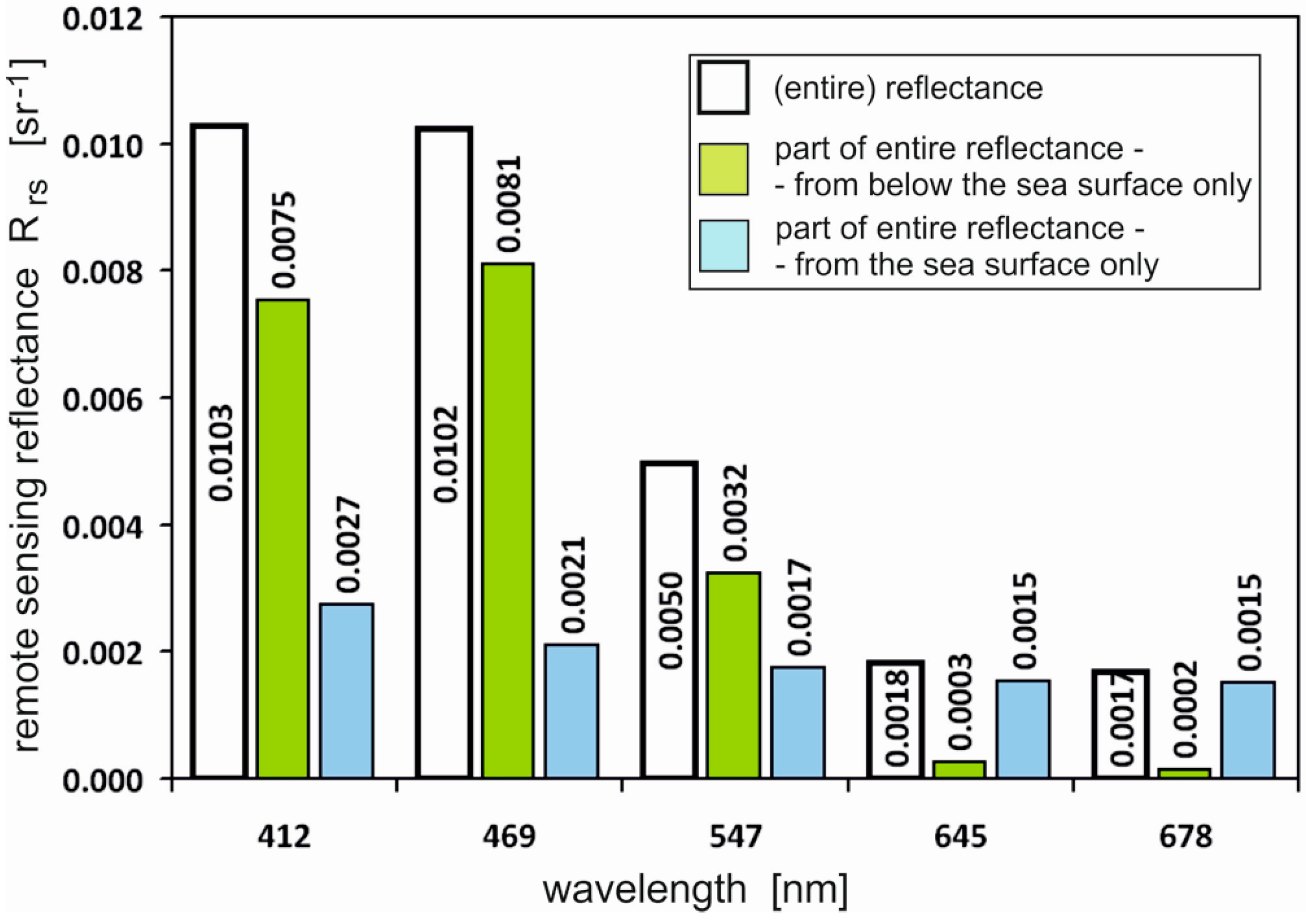
In
Figure 5, apart from reflectance that can detect above-water reflectance meter (white bars), part of the reflectance coming from the sea body is also shown (green bars). Such reflectance would be “visible” for an above-water detector in a theoretical situation with no bordering surface between water and atmosphere (which still reflects a part of the solar light). A similar reflectance would be registered by a detector with an upward radiance meter immersed below the sea surface. On the other hand, blue bars represent the component of reflectance coming from the sea surface only.
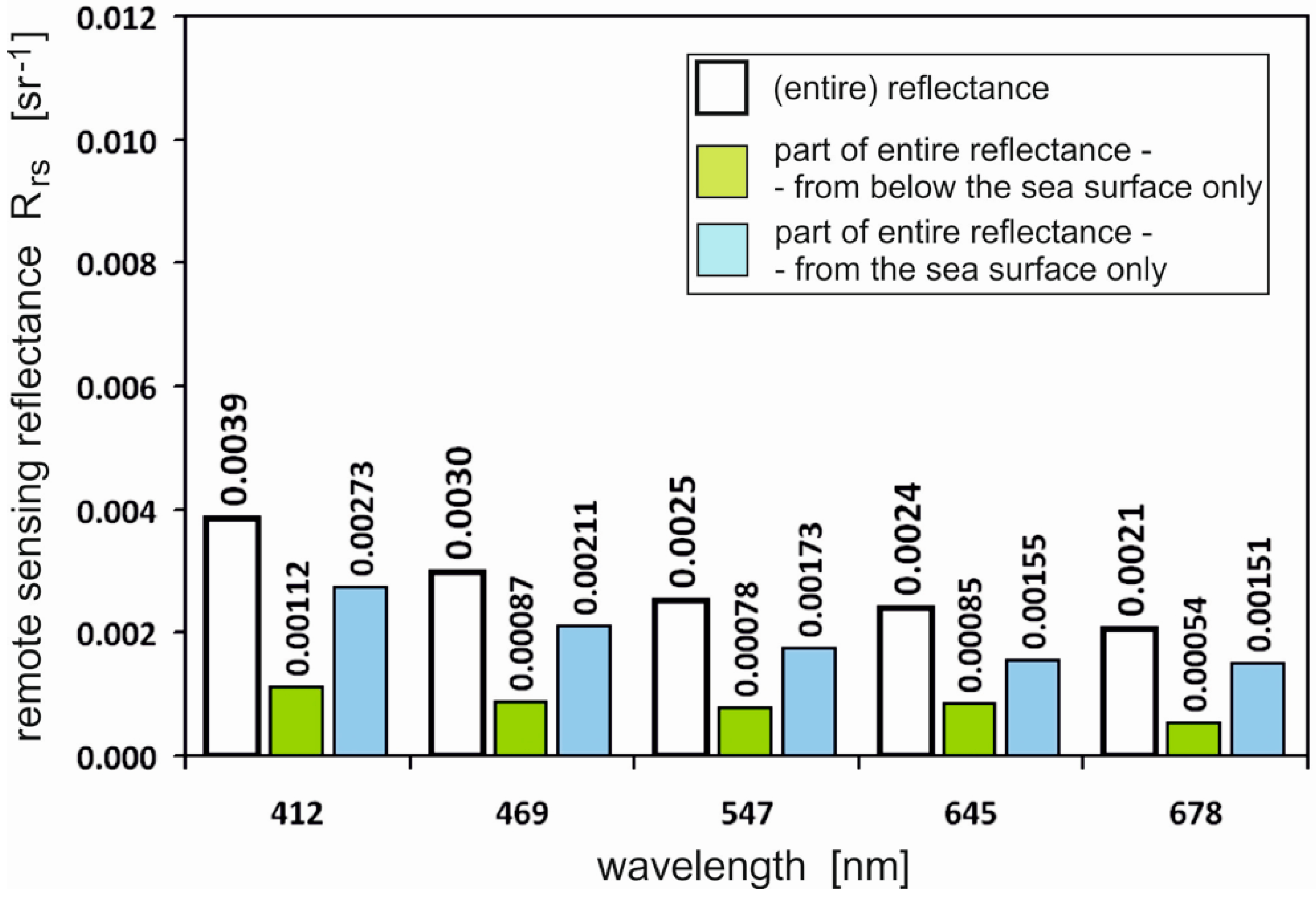
Figure 6 presents the results in a similar way to those presented in
Figure 5, although
Figure 6 presents a case with an oil-contaminated layer under the sea surface.
Of course, the reflectance component related to the sea surface is the same for the clean sea and a deeply-contaminated sea, because the wave slope distribution and light reflection/transmission through the water–atmosphere interface are not disturbed—in contrast to when the surface is covered by an oil film. Reflectance for the polluted sea decreases with the wavelength, and is less than for the clean sea.
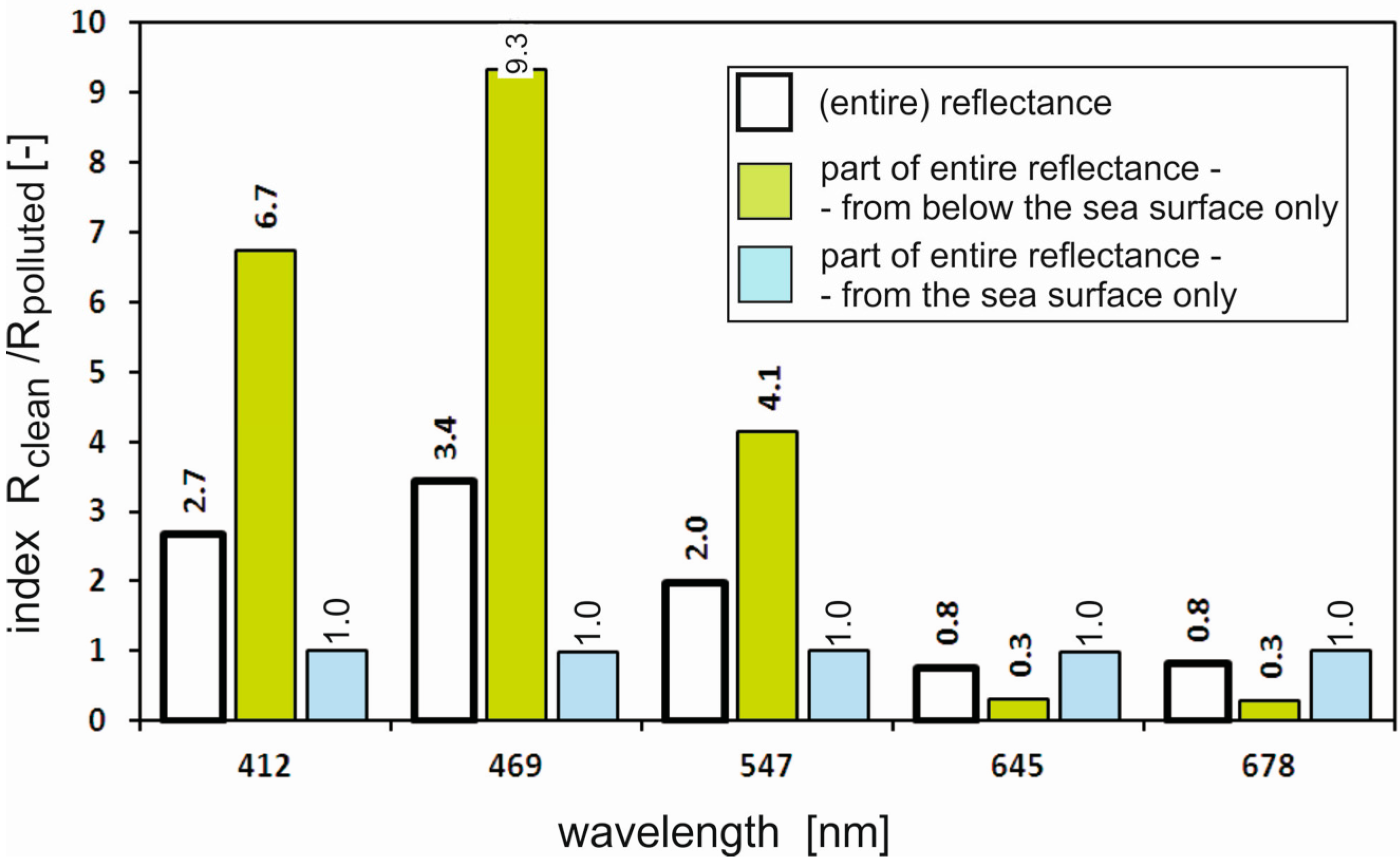
To express how reflectance for the clean sea is greater than for the polluted sea, the quotient of reflectance was calculated and is introduced in
Figure 7 as an index for various wavelengths. The highest value of the index occurs at the wavelength 469 nm, and is slightly lower at 412 nm and 547 nm. However, it is more than twice as much as it would be if the detector was placed below the water surface (green bars).
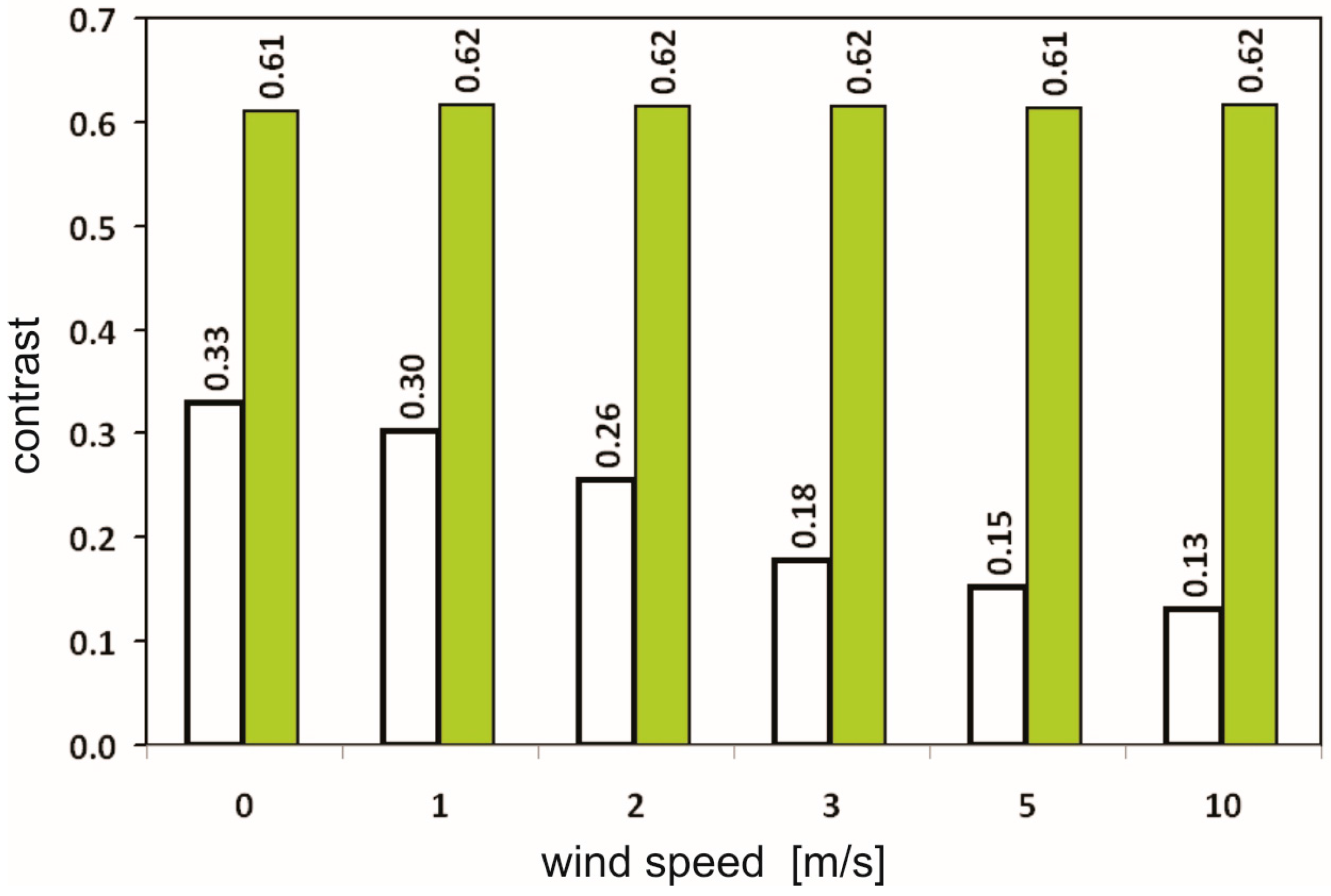
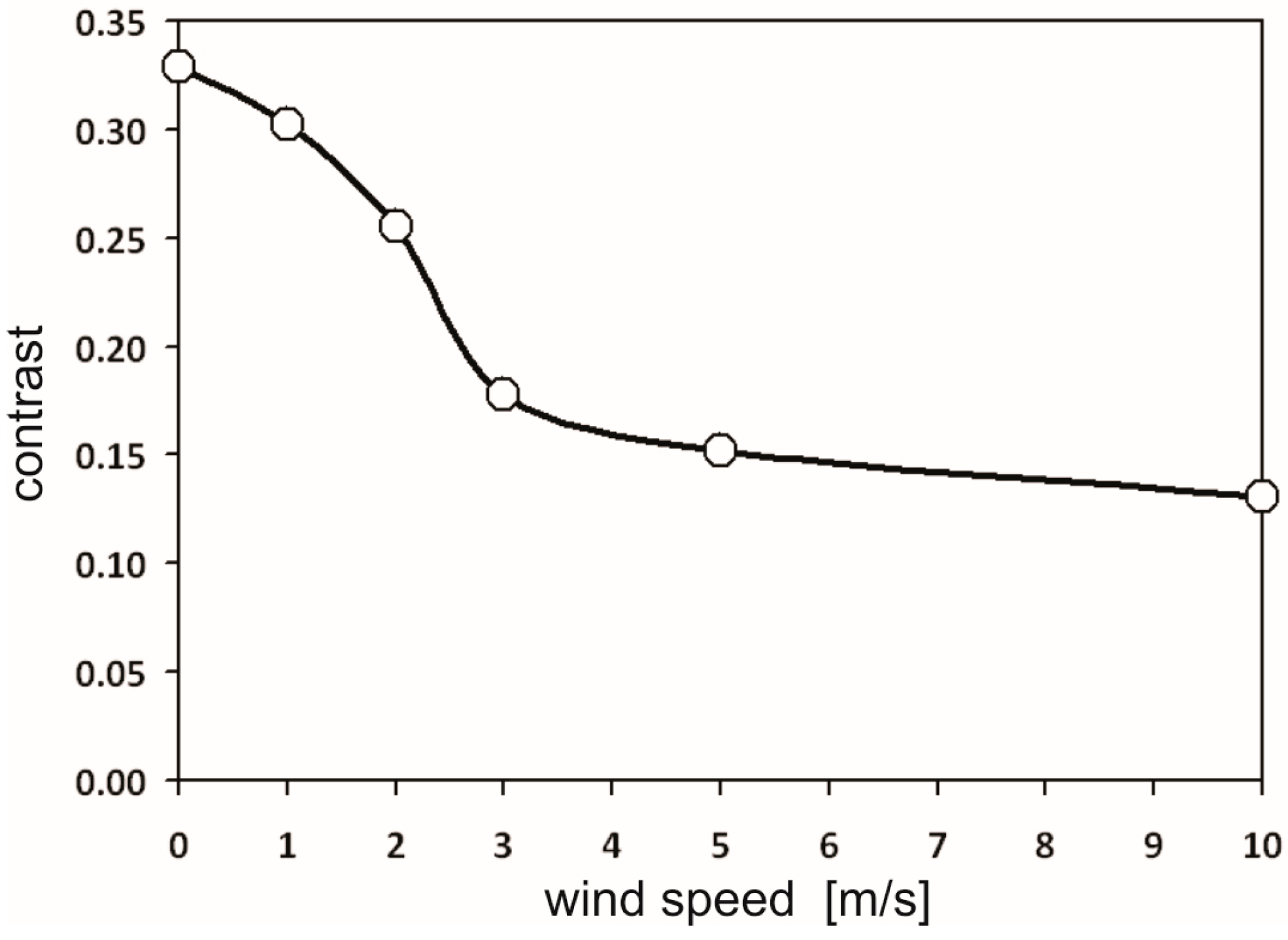
All of the above results relate to calm sea surfaces. If the surface is undulated, the detector also captures solar glints, and the observed reflectance increases. In
Figure 8, the contrast of a polluted area in relation to a clean area for various states of the sea surface is shown. The contrast declines rapidly with the degree of the sea surface undulation (expressed by wind speed [
8]) to only several m/s, because over 5 m/s, it appears to be almost stabilized (
Figure 9).
4. Discussion
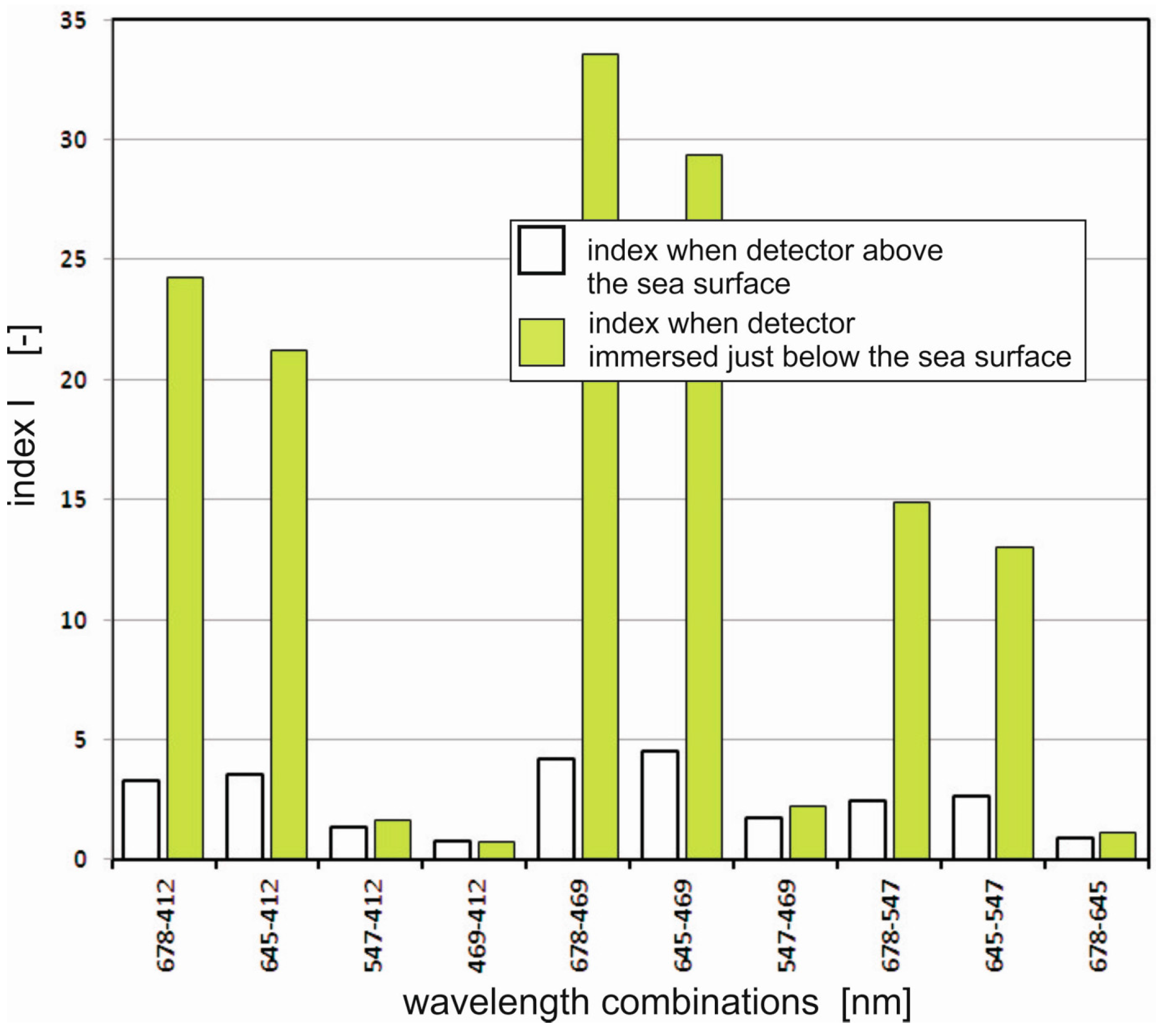
It is unclear at which wavelength the sea should be observed in order to detect a deeply polluted area. In analyzing the graph in
Figure 7, it is possible that in the vicinity of 469 nm, various other factors may decrease the visibility of an oil cloud in specific places. Therefore, the above-presented results were also analyzed in terms of two-wavelengths, setting the index-
I representing the ratio of the reflectance at two wavelengths, as is shown in
Figure 10. The index-
I was calculated according to Equation (4).
where
Rk,
Rn—reflectance used in every combination for the five wavelengths used, numbered by
n and
k (
k <
n).
The index-I achieves maximal value (4.5) at the wavelength combination 645–469 nm for an above-water detector and at combination 678–469 nm for a subsurface detector.
The results in this paper apply to a selected—but realistic—situation, because the oil used to calculate the IOPs of oil-in-water droplet clouds are characteristic for crude oils, fuels, and lubricant oil optical properties [
18]. Furthermore, the applied oil droplet size distribution is typical for oil-in-water emulsions made mechanically in the seawater [
19]. The oil concentration (10 ppm) applied in this study is significant, but relatively not too high (the permissible oil concentration in the vessel waste-waters cannot exceed 15 ppm).
The quantitative indeterminacy of these results in relation to possible fluctuations of IOPs of sea water has not yet been determined. Of course, in high-turbidity waters, deeply-immersed oil clouds will be invisible. On the other hand, in highly-transparent waters, oil clouds will be detectable up to a few dozen meters.
It is worth noting that the possible presence of a suspension of oil in sea water can interfere with the performance of remote sensing measurement processes in the sea (e.g., phytoplankton contents) using algorithms adjusted for pure (not oiled) sea area. It is very possible that signals indicating unnaturally high amounts of green plankton in the Gulf of Mexico reported in 2011 by Hu et al. [
20] were caused by the presence of oil dispersed in the water.
It is possible that an additional factor in improving the ability to remotely detect oil in the depths of the sea is the ability of oil droplets to polarize (or depolarize) light in the scattering process [
21]. It is not yet known to what extent this affects the polarization of light exiting an aquatic environment.
The research described in this paper applies to the detection capabilities of oil substances dispersed in the water column, and additionally when the water surface and the oil underwater cloud are separated by a clean water layer. In situations when the water layer polluted by oil is in contact with the surface, an oil film appears. The reflective properties of the surface then change, which must be included in the optical model of the defined aquatic environment.
Other remote (but not remote sensing) methods of oil detection in the water could also be considered. They will likely include fluorometric or acoustic detectors installed on remotely-controlled underwater vehicles [
22,
23].
5. Conclusions
Following the light field simulation in water contaminated with dispersed oil, it may be concluded that oil floating under the sea surface can be remotely sensed in the visual range of light, even in low concentrations (several ppm), by measuring the radiance reflectance at two wavelengths (470 and 645 nm). However, it should be taken into account that the results presented in this paper apply to only one form of oil-in-water—namely, a dispersed oil forming an underwater cloud. Additionally, it has been confirmed that a clean water layer (about a 1 m thickness) above a polluted layer does not prevent the perception of that pollution. Other variables were not analyzed, such as the thickness of both clean and polluted water layers, oil concentration, size distribution of oil droplet suspension, IOPs of the sea water, geometry of the solar lighting, and direction of the wind in relation to the plane of incidence of solar photons. Since the method used (a Monte Carlo simulation of the tracing of a large number of photons migrating in water) to predict the radiance reflectance is, unfortunately, time consuming, determination of the degree of impact of all of the above-listed factors on the effectiveness of the remote detection of underwater oil pollution does not seem to be realistic. However, it is planned to conduct tests to provide information on the impact of lighting conditions (from clear sky to overclouded) on the visibility of underwater oil. In addition, if other possible suggestions appear, they can be realized in the framework of the above-described method.