A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms
Abstract
:1. Introduction
2. Methodology
2.1. The Problem
2.2. Radiative Transfer Simulations
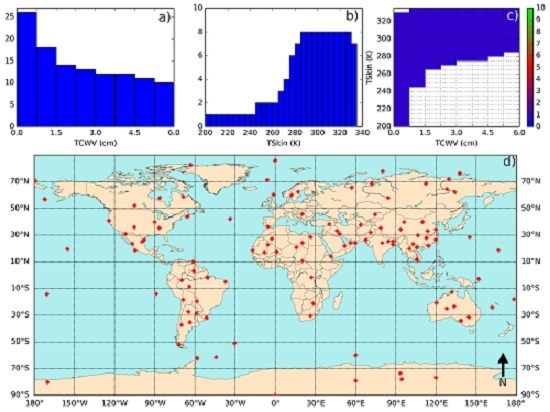
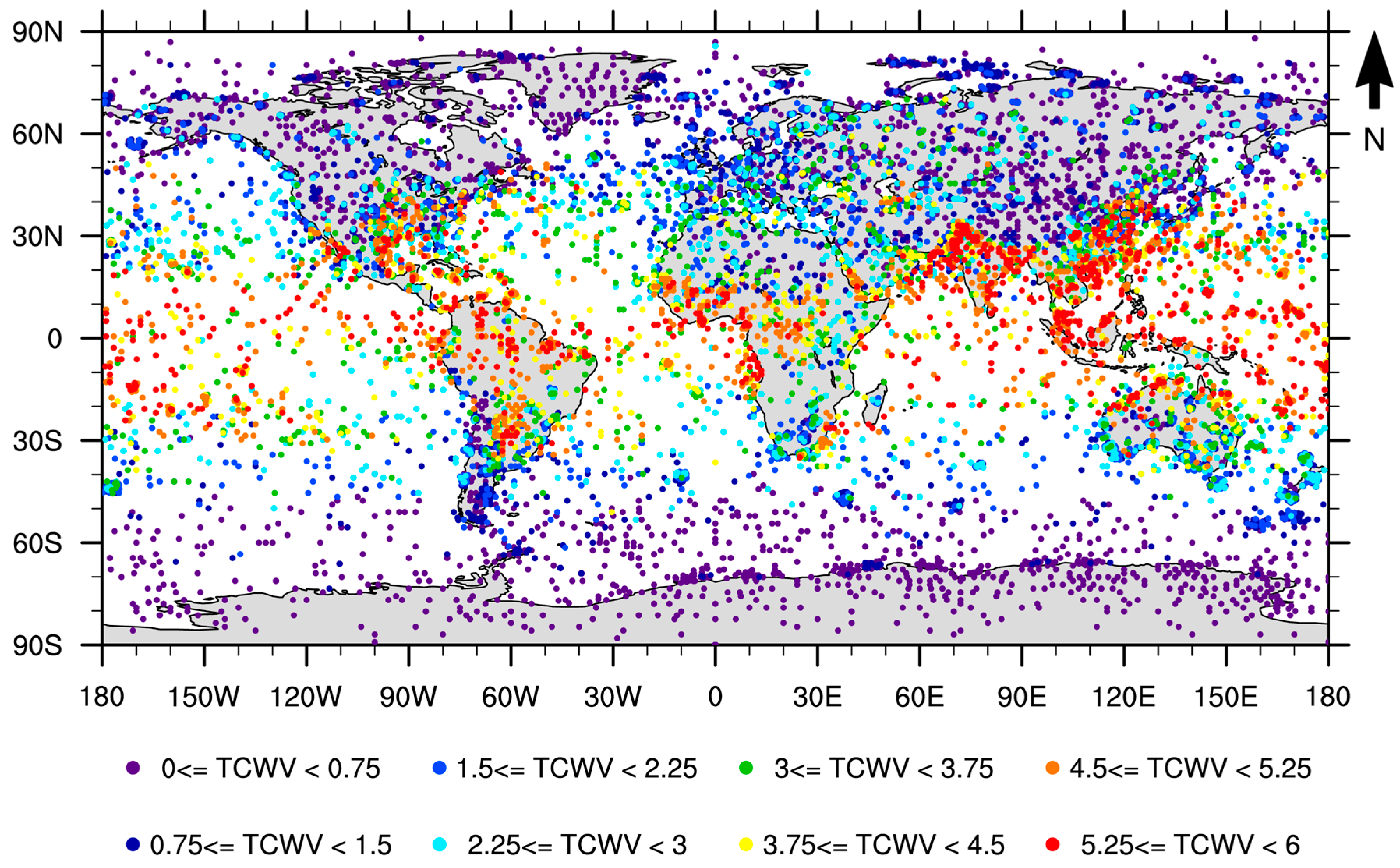
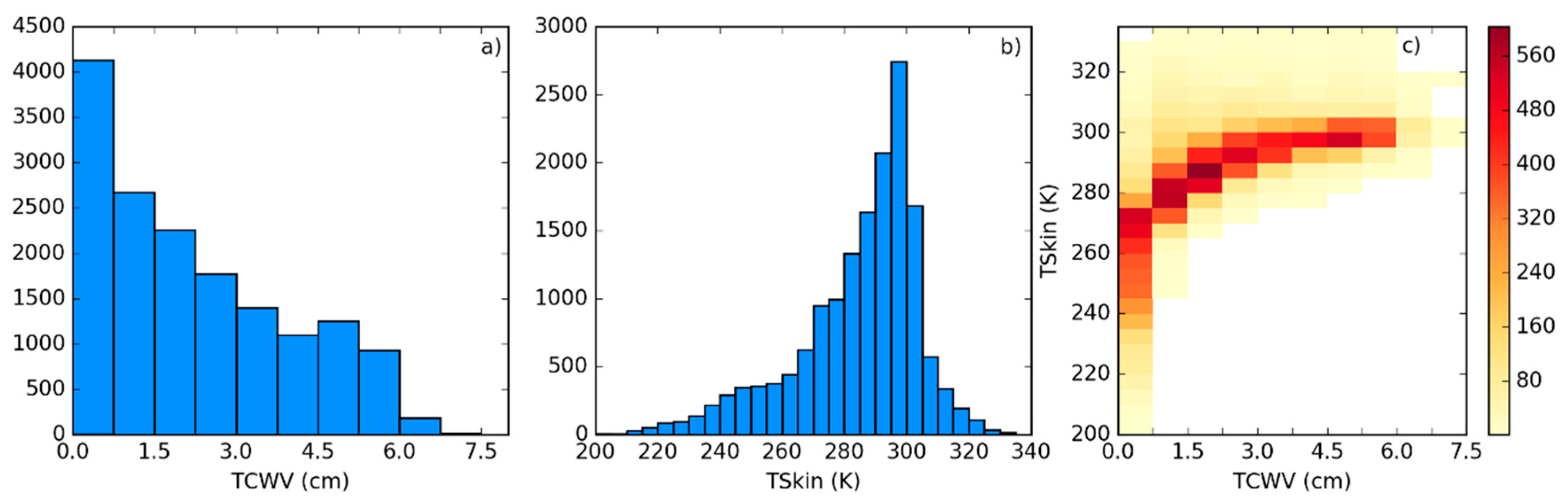
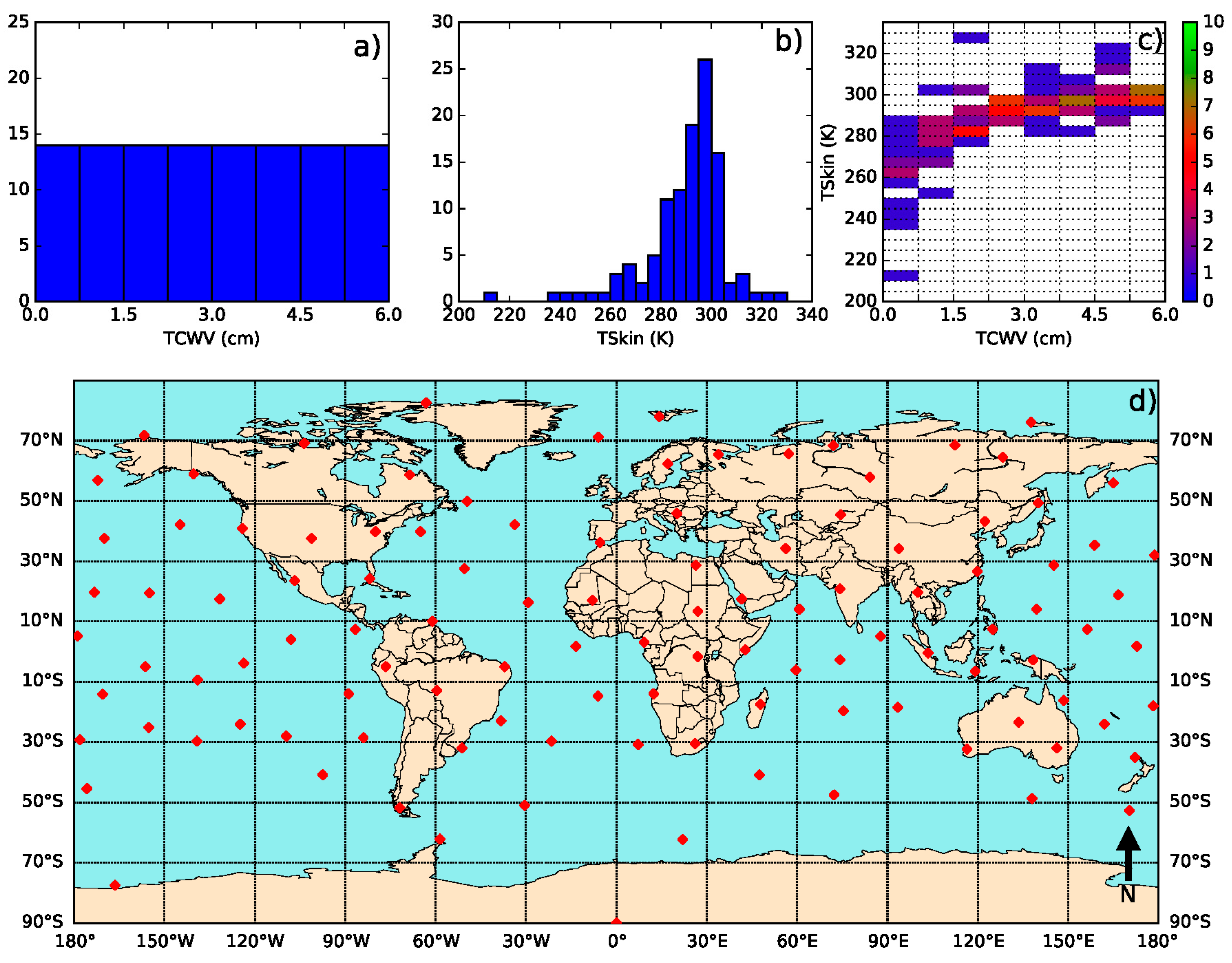
2.3. Characteristics of Atmospheric Profiles Relevant for Radiative Transfer in the TIR Window
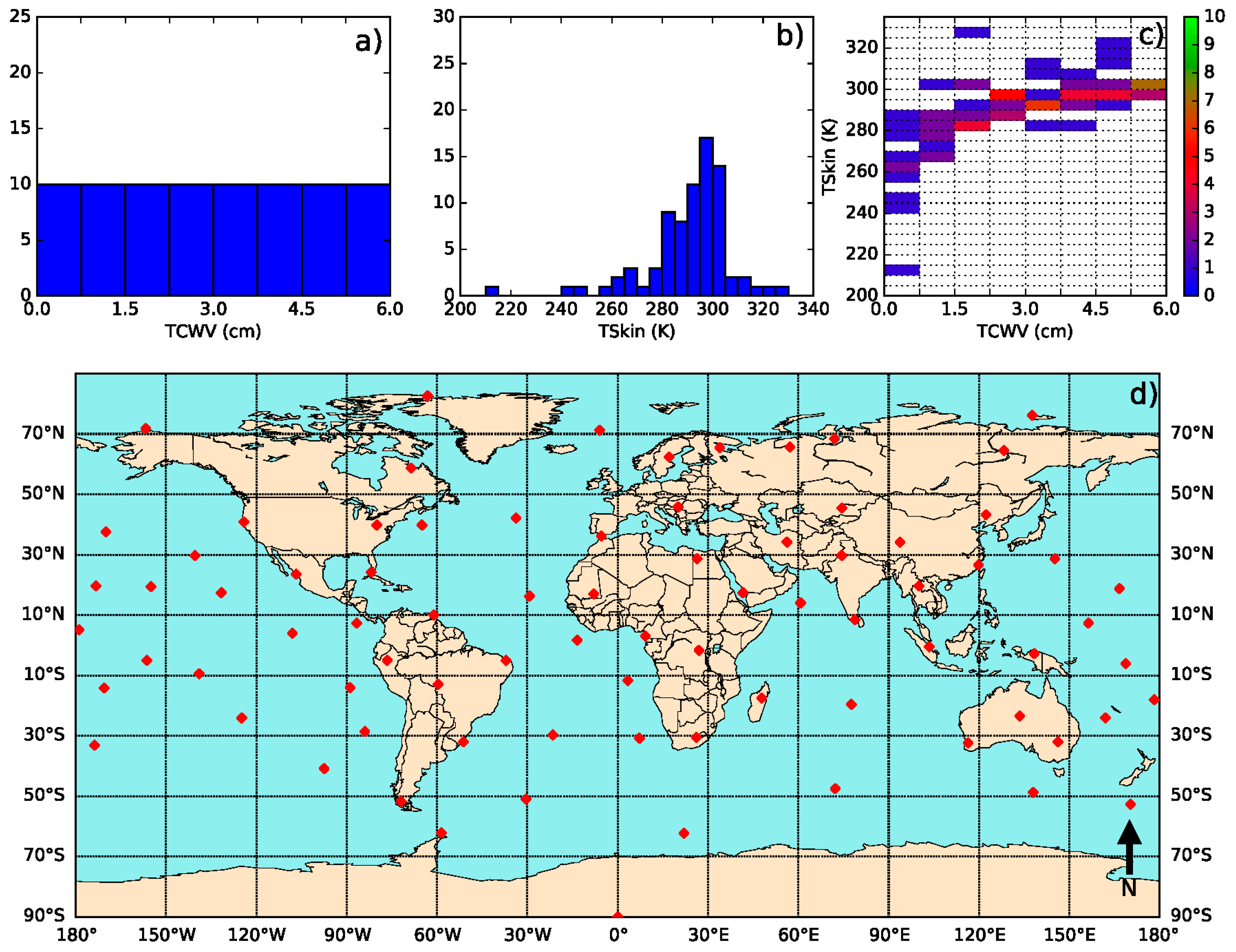
2.4. A Calibration Database
- (1)
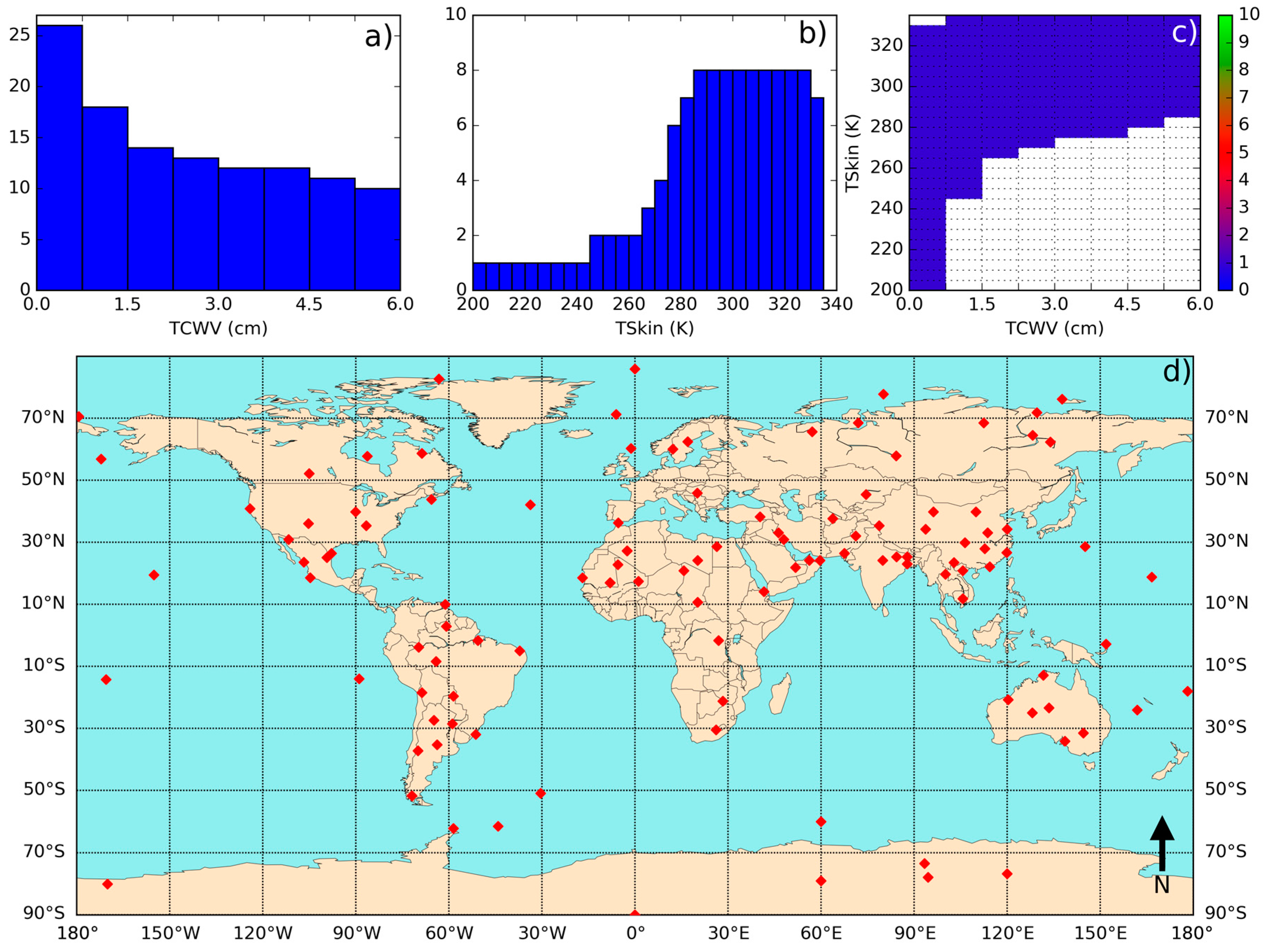
- Define classes of (from 200 K to 330 K in steps of 5 K) and (from 0 to 6 cm in classes of 0.75 cm—values greater than this should be treated with the coefficient corresponding to the last class).
- (2)
- Iterate in the SeeBor clear-sky profile database to fill each class in the phase space (as in Figure 2c) with one case each. When a new profile is selected, it is ensured that its great-circle distance to the already selected profiles is greater than an initial distance of 15 degrees, which guarantees a wide geographical coverage. After a sufficiently large number of tries (in this case 30,000), the distance criterion is relaxed in steps of minus 1 degree, until the whole phase space is filled.
- (3)
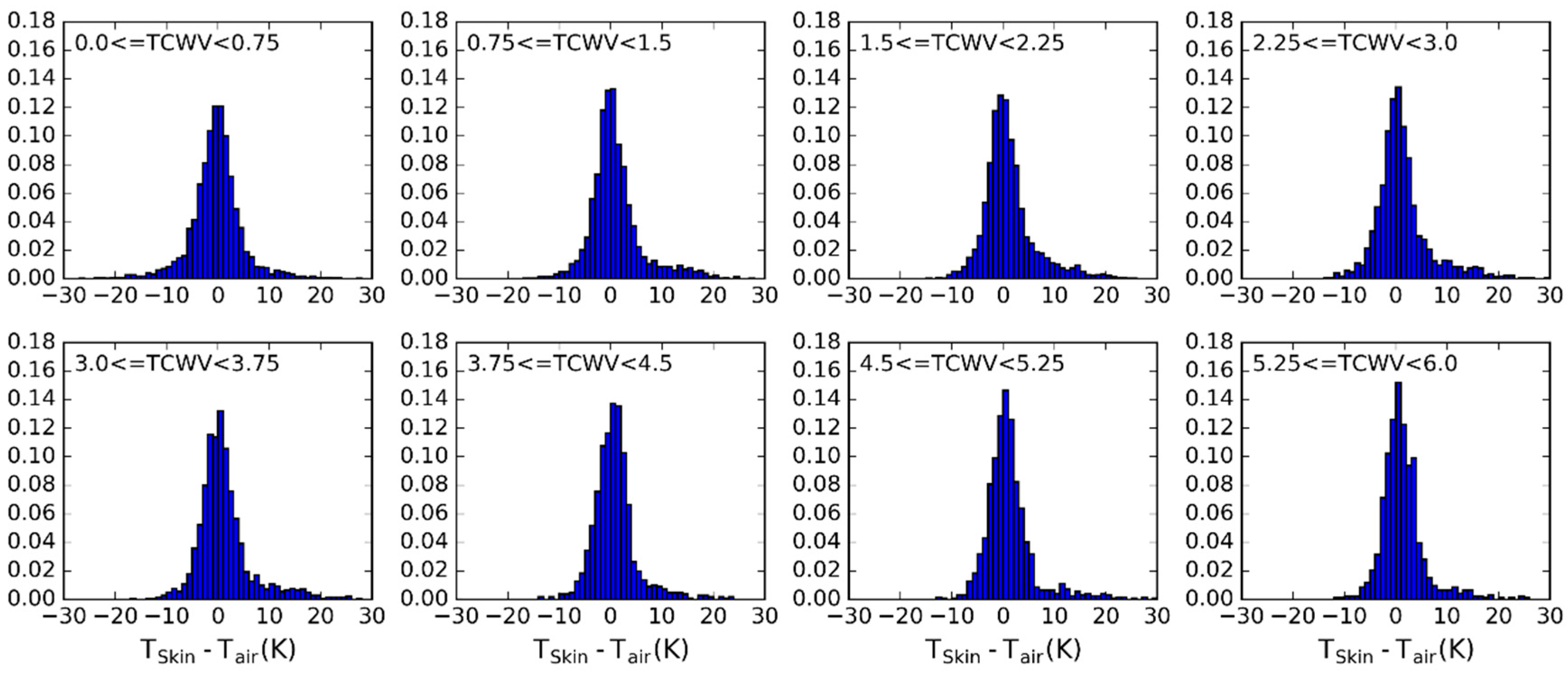
- For each of the previously selected profiles, assign a new based on the ranges of observed in Figure 3. The choice of the range of perturbations to apply is key to the performance of the chosen model and may depend on the region of interest. In the case of this work, a range of ±15 K around in steps of 5 K showed an overall good performance. As will be seen, large biases arise when non-physical cases are included or if the somewhat more extreme cases are not taken into account.
- (4)
- Each of these conditions may be sensed from angles ranging from 0 (nadir view) to 70° in steps of 2.5°. It is important to discretize the viewing geometry in this way because this is an intrinsically non-linear problem. The upper limit of the might be adapted for the sensor under analysis. Previous calibration exercises show that above this viewing angle limit the retrieval errors are generally too high, especially for moister atmospheres [15].
- (5)
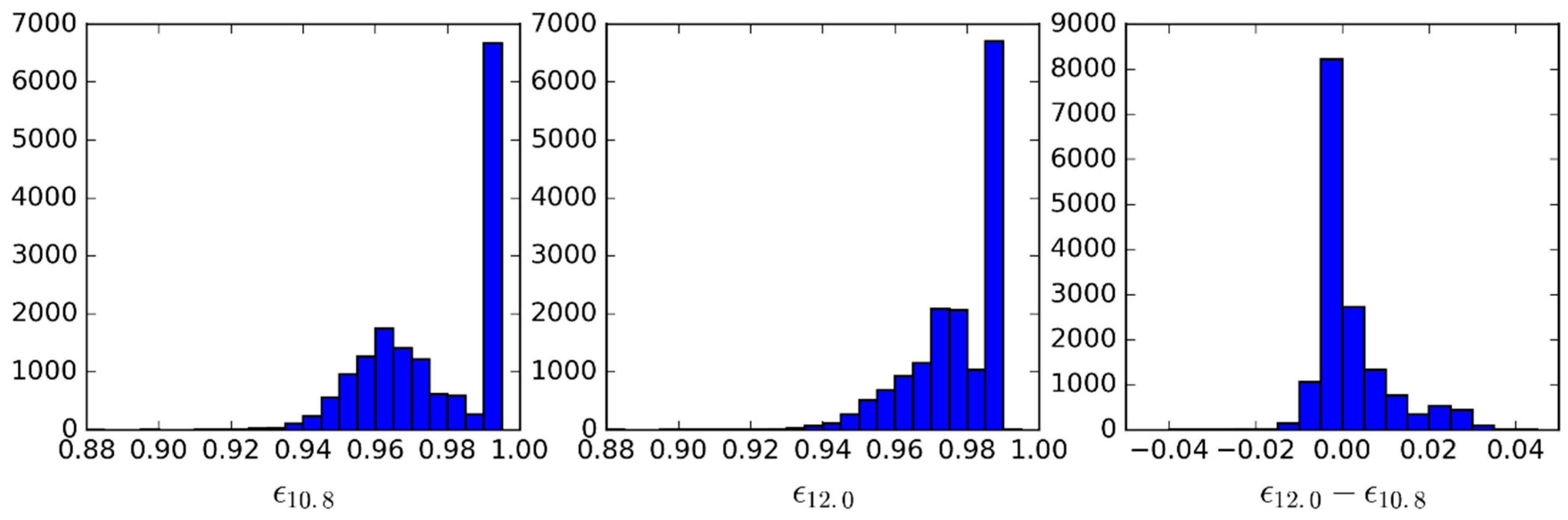
- For the emissivity, a range of possible values are attributed to each of the cases above: values of from 0.93 to 1.0 in steps of 0.01, and then, in the case of a GSW model, it is appropriate to prescribe departures from this value for : −0.015 to 0.035 in steps of 0.01 (excluding cases where ), as suggested by Figure 4.
3. Results
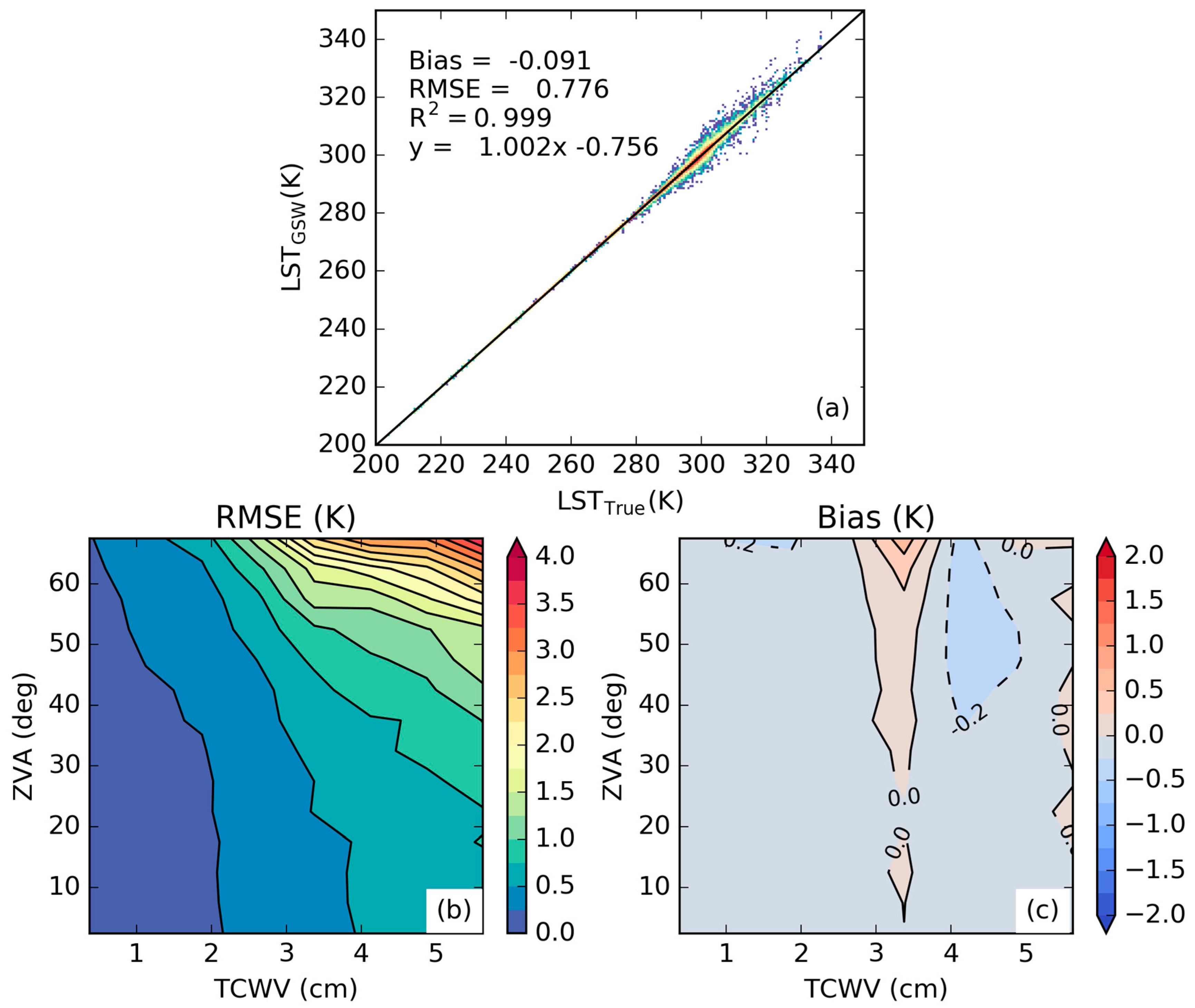
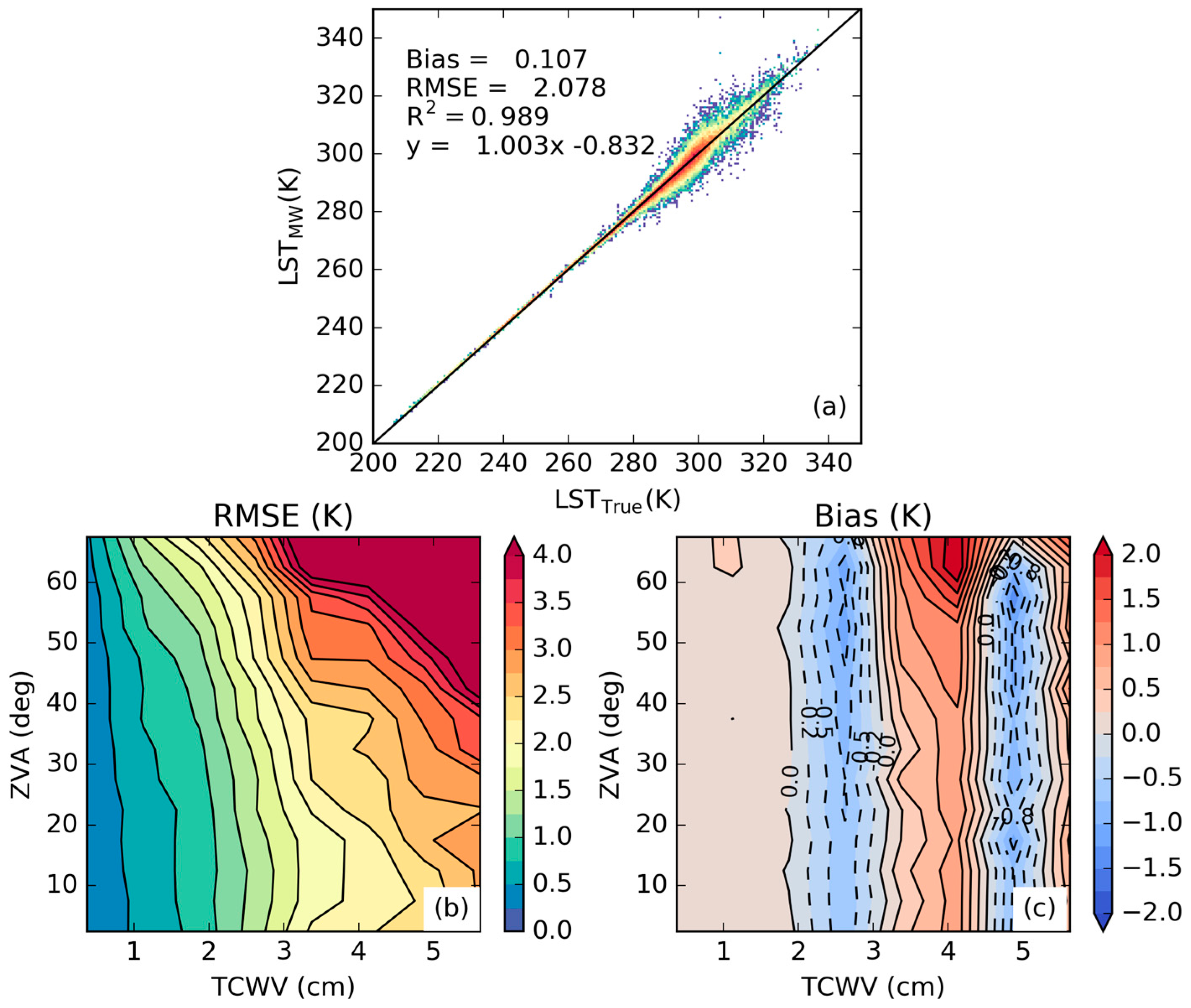
3.1. Error Statistics of the Proposed Calibration Database
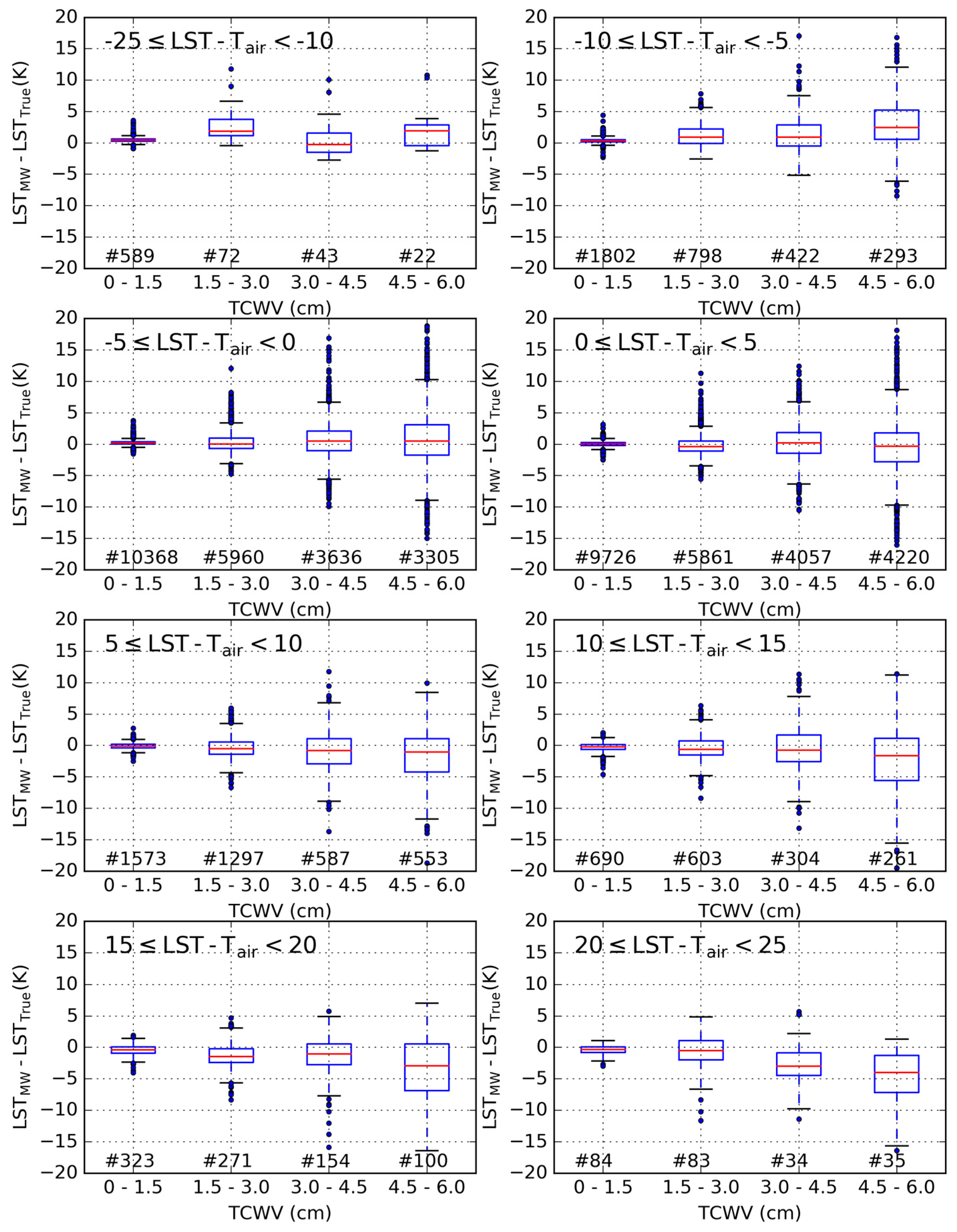
3.2. Sensitivity to the Distribution of Relevant Variables
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dirmeyer, P.A.; Cash, B.A.; Kinter, J.L.; Stan, C.; Jung, T.; Marx, L.; Towers, P.; Wedi, N.; Adams, J.M.; Altshuler, E.L.; et al. Evidence for enhanced land-atmosphere feedback in a warming climate. J. Hydrometeorol. 2012, 13, 981–995. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015, 6, 6443. [Google Scholar] [CrossRef] [PubMed]
- Kustas, W.P.; Norman, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Taylor, C.M.; Gounou, A.; Guichard, F.F.; Harris, P.P.; Ellis, R.J.; Couvreux, F.; De Kauwe, M. Frequency of sahelian storm initiation enhanced over mesoscale soil-moisture patterns. Nat. Geosci. 2011, 4, 430–433. [Google Scholar] [CrossRef]
- Trigo, I.F.; Viterbo, P. Clear-sky window channel radiances: A comparison between observations and the ECMWF model. J. Appl. Meteorol. 2003, 42, 1463–1479. [Google Scholar] [CrossRef]
- Trigo, I.F.; Boussetta, S.; Viterbo, P.; Balsamo, G.; Beljaars, A.; Sandu, I. Comparison of model land skin temperature with remotely sensed estimates and assessment of surface-atmosphere coupling. J. Geophys. Res. Atmos. 2015, 120, 12096–12111. [Google Scholar] [CrossRef]
- Wang, A.; Barlage, M.; Zeng, X.; Draper, C.S. Comparison of land skin temperature from a land model, remote sensing, and in situ measurement. J. Geophys. Res. Atmos. 2014, 119, 3093–3106. [Google Scholar] [CrossRef]
- Zheng, W.; Wei, H.; Wang, Z.; Zeng, X.; Meng, J.; Ek, M.; Mitchell, K.; Derber, J. Improvement of daytime land surface skin temperature over arid regions in the NCEP GFS model and its impact on satellite data assimilation. J. Geophys. Res. Atmos. 2012, 117, D06117. [Google Scholar] [CrossRef]
- Caparrini, F.; Castelli, F.; Entekhabi, D. Variational estimation of soil and vegetation turbulent transfer and heat flux parameters from sequences of multisensor imagery. Water Resour. Res. 2004, 40, 1–15. [Google Scholar] [CrossRef]
- English, S.J. The importance of accurate skin temperature in assimilating radiances from satellite sounding instruments. IEEE Trans. Geosci. Remote Sens. 2008, 46, 403–408. [Google Scholar] [CrossRef]
- Ghent, D.; Kaduk, J.; Remedios, J.; Ardö, J.; Balzter, H. Assimilation of land surface temperature into the land surface model JULES with an ensemble Kalman filter. J. Geophys. Res. 2010, 115, D19112. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Macedo, J.; Barroso, C.; Silva, R.; Perdigão, R. Land surface temperature from multiple geostationary satellites. Int. J. Remote Sens. 2013, 34, 3051–3068. [Google Scholar] [CrossRef]
- Sun, D.; Pinker, R.T. Estimation of land surface temperature from a geostationary operational environmental satellite (GOES-8). J. Geophys. Res. 2003, 108, 4326. [Google Scholar] [CrossRef]
- Duguay-Tetzlaff, A.; Bento, V.; Göttsche, F.; Stöckli, R.; Martins, J.; Trigo, I.; Olesen, F.; Bojanowski, J.; da Camara, C.; Kunz, H. Meteosat land surface temperature climate data record: Achievable accuracy and potential uncertainties. Remote Sens. 2015, 7, 13139–13156. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. 2003, 108, 4688. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C. Land surface temperature retrieval from thermal infrared data: An assessment in the context of the Surface Processes and Ecosystem Changes Through Response Analysis (SPECTRA) mission. J. Geophys. Res. D Atmos. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Bioucas-dias, J.M.; Göttsche, F. Quantifying the uncertainty of land surface temperature retrievals from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2010, 48, 523–534. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Mattar, C.; Durán-Alarcón, C.; Jiménez-Muñoz, J.C.; Santamaría-Artigas, A.; Olivera-Guerra, L.; Sobrino, J.A. Global atmospheric profiles from reanalysis information (GAPRI): A new database for earth surface temperature retrieval. Int. J. Remote Sens. 2015, 36, 5045–5060. [Google Scholar] [CrossRef]
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-de-Coca, F.; Carrer, D.; Freitas, S.C.; García-Haro, J.; et al. The satellite application facility for land surface analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- De La Taille, L.; Rota, S.; Hartley, C.; Stuhlmann, R. Meteosat third generation programme status. In Proceedings of the Annual EUMETSAT Meteorological Satellite Conference, Toulouse, France, 21–25 September 2015.
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Evaluation of split-window land surface temperature algorithms for generating climate data records. IEEE Trans. Geosci. Remote Sens. 2008, 46, 179–192. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An Introduction; Cambridge Univ. Press: Cambridge, UK, 2005. [Google Scholar]
- Crago, R.D.; Qualls, R.J. Use of land surface temperature to estimate surface energy fluxes: Contributions of Wilfried Brutsaert and collaborators. Water Resour. Res. 2014, 50, 3396–3408. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset (ASTER GED): Mapping earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Embury, O.; Merchant, C.J. Sampling uncertainty in gridded sea surface temperature products and Advanced Very High Resolution Radiometer (AVHRR) Global Area Coverage (GAC) data. Remote Sens. Environ. 2016, 177, 287–294. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. Proc. SPIE 1999, 3756, 348–353. [Google Scholar]
- Borbas, E.E.; Seemann, S.W.; Huang, H.L.; Li, J.; Menzel, W.P. Global profile training database for satellite regression retrievals with estimates of skin temperature and emissivity. In Proceedings of International TOVS Study Conference-XIV, Beijing, China, 25–31 May 2005.
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic: Dordrecht, The Netherlands, 1988; p. 666. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Hackensack, NV, USA, 2000; Volume 2. [Google Scholar]
- Maddy, E.S.; Member, A.; Barnet, C.D. Vertical resolution estimates in version 5 of AIRS operational retrievals. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2375–2384. [Google Scholar] [CrossRef]
- Martins, J.P.A.; Teixeira, J.; Soares, P.M.M.; Miranda, P.M.A.; Kahn, B.H.; Dang, V.T.; Irion, F.W.; Fetzer, E.J.; Fishbein, E. Infrared sounding of the trade-wind boundary layer: AIRS and the RICO experiment. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Yu, Y.; Tarpley, D.; Privette, J.L.; Goldberg, M.D.; Rama Varma Raja, M.K.; Vinnikov, K.Y.; Xu, H. Developing algorithm for operational GOES-R land surface temperature product. IEEE Trans. Geosci. Remote Sens. 2009, 47, 936–951. [Google Scholar]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. Error sources on the land surface temperature retrieved from thermal infrared single channel remote sensing data. Int. J. Remote Sens. 2006, 27, 999–1014. [Google Scholar] [CrossRef]
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]

| Database | Selection of Profiles | Number of Profiles | Prescribed Range (K) |
|---|---|---|---|
| Baseline: WTS_−15_15 | Full coverage of the LST/TCWV phase space | 116 | −15 to +15 |
| FLAT14_−15_15 | Flat distribution of TCWV with 14 profiles per TCWV class | 112 | −15 to +15 |
| FLAT10_−15_15 | Flat distribution of TCWV with 10 profiles per TCWV class | 80 | −15 to +15 |
| WTS_−10_10 | Full coverage of the LST/TCWV phase space | 116 | −10 to +10 |
| WTS_−10_15 | Full coverage of the LST/TCWV phase space | 116 | −10 to +15 |
| WTS_−10_20 | Full coverage of the LST/TCWV phase space | 116 | −10 to +20 |
| WTS_−15_20 | Full coverage of the LST/TCWV phase space | 116 | −15 to +20 |
| WTS_−20_15 | Full coverage of the LST/TCWV phase space | 116 | −20 to +15 |
| WTS_−20_20 | Full coverage of the LST/TCWV phase space | 116 | −20 to +20 |
| WTS_−20_25 | Full coverage of the LST/TCWV phase space | 116 | −20 to +25 |
| WTS_−25_25 | Full coverage of the LST/TCWV phase space | 116 | −25 to +25 |
| Database | Bias (K) | RMSE (K) | Bias Stdev (K) | RMSE Stdev (K) |
|---|---|---|---|---|
| Baseline: WTS_−15_15 | −0.09 | 0.78 | 0.14 | 0.67 |
| FLAT14_−15_15 | −0.12 | 0.81 | 0.38 | 0.70 |
| FLAT10_−15_15 | −0.11 | 0.82 | 0.32 | 0.72 |
| WTS_−10_10 | 0.05 | 0.74 | 0.26 | 0.64 |
| WTS_−10_15 | 0.07 | 0.76 | 0.34 | 0.69 |
| WTS_−10_20 | 0.09 | 0.81 | 0.41 | 0.73 |
| WTS_−15_20 | −0.02 | 0.76 | 0.21 | 0.67 |
| WTS_−20_15 | −0.11 | 0.79 | 0.14 | 0.68 |
| WTS_−20_20 | −0.12 | 0.78 | 0.14 | 0.68 |
| WTS_−20_25 | −0.11 | 0.78 | 0.15 | 0.68 |
| WTS_−25_25 | −0.25 | 0.87 | 0.22 | 0.73 |
| Database | Bias (K) | RMSE (K) | Bias Stdev (K) | RMSE Stdev (K) |
|---|---|---|---|---|
| Baseline: WTS_−15_15 | 0.09 | 2.02 | 0.71 | 1.63 |
| FLAT14_−15_15 | 0.11 | 2.08 | 0.73 | 1.42 |
| FLAT10_−15_15 | −0.04 | 2.05 | 0.69 | 1.38 |
| WTS_−10_10 | 0.55 | 1.97 | 0.70 | 1.35 |
| WTS_−10_15 | 0.76 | 2.19 | 0.92 | 1.54 |
| WTS_−10_20 | 0.89 | 2.39 | 1.09 | 1.72 |
| WTS_−15_20 | 0.43 | 2.28 | 0.83 | 1.69 |
| WTS_−20_15 | −0.13 | 2.23 | 0.71 | 1.67 |
| WTS_−20_20 | 0.04 | 2.34 | 0.76 | 1.68 |
| WTS_−20_25 | 0.16 | 2.46 | 0.83 | 1.89 |
| WTS_−25_25 | −0.28 | 2.67 | 0.89 | 2.07 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, J.P.A.; Trigo, I.F.; Bento, V.A.; Da Camara, C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sens. 2016, 8, 808. https://doi.org/10.3390/rs8100808
Martins JPA, Trigo IF, Bento VA, Da Camara C. A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sensing. 2016; 8(10):808. https://doi.org/10.3390/rs8100808
Chicago/Turabian StyleMartins, João P. A., Isabel F. Trigo, Virgílio A. Bento, and Carlos Da Camara. 2016. "A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms" Remote Sensing 8, no. 10: 808. https://doi.org/10.3390/rs8100808
APA StyleMartins, J. P. A., Trigo, I. F., Bento, V. A., & Da Camara, C. (2016). A Physically Constrained Calibration Database for Land Surface Temperature Using Infrared Retrieval Algorithms. Remote Sensing, 8(10), 808. https://doi.org/10.3390/rs8100808