Modeling and Mapping Agroforestry Aboveground Biomass in the Brazilian Amazon Using Airborne Lidar Data
Abstract
:1. Introduction
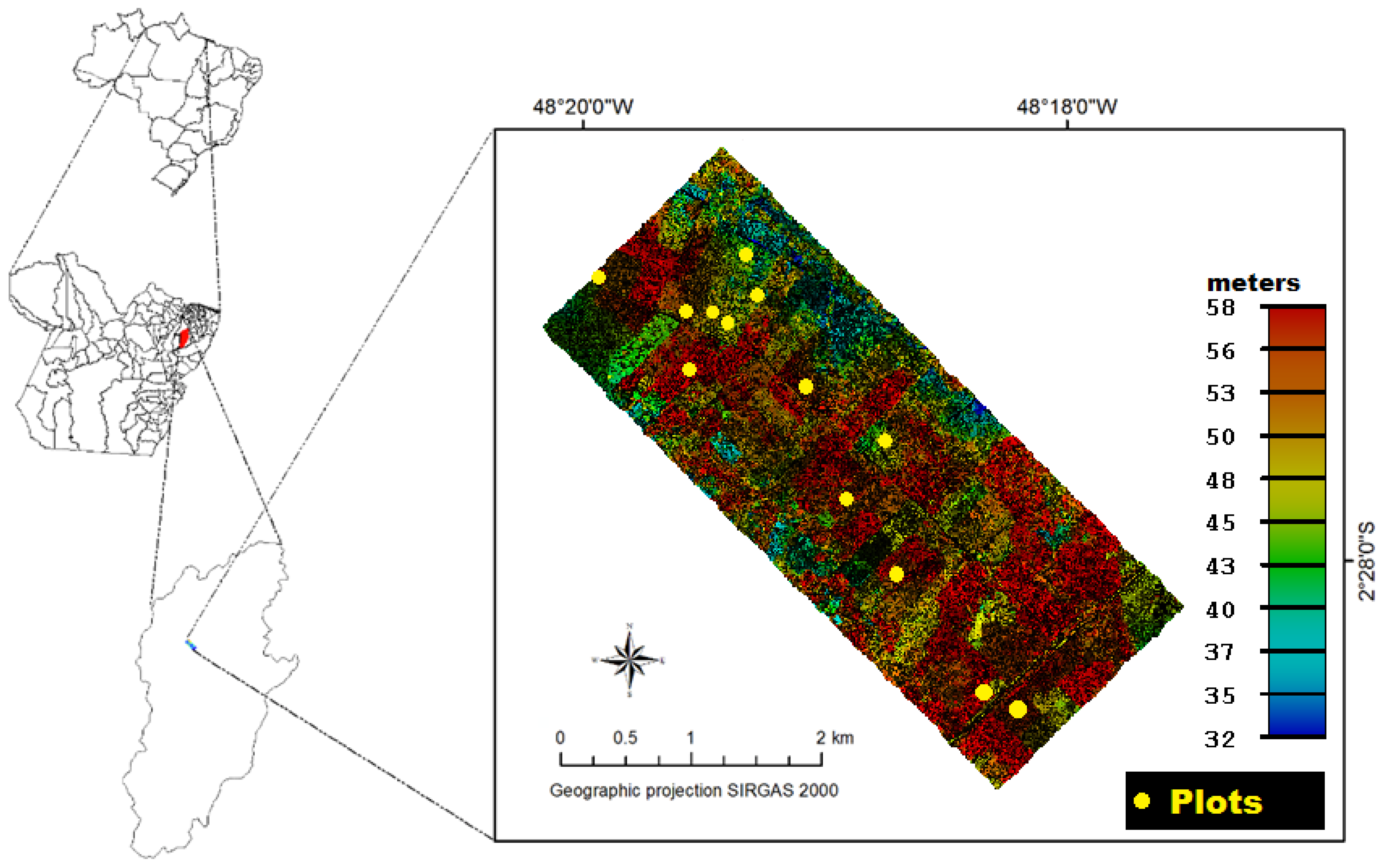
2. Study Area
3. Methods
3.1. Field Data Collection and AGB Estimation
| Common Name | Scientific Name | Tree Count | ρ (g/cm3) | Type |
|---|---|---|---|---|
| Acai | Euterpe oleracea | 287 | 0.41 | Palm |
| Ameixa (Tallow plum) | Ximenia americana | 108 | 0.64 | Other |
| Andiroba | Carapa guianensis | 7 | 0.57 | Other |
| Cacau (Cocoa) | Theobroma glaucum | 408 | 0.53 | Other |
| Castanha dopara (Brazil nut) | Bertholletia excelsa | 4 | 0.64 | Other |
| Cupuacu | Theobroma grandiflorum | 72 | 0.53 | Other |
| Dende (American oil palm) | Elaeis oleifera | 13 | 0.41 | Palm |
| Embauba | Cecropia ficifolia | 5 | 0.27 | Other |
| Freijo cinza | Cordia goeldiana | 1 | 0.50 | Other |
| Goiaba (Guava) | Myrciaria floribunda | 6 | 0.77 | Other |
| Guariuba | Clarisia racemosa | 5 | 0.59 | Other |
| Ipe | Tabebuia chrysotricha | 34 | 0.64 | Other |
| Ipe rosa | Tabebuia roseo-alba | 2 | 0.52 | Other |
| Mogno (Mahogany) | Swietenia macrophylla | 11 | 0.51 | Other |
| Molongo | Ambelania acida | 2 | 0.52 | Other |
| Murta | Strychnos subcordata | 1 | 0.54 | Other |
| Paliteira | Clitoria fairchildiana | 2 | 0.64 | Other |
| Parica | Schizolobium amazonicum | 2 | 0.49 | Other |
| Pelo de Cutia | Banara guianensis | 24 | 0.61 | Other |
| Seringa (Rubber) | Hevea brasiliensis | 35 | 0.49 | Other |
| Tamanqueira | Zanthoxylum rhoifolium | 1 | 0.49 | Other |
| Teca (Teak) | Tectona grandis | 143 | 0.64 | Other |
| Plot ID | Species (Tree Count) | Type | AGB (Mg/ha) | H (m) | BA (m2/ha) | (g/cm3) |
|---|---|---|---|---|---|---|
| 1 | Acai (90), Cacau (95) | Polyculture | 46.0 | 6.8 | 18.9 | 0.44 |
| 3 | Cacau (59), Ipe (29), Parica (2) | Polyculture | 78.0 | 8.6 | 17.8 | 0.58 |
| 5 | Cacau (50), Seringa (35), other (2) | Polyculture | 107.7 | 9.6 | 21.1 | 0.49 |
| 7 | Cacau (51), Andiroba (7), Ipe Rosa (2), Molongo (2), Paliteira (2), Cupuacu (1) | Polyculture | 159.4 | 7.4 | 23.3 | 0.56 |
| 8 | Acai (69), Cacau (63), Cupuacu (25) | Polyculture | 124.3 | 8.0 | 25.6 | 0.57 |
| 9 | Teca (30) | Monoculture | 178.4 | 18.9 | 21.1 | 0.64 |
| 10 | Teca (113) | Monoculture | 255.5 | 17.7 | 31.1 | 0.64 |
| 11 | Dende (13) | Monoculture | 219.8 | 11.2 | 103.3 | 0.41 |
| 12 | Cacau (45), IPE (3) | Polyculture | 13.1 | 3.9 | 6.7 | 0.52 |
| 13 | Acai (70), Pelo de Cutia (23), Ameixa (14), Guariuba (5), Goiaba (2), other (2) | Polyculture | 41.7 | 7.5 | 11.1 | 0.56 |
| 14 | Ameixa (94), Acai (54), Embauba (4), Goiaba (4), other(1) | Polyculture | 105.1 | 9.2 | 22.2 | 0.61 |
| 15 | Cupuacu (46) | Monoculture | 28.1 | 4.5 | 15.6 | 0.53 |
| 16 | Cacau (45), Mogno (5), Ipe (2) | Polyculture | 10.6 | 3.5 | 5.6 | 0.53 |
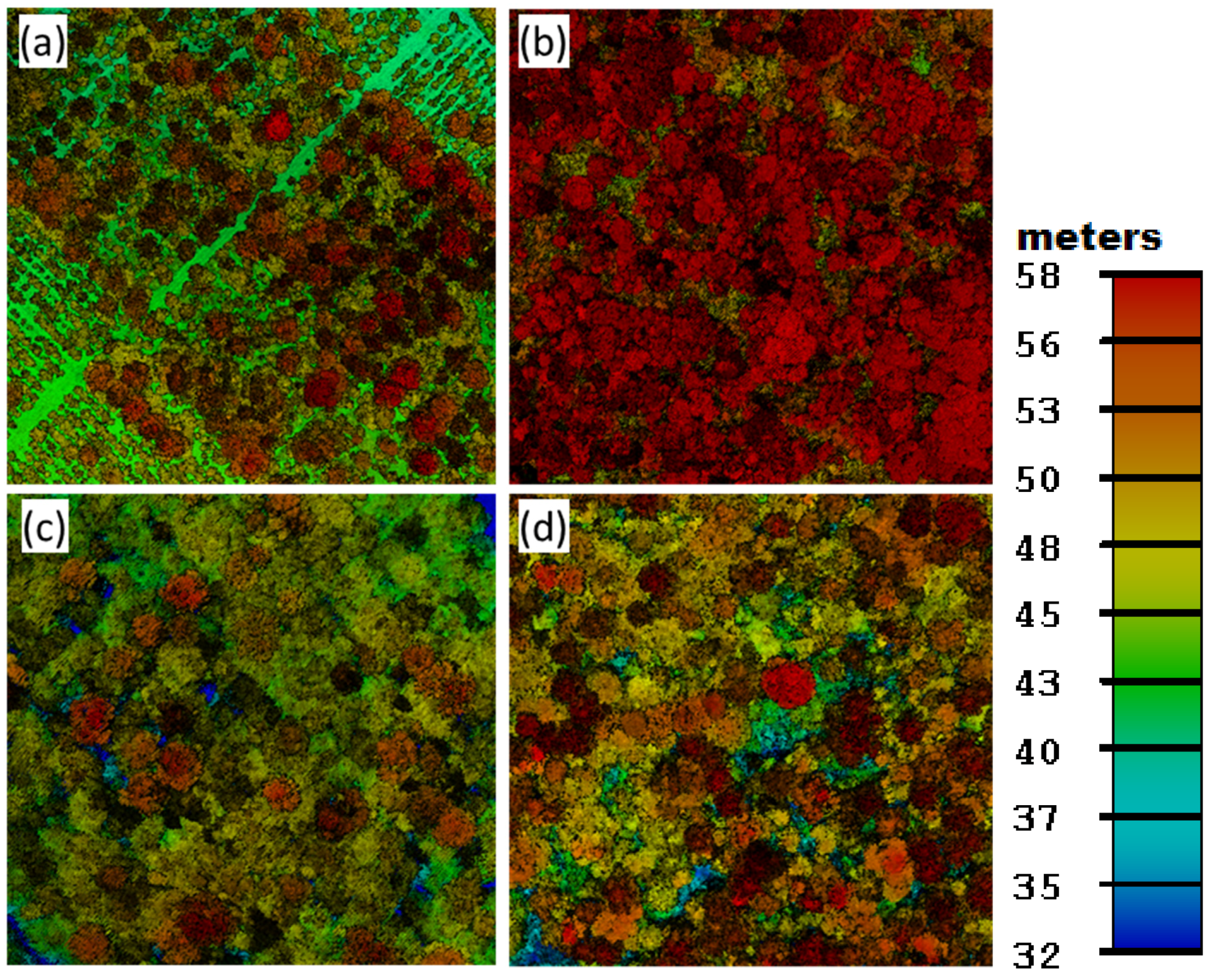
3.2. Airborne Lidar Data Acquisition and Processing
3.3. Lidar-Based AGB Modeling and Mapping
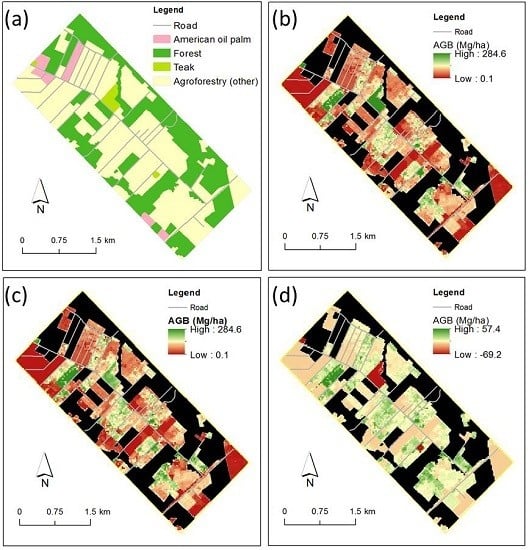
3.4. Mapping Agroforest Distribution with Visual Interpretation
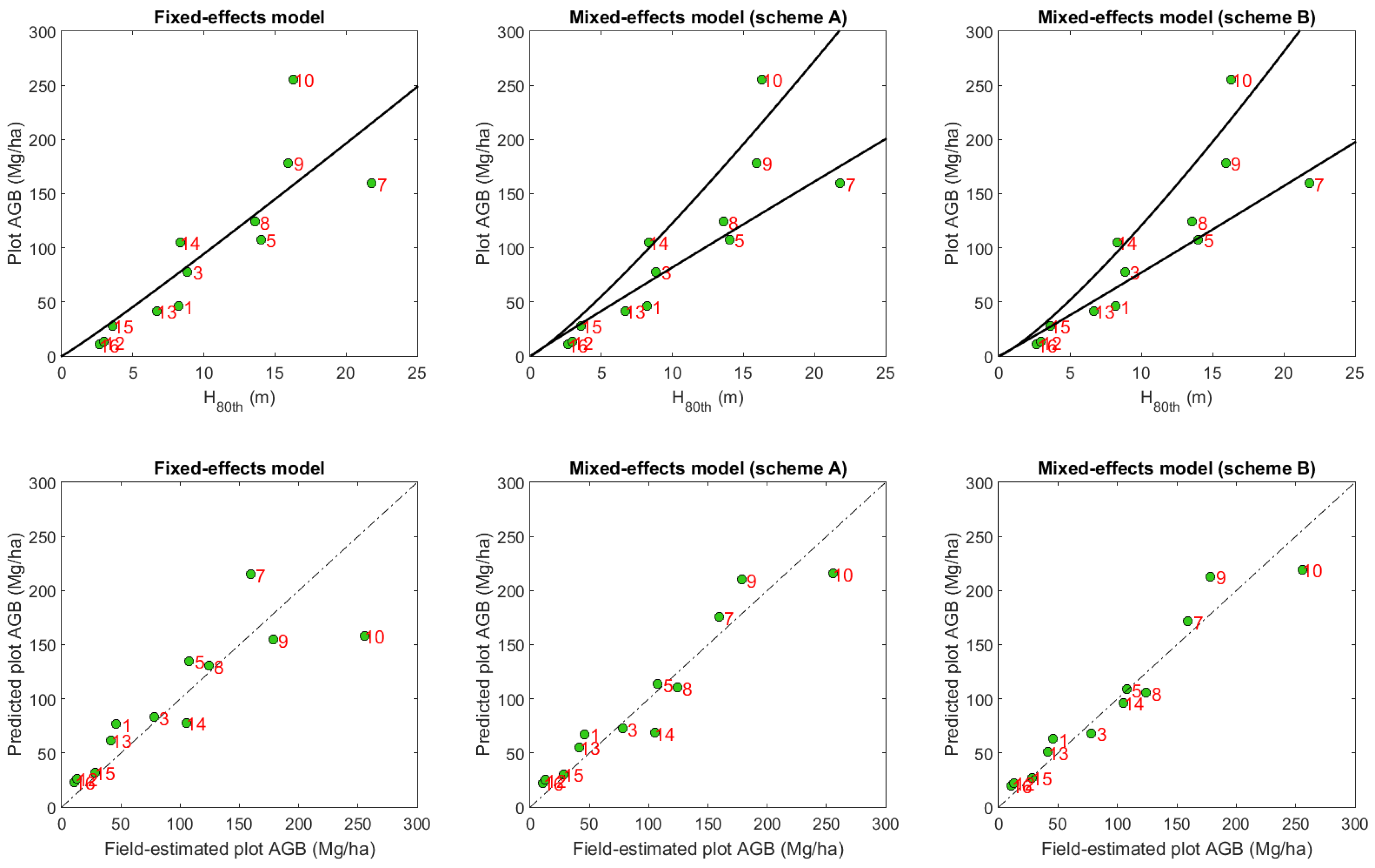
4. Results
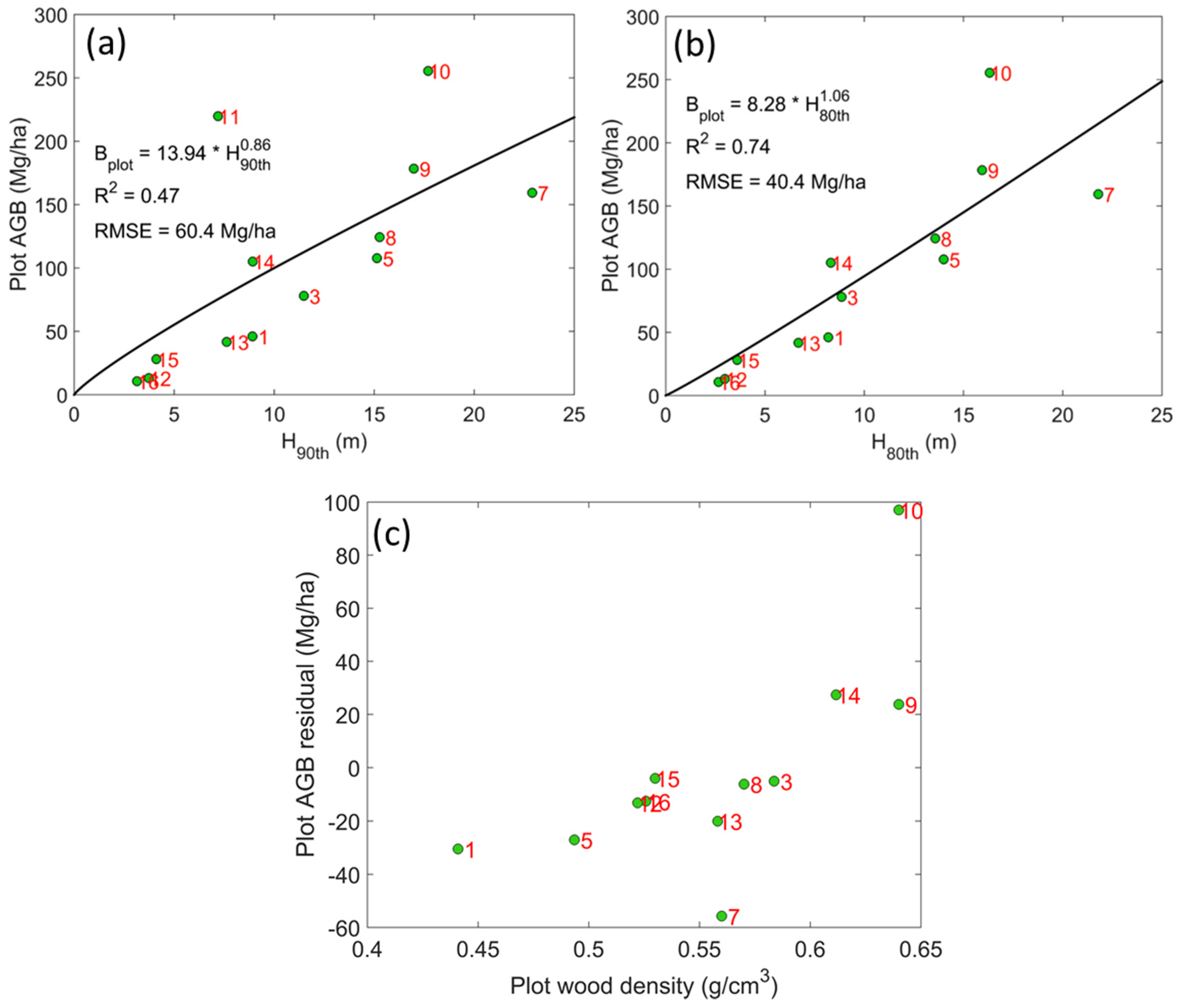
| Scheme | Group#1 | Group#2 |
|---|---|---|
| A | Teak plantation (plot 9, 10) | Non-teak (other plots) |
| B | High wood density plots (plot 9, 10, 14) | Other (other plots) |
| Model Type | Re-Substitution | Cross-Validation | |||
|---|---|---|---|---|---|
| R2 | RMSE (Mg/ha) | AIC | R2 | RMSE (Mg/ha) | |
| Fixed-effects model | |||||
| 0.74 | 40.4 | 122.6 | 0.38 | 56.4 | |
| Mixed-effects model | |||||
| Scheme A | 0.91 | 25.9 | 122.0 | 0.64 | 42.9 |
| Scheme B | 0.94 | 21.6 | 118.7 | 0.75 | 35.9 |

5. Discussion
5.1. Tree DBH-H Relationship

5.2. Allometry
5.3. Mixed-Effects Modeling
6. Conclusions
- (1)
- We found strong evidence to support the stratification of vegetation types in agroforestry fields for AGB modeling and mapping. This is in contrast to the widespread use of statistical models with no awareness of different vegetation types in most studies of tropical forest AGB using airborne lidar. Different from forests where trees are selected or adapted via natural processes, the trees in agroforestry are selected and planted by people to maximize economic and other benefits on purpose. Thus, the trees in agroforestry systems usually show more spatially-regularized patterns with a few co-occurring species. The species and structural diversities within agroforestry fields are usually smaller than the ones within forests while the diversities across different agroforestry fields may be larger. Therefore, the need for stratifying vegetation types in agroforestry is stronger than in forests for AGB studies.
- (2)
- This study analyzed the residual errors resulted from regular fixed-effects models and found that the errors have a pattern related to the variations in plot-level wood density. Based on this pattern, agroforestry fields were classified for lidar-based AGB modeling. This is an improvement over previous studies (e.g., [50]) that used existing vegetation classification schemes not specifically developed for lidar-based AGB modeling and mapping.
- (3)
- This study reinforced the utility of mixed-effects models for biomass modeling and mapping. Mixed-effects models can naturally incorporate how different species or groups have different wood densities and thus distinct lidar height—tree AGB relationships. Mixed-effects models also can elegantly cope with the issue of small sample size via adjustment of model parameters as a combination of fixed and random effects. With the classification of agroforestry into teak plantations and other types, we found the mixed-effects models improved the R2 of AGB prediction from 0.38 to 0.64 and reduced the RMSE from 56.4 Mg/ha to 42.9 Mg/ha in comparison to fixed-effects models. We expect this study will encourage the further use of this under-investigated tool in the community of remote sensing of biomass and carbon.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nair, P.R. An Introduction to Agroforestry; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Negash, M.; Kanninen, M. Modeling biomass and soil carbon sequestration of indigenous agroforestry systems using CO2FIX approach. Agric. Ecosyst. Environ. 2015, 203, 147–155. [Google Scholar] [CrossRef]
- Zomer, R.J.; Trabucco, A.; Coe, R.; Place, F. Trees on Farms: Analysis of the Global Extent and Geographical Patterns of Agroforestry; ICRAF Working Paper No. 89; World Agroforestry Centre: Nairobi, Kenya, 2009. [Google Scholar]
- Mbow, C.; van Noordwijk, M.; Luedeling, E.; Neufeldt, H.; Minang, P.A.; Kowero, G. Agroforestry solutions to address food security and climate change challenges in Africa. Curr. Opin. Environ. Sustain. 2014, 6, 61–67. [Google Scholar] [CrossRef]
- Albrecht, A.; Kandji, S.T. Carbon sequestration in tropical agroforestry systems. Agric. Ecosyst. Environ. 2003, 99, 15–27. [Google Scholar] [CrossRef]
- Thorlakson, T.; Neufeldt, H.; Dutilleul, F.C. Reducing subsistence farmers’ vulnerability to climate change: Evaluating the potential contributions of agroforestry in western Kenya. Agric. Food Secur. 2012, 1, 1–13. [Google Scholar] [CrossRef]
- Nguyen, Q.; Hoang, M.H.; Öborn, I.; van Noordwijk, M. Multipurpose agroforestry as a climate change resiliency option for farmers: An example of local adaptation in Vietnam. Clim. Change 2013, 117, 241–257. [Google Scholar] [CrossRef]
- McNeely, J.A. Nature vs. nurture: Managing relationships between forests, agroforestry and wild biodiversity. Agrofor. Syst. 2004, 61, 155–165. [Google Scholar]
- Jose, S. Agroforestry for conserving and enhancing biodiversity. Agrofor. Syst. 2012, 85, 1–8. [Google Scholar] [CrossRef]
- Ramos, N.C.; Gastauer, M.; de Cordeiro, A.A.C.; Meira-Neto, J.A.A. Environmental filtering of agroforestry systems reduces the risk of biological invasion. Agrofor. Syst. 2015, 89, 279–289. [Google Scholar] [CrossRef]
- Anderson, S.H.; Udawatta, R.P.; Seobi, T.; Garrett, H.E. Soil water content and infiltration in agroforestry buffer strips. Agrofor. Syst. 2009, 75, 5–16. [Google Scholar] [CrossRef]
- Hernandez, G.; Trabue, S.; Sauer, T.; Pfeiffer, R.; Tyndall, J. Odor mitigation with tree buffers: Swine production case study. Agric. Ecosyst. Environ. 2012, 149, 154–163. [Google Scholar] [CrossRef]
- Asbjornsen, H.; Hernandez-Santana, V.; Liebman, M.; Bayala, J.; Chen, J.; Helmers, M.; Ong, C.; Schulte, L. Targeting perennial vegetation in agricultural landscapes for enhancing ecosystem services. Renew. Agric. Food Syst. 2014, 29, 101–125. [Google Scholar] [CrossRef]
- Pandey, D.N. Carbon sequestration in agroforestry systems. Clim. Policy 2002, 2, 367–377. [Google Scholar] [CrossRef]
- Sharrow, S.H.; Ismail, S. Carbon and nitrogen storage in agroforests, tree plantations, and pastures in western Oregon, USA. Agrofor. Syst. 2004, 60, 123–130. [Google Scholar] [CrossRef]
- Kirby, K.R.; Potvin, C. Variation in carbon storage among tree species: Implications for the management of a small-scale carbon sink project. For. Ecol. Manag. 2007, 246, 208–221. [Google Scholar] [CrossRef]
- Nair, P.K.R. Carbon sequestration studies in agroforestry systems: A reality-check. Agrofor. Syst. 2012, 86, 243–253. [Google Scholar] [CrossRef]
- Lorenz, K.; Lal, R. Soil organic carbon sequestration in agroforestry systems: A review. Agron. Sustain. Dev. 2014, 34, 443–454. [Google Scholar] [CrossRef]
- Smith, P.; Bustamante, M.; Ahammad, H.; Clark, H.; Dong, H.; Elsiddig, E.A.; Haberl, H.; Harper, R.; House, J.; Jafari, M.; et al. Agriculture, Forestry and Other Land Use (AFOLU). In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Mdruga, R., Sokana, Y., Minx, J.C., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Skole, D.L.; Samek, J.H.; Chomentowski, W.; Smalligan, M. Forest, carbon, and the global environment: New directions in research. In Land Use and the Carbon Cycle: Advances in Integrated Science, Management, and Policy; Brown, D.G., Robinson, D.T., French, N.H.F., Reed, B.C., Eds.; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014. [Google Scholar] [CrossRef]
- Bolfe, É.L.; Batistella, M.; Ferreira, M.C. Correlation of spectral variables and aboveground carbon stock of agroforestry systems. Pesqui. Agropecu. Bras. 2012, 47, 1261–1269. [Google Scholar] [CrossRef]
- Czerepowicz, L.; Case, B.S.; Doscher, C. Using satellite image data to estimate aboveground shelterbelt carbon stocks across an agricultural landscape. Agric. Ecosyst. Environ. 2012, 156, 142–150. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Meir, P.; Ryan, C.M.; Woollen, E.S.; Williams, M.; Goodman, L.E.; Mucavele, J.A.; Watts, P.; Woodhouse, I.H.; Saatchi, S.S. A novel application of satellite radar data: Measuring carbon sequestration and detecting degradation in a community forestry project in Mozambique. Plant Ecol. Divers. 2013, 6, 159–170. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Chen, Q. Lidar remote sensing of vegetation biomass. In Remote Sensing of Natural Resources; Wang, G., Weng, Q., Eds.; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2013; pp. 399–420. [Google Scholar]
- Montesano, P.M.; Nelson, R.F.; Dubayah, R.O.; Sun, G.; Cook, B.D.; Ranson, K.J.R.; Næsset, E.; Kharuk, V. The uncertainty of biomass estimates from LiDAR and SAR across a boreal forest structure gradient. Remote Sens. Environ. 2014, 154, 398–407. [Google Scholar] [CrossRef]
- Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.E.; Wulder, M. Combining Satellite Lidar, Airborne Lidar and Ground Plots to Estimate the Amount and Distribution of Aboveground Biomass in the Boreal Forest of North America. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Indirect and direct estimation of forest biomass change using forest inventory and airborne laser scanning data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.; Koch, B. Forest structure modeling with combined airborne hyperspectral and LiDAR data. Remote Sens. Environ. 2012, 121, 10–25. [Google Scholar] [CrossRef]
- Chen, Q. Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 2015, 106, 95–106. [Google Scholar] [CrossRef]
- Asner, G.P.; Clark, J.K.; Mascaro, J.; Galindo García, G.A.; Chadwick, K.D.; Navarrete Encinales, D.A.; Paez-Acosta, G.; Montenegro, E.C.; Kennedy-Bowdoin, T.; Duque, Á.; et al. High-resolution mapping of forest carbon stocks in the Colombian Amazon. Biogeosciences 2012, 9, 2683–2696. [Google Scholar] [CrossRef]
- D’Oliveira, M.V.; Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E. Estimating forest biomass and identifying low-intensity logging areas using airborne scanning lidar in Antimary State Forest, Acre State, Western Brazilian Amazon. Remote Sens. Environ. 2012, 124, 479–491. [Google Scholar] [CrossRef]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J.; d’Oliveira, M.V.; Keller, M. Monitoring selective logging in western Amazonia with repeat lidar flights. Remote Sens. Environ. 2014, 151, 157–165. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Yamada, M.; Gholz, H.L. An evaluation of agroforestry systems as a rural development option for the Brazilian Amazon. Agrofor. Syst. 2002, 55, 81–87. [Google Scholar] [CrossRef]
- Rodrigues, T.E.; dos Santos, P.L.; Rolim, P.A.M.; Santos, E.; Rego, R.S.; da Silva, J.M.L.; Valente, M.A.; Gama, J.R.N.F. Caracterização e Classificação dos Solos do Município de Tomé-Açu, Pará; Embrapa Amazônia Oriental: Belém, Pará, Brazil, 2001; p. 49. [Google Scholar]
- Homma, A.K.O. História da Agricultura na Amazônia: Da era Pré-Colombiana ao Terceiro Milênio; Embrapa Informação Tecnológica: Brasília, Distrito Federal, Brazil, 2003; p. 274. [Google Scholar]
- Homma, A.K.O. Dinâmica dos sistemas agroflorestais: O caso da Colônia Agrícola de Tomé-Açu, Pará. Rev. Inst. Estud. Super. Amazôn. 2004, 2, 57–65. [Google Scholar]
- Walker, W.; Baccini, A.; Nepstad, D.; Horning, N.; Knight, D.; Braun, E.; Bausch, A. Field Guide for Forest Biomass and Carbon Estimation, Version 1.0; Woods Hole Research Center: Falmouth, MA, USA, 2011. [Google Scholar]
- Keller, M.; Palace, M.; Hurtt, G. Biomass estimation in the Tapajos National Forest, Brazil: Examination of sampling and allometric uncertainties. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Nascimento, H.E.; Laurance, W.F. Total aboveground biomass in central Amazonian rainforests: A landscape-scale study. For. Ecol. Manag. 2002, 168, 311–321. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Zanne, A.E.; Lopez-Gonzalez, G.; Coomes, D.A.; Ilic, J.; Jansen, S.; Lewis, S.L.; Miller, R.B.; Swenson, N.G.; Wiemann, M.C.; Chave, J. Global Wood Density Database. Dryad. Available online: http://hdl.handle.net/10255/dryad, 235 (accessed on 21 September 2015).
- Fathi, L. Structural and Mechanical Properties of the Wood from Coconut Palms, Oil Palms and Date Palms. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2014. [Google Scholar]
- Chen, Q. Airborne lidar data processing and information extraction. Photogramm. Eng. Remote Sens. 2007, 73, 109–112. [Google Scholar]
- Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of airborne lidar and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from lidar data. Photogramm. Eng. Remote Sens. 2007, 73, 1355–1365. [Google Scholar] [CrossRef]
- Goodman, R.C.; Phillips, O.L.; del Castillo Torres, D.; Freitas, L.; Cortese, S.T.; Monteagudo, A.; Baker, T.R. Amazon palm biomass and allometry. For. Ecol. Manag. 2013, 310, 994–1004. [Google Scholar] [CrossRef]
- Wang, G.; Oyana, T.; Zhang, M.; Adu-Prah, S.; Zeng, S.; Lin, H.; Se, J. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. For. Ecol. Manag. 2009, 258, 1275–1283. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Laurin, G.V.; Saah, D. Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. For. Res. 2012. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Westfall, J.A. Effects of uncertainty in model predictions of individual tree volume on large area volume estimates. For. Sci. 2014, 60, 34–42. [Google Scholar] [CrossRef]
- Lu, D.; Hetrick, S.; Moran, E. Land cover classification in a complex urban-rural Landscape with QuickBird imagery. Photogramm. Eng. Remote Sens. 2010, 76, 1159–1168. [Google Scholar] [CrossRef]
- Bigdeli, B.; Samadzadegan, F.; Reinartz, P. A decision fusion method based on multiple support vector machine system for fusion of hyperspectral and LIDAR data. Int. J. Image Data Fusion 2014, 5, 196–209. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Phinn, S. Land-cover classification using both hyperspectral and LiDAR data. Int. J. Image Data Fusion 2015, 6, 189–215. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Lu, D.; Keller, M.; Dos-Santos, M.N.; Bolfe, E.L.; Feng, Y.; Wang, C. Modeling and Mapping Agroforestry Aboveground Biomass in the Brazilian Amazon Using Airborne Lidar Data. Remote Sens. 2016, 8, 21. https://doi.org/10.3390/rs8010021
Chen Q, Lu D, Keller M, Dos-Santos MN, Bolfe EL, Feng Y, Wang C. Modeling and Mapping Agroforestry Aboveground Biomass in the Brazilian Amazon Using Airborne Lidar Data. Remote Sensing. 2016; 8(1):21. https://doi.org/10.3390/rs8010021
Chicago/Turabian StyleChen, Qi, Dengsheng Lu, Michael Keller, Maiza Nara Dos-Santos, Edson Luis Bolfe, Yunyun Feng, and Changwei Wang. 2016. "Modeling and Mapping Agroforestry Aboveground Biomass in the Brazilian Amazon Using Airborne Lidar Data" Remote Sensing 8, no. 1: 21. https://doi.org/10.3390/rs8010021
APA StyleChen, Q., Lu, D., Keller, M., Dos-Santos, M. N., Bolfe, E. L., Feng, Y., & Wang, C. (2016). Modeling and Mapping Agroforestry Aboveground Biomass in the Brazilian Amazon Using Airborne Lidar Data. Remote Sensing, 8(1), 21. https://doi.org/10.3390/rs8010021