Abstract
Empirical relationships between field-derived Leaf Area Index (LAI) and Leaf Angle Distribution (LAD) and polarimetric synthetic aperture radar (PolSAR) based biophysical indicators were created and applied to map S. alterniflora marsh canopy structure. PolSAR and field data were collected near concurrently in the summers of 2010, 2011, and 2012 in coastal marshes, and PolSAR data alone were acquired in 2009. Regression analyses showed that LAI correspondence with the PolSAR biophysical indicator variables equaled or exceeded those of vegetation water content (VWC) correspondences. In the final six regressor model, the ratio HV/VV explained 49% of the total 77% explained LAI variance, and the HH-VV coherence and phase information accounted for the remainder. HV/HH dominated the two regressor LAD relationship, and spatial heterogeneity and backscatter mechanism followed by coherence information dominated the final three regressor model that explained 74% of the LAD variance. Regression results applied to 2009 through 2012 PolSAR images showed substantial changes in marsh LAI and LAD. Although the direct cause was not substantiated, following a release of freshwater in response to the 2010 Deepwater Horizon oil spill, the fairly uniform interior marsh structure of 2009 was more vertical and dense shortly after the oil spill cessation. After 2010, marsh structure generally progressed back toward the 2009 uniformity; however, the trend was more disjointed in oil impact marshes.
Keywords:
polarimetric radar; marsh structure mapping; LAI; LAD; UAVSAR; Deepwater Horizon oil spill 1. Introduction
1.1. Optical Landcover Mapping and Canopy Structure
Marshes occupy a unique interface between water bodies and upland landscapes. They are critical and essential for exchange of land-to-water fluxes, for providing habitat, and, in coastal settings, protection of people and facilities. In the coastal interface, they experience high frequency shifts in inundation modulated by terrestrial runoff and coastal ocean tides and storms. These dynamic modulations create a spatially complex landscape exhibiting various wetland communities and canopy structure forms, even within monotypic marshes in the same region. In addition, the details of wetland management can have substantial impacts on the biophysical and compositional structure of the marshes and the animal communities dependent on these habitats. The biophysical and structural characteristics of these coastal marshes must be monitored and documented to track their health and function.
Remote sensing can provide this information by linking the optical canopy reflectance to wetland status on multiple spatial and temporal scales. However, multiple canopy contributors such as plant cover percent and background variability [1,2,3,4] complicate the linking the plant leaf condition to canopy reflectance. Even accounting for background influences, the canopy reflectance as represented in the remote sensing signal reflects the intertwined contributions of the leaf optical properties and plant canopy structure, i.e., density and orientation [5,6,7,8,9,10,11,12]. Structure information can be purposely incorporated into the classification by fusing radar backscatter and optical image data [13,14,15]. In other cases where the target canopies exhibit largely “full and uniform coverage” or the leaf and structure are considered a combined land class unit, the decoupling of the leaf optical and plant-canopy structure contributions to the canopy reflectance can be of little consequence. However, when the objective is mapping the canopy structure or capturing subtle changes in plant leaf pigments that accompany changes in canopy condition, the determination of canopy structure or its contribution, including background, to the canopy reflectance can be critical to detecting desired changes. The incorporation of canopy structure into calibration advances remote sensing mapping of subtle changes as well as bulk canopy changes.
1.2. Standardization of Canopy Architecture
Common methods used to transform remote sensing data to estimates of biomass are based on vegetation indexes (VI) adapted from the concept of Tucker [16]. Successful application of VI to map biomass, however, has necessitated widespread modifications of the simple VI index that include changes in form and variable input (e.g., [17]) or optimization (e.g., [18]). These modifications enhance performance for specific landscapes but lead to a plethora of vegetation indexes, particularly in complex canopies [19,20,21]. Relationships that link radar backscatter to biomass can also be constrained in specificity of the landscape composition (e.g., [22]). This abundance of vegetation and site specific VI is a limitation of the VI approach, reducing its general applicability.
Even though broadly useful, VI mapping success is to some degree dependent on the consistency of canopy structure throughout the mapped spatial extent so that the biomass composition and canopy reflectance relationship remains substantially unaltered. That consistency and VI-based biomass mapping success at some level appears to be dependent on the live biomass to total biomass composition consistency [14,17,23,24]. While many applications indicate that consistency is often realized, a more robust remote sensing estimator of the canopy structure would insure more complete and timely accounting of biomass changes in complex canopies exhibiting highly variable structures and compositions.
1.3. Marsh Canopy Structure and Vertical Profiling
The vegetative canopy can be represented in terms of its structure as the “spatial arrangement of plant’s aboveground organs in plant communities” [25]. Watson [26] standardized the leaf area index (LAI) as one component of structure describing the total one-sided leaf area per ground area (m2/m2). Since these early works, numerous review articles have documented limitations and advantages of direct and indirect measurement of LAI (e.g., [20,21,23,27,28,29]). Some of those articles have also reported measures related to the orientations of the vegetative canopy elements, dominantly leaves and stems (e.g., [27,30,31]), which in this paper are aggregately represented as the Leaf Angle Distribution (LAD). Of the studies that report vegetation structure, most describe forest and agriculture landscapes. Although advantageous for proper monitoring and development of physical dynamics, incorporation of canopy structure profile measurements into terrestrial mapping strategy is lacking, particularly in grasslands, and within those, especially marshes.
The necessity of tracking marsh structure and vertical profile is not only based on the need for a consistent measure amenable to remote sensing, but also because of the interdependence of the marsh structure and coastal zone biophysical function. Biophysical values such as LAI have proved useful in a number of environmental applications to represent biomass density. LAI and particularly the three-dimensional spatial variability of LAI in grasslands are needed to estimate key components in biochemical cycles [27,32]. These include surface water balance and productivity (and photosynthesis) [28,33,34,35], and ozone and CO2 assimilation [32,35,36]. In addition, the three-dimensional canopy description is useful for improving water flow estimates, advancing optical condition and change mapping, and fire burn dynamics and emission projections. LAI is an essential factor in climate, weather, and ecological studies, and thus, a factor in global climate [28,35].
1.4. Mapping LAI and LAD with Polarimetric Radar Data
The choice of polarimetric radar data as the base for developing a remote sensing marsh structure mapping technology is founded primarily on the requirements for defining canopy structure and density (biomass, water content, LAI, LAD). Although mapping success varies, the advantage of cross polarization backscatter (HV or VH) or cross and like (HH or VV) polarization ratios in explaining density variance is well established (e.g., [13,37,38,39,40,41,42,43,44]). Less experience exists in applying full polarimetric (PolSAR) information in mapping vegetation density, especially in grassland landscapes; however, some operational mapping applications have utilized the full polarimetric information to account for canopy structural changes in grassland or marsh landscapes [22,45,46,47,48]. This research follows those latter studies by exploiting a combination of backscatter intensities, intensity ratios, copolarization correlation and phase, backscatter spatial heterogeneity, and backscatter mechanism obtained by decomposition of the complex polarimetric data for canopy structure mapping development. Information gained from single and dual polarization radar mapping of vegetation density and orientation was also incorporated into the study to evaluate marsh change during a time interval extending from one year before the Deepwater Horizon (DWH) spill to two years after the spill.
1.5. Coastal Description and Site Locations
Located in the deltaic plains of the north-central Gulf of Mexico, the study region encompasses estuarine wetlands [49,50] (Figure 1) located in southern Louisiana. These marshes are scoured by hurricanes that push water with elevated salinity into inland marshes where channels, levees, and impoundments impede overland flow, lengthening marsh exposure to elevated salinity surge water and prolonged inundation that promote marsh alteration and deterioration [51,52]. Features such as water ponding in scattered small depressions are a constant and changing occurrence throughout these coastal marshes. Water masks created one year may over or under estimate previous or future occurrences of these features resulting at times in the over and under correction of input datasets used in landcover classifications. Because of the possible corrupting influence of extreme values in similarity-based classifications, over correction or over removal of the scattered open water ponds is preferred.
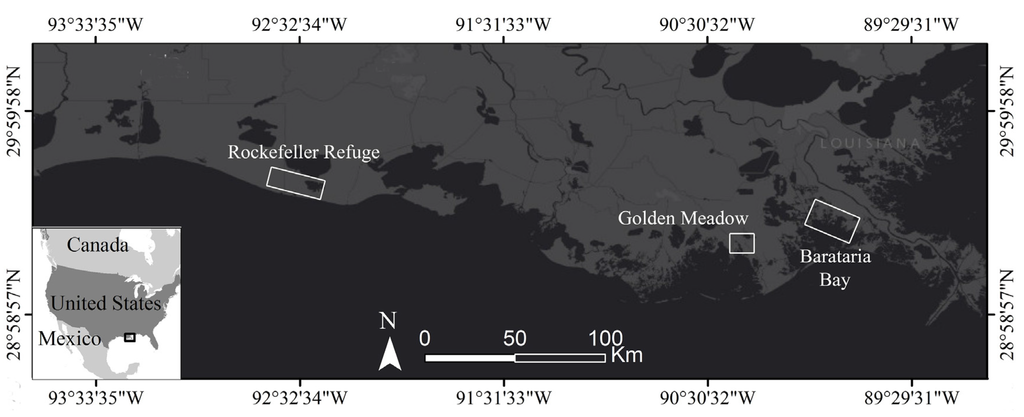
Figure 1.
The coastal marsh region of Louisiana located in the north-central Gulf of Mexico. The boxes locate Barataria Bay, Golden Meadow, and Rockefeller Refuge study regions. Golden Meadow and Rockefeller Refuge S. alterniflora field sites were occupied in 2010–2012 and Barataria Bay field sites in 2011 and 2012. NASA/UAVSAR PolSAR data and field data collections were coordinated. PolSAR collections in Barataria Bay occurred from 2009 to 2012.
As reported in Ramsey et al. [53], marsh canopy structure varies over time and from site to site, sometimes dramatically. This occurs between different marsh species and also within a single species. An added complexity and one core reason for advancing marsh structure mapping is the often abrupt changes in canopy density and orientation within the canopy vertical profile associated with lodging. Lodging is not as pervasive in S. alterniflora as in, for example, S. patens marshes; however, it does occur and can be acute [53]. S. alterniflora marshes also exhibit changes in form (height, leaf width, density) dependent on provenance and growth stage. While variation in form was not a differential variable between the three physiographic regions used in this study, marsh form (not including leaf width) and biomass composition varied highly at each site and from year to year.
2. Objectives
The goal of this research is to develop an operational and robust polarimetric remote sensing estimator of marsh canopy structure. The first objective within that goal is to create an empirical relationship between PolSAR data and marsh canopy structure based on near-coincident PolSAR and field data collections. The relationship is based on field-based LAI and LAD marsh structure and PolSAR-based indicators. The second objective is to apply the empirical relationship in order to provide a direct example of using structure information to track marsh status trends. That objective was accomplished by mapping marsh structural change over a period of time that encompassed the Deepwater Horizon oil spill impact to these marshes. The Deepwater Horizon spill was initiated on 20 April 2010, and continued releasing oil into the Gulf of Mexico approximately 50 miles from the Louisiana coast until the well was capped in July 2010. The radar data set begins in 2009 with images of the Louisiana coast pre-spill, continues in 2010 when data were collected during the spill, and follows with near-anniversary collections in 2011 and 2012. Marsh oiling from the spill was extensive only in the northeastern Barataria Bay. None of the study sites are known to have received direct oiling from the spill, and only the Barataria Bay sites were in close proximity to heavily oiled marshes. In contrast, the PolSAR data for all years covered the extended wetlands, from the coast inland, both oiled and unimpacted.
3. Methods
NASA Uninhabited Aerial Vehicle SAR (UAVSAR) conducted flights over coastal Louisiana in response to the Deepwater Horizon oil spill and its possible long-term effects on exposed coastal resources [54,55]. Specific to this study, PolSAR data were collected in June to July 2010, 2011, and 2012 of the Rockefeller Refuge, Golden Meadow and Barataria Bay study areas (shown in Figure 1). In addition, UAVSAR PolSAR was collected of Barataria Bay in June 2009, prior to the Deepwater Horizon accident. Nearly concurrent with PolSAR summer collections, field data were collected at seven sites in non-impacted and impacted marshes located in the Louisiana coastal zone. In 2010, field data were collected in the Rockefeller Refuge and Golden Meadow sites only, and at all sites in 2011 and 2012.
PolSAR and field data collections are located in three dynamically diverse regions of the coastal landscape. The furthest sites to the east lie within Barataria Bay directly adjacent to the location in the Mississippi River delta that was heavily impacted by the Deepwater Horizon oil spill in 2010 [55]. Outside the oil spill impacted area and further to the west in the Golden Meadow region are located inland marsh sites that are not exposed to wave and storm energy as is marsh in Barataria Bay, although they do experience tidal water level variations. Further west in the Rockefeller Refuge and closer to the shoreline are located the remaining sites, which lie within protected impoundments that while retaining a direct connection to the coastal ocean provide protection from wave erosion. Both the Barataria Bay and Golden Meadow regions are dominated by S. alterniflora marsh while different estuarine marshes create a spatial patchwork of dominance throughout the Rockefeller Refuge [50]. S. alterniflora comprised 100% or nearly 100% of marsh at all seven sites in this study.
3.1. Field Measurements and Post-Analyses
High variability was associated with a regional dieback centered on the Golden Meadow region [14]. Whether this event was also reflected as form and composition variation measured in the Barataria Bay and Rockefeller Refuge marshes is unclear. What was observed, however, was high variability in marsh height, density, live and dead composition, and the vertical distribution of these measures from site to site and year to year. Field data collection within 30 m by 30 m S. alterniflora plots followed a standard sampling strategy that provides reproducible measures within these structurally variable marshes (for detailed descriptions, see Ramsey et al. [14,53,56]). Biomass was measured within a 1 m2 area chosen to represent the typical marsh at each site, separated into live and dead portions, dried, and weighed (for method, see [14,57]). Vertical profiles of photosynthetic active radiation (PAR) attenuation, sampled at 20 cm increments from bottom to top of the canopy, were measured every 3 m along 30 m east–west and north–south transects [14,53,56].
3.1.1. Calculation of Site-specific LAI and LAD
The site averaged PAR vertical profiles were parameterized as marsh canopy LAI profiles and average leaf-stem LAD using the method of Ramsey et al. [56]. For use in calibrating the PolSAR data, the vertical LAI profiles were aggregated as a single total LAI per site and time.
3.1.2. Correction of Biophysical Field Measures for Water Level
At the times of the PolSAR acquisitions, above-surface water levels at the field sites were obtained from nearby hydrologic stations operated by the Coastwide Reference Monitoring System as described in the Strategic Online Natural Resources Information System [58]. Shallow (11 cm) aboveground and subcanopy flooding occurred during the 2012 Rockefeller Refuge UAVSAR overflight. Similarly, in 2009, possible shallow (7 cm) subcanopy flooding was indicated at one of the three hydrologic stations in marshes surrounding Barataria Bay [55]. At Golden Meadow, however, subcanopy surface flooding was present during all UAVSAR collections. To account for the loss of accessible biomass, the LAI profiles and measured water depth were used to adjust measured biomass and LAI remaining above the water surface at the time of the UAVSAR collections [14]. These adjusted biomass metrics offered a more accurate depiction of PolSAR-based variable and biomass relationships, improving interpretability and extendibility of regression results.
3.2. UAVSAR PolSAR Data
The day and night mapping capabilities offered with radar systems are further extended by the UAVSAR airborne platform offering rapid response in emergencies and agility in tracking time-varying features. UAVSAR’s precision repeat-track capability to within 5 m ([54]) enables direct comparison between revisit data collections, and its high transmitted power results in a higher signal-to-noise ratio compared to satellite radars. The high signal-to-noise ratio, a quantity that indicates how much of the measured signal comes from surface backscatter relative to what is generated by noise in the instrument electronics, is particularly important when using HV intensities, which are lower signal level than the HH or VV returns. A previous evaluation of the UAVSAR L-band data found that noise intensities remained below HV backscatter associated with marshes located in the near- to far-range with the possible exception of non-vegetated land covers [54,55]. The L-band 1217.5 to 1297.5 MHz (23.8 cm wavelength) frequency of the SAR system could provide more consistent subcanopy information as suggested in inundation flood mapping [52,59], and its quadrature polarized capability, recording intensities and phases of the HH, VV, and cross-polarization (HV and VH) backscatter, allow a more complete characterization of the scattering properties [60].
This study used UAVSAR’s ground range projected, calibrated, and multilooked complex image data referred to as GRD (georeferenced) products [61]. These image data reflect the amplitude and phase of the electromagnetic wave measured by the PolSAR sensor representing the complex elements of the scattering matrix [55]. The cross-polarized channels, HV and VH, are combined into a single channel based on the assumption that the HV and VH backscatter is equal for natural surfaces [62]. The GRD data at 5.338 m by 6.159 m and effective looks of 3 and 12 in the azimuth and range directions were rectified to a UTM map projection at a 5 m by 5 m pixel resolution. The NASA GRD product provided a readily usable and high fidelity polarimetric data source of high spatial resolution and repeat targeting that enabled determination and direct comparison of canopy structure between the 2009, 2010, 2011, and 2012 revisit data collections.
PolSAR-Based Biophysical Indicators
PolSAR data were extracted at each site by using a 5 by 5 and a 7 by 7 pixel rectangle centered over the field collection areas. The 2009, 2010, 2011, and 2012 PolSAR data were used to calculate site mean HH (horizontal send and receive), VV (vertical send and receive), and HV intensities. These backscatter intensities were combined to form the copolarization ratios, HH/VV, HH/(VV−HH), (HH−VV)/(HH+VV), and VV/(VV+HH), HH/HV and VV/HV, the depolarization ratios, HV/HH, HV/VV, and (HH+VV)/2HV, and ratios related to volume scatter, HV/(HH+HV) and HV/(VV+HV).
The SAR Polarimetric Workstation software module imbedded within the PCI image processing software toolkit [63] provided the site average HH–VV phase difference as a measure of the polarization properties at each marsh site, the HH and VV correlation magnitude and the real and imaginary correlation coefficient components that comprise the HH and VV correlation. In addition, produced were the coefficient of variation related to the maximum and minimum power in the polarization signature, and the pedestal height of the signature plot indicating, somewhat similar to the coefficient of variation, the heterogeneity of scattering properties within the site average.
Following a number of studies (e.g., [39,44,45,46,47,55,64]), decomposition models were applied to the complex polarimetric backscatter components of the GRD data in order to categorize the dominant backscatter into distinct mechanisms that could reveal the structure of the vegetation [65,66]. Freeman–Durden (FD) is a physical model decomposition used to transform the scatter matrix into estimates of surface, volume, and double-bounce scatter mechanism. Cloude–Pottier (CP) decomposition extracts three eigenvectors from either the covariance or coherence matrix representation of the scatter matrix. The eigenvector values and angles are used to derive secondary variables, namely entropy, anisotropy, and alpha and beta angles that combined represent different scatter mechanisms. Revised solutions to improve FD overestimation of volume scatter (negative nonphysical solutions) in certain environments have been offered [67,68]; however, overestimation of volume scatter was not observed in the land applications.
3.3. Defining the PolSAR-Based Indicators and Marsh Structure Relationship
Development of the empirical relationship between marsh structure and PolSAR data is based on multivariate regression analyses. The use of statistical means for this development is a first step in identifying PolSAR-based variable interactions that provide marsh structure information. First, identification should advance understanding of the physical mechanism underlying these interactions, enhancing transition to operational physical models (after Titin-Schnaider [69]). Second, sound regression models fulfill an immediate need to advance marsh condition monitoring while building a body of knowledge concerning PolSAR marsh structure mapping (after Titin-Schnaider [69]).
3.3.1. Examining the PolSAR-Based Indicator Dataset
Simple relationships were examined within and between all biophysical measurements and PolSAR-based indicators in order to identify errors in data entry and variable redundancies, and reveal simple correspondences. Entry errors were corrected and redundant PolSAR variables removed before conducting multiple regression analyses.
3.3.2. Developing Statistical Predictor Equations
Stepwise regressions (SAS® Enterprise) were conducted to determine the best set of PolSAR indicator variables for explaining the Biomass, LAI and LAD variances. To decrease autocorrelation of PolSAR-based regressor variables entered into the regression analyses, PolSAR indicator variables were eliminated that exhibited direct correspondence as noted in the scatter plots. Not all autocorrelations in the PolSAR variables were removed. In order to estimate autocorrelation of the regressors, the tolerance (TOL) and variance inflation factor (VIF) were calculated within the stepwise procedure. The TOL and VIF indicate multicolinearity of the regression coefficients and a TOL < 0.1 and a corresponding VIF > 10 indicate that the importance of the regression variable cannot be interpreted based solely on the associated coefficient magnitude (e.g., [70,71,72]). In order to strengthen interpretation and robustness of the regression relationship and promote comparisons, the stepwise regressions were limited to those with maximum TOL ≥ 0.1 and VIF ≤ 10.
3.3.3. Mapping Marsh Canopy LAI and LAD
Regression equations and the corresponding regression coefficients were applied to the stepwise selected PolSAR indicator images (independent regression image variables). The resultant LAI and LAD images were calculated by multiplying the coefficient and associated image data of each independent regression variable and then summing these products and the regression intercept to obtain the LAI or LAD pixel value. Calculations were carried-out with embedded image processing tools [63]. As a demonstration of LAI and LAD capabilities for monitoring marsh structural change, the study used UAVSAR PolSAR image data collected in 2009, 2010, 2011, and 2012 before and after the 2010 Deepwater Horizon oil spill.
Composite LAI and LAD classifications were obtained by applying a centroid-based clustering procedure [63]. The cluster procedure simply identified spatially covarying groups within each yearly set of LAI and LAD images and produced a set of classes representing these groupings for each year. Individual classifications by year were used in order to emphasize the unique LAI-LAD features comprising each year’s marsh landscape. Comparison then involved describing similar and unique classes and their changing coverages throughout the four-year period. Changes within the extensive interior marshes outside the expected oil penetration and those exposed and potentially exposed to oil during the 2010 Deepwater Horizon oil spill were described.
4. Results
4.1. Site-Specific Biophysical Data
Marsh biomass quantity and composition and calculated LAI and LAD varied highly between sites and over time (Table 1) [56]. Live and dead dry weight compositions highly aligned with total biomass (R2 > 0.87, n = 17, Figure 2), while LAI exhibited weak correspondence with dead biomass (R2 = 0.29, n = 17) and no correspondence with total or live biomass. Although a marsh dieback was documented for the Golden Meadow region [14], and the Deepwater Horizon oil spill impacted Barataria Bay marshes [55] over this time period, no noticeable pattern of biomass and composition grouping was clearly exhibited in the field data per region or time. The S. alterniflora marsh dataset exhibited a broadly distributed dataset range well suited for accomplishing the study objectives [56].
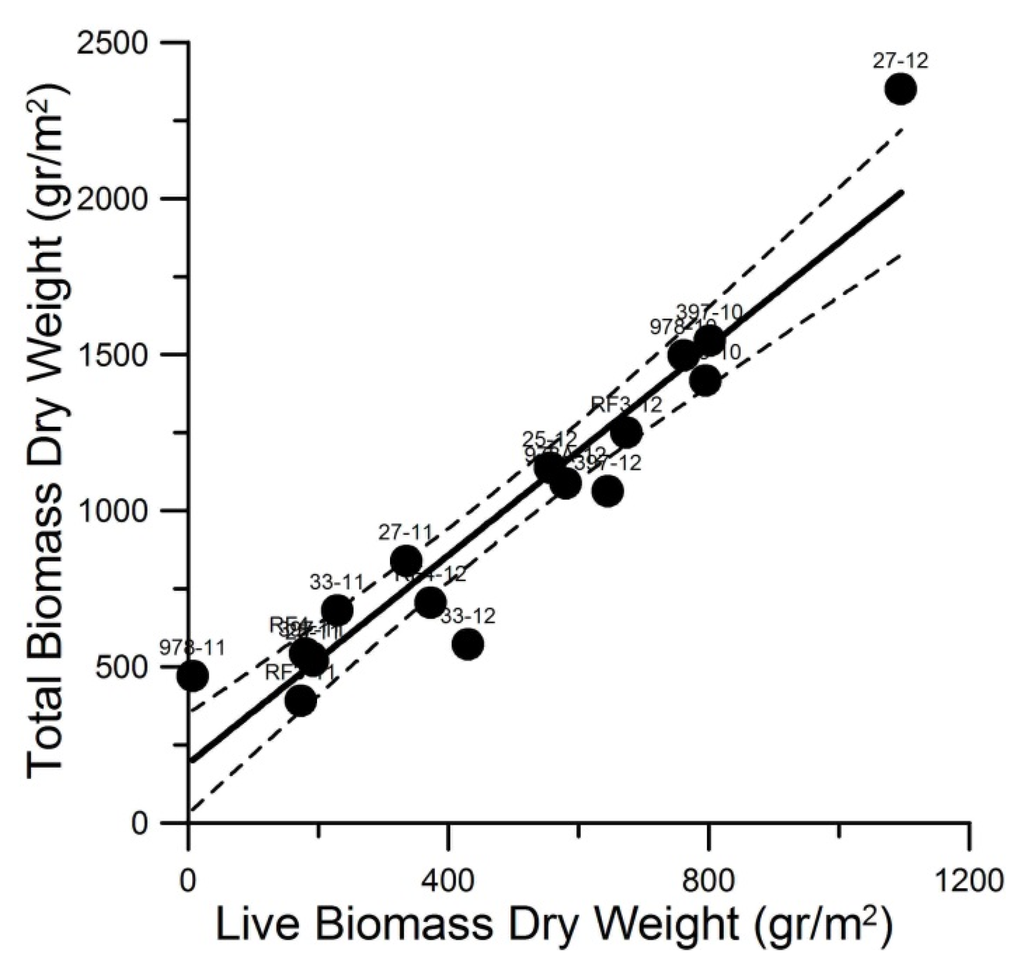
Figure 2.
Total Biomass Dry Weight = 1.67 × Live Biomass Dry Weight + 190.28, R2 = 0.91, MSE = 26,716.40 (gr/m2) (n = 17). Dashed line represents the 95% confidence limits. For data and site labels refer to Table 1.

Table 1.
Field Measured and Calculated Biophysical Variables. Site labels include the site name and year collected (RF = Rockefeller Refuge, BA = Barataria Bay, GM = Golden Meadow). All entries were adjusted for the water level recorded at the time of UAVSAR collection. The Biomass Percent refers to the magnitude of that adjustment. Note: There are two biomass weights, the dry weights and water weights.
| Site | Dried Biomass Weight | Structure | Biomass Water Weight | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | Live | Dead | Biomass | LAI | LAD | Total | Live | Dead | |
| gr/m2 | gr/m2 | gr/m2 | Percent | gr/m2 | gr/m2 | gr/m2 | |||
| RF3-10 | 1417.1 | 795 | 622.1 | 100% | 2.75 | 0.88 | 3238 | 1792.8 | 1445.1 |
| RF3-11 | 392.3 | 173 | 219.3 | 100% | 2.6 | 0.69 | 346.6 | 234.4 | 112.3 |
| RF4-11 | 543.4 | 179.5 | 364 | 100% | 2.41 | 0.72 | 485.8 | 284 | 201.8 |
| RF3-12 | 1113.6 | 600.2 | 513.4 | 89% | 2.13 | 0.67 | 1149.2 | 725.6 | 423.6 |
| RF4-12 | 623.9 | 328.8 | 295.1 | 89% | 1.9 | 0.82 | 781.7 | 428 | 353.7 |
| BA25-11 | 520.3 | 191.6 | 328.7 | 100% | 5.03 | 0.5 | |||
| BA27-11 | 839.9 | 334.9 | 505.1 | 100% | 3.15 | 0.78 | |||
| BA33-11 | 681.4 | 229 | 452.4 | 100% | 3.46 | 0.39 | |||
| BA25-12 | 1137.7 | 555.8 | 581.9 | 100% | 3.92 | 0.31 | 3634.6 | 1297 | 2337.6 |
| BA27-12 | 2351.1 | 1095.1 | 1256 | 100% | 4.34 | 0.58 | 4417.5 | 2045 | 2372.6 |
| BA33-12 | 571.9 | 429.8 | 142.1 | 100% | 1.24 | 0.38 | 2408.2 | 1590.9 | 817.3 |
| GM397-10 | 1020.8 | 529.3 | 491.5 | 66% | 3.26 | 1.04 | 444.8 | 252.7 | 192.1 |
| GM978-10 | 1320 | 670.3 | 649.7 | 88% | 3.91 | 0.52 | 3755.2 | 2023.5 | 1731.7 |
| GM397-11 | 496 | 177.8 | 318.2 | 94% | 3.07 | 0.59 | 587.3 | 272 | 315.3 |
| GM978-11 | 353.7 | 5.3 | 348.3 | 75% | 2.38 | 0.67 | 305.2 | 10.7 | 294.5 |
| GM397-12 | 412 | 249.9 | 162.1 | 39% | 1.6 | 0.4 | 270.6 | 118.2 | 152.3 |
| GM978A-12 | 313.1 | 166.8 | 146.3 | 29% | 0.94 | 0.39 | 247.3 | 82.1 | 165.2 |
4.2. PolSAR-Based Biophysical Indicators
Scatter plots revealed that most of the more complex intensity ratios directly covaried with simpler ratios. The redundant ratios removed from the regression analyses included HH/(VV−HH), (HH−VV)/(HH+VV), and VV/(VV+HH), HV/(HH+HV) and HV/(VV+HV). FD volume scatter was removed because it replicates the HV backscatter variance. In addition, only the linear values associated with each of the FD scatter mechanisms were used in the regression analyses. Close and similar correspondences also were noted between some additional PolSAR-based variables and these are discussed when pertinent to those variables selected in the stepwise regression. Although of interest in analyzing polarimetric mapping of these marshes, a full discussion of the covariances between the PolSAR indicators set is not directly pertinent to this analysis and is not included here. The final PolSAR dataset entered into the regression analyses is contained in Table 2.
4.3. Linking PolSAR Indicators and Site-Specific Marsh Canopy Biophysical Structure
4.3.1. Biomass and PolSAR Data Regressions
First calculated were relationships between dry biomass and biomass water quantities in Table 1 and the set of PolSAR-based variables listed in Table 2. In the dry biomass weight stepwise regressions, site 27-12 (notation is site-year) was an extreme outlier; however, there is no evidence that biomass measurements at that site were incorrect. Including all 17 sites, a four variable solution explained 53% of the live biomass variance and two variable solutions accounted for 42% and 39% of the total and dead biomass variance, respectively. Biomass water weight stepwise regressions used all 14 sites (three sites had missing values). A two variable solution explained 70% of the total biomass water weight, 76% of the dead biomass water weight, and 63% of the live biomass water weight (Table 3). Because water content is commonly used, and its explained variance is substantially higher, only PolSAR-biomass water regression statistics are included in Table 3.
4.3.2. LAI and LAD and PolSAR Data Regressions
All 17 sites were input into the LAI and LAD stepwise regressions (Table 1 and Table 2). The HV/VV PolSAR indicator singularly explained 49% of the LAI variance (Table 3). The prediction equation with the highest explanation (R2 = 0.95) of LAI variance included nine PolSAR-based indicators; however, some variables in the relationship contained TOLs and VIFs indicating high multicolinearity among the selected PolSAR indicators. The maximum TOLs and VIFs included in the prediction was reduced to acceptable levels by eliminating variables selected in the 95% solution. A reduced six variable solution accounted for 77% of the LAI variance (Table 3, Figure 3a). A three variable solution explained 74% of the LAD variance (Table 3, Figure 3b).
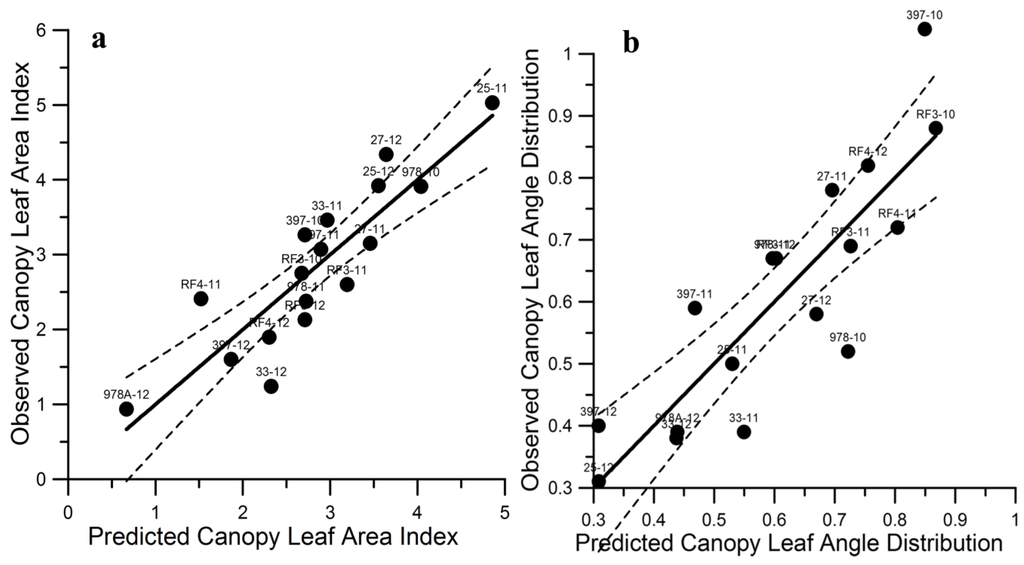
Figure 3.
(a) LAI Observed = 1.00 ± 0.14 (p < 0.001) × LAI Predicted + 2.40E-14 ± 0.416 (p = 1.0) R2 = 0.77, Mean Square Error = 0.30 LAI, (n = 17). (b) LAD Observed = 1.00 ± 0.15 (p < 0.001) × LAD Predicted + 2.24E-14 ± 0.096 (p = 1.0) R2 = 0.74, Mean Square Error = 0.011 LAD, (n = 17). Dashed line represents the 95% confidence limits (SAS® Enterprise). For observed data and site labels refer to Table 1 to Table 2.

Table 2.
PolSAR Biophysical Indicator Variables (Site labels as in Table 1.).
| Site | Average Target Intensity | Average Ratio | (VV+HH) | HH+2HV | Copolar | Pedestal | Coefficient | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HH | HV | VV | HH/VV | HV/HH | HV/VV | /(2HV) | +VV | HH+VV | Height | of | |
| Intensity | Intensity | Intensity | Ratio | Ratio | Ratio | Ratio | Intensity | Intensity | Linear | Variation | |
| RF3-10 | 0.0379 | 0.0038 | 0.0058 | 6.541 | 0.0995 | 0.6506 | 5.796 | 0.0512 | 0.0436 | 0.0051 | 0.0468 |
| RF3-11 | 0.0188 | 0.0031 | 0.0068 | 2.762 | 0.1644 | 0.4541 | 4.142 | 0.0317 | 0.0256 | 0.0041 | 0.0791 |
| RF4-11 | 0.0185 | 0.0018 | 0.0157 | 1.185 | 0.0996 | 0.1180 | 9.260 | 0.0379 | 0.0342 | 0.0061 | 0.0469 |
| RF3-12 | 0.0215 | 0.0036 | 0.0104 | 2.061 | 0.1662 | 0.3424 | 4.470 | 0.0391 | 0.0319 | 0.0066 | 0.0826 |
| RF4-12 | 0.0271 | 0.0033 | 0.0099 | 2.727 | 0.1233 | 0.3362 | 5.543 | 0.0437 | 0.0370 | 0.0061 | 0.0607 |
| 25-11 | 0.0341 | 0.0052 | 0.0079 | 4.341 | 0.1534 | 0.6659 | 4.010 | 0.0525 | 0.0420 | 0.0066 | 0.0678 |
| 27-11 | 0.0185 | 0.0025 | 0.0029 | 6.414 | 0.1324 | 0.8491 | 4.365 | 0.0264 | 0.0214 | 0.0025 | 0.0561 |
| 33-11 | 0.0223 | 0.0035 | 0.0059 | 3.796 | 0.1566 | 0.5943 | 4.035 | 0.0352 | 0.0282 | 0.0051 | 0.0753 |
| 25-12 | 0.0338 | 0.0070 | 0.0103 | 3.294 | 0.2078 | 0.6845 | 3.137 | 0.0581 | 0.0440 | 0.0090 | 0.1037 |
| 27-12 | 0.0215 | 0.0036 | 0.0058 | 3.715 | 0.1667 | 0.6194 | 3.806 | 0.0344 | 0.0272 | 0.0045 | 0.0776 |
| 33-12 | 0.0146 | 0.0032 | 0.0131 | 1.112 | 0.2217 | 0.2466 | 4.282 | 0.0341 | 0.0276 | 0.0058 | 0.1038 |
| 397-10 | 0.0159 | 0.0021 | 0.0105 | 1.508 | 0.1319 | 0.1990 | 6.304 | 0.0305 | 0.0264 | 0.0057 | 0.0650 |
| 978-10 | 0.0154 | 0.0023 | 0.0032 | 4.836 | 0.1496 | 0.7235 | 4.033 | 0.0232 | 0.0186 | 0.0027 | 0.0698 |
| 397-11 | 0.0131 | 0.0033 | 0.0140 | 0.936 | 0.2495 | 0.2334 | 4.147 | 0.0337 | 0.0272 | 0.0064 | 0.1123 |
| 978-11 | 0.0259 | 0.0034 | 0.0068 | 3.827 | 0.1328 | 0.5084 | 4.747 | 0.0396 | 0.0327 | 0.0060 | 0.0623 |
| 397-12 | 0.0060 | 0.0013 | 0.0142 | 0.420 | 0.2223 | 0.0935 | 7.599 | 0.0229 | 0.0202 | 0.0031 | 0.0462 |
| 978A-12 | 0.0093 | 0.0013 | 0.0164 | 0.569 | 0.1448 | 0.0823 | 9.526 | 0.0284 | 0.0257 | 0.0042 | 0.0398 |
| Water | 0.0004 | 0.0002 | 0.0008 | 0.488 | 0.5564 | 0.2715 | 2.740 | 0.0017 | 0.0012 | 0.0003 | 0.1260 |
| Site | Freeman-Durden | Cloude-Pottier | HH + VV | HH+VV Correlation | |||||||
| Double | Surface | Entropy | Anisotropy | Alpha | Beta | Phase | Magnitude | Coefficient | |||
| Bounce | Scatter | Difference | Real | Imaginary | |||||||
| RF3-10 | 0.0001 | 0.0322 | 0.5526 | 0.2009 | 43.51 | 12.77 | 24.96 | 0.2792 | 0.2531 | 0.1178 | |
| RF3-11 | 0.0022 | 0.0141 | 0.7257 | 0.3121 | 40.21 | 16.45 | −5.14 | 0.3737 | 0.3722 | −0.0334 | |
| RF4-11 | 0.0115 | 0.0171 | 0.7185 | 0.7255 | 41.04 | 9.95 | −53.44 | 0.3535 | 0.2105 | −0.2839 | |
| RF3-12 | 0.0060 | 0.0152 | 0.7843 | 0.4382 | 42.41 | 11.22 | −15.44 | 0.2771 | 0.2671 | −0.0738 | |
| RF4-12 | 0.0061 | 0.0209 | 0.7096 | 0.4501 | 41.62 | 9.66 | −23.85 | 0.3075 | 0.2812 | −0.1243 | |
| 25-11 | 0.0263 | 0.0000 | 0.6785 | 0.2466 | 45.99 | 18.16 | −44.36 | 0.2086 | 0.1491 | −0.1458 | |
| 27-11 | 0.0000 | 0.0149 | 0.5884 | 0.1941 | 44.72 | 18.75 | −12.20 | 0.2187 | 0.2137 | −0.0462 | |
| 33-11 | 0.0012 | 0.0165 | 0.7149 | 0.2601 | 45.89 | 15.79 | 5.58 | 0.1636 | 0.1628 | 0.0159 | |
| 25-12 | 0.0000 | 0.0232 | 0.7774 | 0.1649 | 46.60 | 14.18 | −15.94 | 0.2002 | 0.1925 | −0.0550 | |
| 27-12 | 0.0004 | 0.0161 | 0.6999 | 0.2098 | 42.65 | 18.91 | 6.11 | 0.3126 | 0.3108 | 0.0333 | |
| 33-12 | 0.0071 | 0.0108 | 0.8214 | 0.5231 | 41.96 | 19.41 | −36.12 | 0.3047 | 0.2461 | −0.1797 | |
| 397-10 | 0.0071 | 0.0130 | 0.7727 | 0.6266 | 40.22 | 11.77 | 9.75 | 0.2689 | 0.2650 | 0.0455 | |
| 978-10 | 0.0000 | 0.0120 | 0.6463 | 0.1272 | 43.89 | 17.14 | 31.07 | 0.3202 | 0.2743 | 0.1652 | |
| 397-11 | 0.0073 | 0.0101 | 0.8455 | 0.5470 | 42.09 | 29.49 | 9.57 | 0.2244 | 0.2213 | 0.0373 | |
| 978-11 | 0.0199 | 0.0025 | 0.6919 | 0.3491 | 47.66 | 14.50 | 63.17 | 0.1102 | 0.0497 | 0.0983 | |
| 397-12 | 0.0133 | 0.0030 | 0.6683 | 0.5664 | 53.68 | 8.66 | −128.51 | 0.3886 | −0.2419 | −0.3041 | |
| 978A-12 | 0.0162 | 0.0054 | 0.6517 | 0.6491 | 49.94 | 7.35 | −103.38 | 0.4626 | −0.1071 | −0.4500 | |
| Water | 0.0005 | 0.0001 | 0.8635 | 0.3371 | 48.75 | 22.45 | −41.08 | 0.0899 | 0.0678 | −0.0591 | |

Table 3.
Regression models used to estimate the field-based biophysical variables. FDDB = Freeman–Durden Double Bounce, CPAlpha = Cloude–Pottier Alpha angle, HHVVPhDif = Phase difference, HHVVIM = Imaginary Correlation Coefficient, CoefVAR = Coefficient of Variation, MSE = Model Mean Square Error. Highlighted cells denote model parameters used to produce the LAI and LAD images.
| Biophysical | Regression Model | ||||||
|---|---|---|---|---|---|---|---|
| PolSAR Variables | Parameters | Parital R2 | Pr > F | Tol–VIF | R2 (#Obs) | MSE | |
| Dead Biomass Water | Intercept | −317 ± 277 | 0.28 | 0.64 (14) | 2.72E+05 | ||
| HV | 2901 ± 633 | 0.64 | 0.0006 | ||||
| Dead Biomass Water | Intercept | −2767 ± 1062 | 0.0245 | 0.76 (14) | 1.97E+05 | ||
| HV/VV | 5302 ± 1149 | 0.64 | 0.0006 | 0.22– 4.55 | |||
| VV | 151,201 ± 63,919 | 0.12 | 0.0374 | 0.22– 4.55 | |||
| Live Biomass Water | Intercept | 1425 ± 219 | <0.0001 | 0.55 (14) | 2.94E+05 | ||
| FDDB | −90,379 ± 23,653 | 0.55 | 0.0024 | ||||
| Live Biomass Water | Intercept | 709 ± 491 | 0.1765 | 0.63 (14) | 2.60E+05 | ||
| HV/VV | 13,191 ± 822 | 0.09 | 0.137 | 0.56–1.76 | |||
| FDDB | −59,189 ± 29,540 | 0.55 | 0.0704 | 0.56–1.76 | |||
| Total Biomass Water | Intercept | −428 ± 538 | 0.44 | 0.61 (14) | 1.02E+06 | ||
| HV/VV | 5304 ± 1229 | 0.61 | 0.001 | ||||
| Total Biomass Water | Intercept | 921 ± 894 | 0.3249 | 0.70 (14) | 8.61E+05 | ||
| HV/VV | 3521 ± 1497 | 0.61 | 0.0384 | 0.57–1.76 | |||
| FDDB | −97,330 ± 53,790 | 0.09 | 0.0978 | 0.57–1.76 | |||
| Total Biomass Water | Intercept | −2099 ± 2291 | 0.3811 | 0.75 (14) | 7.88E+05 | ||
| HV/VV | 6503 ± 2540 | 0.61 | 0.0284 | 0.18–5.55 | |||
| FDDB | −09253 ± 5157 | 0.09 | 0.103 | 0.56–1.77 | |||
| VV | 182,252 ± 128,231 | 0.05 | 0.1857 | 0.22–4.57 | |||
| LAI | Intercept | 1.45 ± 0.41 | 0.0029 | 0.49 (17) | 0.6624 | ||
| HV/VV | 3.16 ± 0.82 | 0.49 | 0.0016 | ||||
| LAI | Intercept | 1.39 ± 0.40 | 0.0036 | 0.56 (17) | 0.6154 | ||
| HV/VV | 5.98 ± 2.09 | 0.49 | 0.0016 | 0.14–6.89 | |||
| HH/VV | −0.40 ± 0.27 | 0.07 | 0.1651 | 0.14–6.89 | |||
| LAI | Intercept | 6.60 ± 2.59 | 0.029 | 0.77 (17) | 0.4432 | ||
| HV/VV | 6.35 ± 1.86 | 0.49 | 0.0066 | 0.13–7.6 | |||
| HH/VV | −0.437 ± 0.232 | 0.07 | 0.09 | 0.14–7.1 | |||
| FDDB | 69.21 ± 28.00 | 0.03 | 0.033 | 0.58–1.7 | |||
| CPAlpha | −0.126 ± 0.063 | 0.05 | 0.072 | 0.53–1.9 | |||
| HHVVPhDif | −0.0234 ± 0.011 | 0.04 | 0.059 | 0.10–10.2 | |||
| HHVVIM | 7.69 ± 3.23 | 0.09 | 0.038 | 0.10–10.1 | |||
| LAD | Intercept | 2.14 ± 0.43 | 0.0002 | 0.58 (17) | 1.97E−02 | ||
| HV/HH | −2.42 ± 0.84 | 0.38 | 0.008 | 0.95–1.06 | |||
| CPAlpha | −0.026 ± 0.0099 | 0.2 | 0.021 | 0.95–1.06 | |||
| LAD | Intercept | 2.81 ± 0.43 | <0.0001 | 0.74 (17) | 0.0131 | ||
| CoefVAR | −6.47 ± 1.47 | 0.34 | 0.0007 | 0.83–1.21 | |||
| CPAlpha | −0.039 ± 0.0089 | 0.33 | 0.0008 | 0.78–1.28 | |||
| HHVVIM | 0.398 ± 0.196 | 0.08 | 0.0637 | 0.79–1.26 | |||
4.4. Mapping Marsh Canopy LAI and LAD
The black and white 2009 to 2012 continuous images in Figure 4 represent the density (LAI) and average orientation (LAD) of the marshes surrounding Barataria Bay. The LAI images were produced with a common continuous look-up table, providing direct comparability. Higher LAIs are brighter and lower LAIs are darker. Black–white 2009 to 2012 LAD reproductions were produced similarly. LAI and LAD yearly ranges are obtainable from Table 4.
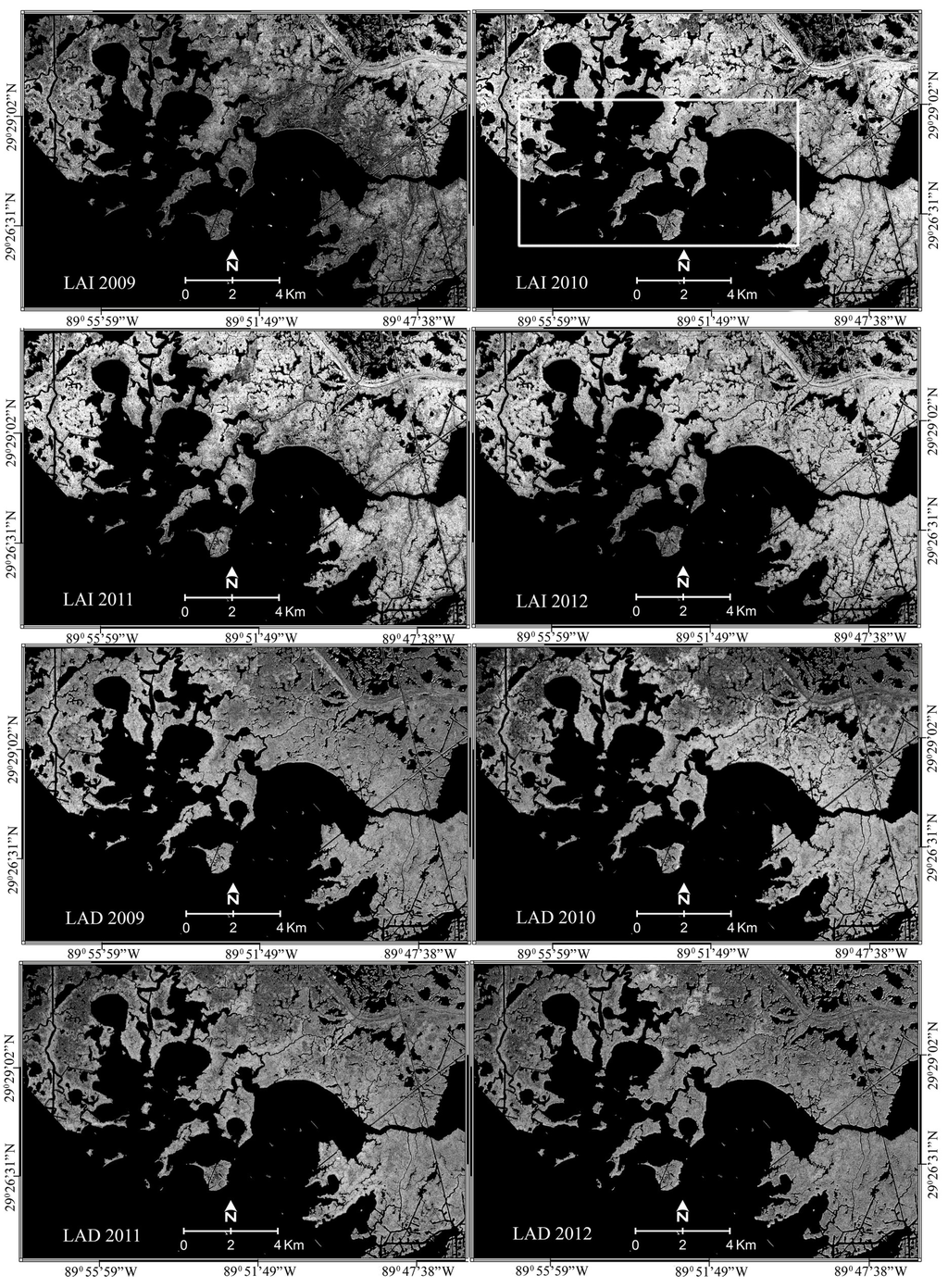
Figure 4.
LAI (top 2009 to 2012) and LAD (bottom 2009 to 2012) were mapped based on regression models shown in Table 3. Brightness representing increasing LAI or LAD (Table 4) is directly comparable from year to year. The box shown on the 2010 LAI map approximately outlines the core oil impact region in Barataria Bay.

Table 4.
Classes are aligned to best match similar LAI and LAD class means from year to year (Figure 5). Grey shading signifies a comparable class was not found in one year that existed in another year. The same color in each year signifies a similar LAI and often a similar LAD. The class colors assigned in the table match the class colors applied in Figure 5. CLS = Class, OBS = the observations (or pixels) comprising each class and MN = Mean.
| 2009 | 2010 | 2011 | 2012 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CLS | OBS | MN LAD | MN LAI | CLS | OBS | MN LAD | MN LAI | CLS | OBS | MN LAD | MN LAI | CLS | OBS | MN LAD | MN LAI |
| 1 | 13,280 | 0.4 | 11 | ||||||||||||
| 2 | 33,362 | 0.4 | 9.2 | 1 | 65,121 | 0.31 | 8.8 | ||||||||
| 3 | 109,761 | 0.43 | 7.9 | 2 | 223,559 | 0.42 | 7.2 | ||||||||
| 1 | 36,353 | 0.42 | 6.5 | 4 | 275,644 | 0.5 | 6.6 | 3 | 501,057 | 0.45 | 5.9 | 1 | 249,634 | 0.41 | 6.3 |
| 2 | 252,305 | 0.44 | 4.8 | 5 | 787,565 | 0.62 | 5.3 | 4 | 912,760 | 0.52 | 4.8 | 2 | 950,110 | 0.45 | 5 |
| 3 | 798,197 | 0.55 | 3.6 | 6 | 1,596,081 | 0.72 | 4 | 5 | 1,201,247 | 0.61 | 3.7 | 3 | 1,392,628 | 0.52 | 3.9 |
| 4 | 1,558,891 | 0.66 | 2.6 | 7 | 867,038 | 0.67 | 2.6 | 6 | 797,528 | 0.68 | 2.5 | 4 | 1,066,460 | 0.61 | 2.8 |
| 5 | 1,178,380 | 0.67 | 1.6 | ||||||||||||
Included in the LAD images were values less than zero. With the exception of the negative values, the lowest LAD values generally were above 0.2. The highest numbers of these negative LADs occurred in 2010 and 2012 grouped in the most interior north and northeast marshes. Although there was possible shallow surface water in 2009 (<7 cm), surface flooding was not indicated in the hydrologic stations surrounding Barataria Bay at the time of the 2010 to 2012 collections. Inspection of the PolSAR image data suggested that the negative LADs could be associated with possible flooding or small open water-filled depressions (ponds). Assessment of the selected PolSAR indicator variables (Table 2) showed that the coefficient of variation, imaginary correlation coefficient, and the copolar phase difference exhibited substantial sensitivity to subcanopy flooding when over 60% of the canopy was submerged. Similar copolar phase difference sensitivity to flooded vegetation has been noted [44]. However, as noted in Table 1, a number of field sites were flooded at the times of PolSAR collections, particularly in Golden Meadow, and these sites did not exhibit abnormal responses in the regression model (Figure 3a,b). It seems more likely that ephemeral features such as ponded open water moved the calibration response outside its operational limits. This would prove a limitation of this polarimetric mapping. The cause of the invalid LAD estimates is being pursued, and once confirmed, the limitation will be reported and avoidance incorporated into the mapping. Neighborhood pixels should also be cautiously interpreted when they exhibit extreme LAI and LAD values. Negative outcomes were excluded from subsequent analyses by combining them into the open-water mask. Excluding the areas covered by the water mask, the LAI and LAD image pairs were used to produce the LAI-LAD 2009 to 2012 classified maps (Figure 5).
Composite Marsh Canopy LAI and LAD Changes
Composite LAI-LAD classifications were created to uncover the spatial relationship between LAI and LAD magnitudes. In order to improve interpretability of the 2009–2012 LAI-LAD classified maps, Table 4 was constructed so as to emphasize the year-to-year relationship of class means (MN) and dominance in the marsh landscape per year. As seen in Table 4, except for Class 7 in the 2010 classification, LAI progressively increases as LAD decreases. The table also reveals the change in marsh complexity as indicated by the number of classes. The least complex marsh landscapes were exhibited in 2009 and 2012, and the most complex in 2010 and 2011. Changes depicted in Table 4 show a shift in dominance in 2009 from a low to moderate LAI (1.6 to 2.5) to a moderately high LAI around 4 in 2010 while retaining a mixed orientation canopy. Although proportionally of low abundance, three high LAI and more vertical (LAI > 7, LAD ~ 0.4, Table 4) classes appeared in 2010 as well as the loss of the lowest LAI (highest LAD) class occurring in 2009. By 2011, class dominance had shifted to a slightly decreased LAI and LAD, and while two of the highest LAI classes remained, the extreme LAI and LAD class (LAI = 11, LAD = 0.4) appearing in 2010 was absent. The class composition of 2012 retained only the lowest four of the six 2011 LAI classes, and aside from lacking the lowest LAI class, its class distribution displayed progressive similarity to that exhibited in 2009.

Figure 5.
LAI-LAD classes (2009 to 2012). See Table 4 for the LAI-LAD color legend, which specifies the classes by number and color code, and their LAI and LAD means. The approximate core oil impact area is depicted in Figure 4 (LAI 2010). Most pixels fall into the moderate to moderate-high LAI classes (green through brown). Within these classes, the green classes have higher LAI than the brown (bright green = highest, dark brown = lowest), and lower LAD, although for LAD the brighter (darker) of the two green (brown) classes is not always the lowest (highest) LAD (exception in 2010). Red pixels have the highest (lowest) LAI (LAD). A detailed discussion is given in Section 4.4.1.
The produced LAI-LAD maps exhibited substantial changes from 2009 to 2012 (Figure 5). As in construction of Table 4, yearly comparability of class distributions and changes are promoted by using the same color from year to year for similar classes. The 2009 classified map displayed a low LAI and high LAD class that although spatially extensive in 2009 was not uniquely present after 2009. By 2010, there was a fairly dramatic and ubiquitous increase in LAI accompanied by a slight increase in LAD. Associated with the overall density increase, marsh exhibiting the highest LAIs (LAI = 6.5 and 4.8, Table 4) found in the northeast of the 2009 map now extended throughout the interior marsh. A minor component contained within the heart of this expansion included more vertically oriented marshes of much higher LAIs (LAI > 7, Table 4, Figure 5). These highest LAI (lowest LAD) classes were spatially associated with the out-of-bounds LADs that indicated incompatibility of the inferred LAD relationship. Although invalid LADs were eliminated from the landcover classifications, their spatial alignment with the most extreme 2010 LAI-LAD classes warrants caution in interpreting these highest values. Also in 2010, LAI increases in the core oil impacted marshes (Figure 5) followed the overall trend of the non-impacted and more interior marsh; however, within some core islands LAI increases in the interior marsh lagged those in the more nearshore marsh facing the Barataria Bay entrance.
There was a slight LAI and accompanying LAD decrease by 2011 in all marsh classes (Table 4, Figure 5). Within the overall LAI and LAD decreases, the most extreme 2010 LAI marsh class disappeared and the two remaining extreme classes of 2010 had diminished by 2011. The number of pixels containing invalid LADs also decreased from 2010 to 2011. The 2009 to 2010 spatial extension of the next highest LAI classes continued in 2011, increasingly dominating the interior marshes and occupying some nearshore marshes as well. Core island marshes tended to exhibit somewhat lower nearshore LAIs than in 2010, resulting in a more uniform marsh. Overall the 2011 classified map portrayed decreased extreme classes, a spatial expansion of moderately higher LAI and lower LAD marshes, and good preservation of marshes exhibiting somewhat lower LAIs and LADs relative to the 2010 map.
By 2012, the extreme classes first appearing in 2010 had disappeared and the expansion of moderately higher LAI classes had reversed. As a result, the lower classes expanded; however, the transforming marsh structure was associated with a more heterogenic interior marsh landscape than observed in 2010 to 2011. Within the oil impact core region, however, the 2012 marsh landscape was reminiscent of 2009. High uniformity of the core marshes, particularly island marshes, was reestablished. Overall, the 2012 marsh landscape seemed to be reverting toward the landscape of 2009.
5. Discussion
5.1. Regression Models
S. alterniflora marsh canopy structure was related to PolSAR data by deriving empirical relationships between polarimetric SAR scattering properties and site-specific canopy biomass, LAI (density), and LAD (orientation) structure indicators. The site-specific polarimetric backscatter was represented by a combination of backscatter intensities, intensity ratios, copolarization correlation and phase, backscatter spatial heterogeneity, and backscatter mechanisms obtained by decomposition of the complex polarimetric data.
5.1.1. Regression Model Accuracy, Error, and Uncertainty
Residual quantile and distribution of the residual plots indicate normality of the error in both the LAI and LAD regression models listed in Table 3. Residuals versus PolSAR independent variable plots are well distributed about zero also satisfying the statistical requirements for conducting regression analysis. The mean-square-error values indicate prediction accuracies of ±0.44 for LAI and ±0.13 for LAD with the suite of PolSAR-biophysical variables input into each regression. The observed vs. predicted plots confirm a one-to-one correspondence and zero bias on the prediction (Figure 3). The TOL and VIF values indicate low collinearity of the independent variables entered into the LAD regression, and although acceptable, higher collinearity of the independent variables in the LAI regression (Table 3). The higher collinearity means higher uncertainty in assessing the importance of each PolSAR variable in the LAI regression. However, the relatively low prediction errors, normal residual distributions, and nonbiased and one-to-one observed and predicted correlations combined with the stepwise partial regression R2 values allowed cautious examination of the PolSAR variable composition.
5.1.2. Leaf Area Index
PolSAR indicator variables comprising the LAI regression model were a mix of intensity ratios, backscatter mechanisms obtained through decomposition, and copolar phase difference and coherence (Table 3). The series of regression models obtained through incremental increases in the stepwise tolerance criteria shows that HV/VV (or VH/VV, absent in this dataset) dominates explanation of the LAI variance, a result that is well established in the literature. Most often the correspondence is with changes in gravimetric dry biomass weight or vegetation water content (VWC) and incorporates HV intensity singularly or as HV/VV or HV/HH intensity ratios. The result also conforms to the VWC regression results (Table 3). The HV/VV ratio was the dominant or one of the two dominant PolSAR-based regressors in the dead and total biomass stepwise regression models. Although the HH/VV ratio was of secondary importance in explaining LAI variance, the ratio has shown a relationship to biomass and LAI (e.g., [73,74]).
Of the secondary variables, the FDDB and CPAlpha regressors (refer to Table 3 for definitions) captured changes in the scatter mechanism as defined in Freeman–Durden and Cloud–Pottier decompositions, respectively. The imaginary correlation coefficient (range 0.17 to –0.45) has a relatively high model partial R2 value, and, as manifested in borderline TOL and VIF, a high linear correspondence with the HH and VV phase difference (range 63° to –128°) (Table 3). The high covariation reflects the complex correlation influence on the phase difference [75]. Judging by the overall low magnitude real correlation coefficient (range of 0.18 ± 0.15), backscatter at HH and VV are largely uncorrelated [76]. The high ranges of the imaginary coefficient and phase difference and the uncorrelated HH and VV backscatter indicate the diverse structural complexity of the marshes sampled. This diversity is reflected in the regressor set that, although dominated by intensity ratios indicating volume scatter, includes secondary regressors reflecting the scatter coherence and other scatter mechanisms.
5.1.3. Leaf Angle Distribution
The best two regressor solution for mapping LAD included the intensity ratio, HV/HH, and the Cloude–Pottier Alpha angle (CPAlpha) reflecting changes in the scatter mechanism (Table 3). Separate correlation analysis found the HV/HH ratio did not covary with the HV/VV ratio, the dominant LAI regressor. This finding supports uncorrelated backscatter at HH and VV, and shows the independence of the two volume scatter ratios as related to this S. alterniflora dataset. The three regressor model retained CPAlpha, and replaced the HV/HH ratio with the coefficient of variation (CoefVAR) and imaginary correlation coefficient (HHVVIM) (Table 3). In this dataset, HHVVIM is strongly related with the copolar phase difference. The coefficient of variation (range 0.11 to 0.040) corroborates the uncorrelated backscatter at HH and VV indicated by the real correlation coefficient and suggests the backscatter is mostly unpolarized, or that the spatial texture at each marsh site is generally homogenous.
5.2. Applying the Regression Models to Map Marsh Canopy LAI and LAD
The sets of yearly LAI and LAD continuous maps (Figure 4 and Figure 5) and the combined LAI-LAD classified maps exhibit a spatially extensive increase in marsh LAI from 2009 to 2010. Within that overall density increase, LAD, fairly uniform in 2009, divided into two broad groups. Lower LAD signifying more vertical oriented marsh spatially covaried with marsh of higher density (LAI), while more horizontal marshes were associated with the lower LAI ranges. Of the former classes, minor classes exhibiting the most extreme LAIs occupied the heart of the expanded regions and were more spatially aligned with invalid LAD values. While all pixels having invalid LAD’s were excluded in the classification, the highest LAIs represented in these classes should also be interpreted cautiously. However, the remaining classes dominated the relatively more vertical and dense marshes extending far beyond this highest LAI class found at the center of their expansion. The extensiveness and persistence of these more vertical and dense interior marshes through 2011 indicate a pattern of new growth in 2010. Overall, LAD became more spatially uniform and LAI broadly decreased by 2011 with some selectively higher decreases along marsh shorelines impacted in the 2010 oil spill. These trends continued into 2012 with island marshes in the oil impact core portraying the sharpest LAI decline.
Aside from the somewhat disjointed trends of islands marshes within the oil spill core impact, the 2010 abrupt LAI increase in interior marshes may have been part of a regional trend. Optical and UAVSAR image data collected in 2010 to 2012 to the northwest and inland of Barataria Bay captured a dramatic dieback of marsh from 2010 to 2011 [14]. Results of the mapping found that in 2010 dieback marshes contained higher biomass quantity and live composition than surrounding non-dieback marshes. The cause of that 2011 sudden dieback was unresolved; however, in this case, there was an action in response to the oil spill that could have promoted increased coastal marsh growth in both these marshes and marshes surrounding Barataria Bay.
In order to help prevent oil from reaching coastal wetlands during the DWH spill event, freshwater releases from the Mississippi River were increased or initiated from locations ranging from just upriver of New Orleans to downriver in the delta north of Barataria Bay [77,78,79,80]. The largest of these releases began on 30 April 2010, ten days after the DWH spill began, with the specific intent of lessening oil entry into Barataria Bay. The UAVSAR data were acquired during the spill on 23 June 2010. Whether this release or other freshwater releases between the 2009 and 2010 UAVSAR acquisitions were responsible for the increased growth, and thereby a change in marsh structure from 2009 to 2010, has implications on whether backscatter changes in the oil core interior marshes as noted by Ramsey et al. [55] were a direct result of oil presence. Although the high changes in marsh structure were outside the core impact area, moderate increases in LAI also occurred in core oil impact marshes. Shoreline oiling and concurrent backscatter change were confirmed, as was the presence of low concentrations of oil in core interior marshes at the time of the documented backscatter change [81]. However, the causal mechanism of the backscatter change in the core interior marshes located straight inland of the oiled shorelines was not determined. These results indicate changes of backscatter in the interior marshes of the core impact area could have resulted fully or in part from a change in marsh structure from 2009 to 2010.
The possible role of oil distributed into the interior marshes within the core region in combination with structure change is not directly determinable based on the 2009 to 2010 marsh structure maps. While oil related causes of backscatter in the interior marsh in 2010 are not excluded, changes after 2010 suggest there could have been a longer-term differential response of structure within the core region. Nearly immediate changes to marsh have been noted, especially when exposed to oil during the growing season [82]. Longer-term changes associated with oil exposure were reported by Burk [83], and recent findings point to a longer-term response of marsh associated with oil contained in the sediment [84]. A more thorough examination is required into the relationships between the dramatic 2009 to 2010 marsh structure change, elevated freshwater inputs, the 2009 to 2010 backscatter change, and the combined occurrences of oil exposure and marsh structure change. Those relationships are being further explored and will be reported as analyses are completed.
6. Conclusions
Field measurements collected at seven S. alterniflora marsh sites over a two to three year period in coordination with polarimetric synthetic aperture radar (PolSAR) data collected from the NASA UAVSAR platform were used to create empirical relationships between the marsh leaf area index (LAI) and leaf angle distribution (LAD) and PolSAR-based biophysical indicators in order to advance observation of wetland vegetation type and health status through use of radar remote sensing. This study used field data acquired at seven test sites, three in Barataria Bay, two at Golden Meadows, and two at Rockefeller Refuge, and is unique in having one acquisition (2009) a year before the Deepwater Horizon spill occurred, one during the spill (2010), and two post-spill (2011–2012), with the post-spill acquisitions timed to nearly match tidal conditions of the 2010 acquisition. The results show that the explanatory power of the polarimetric relationships with LAI equaled or exceeded relationships with typical field collected data, namely dead, live, and total vegetation water content (VWC). The HV/VV intensity ratio singularly explained 49% of the LAI variance, and in a two regressor solution, HV/HH explained 38% of LAD variance. A six regressor model was necessary to explain 77% and a three regressor model for explaining 74% of the LAI and LAD variance, respectively. Secondary regressors in the six variable LAI regression model were HH and VV coherence and phase difference and variability in backscatter mechanics. Similar secondary information was used in the three variable LAD regression model, but no intensity ratio was included. Instead, a PolSAR-based regressor was selected emphasizing the fractional polarization or the homogeneity of the site area. Results of this work offer a methodology where remote measurements of PolSAR parameters can be used in place of field measurements to increase the spatial extent and information content of marsh classifications.
This study is unique in using data from UAVSAR, which is a fine resolution, low noise, L-band synthetic aperture radar, to obtain higher accuracy and greater sensitivity in the PolSAR parameters, which led to more accurate regression analysis for landscape mapping. Future studies could constrain the classes better if more sites were used. The study demonstrates the improved monitoring performance for appraising wetland condition and dynamics offered by polarimetric data, particularly when used to map canopy structure. Advanced performance was demonstrated in the mapping of previously unknown trends of marsh structure in and near oil impacted coastal wetlands that underwent widespread growth and subsequently a progressive decline in 2009–2012, the years encompassing the Deepwater Horizon spill. The near weather-independent and daylight-independent operational capabilities of radar-based landscape mapping enhance responsiveness to emergencies and adherence to planned collection strategies independent of weather conditions. Combined with optical mapping, these new polarimetric mapping capabilities will more fully describe, and therefore track, wetland status and trends.
Acknowledgments
We thank Francis Fields Jr. of the Apache Louisiana Minerals LLC, a subsidiary of Apache Corporation, for access to their properties, and Jeff Deblieux IV of the Louisiana Land and Exploration Company, a subsidiary of Conoco Phillips, for access to their properties. We are indebted to late Clint Jeske and Steve Hartley of the U.S. Geological Survey for their critical assistance in sample collections, Kevin Jones and PCI Geomatics staff for timely solutions to complex image processing obstacles, and Professor Yong Wang at East Caroline University for his insightful and constructive review. Research was supported in part by the National Aeronautics Space Administration (NASA) Grant #11-TE11-104 and was carried out in collaboration with the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA, and supported in part by U.S. Geological Survey Hurricane Sandy Supplemental Funds. UAVSAR data are provided courtesy of NASA/JPL-Caltech. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Author Contributions
Elijah Ramsey III, Amina Rangoonwala, and Cathleen Jones conceived the study. Elijah Ramsey III and Amina Rangoonwala performed the field collections and PolSAR data analysis. Elijah Ramsey III, Amina Rangoonwala, and Cathleen Jones wrote the manuscript. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Colwell, J. Vegetation canopy reflectance. Remote Sens. Environ. 1974, 3, 175–183. [Google Scholar] [CrossRef]
- Chance, J.; Cantu, J. A Study of Plant Canopy Reflectance Models; Pan American University Library: Edinburg, TX, USA, 1975; p. 61. [Google Scholar]
- Hardisky, M.; Klemas, V.; Smart, R. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Myneni, R.; Maggion, S.; Iaquinta, J.; Privette, J.; Gobron, N.; Pinty, B.; Kimes, D.; Verstraete, M.; Williams, D. Optical remote sensing of vegetation: Modeling, caveats, and algorithms. Remote Sens. Environ. 1995, 51, 169–188. [Google Scholar] [CrossRef]
- Allen, W.; Richardson, A. Interaction of light with a plant canopy. J. Opt. Soc. Am. 1968, 58, 1023–1028. [Google Scholar] [CrossRef]
- Ranson, K.; Daughtry, C.; Biehl, L.; Bauer, M. Sun-view angle effects on reflectance factors of corn canopies. Remote Sens. Environ. 1985, 18, 147–161. [Google Scholar] [CrossRef]
- Huete, A.; Jackson, R. Soil and atmosphere influences on the spectra of partial canopies. Remote Sens. Environ. 1988, 25, 89–105. [Google Scholar] [CrossRef]
- Peterson, D.; Aber, J.; Matson, P.; Card, D.; Swanberg, N.; Wessman, C.; Spanner, M. Remote sensing of forest canopy and leaf biochemical contents. Remote Sens. Environ. 1988, 24, 85–108. [Google Scholar] [CrossRef]
- McCloy, K.; Schoneveld, R.; Kemp, D. Measurement of pasture parameters from reflectance data. Int. J. Remote Sens. 1993, 14, 1107–1118. [Google Scholar] [CrossRef]
- Lorenzen, B.; Jensen, A. Reflectance of blue, green, red and near infrared radiation from wetland vegetation used in a model discriminating live and dead above ground biomass. New Phytol. 1988, 108, 345–355. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant. Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Spanglet, H.; Ustin, S.; Rejmankova, E. Spectral reflectance characteristics of California subalpine marsh plant communities. Wetlands 1998, 18, 307–319. [Google Scholar] [CrossRef]
- Ramsey, E., III; Nelson, G.; Sapkota, S.; Laine, S.; Verdi, J.; Krasznay, S. Using multiple polarization L band radar to monitor marsh burn recovery. IEEE Trans. Geosci. Remote Sens. 1999, 37, 635–639. [Google Scholar] [CrossRef]
- Ramsey, E., III; Rangoonwala, A.; Chi, Z.; Jones, C.E.; Bannister, T. Marsh dieback, loss, and recovery mapped with satellite optical, airborne polarimetric radar, and field data. Remote Sens. Environ. 2014, 152, 364–374. [Google Scholar] [CrossRef]
- Ramsey, E., III; Rangoonwala, A. Image fusion and landcover mapping: Emphasizing radar and optical image data and wetland resources. In Advances in Wetland Classification and Mapping; Tiner, R., Klemas, V., Lang, M., Eds.; CRC Press, Taylor and Francis Group: Boca Rotan, FL, USA, 2015; pp. 155–172. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; Leeuwen, W. MODIS vegetation index (MOD 13) algorithm theoretical basis document version 3, 1999. Available online: http://modis.gsfc.nasa.gov/data/atbd /atbd_mod13.pdf (accessed on 18 June 2013).
- Thenkabail, P.S.; Mariotto, I.; Gumma, M.K.; Middleton, E.M.; Landis, D.R.; Huemmrich, K.F. Selection of hyperspectral narrowbands (HNBs) and composition of hyperspectral twoband vegetation indices (HVIs) for biophysical characterization and discrimination of crop types using field reflectance and Hyperion/EO-1 data. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2013, 6, 427–439. [Google Scholar] [CrossRef]
- Qi, J.; Kerr, Y.; Moran, M.; Weltz, S.; Huete, A.; Sorooshian, S.; Bryant, R. Leaf area index estimates using remotely sensed data and BRDF models in a semiarid region. Remote Sens. Environ. 2000, 73, 18–30. [Google Scholar] [CrossRef]
- Breda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Guo, X. Leaf Area Index estimation using remotely sensed data for Grassland National Park. Prairie Perspect. 2006, 9, 105–117. [Google Scholar]
- Pairman, D.; McNeill, S.; Scott, N.; Belliss, S. Vegetation identification and biomass estimation using AIRSAR data. Geocarto. Int. 1999, 14, 69–77. [Google Scholar] [CrossRef]
- He, Y.; Guo, X.; Wilmshurst, J.F. Comparison of different methods for measuring leaf area index in a mixed grassland. Can. J. Plant Sci. 2007, 87, 803–813. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. The description and measurement of plant canopy structure. In Plant Canopies: Their Growth, Form and Function; Russell, G., Marshall, B., Jarvis, P.G., Eds.; Cambridge University Press: Cambridge, UK, 1989; pp. 1–9. [Google Scholar]
- Watson, D.J. Comparative physiological studies on the growth of field crops. I. Variation in net assimilation rate and leaf area between species and varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar]
- Rakocevic, M.; Sinoquet, H.; Christophe, A.; V-Grancher, C. Assessing the structure of a white clover (Trifolium repens L.) canopy using 3-D digitizing. Ann. Bot. 2000, 86, 519–526. [Google Scholar] [CrossRef]
- Juarez, R.; Rocha, H.; Figueira, A.; Goulden, M.; Miller, S. An improved estimate of leaf area index based on the histogram analysis of hemispherical photographs. Agric. For. Meteorol. 2009, 149, 920–928. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.J.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Wolf, D.D.; Carson, E.; Brown, R.H. Light interception efficiency measurements. J. Agron. Educ. 1972, 1, 40–42. [Google Scholar]
- Lindquist, J.L. Performance of INTERCOM for prediction corn-velvetleaf interference across north-central United States. Weed Sci. 2001, 49, 195–201. [Google Scholar] [CrossRef]
- Lantinga, E.; Nassiri, M.; Kropff, M. Modelling and measuring vertical light absorption with grass-clover mixtures. Agric. For. Meteorol. 1999, 9, 71–83. [Google Scholar] [CrossRef]
- Anwar, M.; Akmal, M.; Shah, A.; Asim, M.; Gohar, R. Growth and yield comparison of perennial grasses as rainfed fodder production. Pak. J. Bot. 2012, 44, 547–552. [Google Scholar]
- McNeill, S.J.; Pairman, D.; Belliss, S.E.; Dalley, D.; Dynes, R. Estimation of pasture biomass using dual-polarization radar imagery; a preliminary study. In Proceedings of the 23rd International Conference Image and Vision Computing, Christchurch, New Zealand, 26–28 November 2008; pp. 1–6.
- Kappas, M.; Propastin, P. Review of available products of leaf area index and their suitability over the formerly Soviet Central Asia. J. Sens. 2012, 2012. [Google Scholar] [CrossRef]
- Jäggi, M.; Ammann, C.; Neftel, A.; Fuher, J. Environmental control of profiles of ozone concentration in grassland canopy. Atmos. Environ. 2006, 40, 5496–5507. [Google Scholar] [CrossRef]
- Brakke, T.W.; Kanemasu, E.T.; Steiner, J.L.; Ulaby, F.T.; Wilson, E. Microwave radar response to canopy moisture, leaf-area index, and dry weight of wheat, corn, and sorghum. Remote Sens. Environ. 1981, 11, 207–220. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Budzynska, M.; Tomaszewska, M.; Bartold, M.; Gatkowska, M.; Malek, I.; Turlej, K.; Napiorkowska, M. Monitoring wetland ecosystems using ALOS PALSAR (L-band, HV) Supplemented by optical Data: A case study of Biebrza Wetland in northeast Poland. Remote Sens. 2014, 6, 1605–1633. [Google Scholar] [CrossRef]
- Koyama, E.N.; Schneider, K. A novel approach to estimate soil moisture under vegetation using partial polarimetric ALOS PALSAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 421–426. [Google Scholar]
- Marghany, M.; Zabidi, N.; Hazli, W.; Kadir, W.; Hashim, M. Polarization synthetic aperture radar (SAR) data for mapping coastal zone vegetation. Int. J. Phys. Sci. 2011, 6, 6623–6629. [Google Scholar]
- Paloxcia, S.; Pampaloni, P.; Macelloni, G.; Sigismondi, S. Microwave remtoe sensing of hydrological parameters on the NOPIX area. Agric. For. Meteorol. 1999, 98, 375–387. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Ballester-Berman, J.D.; Hajnsek, I. Rice monitoring in Spain by means of time series of TerraSAR-X dual-pol images. In Proceedings of the 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry–PoLInSAR, Frascati, Italy, 26–30 January 2009.
- Zhang, L.; Zou, B.; Cai, H. Multiple-component scattering model for polarimetric SAR image decomposition. Geosci. Remote Sens. Lett. 2008, 5, 603–607. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, J.; Li, P.; Zhang, L. Seasonal inundation monitoring and vegetation pattern mapping of the Erguna floodplain by means of a RADARSAT-2 fully polarimetric time series. Remote Sens. Environ. 2014, 152, 426–440. [Google Scholar] [CrossRef]
- Dusseux, P.; Corpetti, T.; Hubert-Moy, L.; Corgne, S. Combined use of multi-temporal optical and radar satellite images for grassland monitoring. Remote Sens. 2014, 6, 6163–6182. [Google Scholar] [CrossRef]
- Henderson, R.M.; Lewis, A.J. Radar detection of wetland ecosystems: A review. Int. J. Remote Sens. 2008, 29, 5809–5835. [Google Scholar] [CrossRef]
- Beijma, S.; Comber, A.; Lamb, A. Random forest classification of salt marsh vegetation habitats using quad-polarimetric airborne SAR, elevation and optical RS data. Remote Sens. Environ. 2014, 149, 118–129. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Phase of target scattering for wetland characterization using polarimetric C-band SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3241–3261. [Google Scholar] [CrossRef]
- Sasser, C.; Visser, J.; Mouton, E.; Linscombe, J.; Hartley, S. Vegetation types in coastal Louisiana in 2007. U.S. Geological Survey Open-File Report 2008-1224. Available online: http://pubs.usgs.gov/of/2008/1224 (accessed on 20 October 2012).
- Sasser, C.; Visser, J.; Mouton, E.; Linscombe, J.; Hartley, S. Vegetation types in coastal Louisiana in 2013. U.S. Geological Survey Scientific Investigations Map 3290. Available online: http://pubs.usgs.gov/sim/3290/ (accessed on 27 March 2014).
- Neyland, R. The effects of Hurricane Rita on the aquatic vascular flora in a large fresh-water marsh in Cameron Parish, Louisiana. Castanea 2007, 72, 1–7. [Google Scholar] [CrossRef]
- Ramsey, E., III; Werle, D.; Lu, Z.; Rangoonwala, A.; Suzuoki, Y. A case of timely satellite image acquisitions in support of coastal emergency environmental response management. J. Coastal Res. 2009, 25, 1168–1172. [Google Scholar] [CrossRef]
- Ramsey, E., III; Nelson, G.; Baarnes, F.; Spell, R. Light attenuation profiling as an indicator of structural changes in coastal marshes. In Remote Sensing and GIS Accuracy Assessment; Lunetta, R.S., Lyon, J.G., Eds.; CRC Press: Boca Raton, FL, USA, 2004; pp. 59–73. [Google Scholar]
- Jones, C.E.; Minchew, B.; Holt, B.; Hensley, S. Studies of the Deepwater Horizon oil spill with the UAVSAR Radar, Monitoring and Modeling of the Deepwater Horizon Oil Spill. In A Record-Breaking Enterprise, American Geoph. Monog. Series; Liu, Y., Macfadyen, A., Ji, Z.-G., Weisberg, R.H., Eds.; American Geophysical Union: Washington, DC, USA, 2011; pp. 33–50. [Google Scholar]
- Ramsey, E., III; Rangoonwala, A.; Suzuoki, Y.; Jones, C.E. Oil detection in a coastal marsh with polarimetric SAR. Remote Sens. 2011, 3, 2630–2662. [Google Scholar] [CrossRef]
- Ramsey, E., III; Rangoonwala, A.; Jones, C.E.; Bannister, T. Marsh canopy leaf area and orientation calculated for improved marsh structure mapping. Photogramm. Eng. Remote Sens. 2015, in press. [Google Scholar]
- Ramsey, E., III; Rangoonwala, A. Site-specific canopy reflectance related to marsh dieback onset and progression in coastal Louisiana. Photogramm. Eng. Remote Sens. 2006, 72, 641–652. [Google Scholar] [CrossRef]
- Strategic Online Natural Resources Information System. SONRIS integrated applications, Louisiana Department of Natural Resources, Baton Rouge, LA, 2009. Available online: http://sonris-www.dnr.state.la.us/www_root/sonris_portal_1.htm (accessed on 24 September 2013).
- Ramsey, E., III; Lu, Z.; Suzuoki, Y.; Rangoonwala, A.; Werle, D. Monitoring duration and extent of storm surge flooding along the Louisiana coast with Envisat ASAR data. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 387–399. [Google Scholar] [CrossRef]
- McCandless, S.W., Jr.; Jackson, C.R. Principles of Synthetic Aperture Radar. In Synthetic Aperture Radar Marine User's Manual; Jackson, C.R., Apel, J.R., Eds.; U.S. Dept. of Commerce NOAA/NESDIS Publication, U.S. Govt. Print. Office: Washington, DC, USA, 2004; pp. 1–25. [Google Scholar]
- Zheng, Y.; Muellerschoen, R.; Michel, T.; Chapman, B.; Hensley, S.; Lou, Y. Geocoding of UAVSAR Data Products. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010.
- Van Zyl, J.; Ulaby, F. Scattering matrix representation for simple targets. In Radar Polarimetry for Geoscience Applications; Ulaby, F.T., Elachi, C., Eds.; Artech House: Norwood, MA, USA, 1990; pp. 17–52. [Google Scholar]
- PCI Geomatics. Geomatica SPW 10.1 User Guide (SAR Polarimetry Workstation); PCI Geomatics Enterprises, Inc: Richmond Hill, ON, Canada, 2007; p. 179. [Google Scholar]
- Wang, Y.; Davis, F.W. Decomposition of polarimetric synthetic aperture radar backscatter from upland and flooded forests. Int. J. Remote Sens. 1997, 18, 1319–1332. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S. A three component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S-E.; Kobayashi, H.; Singh, G. Three-component power decomposition for polarimetric SAR data based on adaptive volume scatter modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Titin-Schnaider, C. Discriminating Polarimetric Parameters for Radar Images and Analysis. In Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS ’99, Hamburg, Germany, 28 June–2 July 1999; pp. 2664–2666.
- Neter, J.; Wasserman, W.; Kutner, M.H. Applied Linear Regression Models; McGraw-Hill: Irwin, IL, USA, 1989. [Google Scholar]
- Hair, J.F., Jr.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis, 3rd ed.; Macmillan: New York, NY, USA, 1995. [Google Scholar]
- O'Brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Kornelsen, K.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 461–474. [Google Scholar] [CrossRef]
- Mitchell, R.; Moser, L.; Moore, K.; Redfeam, D. Tiller demographics and leaf area index of four perennial pasture grasses. Agron. J. 1998, 90, 47–53. [Google Scholar] [CrossRef]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications (Optical Science and Engineering); CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Chernyak, V.S. Fundamentals of Multisite Radar Systems: Multistatic Radars and Multistatic Radar Systems; CRC Press: Boca Raton, FL, USA, 1998; p. 492. [Google Scholar]
- Ball, J. Fresh Water Aimed at Oil Kills Oysters. Wall Str. J. 21 July 2010. Available online: http://www.wsj.com/articles/SB10001424052748704720004575377503611992306 (accessed on: 5 February 2015).
- Bianchi, T.; Cook, R.; Perdue, E.; Kolic, P.; Green, N.; Zhang, Y.; Smith, R.; Kolker, A.; Ameen, A.; King, G.; et al. Impacts of diverted freshwater on dissolved organic matter and microbial communities in Barataria Bay, Louisiana, USA. Mar. Environ. Res. 2011, 72, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Justic, D.; Inoue, M.; Hoda, A.; Huang, H.; Park, D. Impacts of Mississippi River diversions on salinity gradients in a deltaic Louisiana estuary: Ecological and management implications. Estuar. Coast. Shelf S. 2012, 111, 17–26. [Google Scholar] [CrossRef]
- O’Connor, B.S. Impacts of the Anomalous Mississippi River Discharge and Diversions on Phytoplankton Blooming in the Northeastern Gulf of Mexico in August 2010. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2013. [Google Scholar]
- Ramsey, E., III; Meyer, B.M.; Rangoonwala, A.; Overton, E.; Jones, C.E.; Bannister, T. Oil source-fingerprinting in support of polarimetric radar mapping of Macondo-252 oil in Gulf Coast marshes. Mar. Pollut. Bul. 2014, 89, 85–95. [Google Scholar] [CrossRef] [PubMed]
- Hershner, C.; Lake, J. Effects of chronic oil pollution on a salt-marsh grass community. Mar. Biol. 1980, 56, 163–173. [Google Scholar] [CrossRef]
- Burk, C.J. A four year analysis of vegetation following an oil spill in a freshwater marsh. J. Appl. Ecol. 1978, 14, 515–522. [Google Scholar] [CrossRef]
- Judy, C.; Graham, S.; Lin, Q.; Hou, A.; Mendelssohn, I. Impacts of Macondo oil from Deepwater Horizon spill on the growth response of common Phagmities australis: A mesocosm study. Mar. Pollut. Bul. 2014, 79, 69–76. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).