Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth
Abstract
:1. Introduction
2. Goal and Objectives
3. Materials and Methods
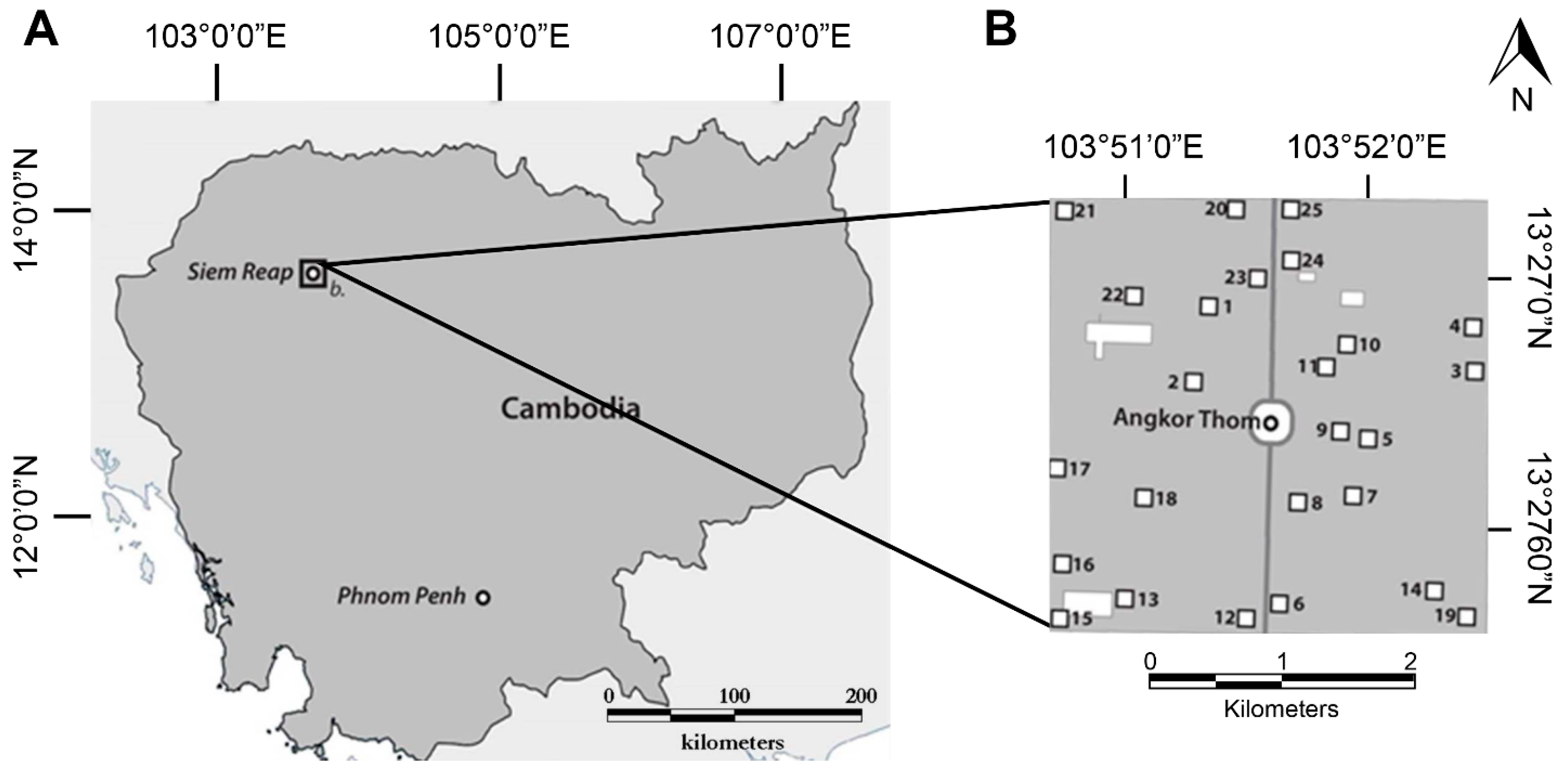
3.1. Study Area
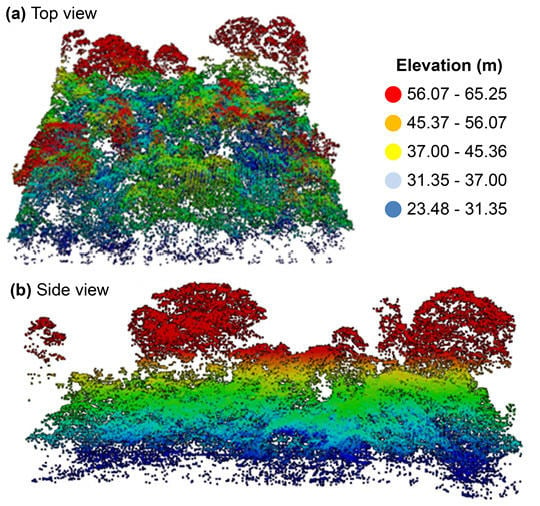
3.2. Field Data Collection
3.3. Analysis of Aerial Imagery Data

3.4. Texture Analysis of Aerial Imagery
3.4.1. Grey Level Co-Occurrence Matrix
3.4.2. Fourier-Based Textural Ordination
3.4.3. Gabor Wavelet-Based Texture Measures
3.5. Machine Learning to Model AGB
3.5.1. Support Vector Regression
3.5.2. Random Forests Models
4. Results
4.1. GLCM-Derived AGB Estimates
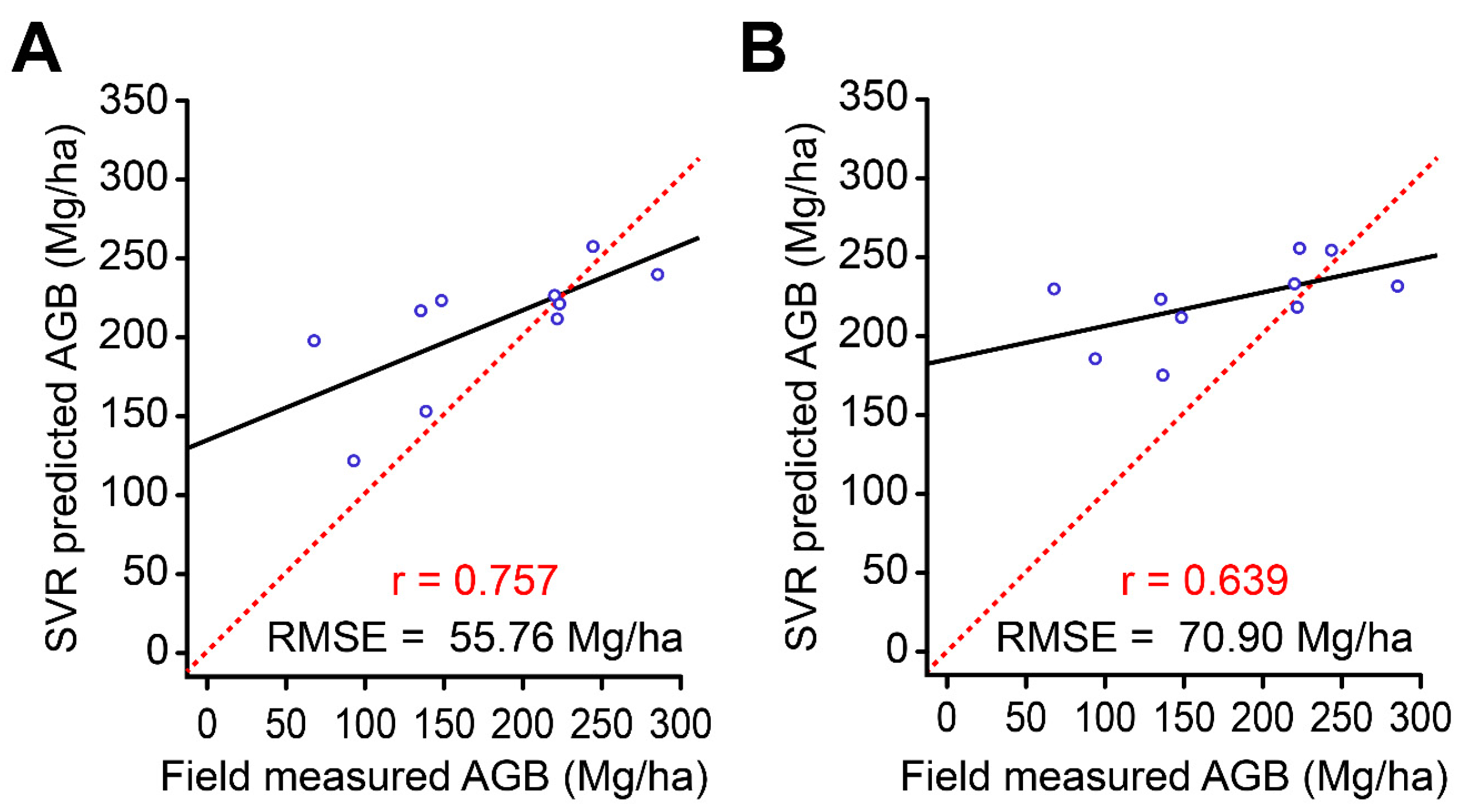
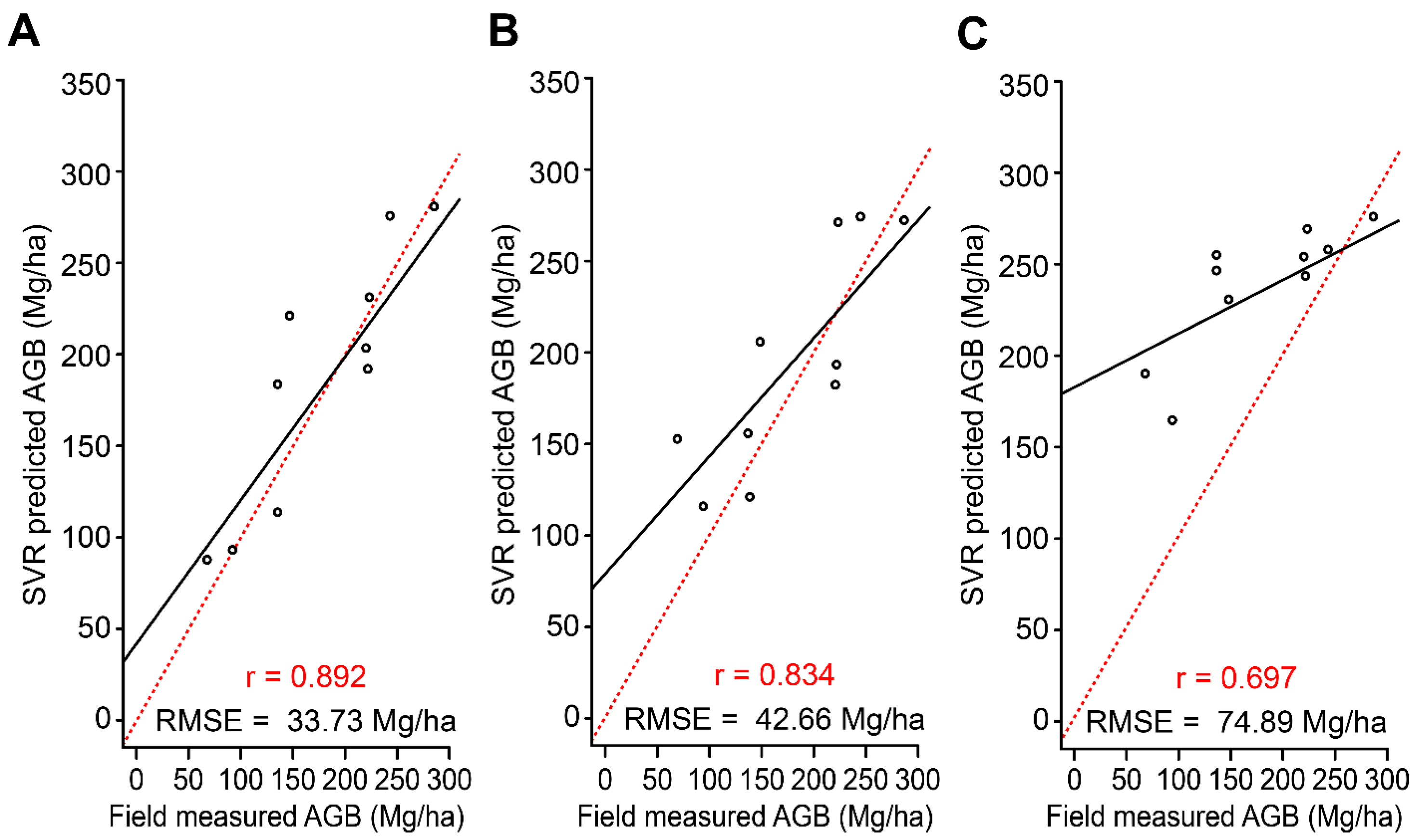
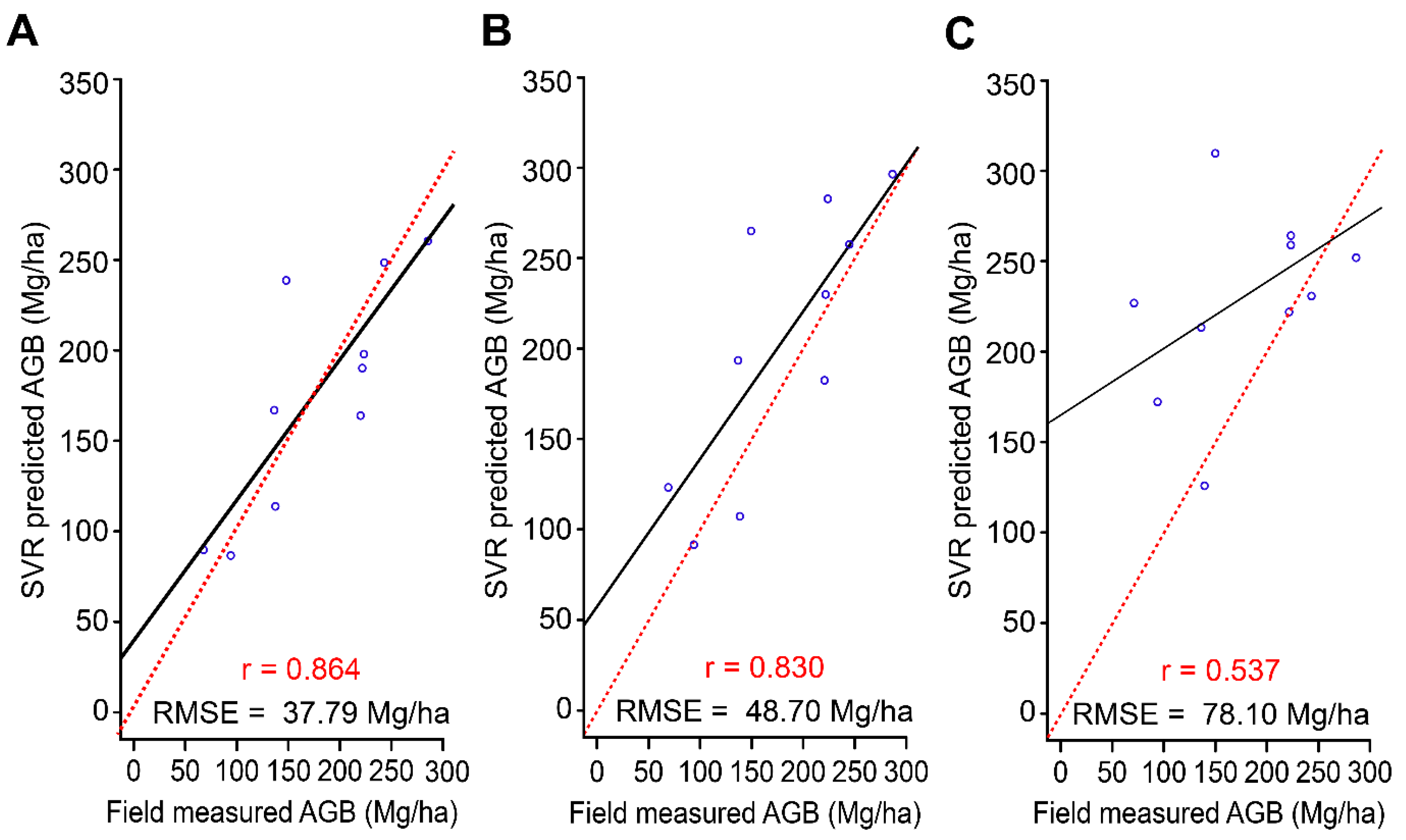
4.2. FOTO-Derived AGB Estimates
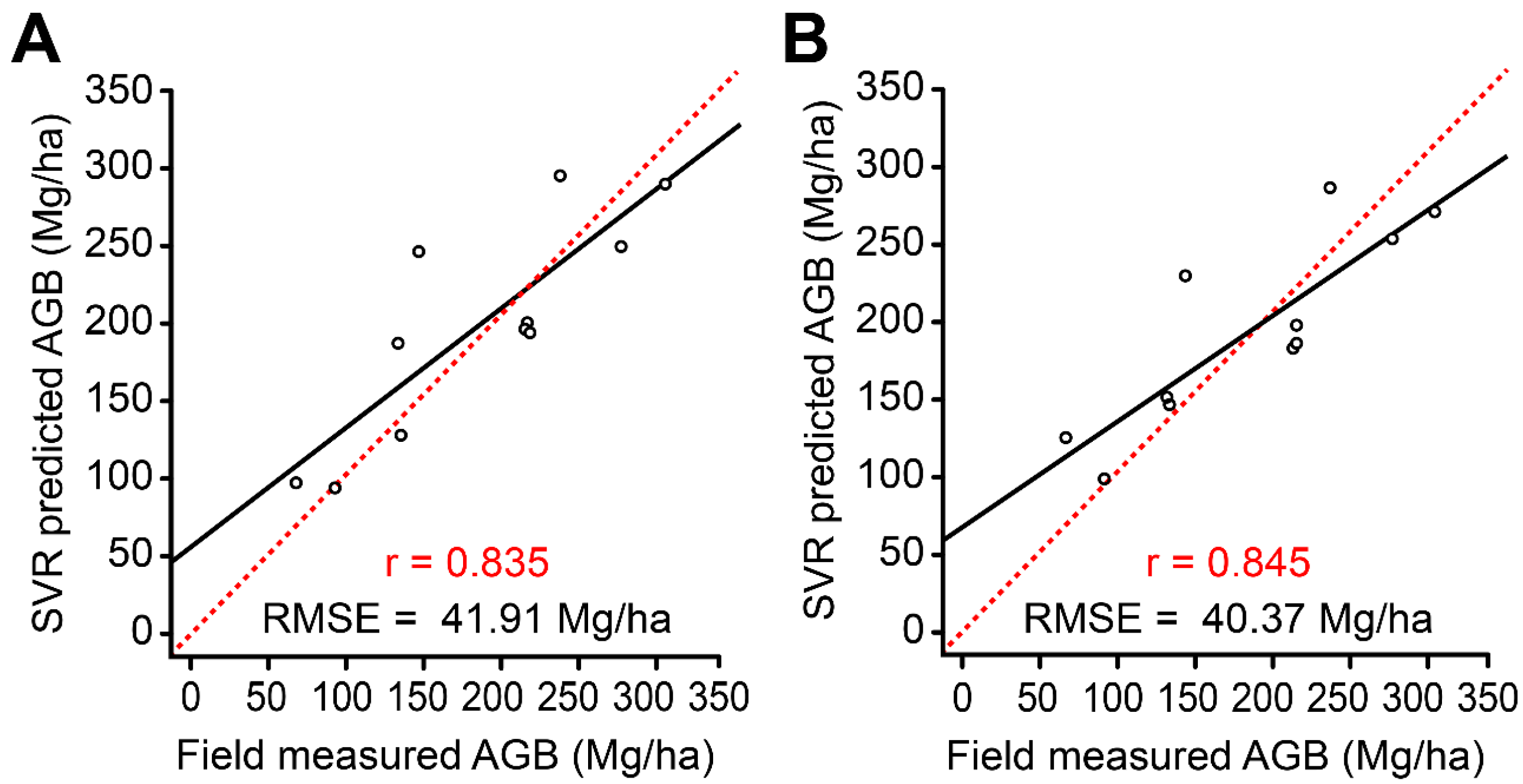
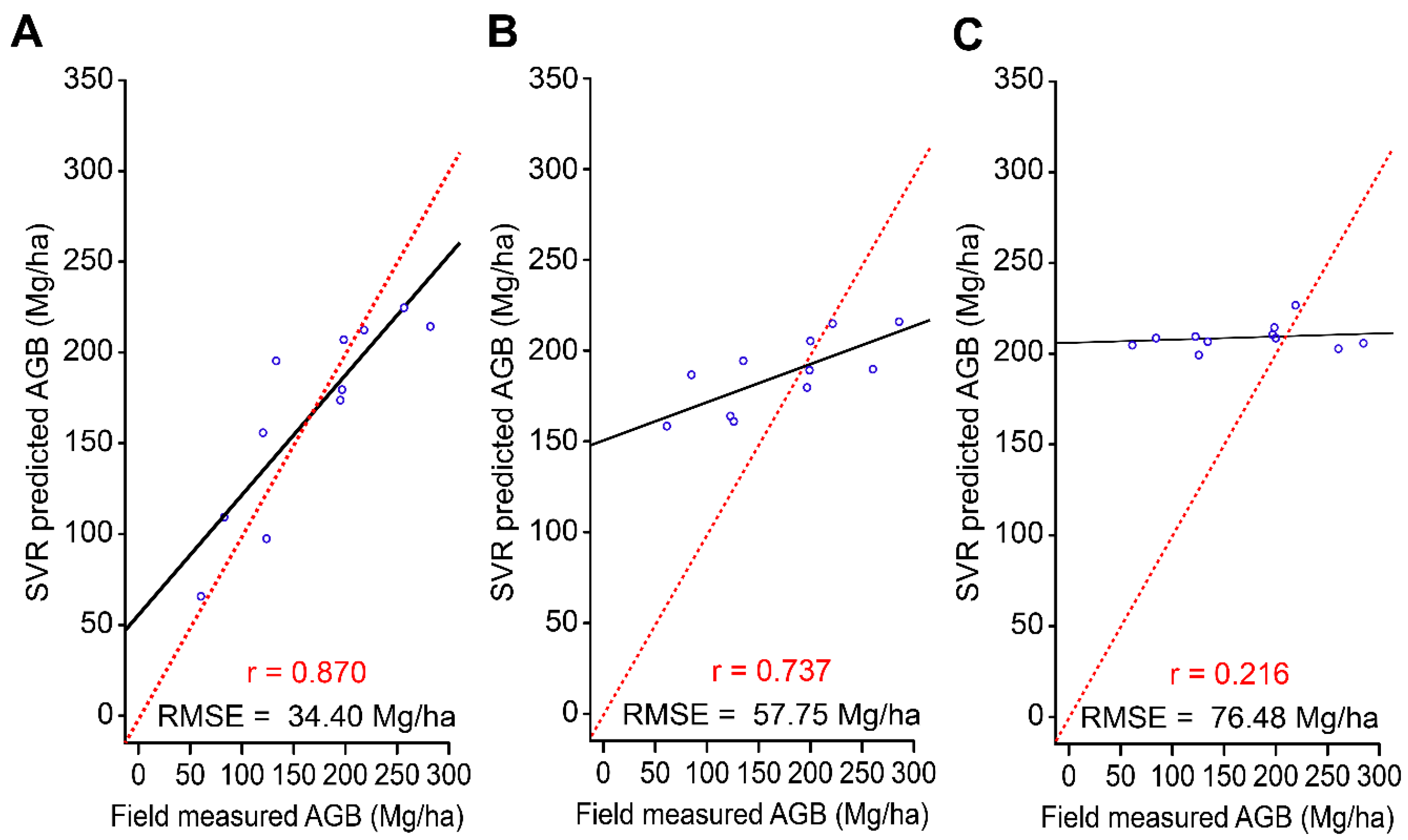
4.3. Gabor Wavelet-Derived AGB Estimates
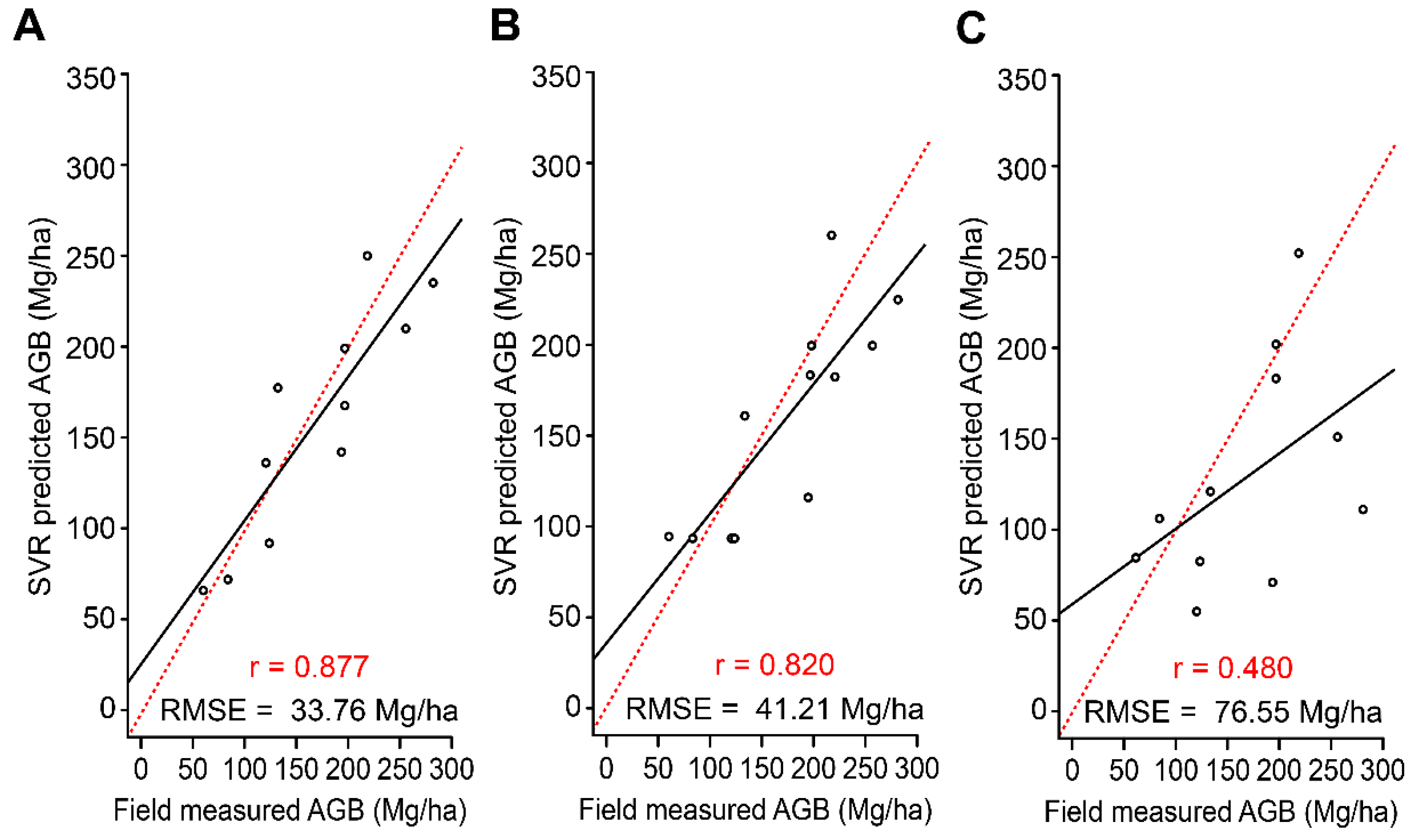
4.4. Mapping AGB
| Model Combination | 50 cm Google Earth | 8 cm Aerial Multispectral | |||
|---|---|---|---|---|---|
| RMSE (Mg/ha) | Association with Field AGB (r) | RMSE (Mg/ha) | Association with Field AGB (r) | ||
| GLCM | |||||
| HCV + VCH | SVR | 33.73 | 0.892 | 55.76 | 0.757 |
| (RF) | (54.34) | (0.793) | (57.8) | (0.787) | |
| HCV only | SVR | 42.66 | 0.834 | 70.90 | 0.639 |
| (RF) | (60.78) | (0.78) | n/a | n/a | |
| TV only | SVR | 74.89 | 0.697 | n/a | n/a |
| (RF) | (76.07) | (0.47) | n/a | n/a | |
| FOTO | |||||
| HCV + VCH | SVR | 41.91 | 0.835 | 37.79 | 0.864 |
| (RF) | (53.2) | (0.758) | (56.039) | (0.732) | |
| HCV only | SVR | 40.37 | 0.845 | 48.70 | 0.830 |
| (RF) | (44.23) | (0.86) | (57.32) | (0.72) | |
| TV only | SVR | n/a | n/a | 78.10 | 0.537 |
| (RF) | n/a | n/a | (74.061) | (0.52) | |
| Gabor | |||||
| HCV + VCH | SVR | 33.76 | 0.87 | 34.40 | 0.870 |
| (RF) | 46.8 | 0.742 | 54.3 | 0.808 | |
| HCV only | SVR | 41.21 | 0.820 | 57.75 | 0.737 |
| (RF) | 60.18 | 0.625 | n/a | 0.68 | |
| TV only | SVR | 76.55 | 0.480 | 76.48 | 0.216 |
| (RF) | 61.1 | 0.54 | n/a | 0.17 | |

5. Discussion
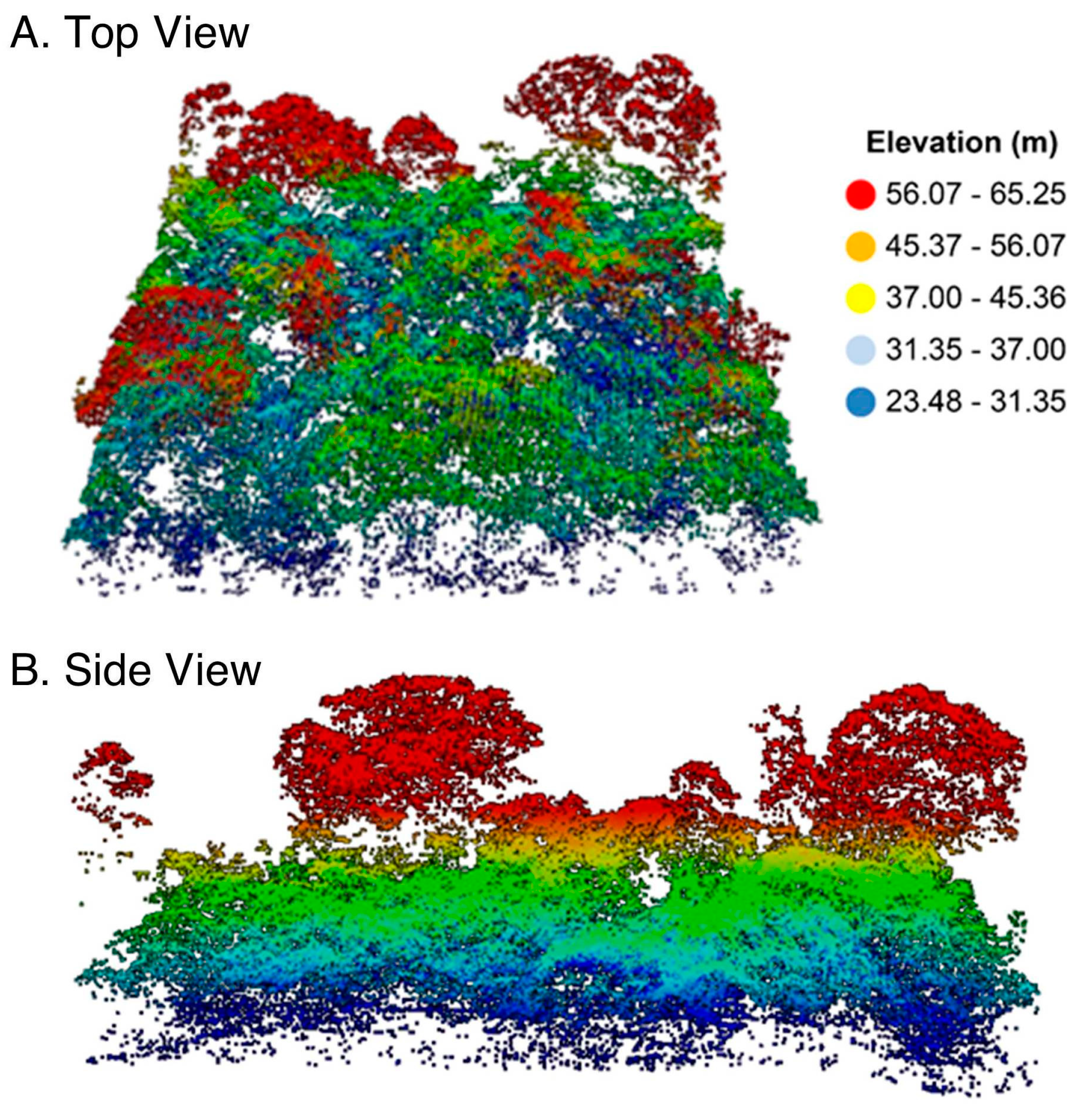
5.1. Spatial Patterns of AGB in Angkor Thom
5.2. The Effectiveness of Different Model Combinations for Estimating AGB
5.2.1. The Importance of Structural Parameters
5.2.2. Performance of Different Modelling Approaches
5.2.3. Performance of Google Earth™ Imagery vs. VHR Imagery for AGB Estimation
5.3. Implications of Freely Available Remote Sensing Imagery for Conservation
6. Conclusions
Acknowledgments
Author Contributions
Supplementary Files
Supplementary File 1Conflicts of Interest
References
- Pan, Y.; Birdsey, R.; Fang, J.; Houghton, R.; Kauppi, P.; Kurz, W.; Phillips, O. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Sodhi, N.; Koh, L.; Brook, B.; Ng, P. Southeast Asian biodiversity: An impending disaster. Trends Ecol. Evol. 2004, 19, 654–660. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.; Potapov, P.; Moore, R.; Hancher, M.; Turubanova, S.; Tyukavina, A.; Thau, D.; Stehman, S.; Goetz, S.; Loveland, T.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Southworth, J.; Nagendra, H.; Cassidy, L. Forest transition pathways in Asia—Studies from Nepal, India, Thailand and Cambodia. J. Land Use Sci. 2012, 7, 51–65. [Google Scholar] [CrossRef]
- Zsombor, P. Loss of Forest in Cambodia among Worst in the World. The Cambodia Daily, 19 November 2013. [Google Scholar]
- Jakubowski, M.; Li, W.; Guo, Q.; Kelly, M. Delineating individual trees from LiDAR data: A comparison of vector-and raster-based segmentation approaches. Remote Sens. 2013, 5, 4163–4186. [Google Scholar] [CrossRef]
- Mumby, P.; Green, E.; Edwards, A.; Clark, C. The cost-effectiveness of remote sensing for tropical coastal resources assessment and management. J. Environ. Manag. 1999, 55, 157–166. [Google Scholar] [CrossRef]
- Friess, D.; Kudavidanage, E.; Webb, E. The digital globe is our oyster. Front. Ecol. Environ. 2011, 9, 542–552. [Google Scholar] [CrossRef]
- Singh, M.; Malhi, Y.; Bhagwat, S. Evaluating land use and aboveground biomass dynamics in an oil palm-dominated landscape in Borneo using optical remote sensing. J. Appl. Remote Sens. 2014, 8, 83695–83695. [Google Scholar] [CrossRef]
- Bastin, J.; Barbier, N.; Couteron, P.; Adams, B.; Shapiro, A.; Bogaert, J.; de Cannière, C. Aboveground biomass mapping of African forest mosaics using canopy texture analysis: Towards a regional approach. Ecol. Appl. 2014, 24, 1984–2001. [Google Scholar] [CrossRef]
- Drake, J.; Knox, R.; Dubayah, R.; Clark, D.; Condit, R.; Blair, J.; Hofton, M. Above-ground biomass estimation in closed canopy neotropical forests using LiDAR remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
- Wijaya, A.; Kusnadi, S.; Gloaguen, R.; Heilmeier, H. Improved strategy for estimating stem volume and forest biomass using moderate resolution remote sensing data and GIS. J. For. Res. 2010, 21, 1–12. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenges of remote sensing based biomass estimates. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Singh, M.; Malhi, Y.; Bhagwat, S. Biomass estimation of mixed forest landscape using a Fourier transform texture-based approach on very-high-resolution optical satellite imagery. Int. J. Remote Sens. 2014, 35, 3331–3349. [Google Scholar] [CrossRef]
- Proisy, C.; Couteron, P.; Fromard, F. Predicting and mapping mangrove biomass from canopy grain analysis using Fourier-based textural ordination of IKONOS images. Remote Sens. Environ. 2007, 109, 379–392. [Google Scholar] [CrossRef]
- Kennel, P.; Tramon, M.; Barbier, N.; Vincent, G. Canopy height model characteristics derived from airborne laser scanning and its effectiveness in discriminating various tropical moist forest types. Int. J. Remote Sens. 2013, 34, 8917–8935. [Google Scholar] [CrossRef]
- Wang, Z.; Boesch, R.; Ginzler, C. Forest delineation of aerial images with Gabor wavelets. Int. J. Remote Sens. 2012, 33, 2196–2213. [Google Scholar] [CrossRef]
- Goetz, S.; Baccini, A.; Laporte, N.; Johns, T.; Walker, W.; Kellndorfer, J.; Houghton, R.; Sun, M. Mapping and monitoring carbon stocks with satellite observations: A comparison of methods. Carbon Balance Manag. 2009, 4, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, S.; Hogg, E.; Lieffers, V.; Qin, Y.; He, F. Estimating spatial variation in Alberta forest biomass from a combination of forest inventory and remote sensing data. Biogeosciences 2014, 11, 2793–2808. [Google Scholar] [CrossRef]
- Maxwell, J. Vegetation and vascular flora of the Ban Saneh Pawng area, Lai Wo subdistrict, Sangklaburi district, Kanchanaburi Province, Thailand. Nat. Hist. Bull. Siam Soc. 1995, 43, 131–170. [Google Scholar]
- Wales, N. Combining Remote Sensing Change Detection and Qualitative Data to Examine Landscape Change in the Context of World Heritage. Ph.D. Thesis, University of Sydney, Sydney, Australia, October 2012. [Google Scholar]
- Marthews, T.; Metcalfe, D.; Malhi, Y.; Phillips, O.; Huasco, W.; Riutta, T.; Jaén, M.; Girardin, C.; Urrutia, R.; Butt, N. Measuring Tropical Forest Carbon Allocation and Cycling: A RAINFOR-GEM Field Manual for Intensive Census Plots (v2.2); University of Oxford: Oxford, UK, 2012. [Google Scholar]
- Asner, G.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Meyer, V.; Saatchi, S.; Chave, J.; Dalling, J.; Bohlman, S.; Fricker, G.; Robinson, C.; Neumann, M.; Hubbell, S. Detecting tropical forest biomass dynamics from repeated airborne LiDAR measurements. Biogeosciences 2013, 10, 1957–1992. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.; Chambers, J.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.; Iverson, L.; Prasad, A.; Liu, D. Geographical distributions of carbon in biomass and soils of tropical Asian forests. Geocarto Int. 1993, 8, 45–59. [Google Scholar] [CrossRef]
- Google Satellite Maps Downloader. Available online: http://www.allallsoft.com/gsmd/ (accessed on (20 December 2012).
- McGaughey, R. Fusion/ldv: Software for LiDAR Data Analysis and Visualization [Computer Program]; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Seattle, WA, USA, 2010. [Google Scholar]
- St-Louis, V.; Pidgeon, A.; Radeloff, V.; Hawbaker, T.; Clayton, M. High-resolution image texture as a predictor of bird species richness. Remote Sens. Environ. 2006, 105, 299–312. [Google Scholar] [CrossRef]
- Couteron, P.; Pélissier, R.; Nicolini, E.; Paget, D. Predicting tropical forest stand structure parameters from Fourier transform of very high-resolution remotely sensed canopy images. J. Appl. Ecol. 2005, 42, 1121–1128. [Google Scholar] [CrossRef]
- Yu, P.; Chen, S.; Chang, I. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Yu, X.; Wang, X.; Chen, J. Support vector machine regression for reactivity parameters of vinyl monomers. J. Chil. Chem. Soc. 2011, 56, 746–751. [Google Scholar] [CrossRef]
- Paneque-Gálvez, J.; Mas, J.-F.; More, G.; Cristobal, J.; Orta-Martinez, M.; Luz, A.C.; Gueze, M.; Macia, M.J.; Reyes-Garcia, V. Enhanced land use/cover classification of heterogeneous tropical landscapes using support vector machines and textural homogeneity. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 372–383. [Google Scholar] [CrossRef]
- Zeng, Z.; Hsieh, W.W.; Shabbar, A.; Burrows, W.R. Seasonal prediction of winter extreme precipitation over Canada by support vector regression. Hydrol. Earth Syst. Sci. 2011, 15, 65–74. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training, R package version 4.58 2014; Available online: http://CRAN.R-project.org/package=caret (accessed on 21 April 2015).
- Lantz, B. Machine Learning with R; Packt Publishing Ltd.: Birmingham, UK, 2013. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.; Muller-Landau, H. Evaluating uncertainty in mapping forest carbon with airborne LiDAR. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Townend, J. Practical Statistics for Environmental and Biological Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chen, G.; Hay, G.; St-Onge, B. A GEOBIA framework to estimate forest parameters from LiDAR transects, QuickBird imagery and machine learning: A case study in Quebec, Canada. Int. J. Appl. Earth Obs. Geoinf. 2012, 15, 28–37. [Google Scholar] [CrossRef]
- Shataee, J. Forest attributes estimation using aerial laser scanner and TM data. For. Syst. 2013, 22, 484–496. [Google Scholar]
- Ploton, P.; Pélissier, R.; Proisy, C.; Flavenot, T.; Barbier, N.; Rai, S.N.; Couteron, P. Assessing aboveground tropical forest biomass using Google Earth canopy images. Ecol. Appl. 2012, 22, 993–1003. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Lövbrand, E.; Turnhout, E.; Vijge, M. In pursuit of carbon accountability: The politics of REDD+ measuring, reporting and verification systems. Curr. Opin. Environ. Sustain. 2012, 4, 726–731. [Google Scholar] [CrossRef]
- Friess, D.; Phelps, J.; Garmendia, E.; Gómez-Baggethun, E. Payments for ecosystem services (PES) in the face of external biophysical stressors. Glob. Environ. Chang. 2015, 30, 31–42. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, M.; Evans, D.; Friess, D.A.; Tan, B.S.; Nin, C.S. Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth. Remote Sens. 2015, 7, 5057-5076. https://doi.org/10.3390/rs70505057
Singh M, Evans D, Friess DA, Tan BS, Nin CS. Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth. Remote Sensing. 2015; 7(5):5057-5076. https://doi.org/10.3390/rs70505057
Chicago/Turabian StyleSingh, Minerva, Damian Evans, Daniel A. Friess, Boun Suy Tan, and Chan Samean Nin. 2015. "Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth" Remote Sensing 7, no. 5: 5057-5076. https://doi.org/10.3390/rs70505057
APA StyleSingh, M., Evans, D., Friess, D. A., Tan, B. S., & Nin, C. S. (2015). Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth. Remote Sensing, 7(5), 5057-5076. https://doi.org/10.3390/rs70505057