The Effect of Topography on Target Decomposition of Polarimetric SAR Data
Abstract
:1. Introduction
2. Model-Fitting-Based POLSAR Decomposition
3. Experimental Results
3.1. Simulation of Polarimetric Scattering from Mountainous Forests
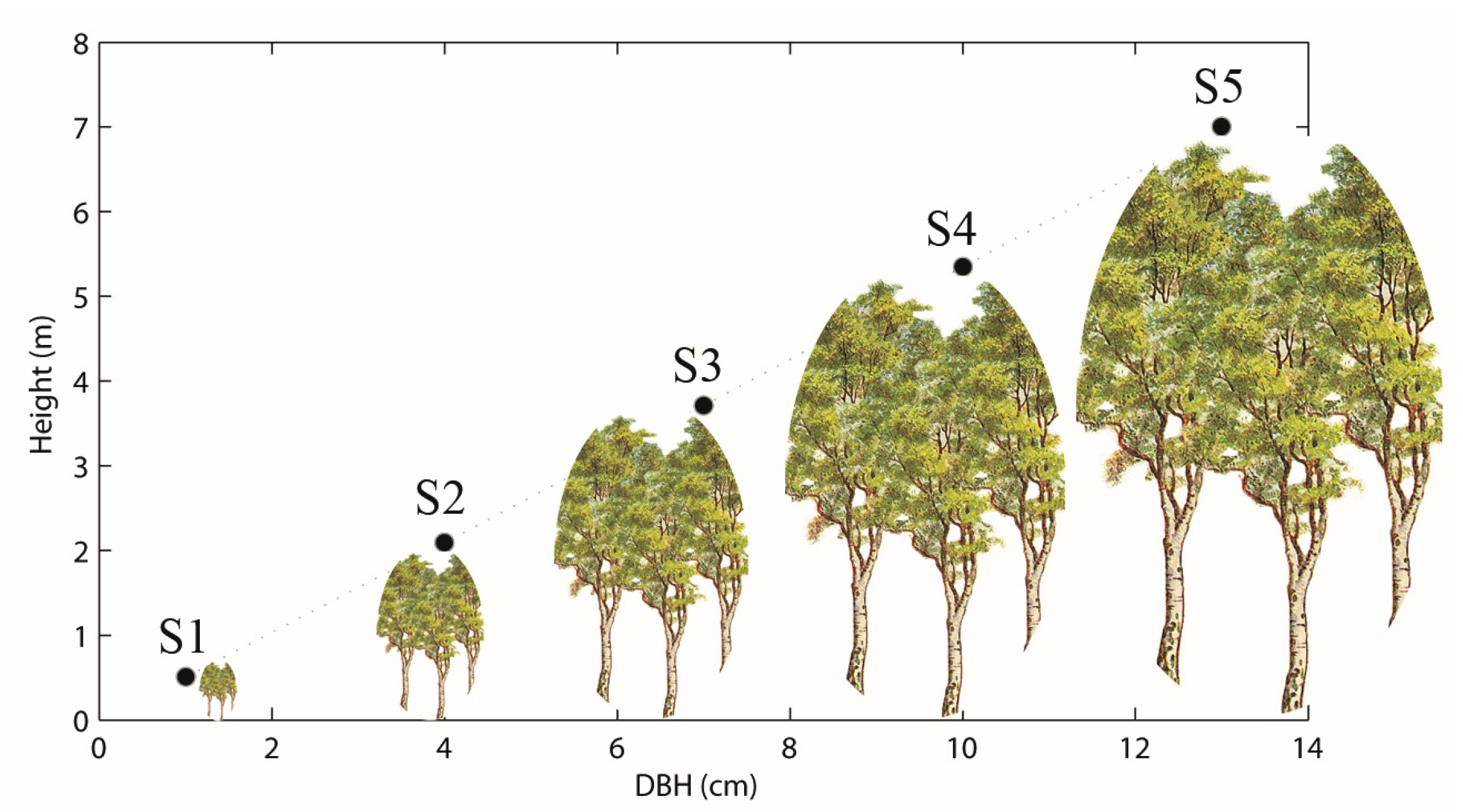
| Parameters | Crown Layer | Trunk Layer | ||||||
|---|---|---|---|---|---|---|---|---|
| Leaf | Stem | Branch 2 | Branch 1 | Trunk | ||||
| Radius (cm) | S1 | 5 | 0.1 | 0.12 | 0.31 | 0.5 | ||
| S2 | 5 | 0.1 | 0.31 | 1.08 | 2.0 | |||
| S3 | 5 | 0.1 | 0.46 | 1.79 | 3.5 | |||
| S4 | 5 | 0.1 | 0.59 | 2.46 | 5.0 | |||
| S5 | 5 | 0.1 | 0.71 | 3.11 | 6.5 | |||
| ½Length (cm) | S1 | 0.01 | 0.51 | 1.35 | 5.0 | 10.0 | ||
| S2 | 0.01 | 2.09 | 5.58 | 21.0 | 42.0 | |||
| S3 | 0.01 | 3.71 | 9.90 | 37.0 | 74.0 | |||
| S4 | 0.01 | 5.35 | 14.26 | 54.0 | 107.0 | |||
| S5 | 0.01 | 7.00 | 18.69 | 70.0 | 140.0 | |||
| Orientation (°) | 70–90 | 0–90 | 15–80 | 0–40 | 0–10 | |||
| Density (number/m3) | 200 | 100 | 4.5 | 0.35 | 0.01 | |||
| Height (m) | S1 | 0.3 | 0.2 | |||||
| S2 | 1.3 | 0.8 | ||||||
| S3 | 2.2 | 1.5 | ||||||
| S4 | 3.2 | 2.1 | ||||||
| S5 | 4.2 | 2.8 | ||||||
3.2. Topography Effects on Model-Fitting-Based Decomposition
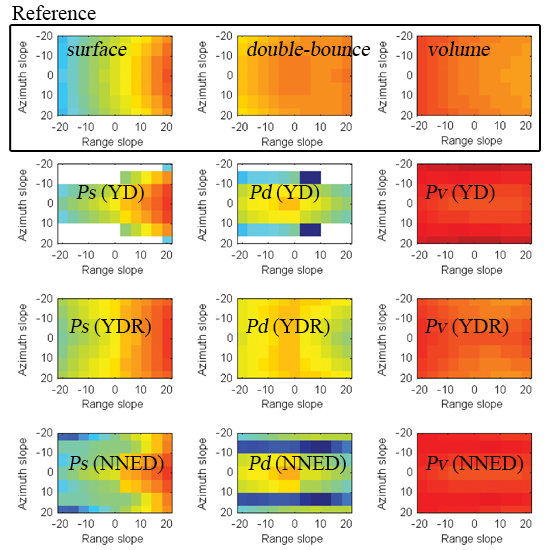
3.2.1. Changes of Scattering Mechanisms in Sloping Terrain

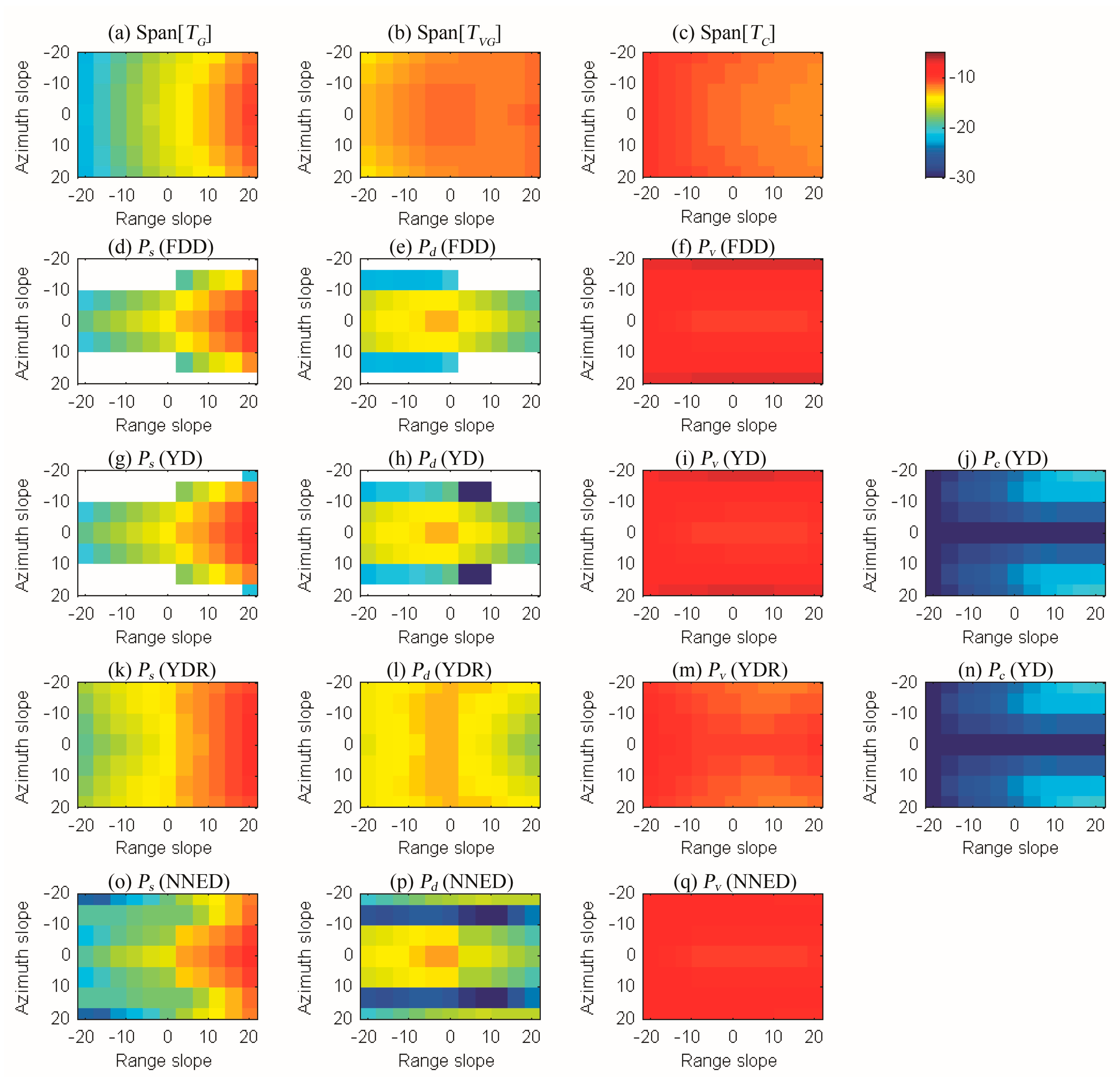
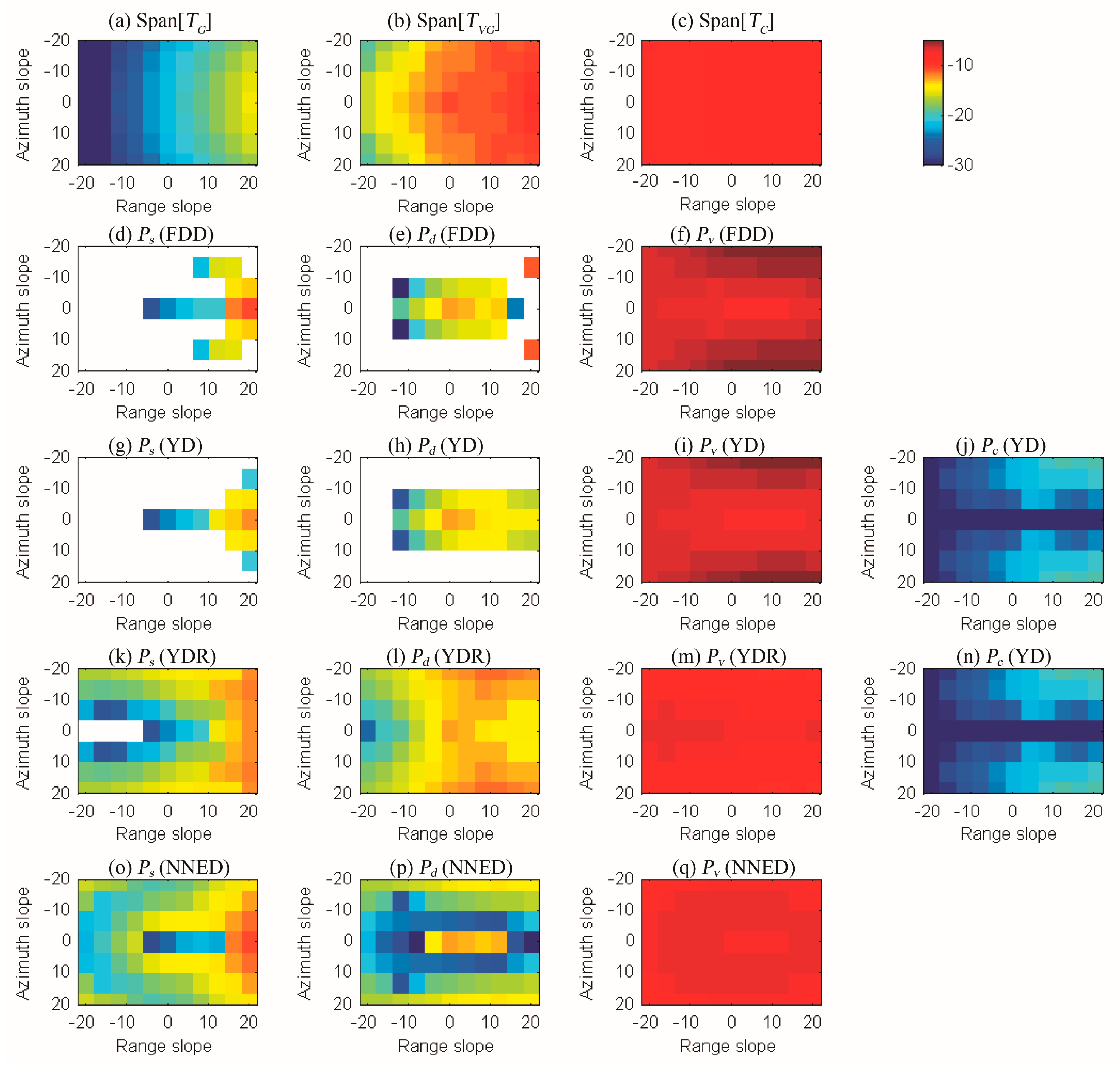
3.2.2. Effect of Range Slope on Decomposition Results
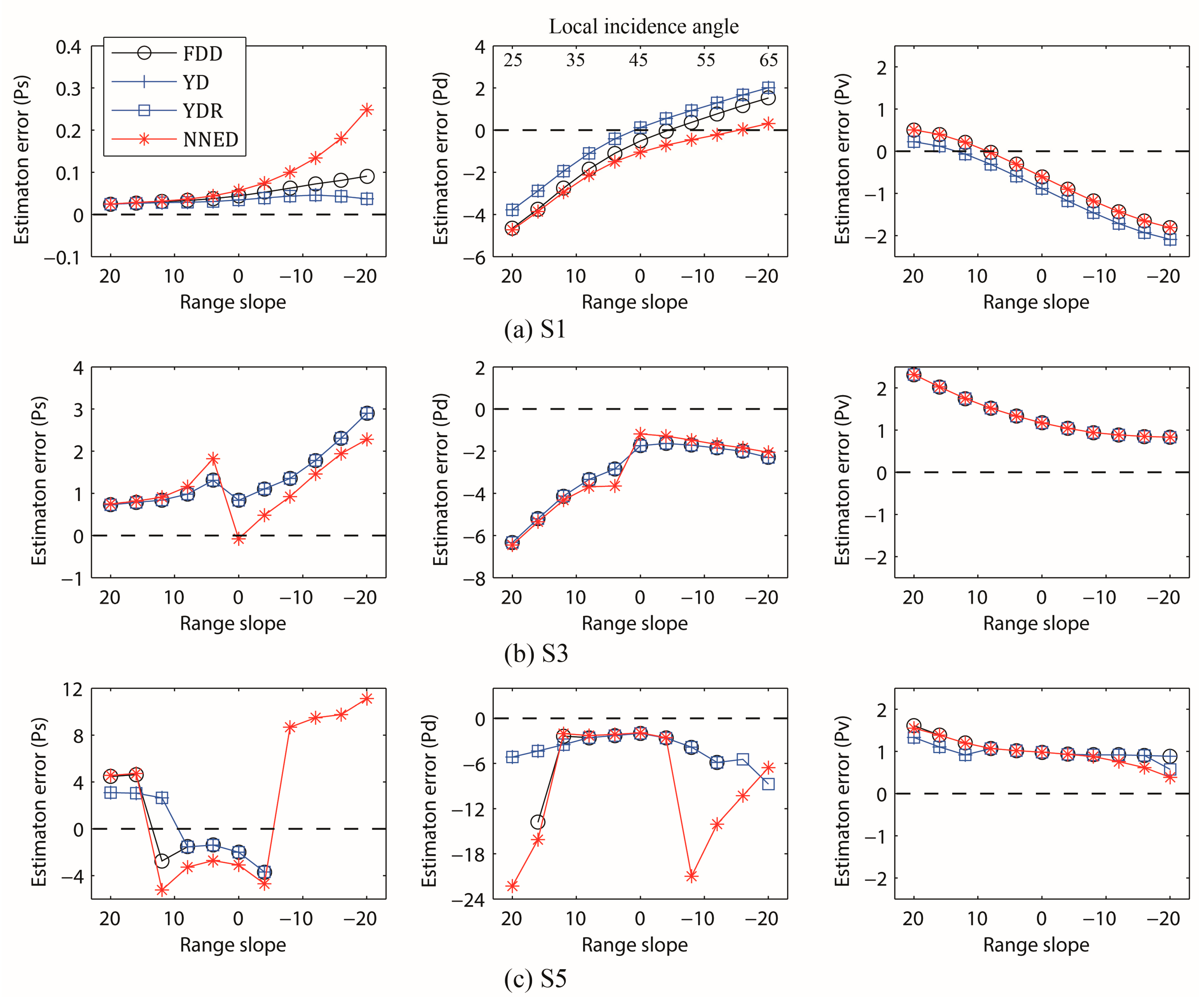
| S1 | S2 | S3 | S4 | S5 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | |
| 0.06 | 0.04 | 0.04 | 0.11 | 0.73 | 0.73 | 0.73 | 0.84 | 1.51 | 1.51 | 1.51 | 1.31 | 10.13 | 10.10 | 10.10 | 3.44 | 19.02 | 18.97 | 18.97 | 6.77 | |
| 2.19 | 1.85 | 1.85 | 2.23 | 2.49 | 2.49 | 2.49 | 2.63 | 3.37 | 3.37 | 3.37 | 3.46 | 4.39 | 3.03 | 3.03 | 7.45 | 24.92 | 19.38 | 4.62 | 11.94 | |
| 1.01 | 1.20 | 1.20 | 1.01 | 1.21 | 1.21 | 1.21 | 1.21 | 1.42 | 1.42 | 1.42 | 1.42 | 1.21 | 1.11 | 1.11 | 1.21 | 1.10 | 1.01 | 0.99 | 1.03 | |
3.2.3. Effect of Azimuth Slope on Decomposition Results
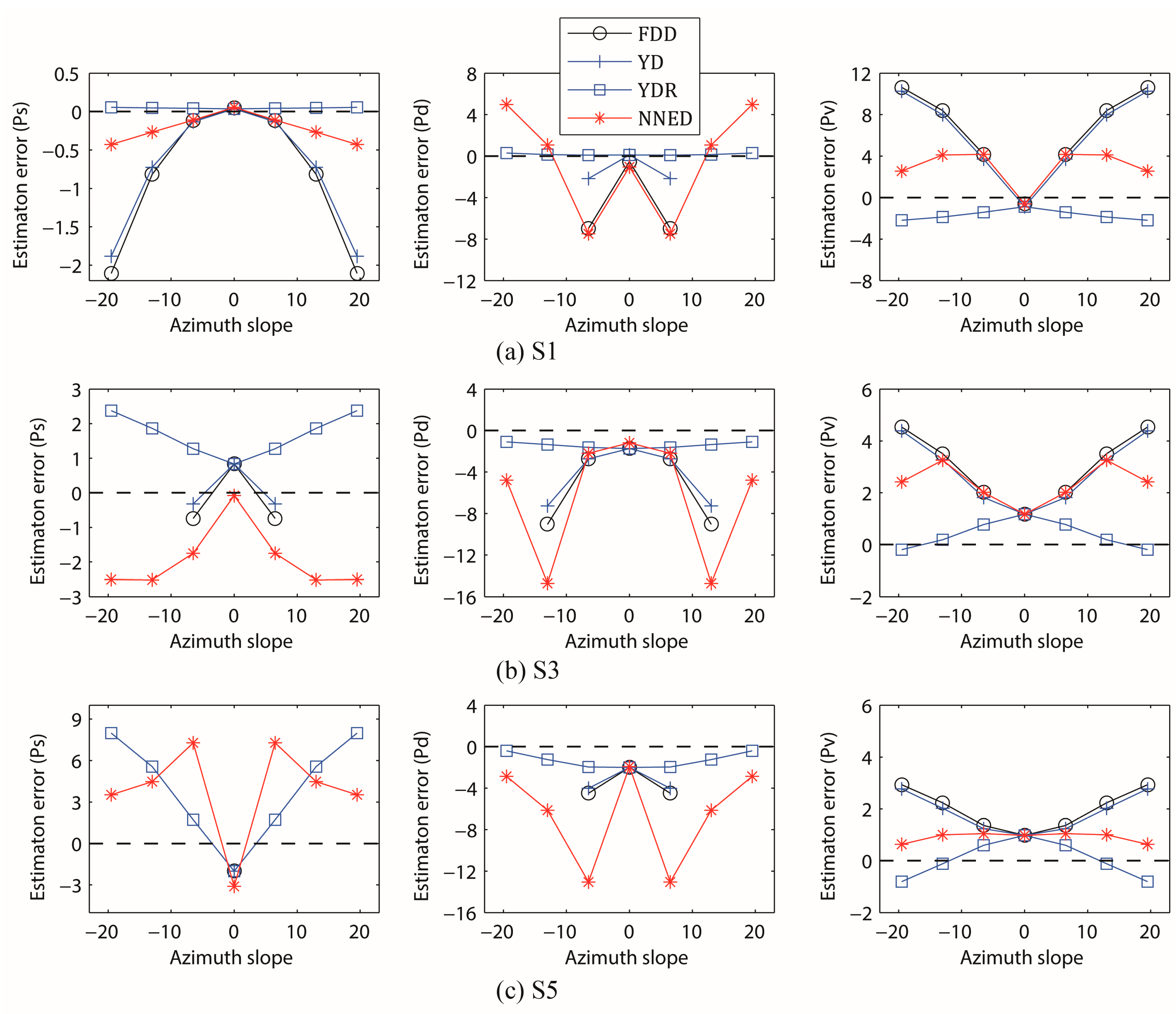
| S1 | S2 | S3 | S4 | S5 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | FDD | YD | YDR | NNED | |
| 1.21 | 1.08 | 0.05 | 0.28 | 6.03 | 5.06 | 0.50 | 1.03 | 33.33 | 33.33 | 1.78 | 2.12 | 31.33 | 31.24 | 3.29 | 3.76 | 34.95 | 34.95 | 5.33 | 5.07 | |
| 24.29 | 24.03 | 0.18 | 4.86 | 24.14 | 24.13 | 1.40 | 5.78 | 26.13 | 25.97 | 1.43 | 8.37 | 37.11 | 37.11 | 1.34 | 4.95 | 36.28 | 36.26 | 1.47 | 7.89 | |
| 7.58 | 7.24 | 1.75 | 3.43 | 3.52 | 3.36 | 0.58 | 2.79 | 3.28 | 3.12 | 0.62 | 2.46 | 2.80 | 2.65 | 0.57 | 1.61 | 2.13 | 1.98 | 0.66 | 0.92 | |
4. Conclusions
Acknowledgments
Conflicts of Interest
References and Notes
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Park, S.-E.; Moon, W.M. Unsupervised classification of scattering mechanisms in polarimetric SAR data using fuzzy logic in entropy and alpha plane. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2652–2664. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar]
- Shan, Z.; Zhang, H.; Wang, C.; An, W.; Wu, T.; Chen, X. Four-component model-based decomposition of polarimetric SAR data for special ground objects. IEEE Geosci. Remote Sens. Lett. 2012, 9, 989–993. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.-E. Four-component scattering power decompo-sition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Chen, S.; Ohk, M.; Shimada, M.; Sato, M. Deorientation effect investigation for model-based decomposition over oriented built-up areas. IEEE Geosci. Remote Sens. Lett. 2013, 10, 273–277. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Chapman, B.D.; Dubois, P.; Shi, J. The effect of topography on SAR calibration. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1036–1043. [Google Scholar] [CrossRef]
- Ulander, L.M.H. Radiometric slope correction of synthetic aperture radar images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1115–1122. [Google Scholar] [CrossRef]
- Park, S.-E.; Moon, W.M.; Pottier, E. Assessment of scattering mechanism of polarimetric SAR signal from mountainous forest areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4711–4719. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Vol. II; Addison-Wesley, Advanced Book Program: Reading, MA, USA, 1982; pp. 949–966. [Google Scholar]
- Lee, J.S.; Shuler, D.L.; Ainsworth, T.L.; Krogager, E.; Kasilingam, D.; Boerner, W.M. On the estimation of radar polarization orientation shifts induced by terrain slopes. IEEE Trans. Geosci. Remote Sens. 2002, 40, 30–41. [Google Scholar] [CrossRef]
- Arii, M.; Van Zyl, J.J.; Kim, Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1104–1113. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modeling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-component power decomposition for polarimetric SAR data based on adaptive volume scattering modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Li, Y.-Z.; Sato, M. Adaptive model-based polarimetric decomposition using PolInSAR coherence. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1705–1718. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-E. The Effect of Topography on Target Decomposition of Polarimetric SAR Data. Remote Sens. 2015, 7, 4997-5011. https://doi.org/10.3390/rs70504997
Park S-E. The Effect of Topography on Target Decomposition of Polarimetric SAR Data. Remote Sensing. 2015; 7(5):4997-5011. https://doi.org/10.3390/rs70504997
Chicago/Turabian StylePark, Sang-Eun. 2015. "The Effect of Topography on Target Decomposition of Polarimetric SAR Data" Remote Sensing 7, no. 5: 4997-5011. https://doi.org/10.3390/rs70504997
APA StylePark, S.-E. (2015). The Effect of Topography on Target Decomposition of Polarimetric SAR Data. Remote Sensing, 7(5), 4997-5011. https://doi.org/10.3390/rs70504997