Geo-Positioning Accuracy Using Multiple-Satellite Images: IKONOS, QuickBird, and KOMPSAT-2 Stereo Images

Abstract

This paper investigates the positioning accuracy of image pairs achieved by integrating images from multiple satellites. High-resolution satellite images from IKONOS, QuickBird, and KOMPSAT-2 for Daejeon, Korea were combined to produce pairs of stereo images. From single-satellite stereo pairs to multiple-satellite image pairs, all available combinations were analyzed via a rational function model (RFM). The positioning accuracy of multiple-satellite pairs was compared to a typical single-satellite stereo pair. The results show that dual-satellite integration can be an effective alternative to single-satellite stereo imagery for horizontal position mapping, but is less accurate for vertical mapping. The integration of additional higher-resolution images can improve the overall accuracy of the existing two images, but, conversely, may result in lower accuracy when very weak convergence or bisector elevation (BIE) angles occur. This highlights that the use of higher resolution images may not ensure improved accuracy, as it can result in very weak geometry. The findings confirm that multiple-satellite images can replace or enhance typical stereo pairs, but also suggest the need for careful verification, including consideration of various geometric elements and image resolution. This paper reveals the potential, limitations, and important considerations for mapping applications using images from multiple satellites.

1. Introduction

High-resolution satellite images are widely used as the primary source for geo-positioning because they provide many advantages such as wide coverage, short revisit time, and appropriate spatial resolution required for large-scale mapping. Many studies have investigated the potential of high-resolution satellite images for geo-positioning. Their positioning accuracy was preferentially examined using ground points generated from IKONOS imagery [1,2]. Noguchi et al. [3] and Tong et al. [4] investigated mapping accuracy from the geometric correction of QuickBird images [3,4]. The studies found that an accuracy of about 1–2 m or better could be achieved from precisely geo-referenced IKONOS and QuickBird images. Similar investigations were carried out for various images, such as SPOT-5 and FORMOSAT-2 [5,6]. Recently, the geo-referencing accuracy of Geoeye-1 and WorldView-1/2 imagery was described as around sub-meter in both the horizontal and vertical planes [7,8,9,10].

The investigations listed above have sufficiently demonstrated the potential of high-resolution satellite images for accurate geo-positioning. However, they are based on the convention of using single-satellite image pairs obtained within the same satellite. The availability of pairs from the same sensor cannot be assumed at all times, and in particular, heavy reliance on such pairs can impose some limitations on the broad applications of satellite images. To overcome such limitations, it is necessary to develop methods of integrating images obtained from multiple satellites. The replacement or improvement of conventional single-satellite stereo images by multi-satellite images will be very useful for real mapping applications. For example, dual-satellite integration might address the absence of single-satellite stereo images or the integration of additional images to improve the accuracy of existing stereo images. In this respect, it is important to investigate the positioning accuracy achievable by multiple-satellite images.

So far, few studies have integrated multiple-satellite images for geo-positioning. Li et al. [11] investigated geo-positioning accuracy for different combinations of IKONOS and QuickBird stereo images, and analyzed the relationship between satellite-borne pointing geometry and attainable positioning accuracy [11]. Another study analyzed topographic mapping accuracy achieved by integrating two images at different resolutions using single images from IKONOS, QuickBird, and SPOT-5 [12]. However, those studies focused more on the applicability of the 3D affine model for satellite sensor modeling than on image integration. Recently, Jeong and Kim (2014) investigated imaging geometry and positioning accuracy of dual-sensor stereo data by integrating two different satellites [13]. They mainly compared differences in geometric characteristics between single-sensor and dual-sensor stereo pairs, and highlighted that such differences should be regarded as important when handling dual-sensor stereo images.

Previous studies have revealed the geo-positioning accuracy and geometric characteristics from multiple-satellite images. In particular, Li et al. [11] provided the accuracy of geo-positioning using results from integration of three or more images, whereas other studies tested integration of only two images. However, their primary concern was to confirm the potential of IKONOS-QuickBird integration for geo-positioning and verify its accuracy. Issues of validity, practical cases, and important considerations have not been investigated thoroughly. This paper argues that accuracy performance relative to that of conventionally used pairs, useful examples, and some guidelines need to be investigated or reviewed before the use of multiple satellite images can be recommended to remote sensing users as the major source for mapping applications.

This paper therefore investigates the positioning accuracy of multiple-satellite images and evaluates their suitability for geo-positioning by comparing their accuracy with that of typical single-satellite stereo images. Firstly, dual-satellite integration is compared with single-satellite stereo imaging. This experiment checks whether there is any difference between the attainable accuracies, and whether the former can replace the latter for real mapping applications. Secondly, accuracy variation is examined when additional images are integrated into single-satellite stereo. This experiment checks whether the integration of higher resolution images is always an effective means of improving the accuracy of existing stereo images. Our analysis suggests the potential and limitations of this approach, and important considerations for handling multiple-satellite images in mapping applications.

This paper is organized as follows: Section 2 describes the experimental data and sensor model used in this study; Section 3 describes our test cases for the use of multiple images; Section 4 presents the experimental results; Section 5 presents our discussion, and Section 6 our conclusions.

2. Experimental Data and Sensor Model

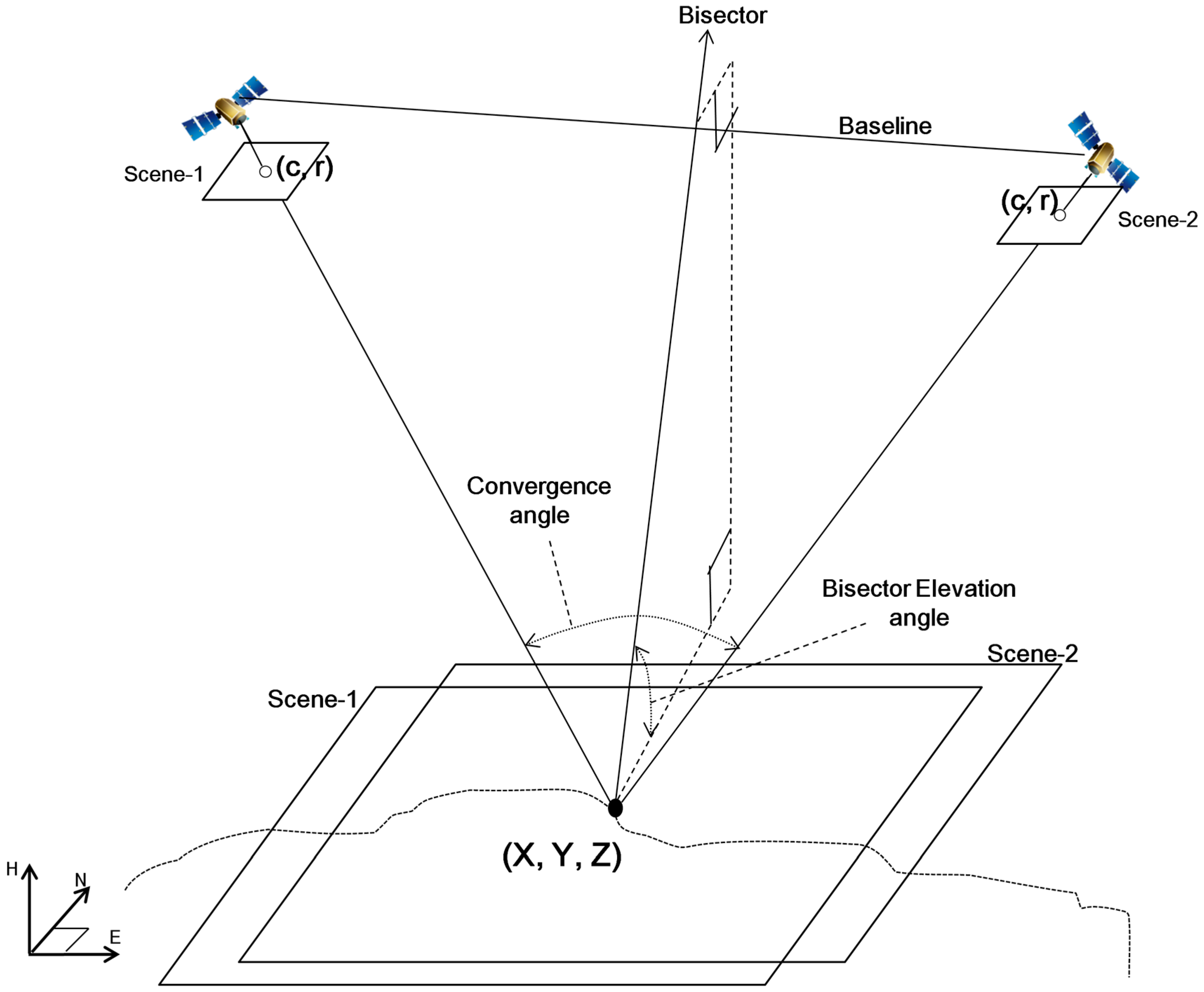
Three pairs of stereo IKONOS, stereo QuickBird, and stereo KOMPSAT-2 images of Daejeon, Korea, were collected and used for our experiments. The properties of the images are shown in Table 1, with the scenes numbered in order of acquisition. For each stereo pair, convergence angle and bisector elevation (BIE) angle were presented to indicate stability of imaging geometry. The two angles are described in Figure 1. Convergence angle is the angle between two rays of a stereo pair, whereas BIE angle is the elevation angle of the bisector of the convergence angle. BIE angle generally indicates the obliqueness of the epipolar plane. Convergence angle and its effect on stereo mapping have been continuously addressed, but the effect of BIE angle has been only recently introduced [13]. Previous studies showed that small BIE can degrade the mapping accuracy of stereo data. The present study considers that such effects of BIE angle may also be important for the integration of three or more data sources as well as stereo data. The two angles are included in metadata or can be calculated via azimuth and elevation angles [11,13].

Most satellites produce stereo pairs via their particular principles of image acquisition. For example, QuickBird stereo is obtained by tilting forward and backward along the pitch axis while maintaining a roll angle close to 0°, whereas KOMPSAT-2 stereo is obtained by tilting the angle along the roll axis while maintaining pitch angles close to 0°. These approaches achieve sufficient convergence angle, and nearly 90° BIE angle as in Table 1. In the case of IKONOS stereo, the convergence and BIE angles are also confined within normal ranges by using two images taken at regular azimuth angle intervals, although they are taken by tilting the sensor along the roll and pitch axes simultaneously.

Figure 1. Representation of convergence and BIE angles on stereo geometry.

Figure 1. Representation of convergence and BIE angles on stereo geometry.

Table 1. Properties of experimental data.

	IKONOS		QuickBird		KOMPSAT-2
	Scene-1	Scene-2	Scene-1	Scene-2	Scene-1	Scene-2
Date of acquisition	7 February 2002	7 February 2002	16 January 2005	16 January 2005	10 May 2007	6 May 2008
Azimuth angle	338.1°	234.9°	199.5°	5.2°	79.7°	256.7°
Elevation angle	66.5°	68.4°	59.5°	58.7°	58.2°	74.1°
Convergence angle	35.00°		61.27°		47.68°
BIE angle	75.53°		85.74°		89.34°
GSD (column/row)	0.90 m/0.96 m	0.92 m/0.90 m	0.71 m/0.79 m	0.71 m/0.83 m	1.30 m/1.10 m	1.04 m/1.01 m

Table 1. Properties of experimental data.

	IKONOS		QuickBird		KOMPSAT-2
	Scene-1	Scene-2	Scene-1	Scene-2	Scene-1	Scene-2
Date of acquisition	7 February 2002	7 February 2002	16 January 2005	16 January 2005	10 May 2007	6 May 2008
Azimuth angle	338.1°	234.9°	199.5°	5.2°	79.7°	256.7°
Elevation angle	66.5°	68.4°	59.5°	58.7°	58.2°	74.1°
Convergence angle	35.00°		61.27°		47.68°
BIE angle	75.53°		85.74°		89.34°
GSD (column/row)	0.90 m/0.96 m	0.92 m/0.90 m	0.71 m/0.79 m	0.71 m/0.83 m	1.30 m/1.10 m	1.04 m/1.01 m

Figure 2 shows the ground coverage of all images used and the configurations of the ground control points (GCPs). In total, 30 GCPs were used for experiments, comprising two types: 12 model GCPs and 18 independent check points (ICPs). The model GCPs are used for updating the initial model coefficients provided in the metadata and for establishing the sensor models, whereas the ICPs are used separately to assess the geo-positioning accuracy of the stereo pairs. All GCPs were acquired by global positioning system (GPS) measurements in the field and processed by differential GPS processing to ensure an accuracy of better than 10 cm.

In this paper, a rational function model (RFM) sensor model proposed by Grodecki and Dial [2] was used for modeling and integrating multiple satellite images. Since the sensor models used have been fully described in the previous work, only a brief description is provided here. The model equations are expressed as below:

$$r_{\mathrm{n}} = \frac{{\mathrm{P}}_1\left(X_{\mathrm{n}}, Y_{\mathrm{n}}, Z_{\mathrm{n}}\right)}{{\mathrm{P}}_2\left(X_{\mathrm{n}}, Y_{\mathrm{n}}, Z_{\mathrm{n}}\right)}$$

(1)

$$c_{\mathrm{n}} = \frac{{\mathrm{P}}_3\left(X_{\mathrm{n}}, Y_{\mathrm{n}}, Z_{\mathrm{n}}\right)}{{\mathrm{P}}_4\left(X_{\mathrm{n}}, Y_{\mathrm{n}}, Z_{\mathrm{n}}\right)}$$

(2)

$$\begin{gathered} {\mathrm{P}}_1\left(X_{\mathrm{n}}, Y_{\mathrm{n}}, Z_{\mathrm{n}}\right)= a_1+a_2{X}_{\mathrm{n}}+a_3{Y}_{\mathrm{n}}+a_4{Z}_{\mathrm{n}}+ a_5{X}_{\mathrm{n}}{Y}_{\mathrm{n}}+a_6{X}_{\mathrm{n}}{Z}_{\mathrm{n}}+a_7{Y}_{\mathrm{n}}{Z}_{\mathrm{n}}+ a_8{X_{\mathrm{n}}}^2+a_9{Y_{\mathrm{n}}}^2 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+a_{10}{Z_{\mathrm{n}}}^2+a_{11}{X}_{\mathrm{n}}{Y}_{\mathrm{n}}{Z}_{\mathrm{n}}+a_{12}{X_{\mathrm{n}}}^3+a_{13}{X}_{\mathrm{n}}{Y_{\mathrm{n}}}^2+a_{14}{X}_{\mathrm{n}}{Z_{\mathrm{n}}}^2+a_{15}{X_{\mathrm{n}}}^2{Y}_{\mathrm{n}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+a_{16}{Y_{\mathrm{n}}}^3+a_{17}{Y}_{\mathrm{n}}{Z_{\mathrm{n}}}^2+a_{18}{X_{\mathrm{n}}}^2{Z}_{\mathrm{n}}+a_{19}{Y_{\mathrm{n}}}^2{Z}_{\mathrm{n}}+a_{20}{Z_{\mathrm{n}}}^2 \end{gathered}$$

(3)

where (${\mathrm{r}}_{\mathrm{n}}$, ${\mathrm{c}}_{\mathrm{n}}$) are the normalized row and column on the image space; $\left({\mathrm{X}}_{\mathrm{n}}, {\mathrm{Y}}_{\mathrm{n}}, {\mathrm{Z}}_{\mathrm{n}}\right)$ are the normalized longitude, latitude, and ellipsoidal height of their corresponding ground coordinates on the object space. Parameters ${\mathrm{a}}_1, {\mathrm{a}}_2, \dots \mathrm{and} {\mathrm{a}}_{20}$are the coefficients of the polynomial function ${\mathrm{P}}_1$ and the coefficients of ${\mathrm{P}}_2, {\mathrm{P}}_3$, and ${\mathrm{P}}_4$ are defined similarly. The model coefficients were extracted from the rational polynomial coefficient (RPC) files provided by the vendor. Twelve model GCPs were used to compensate for errors in the model coefficients and then the model equations were precisely updated. The following equations were used for error compensation in the image space [2]:

$$∆p = a_0 + a_{\mathrm{c}}\bullet \mathrm{Column}+ a_{\mathrm{r}}\bullet \mathrm{Row}$$

(4)

$$∆r = b_0 + b_{\mathrm{c}}\bullet \mathrm{Column}+ b_{\mathrm{r}}\bullet \mathrm{Row}$$

(5)

where ∆p and ∆r are the adjustable functions in the column and row directions respectively, and $a_0$, $a_{\mathrm{c}}$, $a_{\mathrm{r}}$, $b_0$, $b_{\mathrm{c}}$, $b_{\mathrm{r}}$ are the image adjustment parameters that can be estimated by a least-square adjustment.

Figure 2. Image coverage and GCPs’ distribution.

Figure 2. Image coverage and GCPs’ distribution.

3. Test Cases for the Use of Multiple-Satellite Images

Two integration scenarios were examined to check the applicability of multiple-satellite images for geo-positioning. The first case includes dual-satellite integration using two different satellite images. The attained mapping accuracies were compared with those from single-satellite stereo. It will be interesting to compare dual-satellite stereo integrated at two different resolutions with single-satellite stereo images taken at higher or lower resolutions. Such comparison examines whether dual-satellite integration can be used to fully compensate for an absence of single-satellite stereo imagery.

The second case integrates three or more images. The resulting mapping accuracy was also compared with that of single-satellite stereo, including comparison of mapping accuracies before and after the integration of higher resolution images. In real mapping applications, it can be very useful to check cases in which integration of additional images enhances the accuracy of single-satellite stereo, and to determine whether there are any important considerations for such integration.

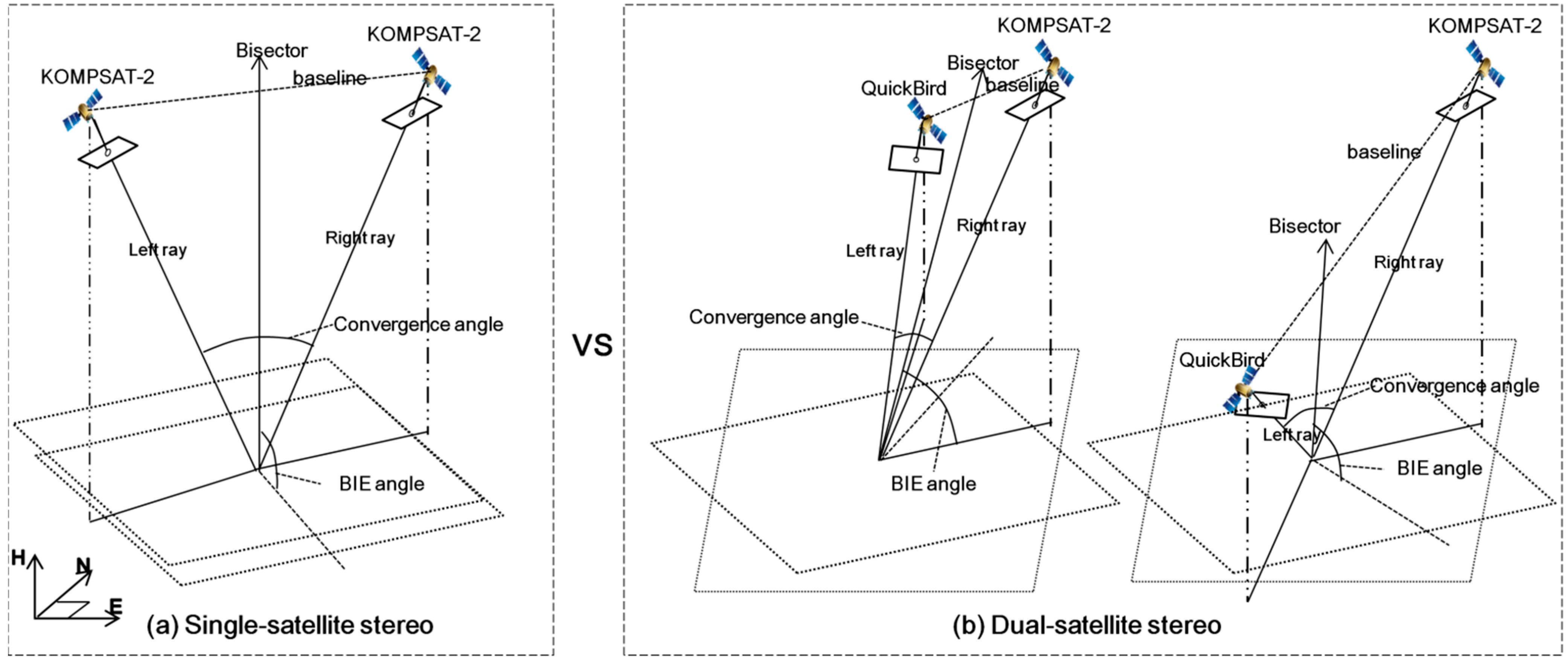
For the first case, we compare, for example, KOMPSAT-2 stereo pair (1 m) with the integrations between one KOMPSAT-2 image (1 m) and one QuickBird image (0.6 m) as in Figure 3. It may be presumed that KOMPSAT-2-QuickBird integration will likely have higher accuracy than the KOMPSAT-2 stereo pair, considering that the absolute positioning accuracy of satellite images has been generally proportional to their image resolutions. However, there is a need to be aware that other elements, for example geometric weakness of dual-satellite integration relative to single-satellite stereo, may produce results that differ from such expectation. The epipolar plane of KOMPSAT-2 stereo pairs has sufficient convergence angle and is nearly orthogonal to the ground plane (BIE angle close to 90°) because of the geometric conditions for acquiring stereo pairs; however, that of KOMPSAT-2-QuickBird integration pairs may have very narrow convergence angle or be highly oblique to the ground plane (small BIE angle) because no geometric conditions are guaranteed due to the arbitrary integration from two different satellites. Such geometric weakness may affect dual-satellite mapping accuracy.

Figure 3. Test cases for comparison between single-satellite stereo and dual-satellite integration. (a) single-satellite stereo, (b) dual-satellite stereo.

Figure 3. Test cases for comparison between single-satellite stereo and dual-satellite integration. (a) single-satellite stereo, (b) dual-satellite stereo.

In addition, we need to consider another element that may affect dual-satellite mapping. Since the mapping accuracy of dual-satellite stereo, unlike single-satellite stereo pairs, has not been investigated thoroughly, many variables need to be considered. In particular, the results—when geometries of single-satellite and dual-satellite stereos are similar or both stable—are used to check whether mapping accuracy is influenced by another element in addition to image resolution and geometry. For this experiment, we analyze three single-satellite stereo pairs and 12 dual-satellite integrations.

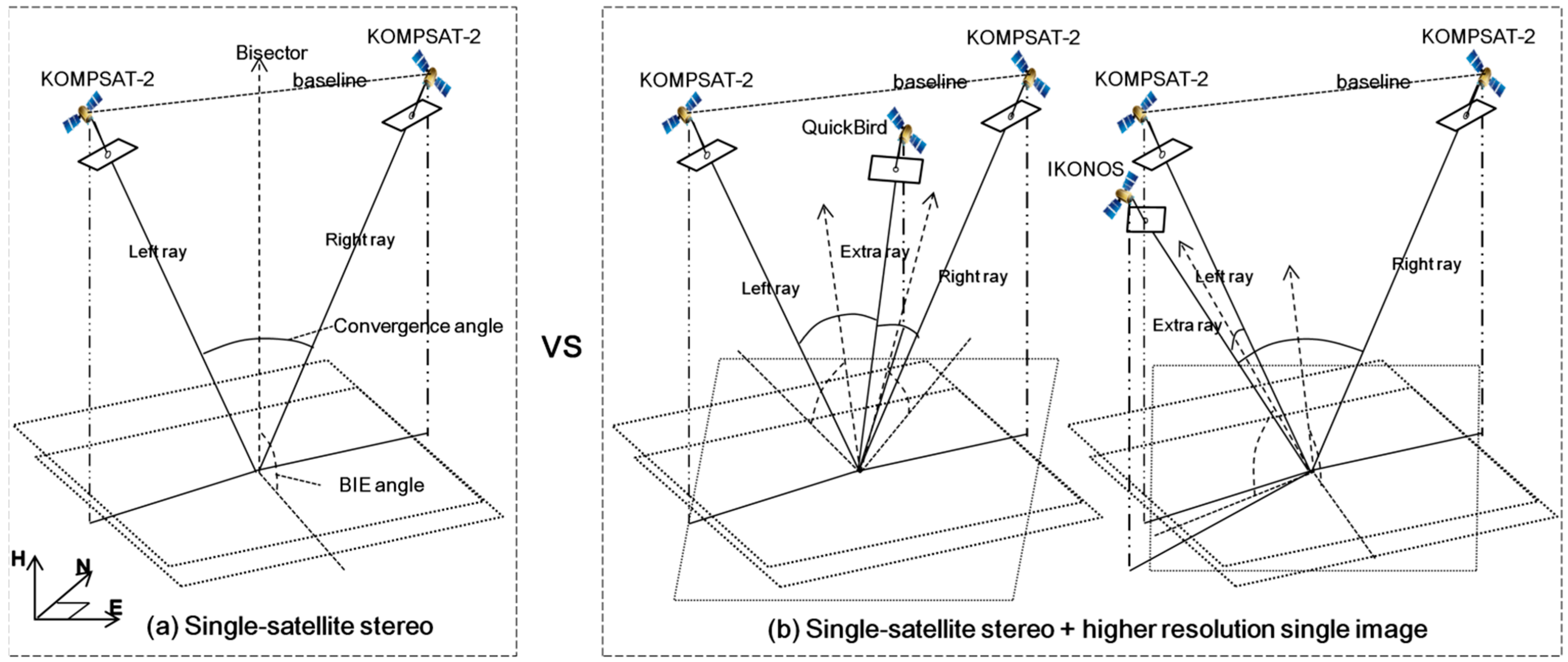
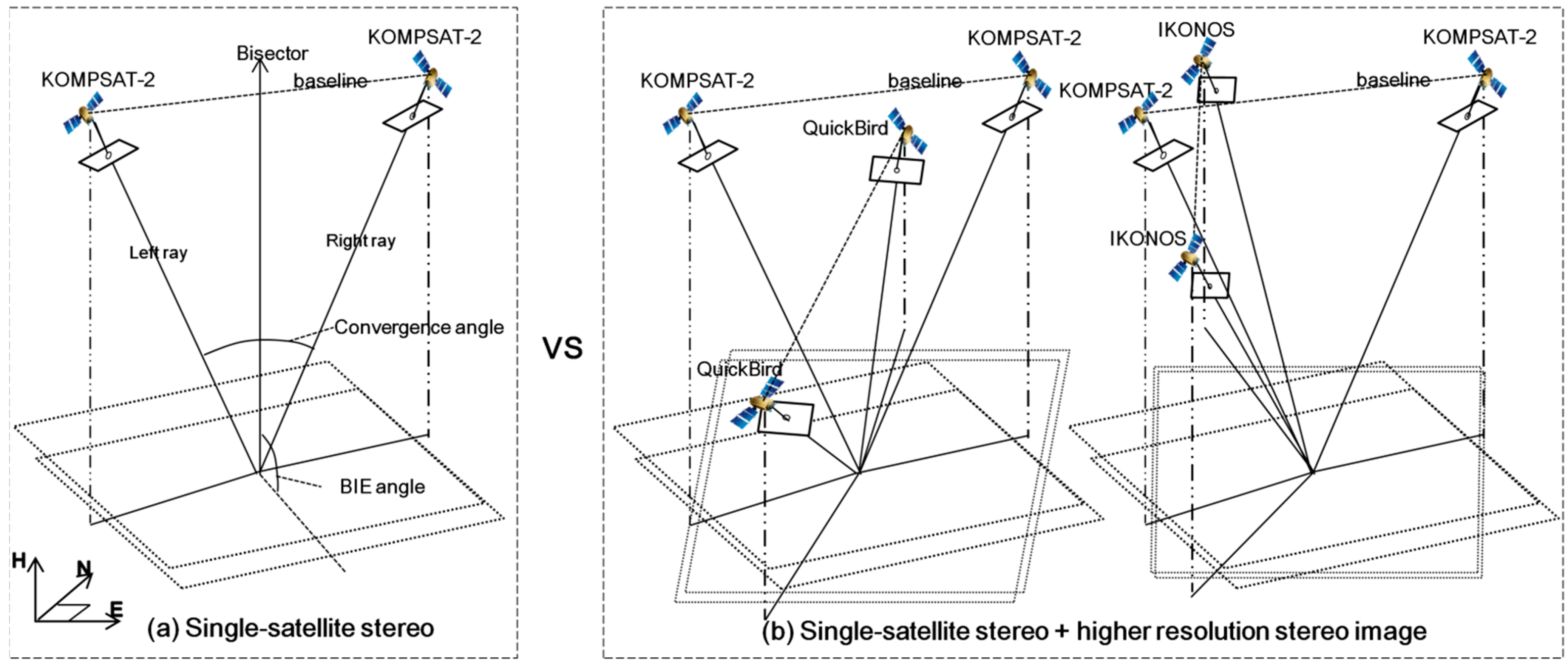
For the second case, we examine, for example, the variations in accuracy when higher resolution QuickBird or IKONOS single images (Figure 4) or stereo images (Figure 5) are integrated into KOMPSAT-2 stereo images. As before, when considering image resolution, it may be expected that such integrations would increase the accuracy of KOMPSAT-2 stereo images. However, in this case there is a need to be aware that geometric relationships between all images may influence the mapping accuracy, and we therefore need to check whether the additional image might result in weak geometry with either of the existing images. We also examine whether there is any difference between the integration of a single image and that of stereo images. For the experiments, we conduct six types of integrations for test cases as in Figure 4 and four types of integrations for test cases as in Figure 5.

In addition, we initially considered various other integration cases, for example the integration of three different satellite images or the integration of lower-resolution images, from multiple satellite images. However, we could not extract any useful information from such integrations. For example, the integration of lower-resolution images always decreased the accuracy of existing pairs, and hence we did not consider their results further in this paper.

Figure 4. Test cases for comparison before and after the integration of higher resolution single image. (a) single-satellite stereo, (b) single-satellite stereo + higher resolution single image.

Figure 4. Test cases for comparison before and after the integration of higher resolution single image. (a) single-satellite stereo, (b) single-satellite stereo + higher resolution single image.

Figure 5. Test cases for comparison before and after the integration of higher resolution stereo image. (a) single-satellite stereo, (b) single-satellite stereo + higher resolution stereo image.

Figure 5. Test cases for comparison before and after the integration of higher resolution stereo image. (a) single-satellite stereo, (b) single-satellite stereo + higher resolution stereo image.

4. Experimental Results

Using IKONOS, QuickBird, and KOMPSAT-2 images, we conducted various integrations using multiple satellite images, and analyzed their convergence and BIE angles and positioning accuracy. Accuracy was evaluated by comparison with 18 ICPs after 3D ground points were determined from each integration pair. Table 3 and Table 4 present the accuracies of each integration pair, using root mean square error (RMSE). These results were mainly compared to those of the three single-satellite stereo pairs shown in Table 2. The positioning accuracy of the single-satellite stereo pairs was explained well by image resolution or ground sampling distance.

Table 2. Mapping accuracy of single-satellite stereo images.

	Convergence Angle	BIE Angle	Horizontal Accuracy	Vertical Accuracy
KOMPSAT-2 stereo	47.7°	89.3°	2.15 m	1.75 m
IKONOS stereo	35.0°	75.5°	1.53 m	0.86 m
QuickBird stereo	61.3°	85.7°	1.15 m	0.63 m

Table 2. Mapping accuracy of single-satellite stereo images.

	Convergence Angle	BIE Angle	Horizontal Accuracy	Vertical Accuracy
KOMPSAT-2 stereo	47.7°	89.3°	2.15 m	1.75 m
IKONOS stereo	35.0°	75.5°	1.53 m	0.86 m
QuickBird stereo	61.3°	85.7°	1.15 m	0.63 m

The mapping accuracy of dual-satellite images is presented in Table 3. The results show three cases of dual-satellite integration. The first case is four combinations from two KOMPSAT-2 and two IKONOS images, the second case combines two KOMPSAT-2 and two QuickBird images, and the third case considers two IKONOS and two QuickBird images.

The results reveal the influence of convergence and BIE angle on mapping accuracy. The fourth combination, between KOMPSAT-2 and IKONOS, clearly shows the degradation of accuracy due to very narrow convergence angle. The second combination between IKONOS and QuickBird also showed lower accuracy because of the smallest convergence and BIE angles. There were no severe variations in accuracy for KOMPSAT-2/QuickBird integration because the two angles were either within a relatively small range, but in this case, the effect of BIE angle on mapping accuracy could be confirmed from the lower accuracy of the third combination compared to the fourth combination. The convergence angles of the two combinations were similar but the BIE angles were very different. Overall, the results show that convergence and BIE angles are important considerations for mapping using dual-satellite integration, and also agree well with previous findings that checked the effects of the angles using other combination pairs [13].

Table 3. Mapping accuracy of two different satellite images.

Image 1	Image 2	Convergence Angle	BIE Angle	Horizontal Accuracy	Vertical Accuracy
K2-s1	IK-s1	42.5°	71.7°	1.65 m	2.74 m
K2-s1	IK-s2	52.0°	83.9°	1.78 m	2.39 m
K2-s2	IK-s1	26.1°	74.8°	1.86 m	2.87 m
K2-s2	IK-s2	8.90°	71.6°	3.87 m	12.10 m
K2-s1	QB-s1	53.2°	73.2°	1.88 m	1.65 m
K2-s1	QB-s2	25.3°	69.4°	1.83 m	2.80 m
K2-s2	QB-s1	36.9°	64.0°	2.12 m	2.71 m
K2-s2	QB-s2	39.1°	75.7°	1.51 m	2.02 m
IK-s1	QB-s1	50.4°	79.8°	1.39 m	1.07 m
IK-s1	QB-s2	14.5°	63.2°	2.80 m	3.59 m
IK-s2	QB-s1	17.6°	65.1°	1.95 m	2.86 m
IK-s2	QB-s2	47.8°	78.2°	1.30 m	1.54 m

Table 3. Mapping accuracy of two different satellite images.

Image 1	Image 2	Convergence Angle	BIE Angle	Horizontal Accuracy	Vertical Accuracy
K2-s1	IK-s1	42.5°	71.7°	1.65 m	2.74 m
K2-s1	IK-s2	52.0°	83.9°	1.78 m	2.39 m
K2-s2	IK-s1	26.1°	74.8°	1.86 m	2.87 m
K2-s2	IK-s2	8.90°	71.6°	3.87 m	12.10 m
K2-s1	QB-s1	53.2°	73.2°	1.88 m	1.65 m
K2-s1	QB-s2	25.3°	69.4°	1.83 m	2.80 m
K2-s2	QB-s1	36.9°	64.0°	2.12 m	2.71 m
K2-s2	QB-s2	39.1°	75.7°	1.51 m	2.02 m
IK-s1	QB-s1	50.4°	79.8°	1.39 m	1.07 m
IK-s1	QB-s2	14.5°	63.2°	2.80 m	3.59 m
IK-s2	QB-s1	17.6°	65.1°	1.95 m	2.86 m
IK-s2	QB-s2	47.8°	78.2°	1.30 m	1.54 m

The results also show that the accuracy of dual-satellite data relative to single-satellite data differs significantly between the horizontal and vertical planes. We observed horizontal accuracy first. In KOMPSAT-2/IKONOS integrations, except for the first pair, horizontal accuracy was generally higher than that for KOMPSAT-2 stereo pairs, although lower than that of IKONOS stereo or QuickBird stereo pairs. The KOMPSAT-2/QuickBird integrations also generally achieved levels of accuracy between those of the KOMPSAT-2 stereo pairs and QuickBird stereo pairs. These observations were also supported for IKONOS/QuickBird integrations, except that their second and third pairs created very small convergence or BIE angles. Overall, the horizontal accuracy of dual-satellite integration conformed well according to expectations based on image resolution, except in the cases involving very weak convergence and BIE angles. Dual-satellite integration without weak geometry showed comparable performance to single-satellite stereo for horizontal position mapping if image resolution is accounted for. On the other hand, vertical accuracy was somewhat contradictory to such expectation. In KOMPSAT-2/IKONOS integrations, the accuracy of all combinations (including the third combination with the largest convergence and BIE angle) was lower than that of KOMPSAT-2 stereo pairs. This phenomenon was also maintained for KOMPSAT-2/QuickBird and IKONOS/QuickBird integrations. For example, the best vertical accuracies for both integrations were also worse than those of single-satellite stereo images obtained from lower-resolution satellites. Overall, dual-satellite integration showed disappointing performance compared to single-satellite stereo, and produced significantly larger vertical errors than expected. This is further discussed in Section 5.

Overall, the comparisons showed that dual-satellite integration can be an effective alternative for horizontal mapping but presently has low accuracy in vertical mapping. This was true even among the integration scenarios with sufficient convergence and BIE geometry.

Secondly, the accuracy achieved by using additional images is presented in Table 4. The upper part of Table 4 shows the accuracy when a single, higher resolution image was integrated into single-satellite stereo images. Each result includes the convergence and BIE angles that are created between all images integrated. The first case is the integration between KOMPSAT-2 stereo and IKONOS single images. In terms of overall accuracy, that of KOMPSAT-2 stereo was improved by the first integration but not by the second integration. This is probably because very weak geometry (e.g., 8.90° convergence angle) was created between IKONOS scene-2 and KOMPSAT-2 scene-2. This phenomenon can also be observed from the third case that integrated IKONOS stereo and QuickBird single images. The accuracy of IKONOS stereo was improved both horizontally and vertically in the first integration but not in the second integration that created the smallest convergence (14.53°) and BIE angles (63.23°). In the second case (the integration of KOMPSAT-2 stereo and QuickBird single image), the first and second integrations of QuickBird both improved the accuracy of KOMPSAT-2 stereo. These two integrations also showed the effect of BIE angle. Although the second integration has the advantage in terms of overall convergence angles, the improvement in accuracy of the first integration that includes the smallest BIE angle was less than that of the second integration. Overall, the results show that an additional single image with higher resolution could enhance the accuracy of existing stereo mapping by appropriate image selection with consideration of convergence or BIE angles. This points out that consideration of the angles needs to be extended to the use of three images as well as two images. More importantly, however, avoiding the creation of very small or weak angles should be a higher priority than selecting pairs with high average angles.

Table 4. Mapping accuracy of three or more satellite images.

Integration of Three Images (Single-Satellite Stereo + Higher Resolution Single Image)

1

2

3

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

1-2

1-3

2-3

1-2

1-3

2-3

K2-s1

K2-s2

IK-s1

47.7°

42.5°

26.1°

89.3°

71.7°

74.8°

1.66 m

1.65 m

K2-s1

K2-s2

IK-s2

47.7°

52.0°

8.9°

89.3°

83.9°

71.6°

1.72 m

2.37 m

K2-s1

K2-s2

QB-s1

47.7°

53.2°

36.9°

89.3°

73.1°

64.0°

1.56 m

1.60 m

K2-s1

K2-s2

QB-s2

47.7°

25.3°

39.1°

89.3°

69.4°

75.7°

1.43 m

1.27 m

IK-s1

IK-s2

QB-s1

35.0°

50.4°

17.6°

75.5°

79.8°

65.1°

1.31 m

0.70 m

IK-s1

IK-s2

QB-s2

35.0°

14.5°

47.8°

75.5°

63.2°

78.2°

1.65 m

0.89 m

Integration of Four or More Images (Single-Satellite Stereo + Higher Resolution Stereo Image)

1

2

3

4

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

1-2

1-3

1-4

1-2

1-3

1-4

2-3

2-4

3-4

2-3

2-4

3-4

K2-s1

K2-s2

IK-s1

IK-s2

47.7°

42.5°

52.0°

89.3°

71.7°

83.9°

1.62 m

1.45 m

26.1°

8.90°

35.0°

74.8°

71.6°

75.5°

K2-s1

K2-s2

QB-s1

QB-s2

47.7°

53.2°

25.3°

89.3°

73.2°

69.4°

1.37 m

0.92 m

36.9°

39.1°

61.3°

64.0°

75.7°

85.7°

IK-s1

IK-s2

QB-s1

QB-s2

35.0°

50.4°

14.5°

75.5°

79.8°

63.2°

1.21 m

0.65 m

17.6°

47.8°

61.3°

65.1°

78.2°

85.7°

Integration of All Images (Three Stereo Pairs)

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

K2stereo + IKstereo + QBstereo

-

-

1.35 m

0.68 m

Table 4. Mapping accuracy of three or more satellite images.

Integration of Three Images (Single-Satellite Stereo + Higher Resolution Single Image)

1

2

3

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

1-2

1-3

2-3

1-2

1-3

2-3

K2-s1

K2-s2

IK-s1

47.7°

42.5°

26.1°

89.3°

71.7°

74.8°

1.66 m

1.65 m

K2-s1

K2-s2

IK-s2

47.7°

52.0°

8.9°

89.3°

83.9°

71.6°

1.72 m

2.37 m

K2-s1

K2-s2

QB-s1

47.7°

53.2°

36.9°

89.3°

73.1°

64.0°

1.56 m

1.60 m

K2-s1

K2-s2

QB-s2

47.7°

25.3°

39.1°

89.3°

69.4°

75.7°

1.43 m

1.27 m

IK-s1

IK-s2

QB-s1

35.0°

50.4°

17.6°

75.5°

79.8°

65.1°

1.31 m

0.70 m

IK-s1

IK-s2

QB-s2

35.0°

14.5°

47.8°

75.5°

63.2°

78.2°

1.65 m

0.89 m

Integration of Four or More Images (Single-Satellite Stereo + Higher Resolution Stereo Image)

1

2

3

4

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

1-2

1-3

1-4

1-2

1-3

1-4

2-3

2-4

3-4

2-3

2-4

3-4

K2-s1

K2-s2

IK-s1

IK-s2

47.7°

42.5°

52.0°

89.3°

71.7°

83.9°

1.62 m

1.45 m

26.1°

8.90°

35.0°

74.8°

71.6°

75.5°

K2-s1

K2-s2

QB-s1

QB-s2

47.7°

53.2°

25.3°

89.3°

73.2°

69.4°

1.37 m

0.92 m

36.9°

39.1°

61.3°

64.0°

75.7°

85.7°

IK-s1

IK-s2

QB-s1

QB-s2

35.0°

50.4°

14.5°

75.5°

79.8°

63.2°

1.21 m

0.65 m

17.6°

47.8°

61.3°

65.1°

78.2°

85.7°

Integration of All Images (Three Stereo Pairs)

Convergence Angle

BIE Angle

Horizontal Accuracy

Vertical Accuracy

K2stereo + IKstereo + QBstereo

-

-

1.35 m

0.68 m

The three cases in the middle part of Table 4 show the mapping accuracy when higher resolution stereo image, rather than a single image, was integrated into existing stereo images. The results include convergence and BIE angles between all images integrated. The first case is the integration of an IKONOS stereo image into an existing KOMPSAT-2 stereo image, the second case integrates a QuickBird stereo image into a KOMPSAT-2 stereo image, and the third case integrates a QuickBird stereo image into an IKONOS stereo image. From the three cases, the accuracy of existing stereo pairs was improved by the integration of additional stereo images. Although such integration also includes very weak convergence or BIE geometry, these did not degrade the accuracy. In our cases, the integration of additional stereo images of higher resolution always enhanced mapping accuracy. In addition, the integration between all three stereo pairs was checked. Such integration also showed accurate mapping but was slightly less accurate than that of the IKONOS stereo/QuickBird stereo integration.

Our analysis shows that appropriate integration of higher resolution images can be very effective in improving the accuracy of existing stereo images. We also point out that there are differences between the integration using a single image and that using stereo imagery. When integrating higher resolution images into existing stereo pairs: The addition of a single image may degrade accuracy if the image creates very weak convergence or BIE angle with either of the existing stereo images, whereas the integration of a stereo image does not degrade accuracy.

Meanwhile, in addition to the finding that very weak convergence or BIE angle may degrade accuracy, more specific definition of weak geometry may be required for real mapping applications. Nevertheless, it is difficult to clearly define such weak geometry and this remains a challenging problem in this field. Based on the results in Table 4, it is recommended that remote sensing users avoid single image integration that creates a convergence angle smaller than 20° and a BIE angle smaller than 70°.

In this section, the accuracy of the geo-positioning using multiple satellite images has been analyzed in comparison with that using typical single-sensor stereo imagery. Overall, dual-sensor integration provided the anticipated improvement in accuracy for the horizontal direction but performed worse than expected for the vertical direction. Our results also show that the integration of multiple satellite images can enhance conventional single-satellite models through the appropriate use of higher resolution images.

5. Discussion

As previously suggested, for the mapping from dual-satellite integration, horizontal accuracy met expectations based on image resolution unless very weak geometry was created, but the resulting vertical accuracy was contradictory to such expectation. More specifically, the vertical errors were larger than those of single-satellite stereo pairs even in cases where geometric stability is comparable to, and average resolution is averagely higher than, single-satellite stereo images. This section discusses the main source of this phenomenon.

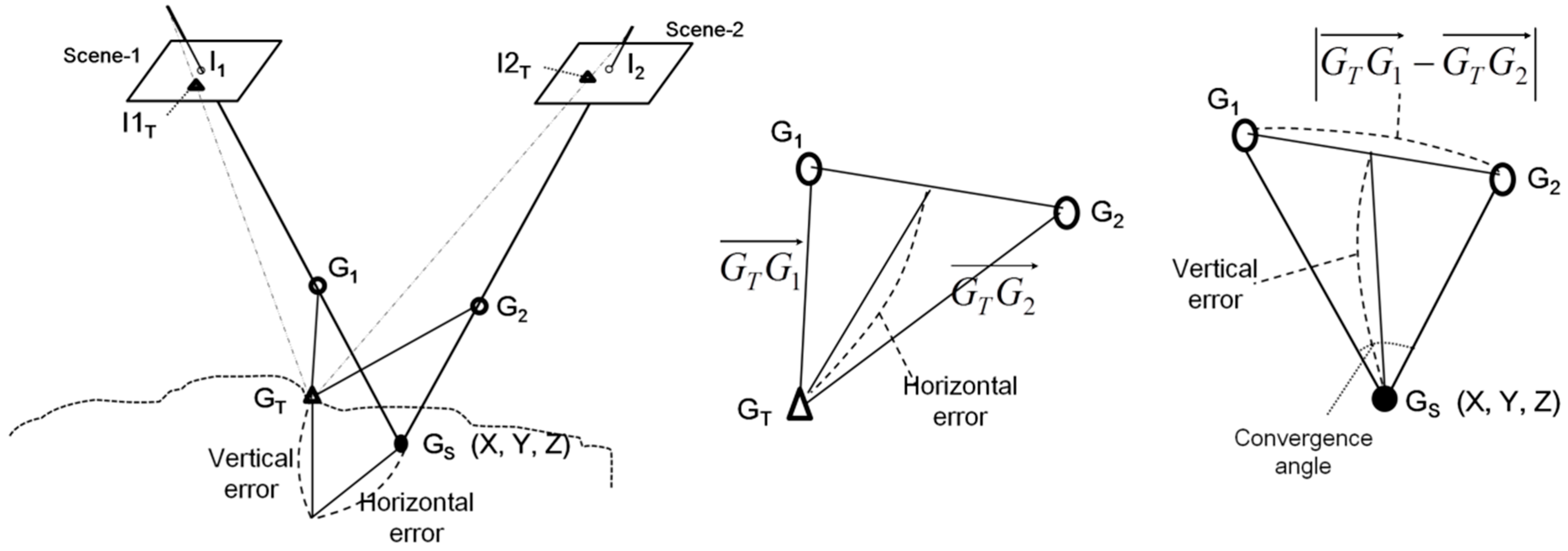
As shown in Figure 6, geo-positioning using stereo pairs is performed by achieving a 3D intersection point, G_S, estimated using two rays. In the left panel, if the two rays have no errors (the error-free scenario is represented by dashed lines), the two rays will intersect exactly at the true ground point G_T. However, the rays generally have individual pointing errors (represented in the middle panel as $\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_{\mathrm{1}}}$ and $\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_{\mathrm{2}}}$) that generate horizontal and vertical errors in object space. G₁ and G₂ are the intersection points of the two rays of scene-1 and scene-2, respectively, with the horizontal plane containing G_T. The individual pointing errors were previously represented to describe the horizontal and vertical errors [13] but their relationship was not discussed. Here, we discuss how the pointing errors relate to horizontal and vertical accuracy as shown in Figure 6.

Figure 6. Relationship between pointing error vectors of individual image and 3D position errors.

Figure 6. Relationship between pointing error vectors of individual image and 3D position errors.

The middle panel of Figure 6 shows that horizontal error mainly depends on the magnitude of the sum of the two error vectors $\left|\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_1}+\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_2}\right|$, which are generally proportional to the resolution of the individual image used. This interpretation supports our observation that the horizontal errors were explained well with image resolution. On the other hand, the right panel shows that vertical error can be expressed as the function of convergence angle and $\left|\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_1}-\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_2}\right|$, which is obtained by subtracting the two error vectors. The magnitude of the subtracting vector depends on the correlation or similarity of pattern between the two error vectors. For example, more similar patterns result in larger magnitude of subtracting vector. The correlation between convergence angle and vertical error has been previously suggested [11,14]. This paper suggests that the similarity of pointing error patterns between stereo images is also highly correlated with vertical error. This would explain why the vertical error could not be explained by image resolution. The vertical error, unlike horizontal error, is not closely related to the magnitude of the error vectors, but rather their correlation or similarity.

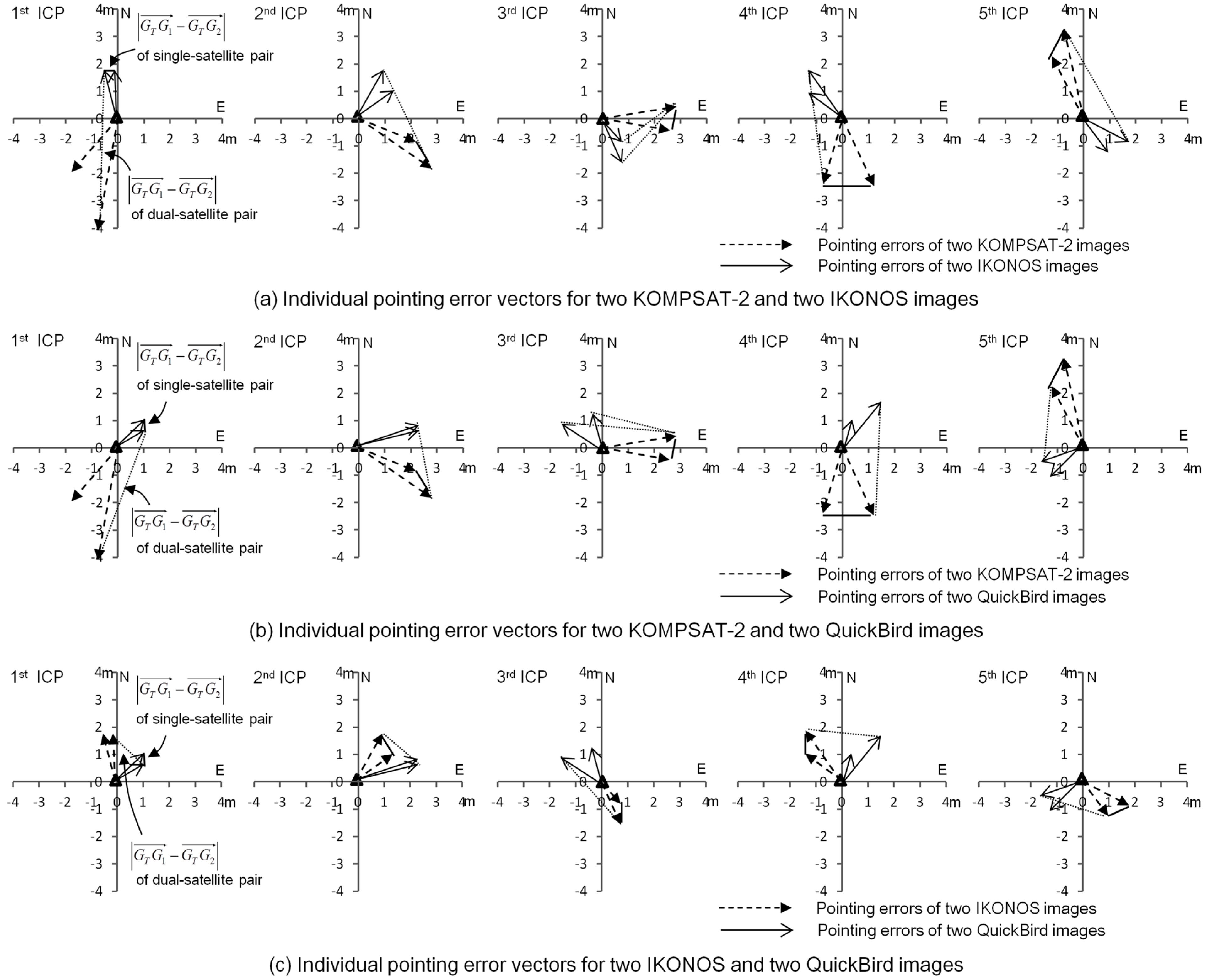
It was established empirically that such similarity of pointing errors is significantly different between single-satellite stereo and dual-satellite integration. In Figure 7, individual pointing errors of the images used are plotted for five ICPs. Figure 7a shows the results of two KOMPSAT-2 and two IKONOS images. The patterns of pointing errors between two KOMPSAT-2 images or those between two IKONOS images are very similar. However, the patterns of pointing errors were very different between one KOMPSAT-2 and one IKONOS image. Therefore, the distances between the ends of the pointing error vector, called the subtracting vector magnitude $\left|\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_1}-\overrightarrow{{\mathrm{G}}_{\mathrm{T}}{\mathrm{G}}_2}\right|$, in KOMPSAT-2/IKONOS integration were larger than those obtained by integrating two KOMPSAT-2 as well as two IKONOS images. This led to unexpectedly low vertical accuracy of KOMPSAT-2/IKONOS integration, which is even lower than that of the KOMPSAT-2 stereo pair. Figure 7b presents pointing errors of two KOMPSAT-2 and two QuickBird images, and Figure 7c of two IKONOS and two QuickBird images. These two cases also produced similar results to those described. Overall, the patterns of pointing errors from the same satellite were very similar, whereas those of different satellites were very different; hence, the higher-magnitude subtracting-vector results in larger vertical error from dual-satellite integrations.

Figure 7. Pointing error vectors and their subtracting vectors for single-satellite stereo and dual-satellite stereo (five ICPs). (a) KOMPSAT-2/IKONOS, (b) KOMPSAT-2/QuickBird, (c) IKONOS/QuickBird.

Figure 7. Pointing error vectors and their subtracting vectors for single-satellite stereo and dual-satellite stereo (five ICPs). (a) KOMPSAT-2/IKONOS, (b) KOMPSAT-2/QuickBird, (c) IKONOS/QuickBird.

Table 5 shows quantitative analysis using all 18 ICPs. Using coordinates of error vector ends, the correlation coefficients and the subtracting vector magnitudes were calculated between two error vectors. The table supports our visual analysis and interpretation very well. The correlations (similarity) of dual-satellite integrations were very low and their subtracting vector magnitudes were very large, compared to the three single-satellite stereo pairs.

This section has revealed that the similarity or dissimilarity of patterns between individual pointing errors is an important consideration for mapping accuracy when using two satellite images. The findings demonstrate that dual-satellite integration may not provide sufficient accuracy for vertical position mapping, and show that dissimilarity of error patterns between two different satellite images was the major reason for this phenomenon. However, this phenomenon is not clearly observed if integrating three or more images. We will give further consideration to such scenarios in future research on another major theme.

Table 5. Similarity of pointing error patterns for single-satellite stereo and dual-satellite stereo (18 ICPs).

	Image 1	Image 2	Correlation	$\left|\overrightarrow{G_T{G}_1}-\overrightarrow{G_T{G}_2}\right|$
Single-satellite stereo pairs	K2-s1	K2-s2	0.651	1.26 m
	IK-s1	IK-s2	0.810	0.69 m
	QB-s1	QB-s2	0.760	0.83 m
Dual-satellite integrations	K2-s1	IK-s1	0.256	1.92 m
	K2-s1	IK-s2	0.213	2.11 m
	K2-s2	IK-s1	0.292	1.75 m
	K2-s2	IK-s2	0.310	1.69 m
	K2-s1	QB-s1	0.233	2.25 m
	K2-s1	QB-s2	0.320	2.16 m
	K2-s2	QB-s1	0.342	1.83 m
	K2-s2	QB-s2	0.370	1.91 m
	IK-s1	QB-s1	0.351	1.63 m
	IK-s1	QB-s2	0.392	1.57 m
	IK-s2	QB-s1	0.311	1.81 m
	IK-s2	QB-s2	0.345	1.60 m

Table 5. Similarity of pointing error patterns for single-satellite stereo and dual-satellite stereo (18 ICPs).

	Image 1	Image 2	Correlation	$\left|\overrightarrow{G_T{G}_1}-\overrightarrow{G_T{G}_2}\right|$
Single-satellite stereo pairs	K2-s1	K2-s2	0.651	1.26 m
	IK-s1	IK-s2	0.810	0.69 m
	QB-s1	QB-s2	0.760	0.83 m
Dual-satellite integrations	K2-s1	IK-s1	0.256	1.92 m
	K2-s1	IK-s2	0.213	2.11 m
	K2-s2	IK-s1	0.292	1.75 m
	K2-s2	IK-s2	0.310	1.69 m
	K2-s1	QB-s1	0.233	2.25 m
	K2-s1	QB-s2	0.320	2.16 m
	K2-s2	QB-s1	0.342	1.83 m
	K2-s2	QB-s2	0.370	1.91 m
	IK-s1	QB-s1	0.351	1.63 m
	IK-s1	QB-s2	0.392	1.57 m
	IK-s2	QB-s1	0.311	1.81 m
	IK-s2	QB-s2	0.345	1.60 m

6. Conclusions

This paper reports on the geo-positioning accuracy achieved from multiple satellite images in comparison with that achieved from conventional single-satellite stereo imagery, in order to check the suitability for real mapping applications. Our analysis showed that dual-satellite integration can be effective in mapping horizontal position, but has some limitations in mapping vertical position. It was found that dissimilarity of pointing error patterns between two different satellite images is the major source of such limitation. Our analysis also showed that the integration of additional images with higher resolution can improve the overall accuracy of existing single-satellite stereo imagery. In this application, the integration of a single image should be carried out very carefully by checking whether the integration creates very weak convergence or BIE angles, while the integration of stereo images always needs to be approved. Overall, our study verified that appropriate use of multiple satellite images can be effective for geo-positioning. Conversely, it was also found that, unlike conventional stereo data, higher resolution is not a pre-requisite for accurate mapping, and therefore various geometric elements need to be considered when handling multiple-satellite data. We hope our findings can improve understanding of the use of multiple-satellite images, and suggest guidelines for effective use of satellite images in real mapping applications.