A Practical Split-Window Algorithm for Retrieving Land Surface Temperature from Landsat-8 Data and a Case Study of an Urban Area in China
Abstract
:1. Introduction
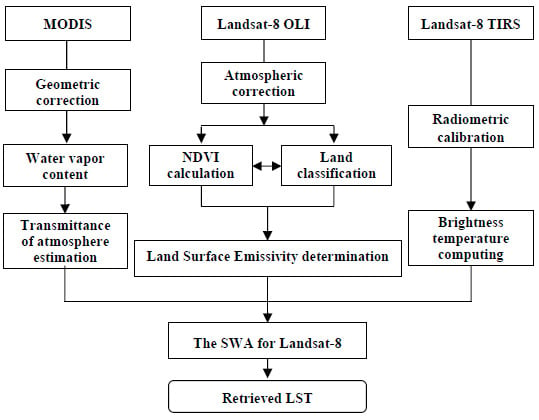
2. The SWA for Landsat-8 TIRS
2.1. Theoretical Derivation of the SWA
2.2. Determination of Coefficients
2.2.1. Determination of the Fitting Parameters for and
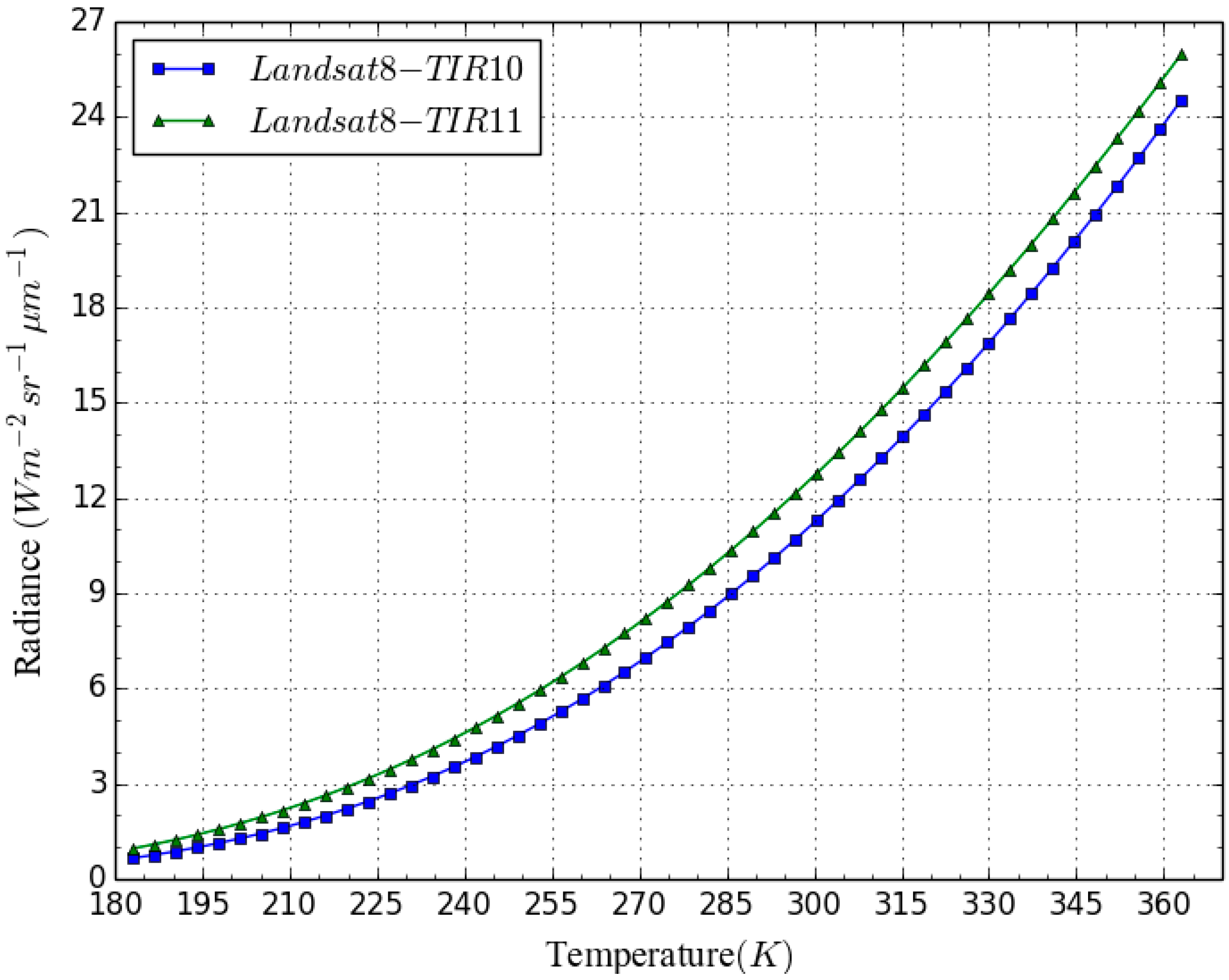
| TIRS | Quadratic Fitting Expression | R2 | SEE |
|---|---|---|---|
| band10 | 0.999979 | 0.0309 | |
| band11 | 0.999997 | 0.0117 |
| TIRS | Linear Regression Results | R2 | SEE |
|---|---|---|---|
| band10 | 0.9465 | 1.6404 | |
| band11 | 0.9584 | 1.5193 |
| TIRS | Fitting Parameters | |
|---|---|---|
| Quadratic Fitting Parameters | Linear Regression Parameters | |
| band10 | a10 = 0.0006678 b10 = −0.2333226 c10 = 21.1666266 | k10 = 0.1312942 d10 = −26.7808503 |
| band11 | a11 = 0.0006188 b11 = −0.1990475 c11 = 16.7224278 | k11 = 0.1387986 d11 = −27.7043284 |
2.2.2. Determination of Atmospheric Transmittance
| Water Vapour Content (g·cm−2) | TIR10- | TIR11- |
|---|---|---|
| 0.5 | 0.93542 | 0.89660 |
| 0.6 | 0.92903 | 0.88448 |
| 0.7 | 0.92217 | 0.87220 |
| 0.8 | 0.91483 | 0.85967 |
| 0.9 | 0.90700 | 0.84686 |
| 1.0 | 0.89869 | 0.83372 |
| 1.1 | 0.88990 | 0.82021 |
| 1.2 | 0.88064 | 0.80637 |
| 1.3 | 0.87093 | 0.79215 |
| 1.4 | 0.86076 | 0.77758 |
| 1.5 | 0.85015 | 0.76266 |
| 1.6 | 0.83913 | 0.74742 |
| 1.7 | 0.82769 | 0.73187 |
| 1.8 | 0.81588 | 0.71603 |
| 1.9 | 0.80370 | 0.69993 |
| 2.0 | 0.79117 | 0.68360 |
| 2.1 | 0.77830 | 0.66706 |
| 2.2 | 0.76514 | 0.65034 |
| 2.3 | 0.75168 | 0.63347 |
| 2.4 | 0.73798 | 0.61649 |
| 2.5 | 0.72401 | 0.59941 |
| 2.6 | 0.70983 | 0.58229 |
| 2.7 | 0.69546 | 0.56512 |
| 2.8 | 0.68092 | 0.54797 |
| 2.9 | 0.66622 | 0.53084 |
| 3.0 | 0.65140 | 0.51378 |
| TIRS | Cubic Regression Results | R2 | SEE |
|---|---|---|---|
| band10 | 0.999999 | 0.0001 | |
| band11 | 0.999995 | 0.0003 |
2.2.3. Determination of the Emissivity of the Ground
| εwater | εvegetation | εnon-vegetation | εGalvanized-Steel | |
|---|---|---|---|---|
| TIR-band10 | 0.991 | 0.984 | 0.964 | 0.959 |
| TIR-band11 | 0.986 | 0.980 | 0.970 | 0.962 |
3. Steadiness Analysis and Validation of the SWA
3.1. Steadiness Analysis of the SWA
3.1.1. Steadiness Analysis of Atmospheric Transmittance
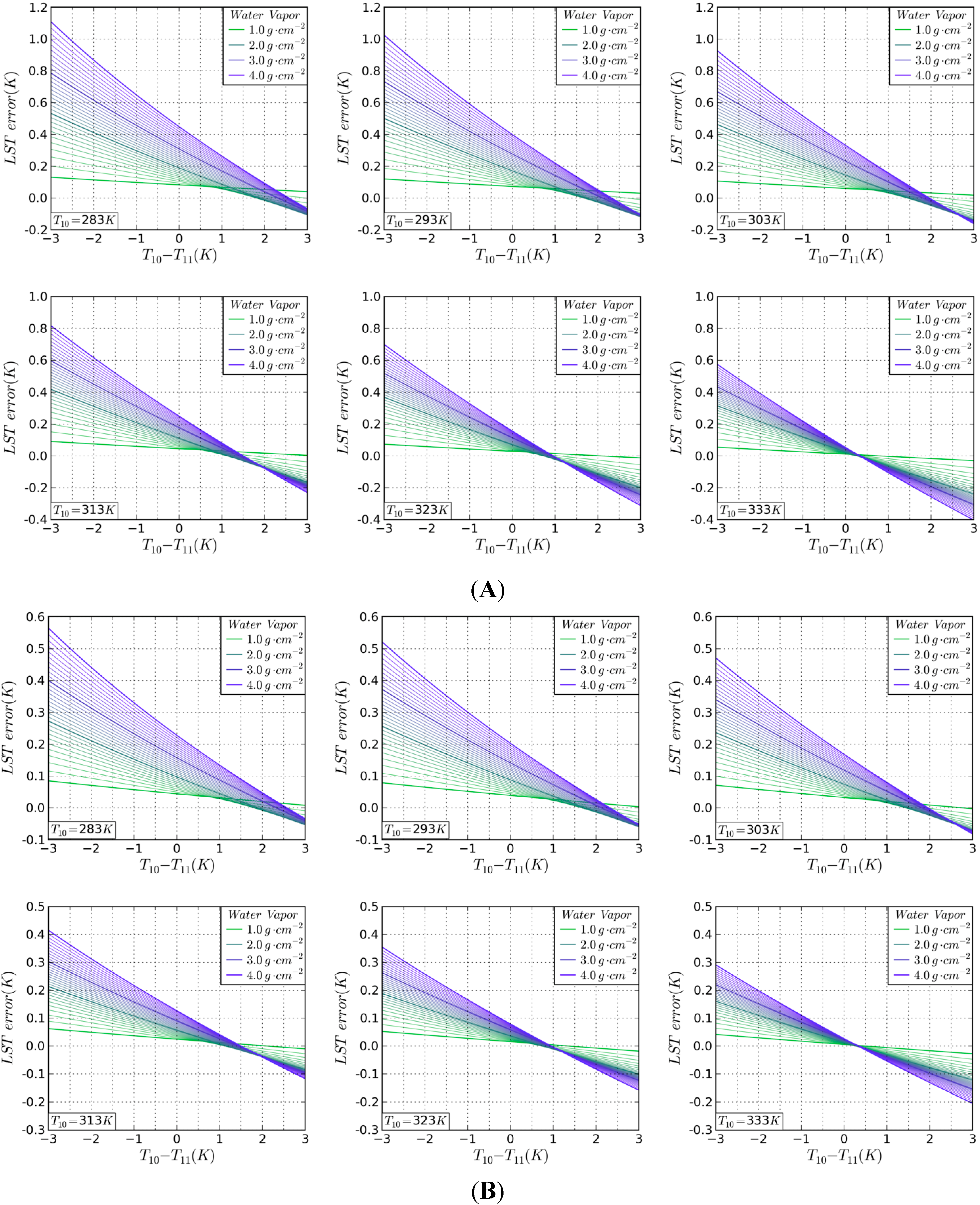
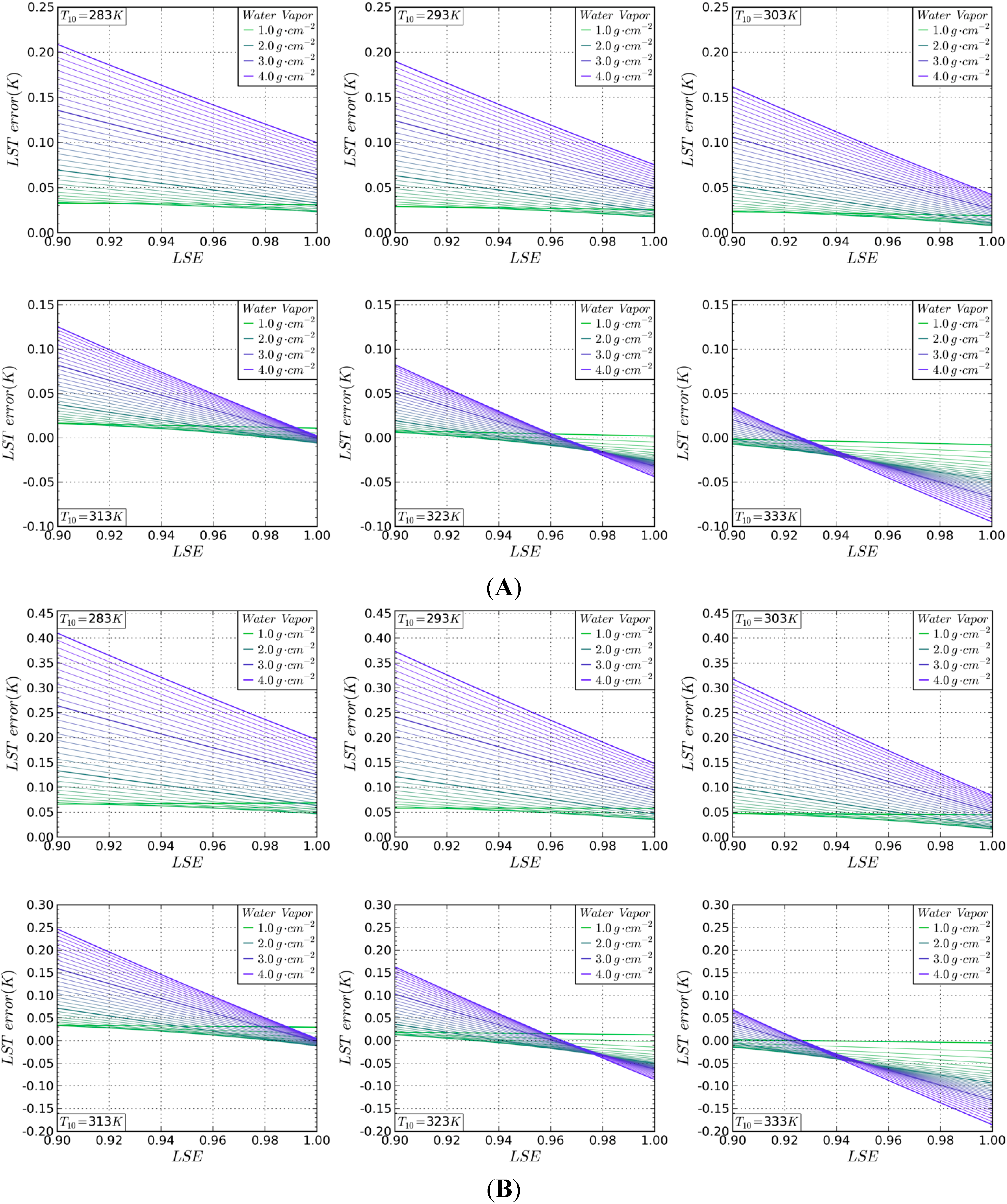
3.1.2. Stability Analysis of LSE
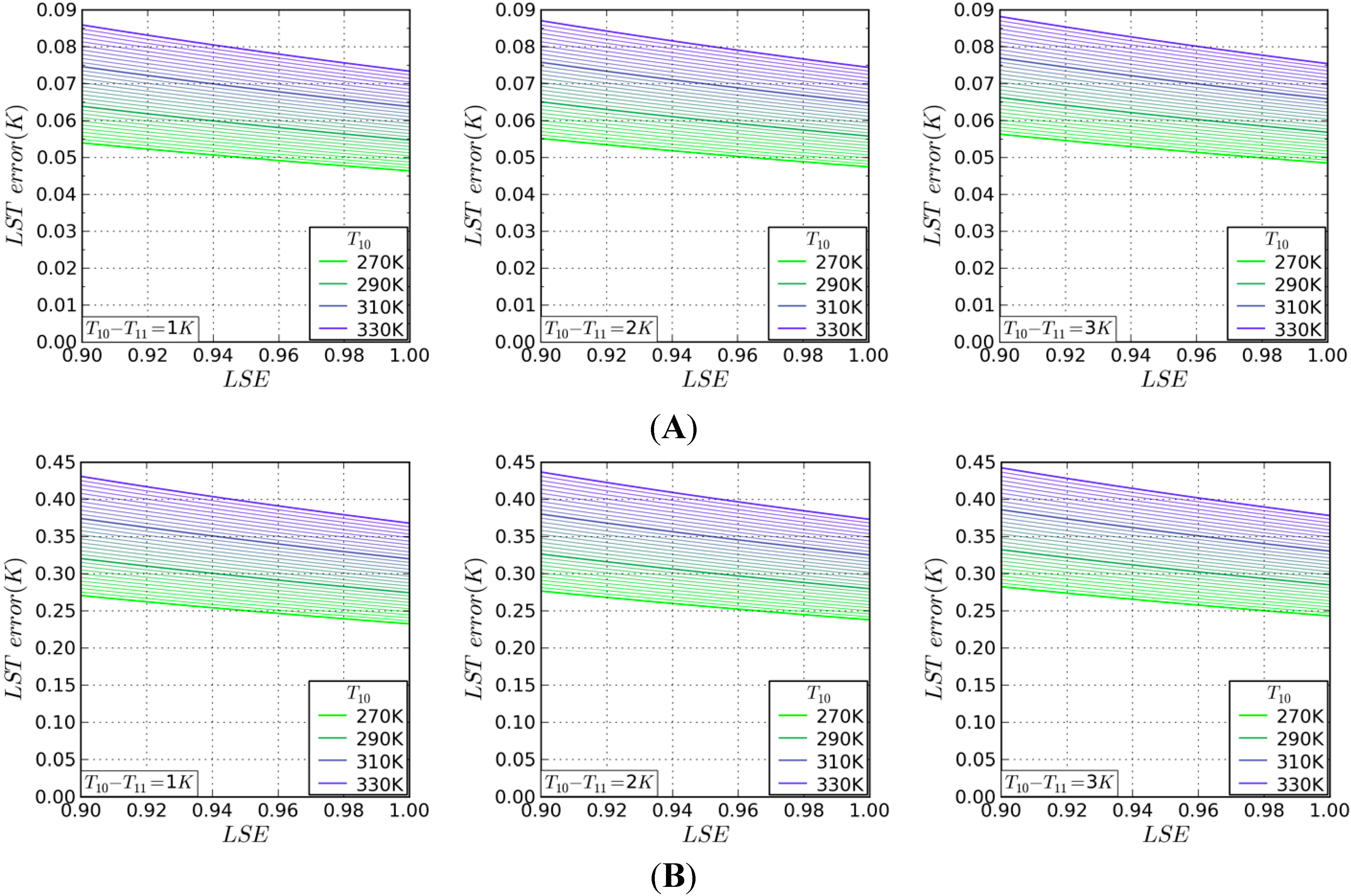
3.2. Evaluation of the Accuracy of the Proposed SWA
| Water Vapour Content (g·cm−2) | LST (°C) | LSE = 0.980 | LSE = 0.970 | LSE = 0.960 | LSE = 0.950 | LSE = 0.940 |
|---|---|---|---|---|---|---|
| 1 | 10 | 0.3710 | 0.3641 | 0.3561 | 0.3492 | 0.3413 |
| 20 | 0.3384 | 0.3302 | 0.3220 | 0.3138 | 0.3056 | |
| 30 | 0.3993 | 0.3914 | 0.3921 | 0.3691 | 0.3700 | |
| 40 | 0.5339 | 0.5348 | 0.5221 | 0.5232 | 0.5103 | |
| 50 | 0.7360 | 0.7350 | 0.7268 | 0.7186 | 0.7178 | |
| 60 | 0.9933 | 0.9870 | 0.9926 | 0.9864 | 0.9731 | |
| 2 | 10 | 0.3235 | 0.2868 | 0.2550 | 0.2231 | 0.1897 |
| 20 | 0.2835 | 0.2605 | 0.2238 | 0.2007 | 0.1635 | |
| 30 | 0.3388 | 0.3250 | 0.2833 | 0.2586 | 0.2450 | |
| 40 | 0.4810 | 0.4671 | 0.4374 | 0.4075 | 0.3936 | |
| 50 | 0.6935 | 0.6682 | 0.6520 | 0.6264 | 0.6102 | |
| 60 | 0.9515 | 0.9278 | 0.9177 | 0.8939 | 0.8611 | |
| 3 | 10 | 0.1532 | 0.0701 | −0.0164 | −0.1170 | −0.2146 |
| 20 | 0.1456 | 0.0527 | −0.0281 | −0.1099 | −0.1927 | |
| 30 | 0.2104 | 0.1390 | 0.0603 | −0.0194 | −0.0933 | |
| 40 | 0.3684 | 0.2865 | 0.2227 | 0.1388 | 0.0734 | |
| 50 | 0.5708 | 0.5059 | 0.4403 | 0.3739 | 0.3067 | |
| 60 | 0.8190 | 0.7716 | 0.7073 | 0.6423 | 0.5933 |
| Water Vapour Content (g·cm−2) | LST (°C) | LSE = 0.980 | LSE = 0.960 | LSE = 0.940 |
|---|---|---|---|---|
| 1.0 | 20 | 0.3130 | 0.2958 | 0.2766 |
| 40 | 0.5476 | 0.5326 | 0.5163 | |
| 60 | 1.0371 | 1.0250 | 1.0122 | |
| 2.0 | 20 | 0.3078 | 0.2415 | 0.1730 |
| 40 | 0.5845 | 0.5282 | 0.4723 | |
| 60 | 1.1176 | 1.0713 | 1.0220 | |
| 3.0 | 20 | 0.2281 | 0.0416 | −0.1486 |
| 40 | 0.6080 | 0.4500 | 0.2914 | |
| 60 | 1.2313 | 1.0958 | 0.9587 |
| Water Vapour Content (g·cm−2) | LST (°C) | LSE = 0.980 | LSE = 0.960 | LSE = 0.940 |
|---|---|---|---|---|
| 1.0 | 20 | 0.3893 | 0.3836 | 0.3762 |
| 40 | 0.5563 | 0.5511 | 0.5439 | |
| 60 | 0.9996 | 0.9940 | 0.9893 | |
| 2.0 | 20 | 0.3129 | 0.2704 | 0.2288 |
| 40 | 0.4576 | 0.4206 | 0.3851 | |
| 60 | 0.8739 | 0.8440 | 0.8145 | |
| 3.0 | 20 | 0.2749 | 0.1358 | −0.0071 |
| 40 | 0.5500 | 0.4310 | 0.3118 | |
| 60 | 1.0849 | 0.9823 | 0.8787 |
4. A Case Study of an Urban Area in China
4.1. Study Area
4.2. Data Used
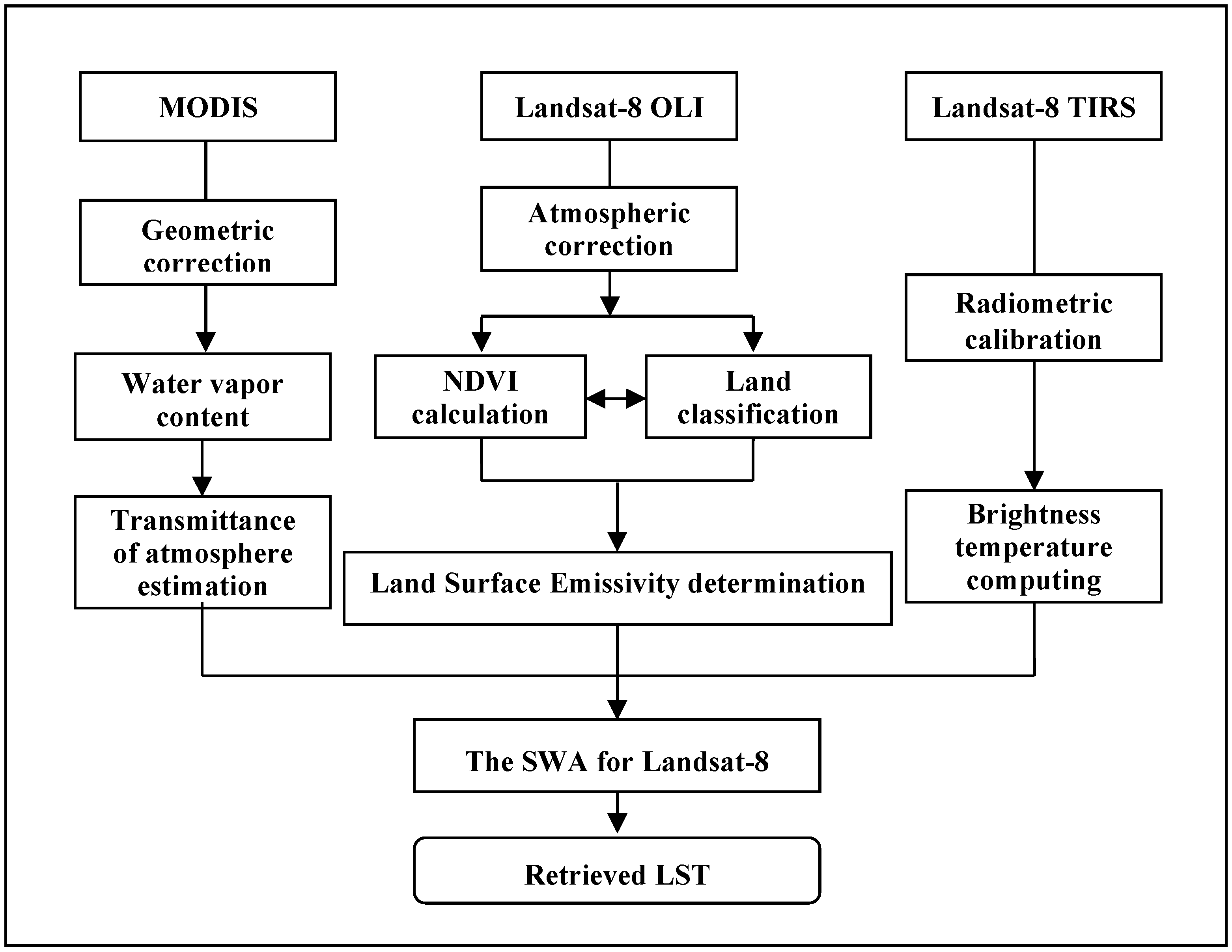
4.3. LST Retrieval
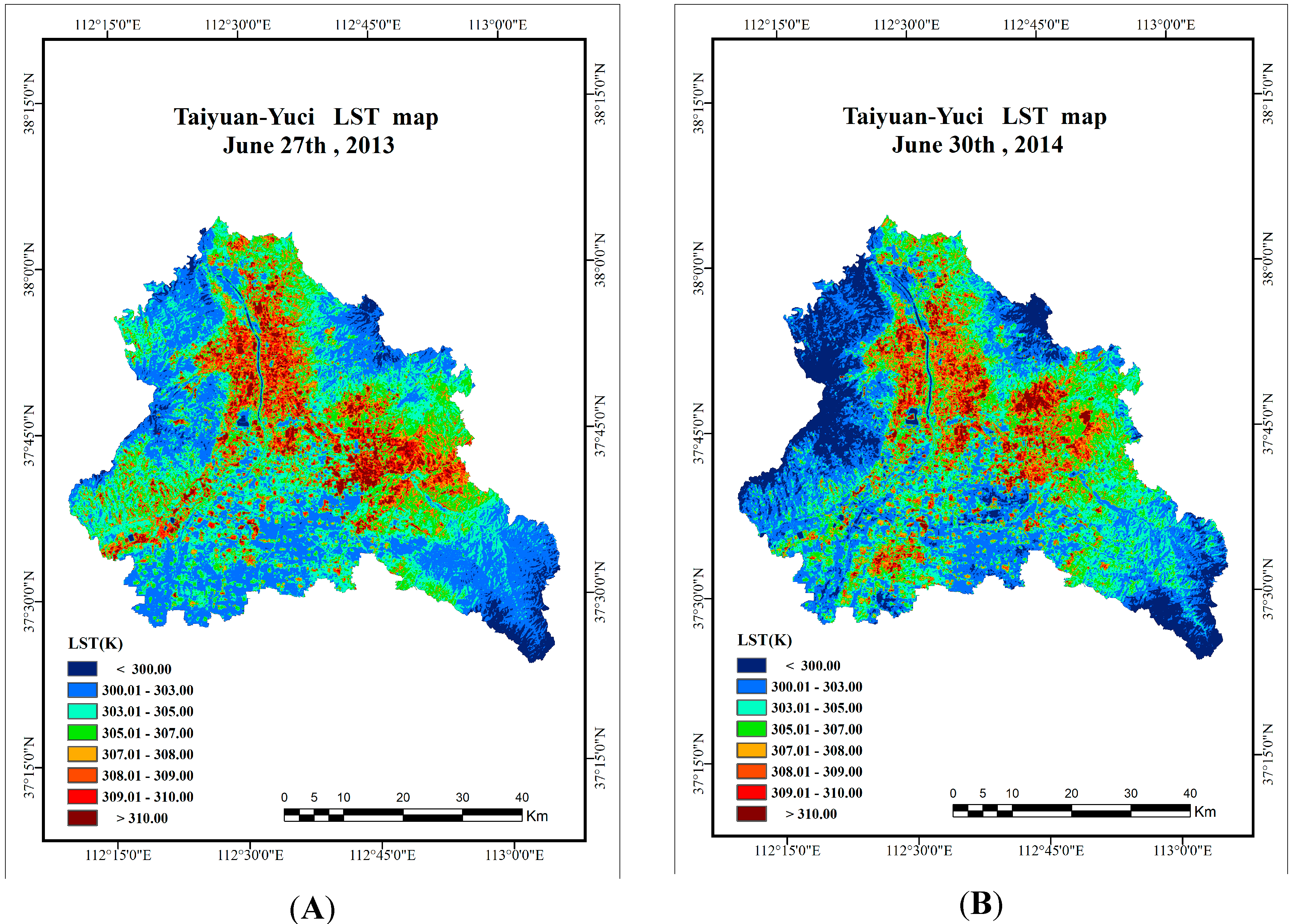
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References and Notes
- Chapin, F.; Sturm, M.; Serreze, M.; McFadden, J.; Key, J.; Lloyd, A.; McGuire, A.; Rupp, T.; Lynch, A.; Schimel, J. Role of Land-Surface Changes in Arctic Summer Warming. Science 2005, 310, 657–660. [Google Scholar] [CrossRef] [PubMed]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use change on climate. Nature 2003, 423, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, V.; Crutzen, P.; Kiehl, J.; Rosenfeld, D. Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the Southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Gallo, K.P.; Owen, T.W. Assessment of urban heat island: A multi-sensor perspective for the Dallas-Ft. Worth, USA region. Geocarto. Int. 1998, 13, 35–41. [Google Scholar] [CrossRef]
- Streutker, D.R. A remote sensing study of the urban heat island of Houston, Texas. Int. J. Remote Sens. 2002, 23, 2595–2608. [Google Scholar] [CrossRef]
- Weng, Q. A Remote sensing-GIS evaluation of urban expansion and its impact on surface temperature in the Zhujiang Delta, China. Int. J. Remote Sens. 2001, 22, 1999–2014. [Google Scholar]
- Chen, X.L.; Zhao, H.; Li, P.; Yin, Z. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2002, 104, 133–146. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and Normalized Difference Vegetation Index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Li, Z.L.; Zhang, R.; Sun, X.; Su, H.; Tang, X.; Zhu, Z. Experimental system for the study of the directional thermal emission of natural surfaces. Int. J. Remote Sens. 2004, 25, 195–204. [Google Scholar] [CrossRef]
- Ottlé, C.; Vidal-Madjar, D. Estimation of land surface temperature with NOAA9 data. Remote Sens. Environ. 1992, 40, 27–41. [Google Scholar] [CrossRef]
- Price, J.C. Estimating surface temperatures from satellite thermal infrared data—A simple formulation for the atmospheric effect. Remote Sens. Environ. 1983, 13, 353–361. [Google Scholar] [CrossRef]
- Price, J.C. Land surface temperature measurements from the split window channels of the NOAA 7 AVHRR. J. Geophys. Res. 1984, 89, 7231–7237. [Google Scholar] [CrossRef]
- Becker, F. The impact of spectral emissivity on the measurement of land surface temperature from a satellite. Int. J. Remote Sens. 1987, 8, 1509–1522. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surfaces. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Coll, C.; Caselles, V. Atmospheric correction for land surface temperature using NOAA-11 AVHRR Channels 4 and 5. Remote Sens. Environ. 1991, 38, 19–34. [Google Scholar] [CrossRef]
- Coll, C.; Caselles, V.; Sobrino, J.A.; Valor, E. On the atmospheric dependence of the split-window equation for land surface temperature. Int. J. Remote Sens. 1994, 15, 105–122. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.L.; Stoll, M.P.; Becker, F. Improvements in the split-window technique for land surface temperature determination. IEEE Trans. Geosci. Remote Sens. 1994, 32, 243–253. [Google Scholar] [CrossRef]
- Prata, A.J. Land surface temperature determination from satellites. Adv. Space Res. 1994, 14, 15–26. [Google Scholar] [CrossRef]
- Ulivieri, C.; Castronuovo, M.M.; Francioni, R.; Cardillo, A. A split window algorithm for estimating land surface temperature from satellites. Adv. Space Res. 1994, 14, 59–65. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Li, Z.L.; Stoll, M.P.; Becker, F. Multi-channel and multi-angle algorithms for estimating sea and land surface temperature with ATSR data. Int. J. Remote Sens. 1996, 17, 2089–2114. [Google Scholar] [CrossRef]
- Tang, B.H.; Li, Z.L. Retrieval of land surface bidirectional reflectivity in the mid-infrared from MODIS Channels 22 and 23. Int. J. Remote Sens. 2008, 29, 4907–4925. [Google Scholar] [CrossRef]
- Atitar, M.; Sobrino, J.A. A split-window algorithm for estimating LST from Meteosat 9 Data: Test and comparison with in situ data and MODIS LSTs. IEEE Geosci. Remote Sens. 2009, 6, 122–126. [Google Scholar] [CrossRef]
- Mao, K.; Qin, Z.; Shi, J.; Gong, P. A practical split-window algorithm for retrieving land-surface temperature from MODIS data. Int. J. Remote Sens. 2005, 26, 3181–3204. [Google Scholar] [CrossRef]
- Chédin, A.; Scott, N.A.; Berroir, A. A single-channel, double-viewing angle method for sea surface temperature determination from coincident Meteosat and TIROS-N radiometric measurements. J. Appl. Meteorol. 1982, 21, 613–618. [Google Scholar] [CrossRef]
- Prata, A.J. Surface temperatures derived from the Advanced Very High Resolution Radiometer and the Along Track Scanning Radiometer. 1. Theory. J. Geophys. Res. 1993, 98, 16689–16702. [Google Scholar] [CrossRef]
- Prata, A.J. Land surface temperatures derived from the Advanced Very High Resolution Radiometer and the Along-Track Scanning Radiometer 2. Experimental results and validation of AVHRR algorithms. J. Geophys. Res. 1994, 99, 13025–13058. [Google Scholar] [CrossRef]
- Li, Z.L.; Stoll, M.P.; Zhang, R.H.; Jia, L.; Su, Z.B. On the separate retrieval of soil and vegetation temperatures from ATSR data. Sci. China Series D: Earth Sci. 2001, 44, 97–111. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Romaguera, M. Land surface temperature retrieval from MSG1-SEVIRI data. Remote Sens. Environ. 2004, 92, 247–254. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat Data Continuity Mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Cuenca, R.H.; Ciotti, S.P.; Hagimoto, Y. Application of Landsat to evaluate effects of irrigation forbearance. Remote Sens. 2013, 5, 3776–3802. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Matter, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 Thermal Infrared Sensor data. IEEE Geosci. Remote Sens. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Du, C.; Ren, H.Z.; Qin, Q.M.; Meng, J.J.; Li, J. Split-window algorithm For estimating land surface temperature from Landsat 8 TIRs data. In Proceedings of 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3578–3581.
- Rybicki, G.B.; Lightman, A.P. Fundamental of Radiative Transfer. Radiative Processes in Astrophysics; John Wiley & Sons, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Ottle, C.; Stoll, M. Effect of atmospheric absorption and surface emissivity on the determination of land surface temperature from infrared satellite data. Int. J. Remote Sens. 1993, 14, 2025–2037. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A. A Mono-Window Algorithm for Retrieving Land Surface Temperature from Landsat TM Data and Its Application to the Israel-Egypt Border Region. Int. J. Remote Sens. 2001, 22, 3722–3723. [Google Scholar]
- Jiménez-MuÌoz, J.C.; Sobrino, J.A. A generalized single 2 channel method for retrieving land surface temperature from remote sensing Data. J. Geophys. Res. 2003, 8. [Google Scholar] [CrossRef]
- Qin, Z.; Dall’Olmo, G.; Karnieli, A.; Berliner, P. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-Advanced very High Resolution Radiometer data. Geophys. Res. Atmos. 2001, 106, 22655–22670. [Google Scholar] [CrossRef]
- Kaufmann, Y.J.; Gao, B.C. Remote sensing of water in the Near IR from EOS/MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z.L. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Aster Spectral Library. Available online: http://speclib.jpl.nasa.gov/ (accessed on 4 June 2014).
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Caselles, V.; Becker, F. Significance of the remotely sensed thermal infrared measurements obtained over a citrus orchard. Photogramm. Eng. Remote Sens. 1990, 44, 343–354. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, M.; Li, J.; Wang, C.; Shang, R. A Practical Split-Window Algorithm for Retrieving Land Surface Temperature from Landsat-8 Data and a Case Study of an Urban Area in China. Remote Sens. 2015, 7, 4371-4390. https://doi.org/10.3390/rs70404371
Jin M, Li J, Wang C, Shang R. A Practical Split-Window Algorithm for Retrieving Land Surface Temperature from Landsat-8 Data and a Case Study of an Urban Area in China. Remote Sensing. 2015; 7(4):4371-4390. https://doi.org/10.3390/rs70404371
Chicago/Turabian StyleJin, Meijun, Junming Li, Caili Wang, and Ruilan Shang. 2015. "A Practical Split-Window Algorithm for Retrieving Land Surface Temperature from Landsat-8 Data and a Case Study of an Urban Area in China" Remote Sensing 7, no. 4: 4371-4390. https://doi.org/10.3390/rs70404371
APA StyleJin, M., Li, J., Wang, C., & Shang, R. (2015). A Practical Split-Window Algorithm for Retrieving Land Surface Temperature from Landsat-8 Data and a Case Study of an Urban Area in China. Remote Sensing, 7(4), 4371-4390. https://doi.org/10.3390/rs70404371