1. Introduction
The alignments of sensors and actuators inside a spacecraft are measured carefully in laboratory before launch. The alignment between the attitude frame and the camera frame is called boresight alignment [
1]. Since it is essential for the quality of earth-observation satellites [
2], several studies have already developed various methods for the precise alignment in laboratory [
3,
4,
5].
Despite the efforts to the precise alignment before launch, on-orbit calibration is mandatory because additional errors may be introduced after launch by launch shock, outgassing, zero-gravity, thermal effect,
etc. Therefore, it is common for earth-observation satellite programs to calibrate the alignment during the initial commissioning period [
2,
3,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. However, it is difficult to obtain an accurate alignment because the alignment error is measured as the sum of various error sources [
6].
A common approach for on-orbit boresight alignment calibration is based on the usage of ground control points (GCPs) and a physical sensor model. Breton and Bouillon used multiple GCPs and a physical model of the spacecraft to estimate the alignment of SPOT-5 [
7,
8]. Radhadevi also used a similar approach for IRS-P6 [
6] which requires as many data samples as possible in order to obtain reliable results. However, the number of GCPs hardly exceeded hundreds because their GCPs relied on spots or landmarks prepared beforehand [
6,
7,
8,
9,
10,
11].
Some researchers tried an automatic GCP extraction technique using reference ortho-photos and image-based feature matching to get a much higher number of GCPs [
12,
13,
14,
21,
22]. Robertson
et al. even included the automated GCP extraction step to RapidEye’s ground processing chain for alignment calibration [
14]. However, the alignment was calculated for individual images, and the system’s alignment was simply taken from the average of individual measurements. This approach can cause biased measurement in case that GCPs are distributed unevenly in an image. It is also unable to consider different alignment characteristics of attitude sensors. Müller
et al. proposed a processing chain for automated geo-referencing that includes automatic GCP extraction and sensor model improvement [
21]. They successfully geo-referenced thousands of images from SPOT-4, SPOT-5, and IRS-P6 using automatically extracted GCPs. However, their study used thousands of images that were already taken, and they did not cover the considerations for effective on-orbit calibration. Klančar
et al. suggested an image-based attitude control mechanism that correlates the spacecraft camera image and the reference image on the fly [
22]. Although this approach eliminates the need of measuring the boresight alignment, it is impractical due to the limited on-board resource to have a high-resolution GCP database on-board and perform the real-time feature matching.
Several interesting approaches were proposed for Pleiades-HR, such as single-track reverse imaging and star imaging, as well as the GCP method [
16,
17,
18]. The single-track reverse imaging method, which is called auto-reverse, utilizes the spacecraft’s high agility to rotate the spacecraft 180 degrees after imaging and to take a second image of the same spot [
16]. This method looks quite promising and has several strengths over the GCP method. However, it is only applicable to high performance satellites such as Pleiades-HR. The star-imaging method is an operationally efficient method which could be performed during the eclipse period without interfering daylight imaging operation [
17]. It is, however, still in a conceptual stage and not developed yet for practical applications. It also has a potential risk to measure different or unwanted error, as space imaging is different from ground imaging. Despite the proposal of new calibration methods, the baseline method for alignment calibration of Pleiades-HR was the GCP-based method [
18] which used only 20 GCPs on average per site from 20 spots across the world.
The latest research on alignment calibration concerns reports on ZY1-02C [
19,
20]. Wang
et al. provided a well-written explanation of the interior and exterior orientation error determination and an estimation model that uses many GCPs extracted from an ortho-photo [
19]. Although it is essential to use multiple images to estimate misalignment from noisy data, they used a single image for estimation in the experiment. The acquisition planning to build proper estimation dataset is also important as the coverage of spacecraft attitude and attitude sensors affect the accuracy and robustness of the estimation; however, they did not consider this aspect. Jiang
et al. tried to correct dynamic attitude error by correlating overlapped CCD images [
20]. In their article, the GCPs were collected from ortho-photo manually, which led them to a small number of available GCPs for experiment.
Camera misalignment is the misalignment between the attitude frame and the true camera frame. The camera frame is calculated from the spacecraft attitude and pre-launch alignment measurement data, whereas the true camera frame is where the boresight vector is actually pointing. The static error between those two frames is observed as if the spacecraft has a biased error on its attitude. The boresight alignment calibration could be done by finding the camera misalignment and compensating it from the spacecraft attitude.
In this paper, a framework for on-orbit camera misalignment estimation of earth-observation satellites is presented. It provides an all-in-one solution from the planning of ground-target image acquisition to the estimation of the camera misalignment. Some of the important aspects when choosing the calibration targets are discussed, as well as the distribution of tilt angles and sensor selections for effective calibration. A proven robust automatic approach for the extraction of many GCPs from ortho-photos is explained in detail. Investigating the pattern of localization errors of GCPs is essential. Sometimes misalignments of attitude sensors are not the same, generating different error patterns depending on which set of attitude sensors were used. The images must be grouped by parameters showing similar error patterns (e.g., sensors, imaging modes, target locations), and the bias must be estimated separately for each group. The mathematical model, which was derived from colinearity to solve the camera misalignment, is explained comprehensively. Simulation tests with sophisticated simulation setup are conducted to prove validity of the framework. Finally, the application results to the Deimos-2 camera misalignment estimation during the initial commissioning phase are presented to show the effectiveness of the proposed framework.
In
Section 2, the overview of the camera misalignment estimation is described, followed by the necessary background knowledge using Deimos-2 as an example. The steps of camera misalignment estimation such as image planning, automated GCP extraction, localization error pattern analysis, and the mathematical model for camera misalignment estimation are also explained.
Section 3 describes the results of the experiments to evaluate the proposed framework. The accuracy of the mathematical model was evaluated using simulation data. The results of the application to Deimos-2 are demonstrated as well. In
Section 4, the summary of the work is presented.
2. Camera Misalignment Estimation Framework
2.1. Overview
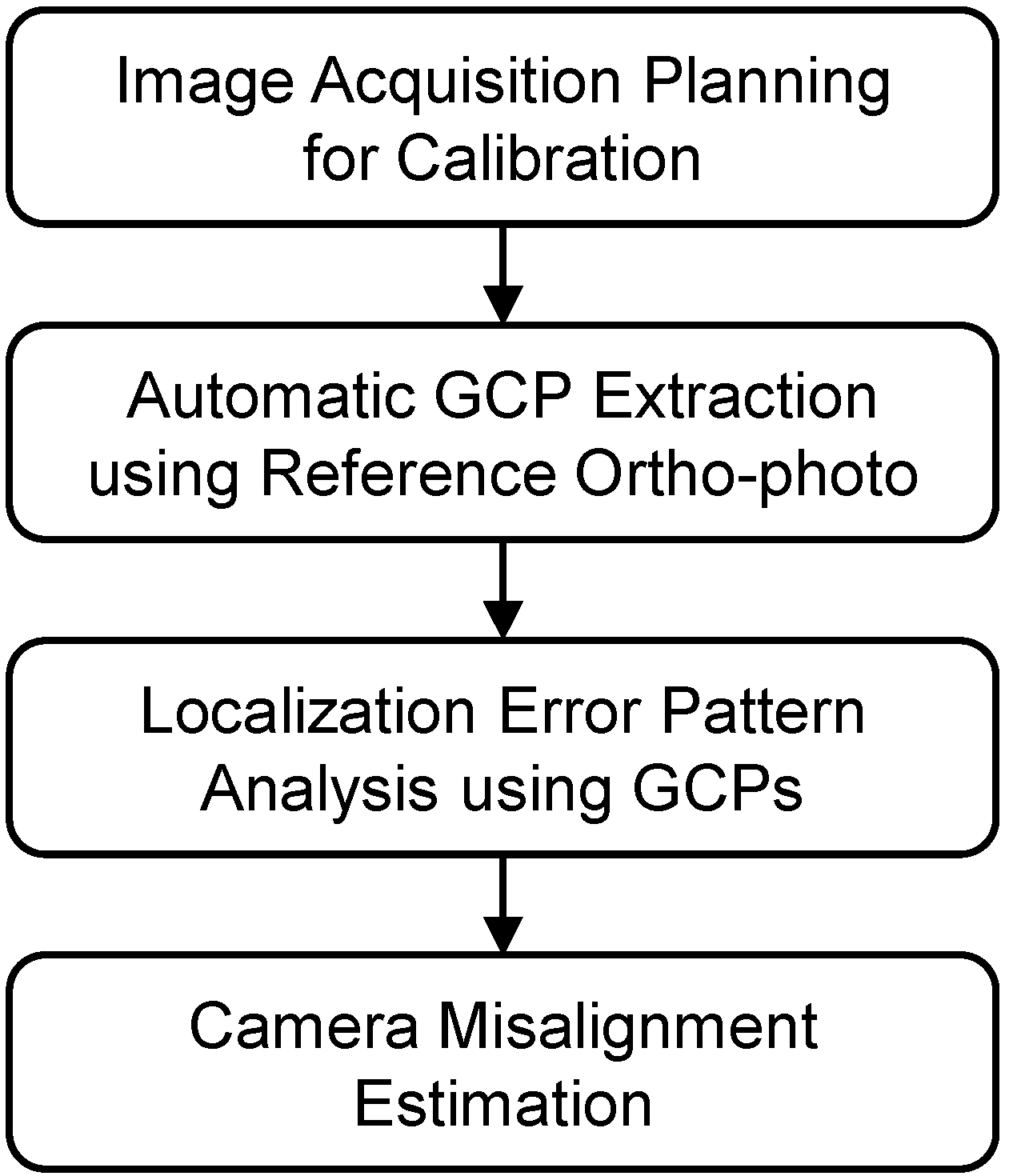
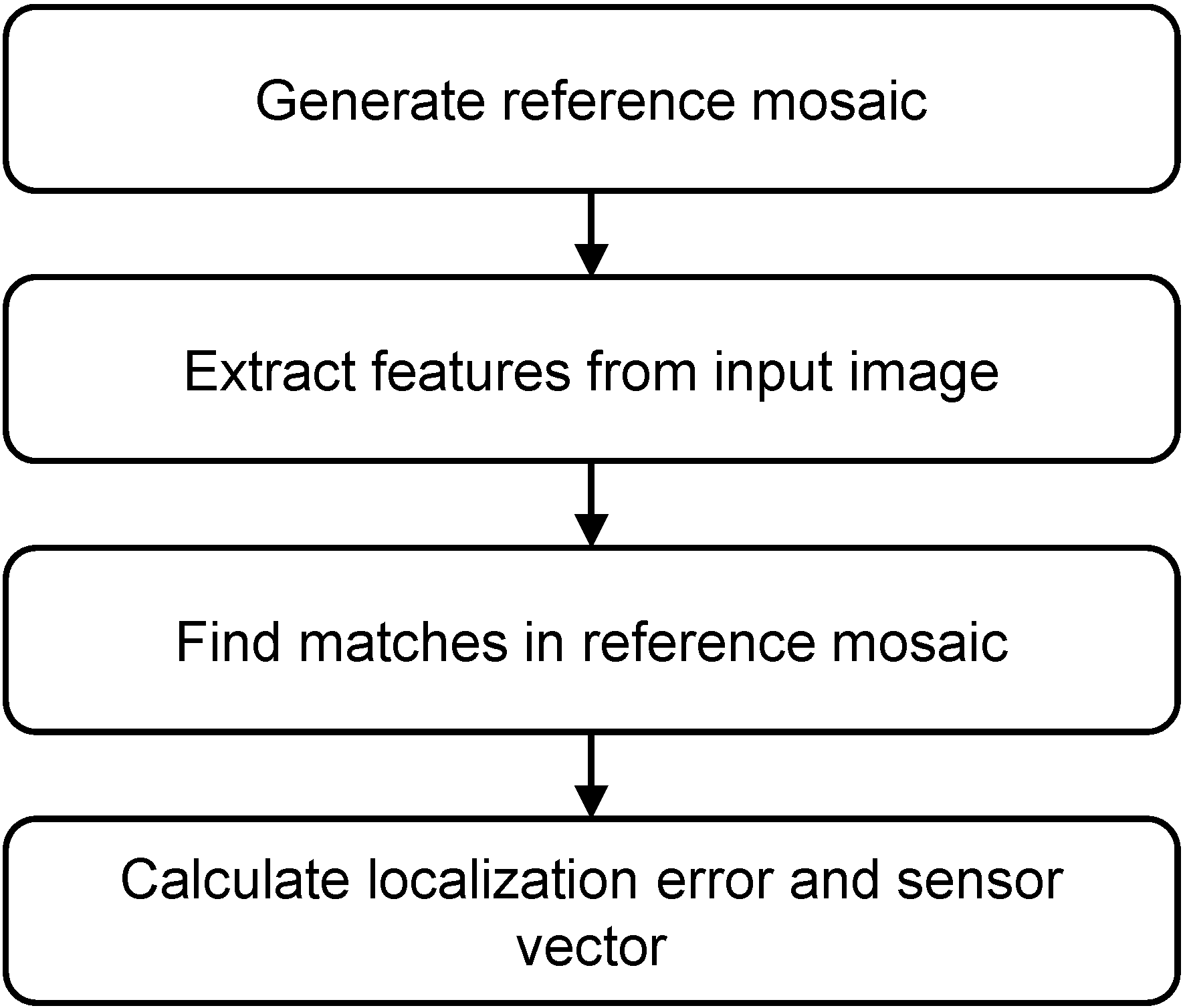
Conceptually, the estimation process of camera misalignment consists of four major steps. The first step is planning the satellite’s imaging operation to acquire image data for the camera misalignment estimation. Extracting GCPs from the images is the next step. Analyzing the error pattern of GCPs and confirming the existence of misalignment are followed. The last step is to estimate the camera misalignment using the GCPs and spacecraft ancillary, which contains spacecraft position and attitude data.
Figure 1 shows the conceptual process of the camera misalignment estimation.
Figure 1.
Conceptual process of camera misalignment estimation.
Figure 1.
Conceptual process of camera misalignment estimation.
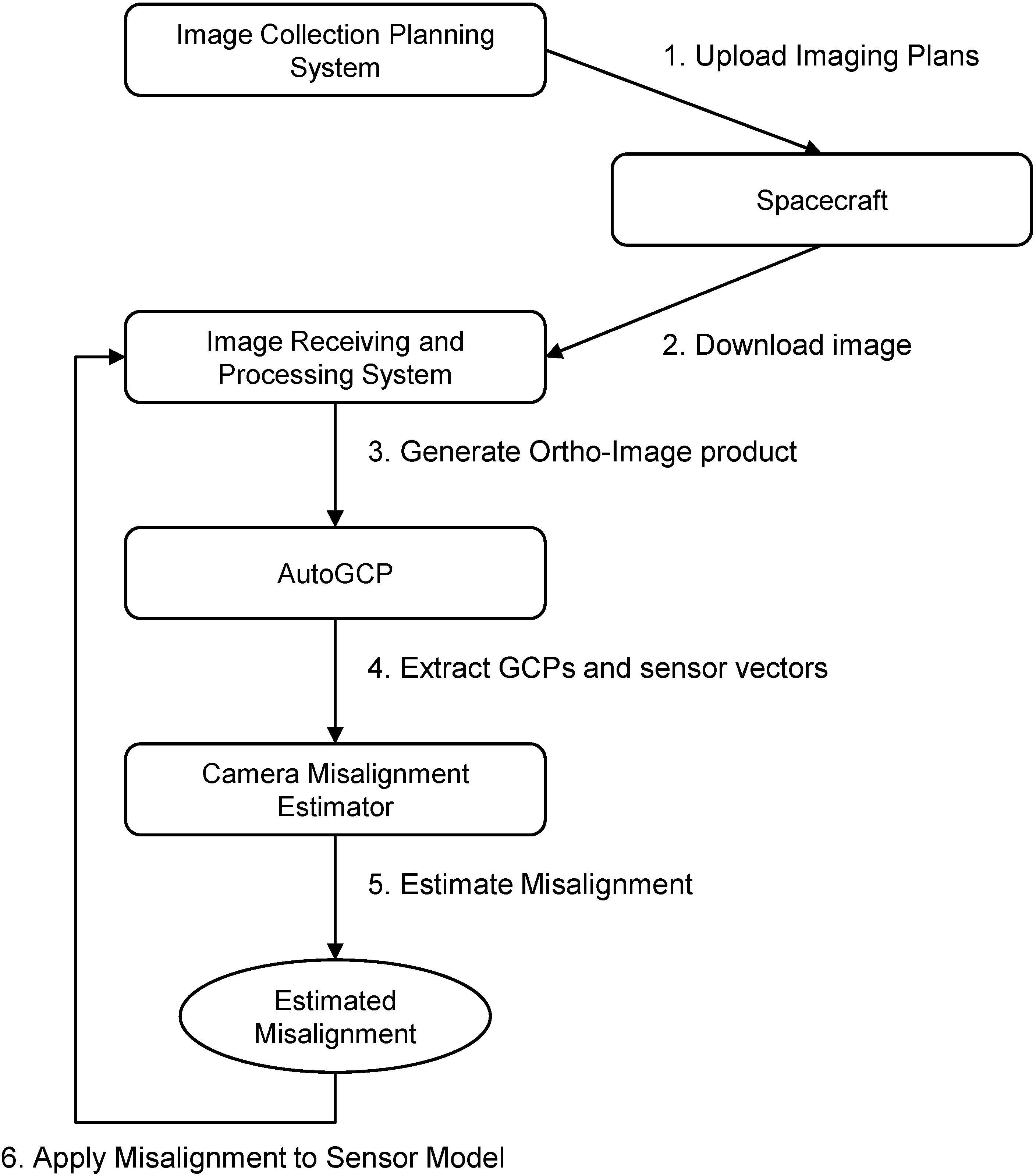
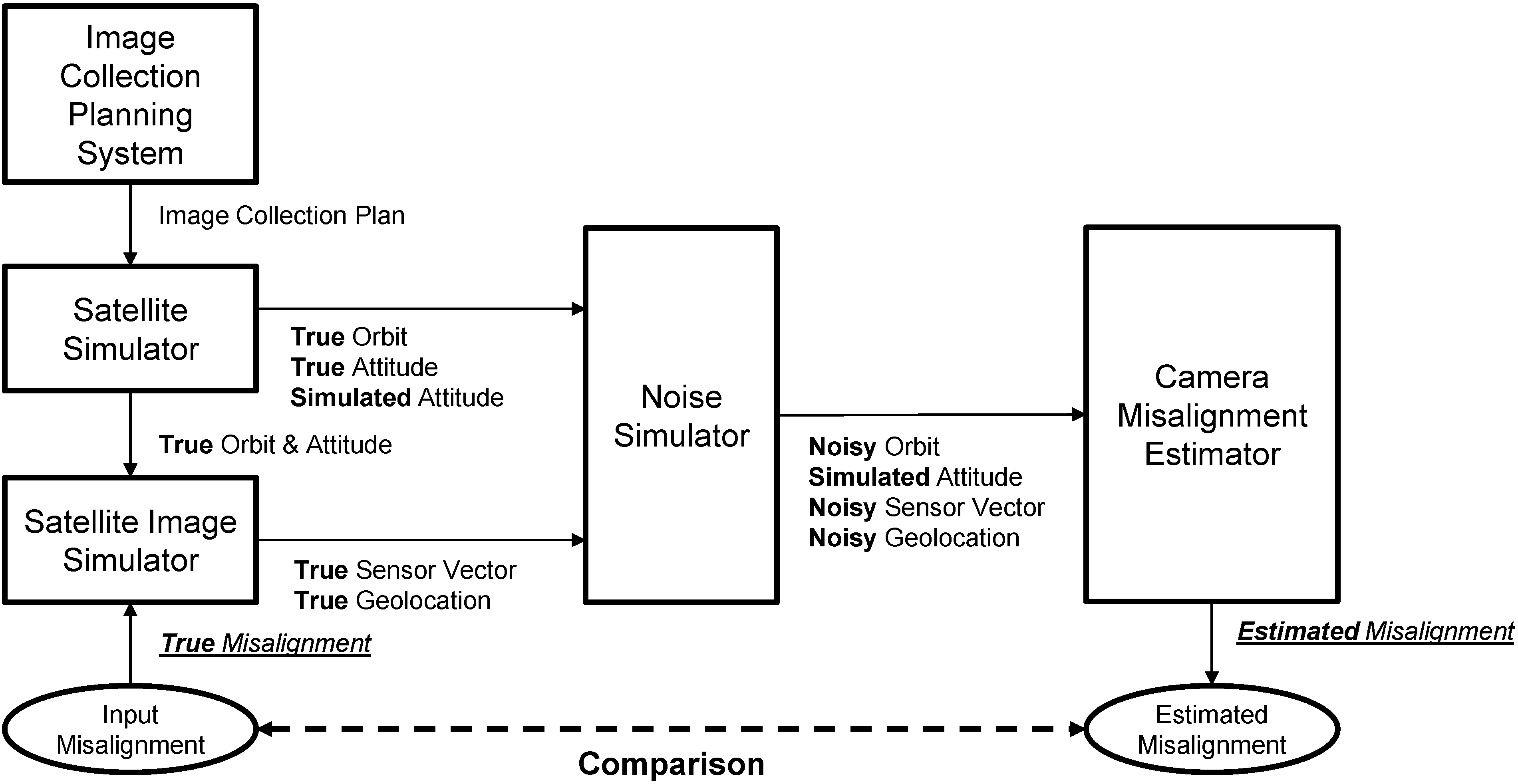
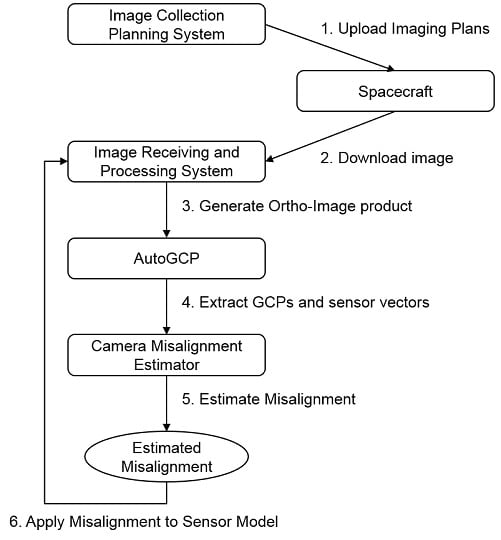
Whereas the simple four steps are provided from a conceptual view, the structural view of camera misalignment estimation involves a couple of additional steps as illustrated in
Figure 2.
After planning imaging scenarios for calibration, the image collection planning system (ICPS) uploads the plans to the spacecraft (1). After the spacecraft takes images, the images are downloaded to the ground station from the spacecraft (2); thereafter, the image receiving and processing system (IRPS) generates ortho-image products, which consist of geometrically corrected images and spacecraft ancillary data (3). AutoGCP software correlates the images with a reference ortho-photo database and generates GCPs and sensor vectors (4). Camera Misalignment Estimator estimates the camera misalignment by using the results of AutoGCP and spacecraft ancillary data (5). The estimated camera misalignment is then set to IRPS in order to adjust the sensor model (6).
It is recommended to iterate the process (3)–(6) at least a couple of times, because large camera misalignment can make the IRPS use a wrong location for the DEM for geometric correction, which influences the accuracy of the calculated geo-location. Therefore, the camera misalignment needs to be re-estimated after applying the misalignment estimate. The iteration may stop when the change of misalignment estimate is less than the desired accuracy.
Figure 2.
Structural process of camera misalignment estimation.
Figure 2.
Structural process of camera misalignment estimation.
2.2. Background: Deimos-2
The proposed framework was applied to Deimos-2 which is a high-resolution earth observation satellite equipped with push-broom type CCD sensors providing 1.0 m resolution panchromatic band (PAN) and 4.0 m resolution multispectral band images (blue, green, red, and near-infrared) with 12 km swath width. Since the estimation is done using attitude measurement and image GCPs, it is important to understand the target system’s camera geometry, attitude determination mechanism, and the definitions of attitude and camera frames.
2.2.1. Attitude Sensors
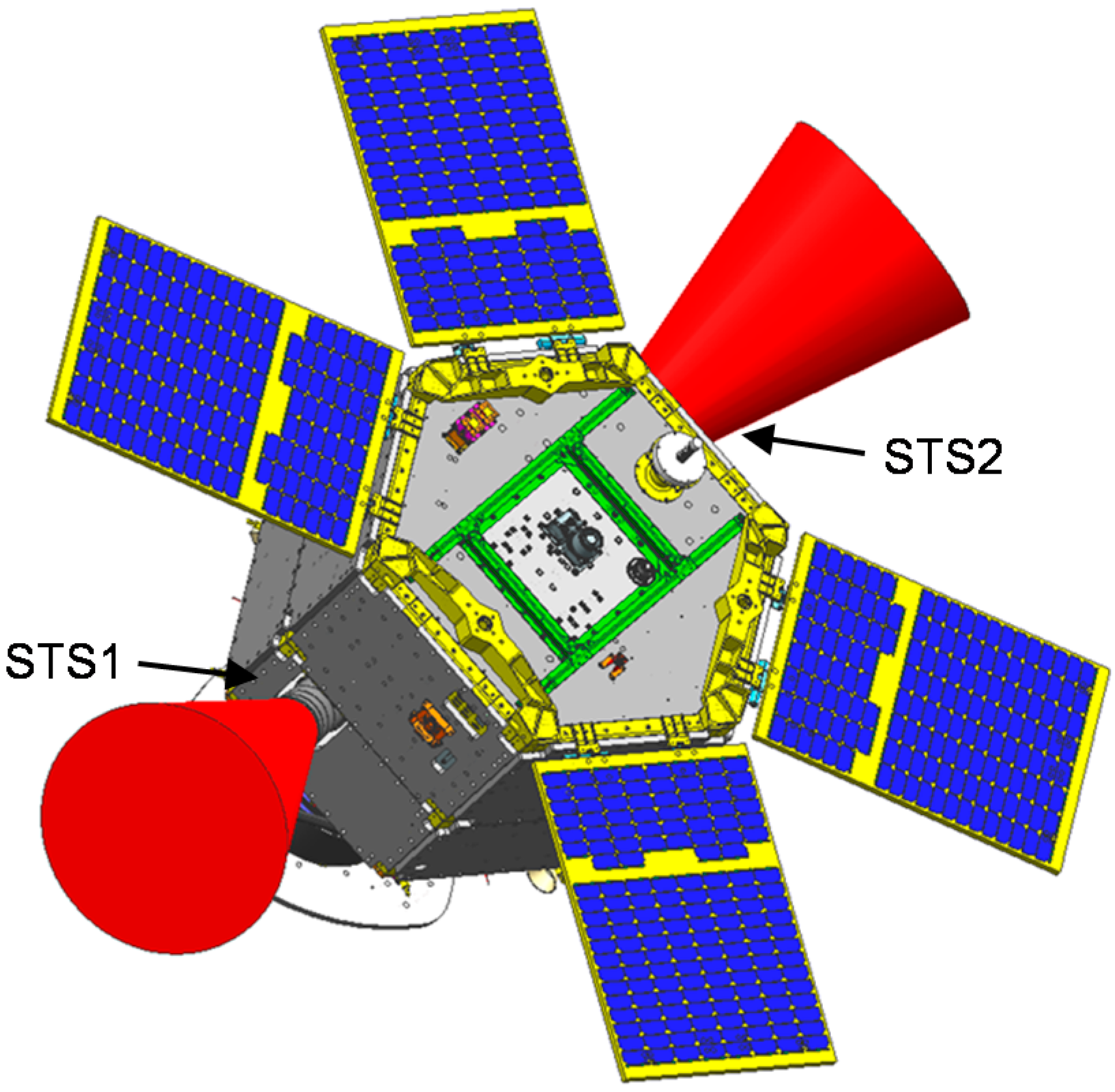
Deimos-2 has two star-trackers for absolute attitude sensing, as well as four gyroscopes for relative attitude sensing.
Figure 3 illustrates the exterior configuration of Deimos-2. The red cones are the field-of-view of star-trackers. The gyroscopes are internally equipped. Because the star-trackers are embedded at the opposite side to each other, one of or both star-trackers are selected for the absolute attitude sensing depending on the position and attitude of the satellite during imaging. The electro-optical camera, which is the main payload of Deimos-2, is at the opposite side of the solar panels.
Figure 3.
Mounting configuration of Deimos-2 star trackers.
Figure 3.
Mounting configuration of Deimos-2 star trackers.
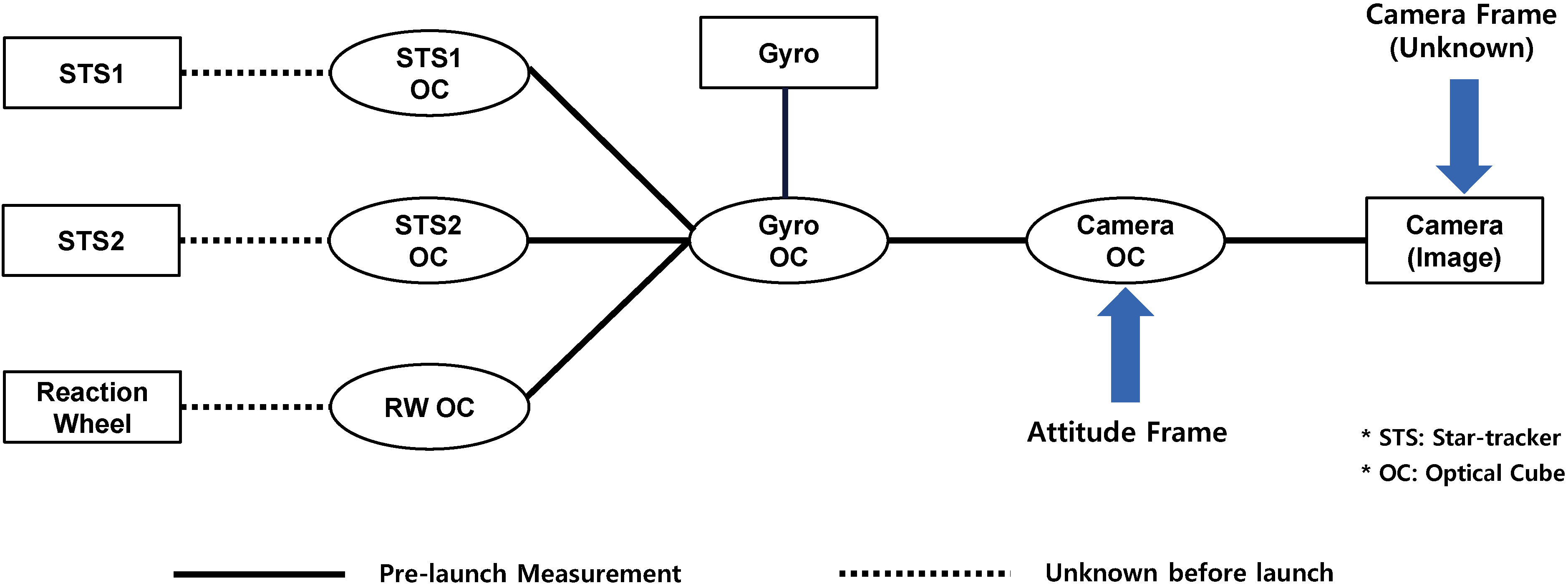
Figure 4 shows the relationship of sensors/actuators and the optical cubes. The sensors and actuators for attitude determination and control are aligned by using optical cubes (OC) before launch. Optical cubes are used as a reference object for precision alignment in satellite manufacturing. The components that need inter-alignment such as imaging sensors and attitude sensors have their own optical cubes that are carefully aligned with them. The alignment between optical cubes are precisely measured using theodolites. Although pre-launch measurement was done for some components, the alignment needs to be calibrated after launch due to launch shock, outgassing, zero-gravity, thermal effect,
etc. The alignment between the star-trackers and their optical cubes were unknown due to difficulty in ground measurement. The measurement of angles between optical cubes is used to build a rotation matrix that converts a vector of one component’s frame to the vector of another component’s frame. For Deimos-2, the attitude data in spacecraft ancillary which IRPS uses is based on Camera OC frame, which is also known as Attitude frame. The attitude measured using star-trackers is converted to Camera OC frame. The camera misalignment estimation that described in this paper estimates the discrepancy between this attitude and the GCPs acquired from the image that is in the unknown Camera frame. Hence, the combined error between the attitude sensor and the camera is estimated.
Figure 4.
Alignment map of attitude sensors and camera.
Figure 4.
Alignment map of attitude sensors and camera.
The alignments between sensors/actuators and optical cubes are calibrated after launch by space-level calibration. Space-level calibration is a series of operations performed during early operation phase, which consists of attitude calibration maneuver and stellar imaging for alignment calibration.
2.2.2. Camera Geometry
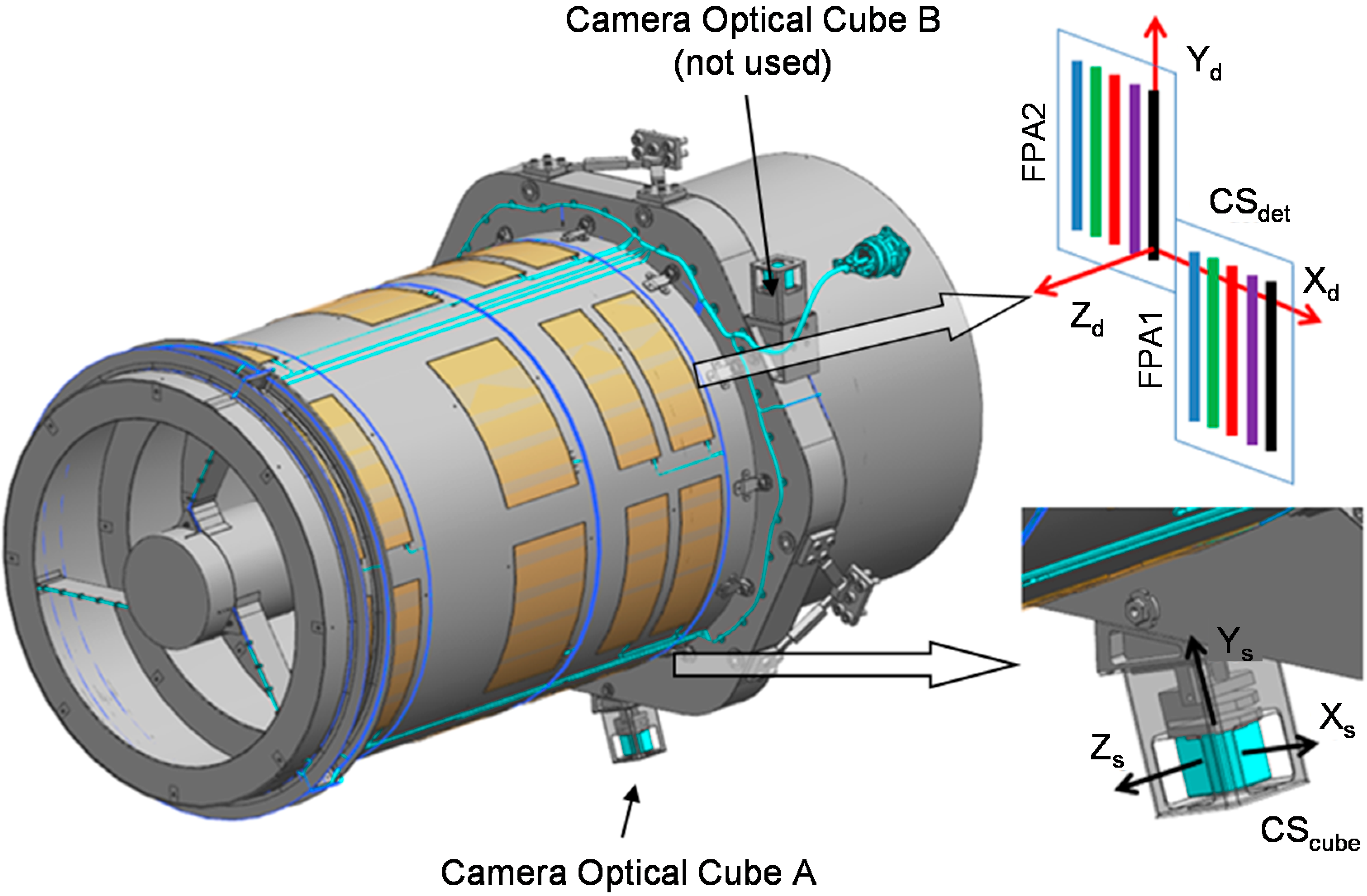
Figure 5 shows the sensor geometry of Deimos-2 camera system. The alignment of the camera system is aligned with the spacecraft body using the Camera OC (Optical Cube) A. The alignment between the coordinates system of Camera OC A, CS
cube, and the coordinates system of the camera focal plane, CS
det, is measured before launch. Two focal plane assemblies (FPA1, FPA2) are aligned to have ground footprints perpendicular to the flight direction with a small overlap (100 panchromatic pixels). The linear TDI CCD arrays are positioned with the order of panchromatic, blue, green, red, and near-infrared in along-track direction. The 6115-th pixel in panchromatic FPA2 is the reference detector that defines the origin and Z-axis direction of the camera frame, which is CS
det.
Figure 5.
Geometry of Deimos-2 camera.
Figure 5.
Geometry of Deimos-2 camera.
2.2.3. Reference Frames
In this section, the reference frames (a.k.a. reference coordinate systems) used in this paper are defined in detail. For well-known frames such as Earth-centered inertial (ECI) and earth-centered earth-fixed (ECEF), J2000 and WGS-84 are used respectively. The definitions of the Deimos-2 attitude frame and camera frame are presented in
Table 1.
The attitude frame is the basis of attitude information in spacecraft ancillary data. It is defined by Camera OC in Deimos-2 as shown in
Figure 4. Note that the definitions of the camera system and attitude reference system in
Table 1 are the same for Deimos-2. Other spacecrafts may employ different definitions, requiring a rotation matrix to calculate the camera frame from a spacecraft attitude. It is represented by the rotation matrix
and its inverse
in this paper. They are identity matrices for Deimos-2.
Table 1.
Definitions of Attitude Frame and Camera Frame.
Table 1.
Definitions of Attitude Frame and Camera Frame.
| Attitude Frame | Camera Frame |
|---|
| Origin | Spacecraft center of mass | Reference detector |
| Z | Boresight vector of the reference detector | Boresight vector of the reference detector |
| Y | Longitudinal direction of linear CCD (along with Geometric Y axis direction) | Longitudinal direction of linear CCD (along with Geometric Y axis direction) |
| X | Y × Z (right hand rule) | Y × Z (right hand rule) |
The camera frame is used by sensor vectors, which point at the corresponding detector cells. IRPS and AutoGCP use sensor vectors to convert image coordinates to geographic coordinates and vice versa.
2.3. Image Planning
The first step is planning imaging scenarios for camera misalignment estimation. It is important to cover all of the possible imaging scenarios that can occur during normal operation. The criteria that needs to be considered for a reliable and accurate estimation are as below.
Tilt angle coverage
Attitude sensor coverage
Global coverage
Terrain variation
Visual distinctiveness
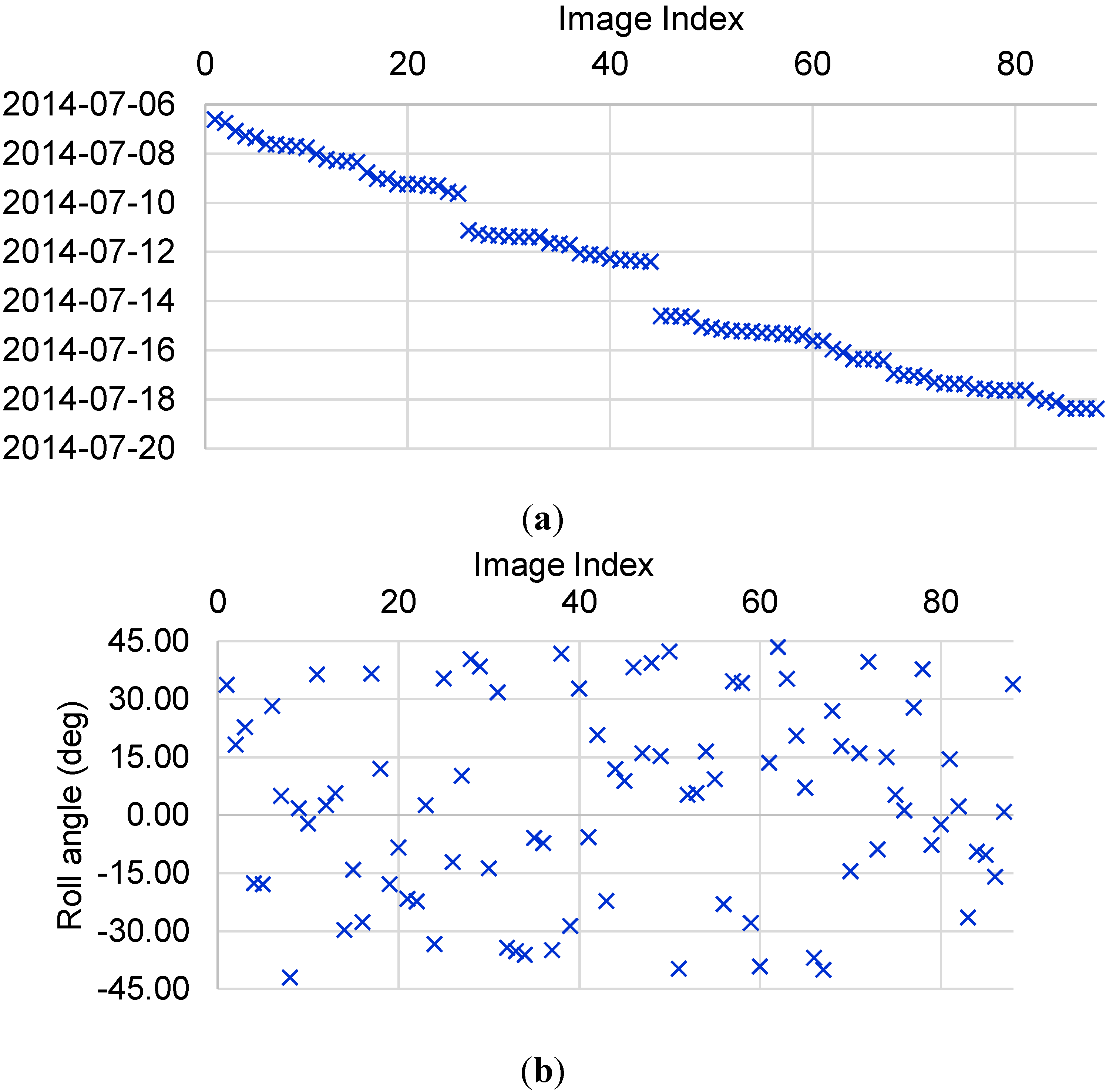
Tilt angle coverage: The image dataset for camera misalignment estimation needs to use various tilt angles that the spacecraft provides to get a reliable estimation result.
Attitude sensor coverage: If the spacecraft has multiple attitude sensors, those sensors are likely to have different misalignment toward the attitude frame. Since the attitude misalignment also introduces localization error like the camera misalignment, the estimation of the camera misalignment is influenced by the misalignment of attitude sensors. Therefore, the camera misalignment needs to be estimated separately for each sensor group. Deimos-2 is equipped with two star-trackers, and one or both of them are selected depending on the position and attitude of the spacecraft at the time of imaging.
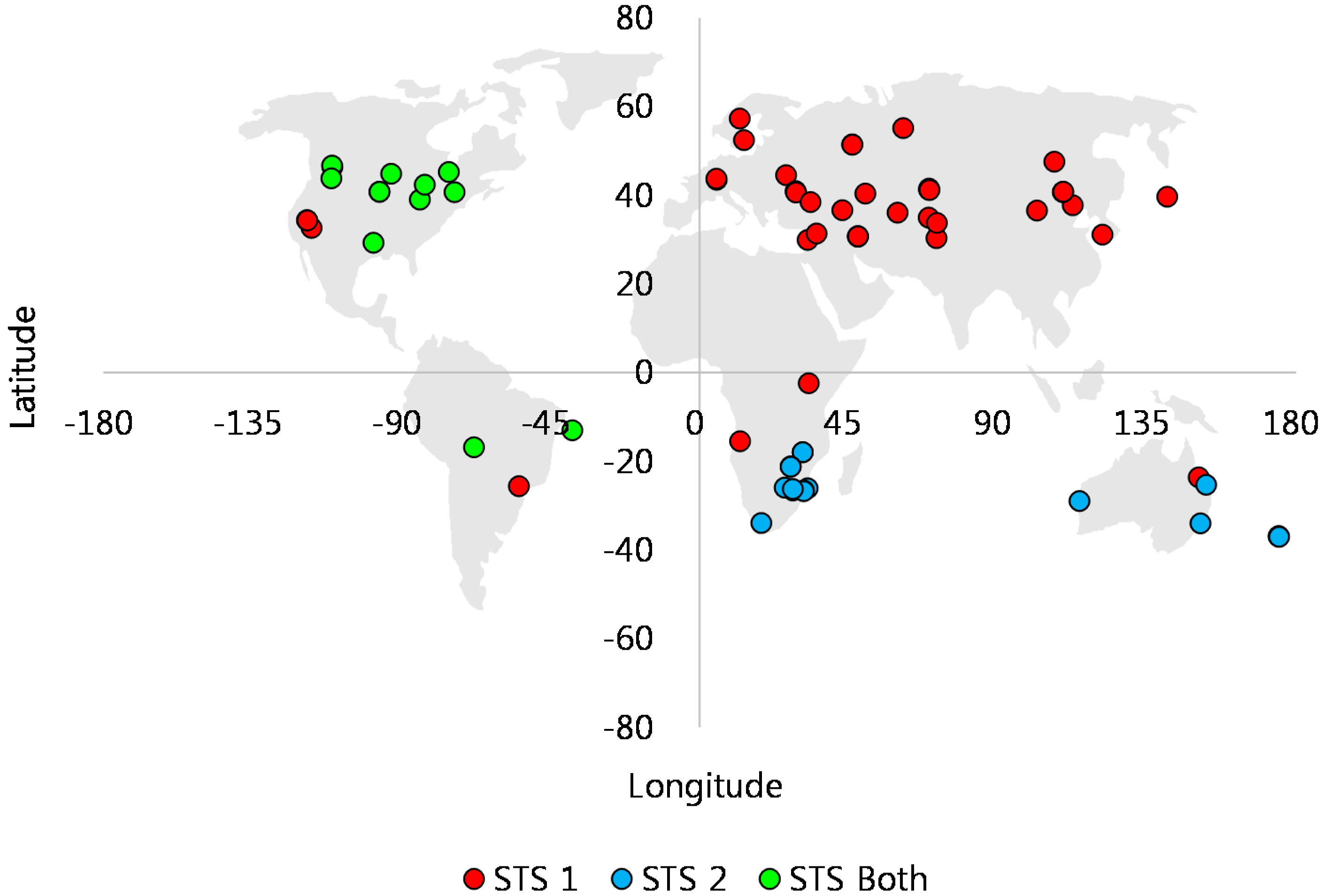
Global coverage: Ground targets needs to be distributed all over the world covering all longitude and latitude ranges. It is not only beneficial for obtaining reliable results, but it can also show a possible relationship between the localization error and the location of a target.
Terrain variation: For the characteristics of ground targets, flat terrain is preferred in order to avoid possible discrepancy of digital elevation model (DEM) and real terrain.
Visual distinctiveness: Area with many visual features are also preferred. However, downtown areas with sky-scrappers are not recommended as tall buildings may add additional localization error, especially at a high tilt angle.
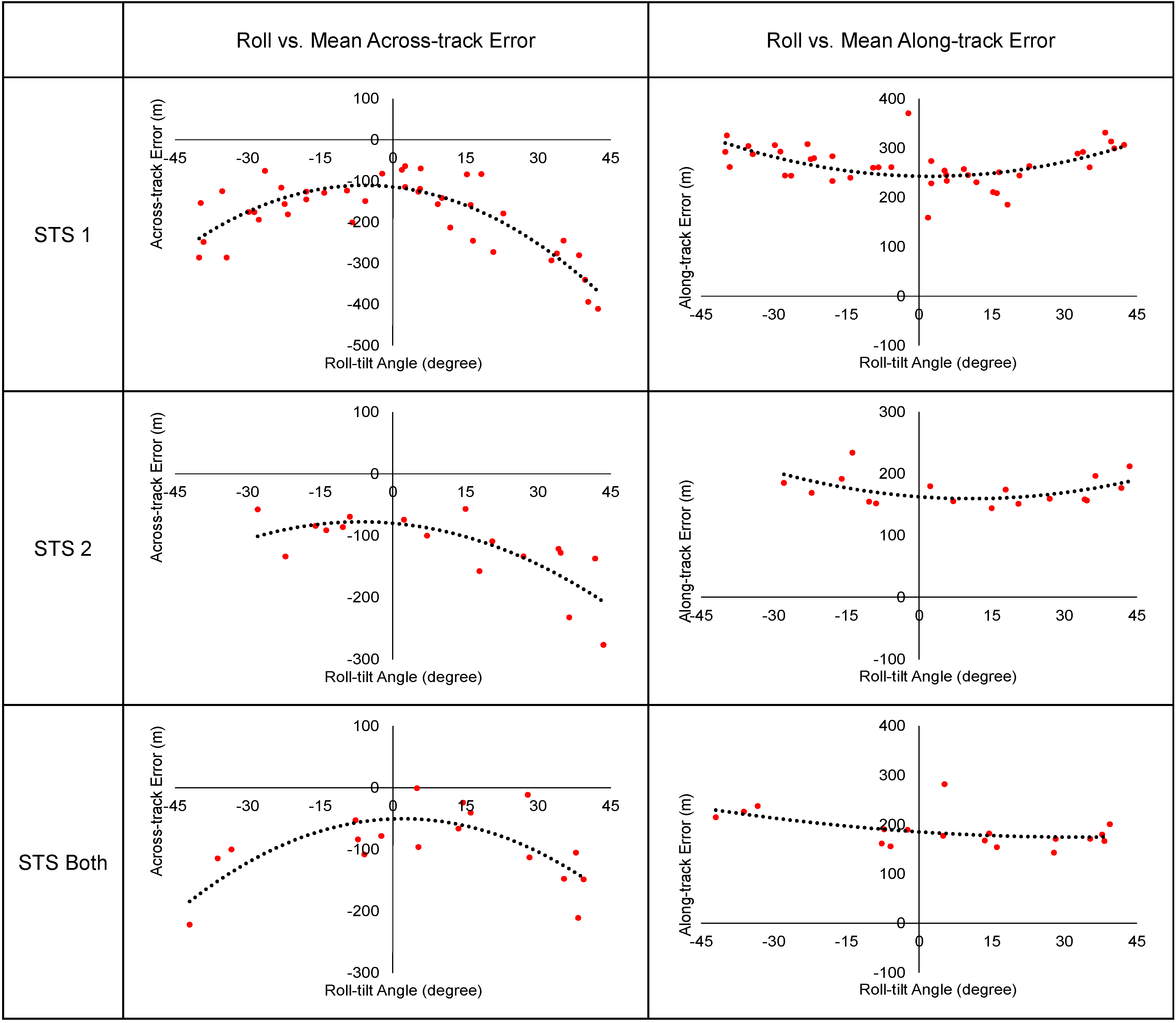
2.5. Error Pattern Analysis
Analyzing the pattern of localization error helps to find the existence of camera misalignment as well as other issues such as time drift. The estimation and correction of camera misalignment is meaningful when there is an obvious pattern of camera misalignment. It also is useful to know what type and amount of camera misalignment are there before estimation.
If a camera misalignment exists, a correlation between the tilt angle and localization error can be observed.
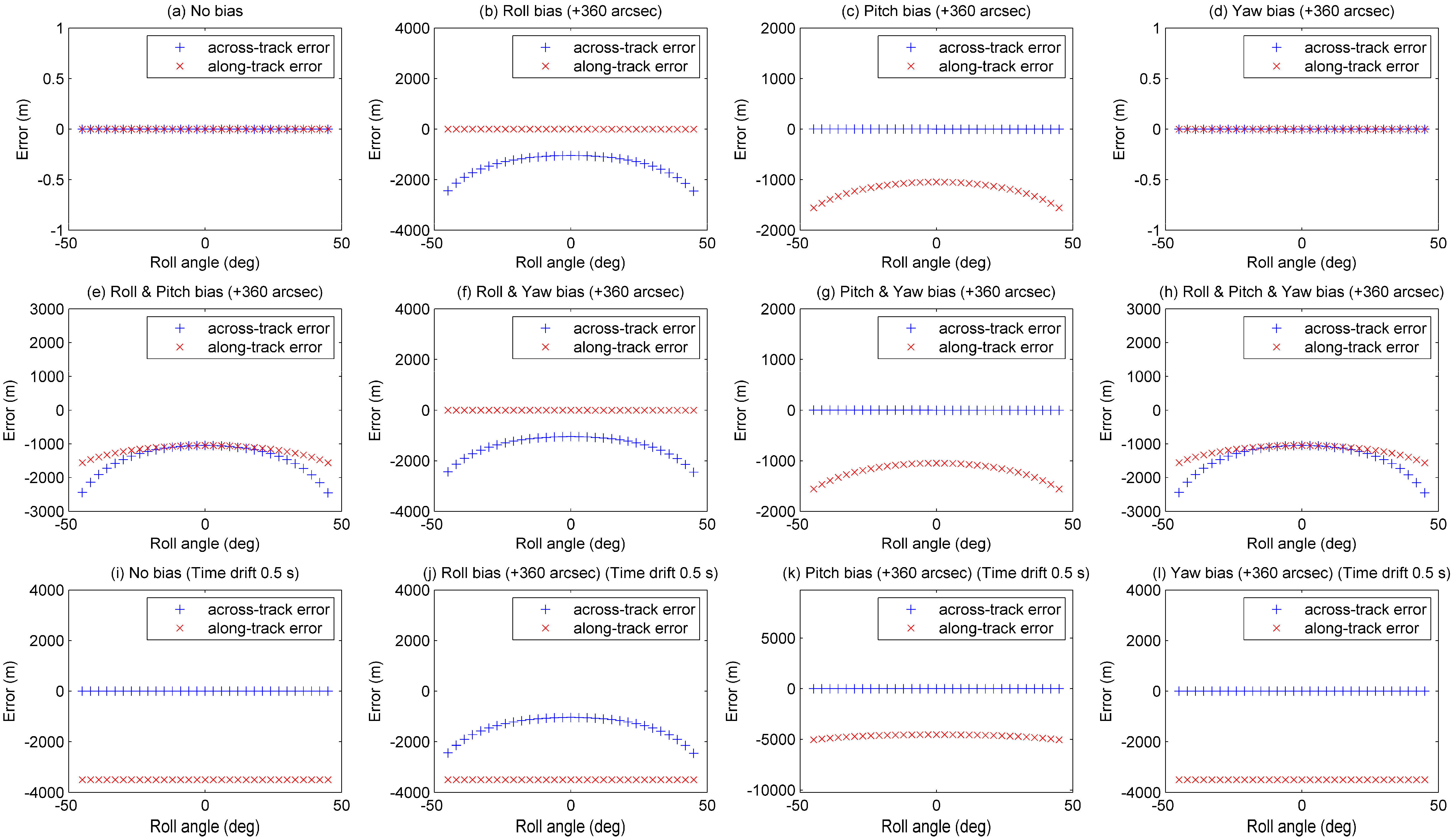
Figure 11 shows the plots of localization error on various camera misalignments. Note that changing the sign of the misalignment will create localization errors of the opposite sign.
Figure 11.
Localization errors by camera misalignment: (a) No bias, (b) Roll bias (+360 arcsec), (c) Pitch bias (+360 arcsec), (d) Yaw bias (+360 arcsec), (e) Roll & Pitch bias (+360 arcsec), (f) Roll & Yaw bias (+360 arcsec), (g) Pitch & Yaw bias (+360 arcsec), (h) Roll & Pitch & Yaw bias (+360 arcsec), (i) No bias (Time drift 0.5 s),(j) Roll bias (+360 arcsec) (Time drift 0.5 s), (k) Pitch bias (+360 arcsec) (Time drift 0.5 s), (l) Yaw bias (+360 arcsec) (Time drift 0.5 s).
Figure 11.
Localization errors by camera misalignment: (a) No bias, (b) Roll bias (+360 arcsec), (c) Pitch bias (+360 arcsec), (d) Yaw bias (+360 arcsec), (e) Roll & Pitch bias (+360 arcsec), (f) Roll & Yaw bias (+360 arcsec), (g) Pitch & Yaw bias (+360 arcsec), (h) Roll & Pitch & Yaw bias (+360 arcsec), (i) No bias (Time drift 0.5 s),(j) Roll bias (+360 arcsec) (Time drift 0.5 s), (k) Pitch bias (+360 arcsec) (Time drift 0.5 s), (l) Yaw bias (+360 arcsec) (Time drift 0.5 s).
Whilst roll and pitch biases display distinct patterns, yaw bias does not show a strong pattern in
Figure 11d. It is because the yaw angle of the camera misalignment has small effect in localization error. The localization error
that is generated by the yaw error at the end of the CCD array can be calculated as follows,
where
is the yaw-bias in radian,
is the CCD array length, and D is the pixel GSD. Because of its relatively small error even with high tilt angles, it is difficult to estimate the yaw bias.
Sometimes, the ancillary data, which contains position and attitude, can have time offset or drift error. If time offset exists, along-track error has an offset as depicted in
Figure 11i–l. In this case, it is difficult to relate to one of the biases in
Figure 11b–h. In case of time drift, it should be corrected before estimating the camera misalignment. Since there are many sources that can cause time drift phenomena, the estimation of time drift is not discussed in this paper.
Another major source of localization error that can be confused with camera misalignment is attitude misalignment. The misalignment in the attitude frame affects the control and determination of the spacecraft attitude, resulting localization errors.
Figure 12 shows the plots of localization error on various attitude misalignments. While the localization error induced by the yaw bias in the camera frame is hardly observable due to narrow field of view as shown in
Figure 11d, it is clearly visible in
Figure 12c that the yaw bias in the attitude frame generates large error as the tilt-angle increases.
Figure 12.
Localization errors by attitude misalignment: (a) Roll bias (+360 arcsec), (b) Pitch bias (+360 arcsec), (c) Yaw bias (+360 arcsec).
Figure 12.
Localization errors by attitude misalignment: (a) Roll bias (+360 arcsec), (b) Pitch bias (+360 arcsec), (c) Yaw bias (+360 arcsec).
There are many other error sources of localization error such as star-trackers, gyroscopes, focal plane assemblies, sensor arrays, or somewhere between them. Only the sum of all misalignments from the attitude sensors to the camera image plane could be observed from image GCPs and attitude data. It is important to categorize datasets that can have different misalignment for effective analysis. In
Section 3.2, Since Deimos-2 has two star-trackers and they are selected depending on the spacecraft attitude, its localization errors were analyzed for star-tracker selections.
In case that localization errors and tilt angles cannot be correlated, the cause of error may not be camera misalignment. They can be sensor malfunctioning, on-board software errors, or inconsistency of ancillary data. It is also recommended to analyze the relationship between the localization errors and target locations (longitude, latitude). Depending on the thermo-elastic characteristics of the spacecraft or the orbit design, the location of the target can affect the localization error.
2.6. Camera Misalignment Estimation
This section describes a mathematical model for camera misalignment estimation. The model describes the relationship between spacecraft position, attitude, sensor vector, and GCP. The key idea of the proposed estimation model is to calculate the boresight misalignment, which is the angular error between the camera frame and the true camera frame, using GCPs and spacecraft positions/attitudes. In order to simplify the problem, the origins of the attitude frame and the camera frame are assumed to be the same.
Assuming that there is no camera misalignment, the geometrical relationship can be modelled as follows:
where,
is a sensor vector, which is a unit vector of the vector , which points the detector pixel on the focal plane at which a GCP is located. and are rotation matrices from attitude frame to camera frame, and from ECI frame to attitude frame, respectively, at time . is an object vector in ECI frame pointing the GCP from the spacecraft. is a position vector of ground object G in ECI frame. is a position vector of spacecraft in ECI frame at time . Since the geo-locations of GCPs are generally in LLH or ECEF, it is important to convert the coordinate system to ECI to get .
In order to take account for the camera misalignment, a bias-correction matrix
is added:
In practice, the amount of misalignment is less than one degree (
i.e., 3600 arcsec). Therefore, an approximation for infinitesimal rotations can be used to solve Equation (7). Supposed that the misalignment is an Euler-angle rotation
,
where
,
,
are roll, pitch, yaw bias respectively, it can be approximated as follows [
25,
26]:
The error of the small angle approximation of sine and cosine function is less than 1% for angles smaller than 14 degrees (≈50,000 arcsec).
In consequence, the equation for a sensor vector and a unit object vector in the Equation (7) can be expanded as below.
Equation (13) can be rewritten as follows, which forms a normal equation for linear least squares (Ax = b):
In addition to the Equation (14), a weight matrix
is introduced to adjust weight of each observation and to force pre-defined bias to certain axes as below:
where the weight matrix
is defined as:
Other elements (
i.e.,
,
,
) in the Equation (15) are also extended as follows,
sets the weight for each observation in accordance with the accuracy of observation. In case that every observation has the same accuracy, the weight is set to 1.0. However, it can also be set to a certain weight calculated from the accuracy of observation, such as the geo-accuracy of a GCP, sensor vector, and position/attitude knowledge.
and could be used to set the bias of some axes to given values. is a parameter for choosing whether the pre-assigned bias will be enforced or not. Setting the element of to a very small number (e.g., 10−1°) forces the assigned angle in to be the bias of the given axis, whereas setting it to a very large number (e.g., 101°) means is ignored. It is useful when the visibility of a certain axis is expected to be very low due to narrow field of view; for instance, the yaw axis of high-resolution push-broom imaging sensors.
Solving Equation (15) gives a least squares solution of
, which contains estimated camera misalignment angles in radian. In order to compensate the camera misalignment during ortho-image generation, the alignment of camera frame from attitude frame needs to be updated using
. The new rotation matrix
is calculated as follows,
where
is a direction cosine matrix for
, and
is the original rotation matrix. The order of rotations is irrelevant for infinitesimal angles [
25,
26].
4. Conclusions
This paper presented a framework for camera misalignment estimation and supporting results. The proposed framework consists of four steps: image planning, automated GCP extraction, error pattern analysis, and camera misalignment estimation.
A set of simulation experiments was performed to verify the validity of the proposed mathematical model. A satellite simulator and an image simulator were used for the generation of realistic simulation data. Various camera misalignment settings were simulated and compared with the estimation results. In this simulation experiments, it was proven that the proposed estimation model can achieve a sub-meter geo-location accuracy in ideal cases and respond to the characteristics of sensor noise specifications very well.
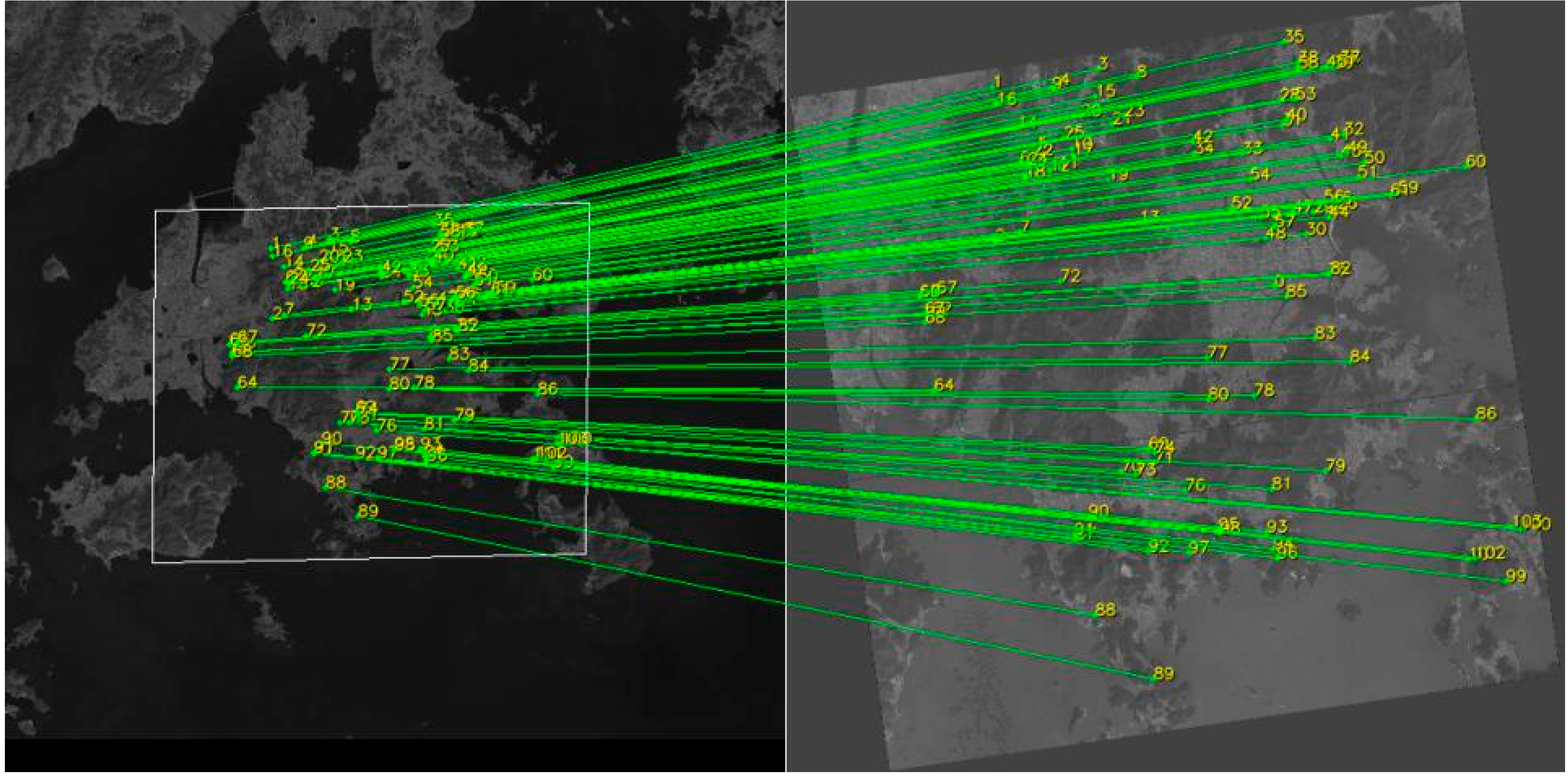
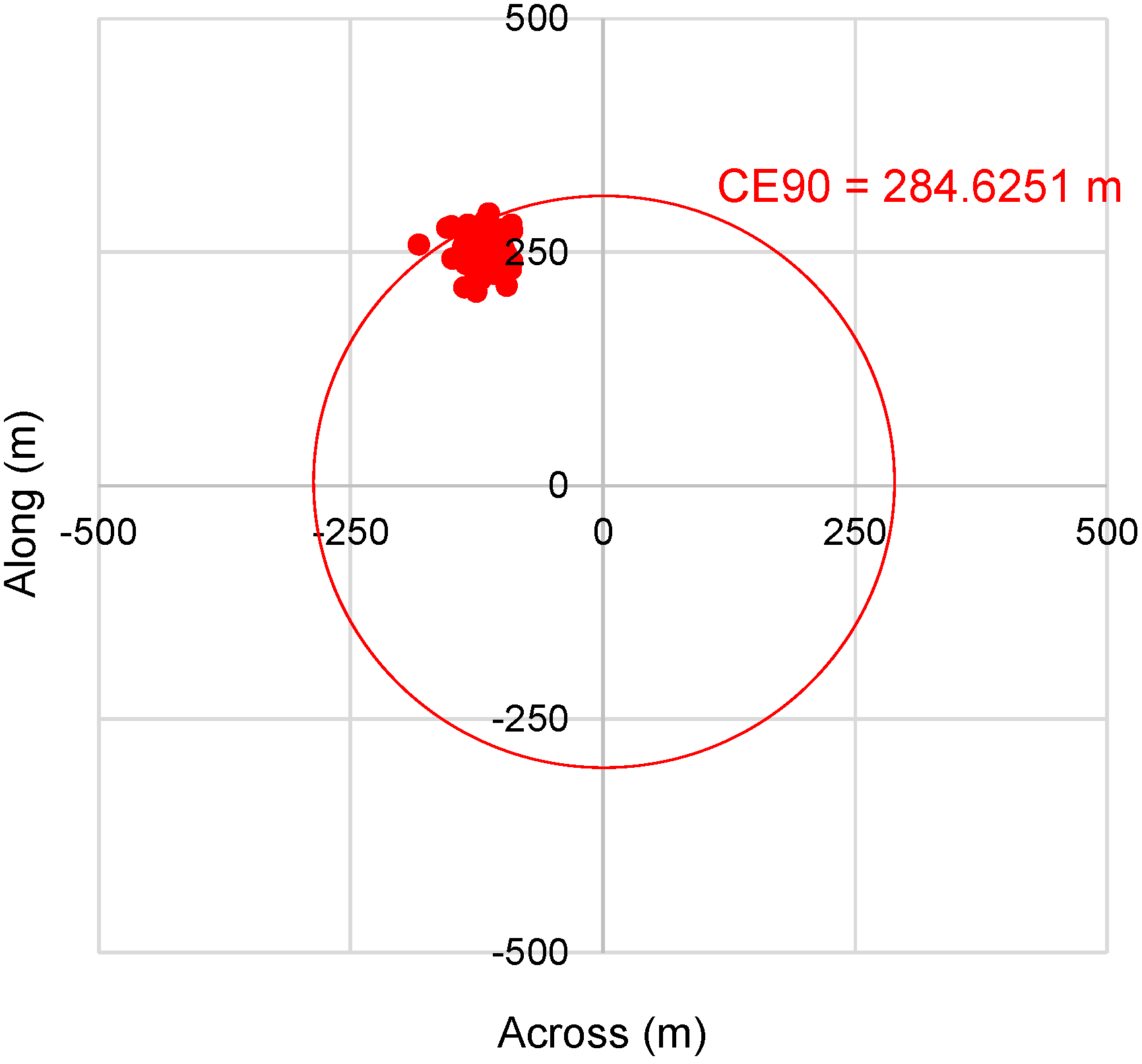
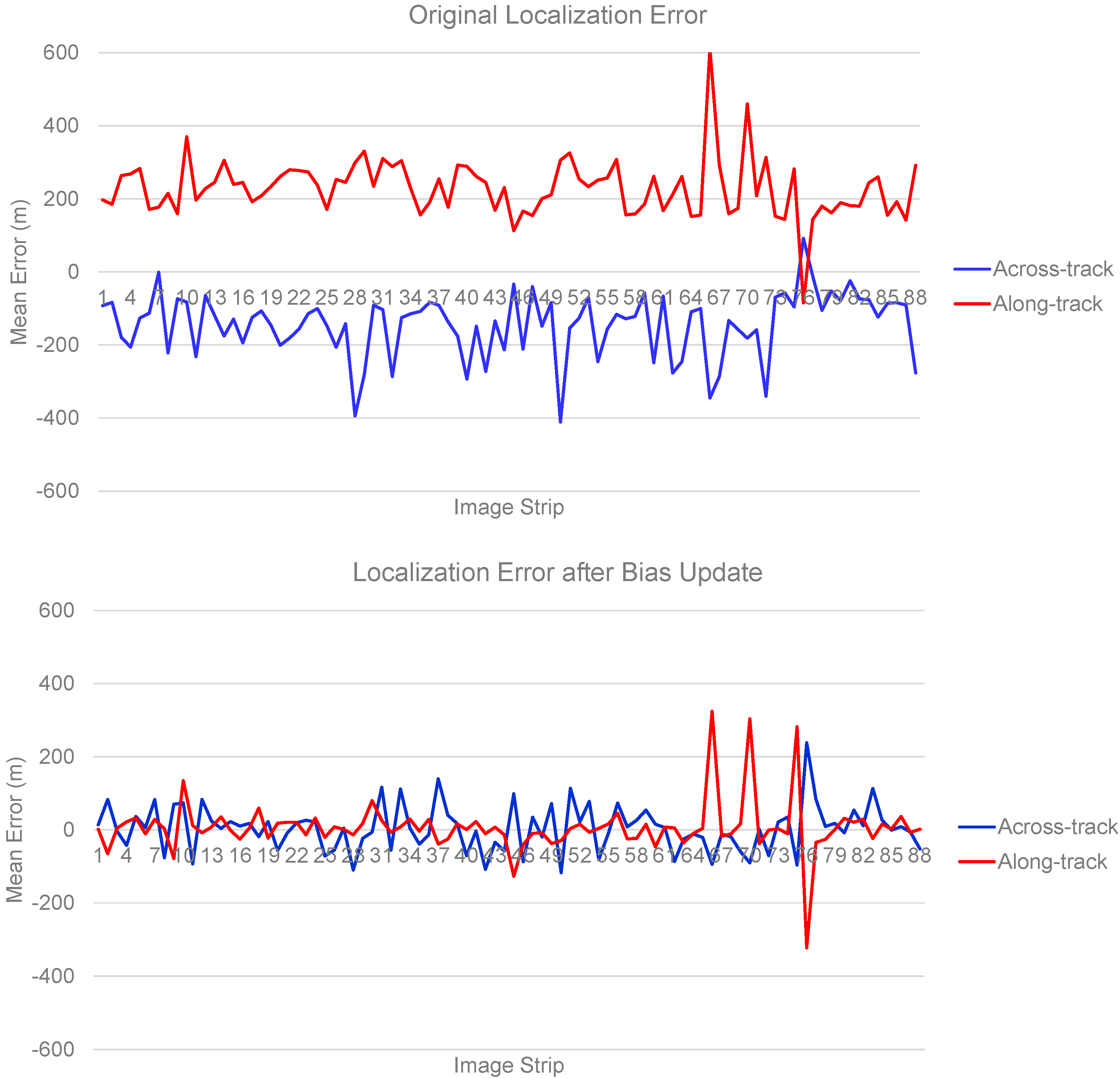
The application of the entire framework was demonstrated by using several tens of real image data covering all operational cases of the satellite in order to prove the feasibility of the proposed framework. The imaging planning decisions and the pattern analysis schemes in the proposed framework provided a guideline for the camera misalignment estimation activity during the initial commissioning period of a high-resolution satellite program. Hundreds of GCPs per image were extracted automatically for camera misalignment estimation. The estimated misalignment was applied to the ground image processor so that the localization error was reduced from 405.97 to 119.33 m in CE90.
The proposed framework is an effective and efficient method to estimate an accurate camera misalignment during a post-launch calibration and validation phase. As it provides precise and reliable measurements and estimation results, it may also reduce the efforts to pre-launch calibration activities. Although this paper focused on the camera misalignment estimation, the presented ideas can be applied to a wide range of applications. The presented GCP extraction algorithm provides many GCPs automatically which can be used for the calibration of other parameters such as focal length, line rate, and image distortion. It can also be attached to the image processing chain to improve the geo-location accuracy of images through a systematic geo-correction using GCPs. The analysis of localization error patterns is useful to discover many other errors such as telemetry error, time drift, gyro scale factor error, and other hardware or software errors of the satellite.