Abstract
The high importance of bathymetric character for many processes on reefs means that high-resolution bathymetric models are commonly needed by marine scientists and coastal managers. Empirical and optimisation methods provide two approaches for deriving bathymetry from multispectral satellite imagery, which have been refined and widely applied to coral reefs over the last decade. This paper compares these two approaches by means of a geographical error analysis for two sites on the Great Barrier Reef: Lizard Island (a continental island fringing reef) and Sykes Reef (a planar platform reef). The geographical distributions of model residuals (i.e., the difference between modelled and measured water depths) are mapped, and their spatial autocorrelation is calculated as a basis for comparing the performance of the bathymetric models. Comparisons reveal consistent geographical properties of errors arising from both models, including the tendency for positive residuals (i.e., an under-prediction of depth) in shallower areas and negative residuals in deeper areas (i.e., an over-prediction of depth) and the presence of spatial autocorrelation in model errors. A spatial error model is used to generate more reliable estimates of bathymetry by quantifying the spatial structure (autocorrelation) of model error and incorporating this into an improved regression model. Spatial error models improve bathymetric estimates derived from both methods.
Keywords:
coral reef; landscape; WorldView-2; water depth; spatial error; Great Barrier Reef; Lizard Island; Sykes Reef 1. Introduction
Bathymetric character lies at the heart of many important biophysical processes on coral reefs, such as primary production and coral calcification that are influenced by the varying levels of light with depth, and also the effects of sediment and nutrient loading, which are related to depth and energy regimes across a reef [1,2]. Spatial variation in bathymetry defines reef structural properties, such as rugosity, slope, terrain ruggedness, aspect and bathymetric position index [3]. In turn, these properties determine the biological character of benthic communities inhabiting reef environments [4] and their associated fish populations [5]. Information on the bathymetric character of reef platforms is therefore critical to reef management and science.
Procedures for the estimation of bathymetry across large, shallow (<30 m) platforms through clear water using remote sensing data have developed over two decades. Table 1 ([7,8,9,10,16,17,18,19,20,21,22,23,24,25,26]) summarises developments in this area, also reviewed by Dekker et al. [6]. Major methodologies include empirical approaches [7,8], semi-analytical and radiative transfer-based optimisation approaches [9,10].
Empirical approaches assume that light is attenuated exponentially with depth through surface waters and rely on the varying extent to which this occurs for light at different wavelengths to derive estimates of water depth. Coefficients of attenuation are unknown and are therefore derived empirically through regression of band ratios against in situ depth data. The empirical derivation is unconstrained, and coefficients are assumed to be constant across the entire image. Optimisation approaches aim to deconstruct measured spectra into components relating to water depth, bottom type and water quality. The physics-based optimisation methods replace the unknown coefficients with a more constrained system in which the spectral attenuation of the water column is restricted by physical ranges based on knowledge of the nature of typical water constituents. The physics-based method assumes that water optical properties can vary from pixel to pixel across the image and coefficients, along with other retrievable parameters (water quality, benthic community endmember composition, water depth), which are deduced for every pixel by the best model fit within the constraints.
The aim of the present study was to compare bathymetric estimates derived from empirical and optimisation methods through a geographical analysis of the model errors for two sites on the Great Barrier Reef, Australia. The study of errors, in particular the spatial distribution and geostatistical properties of the model residuals, can reveal critical insight into model performance [11]. Geographical or spatial analysis refers to a collection of techniques and statistical models that explicitly use the spatial referencing associated with each data value or object that is specified within the system under study [12,13]. Exploratory spatial data analysis (ESDA) enables the detection of spatial patterns and the formulation of hypotheses based on the geography of the data and the assessment of spatial models through visual, numerical, graphical and cartographic treatment of a dataset [14]. In ESDA, the map becomes crucial, and valuable insight is generated from the ability to view both extreme incidences and general trends within their geographical context. Computer visualisation techniques draw on the continuity and structure often found in spatially-referenced datasets described by Tobler’s first law of geography: that observations geographically close together tend to be more alike than those that are further apart [15]. Often this structure can be expressed statistically by calculating the spatial autocorrelation of a dataset. Spatial autocorrelation is the correlation among values of a single variable directly related to their locational positions on a two-dimensional surface. Autocorrelation is a statistically-quantifiable property that expresses the idea of near things being more alike than far things with respect to one single variable. It can be loosely defined as the coincidence of value similarity with locational similarity. Like spatial dependency, it arises because of the pervasive continuity and structure to the real world, which means that things rarely change dramatically over short distances. This generic property of geographic space is exploited in the present study to analyse the error associated with bathymetric models derived using both empirical and optimisation approaches. Such an investigation seeks to answer questions, such as: “Where is the model under- or over-predicting? Are the statistical assumptions valid? Is there any discernible spatial structure or pattern associated with the model error? Can this structure be characterised and utilised in a spatial error model?”

Table 1.
Developments in the derivation of shallow water bathymetry from remote sensing imagery.
| Bathymetric Mapping Development | Reference |
|---|---|
| “Depth of penetration” zones mapped from the range of depths to which light penetrates through the water column at different wavelengths. | Jupp, 1988 [16] |
| Pair-wise waveband correction of absorption and scattering in the water column to derive a single depth-invariant index. Light transfer is assumed to decrease exponentially with vertical depth. | Lyzenga, 1978; 1981 [7,17] |
| A semi-analytical model developed for shallow water remote sensing based on radiative transfer. | Lee et al., 1998 [18] |
| An inversion optimisation approach developed to simultaneously derive water depth and water column properties from hyper-spectral data. | Lee et al., 1999 [19] |
| Empirically deriving the relationship between the changing ratio of two water-penetrating waveband pairs and water depth, independently of bottom albedo. | Stumpf et al., 2003 [8] |
| Linear regression of reflectance principal components, with uniform bottom types | Mishra et al., 2004 [20] |
| A semi-analytical model similar to that of Lee et al. [18] incorporating the assumption of constant water optical properties across the scene. | Adler-Golden et al., 2005 [21] |
| A semi-analytical model similar to that of Lee et al. [18] that included a quantitative comparison of model-derived depth with high-resolution multi-beam acoustic bathymetry data. | Mcintyre et al., 2006 [22] |
| Linear unmixing of the benthic cover incorporated into semi-analytical approaches. | Goodman and Ustin, 2007 [23], Klonowski et al., 2007 [10] |
| Lookup table approach for matching image spectra to a library of spectra corresponding to different combinations of depth, bottom type and water properties. | Louchard et al., 2003 [24], Mobley et al., 2005 [9], Lesser and Mobley, 2007 [25] Hedley et al., 2009 [26] |
| A bio-optical optimization model for simultaneous retrieval of the optical properties of the water column and bottom from remotely-sensed imagery in optically-deep and optically-shallow waters. | Giardino et al., 2012 [27] |
| An assessment of Sentinel-2, a moderate resolution, multispectral satellite sensor for bathymetric mapping, including the propagation of noise and environmental uncertainties through a radiative transfer model inversion to quantify uncertainty in the retrievable parameters. | Hedley et al., 2012 [28] |
2. Methods
2.1. Site Locations
The spatial analysis is carried out at Lizard Island and Sykes Reef on the Great Barrier Reef using a combination of bathymetric echosounder data collected in situ and WorldView-2 satellite imagery (four bands centred at 478 nm, 546 nm, 659 nm and 831 nm). Because only four bands were available for the Sykes Reef image, the estimation methods were only applied to four bands to ensure consistent application of the method across both case study sites.
Lizard Island is the largest of a group of granitic islands located approximately 30 km off the northern Queensland coastline (Figure 1). A complex of reefs has developed around these foundations during the Holocene [29]. The reef flat within the Lizard Island group falls primarily within the three islands and is bordered along the windward aspect by the south-eastern barrier reef, a series of reef patches in the west and a narrower fringing reef rim around the northern boundary of the main island. These reefs enclose a lagoon that is up to 10 m deep and rise from a peripheral platform base at approximately 30 m of depth. Windward reefs along the south-eastern side of Lizard Island, such as South Reef and Coconut Reef (Figure 1), have developed more continuous reef flats with a better defined zonation than their counterparts to the west and north of the island group, exemplified by the patch reefs around Watsons Bay. The reefs exposed to higher energy on the south-eastern side have steeper reef slopes, with reef crests and flats that are just below the lowest astronomical tide (LAT). The reef flats are mostly composed of consolidated rubble, sandy patches and coral heads. The South Reef flat gently slopes into the sandy lagoon, while Coconut Reef is confined between two granitic headlands and meets a sandy beach backed by a coastal plain. The narrower reef flat fringing Lizard Island intersects the steep granitic cliffs plunging into deep water.
The Capricorn Bunker Group lies at the southern end of the Great Barrier Reef and consists of 16 islands and 22 reefs, with eight of these islands being vegetated. The reef platforms in the group have been classified into four different geomorphological types as lagoonal, elongate platform, platform and closed-ring reefs [30]. Within this scheme, Sykes Reef is a platform reef that is approximately 7 km2 in area, which lies in the cluster of reefs at the centre of the group comprised of Wistari, Heron, Sykes and One Tree reefs. Sykes Reef is situated on the eastern, windward side of the group, approximately 82 km from the Queensland coastline.
The Sykes Reef platform formed during the early Pleistocene [31]. The reef communities across the wider platform fall within a distinctive zonation pattern made up of a steep forereef that rises from the surrounding base foundation, an algae rim, an outer reef flat coral zone and an inner reef flat of sand. Structurally, most of the Capricorn Bunker Group reefs are steeper on their windward sides with gentle gradients found on the leeward sides of the reefs [32,33]. This is particularly the case for Sykes Reef, which has a steep forereef slope that drops to a depth of 25 m along the exposed eastern flank, rising to a shallow, plateau-like reef flat at a consistent depth of 4–5 m. Then, it gradually deepens along a gentler slope on the western side, dropping to a depth of approximately 15 m, where sand ripples can be observed traversing a comparatively shallow ridge toward the neighbouring Heron Reef. The reef flat sediments are primarily biotic in nature, sourced from past and existing forams and carbonate producers.
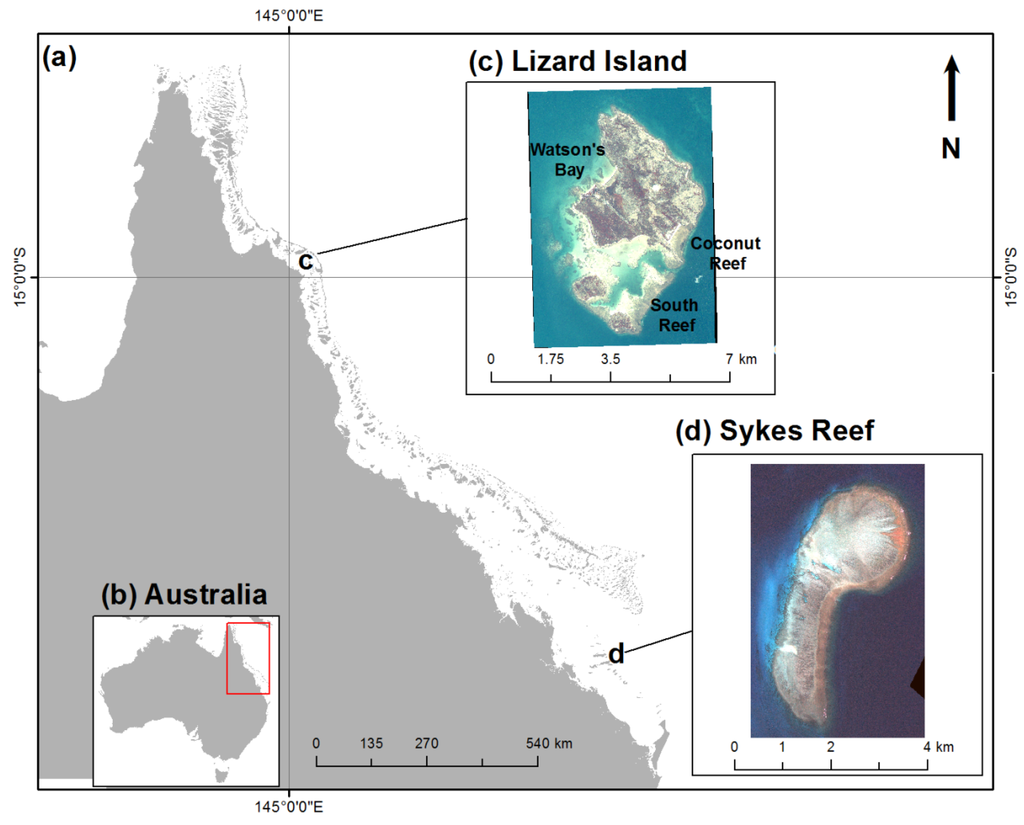
Figure 1.
Locations of study sites selected for analysis of bathymetry models (from left to right): (a) Queensland coastline; (b) Australian continent; (c) Lizard Island (northern Great Barrier Reef, GBR); and (d) Sykes Reef (Capricorn-Bunker Group, southern GBR).
2.2. Collection of in situ Bathymetric Measurements
In situ bathymetric measurements were collected with a single beam echosounder during separate fieldwork campaigns at each site. Bathymetric surveys were carried out at Lizard Island in December 2011 using a Bruttour International Ceeducer Pro single beam echosounder (200 kHz) and at Sykes Reef during May 2014 with a Bruttour International Ceestar single beam echosounder (200 kHz) and a Garmin GPS 550C. In total, 31,816 and 23,738 point measurements of water depth were collected across the reef platforms at Lizard Island and Sykes Reef, respectively (see Figure 2a,d for the locations of survey points). Raw data were imported into Caris HIPS/SIPS V8.1 software for post-processing. A vessel configuration file was created accounting for layback distances between the GPS position and transducer position. Mean sea level (MSL) tides were applied using AusTides predicted tides for Lizard Island and Heron Island, respectively. Overall, bathymetry data are considered to be International Hydrographic Organisation Order 2 compliant using the MSL vertical datum (i.e., in depths <30 m, total vertical uncertainty lies between 1 and 1.2 m) [34]. Data were cleaned of noise, particularly glint emanating from the sea surface, and accepted soundings were exported to an ASCII xyz file for use in calibration and validation. Data were subset into two separate calibration and validation datasets, each comprising half of the survey points, using the subset features tool in ArcGIS 10.2, which randomly assigns points to either of the data subsets.
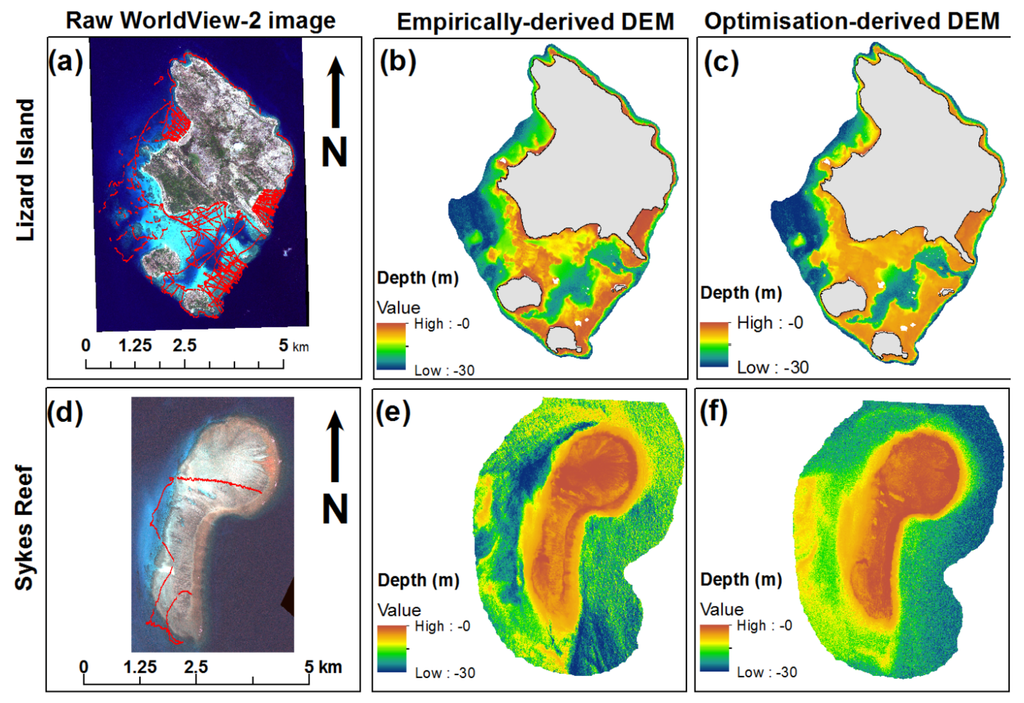
Figure 2.
Raw satellite images and bathymetry estimates for study sites (from left to right, top to bottom): (a) WorldView-2 image of Lizard Island; (b) Empirically-derived bathymetry model for Lizard Island; (c) Optimisation-derived bathymetry model for Lizard Island; (d) WorldView-2 image of Sykes Reef; (e) Empirically-derived bathymetry model for Sykes Reef; (f) Optimisation-derived bathymetry model for Sykes Reef.
2.3. Image Pre-Processing: Atmospheric and Glint Correction
Table 2 provides details of the multispectral satellite images employed for bathymetry estimation by this study. The optimisation approach requires that imagery be pre-processed to physical units of water-leaving reflectance just above the water surface. For consistency, the same imagery was pre-processed and employed by both techniques. The imagery was first converted to top of atmosphere reflectance using the band calibration coefficients supplied in the image metadata plus a correction for solar zenith angle and Earth-Sun distance. The top of atmosphere reflectance was then converted to bottom of atmosphere reflectance using look-up tables for atmospheric reflectance and transmission, as described by Antoine and Morel [35]. The look-up tables for the atmospheric correction were generated with libRadtran [36]; the atmospheric model used was the maritime 99% relative humidity model. Aerosol optical thickness was adjusted manually to bring the darker deep water pixels close to expected reflectance of deep water with low chlorophyll concentration, being approximately 0.04, 0.02 and 0.01 at 443 nm, 490 nm and 510 nm according to Figure 1 in the Antoine and Morel paper [35]. Note that the contribution of aerosol is small compared to the Rayleigh scattering, which is treated as a fixed function of solar-view geometry; the manual adjustment of aerosol optical thickness corresponded to less than 10% of the magnitude of the correction in the blue band. This simple single aerosol model treatment is adequate for these sites that are relatively far from land and where deep waters are clear. Following the atmospheric correction, a sun glint correction was applied to the Sykes Reef image only [37], since the Lizard Island image was largely clear of glint.

Table 2.
Details of the WorldView-2 multispectral satellite images employed for bathymetry estimation using both empirical and optimization methods in this study.
| Lizard Island WorldView-2 Image | Sykes Reef Worldview-2 Image | |
|---|---|---|
| Acquisition date | 10 October 2011 | 14 February 2014 |
| Tidal stage | Mean sea level, rising flood | Mean sea level, rising flood |
| Weather conditions | Low cloud, calm | Low cloud, calm |
2.4. Bathymetric Mapping: Empirical Approach
The empirical approach to bathymetry estimation followed the methodology proposed by Stumpf et al. [8]. Firstly, the green and blue wavebands (centre wavelengths 546 nm and 478 nm) were extracted from the pre-processed WorldView-2 image. The natural logarithm was calculated for each band, before the log green band was divided by the log blue band to create a ratio layer. The ratio layer was then plotted against the bathymetry calibration data measured in the field to generate an empirical relationship between the two. In the case of both sites, this took the form of a second order polynomial regression. These empirically-derived regression equations were then applied to the continuous raster log ratio layers covering the overall study sites generated from the blue and green wavebands to derive an estimate of bathymetry for the entire area covered by the image at both sites. The overall accuracy of these bathymetry estimates was then calculated using an independent set of validation bathymetry data taken in the field and not used in the original empirical process. Accuracy was calculated by regression of the modelled depths against the actual depths and then generating an R2 for the resulting linear scatterplot.
2.5. Bathymetric Mapping: Optimisation Approach
The adaptive look-up table (ALUT) model inversion method was applied as described in Hedley et al. [26,28]. In summary, the equations of Lee et al. [18,19] were used to model the water-leaving reflectance based on six parameters: P, G, X, which quantify the phytoplankton, dissolved organic matter and backscatter; H, the depth; and E and M, where E is an integer that describes which pair of bottom types are present and M (the mix parameter) ranges from 0–1 to set the bottom reflectance as a linear mix of the two bottom types. The analysis included the same six possible bottom reflectances as used in the 6-endmember analysis of Hedley et al. [28] that includes sand, coral, rubble and algae. For each pixel, the values of P, G, X, H, E and M that best reproduce the water-leaving spectral reflectance from the image were estimated. In this case, the ranges were P: 0–0.06, G: 0–0.1, X: 0–0.02, and depth H could range from 0–30 m. These ranges were similar to those used in previous work [26] and were based on values published by Lee et al. [19] and published field data of inherent optical properties of coral reef waters [38]. The ALUT method uses a hierarchically-structured look-up table to perform the spectral matching [26]. For both the Sykes Reef and Lizard Island sites, only the red, green and blue bands were used in the spectral matching. This was because for Sykes Reef, the NIR band was used in the glint correction and no longer contained useful information. Although deducing six parameters from three bands clearly introduces uncertainties, it is important to note that the constrained ranges and form of the model mean that the uncertainties are not equal for all estimated parameters. In particular, bathymetry benefits from the large range of spectral absorption by pure water from blue to red, which is always present. Previous work using uncertainty propagation indicates that the uncertainties associated with optimised estimates of bathymetry are frequently less than estimates of water optical properties or benthic reflectance [39].
2.6. Mapping Model Residuals
Model residuals were mapped as a simple way to visually examine the spatial distribution of the performance of bathymetric estimations [40]. Residuals were calculated as the difference between the optimisation-derived depth values and the validation echosounder bathymetry data. A point shapefile was produced to depict the model residuals in their geographical location at each site. This shapefile was then interpolated to a continuous raster surface (5 m spatial resolution) using a kriging algorithm. Kriging was selected because it has emerged as an optimal spatial interpolation method for mapping point values of residuals in model predictions [41]. A spherical ordinary kriging algorithm was selected to capture both the deterministic and autocorrelated variation in the residual surface, with the assumption of a constant mean. The resultant layer was then used as a visualization tool for examining the spatial distribution of error associated with the bathymetric estimations (note that it was not utilised in the spatial error model).
2.7. Statistical Exploration of Model Residuals: Independent Validation Plots, Moran’s I
Spatial autocorrelation of the model residuals was measured via the Moran’s I statistic using the software GeoDa (version 9.9.8). The Moran’s I statistic ranges from +1 to −1 and is a large and positive statistic in the presence of positive spatial dependence. A large and negative statistic occurs in the presence of negative spatial dependence and is close to zero if the map pattern is random. A scatter plot was constructed to investigate the univariate Moran’s I, with the spatially-lagged residuals on the vertical axis and the residuals on the horizontal axis. Variables were standardised, such that the units along the axes corresponded to standard deviations. The four quadrants in the graph depicted the different types of spatial autocorrelation, with the upper right and lower left quadrants relating to positive spatial autocorrelation (high-high- and low-low-valued neighbour pairings, respectively) and the lower right and upper left quadrants relating to negative spatial autocorrelation (high-low and low-high pairings, respectively). Global Moran’s I across the whole study area was provided at the top of each graph.
2.8. Modelling the Spatially-Structured Component Error Component
A spatial error model was constructed from the initial bathymetry estimates and the Moran’s I values. This model assumed that the unexplained variation in bathymetry estimates could be partially expressed as a spatial autoregressive function, such that an improved estimate of bathymetry (Y) for a given location i could be generated from the existing estimate of bathymetry (Xi) by characterising the spatially-structured component of error (ui) that was evident from the regression maps.
where ρ is a spatially-autocorrelated local Moran’s I parameter characterising the geographic structure observed in the bathymetry residuals, β0 and β1 are empirically-defined coefficients of variation and uj is the sum error (i.e., both spatially-structured unexplained and unexplained components) of the linear regression model for case j.
Yi = β0 + β1Xi + ui
ui = ρΣjєN(i) wi,j uj + ei
The structured component of the error was modelled using a spatially-lagged error term, such that only cases identified as falling within the neighbourhood of location i would be incorporated (j є N(i)). This condition was implemented by drawing explicitly on the location of each individual case through a spatial weights matrix (w(i,j)). This matrix expressed for each data case whether or not other cases belonged to its neighbourhood and were therefore included in the equation, such that wij = 1 when i and j were neighbours and wij = 0 otherwise (for point locations excluded from the model) [42]. To estimate the spatial autoregressive terms in the spatial lag model, all cases and the spatial weights matrix were input into a maximum likelihood procedure that generated consistent estimates of β.
Once the spatial structure of the error term had been modelled using the spatial autocorrelation metric of Moran’s I, this Moran’s I term was then introduced as an additional component to a regression model (Equation (2)) with the aim of improving the bathymetry estimates generated from both the empirical and optimisation routines. In this way, the values of the error associated with estimates of the dependent variable at neighbouring locations were employed within the standard regression equation.
After each regression analysis, diagnostics were recorded (including beta coefficients, R2 and p values), and the resulting final bathymetry estimates were mapped by applying the regression equation and beta coefficients to the initial estimates of bathymetry and locally-calculated estimates of Moran’s I for the model residuals.
3. Results
3.1. Bathymetric Mapping
Figure 2 illustrates the raw WorldView-2 satellite imagery and digital elevation models (DEMs) derived for each study site. For the empirical derivations, strong calibration relationships were established between the ratio of water reflectance and the water depths measured in the field for both Lizard Island (R2 = 0.76) and Sykes Reef (R2 = 0.83).
In terms of validation, the empirical estimates of bathymetry extracted from the DEM explained 74% and 82% of the variation observed within the independent field validation dataset collected with the echosounder for the Lizard Island and Sykes Reef sites, respectively. Bathymetry estimates derived from the optimisation procedure explained 89% of the variation from the validation dataset at both sites.
3.2. Exploration of Model Residuals: Mapping Model Residuals and Exploring Moran’s I
Figure 3 shows the validation plots, with interpolated maps of model residuals as an inset diagram for all four of the predicted DEMs. The spatial distribution of residuals appeared to be relatively unstructured for the empirical model at Lizard Island, with little discernible pattern of under- or over-prediction of depth across shallower and deeper zones from the residuals map (see the inset in Figure 3a). The validation plot suggested an under-estimation of depth in deeper areas.
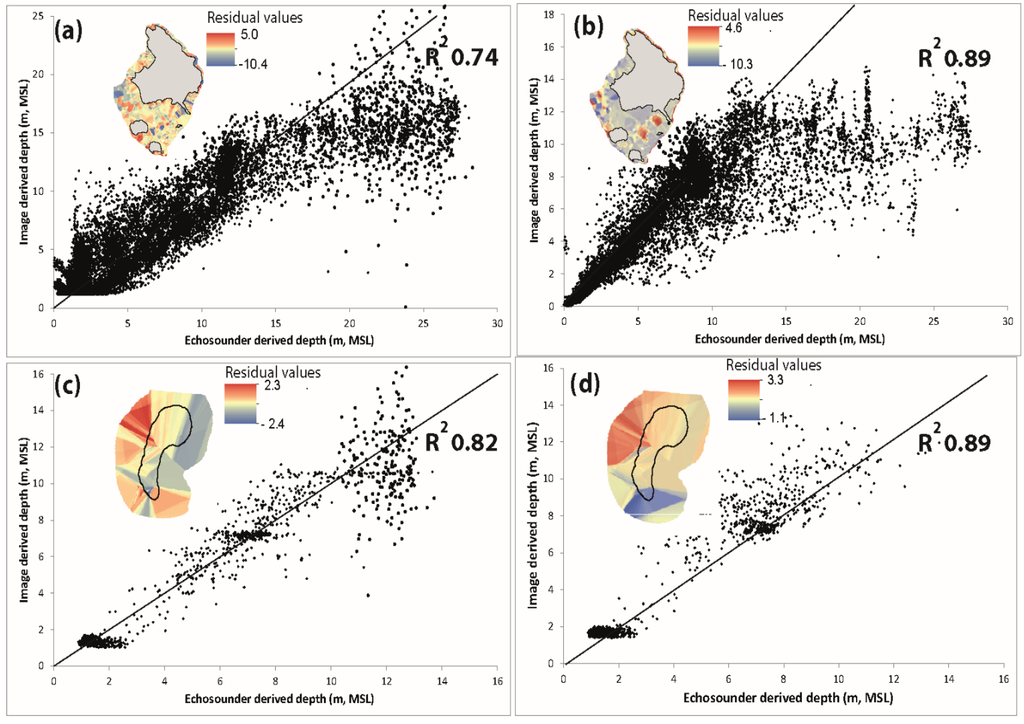
Figure 3.
Validation plots of echosounder-derived depths (x-axis) against image-derived depths (y-axis) derived from the multispectral images, with inset maps of the geographical distribution of residuals across the study sites (from left to right, top to bottom): (a) Lizard Island empirical model; (b) Lizard Island optimisation model; (c) Sykes Reef empirical model; (d) Sykes Reef optimisation model. Note: MSL stands for mean sea level.
The optimisation model appeared to perform better around the Lizard Island site, because the residuals were constrained around a narrower range of values (Figure 3b). These also showed structure with depth zonation, with shallow water bathymetry estimates converging on zero with increasing accuracy and, conversely, a tendency to under-predict depth around the deeper lagoon and reef platform areas at the base of the forereef to the periphery of the study site (Figure 3b). There was a notable overall trend of reduced residuals in shallower regions (i.e., <10-m water depth) in comparison to the deeper regions, as illustrated by the asymmetrical (heteroskedastic) spread of points in Figure 3b.
At the Sykes Reef site, the residuals associated with the empirical estimates of depth had a more distinctive geographical structure. In shallow regions, a cluster of validation points was apparent, for which the model under-predicted depth (Figure 3c), with an even magnitude of positive and negative residuals across the remainder of the study site. These displayed a marked geographic trend of positive residuals to the west and negative residuals to the east of the reef platform itself (see the inset in Figure 3c). This west to east trend was also present for the optimisation model, which tended to over-predict depth in the west, potentially because of unmixing confusion caused by dark benthos, such as coral and algae. Highly accurate clusters of pixels were apparent across both shallow and moderate depths, which likely corresponded to bright sandy areas, for which both the empirical and optimisation routines performed well.
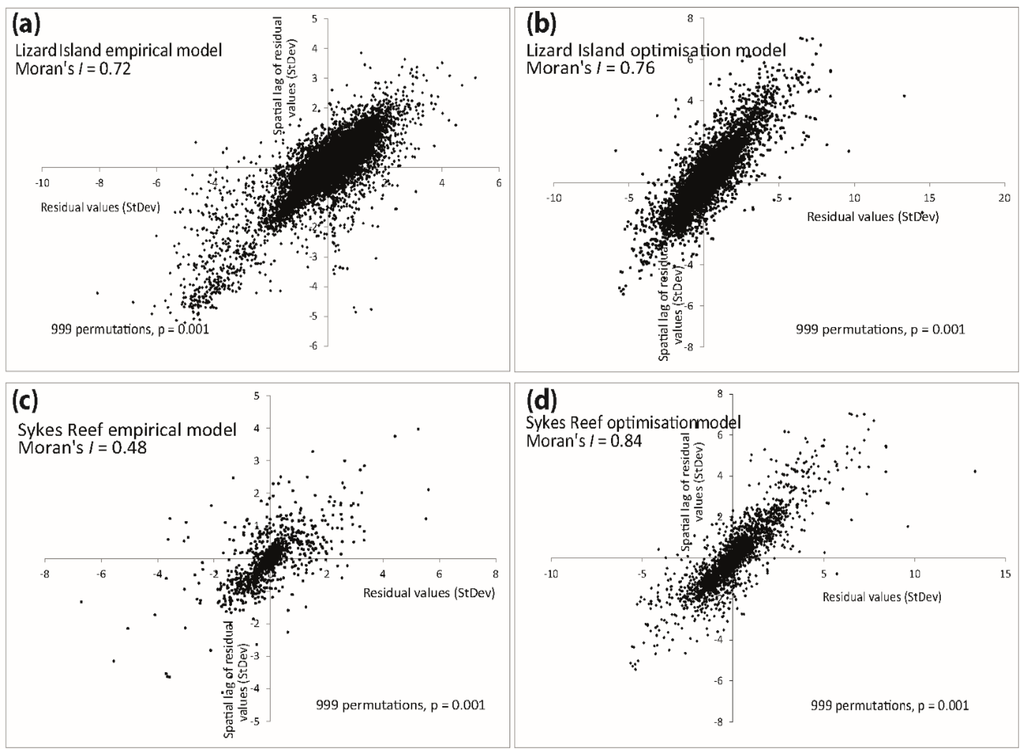
Figure 4.
Spatial autocorrelation of residuals from the bathymetric models, as depicted in plots of the residual values (x-axis) against a spatial lag of the residual values (y-axis) (from left to right, top to bottom): (a) Lizard Island empirical model; (b) Lizard Island optimisation model; (c) Sykes Reef empirical model; (d) Sykes Reef optimisation model. Global Moran’s I estimates of autocorrelation are provided. Axes relate to the standard deviation of true values and indicate the absolute magnitude of the error term.
Figure 4 shows the spatial autocorrelation plots for the residual datasets. All residuals from both the empirical and optimisation models at the Lizard Island and Sykes Reef sites were positively spatially autocorrelated, yielding a Moran’s I between zero and one with points falling in the positive (lower left and upper right) quadrants of the univariate Moran’s I plots (Figure 4). This means that positive residuals and negative residuals tended to cluster together in space, i.e., there was a detectable spatial structure in the model error, which adhered to Tobler’s first law of geography.
Residuals from the empirical analysis at the Lizard Island site were moderately spatially autocorrelated (Moran’s I = 0.72). Slightly stronger spatial autocorrelation was observed for the optimisation model at this site (Moran’s I = 0.75).
A larger difference was notable in the spatial autocorrelation of residuals for the different models at Sykes Reef, with the empirical model showing weak positive autocorrelation (Moran’s I = 0.48) and the optimisation model showing the strongest measured autocorrelation (Moran’s I = 0.84).
3.3. Modelling the Spatially-Structured Error Component
In all four cases, the addition of a spatial error term based on localised measurements of Moran’s I to characterise the spatial structure of the error associated with each model improved the estimates of bathymetry. The most notable improvement was in the application of the empirically-derived depth estimates at Lizard Island (Table 3).

Table 3.
Coefficient of determination values (R2) of bathymetry estimates at Lizard Island and Sykes Reef derived from a standard and a spatial error model when compared to the validation echosounder data. n = the number of depth points used.
| n | Standard Model R2 | Spatial Error Model R2 | |
|---|---|---|---|
| Lizard Island empirical bathymetry estimates. | 14,762 | 0.74 | 0.89 |
| Lizard Island optimisation bathymetry estimates. | 14,762 | 0.89 | 0.91 |
| Sykes Reef empirical bathymetry estimates. | 1168 | 0.82 | 0.95 |
| Sykes Reef optimisation bathymetry estimates. | 1168 | 0.89 | 0.95 |
Improved estimates of bathymetry at both the Lizard Island and Sykes Reef sites were particularly located in the shallower regions that corresponded to focal areas for echosounder bathymetric surveys where the denser field measurements were available. Increased levels of small scale, finer detail were discernible in these areas around networks of individual reef patches (Figure 5). A broader scale trend was also noticeable at the Sykes Reef site, where the spatial error model inverted the east to west trend of residuals, resulting in the identification of deeper areas around the base of the western and southern sections of the reef platform for the empirical model, and reduced estimates of water depth to the east of the reef platform for the optimisation model.
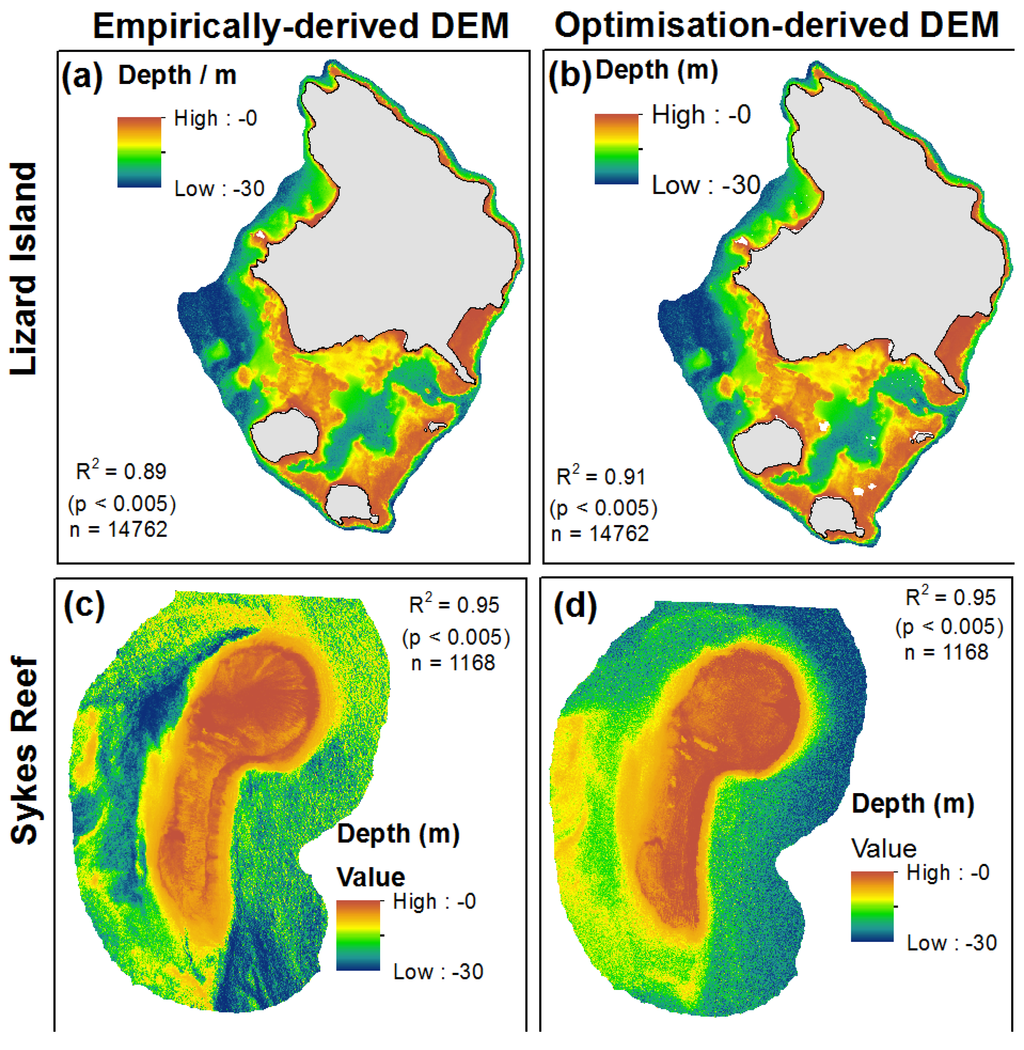
Figure 5.
Final DEMs of Lizard Island and Sykes Reef derived from satellite images after the spatial structure of errors associated with depth estimates have been characterised and accounted for in the DEMs (from left to right, top to bottom): (a) Lizard Island empirical model; (b) Lizard Island optimisation model; (c) Sykes Reef empirical model; (d) Sykes Reef optimisation model.
4. Discussion
The empirical and optimisation models estimated a similar range of depths at both Lizard Island (empirical range −1.15 to −27 m and optimisation range 0 to −30 m) and Sykes Reef (empirical range −0.83 to −28 m and optimisation range −2.21 to −30 m). These estimates of bathymetry correspond broadly to those reported elsewhere for both the Lizard Island site [43] and Sykes Reef site [44]. While bathymetry estimates resulted in maps with a very similar appearance at the Lizard Island site (see Figure 2b compared to Figure 2c), there was a greater distinction between the bathymetry maps estimated for Sykes Reef, particularly for the eastern side of the platform, which was estimated to fall to a deeper depth by the optimisation model than by the empirical model (see Figure 2e compared to Figure 2f). This may be due in part to a tendency for the optimisation model to over-predict depth across deeper sectors of the study area, as indicated by most of the deeper scatter points in the validation plot falling above the line of correspondence (Figure 3d). With both the empirical and the optimisation approaches, validation plots for the Sykes Reef site revealed a horizontal cluster of pixels at about a 2 m water depth (Figure 3c,d), where estimates range from −1 to −3. We interpret these to arise from residual noise associated with glint from the water surface.
At the Lizard Island site, the tendency for both empirical and optimisation bathymetric estimation methods to under-predict depth in deeper regions (i.e., where water depth exceeded 15 m) was likely due to the reduced number of light photons that interacted with the sea floor and were subsequently reflected into the sensor field of view. Beyond a certain depth threshold, which is governed by site-specific environmental conditions such as water quality, the number of photons detected by the sensor that have interacted with the seafloor will become negligibly small. At this point, there will be no information for the estimation of bathymetry. Because of variable water quality conditions and associated optical properties at different sites, this depth threshold will fluctuate, with reliable estimates extending deeper into the water column for clearer waters. The general tendency for reefs to exist in shallow, clear waters suggests that bathymetry estimation methods relying on multispectral satellite imagery will have some measure of success, although this raises the important consideration of the wavelengths at which image bands are configured. Because longer wavelengths of light attenuate more rapidly at shallower depths, satellite images that have wavebands calibrated towards shorter wavelengths (e.g., green and blue, as opposed to red sections of the electromagnetic spectrum) will likely yield more reliable depth estimates.
Other methods that can overcome these limitations include the use of multibeam echosounders and bathymetric LiDAR, which operate by emitting a pulse at wavelengths in the green section of the electromagnetic spectrum to facilitate seawater penetration. Such field-based methods complement satellite image-based methods, because they work well in deeper regions (as opposed to shallow regions, where the image-based methods work well); however, they have associated fieldwork costs, including the operation of a suitable plane- or boat-based platform.
The reefs span areas encompassing a range of long-term and short-term processes that have influenced their topography. These include the underlying antecedent platforms upon which they were initially founded, the modern benthic communities that have colonised the reef surface and have subsequently governed the rate of upward reef accretion and, originally, the broader scale tectonic movements resulting in the horizontal and vertical shifts of the continental crust in reef locations [1]. The resulting highly heterogeneous topography of the reefs reflect these spatial scales of variability superimposed on top of one another in a seafloor environment that may include isolated bommies, broad sand-filled lagoons and steep forereef slopes. In turn, these local scale features support diverse substrate colour and depth variation that gives rise to a challenging environment in which to apply satellite imagery for estimating bathymetry. The spatial distribution of the model residuals can therefore provide useful clues as to the processes that might underpin departures from model estimates (i.e., systematic model error). For example, in reef zones where the model is consistently under-predicting depth, it may be useful to seek reasons as to why this may be the case. Perhaps a localised area of high turbidity or a lighter substrate might underpin this trend? Regardless of the identity of the process causing the departure from in situ bathymetric measurements (i.e., the error), if it has a spatial pattern that can be modelled, then this term can be introduced into the estimation equation to “patch up” this spatially-structured proportion of the error observed (as per Equation (2)).
The most consistent pattern in the geographical distribution of model residuals was observed for Sykes Reef, where models tended to over-predict depth in the west and under-predict depth in the east. A closer examination of the geophysical environment of this region and how this links to assumptions of the empirical and optimisation models may provide an explanation for this. Jell and Webb [44] note that the western side of Sykes Reef is much shallower than the eastern side, due to a broad east to west -aligned shoal that runs between Heron and Sykes reefs, rising to approximately 15 m between the two reefs and dipping as it moves eastward [31]. The platform upon which the modern Sykes Reef sits is therefore an uneven slope that drops from shallower depths in the west to deeper depths in the east. Benthic communities colonising the surface of this shoal include large stands of Acropora spp. coral and algal mats, both of which serve to reduce the amount of light reflected from the seafloor that will be captured in the reflectance values of a satellite image. Both empirical and optimisation routines seek to define a relationship between this reflectance value and water depth, which often becomes confounded with the variable composition of seafloor communities. Often, this relationship can be broadly characterised as a trend in which areas of deeper water are equated with low reflectance and shallower areas are equated with high reflectance. Confusion may therefore arise in shallow areas that support darker substrates, where the depth may be over-predicted (as depicted by the red-coloured regions to the west of the Sykes Reef in the inset maps of Figure 3c,d). The negative residuals associated with the eastern, windward side of the study region represent regions of depth under-prediction, where it is known that the reef base slopes off more rapidly [30]. Combined with a sand-dominated (higher reflectance) platform, this would result in the opposite effect of depth under-prediction. To overcome this systematic error, other studies have suggested the derivation of substrate-specific empirical relationships (i.e., performing individual regressions for uniform bottom types, such as seagrass, sand and coral) [20]. Here, we suggest that the incorporation of a geographically-explicit term into one overall model represents an efficient solution that overcomes the need to run individual models and produces estimates of bathymetry across a range of substrate types, reflecting the diversity of reef benthic character.
Such a marked geographical trend in the performance of the two depth estimation models has a geographical structure that itself was characterised and accounted for in a spatial error model. This was evident in the improvement in the overall correspondence of estimates from the optimisation model of Sykes Reef with an independent validation dataset (a transition from an R2 of 0.89 for the standard model to 0.95 for the spatial error model; see Table 3). The highly autocorrelated nature of the model residuals, as indicated by global Moran’s I values, which ranged from 0.48–0.84, would have contributed to the success of the spatial error model. This is indicated by the fact that the spatial error model that resulted in the biggest improvement was the one that was applied to the optimisation estimates at Sykes Reef, which also yielded the model residuals with the highest levels of autocorrelation (Moran’s I = 0.84).
Quantification of spatial autocorrelation improved estimates of bathymetry generated from multispectral satellite image datasets. In this case, a map of the local Moran’s I was inserted into a spatial error regression model (Equation (2)) as an additional term that characterised the spatial structure of error across the Lizard Island and Sykes Reef sites and adjusted the bathymetry estimates accordingly. While the spatial structure of model residuals can be put to good use, it is also indicative of a violation of the assumptions of the classic regression technique that was used to empirically define the relationship between water depth and the satellite image. At both the calibration and validation stages, empirical regression assumes that observations are independent of each other and that residuals are both normally distributed and randomly located. This is not the case in the presence of spatial dependence because echosounder measurements that are close together are very similar (i.e., they adhere to Tobler’s first law of geography, see Introduction). This means that the effective number of degrees of freedom in both the calibration and validation samples is smaller than the one estimated from the number of observations. Because observations are not independent of each other, they cannot be freely permuted at random to create the reference (null) distribution of the test statistic. As a consequence, statistical tests undertaken in calibration of the bathymetry model generate narrow confidence limits. Regressing autocorrelated data cases therefore increases the likelihood of a Type I error by inflating the goodness of fit measure and underestimating the standard error as a result of allocating some of the effect due to interaction to the existing dependent variables [45]. Given that the empirical relationships defined were relatively strong (an R2 of 0.84 for Lizard island and 0.93 for Sykes Reef), it is possible that some of this is attributable to an underlying spatial effect.
The effects of spatial autocorrelation are also compounded by the tendency for both calibration and validation datasets to be extracted from the same bathymetric survey, thereby originating from the same geographic areas of the reef. The use of these datasets, which are more or less statistically identical, may also inflate the goodness of fit measure. Despite this statistical violation, this narrow geographical range of bathymetric information is a widespread practice among reef researchers and managers, largely due to the practical constraints associated with fieldwork in coral reef environments (e.g., weather and access for fieldwork). This bias can be overcome by ensuring that calibration and validation data are stratified on a geographical basis, such that data points originating from the same areas of reef are not used for both calibration and validation purposes. However, the optimal performance of bathymetric estimates is like to be achieved when points covering a fully-representative range of depths are present in both datasets.
5. Conclusions
A comparison of the empirical and optimisation approaches for estimating bathymetry at both the Lizard Island and Sykes Reef sites reveals that these methods yield very similar estimates overall. Although the optimization approach appeared to perform marginally better than the empirical method, both were subject to the same depth limitations, which are likely governed by the site water characteristics.
It is important to keep in mind that the ability to evaluate the performance of satellite-derived bathymetry models is limited by the data available for evaluation and that sites for which adequate satellite and field data exist in tandem to support model development and evaluation are rare. Consequently, it can be a challenge to evaluate estimates of seafloor topography that have been extrapolated across broader geographic areas using multispectral satellite data [8]. Here, we present a geographical error analysis as a means of comparing model performance across two sites where the requisite data were available. Explicitly spatial approaches, such as the mapping of model residuals and the calculation of spatial autocorrelation, emerged as useful tools for the exploration of error in bathymetry estimation models, particularly given that such models are generally implemented by combining georeferenced images and in situ survey datasets.
Spatial error models demonstrated that it is possible to go beyond evaluating uncertainty to profitably employ the model residuals within the predictive bathymetric modelling procedure using these techniques. While this has been applied before using interpolation algorithms [43,46], our study is the first attempt known to the authors that seeks to do so using geographically-weighted regression. The evaluation of bathymetric modelling error is also useful to subsequent users of bathymetric predictions, because uncertainty will propagate through other models or procedures that utilise output bathymetric data. Using a geographical evaluation approach is of practical value, because it enables the user to explicitly link model performance (and the associated likelihood of the estimate over- or under-prediction) to their location on a map. Given the fundamental importance of water depth as a driver for marine biophysical processes and applications, this geographical approach adds to the tools for critically assessing bathymetric information estimated from remote sensing datasets in coral reef environments.
Acknowledgments
This research would not have been possible without support from a University of Wollongong Return to Work Grant (SH) and a Lizard Island Research Station Fellowship Grant, 2011 (SH). We acknowledge assistance in the field from Russell Graham, Colin Woodroffe, Valerie Harwood, Javier Leon and Rafael Carvalho.
Author Contributions
Sarah M. Hamylton designed the study, collected the data, conducted analysis, and wrote paper. John D. Hedley designed study, conducted analysis, and wrote paper. Robin J. Beaman processed data and wrote paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hubbard, D. Reefs as dynamic systems. In Life and Death of Coral Reefs; Birkeland, C., Ed.; Chapman & Hall: New York, NY, USA, 1997; pp. 43–67. [Google Scholar]
- Kleypas, J.A.; McManus, J.W.; Meñez, L.A. Environmental limits to coral reef development: Where do we draw the line? Am. Zool. 1999, 39, 146–159. [Google Scholar] [CrossRef]
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar., Coastal Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Arias-González, J.E.; Acosta-González, G.; Membrillo, N.; Garza-Pérez, J.R.; Castro-Pérez, J.M. Predicting spatially explicit coral reef fish abundance, richness and Shannon-Weaver index from habitat characteristics. Biodivers. Conserv. 2012, 21, 115–130. [Google Scholar] [CrossRef]
- Harborne, A.R.; Mumby, P.J.; Ferrari, R. The effectiveness of different meso-scale rugosity metrics for predicting intra-habitat variation in coral-reef fish assemblages. Environ. Biol. Fish. 2012, 94, 431–442. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P. Intercomparison of shallow water bathymetry, hydro‐optics, and benthos mapping techniques in australian and caribbean coastal environments. Limnol. Oceanogr. Meth. 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high‐resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.; Reid, R.P. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef] [PubMed]
- Klonowski, W.M.; Fearns, P.R.; Lynch, M.J. Retrieving key benthic cover types and bathymetry from hyperspectral imagery. J. Appl. Remote Sens. 2007, 1, 011505. [Google Scholar] [CrossRef]
- Haining, R.P. Spatial Data Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Upton, G.; Fingleton, B. Spatial Data Analysis by Example. Volume 1: Point Pattern and Quantitative Data; John Wiley & Sons Ltd.: Chichester, UK, 1985. [Google Scholar]
- Fotheringham, S.; Rogerson, P. Spatial Analysis and Gis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tukey, J.W. Exploratory data analysis. Read. Ma 1977. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Jupp, D. Background and extensions to depth of penetration (dop) mapping in shallow coastal waters. In Proceedings of 1988 Remote Sensing of the Coastal Zone International Symposium, Queensland, Australia, 7–9 September 1988.
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [PubMed]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Mishra, D.; Narumalani, S.; Lawson, M.; Rundquist, D. Bathymetric mapping using ikonos multispectral data. GISci. Remote Sens. 2004, 41, 301–321. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Acharya, P.K.; Berk, A.; Matthew, M.W.; Gorodetzky, D. Remote bathymetry of the littoral zone from aviris, lash, and quickbird imagery. IEEE Trans. Geosci. Remote Sens 2005, 43, 337–347. [Google Scholar] [CrossRef]
- McIntyre, M.L.; Naar, D.F.; Carder, K.L.; Donahue, B.T.; Mallinson, D.J. Coastal bathymetry from hyperspectral remote sensing data: Comparisons with high resolution multibeam bathymetry. Mar. Geophys. Res. 2006, 27, 129–136. [Google Scholar] [CrossRef]
- Goodman, J.; Ustin, S.L. Classification of benthic composition in a coral reef environment using spectral unmixing. J. Appl. Remote Sens. 2007, 1, 011501. [Google Scholar]
- Louchard, E.M.; Reid, R.P.; Stephens, F.C.; Davis, C.O.; Leathers, R.A.; T Valerie, D. Optical remote sensing of benthic habitats and bathymetry in coastal environments at lee stocking island, bahamas: A comparative spectral classification approach. Limnol. Oceanogr. 2003, 48, 511–521. [Google Scholar] [CrossRef]
- Lesser, M.; Mobley, C. Bathymetry, water optical properties, and benthic classification of coral reefs using hyperspectral remote sensing imagery. Coral Reefs 2007, 26, 819–829. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Phinn, S.R. Efficient radiative transfer model inversion for remote sensing applications. Remote Sens. Environ. 2009, 113, 2527–2532. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Gagliano, S.; Pepe, M. Bomber: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Koetz, B.; Phinn, S. Capability of the sentinel 2 mission for tropical coral reef mapping and coral bleaching detection. Remote Sens. Environ. 2012, 120, 145–155. [Google Scholar] [CrossRef]
- Rees, S.A.; Opdyke, B.N.; Wilson, P.A.; Fifield, L.K.; Levchenko, V. Holocene evolution of the granite based lizard island and macgillivray reef systems, northern great barrier reef. Coral Reefs 2006, 25, 555–565. [Google Scholar] [CrossRef]
- Maxwell, W. Atlas of the Great Barrier Reef; Elsevier: Amsterdam, NY, USA, 1968. [Google Scholar]
- Jell, J.S.; Flood, P.G. Guide to the Geology of Reefs of the Capricorn and Bunker Groups, Great Barrier Reef Province, with Special Reference to Heron Reef; University of Queensland Press: Brisbane, Australia, 1978. [Google Scholar]
- Marshall, J.F.; Davies, P.J. Submarine lithification on windward reef slopes: Capricorn-bunker group, southern great barrier reef. J. Sediment. Res. 1981, 51, 953–960. [Google Scholar]
- Davies, P.; Marshall, J.; Hekel, H.; Searle, D. Shallow inter-reefal structure of the capricorn group, southern great barrier reef. BMR J. Aust. Geol. Geophys. 1981, 6, 101–105. [Google Scholar]
- Wells, D.E.; Monahan, D. Iho s44 standards for hydrographic surveys and the variety of requirements for bathymetric data. Hydrogr. J. 2002, 44, 9–16. [Google Scholar]
- Antoine, D.; Morel, A. A multiple scattering algorithm for atmospheric correction of remotely sensed ocean colour (meris instrument): Principle and implementation for atmospheres carrying various aerosols including absorbing ones. Int. J. Remote Sens. 1999, 20, 1875–1916. [Google Scholar] [CrossRef]
- Mayer, B.A.; Kylling, A. The libradtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Hedley, J.; Harborne, A.; Mumby, P. Simple and robust removal of sun glint for mapping shallow‐water benthos. Int. J. Remote Sens 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Phinn, S.R.; Mumby, P.J. Environmental and sensor limitations in optical remote sensing of coral reefs: Implications for monitoring and sensor design. Remote Sens. 2012, 4, 271–302. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Phinn, S. Propogating uncertainty through a shallow water mapping algorithm based on radiative transfer model inversion. Ocean Opt. 2010, 12, 24–51. [Google Scholar]
- Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kyriakidis, P.C.; Dungan, J.L. A geostatistical approach for mapping thematic classification accuracy and evaluating the impact of inaccurate spatial data on ecological model predictions. Environ. Ecol. Stat. 2001, 8, 311–330. [Google Scholar] [CrossRef]
- Anselin, L.; Bera, A.K. Spatial dependence in linear regression models with an introduction to spatial econometrics. Stat. Textb. Monogr. 1998, 155, 237–290. [Google Scholar]
- Leon, J.X.; Phinn, S.R.; Hamylton, S.; Saunders, M.I. Filling the “white ribbon”—A multisource seamless digital elevation model for lizard island, northern great barrier reef. Int. J. Remote Sens. 2013, 34, 6337–6354. [Google Scholar] [CrossRef]
- Jell, J.S.; Webb, G.E. Geology of heron island and adjacent reefs, great barrier reef, australia. Episodes 2012, 35, 110–119. [Google Scholar]
- Cliff, A.D.; Ord, J.K. Spatial Autocorrelation; Pion: London, UK, 1973. [Google Scholar]
- Corucci, L.; Masini, A.; Cococcioni, M. Approaching bathymetry estimation from high resolution multispectral satellite images using a neuro-fuzzy technique. J. Appl. Remote Sens. 2011, 5, 053515. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).