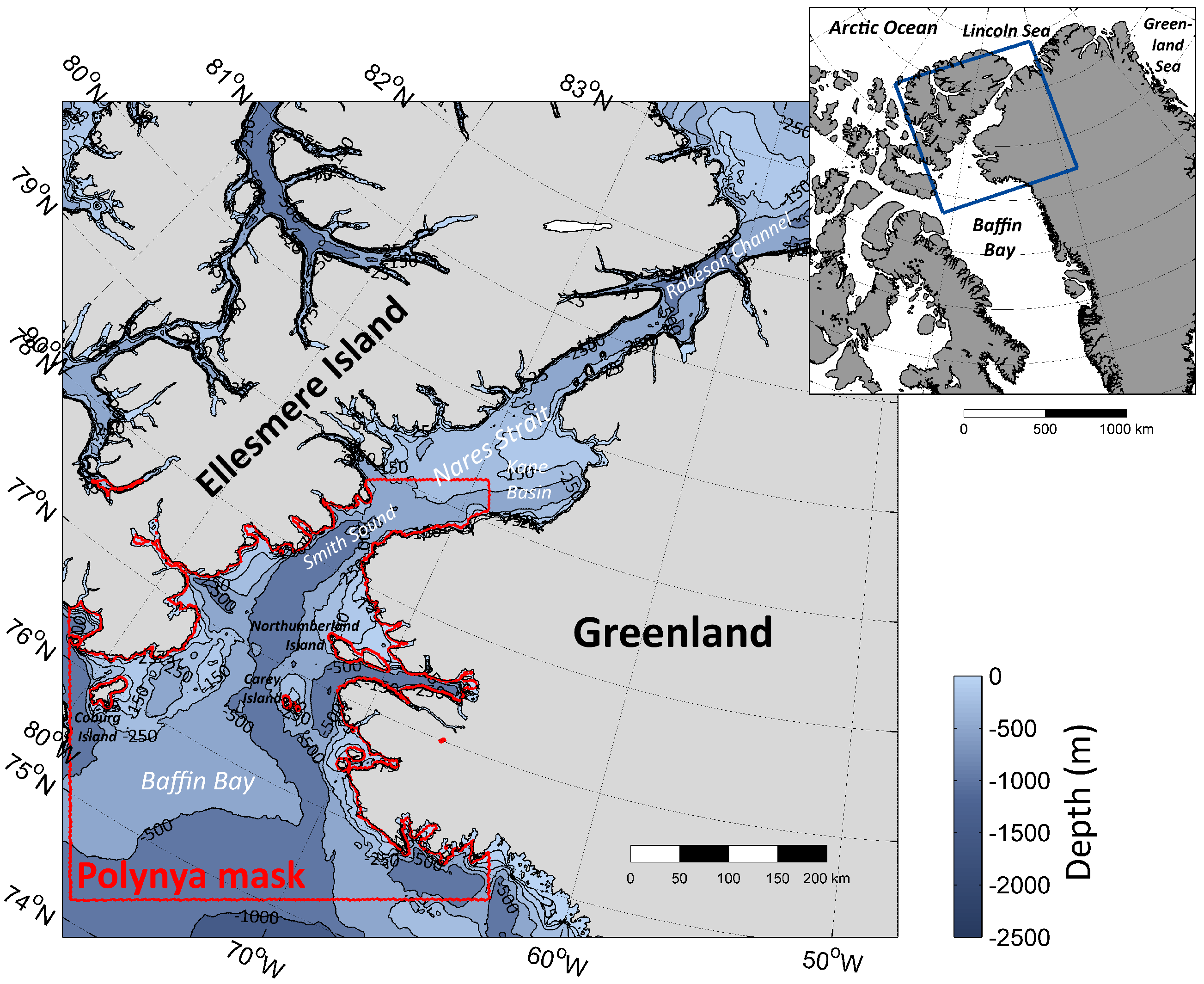
3.1. Sensor Differences in the POLA Retrieval
Concerning the upper value for ice thickness of the PSSM-derived POLA in the NOW region,
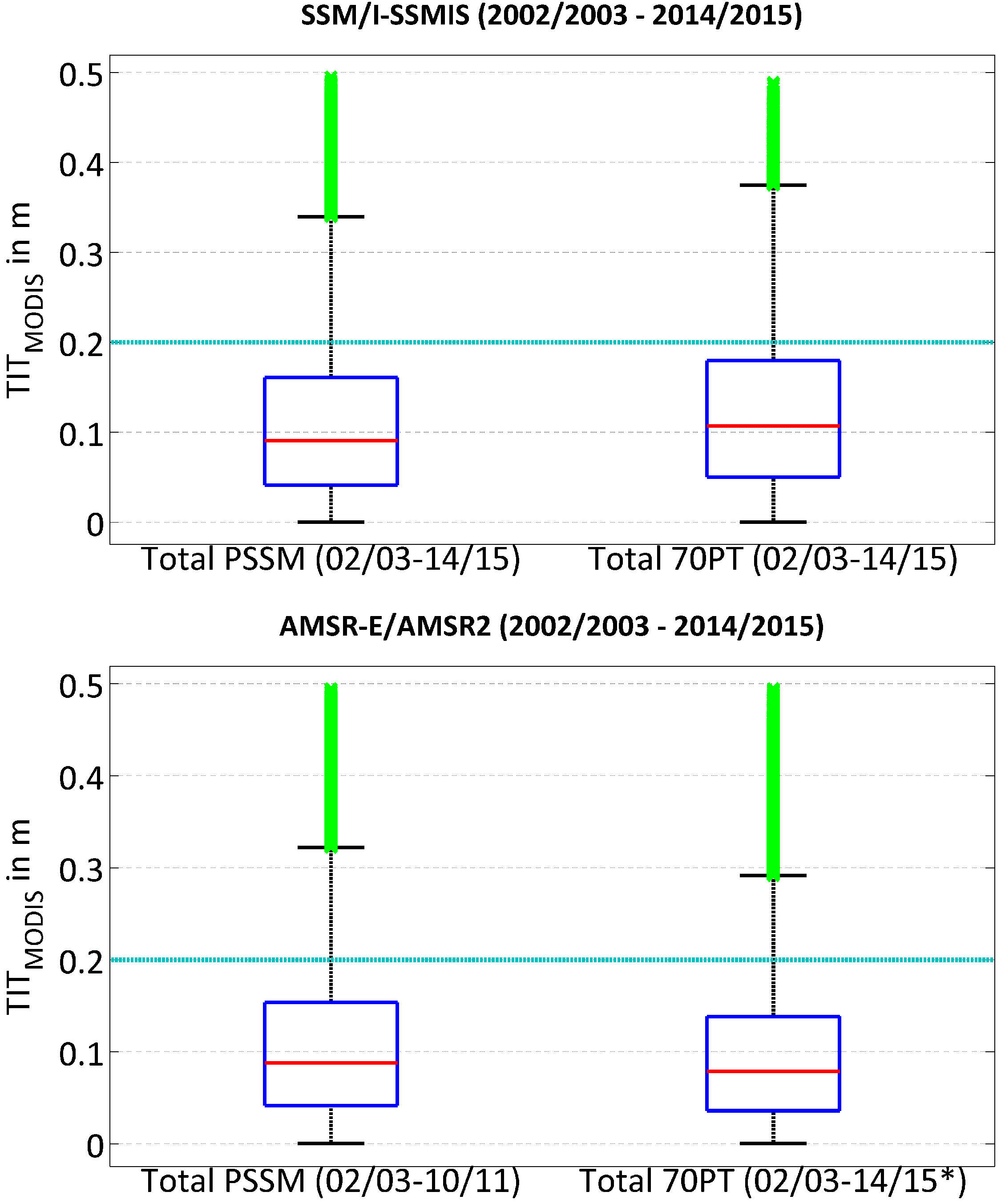
Figure 3 shows a similar analysis as in Kern
et al. [
39] and Willmes
et al. [
30] for both SSM/I, as well as AMSR-E/AMSR2 for the period 2002 to 2015. We notice that the vast majority of thin-ice pixels in the NOW polynya region as defined by PSSM and 70PT does not exceed the 0.2-m threshold, which is in accordance with previous studies, while at the same time, a significant amount of outliers exists. In the case of PSSM, the average TIT amounts to 11.2 ± 9.0 cm and 10.8 ± 8.6 cm for SSM/I-SSMIS and AMSR-E, respectively. When using a 70% SIC-threshold to derive POLA (70PT), similar values of 12.4 ± 9.1 cm (SSM/I-SSMIS) and 9.7 ± 7.8 cm (AMSR-E/AMSR2) are calculated. As these values are gathered over the complete polynya area as prescribed by PSSM and 70PT, these TIT can be seen as areal averages.
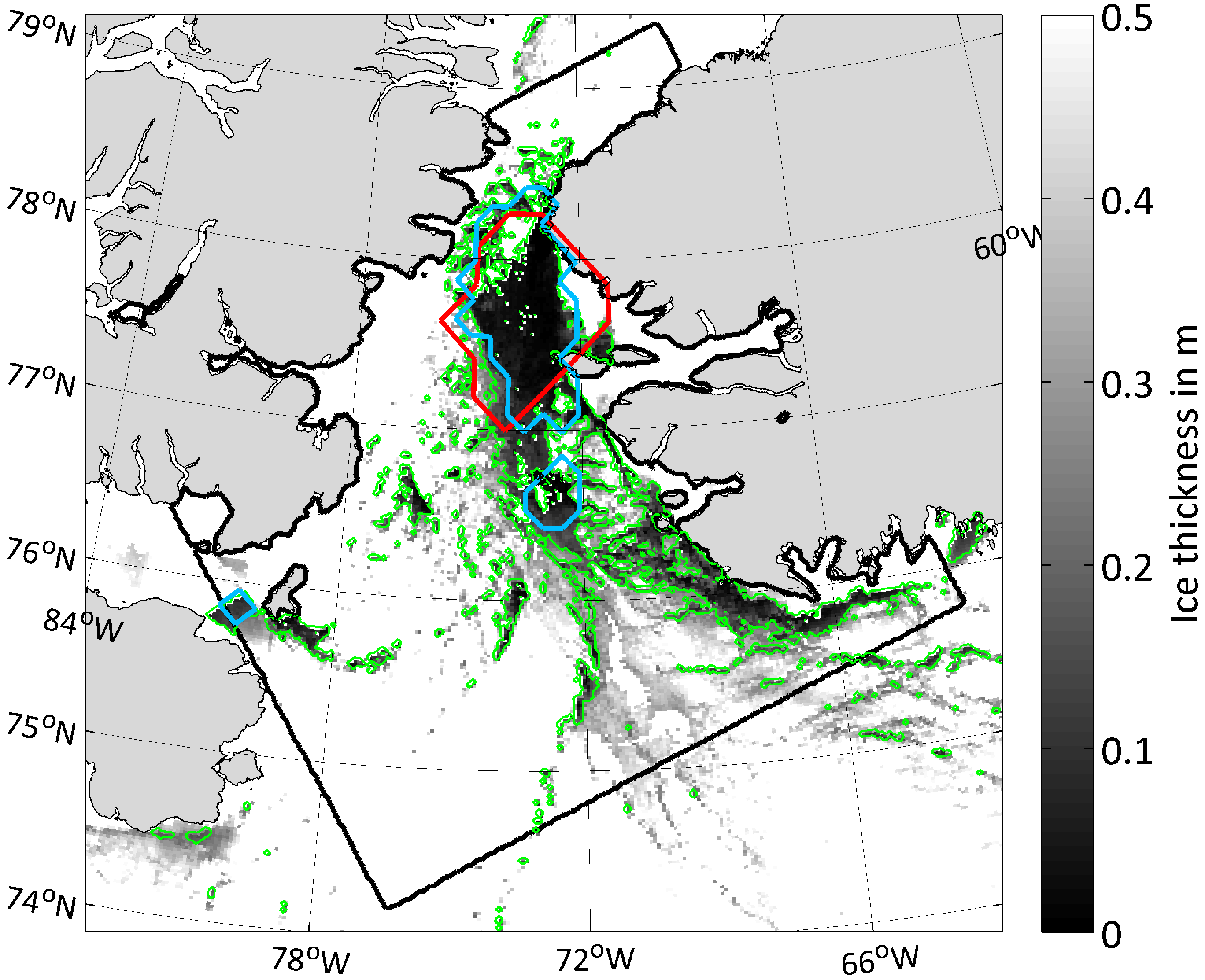
Differences in the retrieved POLA (AMSR-E/2
vs. SMMR/SSM/I-SSMIS
vs. MODIS) can be mostly attributed to the sensor-specific capability to resolve small thin-ice features, such as small coastal polynyas and leads,
i.e., the spatial resolution of each sensor.
Figure 2 illustrates this effect quite nicely by showing an example (14 March 2009) of the retrieved POLA for MODIS (TIT ≤ 0.2 m; green contour; 2 km), SSM/I 70PT (red contour; 25 km) and SSM/I PSSM (blue contour; 12.5 km). While the passive microwave estimates on that given day are comparable (PSSM: 7463 km
; 70PT: 6691 km
), the MODIS-estimates more than double those values (no CC: 17,804 km
; CC (IST-coverage 92.3%): 19,290 km
).
Figure 3.
Box-plots of the daily TIT distribution in polynya areas as detected by passive microwave sensors (upper panel: SSM/I-SSMIS; lower panel: AMSR-E/AMSR2). Boxes on the left side show the MODIS TIT distribution in the PSSM polynya area, while the right-hand boxes show the equivalent information for the 70PT method. The light blue horizontal bar marks the 0.2-m TIT-threshold for the MODIS POLA-retrieval. Red bars indicate the median within the 25th and 75th percentile (inter-quartile range; blue boxes). The whisker length has a default value of 1.5-times the inter-quartile range, and outliers are marked in green (* no AMSR-E/AMSR2 sea ice concentrations available for November to March 2011/2012).
Figure 3.
Box-plots of the daily TIT distribution in polynya areas as detected by passive microwave sensors (upper panel: SSM/I-SSMIS; lower panel: AMSR-E/AMSR2). Boxes on the left side show the MODIS TIT distribution in the PSSM polynya area, while the right-hand boxes show the equivalent information for the 70PT method. The light blue horizontal bar marks the 0.2-m TIT-threshold for the MODIS POLA-retrieval. Red bars indicate the median within the 25th and 75th percentile (inter-quartile range; blue boxes). The whisker length has a default value of 1.5-times the inter-quartile range, and outliers are marked in green (* no AMSR-E/AMSR2 sea ice concentrations available for November to March 2011/2012).
3.2. Assessment of Long-Term POLA Development
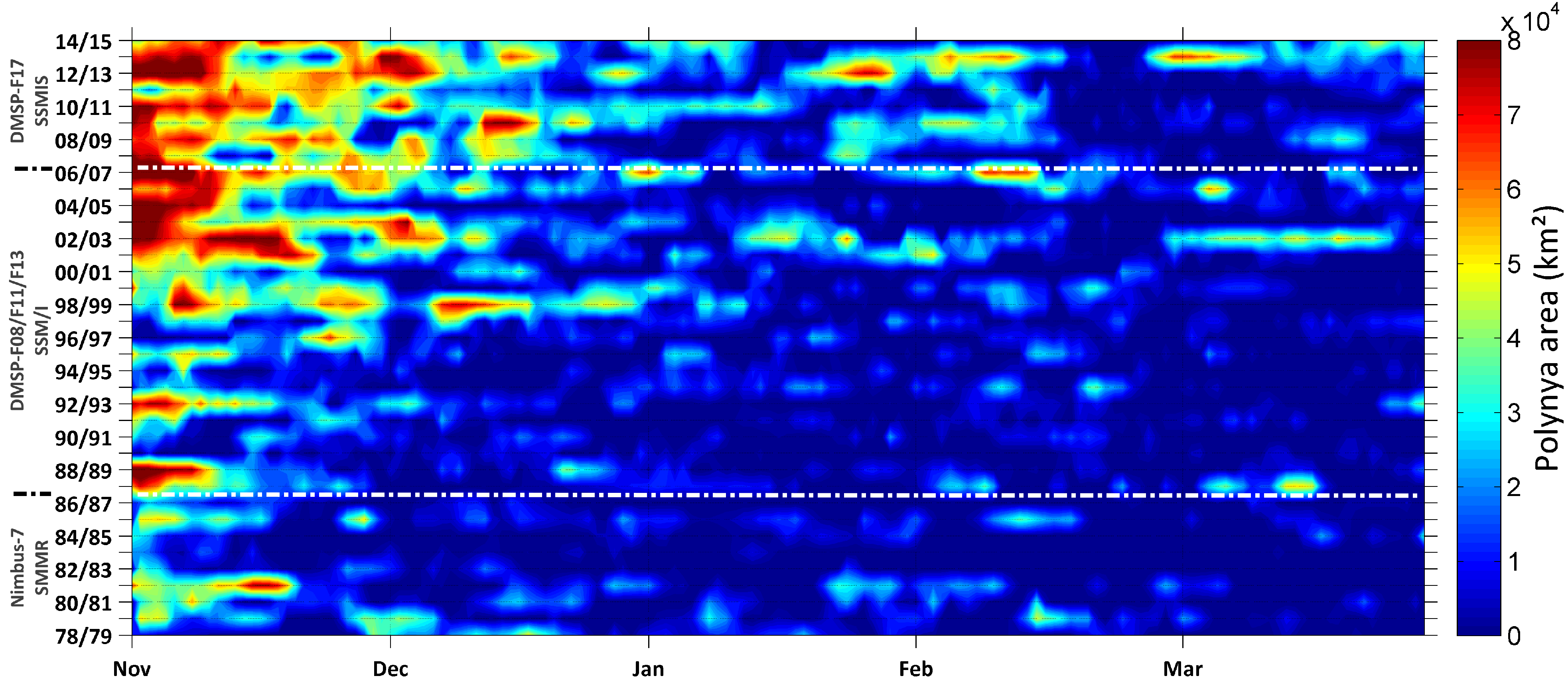
As the coarse-resolution SMMR/SSM/I-SSMIS SIC dataset features by far the longest available satellite record (1978 to 2015),
Figure 4 shows the daily development of
estimates for the NOW polynya. This time series of 37 consecutive winter seasons covers a comparatively long period of time and is therefore better suited for climatological studies than the MODIS and AMSR-E/AMSR2 estimates, which feature only the last 13 winter seasons. It gets clear that the NOW polynya changed significantly during the last three decades, regardless of the absolute accuracy of the underlying SIC dataset [
16]. Until the mid-1990s, the overall polynya-activity was very weak. Larger polynya events occurred mainly at the beginning of a freezing season (November), while the remaining months only featured sparse periods with enhanced activity. Overall, a shift to a later fall freeze-up is observed in the last 15 to 16 years, where the polynya exceeds areal extents of 40,000 to 50,000 km
until the end of December. In addition, also the remaining months of these years show large polynya events. Less polynya activity is generally observed towards the end of an average winter season.
Figure 4.
Hovmöller diagram of daily polynya area (
) in the North Water Polynya between 1978/1979 and 2014/2015. White horizontal dotted lines indicate changing sensors in the sea ice concentration (SIC) dataset by Cavalieri
et al. [
16].
Figure 4.
Hovmöller diagram of daily polynya area (
) in the North Water Polynya between 1978/1979 and 2014/2015. White horizontal dotted lines indicate changing sensors in the sea ice concentration (SIC) dataset by Cavalieri
et al. [
16].
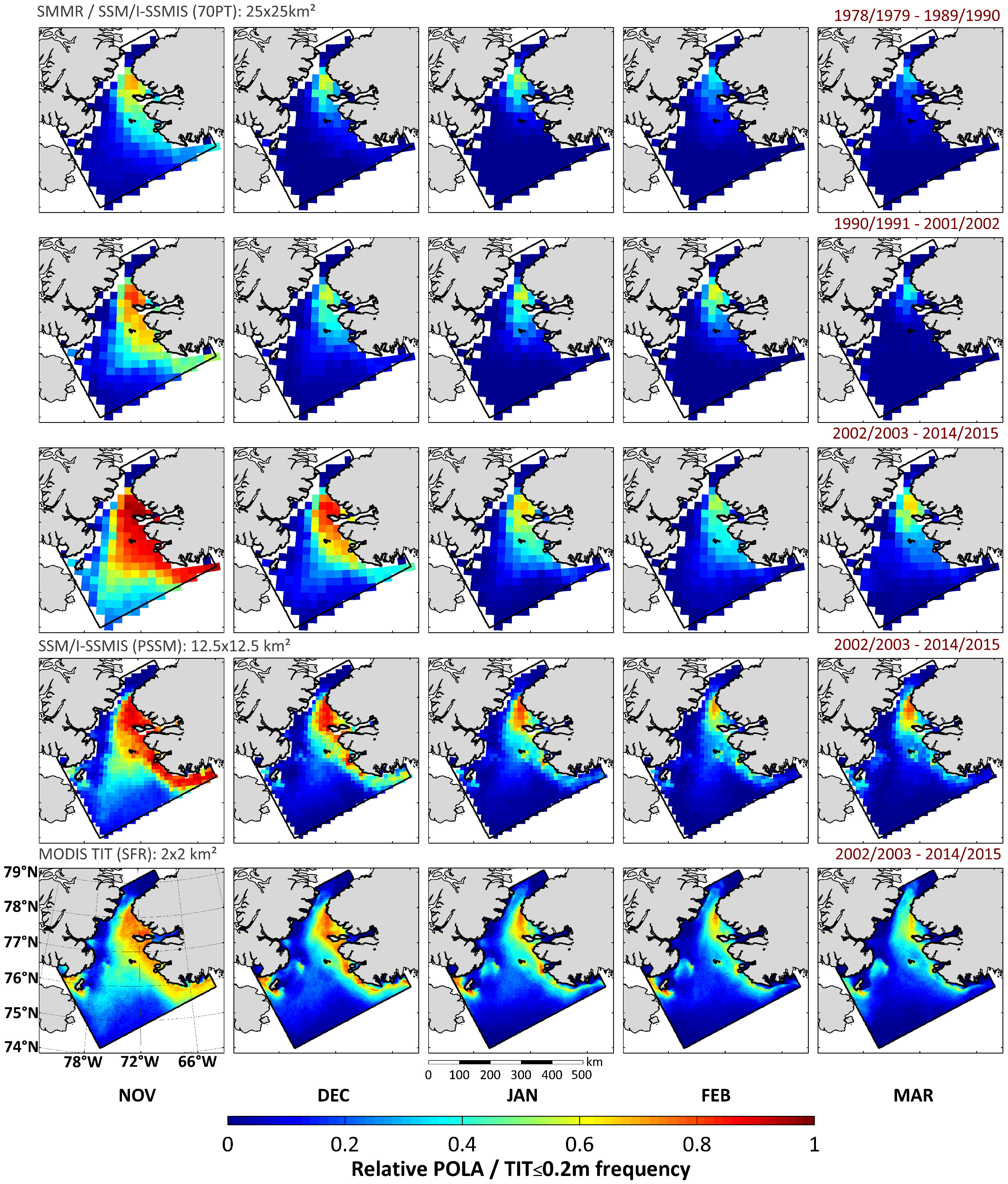
Figure 5 shows spatial overviews of the relative frequency of polynya/thin-ice occurrences on a monthly basis (November to March) based on daily
estimates,
estimates and MODIS TIT (using SFR for gap filling). The upper three rows roughly represent the 1980s (1978/1979 to 1989/1990), the 1990s (1990/1991 to 2001/2002) and the 2000s (2002/2003 to 2014/2015) periods to detect decadal changes of the sea ice in northern Baffin Bay. The lower two rows show equivalent information for the 2000s period based on
and MODIS. In the 1980s, the NOW polynya features an overall low activity. These first 12 winter seasons show appearance rates of around 70% (21 d) in November down to approximately 30% (9 d) in February and March in the area of Smith Sound. The main polynya activity during this period is limited to areas north of 76
N (maximum extent in November). During the 1990s and even more the 2000s, this region vastly expands down to approximately 74
N. Even in January to March, appearance rates of over 20% to 30% extend down to around 76
N. Remarkably, the monthly duration of the polynya in the proximity of Smith Sound increases towards 60% (17 to 19 d) in January to March and up to 90% to 100% (28 to 31 d) in November to December. The finer resolving counterparts from MODIS, SSM/I-SSMIS (PSSM) (
Figure 5; 2000s period) and AMSR-E/AMSR2 (not shown) are certainly able to provide more precise regional differentiations. Not only in the case of MODIS (relative frequencies of TIT ≤ 0.2 m), observed patterns are in accordance with earlier studies (e.g., [
8,
20,
21]) and underline the previously-stated observations based on coarse-resolution SMMR and SSM/I-SSMIS 70PT data. In addition, the detection of small-scale features, like the clearly visible shape of the ice bridge at Smith Sound, as well as larger thin-ice areas at the eastern side of the polynya, profits from the enhanced spatial resolution of MODIS. Also noticeable is a quite large area with values ranging from around 35% to 60% south of Ellesmere Island (eastern entrance of Jones Sound).
Figure 5.
Average monthly relative frequency distribution of polynya-pixels as classified by the 70PT-method (SMMR/SSM/I-SSMIS; top three rows), the PSSM method (SSM/I-SSMIS); fourth row) and based on MODIS thin-ice thicknesses ≤ 0.2 m (daily TIT composites with applied spatial feature reconstruction (SFR); bottom row). Note the reference period over which the monthly relative frequency distributions are calculated, as indicated in the the upper right corner of each row.
Figure 5.
Average monthly relative frequency distribution of polynya-pixels as classified by the 70PT-method (SMMR/SSM/I-SSMIS; top three rows), the PSSM method (SSM/I-SSMIS); fourth row) and based on MODIS thin-ice thicknesses ≤ 0.2 m (daily TIT composites with applied spatial feature reconstruction (SFR); bottom row). Note the reference period over which the monthly relative frequency distributions are calculated, as indicated in the the upper right corner of each row.
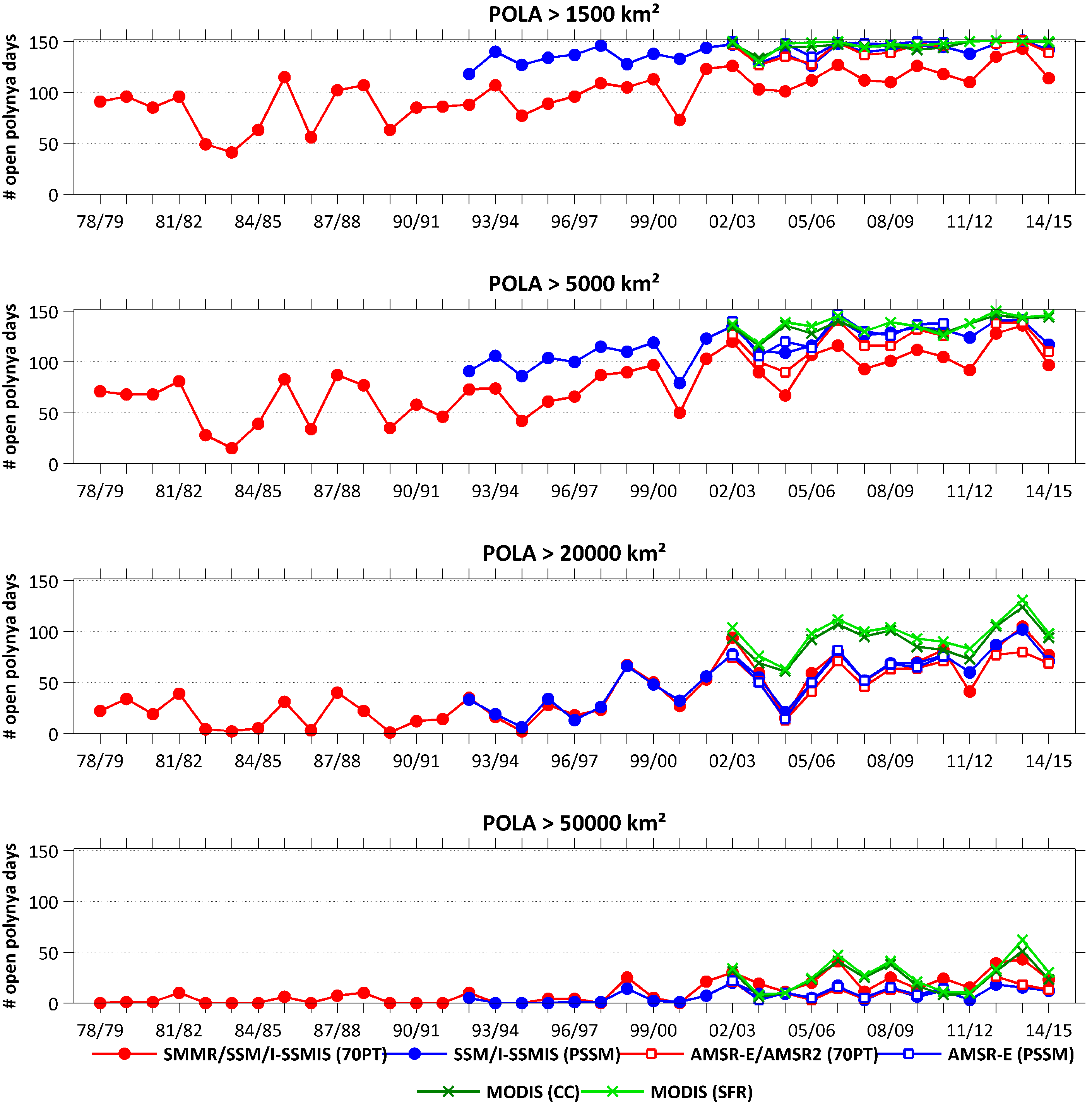
Figure 6 sums up the previous findings for the whole regarded period from 1978 to 2015. It shows the amount of open polynya days (based on POLA estimates from MODIS (CC/SFR), AMSR-E/AMSR2 and SMMR/SSM/I-SSMIS (both 70PT/PSSM)) exceeding a certain areal threshold (POLA ≥1500/5000/20,000/50,000 km
). In the upper panel (POLA ≥1500 km
), days that are falling below a threshold of 1500 km
,
i.e., an almost closed polynya, can be depicted by the difference of given values to the total number of days each winter season (November to March; 151/152 d). In recent winters, the number of very small to almost closed polynyas seems to vanish almost completely (except for the SMMR/SSM/I-SSMIS 70PT retrievals). On the other hand, the number of larger polynyas increases significantly from approximately 1997/1998 onwards, especially those exceeding a threshold of 20,000 km
. Noteworthy is the higher amount of detected polynyas larger than 20,000 km
from MODIS and a good agreement between MODIS and the passive microwave estimates for very large polynyas (≥50,000 km
).
Figure 6.
Number of polynya days with an area of ≥1500 km, ≥5000 km, ≥20,000 km and ≥50,000 km within the applied polynya mask. A comparison is made between POLA estimations based on daily MODIS TIT composites (CC: dark green crosses; SFR: light green crosses) and passive microwave sensors (SMMR/SSM/I-SSMIS 70PT: filled red circles; AMSR-E/AMSR2 70PT: unfilled red squares; SSM/I-SSMIS PSSM: filled blue circles; AMSR-E PSSM: unfilled blue squares). The numbers indicate the amount of polynya days for each area threshold from zero.
Figure 6.
Number of polynya days with an area of ≥1500 km, ≥5000 km, ≥20,000 km and ≥50,000 km within the applied polynya mask. A comparison is made between POLA estimations based on daily MODIS TIT composites (CC: dark green crosses; SFR: light green crosses) and passive microwave sensors (SMMR/SSM/I-SSMIS 70PT: filled red circles; AMSR-E/AMSR2 70PT: unfilled red squares; SSM/I-SSMIS PSSM: filled blue circles; AMSR-E PSSM: unfilled blue squares). The numbers indicate the amount of polynya days for each area threshold from zero.
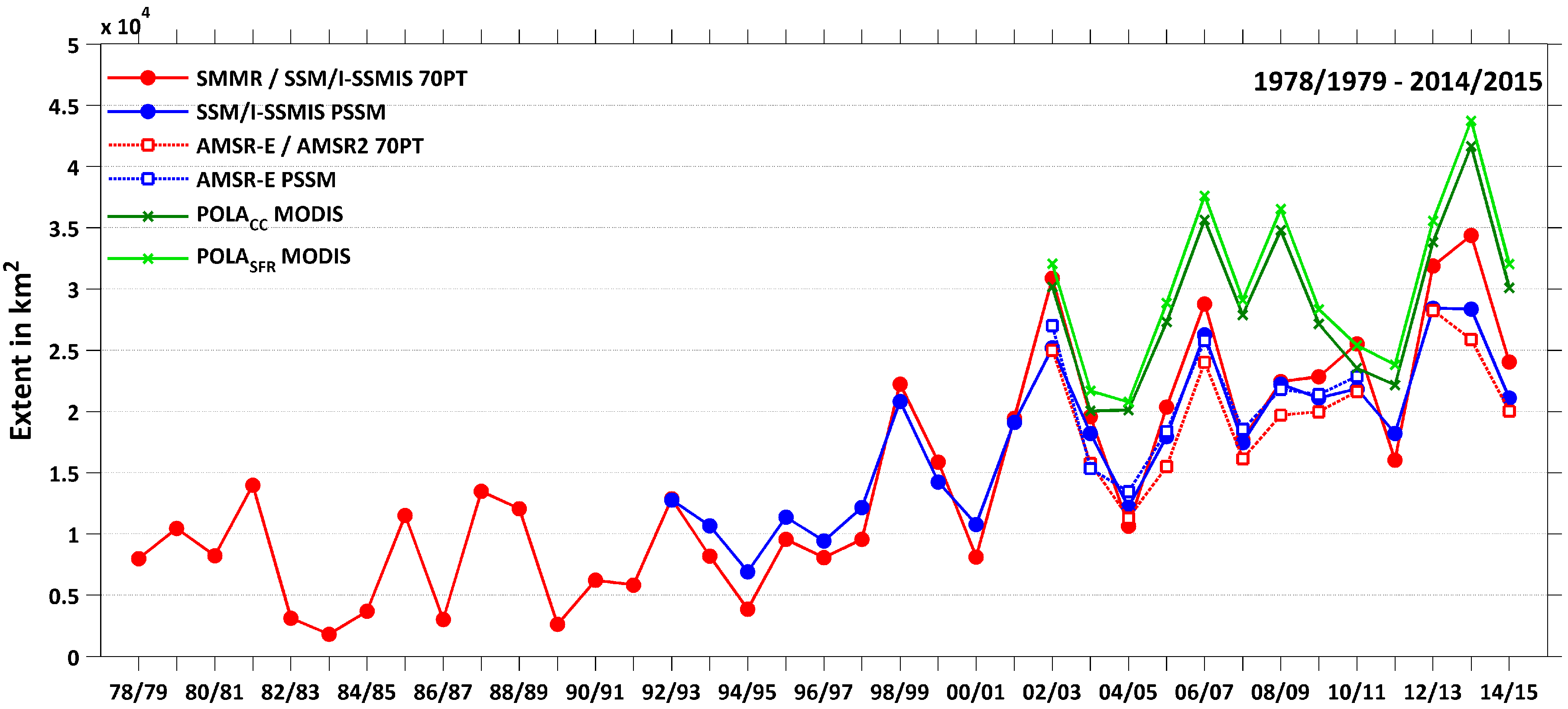
A comparison of the wintertime mean POLA for all available sensors and retrieval-schemes is presented in
Figure 7 for the complete record of 37 winter seasons. In this long-term context, we find coherent patterns between all incorporated satellites and sensors, although absolute mean values are differing. Further, a tendency towards larger areal extents of the NOW polynya becomes very obvious. As could be seen before, the winter seasons around 1996/1997 to 1997/1998 seem to be the periods where the NOW polynya starts to expand from an average level of around 7000 km
in the 1980s and early 1990s up to almost doubled average values in recent years.
Figure 7.
Average wintertime (November to March) polynya area (POLA) for the period from 1978/1979 to 2014/2015. A comparison is made between POLA estimations based on daily MODIS TIT composites (CC: dark green crosses; SFR: light green crosses) and passive microwave sensors (SMMR/SSM/I-SSMIS 70PT: filled red circles; AMSR-E/AMSR2 70PT: unfilled red squares; SSM/I-SSMIS PSSM: filled blue circles; AMSR-E PSSM: unfilled blue squares).
Figure 7.
Average wintertime (November to March) polynya area (POLA) for the period from 1978/1979 to 2014/2015. A comparison is made between POLA estimations based on daily MODIS TIT composites (CC: dark green crosses; SFR: light green crosses) and passive microwave sensors (SMMR/SSM/I-SSMIS 70PT: filled red circles; AMSR-E/AMSR2 70PT: unfilled red squares; SSM/I-SSMIS PSSM: filled blue circles; AMSR-E PSSM: unfilled blue squares).
This sudden “POLA shift” during the mid-1990s may be related to the clear warming trend in northwestern Greenland from 1994 onwards [
41] (associated with an increasing amount of blocking events (high-pressure anomalies) over the Greenland Ice Sheet (GrIS), e.g., [
42]). The North Atlantic Oscillation (NAO) and Arctic Oscillation (AO) are well known and widely used indices that characterize large-scale atmospheric variability in the Northern Hemisphere. While featuring significant interannual and seasonal variability, the NAO experienced a transition to a prevailing more negative phase in 1995/1996, which so far peaked in the most negative wintertime NAO index in 2009/2010 [
43]. These negative phases are associated with a high-pressure anomaly/ridges over the GrIS, which can bring relatively warm southerly winds from lower latitudes to the western side of Greenland [
44]. Although the NAO and AO are very similar from a conceptual point of view and do strongly correlate (r > 0.8), the recently declining nature of the summer NAO is not replicated in the AO index [
45]. Instead, both indexes show enhanced wintertime variability in recent years [
45,
46]. However, extreme negative phases, like in 2009/2010, are evident in both the NAO and AO index. Stroeve
et al. [
46] highlights that winter months (December to January) for the period 1979 to 2009 with a strongly negative AO index tend to show positive air temperature (925-hPa level) anomalies and negative SIC anomalies over Greenland, Baffin Bay, Canada and Alaska. A steady increase in autumn and winter air temperatures from 1995/1996 onwards could slow down or limit ice growth during freeze-up and, hence, lead to prolonged periods with very thin ice in northern Baffin Bay. Following this argumentation, increasing POLA and a later fall freeze-up align well. Therefore, besides having a potentially large influence on summer melt rates on the GrIS and land surface [
41], we assume that increased winter warming and associated negative NAO phases are also linked to sea ice and polynya characteristics in the NOW region.
Overall, it can be noted, that MODIS, as well as both AMSR-E PSSM and SSM/I-SSMIS PSSM all capture the general seasonal development of polynya opening events in good agreement (compare
Table 3). In several cases, MODIS-derived POLA exceeds the passive microwave estimates by a factor of 1.5 to two, especially for polynyas below 40,000 km
. When comparing individual winter seasons, a large interannual variability can be observed.
Table 3.
Comparison of calculated monthly mean polynya area (POLA; in 10
km
) from different sensor types (SSM/I-SSMIS, AMSR-E, MODIS) and methods, averaged over the overlapping period from 2002/2003 to 2010/2011 (November to March). Cloud-cover corrections have been applied to the MODIS data where CC denotes the values after coverage correction and SFR denotes the values after the spatial feature reconstruction (compare
Section 2.6). All values are calculated within the predefined polynya mask (
Figure 1).
Table 3.
Comparison of calculated monthly mean polynya area (POLA; in 10 km) from different sensor types (SSM/I-SSMIS, AMSR-E, MODIS) and methods, averaged over the overlapping period from 2002/2003 to 2010/2011 (November to March). Cloud-cover corrections have been applied to the MODIS data where CC denotes the values after coverage correction and SFR denotes the values after the spatial feature reconstruction (compare Section 2.6). All values are calculated within the predefined polynya mask (Figure 1).
| | SSM/I-SSMIS 70PT (10 km) | SSM/I-SSMIS PSSM (10 km ) | AMSR-E70PT (10 km) | AMSR-EPSSM (10 km) | MODISCC (10 km) | MODISSFR (10 km) |
|---|
| November | 50.5 | 39.3 | 38.5 | 39.1 | 39.3 | 42.8 |
| December | 25.6 | 21.6 | 20.5 | 22.5 | 29.0 | 30.8 |
| January | 12.9 | 15.6 | 13.5 | 15.3 | 26.9 | 28.1 |
| February | 11.4 | 12.6 | 10.8 | 13.5 | 21.8 | 22.5 |
| March | 10.0 | 12.2 | 10.5 | 12.1 | 19.9 | 20.3 |
| Mean | 22.1 | 20.3 | 18.8 | 20.5 | 27.4 | 28.9 |
| SD | 17.0 | 11.3 | 11.8 | 11.2 | 7.6 | 8.8 |
3.3. Thin-Ice Thickness Distribution and Thermodynamic Ice Production for 2002/2003 to 2014/2015
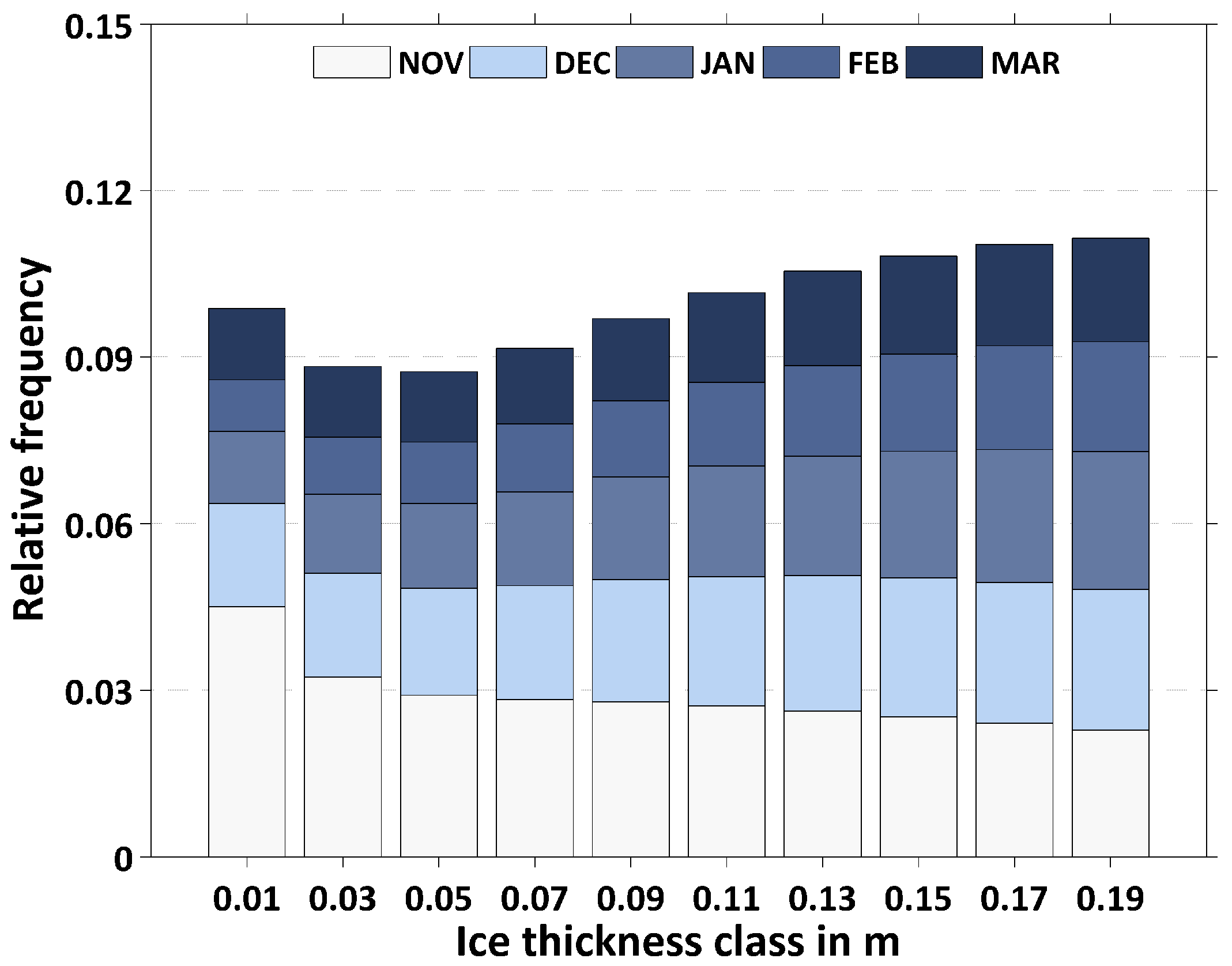
Figure 8 shows a histogram of the total wintertime relative TIT distribution for ice thicknesses below 0.2 m, based on median daily composites. Colors indicate monthly differences. Between November and March, ice thinner than 0.04 m contributes around 9 to 10% to the total polynya area in an average winter season, with the largest proportion being present in November during freeze-up. Thicker ice classes (>0.1 m) show higher contributions of around 10 to 11% in total, therefore covering more than half of the entire NOW polynya predominately from January to March. Concerning the thin-ice thickness distribution in the NOW-polynya region, there is only sparse information available in recent literature. As Ingram
et al. [
5] states, an improved characterization of the ice-thickness distribution is one of the main aspects that needs to be further investigated in the NOW region to get more viable information about the magnitude of heat exchange between ocean and atmosphere. Nevertheless, some information on sea ice types and associated ice thicknesses in the North Water region can be found in an older study by Steffen [
47]. This study had the purpose of investigating the general ice conditions in the winters of 1978/1979 and 1980/1981 by means of an aerial survey performing radiometric temperature measurements of the sea surface. From these measurements, distinct ice types were classified, and their proportion to the sea ice cover was derived. According to Steffen [
47], more than 50% of the NOW polynya (in his study called “Smith Sound polynya”) was covered by young ice (0.1 m to 0.3 m), nilas (0 m to 0.1 m) and open water in the months November to January. This is roughly in accordance to the estimated relative TIT frequencies (TIT ≤ 0.2 m) for November to December derived in this study, where values up to 65% are visible south of Smith Sound. Steffen [
47] also states that in February and March, more white ice (>0.3 m) was present during their flight campaigns. This fits the conclusion made earlier that there is less polynya activity in the NOW region towards the end of the freezing season (
Figure 4 and
Figure 5). While there is no direct comparison available for the TIT distribution shown in
Figure 8, the study of Steffen [
47] also gives an indication that the derived proportion of very thin ice is not far off from his observations (see his
Table 3; categories “ice-free” and “dark nilas” combined), despite a possible bias in this thickness class due to inherent cloud and sea smoke effects [
36].
Figure 8.
Histogram of the relative thin-ice thickness (TIT) distribution in the NOW polynya, with ice-thickness classes of the 2-cm range (x axis). Input data are based on daily TIT composites covering the complete freezing season from November to March. The bars indicate the relative distribution of each thickness class from the total number of TIT ≤ 0.2-m appearances between the winter seasons 2002/2003 and 2014/2015. Contributions of each month with respect to the whole winter season for each thickness class are indicated by the blueish colors (see the legend).
Figure 8.
Histogram of the relative thin-ice thickness (TIT) distribution in the NOW polynya, with ice-thickness classes of the 2-cm range (x axis). Input data are based on daily TIT composites covering the complete freezing season from November to March. The bars indicate the relative distribution of each thickness class from the total number of TIT ≤ 0.2-m appearances between the winter seasons 2002/2003 and 2014/2015. Contributions of each month with respect to the whole winter season for each thickness class are indicated by the blueish colors (see the legend).
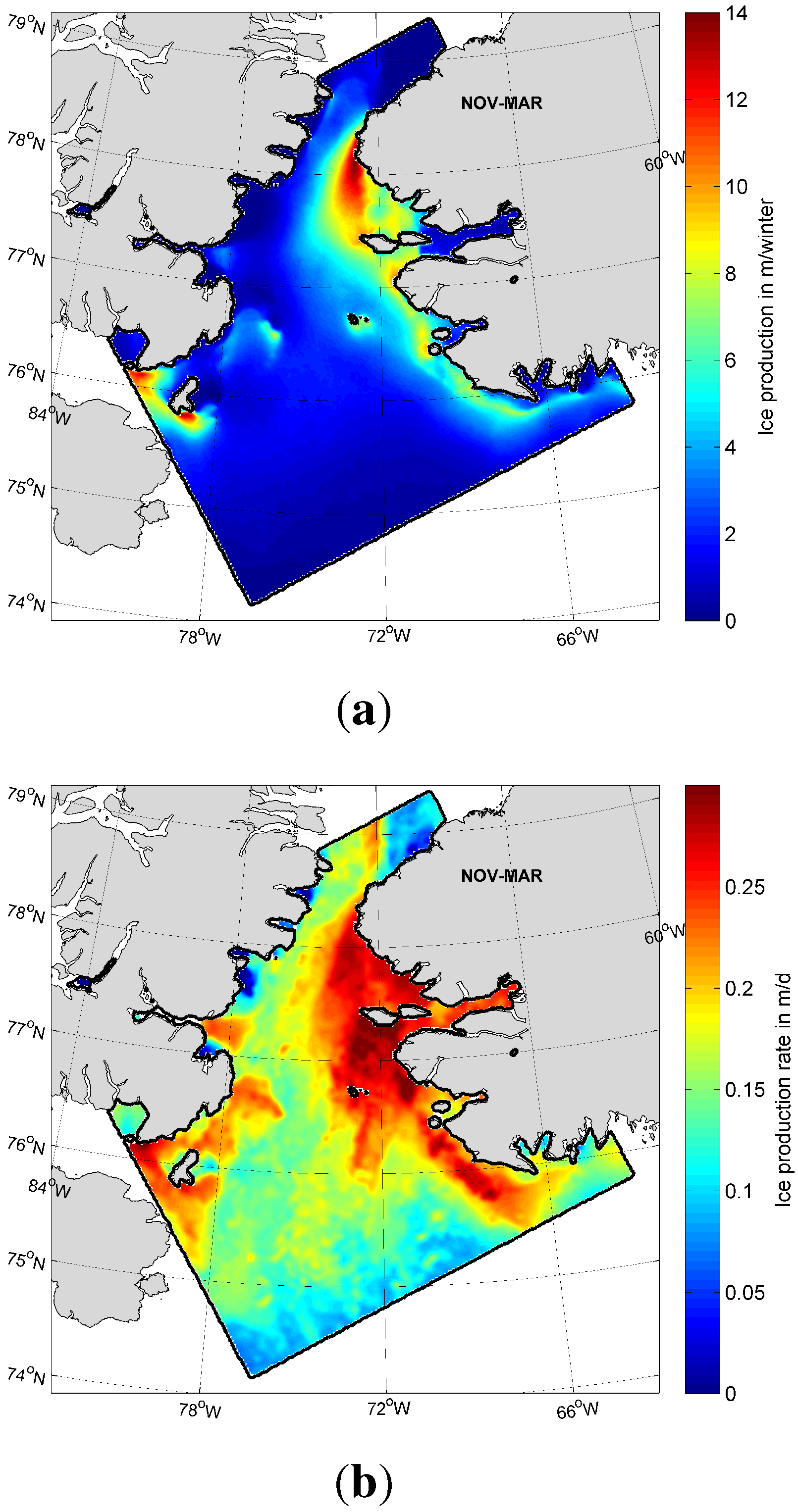
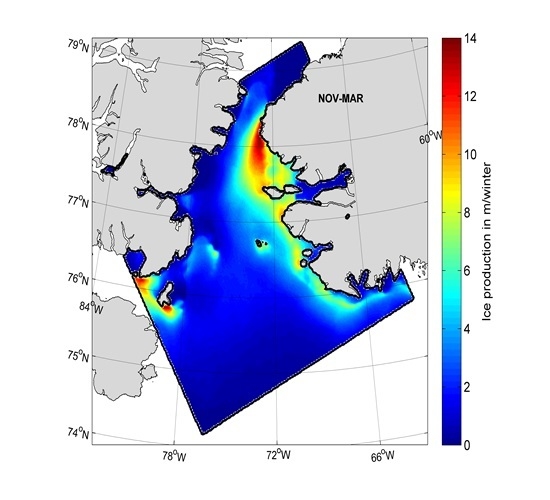
Based on the calculated thin-ice distributions, daily averaged net surface heat loss and associated ice production (rates) are pixel-wise calculated. Spatial overviews of interannual (2002/2003 to 2014/2015) average wintertime ice production (in m·winter
) and the daily maximum ice production rates (in m·d
) are shown in
Figure 9 with the purpose of locating regional differences and typical spatial patterns. The highest values of accumulated ice production (up to 13 to 14 m·winter
;
Figure 9a) occur directly south of the Greenland side of Smith Sound (lee-side) and slightly lower values (around 5 to 8 m·winter
) in proximity of the West Greenland coast. These values compare well to Iwamoto
et al. [
21], who state a maximum rate of 13 m·winter
and are therefore lower than the 19 m·winter
stated by Tamura and Ohshima [
20]. Maximum daily rates at these locations can exceed 20 to 25 cm per day, in certain areas even reaching values as high as 30 cm per day (e.g., south of Northumberland Island at approximately 77
N, 72
W;
Figure 9b). It has to be noted that the typical location of the ice bridge at Smith Sound (see the following
Section 3.3) is well visible and recognizable by its characteristic arch-like shape. However, the main location for high ice formation rates is found at the eastern exit of Smith Sound, indicating the importance of the gap flow dynamics for the polynya formation in that area [
48]. Other prominent features are large areas of high ice production between Ellesmere Island and Devon Island in the west of the polynya domain near Coburg Island. While potentially belonging to individual smaller polynya systems (as implied by Barber and Massom [
1]), these areas are included in our NOW polynya estimates.
Figure 9.
Spatial distribution of (a) the average accumulated ice production (IP, in m·winter) rate, as well as (b) the maximum daily ice production rate (in m·d) in the North Water Polynya for winter seasons (November to March) 2002/2003 to 2014/2015.
Figure 9.
Spatial distribution of (a) the average accumulated ice production (IP, in m·winter) rate, as well as (b) the maximum daily ice production rate (in m·d) in the North Water Polynya for winter seasons (November to March) 2002/2003 to 2014/2015.
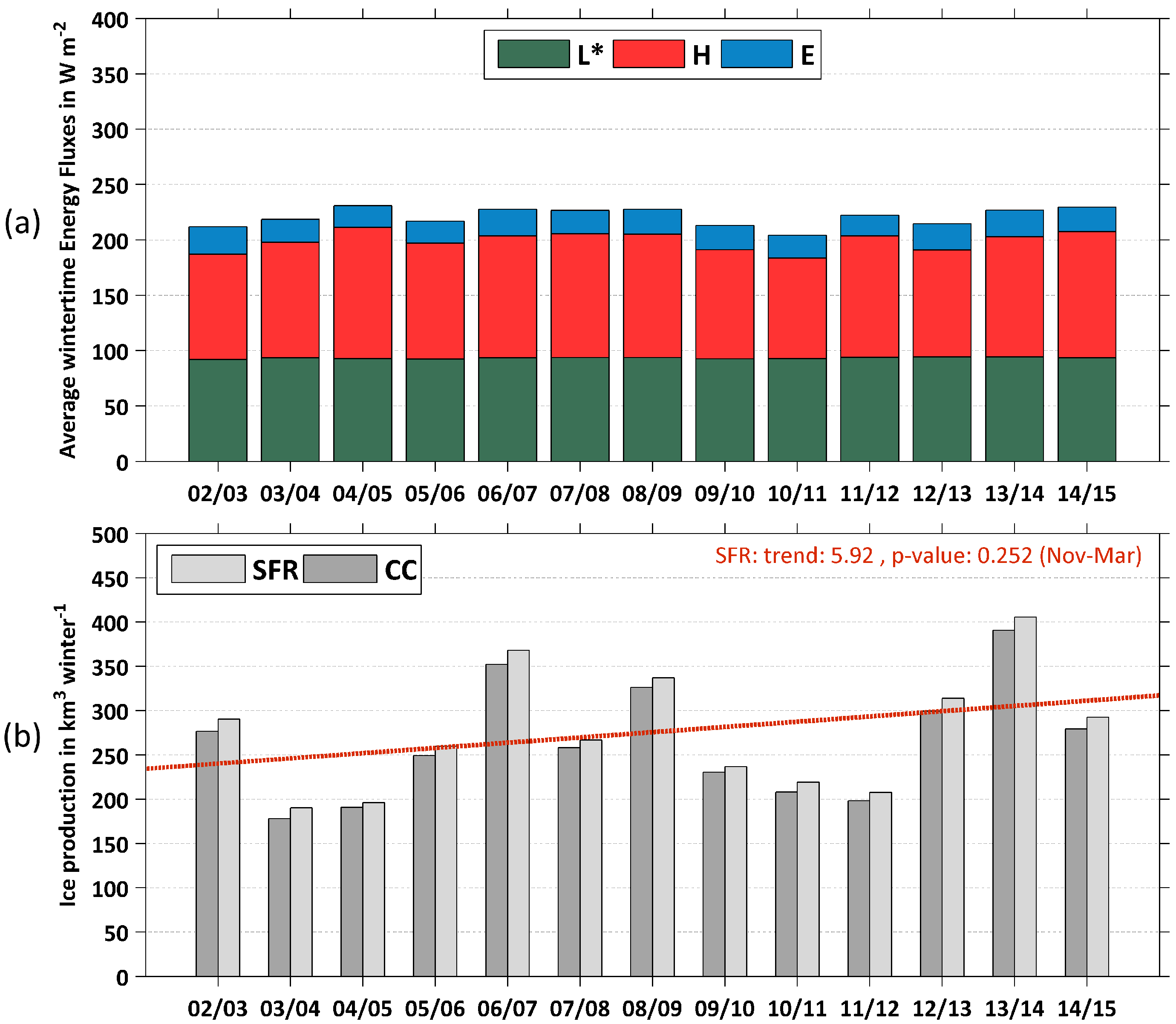
In
Figure 10a,b, average wintertime energy fluxes from the heat flux calculations are shown together with the total accumulated ice production (CC/SFR) per winter season from November to March. A detailed overview on ice production and polynya area (CC/SFR) for each winter season is additionally given in
Table 4. Overall, the average fluxes from both net long-wave radiation and latent heat show almost no interannual variability by ranging around 95 W·m
and 25 W·m
, respectively. The net energy balance during wintertime is therefore strongly controlled by the contribution of the sensible heat flux. In the NOW region, average values for H are ranging between 91 W·m
(2010/2011) and 119 W·m
(2004/2005). Concerning wintertime ice production in the NOW polynya, results from the two correction schemes (CC/SFR) are overall differing by approximately 4%. The average
value amounts to 275.7 ± 67.4 km
(CC: 264.4 ± 65.1 km
). We note a high interannual variability of ice production, with values as low as 190.2 km
(SFR; CC −6.9 %) in 2003/2004 and up to 405.7 km
(SFR; CC
%) in 2013/2014. Large increases in IP occur from winter 2005/2006 to 2006/2007 (SFR: +108 km
) and again from winter 2011/2012 to 2012/2013 (SFR: +106 km
). Regardless of the applied cloud-cover correction, a non-significant positive trend of 5.9 km
·yr
can be observed over the examined 13 winters’ record. The high ice production in 2013/2014 can be partly explained by continuously high frequencies of TIT
m and, therefore, several large polynya events in the NOW area throughout the whole winter season from November to March.
Figure 10.
(a) Average wintertime (November to March) energy fluxes of net long-wave radiation (L*), sensible (H) and latent (E) heat (all in W·m) within the applied polynya mask. (b) Annual wintertime accumulated ice production (IP) in the NOW polynya (in km·winter) for 2002/2003 to 2014/2015. Estimations of IP are based on heat flux calculations using the daily derived TIT composites. Special emphasis is given to the effect of an applied cloud-cover correction (CC/SFR). The red dotted line shows a linear trend estimation for .
Figure 10.
(a) Average wintertime (November to March) energy fluxes of net long-wave radiation (L*), sensible (H) and latent (E) heat (all in W·m) within the applied polynya mask. (b) Annual wintertime accumulated ice production (IP) in the NOW polynya (in km·winter) for 2002/2003 to 2014/2015. Estimations of IP are based on heat flux calculations using the daily derived TIT composites. Special emphasis is given to the effect of an applied cloud-cover correction (CC/SFR). The red dotted line shows a linear trend estimation for .
Table 4.
Accumulated ice production in km
per winter and average polynya area (in 10
km
) for each winter season (November to March) from 2002/2003 to 2014/2015 in the North Water Polynya, together with the interannual average (mean) and its standard deviation (SD). Cloud-cover corrections have been applied where CC denotes the values after coverage correction and SFR denotes the values after the spatial feature reconstruction (see the text). All values are derived from daily MODIS TIT composites after application of the predefined polynya mask (
Figure 1).
Table 4.
Accumulated ice production in km per winter and average polynya area (in 10km) for each winter season (November to March) from 2002/2003 to 2014/2015 in the North Water Polynya, together with the interannual average (mean) and its standard deviation (SD). Cloud-cover corrections have been applied where CC denotes the values after coverage correction and SFR denotes the values after the spatial feature reconstruction (see the text). All values are derived from daily MODIS TIT composites after application of the predefined polynya mask (Figure 1).
| | Acc. (km) | Acc. (km) | (10 km) | (10 km) |
|---|
| 2002 to 2003 | 276.6 | 290.3 | 30.2 | 32.1 |
| 2003 to 2004 | 178.0 | 190.2 | 20.0 | 21.7 |
| 2004 to 2005 | 191.0 | 196.2 | 20.1 | 20.8 |
| 2005 to 2006 | 249.2 | 259.8 | 27.3 | 28.8 |
| 2006 to 2007 | 352.2 | 368.2 | 35.6 | 37.6 |
| 2007 to 2008 | 258.2 | 266.6 | 27.9 | 29.1 |
| 2008 to 2009 | 326.2 | 337.1 | 34.8 | 36.5 |
| 2009 to 2010 | 230.5 | 236.7 | 27.2 | 28.3 |
| 2010 to 2011 | 208.1 | 219.1 | 23.5 | 25.4 |
| 2011 to 2012 | 198.3 | 207.8 | 22.2 | 23.8 |
| 2012 to 2013 | 299.4 | 313.9 | 33.8 | 35.6 |
| 2013 to 2014 | 390.6 | 405.7 | 41.7 | 43.7 |
| 2014 to 2015 | 279.1 | 292.6 | 30.1 | 32.0 |
| Mean | 264.4 | 275.7 | 28.8 | 30.4 |
| SD | 65.1 | 67.4 | 6.5 | 6.7 |
Comparative numbers from previous studies in terms of ice production are hard to find for the NOW polynya. There are recent studies by Tamura and Ohshima [
20] (hereafter TO11) and Iwamoto
et al. [
21] (hereafter I14), who both estimated pan-Arctic ice production in polynyas. Their estimated ice production values are based on newly-developed thin-ice algorithms, which use either SSM/I or AMSR-E brightness-temperature data to calculate thin-ice thicknesses. These algorithms are based on empirical approaches, which incorporate either Advanced Very High Resolution Radiometer (AVHRR) or MODIS-calculated reference-thicknesses (TIT). Similar to our study, these estimated ice thicknesses are then combined with heat-flux calculations (NCEP2 [
49]/ERA-Interim reanalysis serving as the atmospheric dataset) to achieve ice production.
For the NOW polynya, TO11 [
20] and I14 [
21] state an average ice production of 353 ± 69 km
(1992/1993 to 2007/2008) and 186 ± 34 km
(2002/2003 to 2010/2011), respectively. The base-period of these studies is extended by four months each winter season compared to our study (November to March), and the applied polynya masks are differing (similar to the comparisons in [
32]), which makes direct comparisons challenging. For the same averaging interval as I14 and based on
, we achieve a 41% higher value of 263 ± 61 km
. We assume that the values derived here are more accurate, as they profit from the enhanced resolution of MODIS. Additionally, they are presumably far less influenced by ambiguities in heat loss calculations by leaving out the months of September, October, April and May. Regarding the large ice production in TO11 [
20], the study of I14 [
21] refers to a “thin-bias”, which is explained by differences in the applied atmospheric reanalysis data (NCEP2
vs. ERA-Interim). Thereby, larger calculated heat loss and thinner TIT are explained by a lower bias in 2-m-air temperature and a higher bias in wind speed when NCEP2 is compared to ERA-Interim in the the Arctic Ocean domain (also evident in Lindsay
et al. [
50]). Part of the difference from I14 is thought to originate from a smaller areal extent of their polynya mask, which excludes the area of high IP at the eastern entrance of Jones Sound (around 76
N, 81
W; compare
Figure 9). We also applied a smaller polynya mask, which excluded the Jones Sound area for earlier investigations on the NOW polynya, which resulted in slightly lower IP (CC) estimates (about 8%). Taking this into consideration, our presented average accumulated IP values would get closer to I14, while still being higher.
Both TO11 and I14 [
20,
21] state that polynyas located around the Canada Basin (including the NOW polynya) show the largest ice production values in the early stage of the freezing period (October to December), which afterwards gradually decrease towards March. This is also revealed in our data and can be explained by more consolidated pack ice in northern Baffin Bay and several fast-ice areas around Ellesmere Island at the end of a freezing season, which limit the west- and south-ward expansion of the NOW polynya.
3.4. Ice Bridge Dynamics in Nares Strait (2002/2003 to 2014/2015)
According to Kwok
et al. [
51], ice bridges typically form at two distinct locations along Nares Strait. A deeper understanding of the involved mechanisms and temporal patterns is of high value, as the movement of sea ice through Nares Strait and, therefore, the export of old multi-year ice from the north of Greenland is strongly controlled by the timing and location of ice bridge formation.
In the context of the present study, the most prominent location is certainly Smith Sound at the southern exit of the channel, as it usually is associated with the formation of the NOW polynya (e.g., [
5,
8]). According to Barber
et al. [
8], the timing of wintertime ice bridge formation at Smith Sound is quite variable by occurring sometime between November and March. Barber
et al. [
8] analyze time series of SIC north and south of the typical ice bridge location to infer characteristic development stages in the course of a year. While a similar analysis using our data worked reasonably well for the southern ice bridge at Smith Sound, we were not able to apply this analysis to the northern ice bridge locations at Robeson Channel (compare
Figure 1), presumably due to the coarse resolution of the passive microwave data.
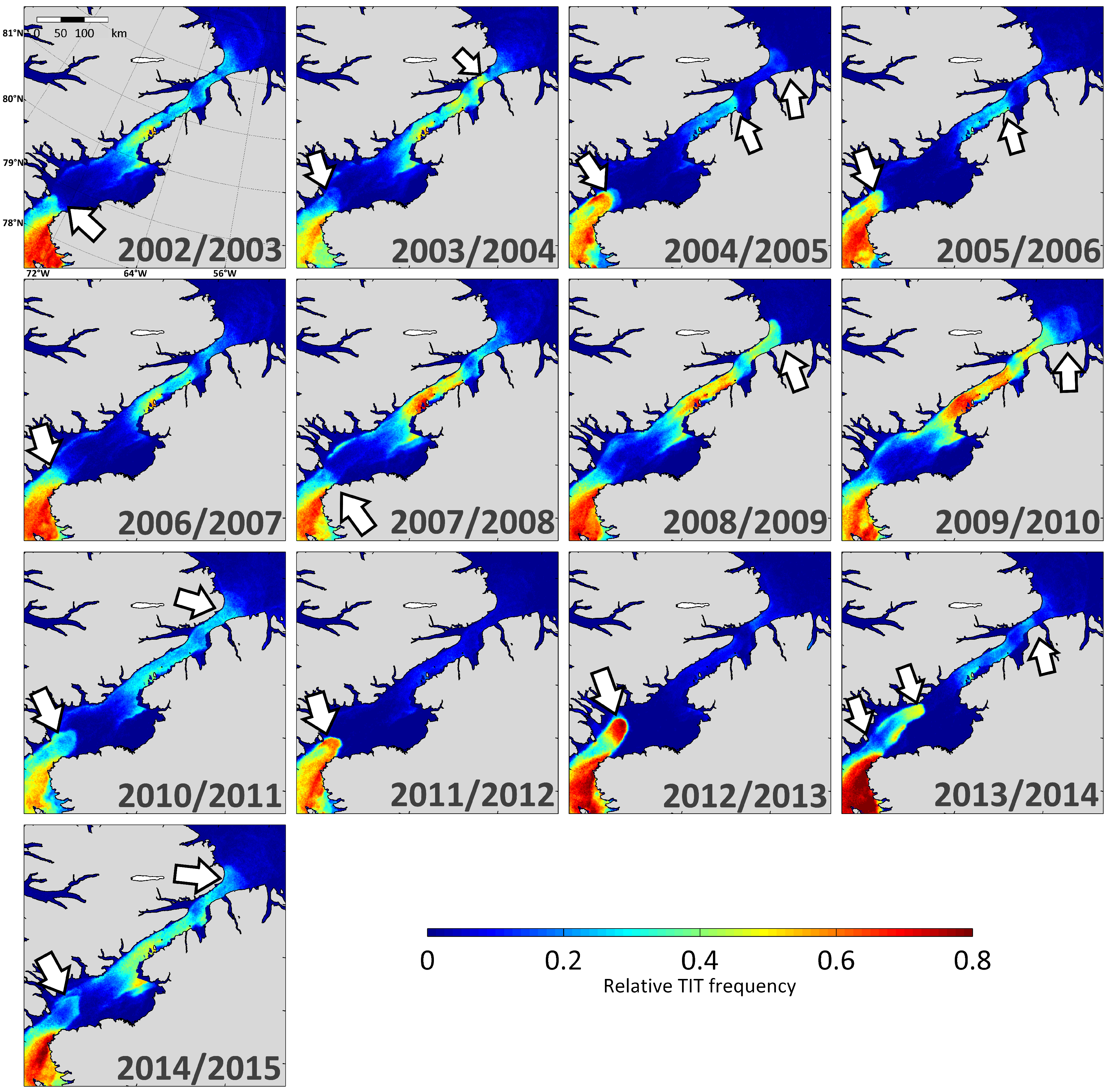
As an alternative approach we decided to take a closer look at the annual (November to March; 151/152 days in total) relative occurrences of MODIS TIT ≤ 0.2 m, in order to relate typical thin-ice locations to nearby ice bridge patterns. The spatial overviews for the winter seasons 2002/2003 to 2014/2015 are presented in
Figure 11. The observed locations of an arch-type pattern during each winter season are marked with a white arrow. The southern ice bridge at Smith Sound is present in every winter season, except the period from 2008/2009 to 2009/2010. Contrary to Kwok
et al. [
51], who also had a closer look at the behavior of the ice bridges in Nares Strait, we cannot confirm the absence of the southern ice bridge in 2006/2007, which was stated as the main reason for a sea ice export anomaly through Nares Strait in 2007. It was assumed that the movement of sea ice was not suppressed by any kind of blocking features both at Smith Sound in the south and Robeson Channel roughly 450 km further north. While the latter is also observable in our study (high TIT frequencies in the northerly part of Nares Strait), an arch-type TIT pattern at the southern end of Nares Strait was present during the whole winter season from November to March, although its location is very variable. In addition, daily TIT maps reveal several events where large patches of ice broke off at Smith Sound and drifting further south, thereby still indicating a less stable ice bridge and enhanced sea ice export at the Canadian side of the channel.
Figure 11.
Relative frequency distribution of thin-ice thickness ≤ 0.2 m in northern Baffin Bay/Smith Sound, Nares Strait and Lincoln Sea for the complete freezing seasons (November to March) 2002/2003 to 2014/2015, based on daily TIT composites. Observed sites of ice bridge appearances between November and March are indicated by white arrows.
Figure 11.
Relative frequency distribution of thin-ice thickness ≤ 0.2 m in northern Baffin Bay/Smith Sound, Nares Strait and Lincoln Sea for the complete freezing seasons (November to March) 2002/2003 to 2014/2015, based on daily TIT composites. Observed sites of ice bridge appearances between November and March are indicated by white arrows.
Barber
et al. [
8] stated that the formation of an ice bridge at Smith Sound seemed to be less regular in the 1990s compared to the 1980s, with a tendency to form later and break up earlier. As we only regard the case of ice bridge formation during winter, we cannot comment on the timing of ice bridge break-up for the 2000s and ongoing. Regarding the later appearing ice bridge formation, we noted a large monthly variability of TIT frequencies in Nares Strait over the last 13 winter seasons, but no sign of a temporal shift.
Using SAR (Synthetic Aperture Radar) satellite imagery from RADARSAT, Kwok
et al. [
51] estimated the average timing of ice bridge formation at Smith Sound to be around 2 February (±44 d), blocking the ice movement in Nares Strait on average for 184 ± 10 d until the summer melt period. Based on monthly TIT frequency distributions (2002/2003 to 2014/2015; not shown), we can confirm that the most regular ice bridge development starts from February onwards. In addition, more than half of the winters between 2002/2003 and 2014/2015 already feature an ice bridge in November and December.
Unfortunately, we are not able to directly relate the ice bridge formation in Nares Strait to the development of the NOW polynya during winter. Years with high wintertime POLA and IP do not necessarily coincide with long ice bridge periods and vice versa. Hence, we expect that the ice bridge at Smith Sound becomes more important around April to June, when the NOW-polynya starts to expand southward.