Magma Pathways and Their Interactions Inferred from InSAR and Stress Modeling at Nyamulagira Volcano, D.R. Congo
Abstract
:1. Introduction

2. Background
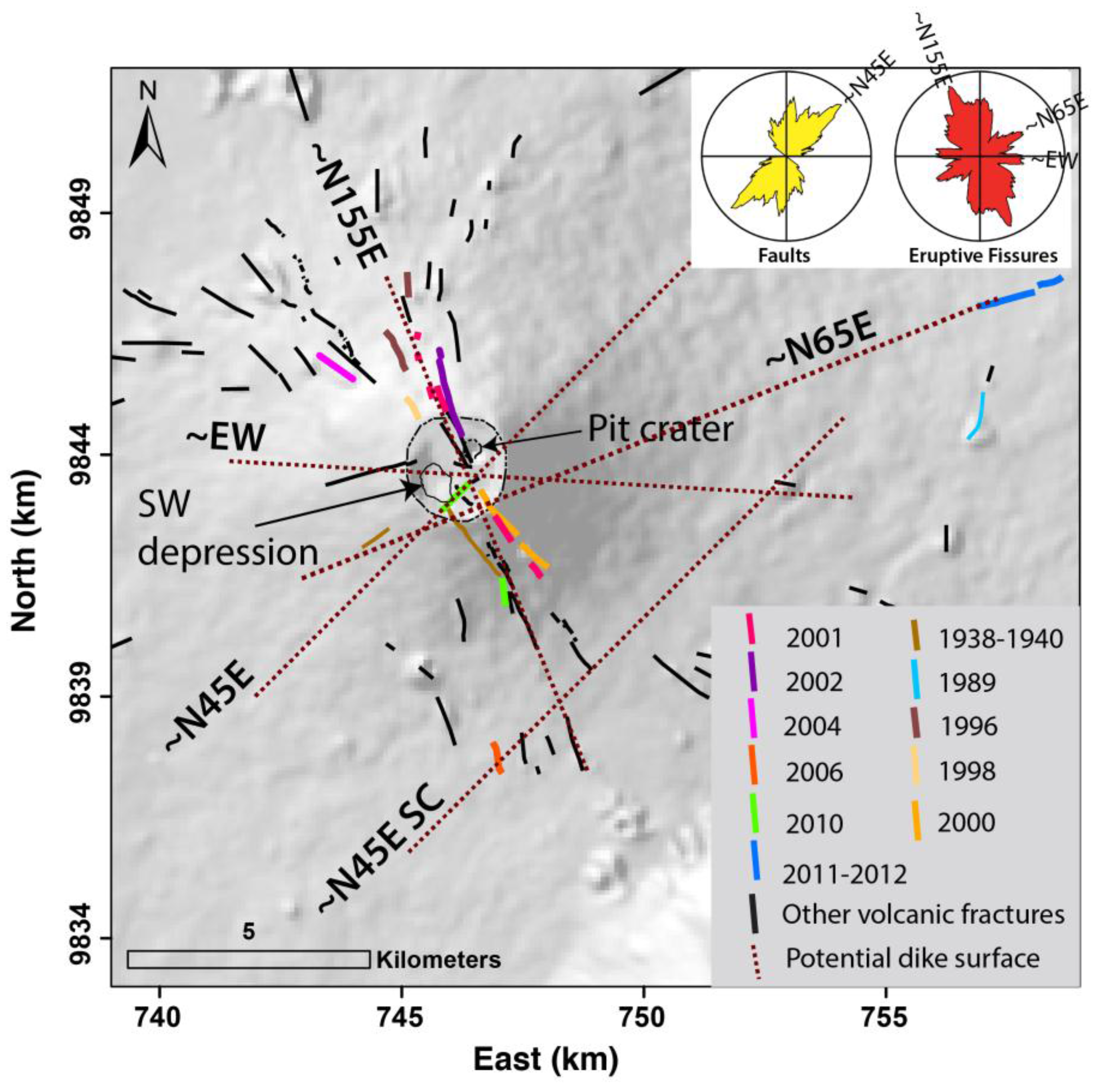
2.1. Geologic Setting
2.2. Characteristics of Recent Eruptions
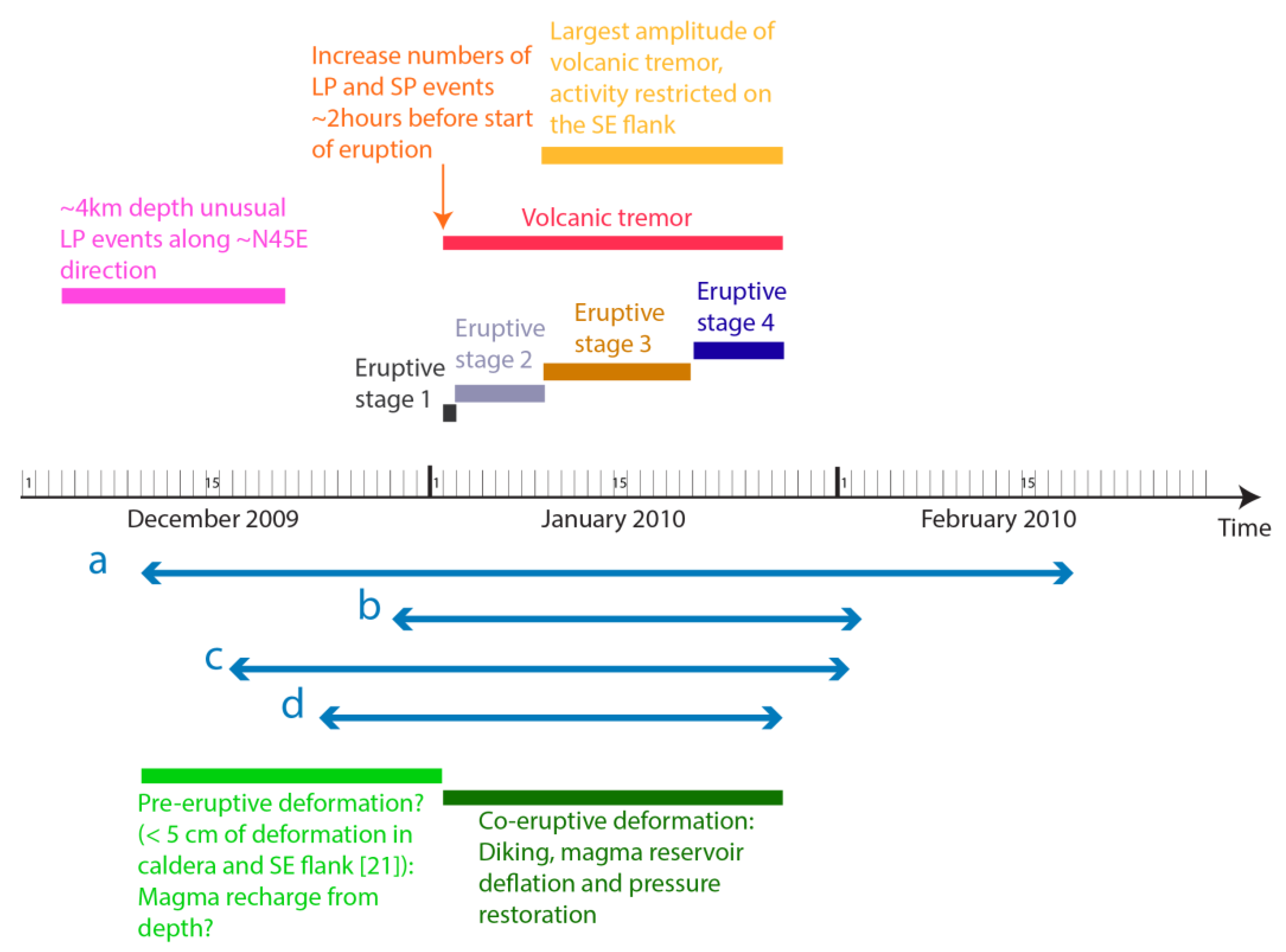
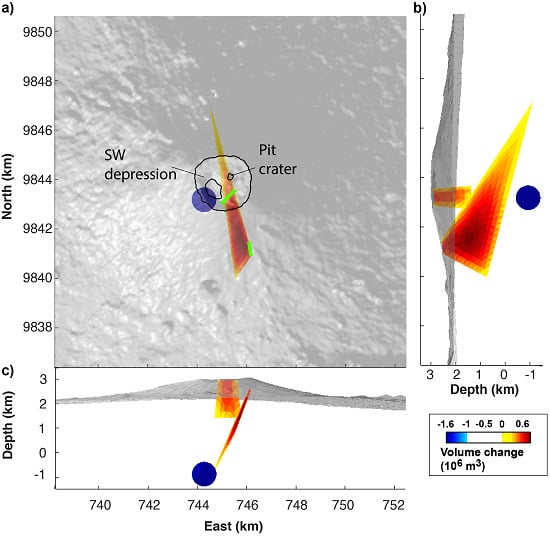
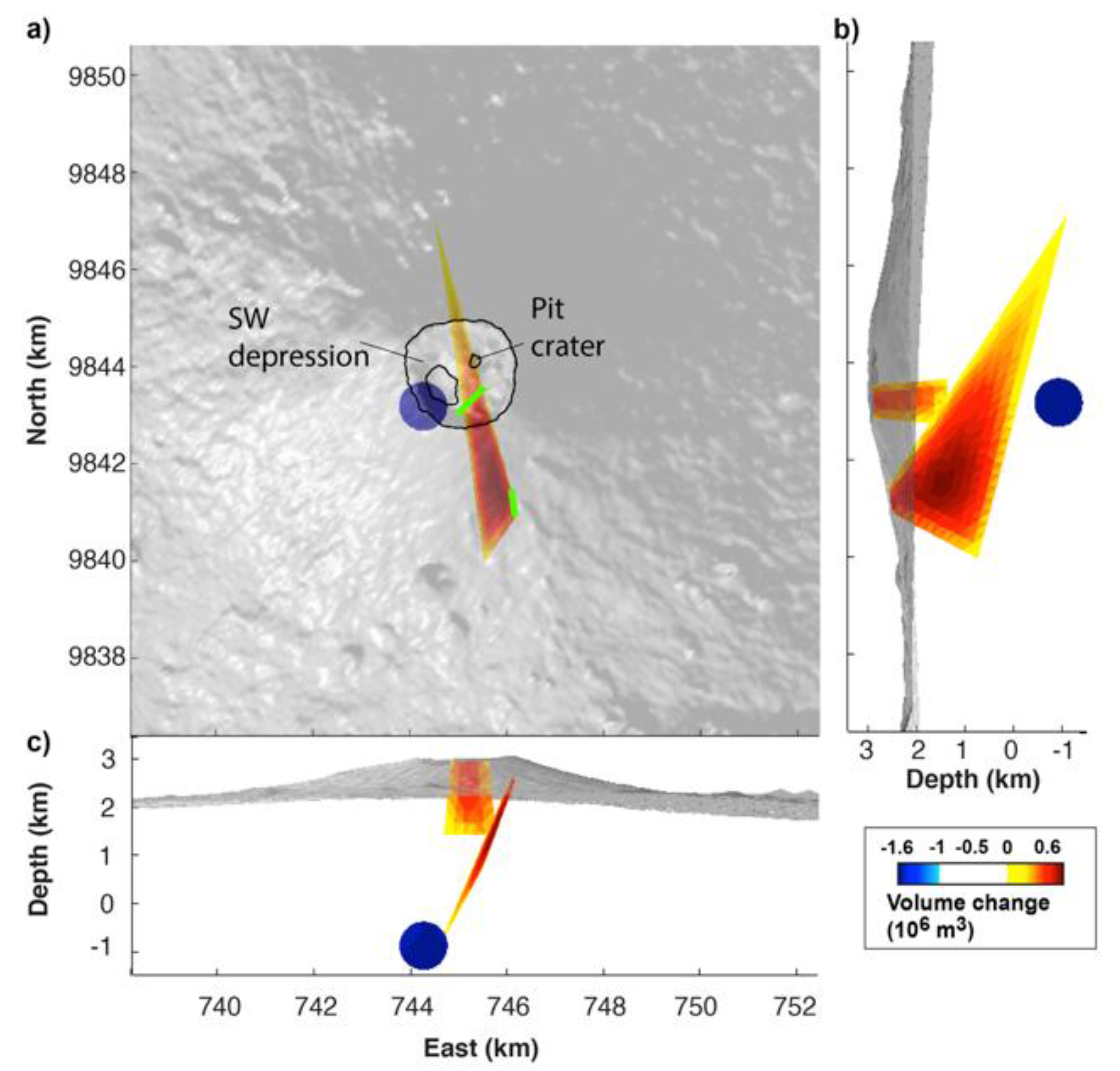
2.3. The January 2010 Eruption
3. Methods
3.1. InSAR Processing
3.2. Boundary Elements Modeling and Non-Linear Inversions
4. Numerical 3D Modeling Results
| Model | Explained Deformation (%) | RMS Error (cm) | AIC |
|---|---|---|---|
| 1 dike | 68 | 2.5 | 702 |
| 2 dikes | 71 | 2.5 | 746 |
| 2 dikes + quadrangular connection | 60 | 2.5 | 1216 |
| 1 dike + circular sill | 83 | 1.9 | 295 |
| 1 dike + rectangular sill | 82 | 2 | 374 |
| 1 dike + spherical reservoir | 86 | 1.7 | 295 |
| 2 dikes + circular sill | 87 | 1.6 | 65 |
| 2 dikes + rectangular sill | 87 | 1.6 | 96 |
| 2 dikes + spherical reservoir* | 90 | 1.5 | 29 |
| 2 dikes + laccolith | 86 | 1.7 | 164 |
| Parameter | Dike Connected to the Caldera Fissure | Dike Connected to Southern Flank Fissure | Reservoir |
|---|---|---|---|
| Static pressure change (MPa) | 1.4 [1, 1.6] | 1.4 [1, 1.6] | −26 [−26, −17] |
| Elevation of the base (middle point) for dikes or center of the reservoir (m a.s.l.) | 1400 [1236, 2314] | −150 [−620, 486] | −890 [−1462, −181] |
| Dip angle (°) | 90 * | 106 [88, 120] | - |
| Angle between the line connecting the top and base middle points and the dipping direction (°) | 0 * | 42 [0.5, 43] | - |
| Length of the base scaled to that of the top | 1.4 [1.3, 1.7] | 13 [10, 13] | - |
| Vertical angle of the base (°) | 0 * | −14 [−33, −6] | - |
| Horizontal position of the reservoir (km) | - | - | 744.2 [744.1, 744.5]; 9843.2 [98430, 9843] |
| Radius of the reservoir (m) | - | - | 500 ** |
5. Discussion
5.1. Sources of Deformation
5.2. Magma Reservoir Size
5.3. Magma Budget
| T (°C) | P (MPa) | SiO2 | TiO2 | Al2O3 | Fe2O3 | FeO | MnO | MgO | CaO | Na2O | K2O | H2O (wt%) | CO2 (wt%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1200 | 87.5 | 45 | 3.5 | 15 | 13.1 | 12 | 0.2 | 4.5 | 11,5 | 3 | 2.2 | 1.25 | 0.1 |
5.4. Stress Analysis
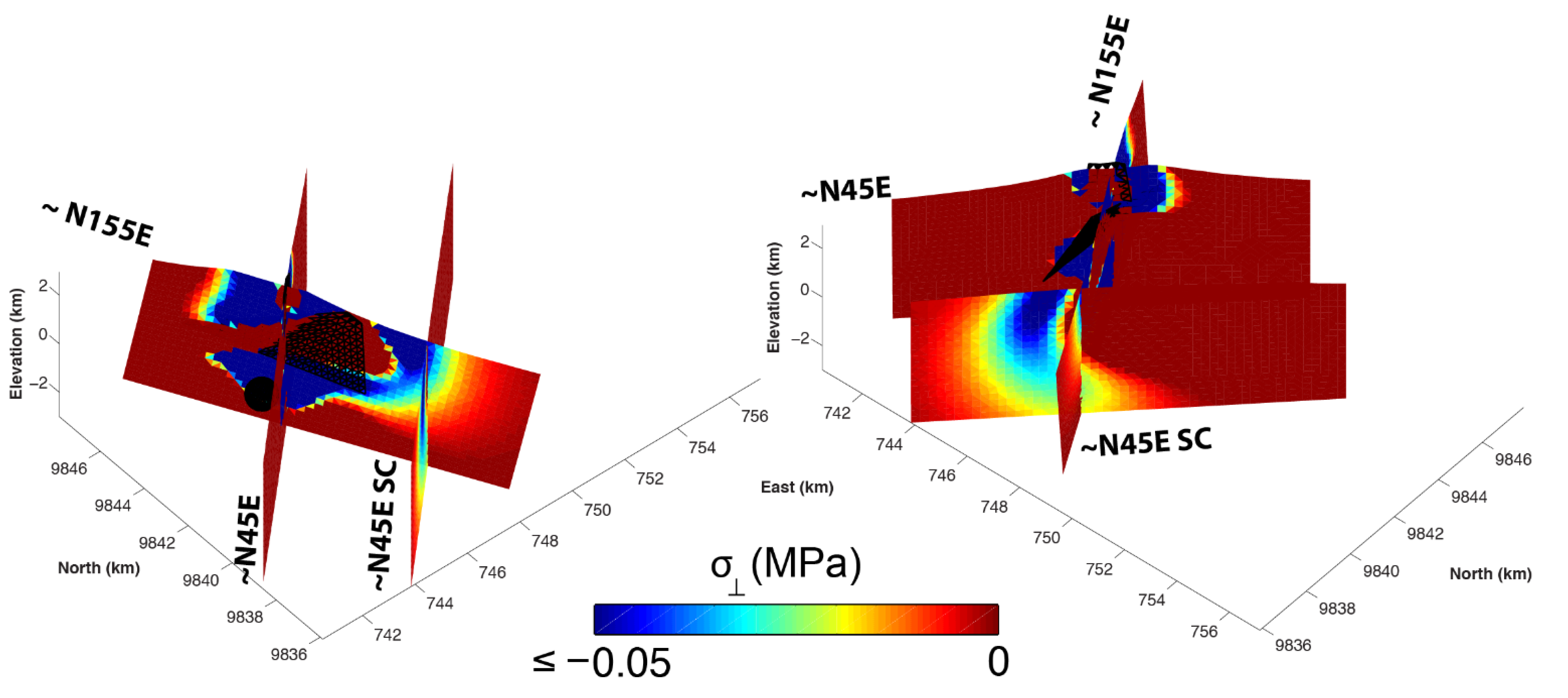
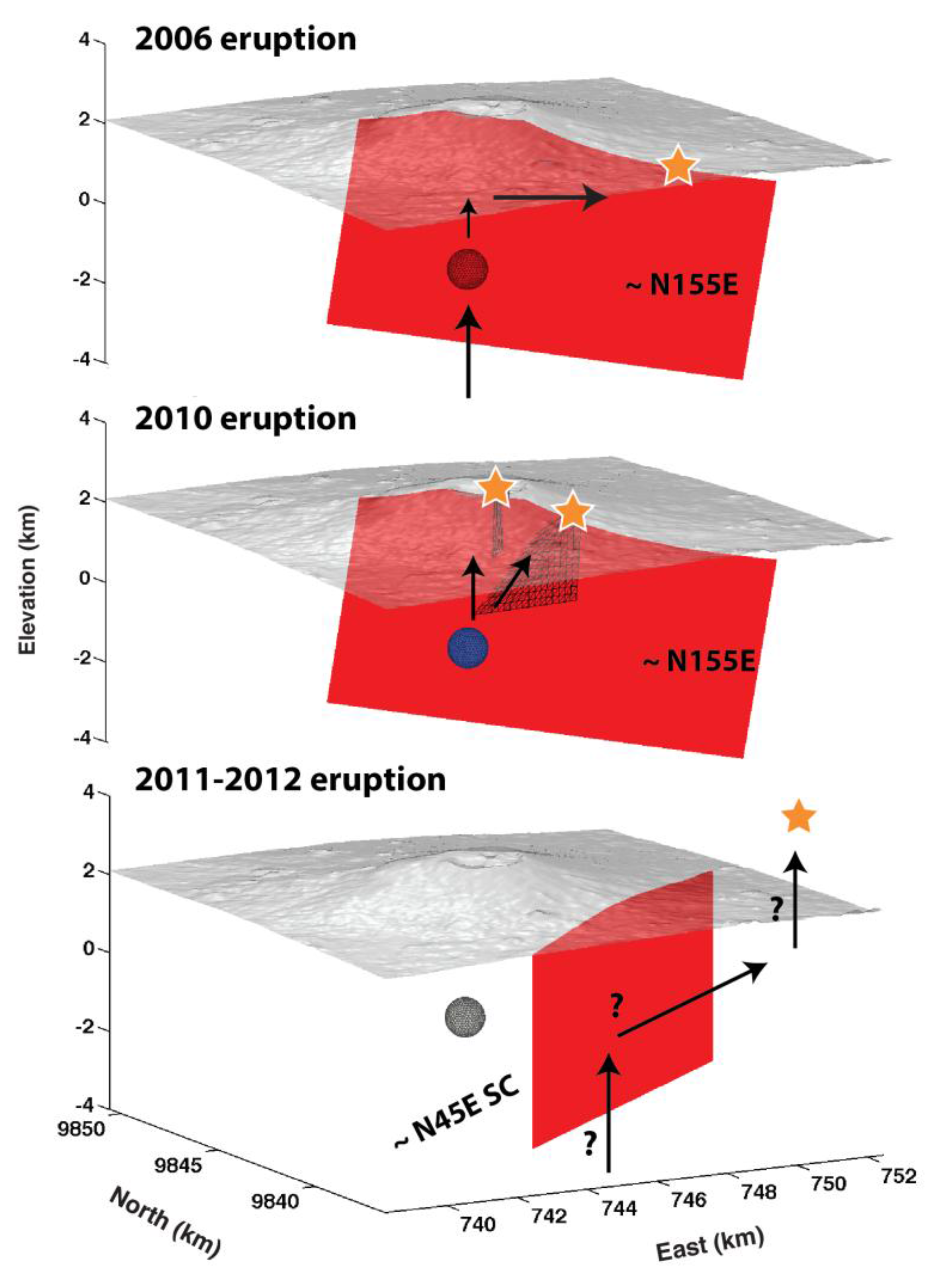
5.5. Influence of the Crustal Extension
5.6. Magma Storage and Transport
6. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A: Ratio of Emitted over Reservoir Volume Change, Taking Lava Erupted at the Surface into Account
References
- Nakamura, K.; Jacob, K.H.; Davies, J.N. Volcanoes as possible indicators of tectonic stress orientation—Aleutians and Alaska. Pure Appl. Geophys. 1977, 115, 87–112. [Google Scholar] [CrossRef]
- Chadwick, W.W.; Dieterich, J.H. Mechanical modeling of circumferential and radial dike intrusion on Galapagos volcanoes. J. Volcanol. Geotherm. Res. 1995, 66, 37–52. [Google Scholar] [CrossRef]
- Chestler, S.R.; Grosfils, E.B. Using numerical modeling to explore the origin of intrusion patterns on Fernandina Volcano, Galapagos Islands, Ecuador. Geophys. Res. Lett. 2013, 40, 4565–4569. [Google Scholar] [CrossRef]
- Bagnardi, M.; Amelung, F.; Poland, M.P. A new model for the growth of basaltic shields based on deformation of Fernandina volcano, Galápagos Islands. Earth Planet. Sci. Lett. 2013, 377–378, 358–366. [Google Scholar] [CrossRef]
- Klein, F.W.; Koyanagi, R.Y.; Nakata, J.S.; Tanigawa, W.R. The seismicity of Kilauea’s magma system. Volcan. Hawaii 1987, 1350, 1019–1185. [Google Scholar]
- Peltier, A.; Bachèlery, P.; Staudacher, T. Magma transport and storage at Piton de La Fournaise (La Réunion) between 1972 and 2007: A review of geophysical and geochemical data. J. Volcanol. Geotherm. Res. 2009, 184, 93–108. [Google Scholar] [CrossRef]
- Smets, B.; Wauthier, C.; d’Oreye, N. A new map of the lava flow field of Nyamulagira (D.R. Congo) from satellite imagery. J. Afr. Earth Sci. 2010, 58, 778–786. [Google Scholar] [CrossRef]
- Wadge, G.; Burt, L. Stress field control of eruption dynamics at a rift volcano: Nyamuragira, D.R.Congo. J. Volcanol. Geotherm. Res. 2011, 207, 1–15. [Google Scholar] [CrossRef]
- Smets, B.; Kervyn, M.; d’Oreye, N.; Kervyn, F. Spatio-temporal dynamics of eruptions in a youthful extensional setting: Insights from Nyamulagira Volcano (D.R. Congo), in the western branch of the East African Rift. Earth-Sci. Rev. 2015, 150, 305–328. [Google Scholar] [CrossRef]
- Smets, B.; d’Oreye, N.; Kervyn, F.; Kervyn, M.; Albino, F.; Arellano, S.R.; Bagalwa, M.; Balagizi, C.; Carn, S.A.; Darrah, T.H.; et al. Detailed multidisciplinary monitoring reveals pre- and co-eruptive signals at Nyamulagira volcano (North Kivu, Democratic Republic of Congo). Bull. Volcanol. 2014, 76, 1–35. [Google Scholar] [CrossRef]
- Stamps, D.S.; Calais, E.; Saria, E.; Hartnady, C.; Nocquet, J.-M.; Ebinger, C.J.; Fernandes, R.M. A kinematic model for the East African Rift. Geophys. Res. Lett. 2008, 35, L05304. [Google Scholar] [CrossRef]
- Saria, E.; Calais, E.; Stamps, D.S.; Delvaux, D.; Hartnady, C.J.H. Present-day kinematics of the East African Rift. J. Geophys. Res. Solid Earth 2014, 119, 1–17. [Google Scholar] [CrossRef]
- Smets, B.; Delvaux, D.; Ross, K.A.; Poppe, S.; Kervyn, M.; d’Oreye, N.; Kervyn, F. The role of inherited crustal structures and magmatism in the development of rift segments: Insights from the Kivu basin, western branch of the East African Rift. Tectonophysics 2015. submitted. [Google Scholar]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Ebinger, C.J. Tectonic development of the western branch of the East African rift system. GSA Bull. 1989, 101, 885–903. [Google Scholar] [CrossRef]
- Ebinger, C.J. Geometric and kinematic development of border faults and accommodation zones, Kivu-Rusizi rift, Africa. Tectonics 1989, 8, 117–133. [Google Scholar] [CrossRef]
- Ebinger, C.; Furman, T. Geodynamical setting of the virunga volcanic province, East Africa. Acta Vulcanol. 2002, 14, 1–8. [Google Scholar]
- Corti, G.; Bonini, M.; Innocenti, F.; Manetti, P.; Piccardo, G.B.; Ranalli, G. Experimental models of extension of continental lithosphere weakened by percolation of asthenospheric melts. J. Geodyn. 2007, 43, 465–483. [Google Scholar] [CrossRef]
- Pouclet, A. Volcanologie du Rift de L’afrique Centrale, le Nyamuragira Dans les Virunga, Essaie de Magmatologie du Rift. Ph.D. Thesis, University of Paris-Sud., Orsay, France, 1976. [Google Scholar]
- Wauthier, C.; Cayol, V.; Poland, M.; Kervyn, F.; d’Oreye, N.; Hooper, A.; Samsonov, S.; Tiampo, K.; Smets, B. Nyamulagira’s magma plumbing system inferred from 15 years of InSAR. Geol. Soc. Lond. Spec. Publ. 2013, 380, 39–65. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar]
- D’Oreye, N.; Gonzalez, P.J.; Shuler, A.; Oth, A.; Bagalwa, L.; Ekstrom, G.; Kavotha, D.; Kervyn, F.; Lucas, C.; Lukaya, F.; et al. Source parameters of the 2008 Bukavu-Cyangugu earthquake estimated from InSAR and teleseismic data. Geophys. J. Int. 2011, 184, 934–948. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Peltzer, G.; Simons, M. Updated repeat orbit interferometry package released. Eos Trans. Am. Geophys. Union 2004, 85, 47. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–43. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the.the epicentral area of the 1999 M_W7. 1 Hector Mine Earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Wright, T.J. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Cayol, V.; Cornet, F.H. 3D mixed boundary elements for elastostatic deformation field analysis. Int. J. Rock Mech. Min. 1997, 34, 275–287. [Google Scholar] [CrossRef]
- Fukushima, Y. Finding realistic dike models from interferometric synthetic aperture radar data: The February 2000 eruption at Piton de la Fournaise. J. Geophys. Res. 2005, 110, B03206. [Google Scholar] [CrossRef]
- Wauthier, C.; Cayol, V.; Kervyn, F.; d’Oreye, N. Magma sources involved in the 2002 Nyiragongo eruption, as inferred from an InSAR analysis. J. Geophys. Res. 2012, 117, B05411. [Google Scholar] [CrossRef]
- Grosfils, E.B. Magma reservoir failure on the terrestrial planets; Assessing the importance of gravitational loading in simple elastic models. J. Volcanol. Geotherm. Res. 2007, 166, 47–75. [Google Scholar] [CrossRef]
- Gerbault, M.; Cappa, F.; Hassani, R. Elasto-plastic and hydromechanical models of failure around an infinitely long magma chamber. Geochem. Geophys. Geosyst. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Cayol, V. Analyse Élastostatique Tridimensionnelle du Champs de Déformations des Édifices Volcaniques Par Éléments Frontières Mixtes; Université de Paris VII: Paris, France, 1996. [Google Scholar]
- Sambridge, M. Geophysical inversion with a neighbourhood algorithm—I. Searching a parameter space. Geophys. J. Int. 1999, 138, 479–494. [Google Scholar] [CrossRef]
- Fukushima, Y. Transferts de Magma au Volcan du Piton de la Fournaise Determines par la Modelisation 3d de Donnees D’interferometrie Radar Entre 1998 et 2000; Universite Blaise-Pascal: Aubière, France, 2006. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- O’Brien, G.S.; Lokmer, I.; Bean, C.J. Statistical selection of the “best” seismic source mechanisms from inversions of synthetic volcanic long-period events. J. Geophys. Res. Solid Earth 2010, 115, 1–13. [Google Scholar] [CrossRef]
- Fukushima, Y.; Cayol, V.; Durand, P.; Massonnet, D. Evolution of magma conduits during the 1998–2000 eruptions of Piton de la Fournaise volcano, Réunion Island. J. Geophys. Res. Solid Earth 2010, 115, 1–21. [Google Scholar] [CrossRef]
- Anderson, K.; Segall, P. Bayesian inversion of data from effusive volcanic eruptions using physics-based models: Application to Mount St. Helens 2004–2008. J. Geophys. Res. Solid Earth 2013, 118, 2017–2037. [Google Scholar] [CrossRef]
- Sambridge, M. Geophysical inversion with a neighbourhood algorithm-II. Appraising the ensemble. Geophys. J. Int. 1999, 138, 727–746. [Google Scholar] [CrossRef]
- Rubin, A.M. Dike-induced faulting and graben subsidence in volcanic rift zones. J. Geophys. Res. 1992, 97, 1839. [Google Scholar] [CrossRef]
- Rubin, A.M.; Pollard, D.D. Dike-induced faulting in rift zones of Iceland and Afar. Geology 1988, 16, 413–417. [Google Scholar] [CrossRef]
- Calais, E.; d’Oreye, N.; Albaric, J.; Deschamps, A.; Delvaux, D.; Déverchère, J.; Ebinger, C.; Ferdinand, R.W.; Kervyn, F.; Macheyeki, A.S.; et al. Strain accommodation by slow slip and dyking in a youthful continental rift, East Africa. Nature 2008, 456, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Wright, T.J.; Ebinger, C.; Biggs, J.; Ayele, A.; Yirgu, G.; Keir, D.; Stork, A. Magma-maintained rift segmentation at continental rupture in the 2005 Afar dyking episode. Nature 2006, 442, 291–294. [Google Scholar] [CrossRef] [PubMed]
- Carracedo, J.C.; Guillou, H.; Nomade, S.; Rodriguez-Badiola, E.; Perez-Torrado, F.J.; Rodriguez-Gonzalez, A.; Paris, R.; Troll, V.R.; Wiesmaier, S.; Delcamp, A.; et al. Evolution of ocean-island rifts: The northeast rift zone of Tenerife, Canary Islands. Geol. Soc. Am. Bull. 2010, 123, 562–584. [Google Scholar] [CrossRef]
- Rubin, A.M. Propagation of Magma-Filled Cracks. Annu. Rev. Earth Planet. Sci. 1995, 23, 287–336. [Google Scholar] [CrossRef]
- Delaney, P.; Pollard, D. Deformation of Host Rocks and Flow of Magma during Growth of Minette Dikes and Breccia-Bearing Intrusions near Ship Rock, New Mexico; U.S. Government Publishing Office (USGPO): Washington, DC, USA, 1981; p. 69. [Google Scholar]
- Traversa, P.; Pinel, V.; Grasso, J.R. A constant influx model for dike propagation: Implications for magma reservoir dynamics. J. Geophys. Res. Solid Earth 2010, 115, 1–19. [Google Scholar] [CrossRef]
- Rivalta, E.; Segall, P. Magma compressibility and the missing source for some dike intrusions. Geophys. Res. Lett. 2008, 35, L04306. [Google Scholar] [CrossRef]
- Johnson, D.J. Dynamics of magma storage in the summit reservoir of Kilauea Volcano, Hawaii. J. Geophys. Res. 1992, 97, 1807. [Google Scholar] [CrossRef]
- Johnson, D.J.; Sigmundsson, F.; Delaney, P.T. Comment on “Volume of magma accumulation or withdrawal estimated from surface uplift or subsidence, with application to the 1960 collapse of Kilauea Volcano”. Bull. Volcanol. 2000, 61, 491–493. [Google Scholar] [CrossRef]
- Huppert, H.E.; Woods, A.W. The role of volatiles in magma chamber dynamics. Nature 2002, 420, 493–495. [Google Scholar] [CrossRef] [PubMed]
- Mastin, L.G.; Roeloffs, E.; Beeler, N.M.; Quick, J.E. Constraints on the Size, Overpressure, and Volatile Content of the Mount St. Helens Magma System from Geodetic and Dome-Growth Measurements During the 2004–2006+ Eruption. US Geol. Surv. Prof. Pap. 2008, 1750, 461–488. [Google Scholar]
- Amelung, F.; Day, S. InSAR observations of the 1995 Fogo, Cape Verde, eruption: Implications for the effects of collapse events upon island volcanoes. Geophys. Res. Lett. 2002, 29, 5–8. [Google Scholar] [CrossRef]
- Grosfils, E.B.; McGovern, P.J.; Gregg, P.M.; Galgana, G.A.; Hurwitz, D.M.; Long, S.M.; Chestler, S.R. Elastic models of magma reservoir mechanics: a key tool for investigating planetary volcanism. Geol. Soc. Lond. Spec. Publ. 2013, 401, SP401-2. [Google Scholar] [CrossRef]
- Mishina, M. Gravity survey in and around volcanoes Nyamuragira and Nyiragongo. In Volcanoes Nyiragongo and Nyamuragia: Geophysical Aspects; Tohoku University: Sendai, Japan, 1983; pp. 69–74. [Google Scholar]
- Hickman, S.H.; Healy, J.H.; Zoback, M.D. In situ stress, natural fracture distribution, and borehole elongation in the Auburn Geothermal Well, Auburn, New York. J. Geophys. Res. 1985, 90, 5497. [Google Scholar] [CrossRef]
- Segall, P. Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Nobile, A.; Pagli, C.; Keir, D.; Wright, T.J.; Ayele, A.; Ruch, J.; Acocella, V. Dike-fault interaction during the 2004 Dallol intrusion at the northern edge of the Erta Ale Ridge (Afar, Ethiopia). Geophys. Res. Lett. 2012, 39, 2–7. [Google Scholar] [CrossRef]
- Sparks, R.S.J. The dynamics of bubble formation and growth in magmas: A review and analysis. J. Volcanol. Geotherm. Res. 1978, 3, 1–37. [Google Scholar] [CrossRef]
- Mastin, L.G.; Ghiorso, M.S. A Numerical Program for Steady-State Flow of Magma-Gas Mixtures through Vertical Eruptive Conduits; Department of the Interior: Washington, DC, USA, 2000.
- Newman, S.; Lowenstern, J.B. VolatileCalc: A silicate melt–H2O–CO2 solution model written in Visual Basic for excel. Comput. Geosci. 2002, 28, 597–604. [Google Scholar] [CrossRef]
- Papale, P.; Moretti, R.; Barbato, D. The compositional dependence of the saturation surface of H2O + CO2 fluids in silicate melts. Chem. Geol. 2006, 229, 78–95. [Google Scholar] [CrossRef]
- Head, E.M.; Shaw, A.M.; Wallace, P.J.; Sims, K.W.W.; Carn, S.A. Insight into volatile behavior at Nyamuragira volcano (D.R. Congo, Africa) through olivine-hosted melt inclusions. Geochem. Geophys. Geosyst. 2011, 12. [Google Scholar] [CrossRef]
- Amelung, F.; Yun, S.-H.; Walter, T.R.; Segall, P.; Kim, S.-W. Stress control of deep rift intrusion at Mauna Loa volcano, Hawaii. Science 2007, 316, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Hamling, I.J.; Wright, T.J.; Calais, E.; Bennati, L.; Lewi, E. Stress transfer between thirteen successive dyke intrusions in Ethiopia. Nat. Geosci. 2010, 3, 713–717. [Google Scholar] [CrossRef]
- Grandin, R.; Socquet, A.; Jacques, E.; Mazzoni, N.; de Chabalier, J.-B.; King, G.C.P. Sequence of rifting in Afar, Manda-Hararo rift, Ethiopia, 2005–2009: Time-space evolution and interactions between dikes from interferometric synthetic aperture radar and static stress change modeling. J. Geophys. Res. 2010, 115, B10413. [Google Scholar] [CrossRef]
- Fialko, Y.A.; Rubin, A.M. Thermal and mechanical aspects of magma emplacement in giant dike swarms. J. Geophys. Res. Solid Earth 1999, 104, 23033–23049. [Google Scholar] [CrossRef]
- Lister, J.R. Steady solutions for feeder dykes in a density-stratified lithosphere. Earth Planet. Sci. Lett. 1991, 107, 233–242. [Google Scholar] [CrossRef]
- Acocella, V.; Neri, M. Dike propagation in volcanic edifices: Overview and possible developments. Tectonophysics 2009, 471, 67–77. [Google Scholar] [CrossRef]
- Poland, M.P.; Moats, W.P.; Fink, J.H. A model for radial dike emplacement in composite cones based on observations from Summer Coon volcano, Colorado, USA. Bull. Volcanol. 2008, 70, 861–875. [Google Scholar] [CrossRef]
- Hurwitz, D.M.; Long, S.M.; Grosfils, E.B. The characteristics of magma reservoir failure beneath a volcanic edifice. J. Volcanol. Geotherm. Res. 2009, 188, 379–394. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wauthier, C.; Cayol, V.; Smets, B.; D’Oreye, N.; Kervyn, F. Magma Pathways and Their Interactions Inferred from InSAR and Stress Modeling at Nyamulagira Volcano, D.R. Congo. Remote Sens. 2015, 7, 15179-15202. https://doi.org/10.3390/rs71115179
Wauthier C, Cayol V, Smets B, D’Oreye N, Kervyn F. Magma Pathways and Their Interactions Inferred from InSAR and Stress Modeling at Nyamulagira Volcano, D.R. Congo. Remote Sensing. 2015; 7(11):15179-15202. https://doi.org/10.3390/rs71115179
Chicago/Turabian StyleWauthier, Christelle, Valérie Cayol, Benoît Smets, Nicolas D’Oreye, and François Kervyn. 2015. "Magma Pathways and Their Interactions Inferred from InSAR and Stress Modeling at Nyamulagira Volcano, D.R. Congo" Remote Sensing 7, no. 11: 15179-15202. https://doi.org/10.3390/rs71115179
APA StyleWauthier, C., Cayol, V., Smets, B., D’Oreye, N., & Kervyn, F. (2015). Magma Pathways and Their Interactions Inferred from InSAR and Stress Modeling at Nyamulagira Volcano, D.R. Congo. Remote Sensing, 7(11), 15179-15202. https://doi.org/10.3390/rs71115179