A Survey of Algorithmic Shapes †
Abstract
:1. Introduction
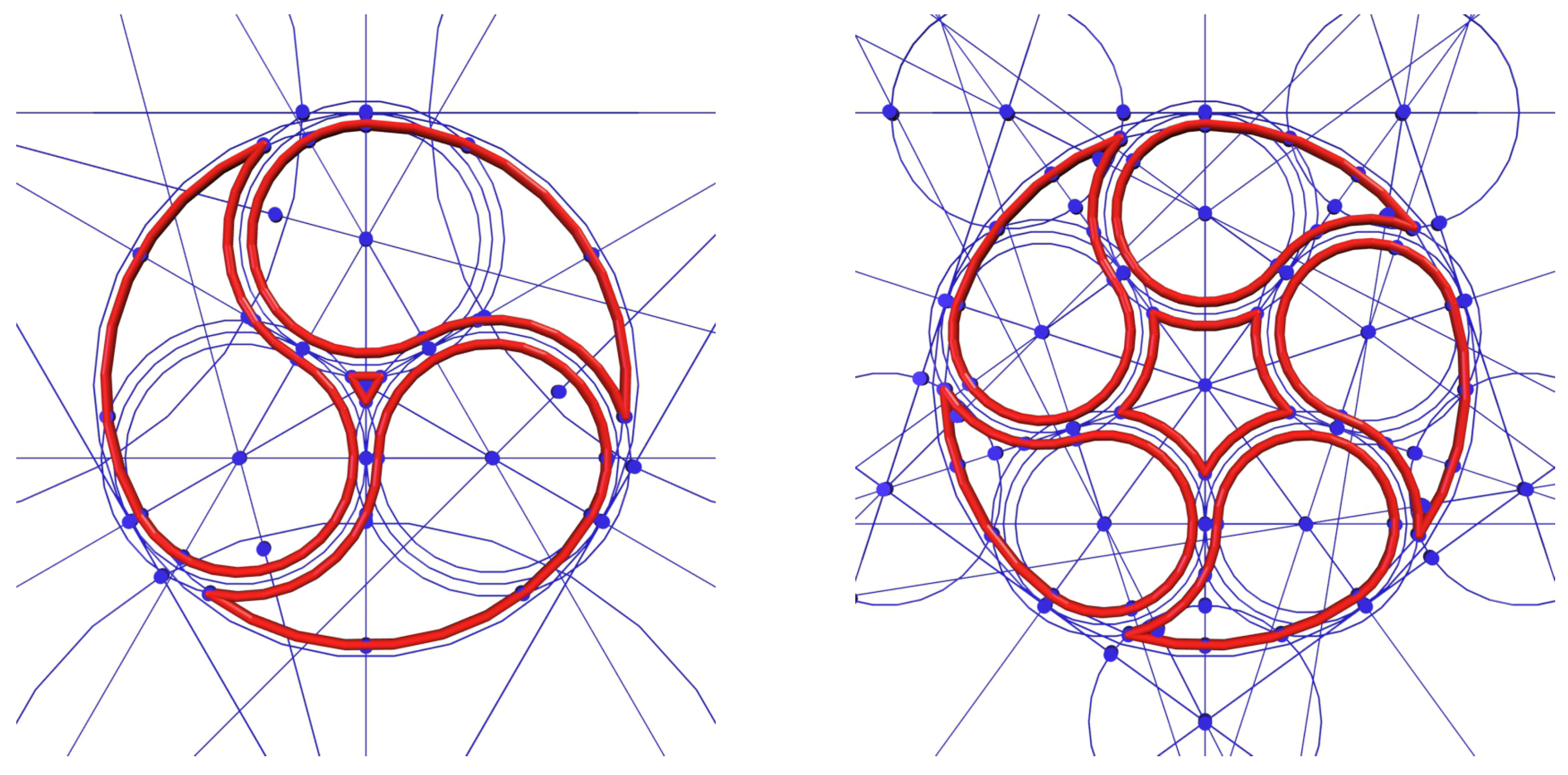
1.1. Ruler and Compass
1.2. Natural Patterns
2. Languages and Grammars
2.1. Language Processing and Compiler Construction
2.2. Scripting Languages for Generative Modeling
- Imperative: Many generative models are described using classical programming paradigms: a programming language is used to generate a specific object, possibly using a library that utilizes some sort of geometry representation and operations to perform changes. Any modeling software that is scriptable by an imperative language or provides some sort of API falls into this category.
- Dataflow based: A generative description can be represented by a directed graph of the data flowing between operations. This graph representation also allows for a graphical representation; visual programming languages (VPLs) allow one to create a program by linking and modifying visual elements. Many VPLs are based on the dataflow paradigm. Examples in the domain of generative modeling are the Grasshopper3D (online) plug-in for the Rhinoceros3D (online) modeling suite, or the work of Gustova Patow et al. built on top of the procedural modeler Houdini (online) [41].
- Rule-based systems: Another different representation for generative modeling is rule-based systems. These systems provide a declarative description of the construction behavior of a model by a set of rules. An example are L-systems, as described in the Introduction. Furthermore, the seminal work of George Stiny and James Gips introduced shape grammars, as a formal description of capturing the design of paintings and sculptures [42]. Similar to formal grammars, shape grammars are based on rule replacement.
2.3. Shape Grammars
2.4. Tools and Environments
| Tool Name | Application Domain | Programming Category | Environment |
|---|---|---|---|
| Blender Scripting | general purpose modeling | python scripting | open source modeling software blender |
| CGAL, The Computational Geometry Algorithms Library [49] | general purpose modeling | C++ | CGAL open source project |
| CityEngine [31] | urban modeling | CGA shape | commercial integrated development environment CityEngine |
| Generalized Grammar [30] | scientific | python scripting | commercial modeling software Houdini |
| Generative Modeling Language (GML) [33] | CAD | postscript dialect | proprietary, integrated development environment for polygonal and subdivision modeling |
| Grasshopper 3D | visual arts, rapid prototyping, architecture | visual programming based on dataflow graphs, Microsoft .NET family of languages | commercial modeling software Rhinoceros3D |
| HyperFun [50] | scientific | specialized high-level programming language | proprietary geometry kernel FRep (Function Representation) |
| Maya Scripting | general purpose modeling | Maya Embedded Language (MEL) and python scripting | commercial modeling software Autodesk Maya |
| OpenSCAD | CAD | OpenSCAD language | open source, based on CGAL geometry kernel |
| PLaSM | scientific | python scripting, Function Level scripting | integrated development environment Xplode |
| Processing | visual arts, rapid prototyping | Java dialect | open source, integrated development environment Processing |
| Tool Name | Application Domain | Programming Category | Environment |
|---|---|---|---|
| PythonOCC | general purpose modeling and CAD | python scripting | Open CASCADE Technology |
| Revit Scripting | architecture | Microsoft .NET family of languages | commercial modeling software Autodesk Revit |
| siteplan [51] | rapid prototyping, architecture | interactive GUI-based modeler | open source, integrated development environment siteplan |
| SketchUp Scripting | architecture, urban modeling and CAD | Ruby scripting | commercial modeling software SketchUp |
| Skyline Engine [41] | urban modeling | visual programming based on dataflow graphs, python scripting | commercial modeling software Houdini |
| speedtree | plants/trees | interactive GUI-based modeler, SDK for C++ | standalone modeler and integration into various game engines |
| Terragen | landscape modeling | interactive GUI-based modeler | free and commercial, integrated development environment Terragen |
| XFrog [11] | plants/trees | interactive GUI-based modeler | integrated development environment, standalone and plugins for Maya and Cinema4D |
3. Modeling by Programming
3.1. Building Blocks and Elementary Data Structures
- Instantiations are operations for creating new shapes.
- Binary creations are operations involving two shapes, such as constructive solid geometry (CSG) operations.
- Deformations and manipulations stand for all deforming and modifying operations, like morphing or displacing.
3.2. Architectural Modeling with Procedural Extrusions
3.3. Deformation-Aware Shape Grammars
3.4. Procedural Shape Modeling

3.5. Variance Analysis
3.6. Semantic Modeling
- Data type: The data type of the object can be of any elementary data structure (e.g. polygons, non-uniform rational b-splines (NURBS), subdivision surfaces, etc.).
- Scale of semantic information: This property describes whether metadata are added for the entire dataset or only for a sub-part of the object.
- Type of semantic information: The type of metadata can be descriptive (describing the content), administrative (providing information regarding creation, storing, provenance, etc.) or structural (describing the hierarchical structure).
- Type of creation: The creation of the semantic information for an object can be done manually (by a domain expert) or automatically (e.g., using a generative description).
- Data organization: The two basic concepts of storing metadata are storing the information within the original object (e.g., Exchangeable Image File Format (Exif) data for images) or storing it separately (e.g., using a database).
- Information comprehensiveness: The comprehensiveness of the semantic information can be declared varying from low to high in any gradation.
- Collada The XML-based Collada format is an ISO standard and allows storing metadata, like title, author, revision, etc., not only on a global scale, but also for parts of the scene [64]. This file format can be found in Google Warehouse where metadata are, for example, used for geo-referencing objects.
- IGES Initial Graphics Exchange Specification (IGES), an American National Standards Institute (ANSI) standard since 1980, allows the definition of annotations, including dimensioning data, as well as labels and notes [65]. This file format is used as a vendor-neutral exchange format among CAD systems.
- JT The Jupiter Tesselation (JT) file format has been an ISO standard since 2012 and is used for product visualization and data exchange in CAD systems [66]. Annotations in the form of attributes and properties, as well as filters are supported by this format. It is accompanied by the XML-based format for product lifecycle management (PLMXML) to represent product structure hierarchy.
- PDF 3D PDF 3D is an ISO standard and allows one to store annotations separated from the 3D data, even allowing annotating of the annotations [67]. An advantage is that the viewer application is widely spread, and PDF documents are the quasi standard for textual documents.
- STEP The standard for the exchange of product model data (STEP) has been an ISO standard since 1994 divided into different parts, data models and environments [68]. The current Application Protocol 242 supports product data and non-geometrical metadata.
- X3D The X3D file format is an XML-based ISO standard for representing 3D computer graphics [69]. It supports a number of different metadata nodes, providing arrays of strongly typed data.
4. Inverse Modeling
4.1. Parsing Shape Grammars
4.2. Model Synthesis
4.3. Inverse Procedural Modeling of Trees
4.4. Parameter Fitting and Shape Recognition
- can the point cloud be described by the generative model, and if so,
- what are the input parameters , such that is a good description of P.
5. Architecture, Engineering and Design
5.1. Generative Architectural Design

5.2. Engineering Design
5.3. Urban Modeling
5.4. Building Information Modeling
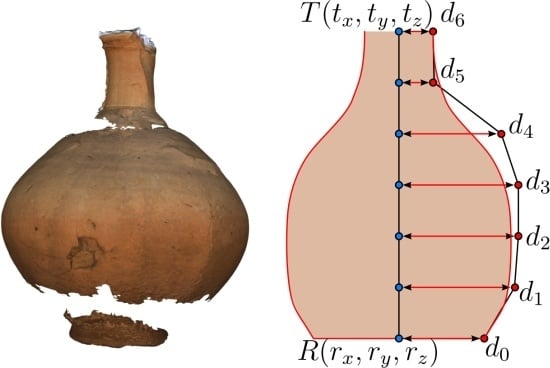
6. Archeology and Cultural Heritage
6.1. Semantic Enrichment
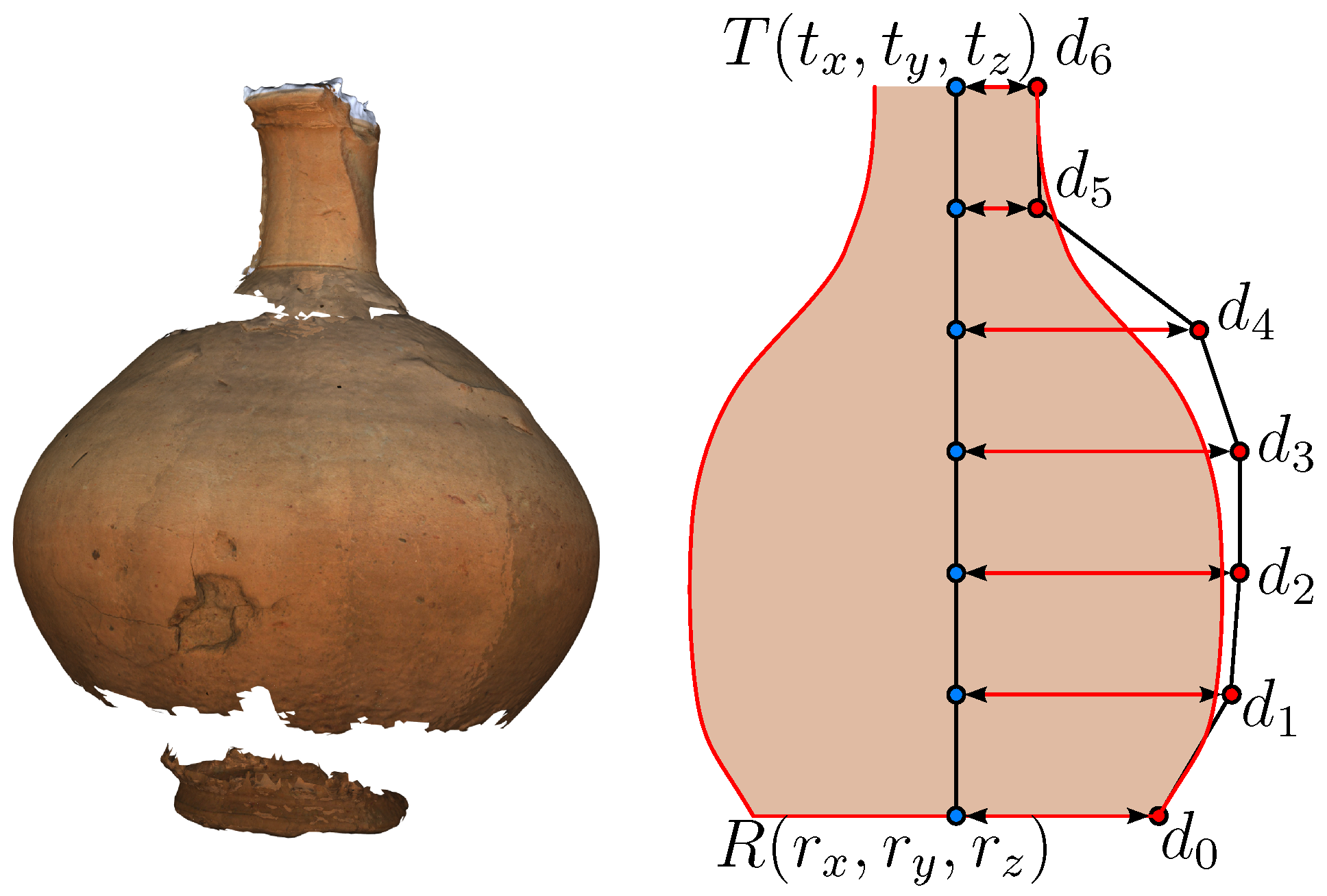
6.2. Cultural Heritage

7. Open Research Questions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heiberg, J. Euclid’s Elements of Geometry; Fitzpatrick Richard: Austin, TX, USA, 2007. [Google Scholar]
- Hartshorne, R. Teaching geometry according to Euclid. Not. AMS 2000, 47, 460–465. [Google Scholar]
- Maxfield, J.E.; Coolidge, J.L. A History of Geometrical Methods, 1st ed.; Dover Publications: New York, NY, USA, 2003. [Google Scholar]
- Scriba, C.J.; Schreiber, P. 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (english: 5000 years of geometry: history, cultures, men); Springer: Berlin, Germany, 2004. [Google Scholar]
- Thaller, W.; Krispel, U.; Zmugg, R.; Havemann, S.; Fellner, D.W. A Graph-Based Language for Direct Manipulation of Procedural Models. Int. J. Adv. Softw 2013, 6, 225–236. [Google Scholar]
- Martin, G.E. Geometric Constructions; Springer: Berlin, Germany, 1998. [Google Scholar]
- Mitchell, W.J. The Logic of Architecture: Design, Computation, and Cognition; MIT Press: Cambridge, UK, 1990. [Google Scholar]
- Havemann, S.; Fellner, D.W. Generative parametric design of gothic window tracery. IEEE Proc. Shape Model. Appl. 2004. [Google Scholar] [CrossRef]
- Berndt, R.; Fellner, D.W.; Havemann, S. Generative 3D models: A key to more information within less bandwidth at higher quality. In Proceedings of the 10th International Conference on 3D Web Technology, Gwynedd, UK, 29 March–1 April 2005.
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer: Berlin, Germany, 1990. [Google Scholar]
- Deussen, O.; Lintermann, B. Digital Design of Nature: Computer Generated Plants and Organics; Springer: Berlin, Germany, 2005. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Co.: New York, NY, USA, 1982. [Google Scholar]
- Tobler, R.F.; Maierhofer, S.; Wilkie, A. A multiresolution mesh generation approach for procedural definition of complex geometry. Proc. Shape Model. Int. 2002, 6, 35–44. [Google Scholar]
- Tobler, R.F.; Maierhofer, S.; Wilkie, A. Mesh-based parametrized L-systems and generalized subdivision for generating complex geometry. Int. J. Shape Model. 2002, 8, 173–191. [Google Scholar] [CrossRef]
- Lipp, M.; Wonka, P.; Wimmer, M. Parallel generation of multiple L-systems. Comput. Graph. 2010, 34, 585–593. [Google Scholar] [CrossRef]
- Brutzman, D. The virtual reality modeling language and Java. Commun. ACM 1998, 41, 57–64. [Google Scholar] [CrossRef]
- Behr, J.; Dähne, P.; Jung, Y.; Webel, S. Beyond the web browser–X3D and immersive VR. IEEE Virtual Real. Tutor. Workshop Proc. 2007, 28, 5–9. [Google Scholar]
- Breuel, F.; Bernd, R.; Ullrich, T.; Eggeling, E.; Fellner, D.W. Mate in 3D – publishing interactive content in PDF3D. In Digital Publishing and Mobile Technologies, Proceedings of the 15th International Conference on Electronic Publishing, Äřstanbul, Turke, 22–24 June 2011.
- Di Benedetto, M.; Ponchio, F.; Ganovelli, F.; Scopigno, R. SpiderGL: A JavaScript 3D graphics library for next-generation WWW. In Proceedings of the 15th International Conference on Web 3D Technology, Los Angeles, CA, USA, 24–25 July 2010.
- Schinko, C.; Strobl, M.; Ullrich, T.; Fellner, D.W. Scripting technology for generative modeling. Int. J. Adv. Softw. 2011, 4, 308–326. [Google Scholar]
- Ousterhout, J.K. Scripting: Higher level pogramming for the 21st century. IEEE Comput. Mag. 1998, 31, 23–30. [Google Scholar] [CrossRef]
- OpenGL Architecture, R.B. OpenGL Reference Manual; Addison-Wesley: Boston, MA, USA, 1993. [Google Scholar]
- NVidia. CUDA C Programming Guide. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/ (accessed on 29 June 2015).
- Reiners, D.; Voss, G.; Behr, J. OpenSG: Basic concepts. OpenSG Symp. 2002, 1, 1–7. [Google Scholar]
- Voß, G.; Behr, J.; Reiners, D.; Roth, M. A multi-thread safe foundation for scene graphs and its extension to clusters. EGPGV 2002, 4, 33–37. [Google Scholar]
- Eckel, B. Thinking in C++: Introduction to Standard C++, Practical Programming; Prentice Hall: New Jersey, NJ, USA, 2003. [Google Scholar]
- Parr, T. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages; Pragmatic Bookshelf: North Carolina, NC, USA, 2010. [Google Scholar]
- Chomsky, N. Three models for the description of language. IRE Trans. Inf. Theory 1956, 2, 113–124. [Google Scholar] [CrossRef]
- Özkar, M.; Kotsopoulos, S. Introduction to shape grammars. In Proceedings of the International Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 11–15 August 2008.
- Krecklau, L.; Pavic, D.; Kobbelt, L. Generalized use of non-terminal symbols for procedural modeling. Comput. Graph. Forum 2010, 29, 2291–2303. [Google Scholar] [CrossRef]
- Müller, P.; Wonka, P.; Haegler, S.; Andreas, U.; van Gool, L. Procedural modeling of buildings. ACM Trans. Graph. 2006, 25, 614–623. [Google Scholar] [CrossRef]
- Snyder, J.M.; Kajiya, J.T. Generative modeling: A symbolic system for geometric modeling. ACM SIGGRAPH Comput. Graph. 1992, 26, 369–378. [Google Scholar] [CrossRef]
- Havemann, S. Generative Mesh Modeling. Ph.D. Thesis, Technische Universit, Braunschweig, Germany, 2005. [Google Scholar]
- Krecklau, L.; Kobbelt, L. Procedural modeling of interconnected structures. Comput. Graph. Forum 2011, 30, 335–344. [Google Scholar] [CrossRef]
- Lipp, M.; Wonka, P.; Wimmer, M. Interactive visual editing of grammars for procedural architecture. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Thaller, W.; Krispel, U.; Havemann, S.; Fellner, D. Implicit nested repetition in dataflow for procedural modeling. In Proceedings of the International Conference on Computational Logics, Algebras, Programming, Tools, and Benchmarking (Computation Tools), Nice, France, 22–27 July 2012; pp. 45–50.
- Schinko, C.; Ullrich, T.; Fellner, D.W. Minimally invasive interpreter construction—How to reuse a compiler to build an interpreter. In Proceedings of the International Conference on Computational Logics, Algebras, Programming, Tools, and Benchmarking (Computation Tools), Nice, France, 22–27 July 2012; pp. 38–44.
- Parish, Y.; Müller, P. Procedural modeling of cities. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 1 August 2001; pp. 301–308.
- Ullrich, T.; Krispel, U.; Fellner, D.W. Compilation of procedural models. In Proceeding of the 13th International Conference on 3D Web Technology, Los Angeles, CA, USA, 9–10 August 2008; pp. 75–81.
- Reas, C.; Fry, B.; Maeda, J. Processing: A Programming Handbook for Visual Designers and Artists; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Patow, G. User-friendly graph editing for procedural modeling of buildings. IEEE Comput. Graph. Appl. 2012, 32, 66–75. [Google Scholar] [CrossRef]
- Stiny, G.; Gips, J. Shape grammars and the generative specification of painting and sculpture. IFIP Congr. 1971, 2, 125–135. [Google Scholar]
- Wonka, P.; Wimmer, M.; Sillion, F.; Ribarsky, W. Instant architecture. IACM Trans. Graph. 2003, 22, 669–677. [Google Scholar] [CrossRef]
- Marvie, J.E.; Buron, C.; Gautron, P.; Hirtzlin, P.; Sourimant, G. GPU Shape grammars. Comput. Graph. Forum 2012, 31, 2087–2095. [Google Scholar] [CrossRef]
- Krecklau, L.; Born, J.; Kobbelt, L. View-dependent realtime rendering of procedural facades with high geometric detail. Comput. Graph. Forum 2013, 32, 479–488. [Google Scholar] [CrossRef]
- Kuang, Z.; Chan, B.; Yu, Y.; Wang, W. A compact random-access representation for urban modeling and rendering. ACM Trans. Graph. 2013. [Google Scholar] [CrossRef]
- Steinberger, M.; Kenzel, M.; Kainz, B.; Müller, J.; Peter, W.; Schmalstieg, D. Parallel generation of architecture on the GPU. Comput. Graph. Forum 2014, 33, 73–82. [Google Scholar] [CrossRef]
- Steinberger, M.; Kenzel, M.; Kainz, B.; Wonka, P.; Schmalstieg, D. On-the-fly generation and rendering of infinite cities on the GPU. Comput. Graph. Forum 2014, 33, 105–114. [Google Scholar] [CrossRef]
- The CGAL Project CGAL User and Reference Manual. Available online: http://doc.cgal.org/latest/Manual/ (accessed on 29 June 2015).
- Pasko, A.; Adzhiev, V. Function-based shape modeling: Mathematical framework and specialized language. Lect. Notes Comput. Sci. 2004, 2930, 132–160. [Google Scholar]
- Kelly, T.; Wonka, P. Interactive architectural modeling with procedural extrusions. ACM Trans. Graph. 2011. [Google Scholar] [CrossRef]
- Aurenhammer, F. Weighted skeletons and fixed-share decomposition. Comput. Geom. 2008, 40, 93–101. [Google Scholar] [CrossRef]
- Watson, B.; Wonka, P. Procedural methods for urban modeling. IEEE Comput. Graph. Appl. 2008, 28, 16–17. [Google Scholar] [CrossRef]
- Whiting, E.; Ochsendorf, J.; Durand, F. Procedural modeling of structurally-sound masonry buildings. ACM Trans. Graph. 2009. [Google Scholar] [CrossRef]
- Edelsbrunner, J.; Krispel, U.; Havemann, S.; Sourin, A.; Fellner, D.W. Constructive roof geometry. In Proceedings of the 2014 International Conference on Cyberworlds, Santander, Spain, 6–8 October 2014.
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. ACM SIGGRAPH Comput. Graph. 1986, 13, 151–160. [Google Scholar] [CrossRef]
- Zmugg, R.; Thaller, W.; Krispel, U.; Edelsbrunner, J.; Havemann, S.; Fellner, D.W. Procedural architecture using deformation-aware split grammars. Visual Comput. 2013, 12, 1–11. [Google Scholar] [CrossRef]
- Berndt, R.; Schinko, C.; Krispel, U.; Settgast, V.; Havemann, S.; Eggeling, E.; Fellner, D.W. Ring’s anatomy—parametric design of wedding rings. Content 2012, 4, 72–78. [Google Scholar]
- Schinko, C.; Berndt, R.; Eggeling, E.; Fellner, D. A scalable rendering framework for generative 3D content. In Proceedings of the 19th International ACM Conference on 3D Web Technologies, Vancouver, BC, Canada, 8–10 August 2014.
- Schinko, C.; Ullrich, T.; Schiffer, T.; Fellner, D.W. Variance analysis and comparison in computer-aided design. In Proceedings of the International Workshop on 3D Virtual Reconstruction and Visualization of Complex Architectures, Rento, Italy, 2–4 March 2011.
- Arnold, D. Procedural methods for 3D reconstruction. Rec. Model. Vis. Cult. Herit. 2006, 1, 355–359. [Google Scholar]
- Ullrich, T.; Settgast, V.; Berndt, R. Semantic enrichment for 3D documents: Techniques and open problems. In the Networked World: Transforming the Nature of Communication, Proceedings of the International Conference on Electronic Publishing, Helsinki, Finland, 16–18 June 2010.
- Settgast, V. Processing Semantically Enriched Content for Interactive 3D Visualizations. Ph.D. Thesis, Technische Universität, Graz, Austria, 2013. [Google Scholar]
- International Organization for Standardization (ISO) / Publicly Available Specification (PAS) 17506:2012 (Industrial Automation Systems and Integration–COLLADA Ddigital Asset Schema Specification for 3D Visualization of Industrial Data). Available online: http://www.iso.org/iso/catalogue_detail.htm?csnumber=59902 (accessed on 29 June 2015).
- U.S. Product Data Association (US PRO), Formerly ANS US PRO/IPO-100-1996 (Initial Graphics Exchange Specification IGES 5.3). Available online: http://webstore.ansi.org/RecordDetail.aspx?sku=SAE+J+1881-2001+(SAE+J1881-2001) (accessed on 29 June 2015).
- International Organization for Standardization (ISO) 14306:2012 (Industrial Automation Systems and Integratio–JT File Format Specification for 3D Visualization). Available online: http://www.iso.org/iso/catalogue_detail.htm?csnumber=60572 (accessed on 29 June 2015).
- International Organization for Standardization (ISO) 32000-1:2008 (Document Management–Portable Document Format–Part 1: PDF 1.7). Available online: http://www.iso.org/iso/catalogue_detail.htm?csnumber=51502 (accessed on 29 June 2015).
- International Organization for Standardization (ISO) 10303-1:1994 (Industrial Automation Systems and Integration–Product Data Representation and Exchange–Part 1: Overview and Fundamental Principles). Available online: http://www.iso.org/iso/catalogue_detail?csnumber=20579 (accessed on 29 June 2015).
- International Organization for Standardization (ISO) / International Electrotechnical Commission (IEC) 19775-1:2013 (Information technology–Computer Graphics, Image Processing and Environmental Data Representation–Extensible 3D (X3D)–Part 1: Architecture and Base Components). Available online: http://www.iso.org/iso/catalogue_detail?csnumber=60760 (accessed on 29 June 2015).
- Boulch, A.; Houllier, S.; Marlet, R.; Tournaire, O. Semantizing complex 3D scenes using constrained attribute grammars. Proc. Eur. Symp. Geom. Proc. 2013, 32, 33–42. [Google Scholar] [CrossRef]
- Haegeler, S.; Müller, P.; Van Gool, L. Procedural modeling for digital cultural heritage. J. Image Video Process. 2009, 9, 1–11. [Google Scholar] [CrossRef]
- Mendez, E.; Schall, G.; Havemann, S.; Fellner, D.W.; Schmalstieg, D.; Junghanns, S. Generating semantic 3D models of underground infrastructure. IEEE Comput. Graph. Appl. 2008, 28, 48–57. [Google Scholar] [CrossRef]
- Thaller, W.; Zmugg, R.; Krispel, U.; Posch, M.; Havemann, S.; Fellner Dieter, W. Creating procedural windowbuilding blocks using the generative fact labeling method. Proc. ISPRS Int. Workshop 3D-ARCH 2013, 5, 235–242. [Google Scholar] [CrossRef]
- Van Gool, L.; Martinovic, A.; Mathias, M. Towards semantic city models. Proc. Photogramm. Week 2013, 1, 217–232. [Google Scholar]
- Yong, L.; Mingmin, Z.; Yunliang, J.; Haiying, Z. Improving procedural modeling with semantics in digital architectural heritage. Comput. Graph. 2012, 36, 178–184. [Google Scholar] [CrossRef]
- Riemenschneider, H.; Krispel, U.; Thaller, W.; Donoser, M.; Havemann, S.; Fellner, D.W.; Bischof, H. Irregular lattices for complex shape grammar facade parsing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012.
- Wu, F.; Yan, D.M.; Dong, W.; Zhang, X.; Wonka, P. Inverse procedural modeling of facade layouts. ACM Trans. Graph. 2014. [Google Scholar] [CrossRef]
- Merrell, P.; Manocha, D. Continuous model synthesis. ACM Trans. Graph. 2008. [Google Scholar] [CrossRef]
- Merrell, P.; Manocha, D. Model Synthesis: A general procedural modeling algorithm. IEEE Trans. Vis. Comput. Graph. 2010, 17, 715–728. [Google Scholar] [CrossRef] [PubMed]
- Stava, O.; Pirk, S.; Kratt, J.; Chen, B.; Měch, R.; Deussen, O.; Benes, B. Inverse procedural modelling of trees. Comput. Graph. Forum 2014, 33, 118–131. [Google Scholar] [CrossRef]
- Talton, J.O.; Lou, Y.; Lesser, S.; Duke, J.; Mech, R.; Koltun, V. Metropolis procedural modeling. ACM Trans. Graph. 2011. [Google Scholar] [CrossRef]
- Vanegas, C.A.; Garcia-Dorado, I.; Aliaga, D.G.; Benes, B.; Waddell, P. Inverse design of urban procedural models. ACM Trans. Graph. 2012. [Google Scholar] [CrossRef]
- Yu, L.F.; Yeung, S.K.; Tang, C.K.; Terzopoulos, D.; Chan, T.F.; Osher, S. Make it home: Automatic optimization of furniture arrangement. ACM Trans. Graph. 2011. [Google Scholar] [CrossRef]
- Ullrich, T.; Fellner, D.W. Generative object definition and semantic recognition. In Proceedings of the Eurographics Workshop on 3D Object Retrieval, Llandudno, UK, 10 April 2011.
- Müller, P.; Vereenooghe, T.; Ulmer, A.; van Gool, L. Automatic reconstruction of Roman housing architecture. Rec. Model. Vis. Cult. Heritage 2006, 1, 287–298. [Google Scholar]
- Müller, P.; Vereenooghe, T.; Wonka, P.; Paap, I.; Van Gool, L. Procedural 3D reconstruction of Puuc buildings in Xkipche. Proc. Eur. Symp. Virtual Real. Archaeol. Cult. Heritage (VAST) 2006, 1, 139–146. [Google Scholar]
- Hohmann, B.; Krispel, U.; Havemann, S.; Fellner, D.W. Cityfit: High-quality urban reconstructions by fitting shape grammars to images and derived textured point clouds. Proc. ISPRS Int. Workshop 3D-ARCH 2009, 3, 61–68. [Google Scholar]
- Ullrich, T.; Silva, N.; Eggeling, E.; Fellner, D.W. Generative Modeling and Numerical Optimization for Energy Efficient Buildings. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013.
- Campbell, M.I.; Shea, K. Guest editorial: Computational design synthesis. AI EDAM 2014, 28, 207–208. [Google Scholar]
- Pugliese, M.; Cagan, J. Capturing a rebel: Modeling the Harley-Davidson brand through a motorcycle shape grammar. Res. Eng. Design 2002, 13, 139–156. [Google Scholar]
- Flager, F.; Soremekun, G.; Adya, A.; Shea, K.; Haymaker, J.; Fischer, M. Fully Constrained Design: A general and scalable method for discrete member sizing optimization of steel truss structures. Comput. Struct. 2014, 140, 55–65. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Shea, K.; Stone, R.; Cagan, J.; Campbell, M.; Vargas-Hernandez, N.; Wood, K.L. Computer-based design synthesis research: An overview. J. Comput. Inf. Sci. Eng. 2011. [Google Scholar] [CrossRef]
- Frank, G.; Hillbrand, C. Automatic support of standardization processes in design models. In Proceedings of the 2012 IEEE International Conference on Intelligent Engineering Systems (INES), Lisbon, Portugal, 13–15 June 2012.
- Musialski, P.; Wonka, P.; Aliaga, D.G.; Wimmer, M.; van Gool, L.; Purgathofer, W. A survey of urban reconstruction. Comput. Graph. Forum 2012, 31, 1–28. [Google Scholar] [CrossRef]
- Génevaux, J.D.; Galin, E.; Guérin, E.; Peytavie, A.; Beneš, B. Terrain generation using procedural models based on hydrology. ACM Trans. Graph. 2013. [Google Scholar] [CrossRef]
- Andújar, C.; Chica, A.; Vico, M.A.; Moya, S.; Brunet, P. Inexpensive reconstruction and rendering of realistic roadside landscapes. Comput. Graph. Forum 2014, 33, 101–117. [Google Scholar] [CrossRef]
- Galin, E.; Peytavie, A.; Marechal, N.; Guerin, E. Procedural generation of roads. Comput. Graph. Forum 2010, 29, 429–438. [Google Scholar] [CrossRef]
- Benes, J.; Wilkie, A.; Krivanek, J. Procedural modelling of urban road networks. Comput. Graph. Forum 2014, 33, 132–142. [Google Scholar] [CrossRef]
- Lipp, M.; Scherzer, D.; Wonka, P.; Wimmer, M. Interactive modeling of city layouts using layers of procedural content. Comput. Graph. Forum 2011, 30, 345–354. [Google Scholar] [CrossRef]
- Vanegas, C.A.; Aliaga, D.G.; Wonka, P.; Müller, P.; Waddell, P.; Watson, B. Modelling the appearance and behaviour of urban spaces. Comput. Graph. Forum 2010, 29, 25–42. [Google Scholar] [CrossRef]
- Bao, F.; Yan, D.M.; Mitra, N.J.; Wonka, P. Generating and exploring good building layouts. ACM Trans. Graph. 2013. [Google Scholar] [CrossRef]
- Musialski, P.; Wimmer, M.; Wonka, P. Interactive coherence-based facade modeling. Comput. Graph. Forum 2012, 31, 661–670. [Google Scholar] [CrossRef]
- Bao, F.; Schwarz, M.; Wonka, P. Procedural facade variations from a single layout. ACM Trans. Graph. 2013. [Google Scholar] [CrossRef]
- Schwarz, M.; Wonka, P. Procedural design of exterior lighting for buildings with complex constraints. ACM Trans. Graph. 2014. [Google Scholar] [CrossRef]
- Merrell, P.; Schkufza, E.; Li, Z.; Agrawala, M.; Koltun, V. Interactive furniture layout using interior design guidelines. ACM Trans. Graph. 2011. [Google Scholar] [CrossRef]
- Abrishami, S.; Goulding, J.S.; Rahimian, F.P.; Ganah, A. Integration of BIM and Generative Design to Exploit AEC Conceptual Design Innovation. Available online: http://clok.uclan.ac.uk/11420/ (accessed on 29 June 2015).
- National Institute of Building Sciences. Frequently Asked Questions About the National BIM Standard. Available online: https://www.nationalbimstandard.org/faqs (accessed on 29 June 2015).
- Abbasnejad, B.; Moud, H.I. BIM and basic challenges associated with its definitions, interpretations and expectations. Int. J. Eng. Res. Appl. 2013, 3, 287–294. [Google Scholar]
- Eastman, C.; Teicholz, P.; Sacks, R.; Liston, K. BIM Handbook, 2nd ed.; John Wiley & Sons: New Jersey, NJ, USA, 2011. [Google Scholar]
- Krispel, U.; Schinko, C.; Ullrich, T. The rules behind—Tutorial on generative modeling. Proc. Symp. Geom. Process. 2014, 12, 1–49. [Google Scholar]
- Schinko, C.; Strobl, M.; Ullrich, T.; Fellner, D.W. Modeling procedural knowledge—A generative modeler for cultural heritage. In Digital Heritage; Springer: Berlin, Germany, 2010. [Google Scholar]
- Hichri, N.; Stefani, C.; De Luca, L.; Veron, P. Review of the "as-built BIM" approaches. ISPRSl Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, XL-5/W1, 107–112. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Cagliari, Sardinia, 26–28 June 2006; pp. 61–70.
- Weyrich, T.; Lawrence, J.; Lensch, H.P.A.; Rusinkiewicz, S.; Zickler, T. Principles of appearance acquisition and representation. Found. Trends. Comput. Graph. Vis. 2009, 4, 75–191. [Google Scholar] [CrossRef]
- Krispel, U.; Evers, H.L.; Tamke, M.; Viehauser, R.; Fellner, D.W. Automatic texture and orthophoto generation from registered panoramic views. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 131–137. [Google Scholar] [CrossRef]
- Tamke, M.; Blümel, I.; Ochmann, S.; Vock, R.; Wessel, R. From point clouds to definitions of architectural space-Potentials of automated extraction of semantic information from point clouds for the building profession. In Proceedings of the 32nd eCAADe Conference, Northumbria, UK, 10–12 September 2014; pp. 557–566.
- Hullo, J.F.; Thibault, G.; Boucheny, C. Advances in Multi-sensor scanning and visualization of complex plants: The utmost case of a reactor building. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 163–169. [Google Scholar] [CrossRef]
- Dore, C.; Murphy, M. Semi-automatic modelling of building Fa with shape grammars using historic building information modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 57–64. [Google Scholar] [CrossRef]
- Dore, C.; Murphy, M.; McCarthy, S.; Brechin, F.; Casidy, C.; Dirix, E. Structural simulations and conservation analysis-Historic building information model (HBIM). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 351–357. [Google Scholar] [CrossRef]
- Quattrini, R.; Malinverni, E.S.; Clini, P.; Nespeca, R.; Orlietti, E. From TLS to HBIM. High quality semantically-aware 3D modeling of complex architecture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-5/W4, 367–374. [Google Scholar] [CrossRef]
- Ladenhauf, D.; Berndt, R.; Eggeling, E.; Ullrich, T.; Battisti, K.; Gratzl-Michlmair, M. From building information models to simplified geometries for energy performance simulation. In In Proceeding of the First International Academic Conference on Places and Technologies, Belgrade, Yugoslavia, 3–4 April 2014.
- Ladenhauf, D.; Berndt, R.; Krispel, U.; Eggeling, E.; Ullrich, T.; Battisti, K.; Gratzl-Michlmair, M. Geometry simplification according to semantic constraints. Comput. Sci. Res. Dev. 2014, 11, 1–7. [Google Scholar] [CrossRef]
- Initiative, D.C.M. Dublin Core Metadata Initiative. Available online: http://dublincore.org/ (accessed on 29 June 2015).
- Settgast, V.; Ullrich, T.; Fellner, D.W. Information technology for cultural heritage. IEEE Potentials 2007, 26, 38–43. [Google Scholar] [CrossRef]
- Fellner, D.W. Graphics content in digital libraries: Old problems, recent solutions, future demands. J. Univers. Comput. Sci. 2001, 7, 400–409. [Google Scholar]
- Fellner, D.W.; Saupe, D.; Krottmaier, H. 3D documents. IEEE Comput. Graph. Appl. 2007, 27, 20–21. [Google Scholar] [CrossRef]
- Maybury, M.T. Multimedia Information Extraction; John Wiley & Sons: New Jersey, NJ, USA, 2012. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2007. [Google Scholar]
- Ulusoy, I.; Bishop, C.W. Generative versus discriminative methods for object recognition. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2015.
- Bustos, B.; Keim, D.; Saupe, D.; Schreck, T. Content-based 3D object retrieval. IEEE Comput. Graph. Appl. 2007, 27, 22–27. [Google Scholar] [CrossRef] [PubMed]
- King, B.D.; Wertheimer, M. Max Wertheimer & Gestalt Theory; Transaction Publishers: New Jersey, NJ, USA, 2005. [Google Scholar]
- Hilaga, M.; Shinagawa, Y.; Kohmura, T.; Kunii, T.L. Topology matching for fully automatic similarity estimation of 3D shapes. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2011; pp. 203–212.
- Pauly, M.; Mitra, N.J.; Wallner, J.; Pottmann, H.; Guibas, L.J. Discovering structural regularity in 3D geometry. ACM Trans. Graph. 2008, 27, 1–11. [Google Scholar] [CrossRef]
- Bokeloh, M.; Wand, M.; Seidel, H.P. A connection between partial symmetry and inverse procedural modeling. In Proceedings of the ACM SIGGRAPH 2010, Los Angeles, CA, USA, 27–29 July 2010.
- Mitra, N.J.; Guibas, L.J.; Pauly, M. Partial and approximate symmetry detection for 3D geometry. ACM Trans. Graph. 2006, 25, 560–568. [Google Scholar] [CrossRef]
- Mitra, N.J.; Guibas, L.J.; Pauly, M. Symmetrization. Int. Conf. Comput. Graph. Interact. Tech. 2007, 26, 1–8. [Google Scholar]
- Ullrich, T.; Schinko, C.; Fellner, D.W. Procedural modeling in theory and practice. In Proceedings of the 18th WSCG International Conference on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 27 March 2010.
- Autodesk. Autodesk Maya API. Available online: http://docs.autodesk.com/MAYAUL/2014/ENU/Maya-API-Documentation/index.html (accessed on 29 June 2015).
- Ramamoorthi, R.; Arvo, J. Creating generative models from range images. Proc. ACM SIGGRAPH 1999, 1, 195–204. [Google Scholar]
- Ullrich, T. Reconstructive Geometry. Ph.D. Thesis, Technische Universität, Graz, Austria, 2011. [Google Scholar]
- Arnold, D. Computer graphics and cultural heritage: From one-way inspiration to symbiosis. Comput. Graph. Appl. 2014, 34, 76–86. [Google Scholar] [CrossRef]
- Havemann, S.; Settgast, V.; Krottmaier, H.; Fellner, D.W. On the integration of 3D models into digital cultural heritage libraries. In Proceedings of the 7th International Symposium on Virtual Reality, Archaeology and Cultural Heritage (VAST), Nicosia, Cyprus, 30 October–4 November 2006.
- Niccolucci, F. XML and the future of humanities computing. ACM SIGAPP Appl. Comput. Rev. 2002, 10, 43–47. [Google Scholar] [CrossRef]
- Niccolucci, F.; D’Andrea, A. An ontology for 3D cultural objects. In Proceedings of the 7th International Symposium on Virtual Reality, Archaeology and Cultural Heritage (VAST), Nicosia, Cyprus, 30 October–4 November 2006.
- Arnold, D. Computer graphics and cultural heritage: Continuing inspiration for future tools. Comput. Graph. Appl. 2014, 34, 70–79. [Google Scholar] [CrossRef] [PubMed]
- Berndt, R.; Gerth, B.; Havemann, S.; Fellner, D.W. 3D modeling for non-expert users with the castle construction kit v0.5. In Proceedings of the 6th International Symposium on Virtual Reality, Archaeology and Cultural Heritage (VAST), Pisa, Italy, 8–11 Novermber 2005.
- Ullrich, T.; Settgast, V.; Fellner, D.W. Semantic fitting and reconstruction. J. Comput. Cult. Heritage 2008, 1, 1201–1220. [Google Scholar] [CrossRef]
- Ullrich, T.; Schinko, C.; Schiffer, T.; Fellner, D.W. Procedural descriptions for analyzing digitized artifacts. Appl. Geomat. 2013, 5, 185–192. [Google Scholar] [CrossRef]
- Schinko, C.; Ullrich, T.; Fellner, D.W. Modeling with high-level descriptions and low-level details. In Proceeding of the International Conference on Computer Graphics, Visualization, Computer Vision and Image Processing, Lisbon, Portugal, 15–19 July 2014.
- Calogero, E.; Arnold, D. Generating alternative proposals for the louvre using procedural modeling. In Proceedings of the 4th ISPRS International Workshop 3D-ARCH, Trento, Italy, 2–4 March 2011.
- Saldana, M.; Johanson, C. Procedural modeling for rapid-prototyping of multiple building phases. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 205–210. [Google Scholar] [CrossRef]
- Fellner, D.W.; Havemann, S. Striving for an adequate vocabulary: Next generation metadata. In Proceedings of the 29th Annual Conference of the German Classification Society, Magdeburg, Germany, 9–11 March 2005.
- Havemann, S.; Fellner, D.W. Seven research challenges of generalized 3D documents. IEEE Comput. Graph. Appl. 2007, 3, 70–76. [Google Scholar] [CrossRef]
- Havemann, S.; Ullrich, T.; Fellner, D.W. The meaning of shape and some techniques to extract it. Multimed. Inf. Extr. 2012, 1, 81–98. [Google Scholar]
- Marcheix, D.; Pierra, G. A survey of the persistent naming problem. In Proceedings of the ACM Symposium on Solid Modeling and Applications, Saarbrucken, Germany, 17–21 June 2002.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krispel, U.; Schinko, C.; Ullrich, T. A Survey of Algorithmic Shapes. Remote Sens. 2015, 7, 12763-12792. https://doi.org/10.3390/rs71012763
Krispel U, Schinko C, Ullrich T. A Survey of Algorithmic Shapes. Remote Sensing. 2015; 7(10):12763-12792. https://doi.org/10.3390/rs71012763
Chicago/Turabian StyleKrispel, Ulrich, Christoph Schinko, and Torsten Ullrich. 2015. "A Survey of Algorithmic Shapes" Remote Sensing 7, no. 10: 12763-12792. https://doi.org/10.3390/rs71012763
APA StyleKrispel, U., Schinko, C., & Ullrich, T. (2015). A Survey of Algorithmic Shapes. Remote Sensing, 7(10), 12763-12792. https://doi.org/10.3390/rs71012763